High-Dynamic-Range Integrated NV Magnetometers
Abstract
:1. Introduction
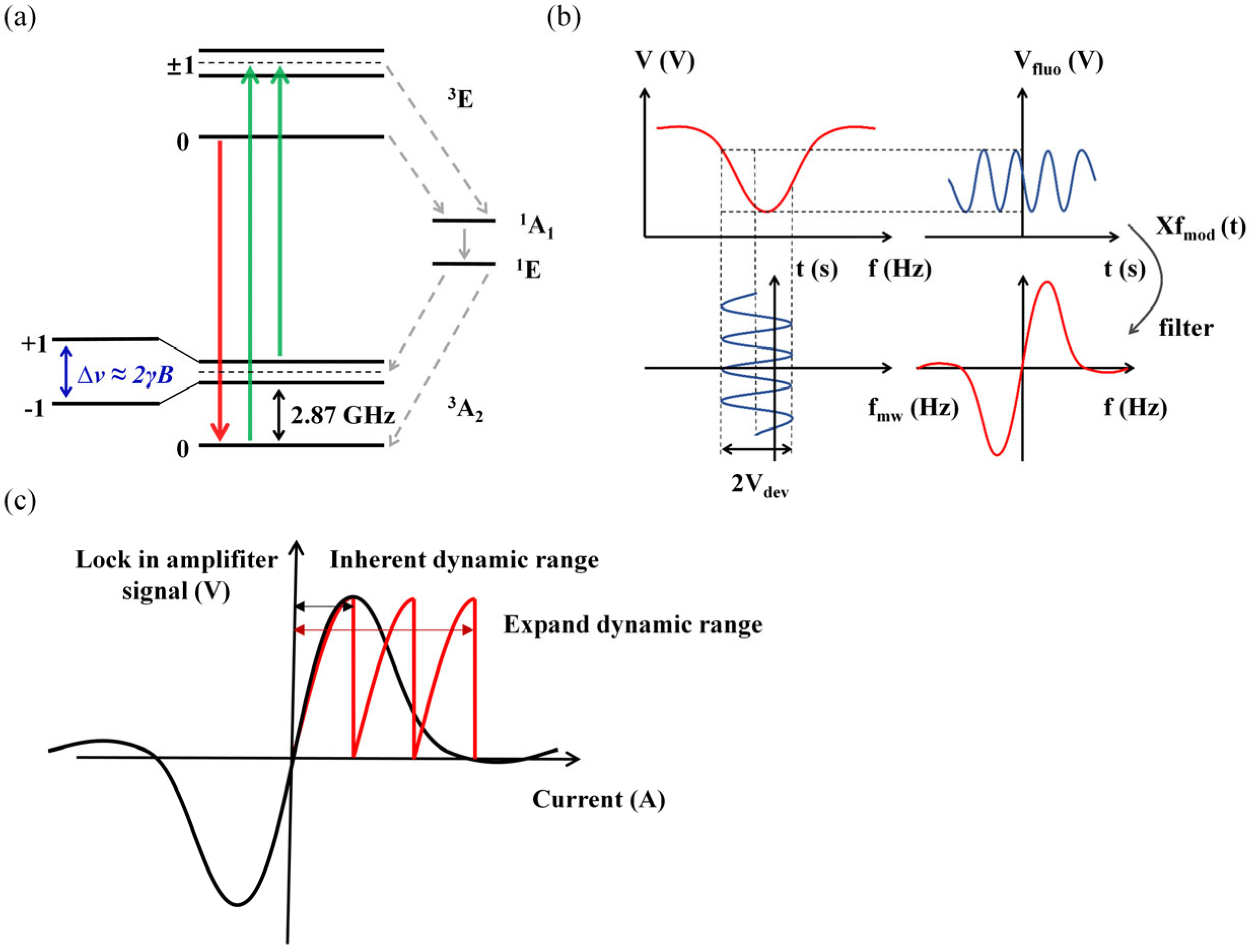
2. Principle
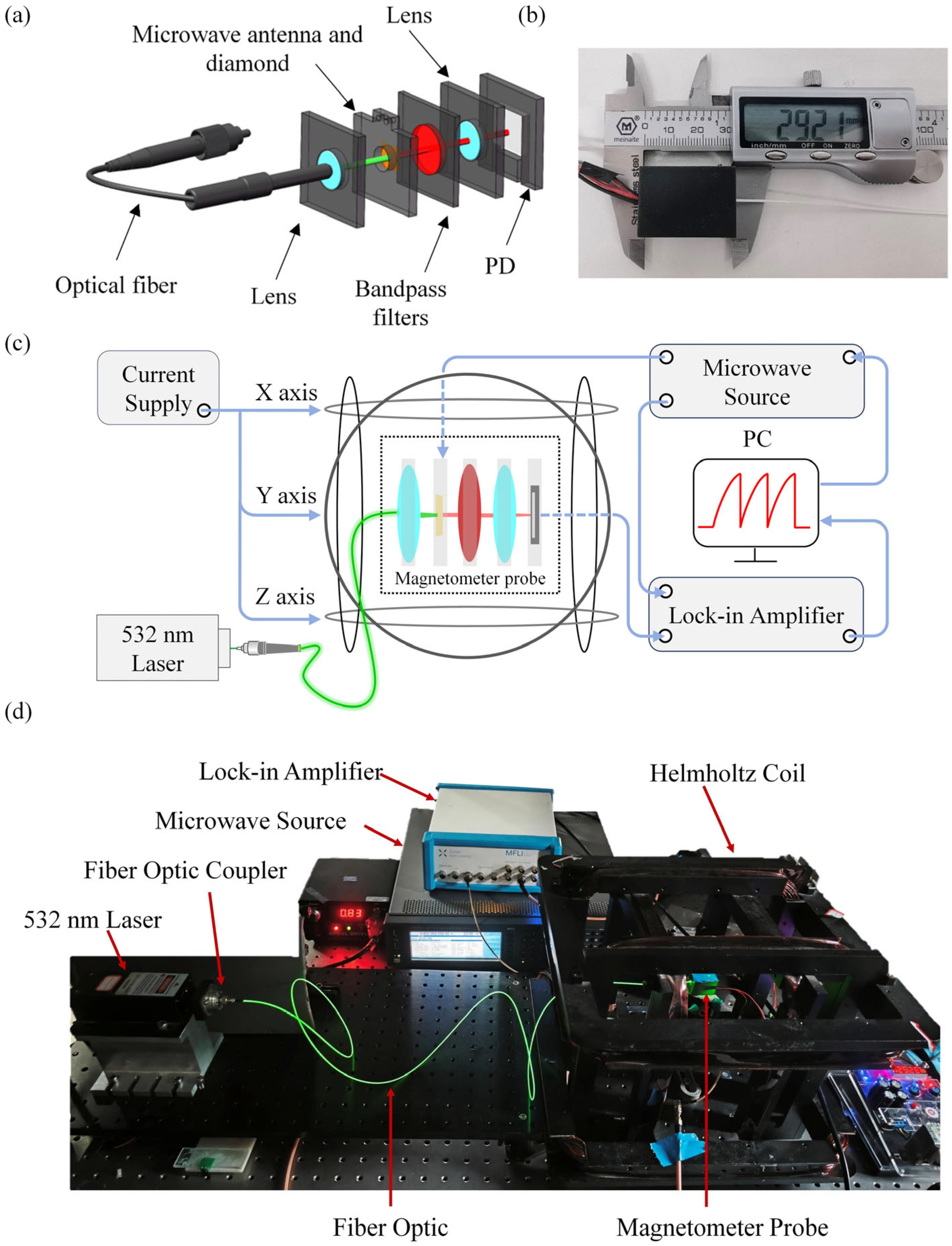
3. Experimental Setup Design
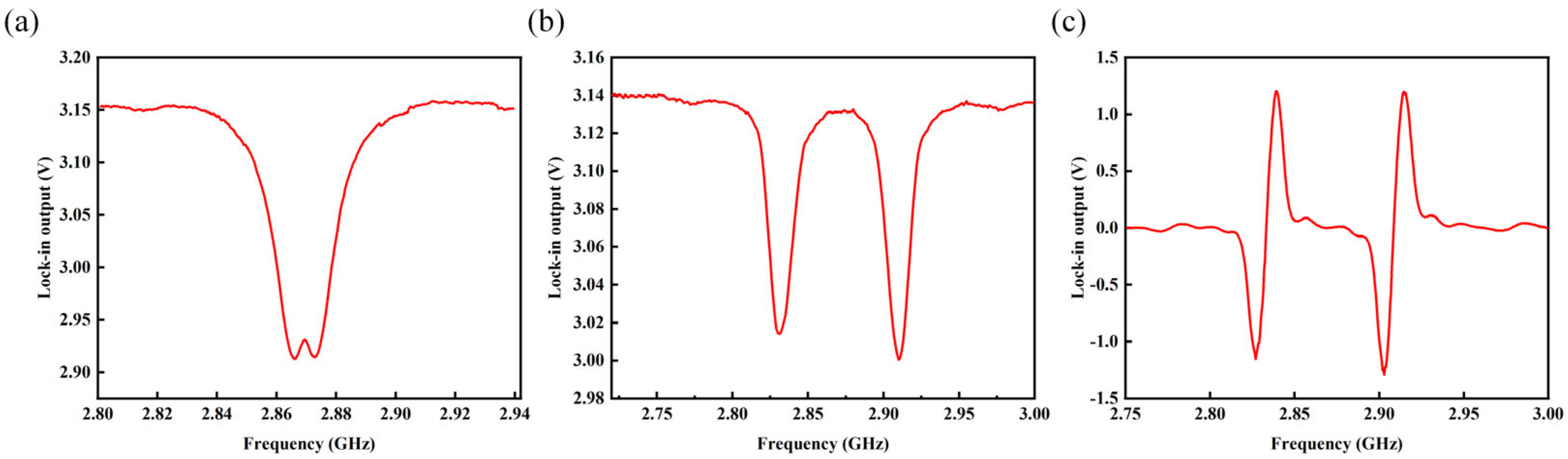
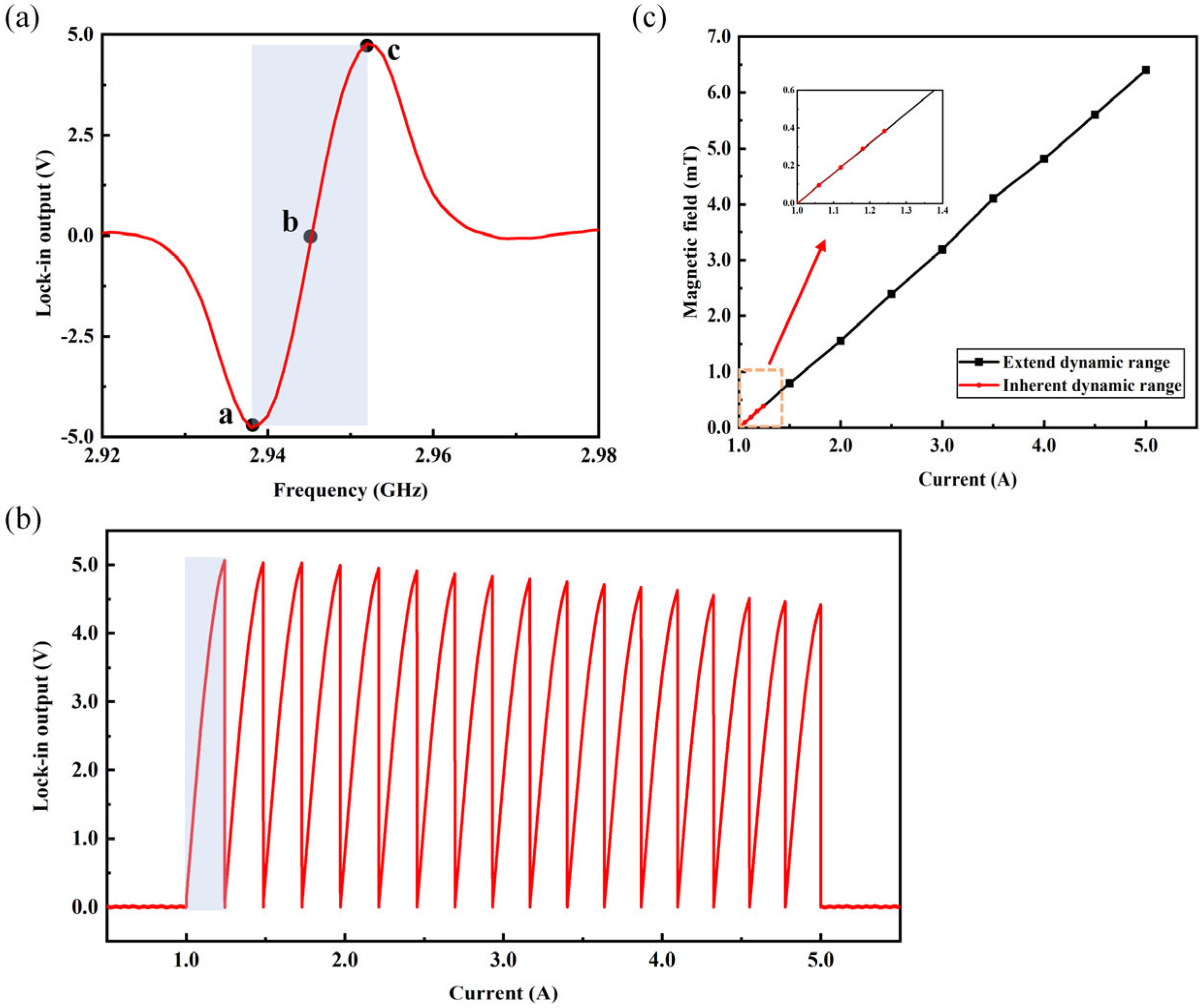
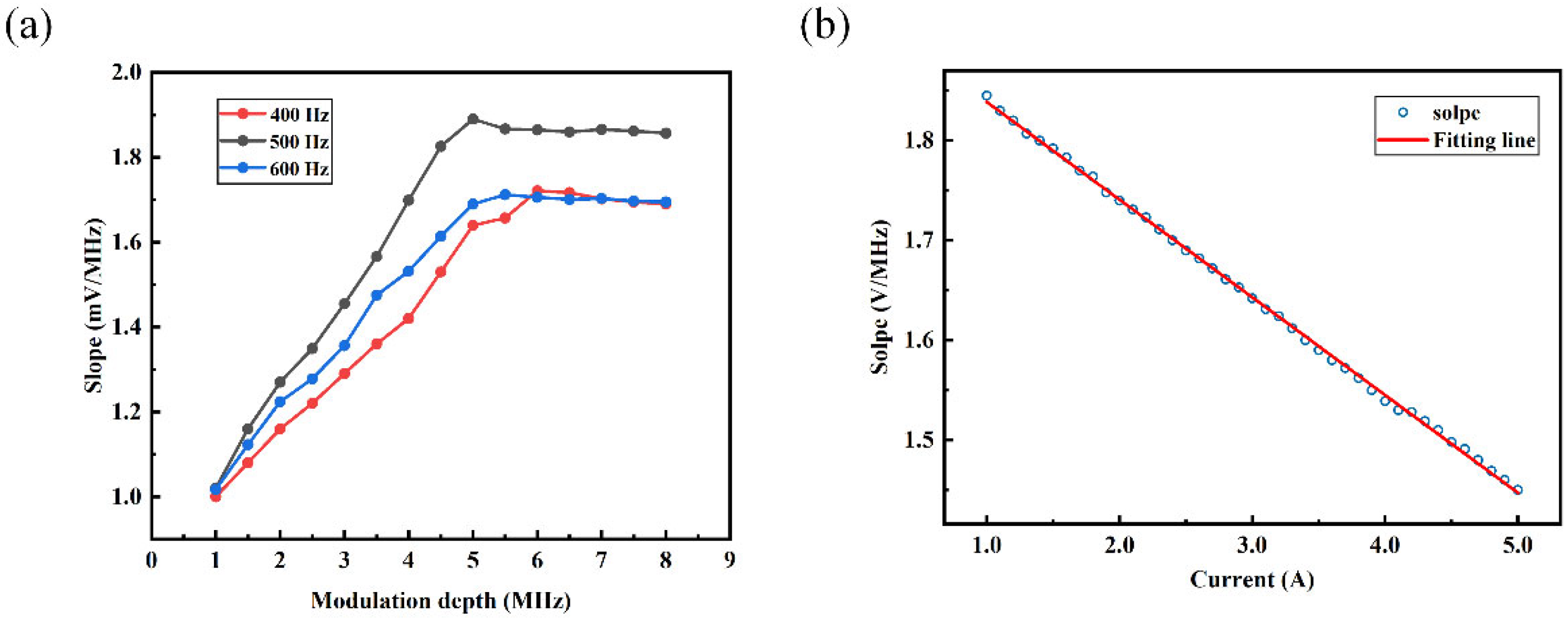
4. Experimental Details and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R.; Vacoby, A.; Walsworth, R.; Lukin, M.D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- Maze, J.R.; Stanwix, P.L.; Hodges, J.S.; Hong, S.; Taylor, J.M.; Cappellaro, P.; Jiang, L.; Dutt, M.V.G.; Togan, E.; Zibrov, A.S. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef]
- Balasubramanian, G.; Chan, I.Y.; Kolesov, R.; Al-Hmoud, M.; Tisler, J.; Shin, C.; Kim, C.; Wojcik, A.; Hemmer, P.R.; Krueger, A. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 2008, 455, 648–651. [Google Scholar] [CrossRef] [PubMed]
- Schoenfeld, R.S.; Harneit, W. Real time magnetic field sensing and imaging using a single spin in diamond. Phys. Rev. Lett. 2011, 106, 030802. [Google Scholar] [CrossRef]
- Dréau, A.; Lesik, M.; Rondin, L.; Spinicelli, P.; Arcizet, O.; Roch, J.F.; Jacques, V. Avoiding power broadening in optically detected magnetic resonance of single NV defects for enhanced dc magnetic field sensitivity. Phys. Rev. B 2011, 84, 195204. [Google Scholar] [CrossRef]
- Dolde, F.; Fedder, H.; Doherty, M.W.; Noebauer, T.; Rempp, F.; Balasubramanian, G.; Wolf, T.; Reinhard, F.; Hollenberg, L.C.L.; Jelezko, F.; et al. Electric-field sensing using single diamond spins. Nat. Phys. 2011, 7, 459–463. [Google Scholar] [CrossRef]
- Steinert, S.; Dolde, F.; Neumann, P.; Aird, A.; Naydenov, B.; Balasubramanian, G.; Jelezko, F.; Wrachtrup, J. High sensitivity magnetic imaging using an array of spins in diamond. Rev. Sci. Instrum. 2010, 81, 043705. [Google Scholar] [CrossRef] [PubMed]
- Braukmann, D.; Glaser, E.R.; Kennedy, T.A.; Bayer, M.; Debus, J. Circularly polarized zero-phonon transitions of vacancies in diamond at high magnetic fields. Phys. Rev. B 2018, 97, 195448. [Google Scholar] [CrossRef]
- Wood, B.D.; Stimpson, G.A.; March, J.E.; Lekhai, Y.N.D.; Stephen, C.J.; Green, B.L.; Frangeskou, A.C.; Gines, L.; Mandal, S.; Williams, O.A.; et al. Long spin coherence times of nitrogen vacancy centers in milled nanodiamonds. Phys. Rev. B 2022, 105, 205401. [Google Scholar] [CrossRef]
- Bar-Gill, N.; Pham, L.M.; Jarmola, A.; Budker, D.; Walsworth, R.L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 2013, 4, 1743. [Google Scholar] [CrossRef]
- Trusheim, M.E.; Li, L.; Laraoui, A.; Chen, E.H.; Bakhru, H.; Schroeder, T.; Gaathon, O.; Meriles, C.A.; Englund, D. Scalable fabrication of high purity diamond nanocrystals with long-spin-coherence nitrogen vacancy centers. Nano Lett. 2014, 14, 32–36. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Umeda, T.; Watanabe, K.; Onoda, S.; Markham, M.L.; Twitchen, D.J.; Naydenov, B.; McGuinness, L.P.; Teraji, T.; Koizumi, S.; et al. Extending spin coherence times of diamond qubits by high-temperature annealing. Phys. Rev. B 2013, 88, 075206. [Google Scholar] [CrossRef]
- Herbschleb, E.D.; Kato, H.; Maruyama, Y.; Danjo, T.; Makino, T.; Yamasaki, S.; Ohki, I.; Hayashi, K.; Morishita, H.; Fujiwara, M.; et al. Ultra-long coherence times amongst room-temperature solid-state spins. Nat. Commun. 2019, 10, 3766. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, G.; Neumann, P.; Twitchen, D.; Markham, M.; Kolesov, R.; Mizuochi, N.; Isoya, J.; Achard, J.; Beck, J.; Tissler, J.; et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 2009, 8, 383–387. [Google Scholar] [CrossRef] [PubMed]
- Hodges, J.S.; Li, L.; Lu, M.; Chen, E.H.; Trusheim, M.E.; Allegri, S.; Yao, X.; Gaathon, O.; Bakhru, H.; Englund, D. Long-lived NV−spin coherence in high-purity diamond membranes. New J. Phys. 2012, 14, 093004. [Google Scholar] [CrossRef]
- Hall, L.T.; Beart, G.C.G.; Thomas, E.A.; Simpson, D.A.; McGuinness, L.P.; Cole, J.H.; Manton, J.H.; Scholten, R.E.; Jelezko, F.; Wrachtrup, J.; et al. High spatial and temporal resolution wide-field imaging of neuron activity using quantum NV-diamond. Sci. Rep. 2012, 2, 401. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Grinolds, M.S.; Pham, L.M.; Le Sage, D.; Luan, L.; Walsworth, R.L.; Yacoby, A. Nanoscale magnetometry with NV centers in diamond. MRS Bull. 2013, 38, 155–161. [Google Scholar] [CrossRef]
- Ninio, Y.; Waiskopf, N.; Meirzada, I.; Romac, Y.; Haim, G.; Yochelis, S.; Banin, U.; Bar-Gill, N. High-sensitivity, high-resolution detection of reactive oxygen species concentration using nv centers. ACS Photonics 2021, 8, 1917–1921. [Google Scholar] [CrossRef]
- Hayashi, K.; Matsuzaki, Y.; Taniguchi, T.; Shimo-Oka, T.; Nakamura, I.; Onoda, S.; Ojshima, T.; Morishita, H.; Fujiwara, M.; Saito, S.; et al. Optimization of temperature sensitivity using the optically detected magnetic-resonance spectrum of a nitrogen-vacancy center ensemble. Phys. Rev. Appl. 2018, 10, 034009. [Google Scholar] [CrossRef]
- Robinson, M.E.; Ng, J.D.; Zhang, H.; Buchman, J.T.; Shenderova, O.A.; Haynes, C.L.; Ma, Z.Q.; Goldsmith, R.H.; Hamers, R.J. Optically detected magnetic resonance for selective imaging of diamond nanoparticles. Anal. Chem. 2018, 90, 769–776. [Google Scholar] [CrossRef]
- Zhang, H.; Belvin, C.; Li, W.; Wang, J.; Wainwright, J.; Berg, R.; Bridger, J. Little bits of diamond: Optically detected magnetic resonance of nitrogen-vacancy centers. Am. J. Phys. 2018, 86, 225–236. [Google Scholar] [CrossRef]
- Titkov, S.V.; Yakovleva, V.V.; Breev, I.D.; Babunts, R.A.; Baranov, P.G.; Bortnikov, N.S. NV−center in natural diamonds: Optically detected magnetic resonance study. Diam. Relat. Mater. 2023, 136, 109938. [Google Scholar] [CrossRef]
- Lazda, R.; Busaite, L.; Berzins, A.; Smits, J.; Gahbauer, F.; Auzinsh, M.; Budker, D.; Ferber, R. Cross-relaxation studies with optically detected magnetic resonances in nitrogen-vacancy centers in diamond in external magnetic field. Phys. Rev. B 2021, 103, 134104. [Google Scholar] [CrossRef]
- Matsuzaki, Y.; Morishita, H.; Shimooka, T.; Tshima, T.; Kakuyanagi, K.; Semba, K.; Munro, W.J.; Yamaguchi, H.; Mizuochi, N.; Saito, S. Optically detected magnetic resonance of high-density ensemble of NV−centers in diamond. J. Phys. Condens. Matter 2016, 28, 275302. [Google Scholar] [CrossRef]
- Simanovskaia, M.; Jensen, K.; Jarmola, A.; Aulenbacher, K.; Manson, N.; Budker, D. Sidebands in optically detected magnetic resonance signals of nitrogen vacancy centers in diamond. Phys. Rev. B 2013, 87, 224106. [Google Scholar] [CrossRef]
- Ambal, K.; McMichael, R.D. A differential photon-rate meter for real-time peak tracking in optically detected magnetic resonance at low photon-count rates. Rev. Sci. Instrum. 2019, 90, 023907. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, D.; Wang, X.C.; Liu, X.Y.; Wang, Q.M.; Zhao, J.Z.; Guo, H.; Qin, L.; Tang, J.; Ma, Z.M.; et al. Portable diamond NV magnetometer head integrated with 520 nm diode laser. IEEE Sens. J. 2022, 22, 5580–5587. [Google Scholar] [CrossRef]
- Frontera, P.; Alessandrini, S.; Stetson, J. Shipboard calibration of a diamond nitrogen vacancy magnetic field sensor. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Wang, C.; Liu, Q.H.; Hu, Y.Q.; Xie, F.; Krishna, K.; Wang, N.; Wang, L.H.; Wang, L.H.; Wang, Y.; Toussaint, K.C.; et al. Realization of high-dynamic-range broadband magnetic-field sensing with ensemble nitrogen-vacancy centers in diamond. Rev. Sci. Instrum. 2023, 94, 015109. [Google Scholar] [CrossRef]
- Ambal, K.; McMichael, R.D. Locking and Tracking Magnetic Resonance Spectra of NV-Center for Real-time Magnetometry using a Differential Photon-Rate Meter. arXiv 2018, arXiv:1808.05580. [Google Scholar]
- Clevenson, H.; Pham, L.M.; Teale, C.; Johnson, K.; Englund, D.; Braje, D. Robust high-dynamic-range vector magnetometry with nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 2018, 112, 252406. [Google Scholar] [CrossRef]
- Hatano, Y.; Shin, J.; Tanigawa, J.; Shigenobu, Y.; Nakazono, A.; Sekiguchi, T.; Onoda, S.; Ohshima, T.; Arai, K.; Iwasaki, T.; et al. High-precision robust monitoring of charge/discharge current over a wide dynamic range for electric vehicle batteries using diamond quantum sensors. Sci. Rep. 2022, 12, 13991. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zheng, D.D.; Liu, Z.H.; Wang, H.; Liu, Y.K.; Hou, C.Y.; Guo, H.; Li, Z.H.; Sugawara, Y.; Tang, J.; et al. Noise Suppression of Nitrogen-Vacancy Magnetometer in Lock-In Detection Method by Using Common Mode Rejection. Micromachines 2023, 14, 1823. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.Z.; Li, Y.; Liu, X.Y.; Gao, Y.X.; Zheng, D.D.; Wang, Q.M.; Liu, Z.H.; Li, Z.H.; Guo, H.; Yasuhiro, S.; et al. Pico-tesla Magnetic Field Detection with integrated Flux Concentrators using Multi-Frequency Modulation technique on Solid Nuclear Spin in Diamonds. Appl. Opt. 2023, 62, 3967–3975. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Liu, Z.; Liu, Y.; Wang, B.; Shen, Y.; Qin, L. High-Dynamic-Range Integrated NV Magnetometers. Micromachines 2024, 15, 662. https://doi.org/10.3390/mi15050662
Wang T, Liu Z, Liu Y, Wang B, Shen Y, Qin L. High-Dynamic-Range Integrated NV Magnetometers. Micromachines. 2024; 15(5):662. https://doi.org/10.3390/mi15050662
Chicago/Turabian StyleWang, Tianning, Zhenhua Liu, Yankang Liu, Bo Wang, Yuanyuan Shen, and Li Qin. 2024. "High-Dynamic-Range Integrated NV Magnetometers" Micromachines 15, no. 5: 662. https://doi.org/10.3390/mi15050662
APA StyleWang, T., Liu, Z., Liu, Y., Wang, B., Shen, Y., & Qin, L. (2024). High-Dynamic-Range Integrated NV Magnetometers. Micromachines, 15(5), 662. https://doi.org/10.3390/mi15050662




