Electro-Osmotic Flow and Mass Transfer through a Rough Microchannel with a Modulated Charged Surface
Abstract
:1. Introduction
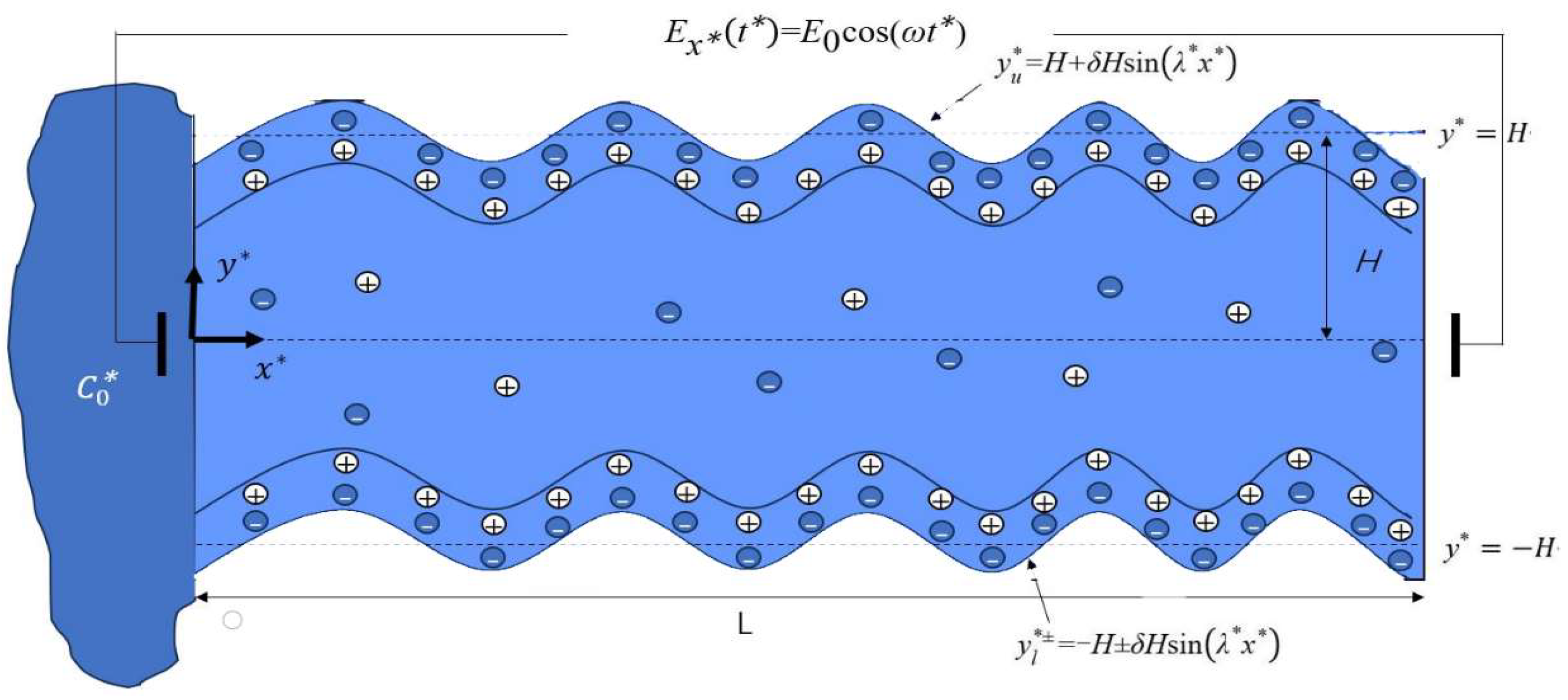
2. Mathematics Model
2.1. Velocity Distribution
2.1.1. The Zeroth-Order Equations
2.1.2. The First-Order Equations
2.1.3. The Second-Order Equations
2.2. Concentration Distribution
3. Results and Discussion
3.1. Electric Potential Field
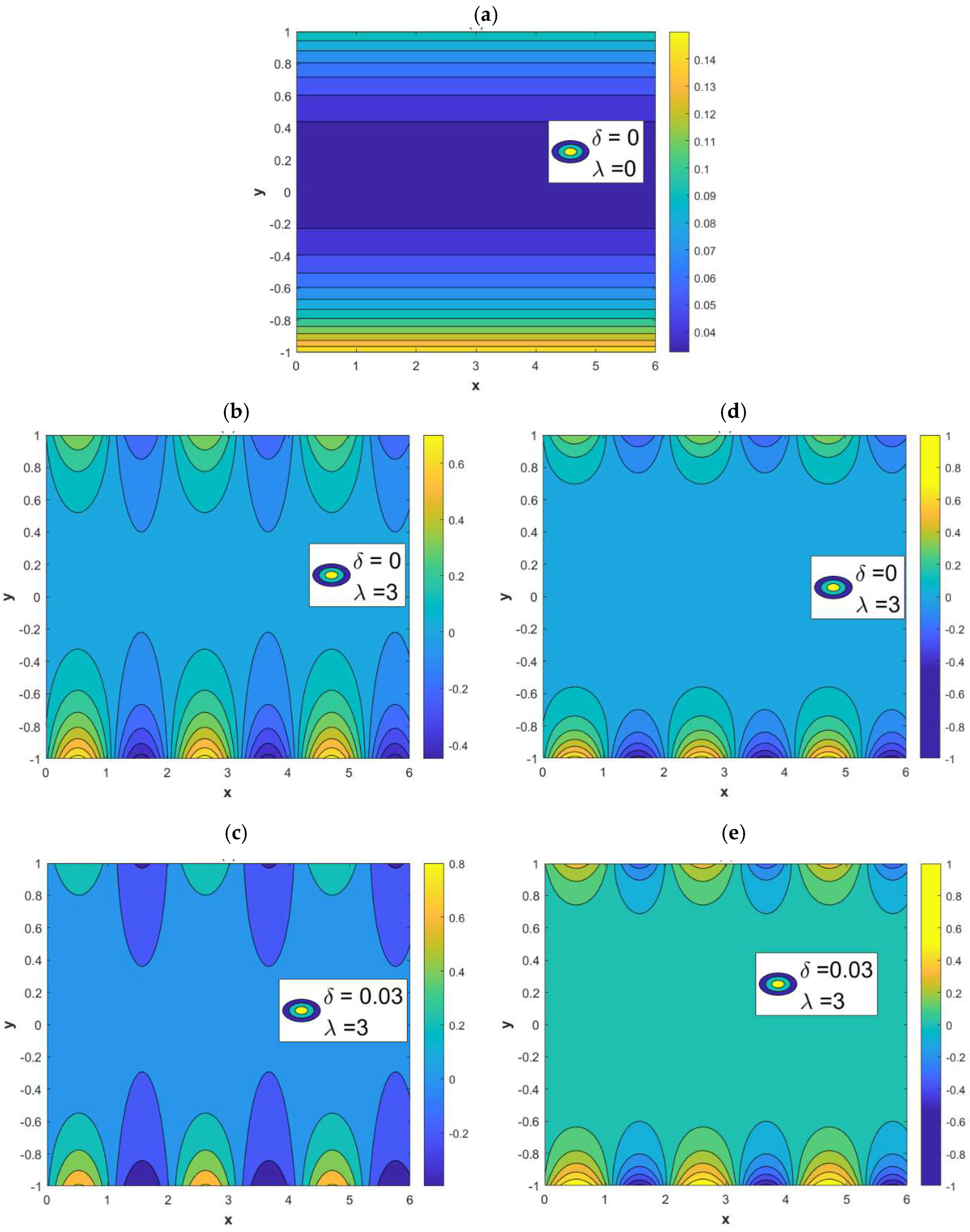
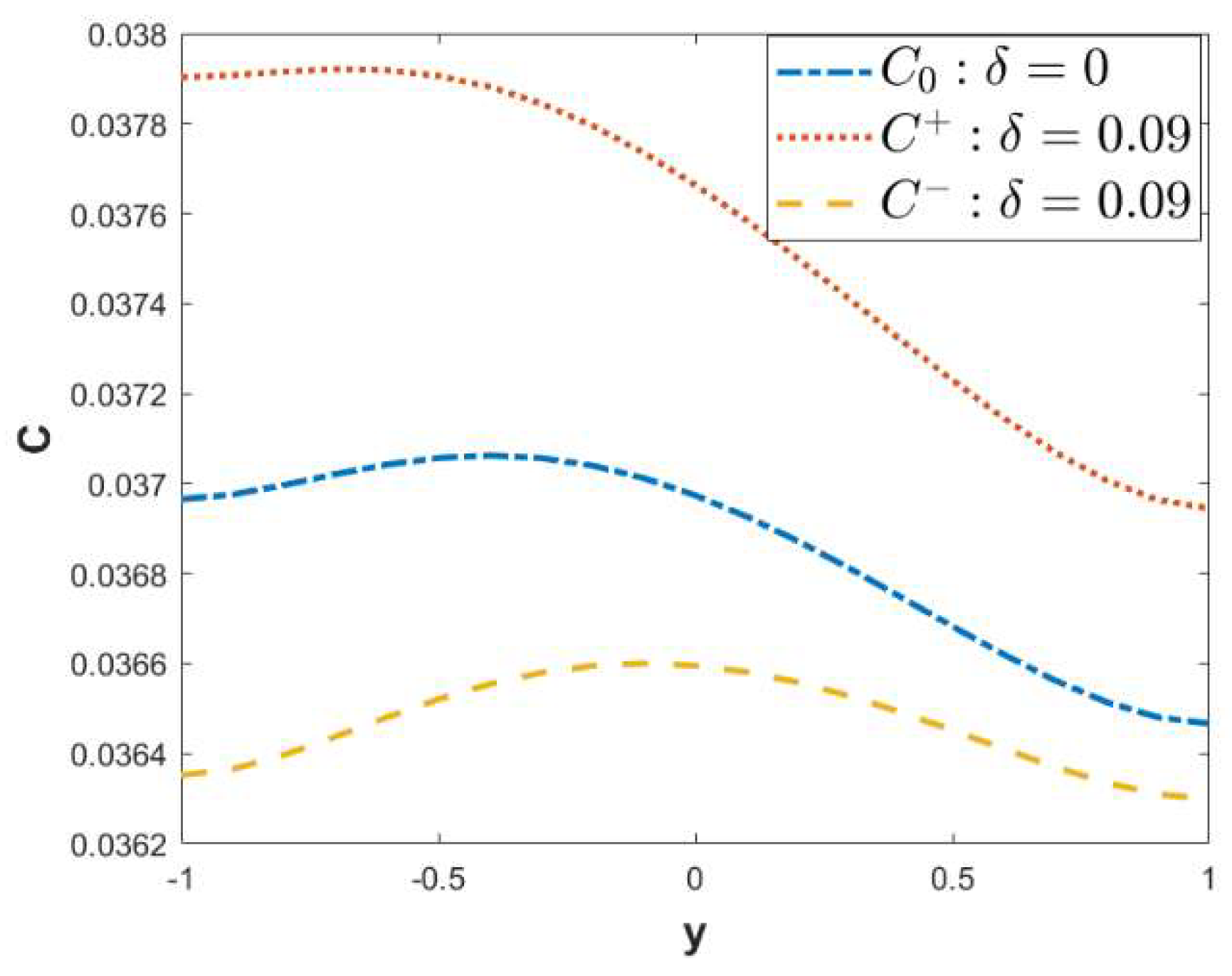
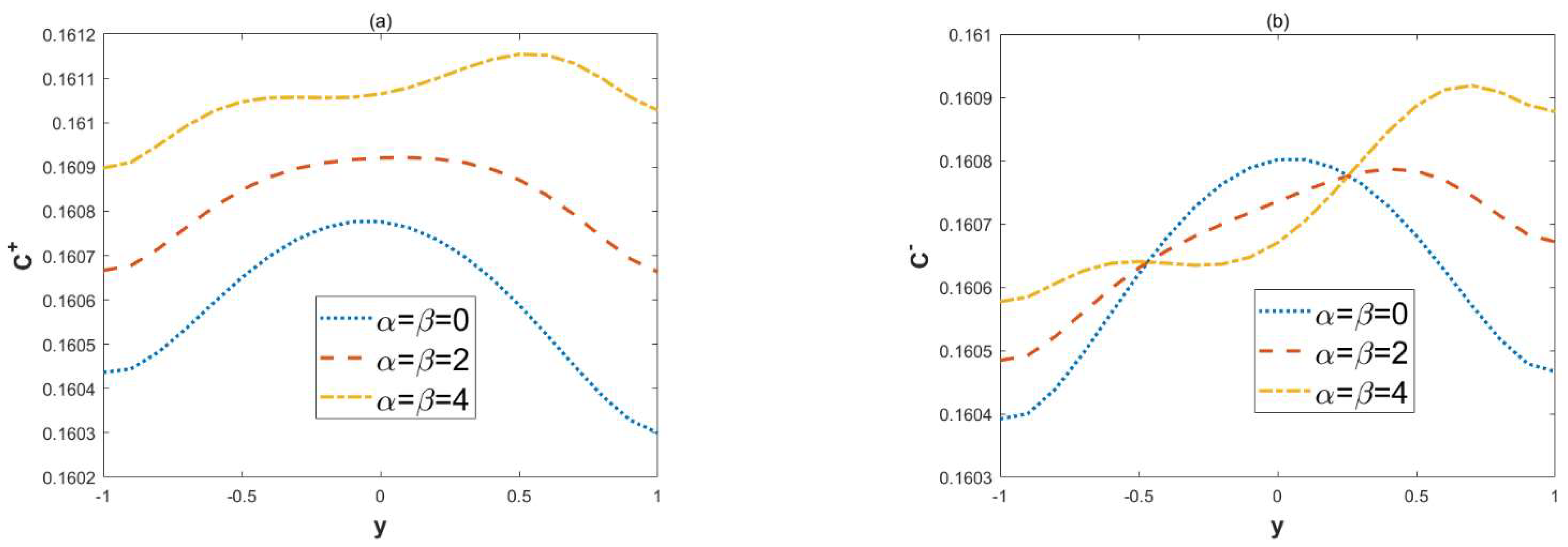
3.2. Concentration Field
4. Conclusions
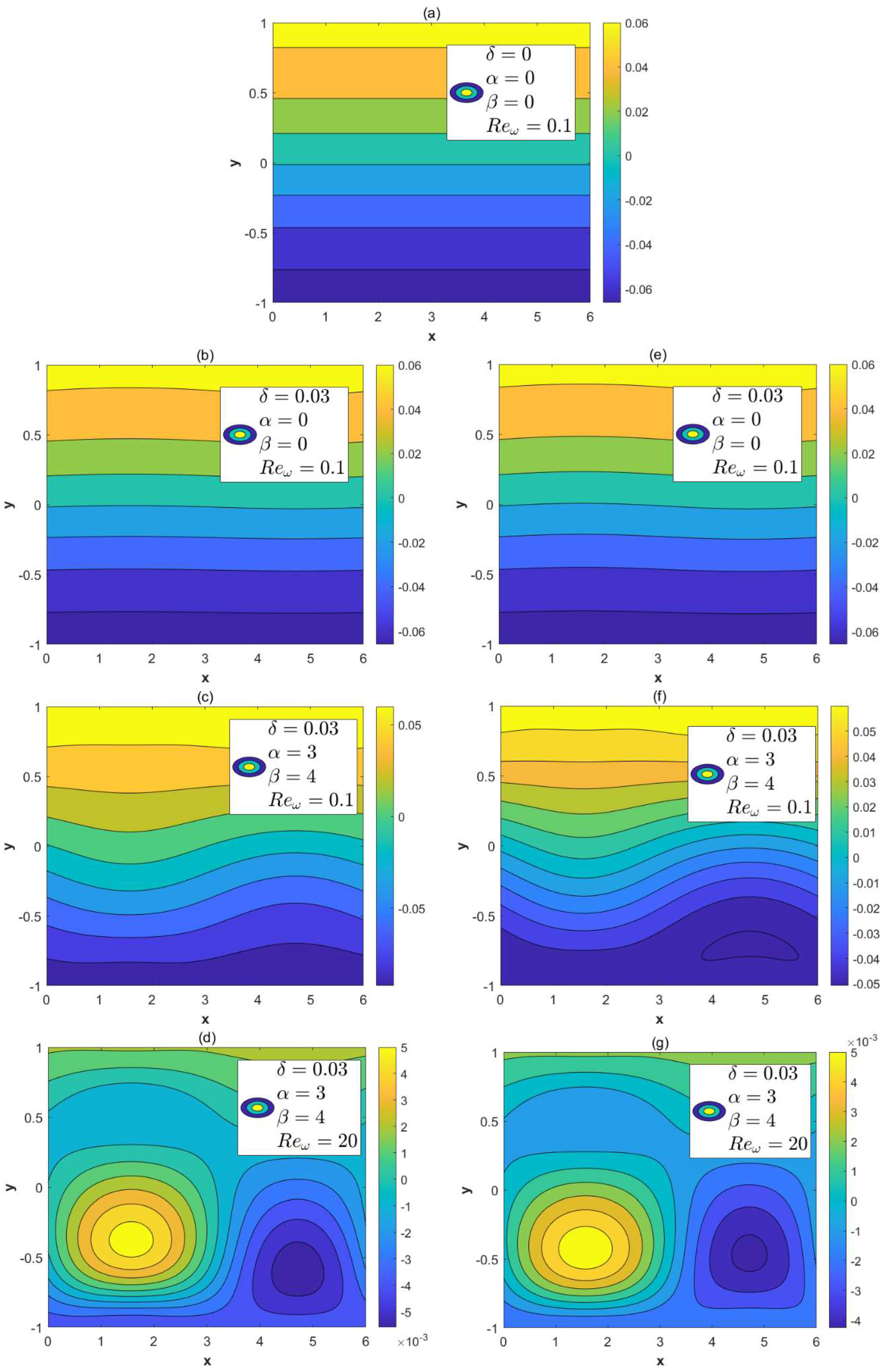
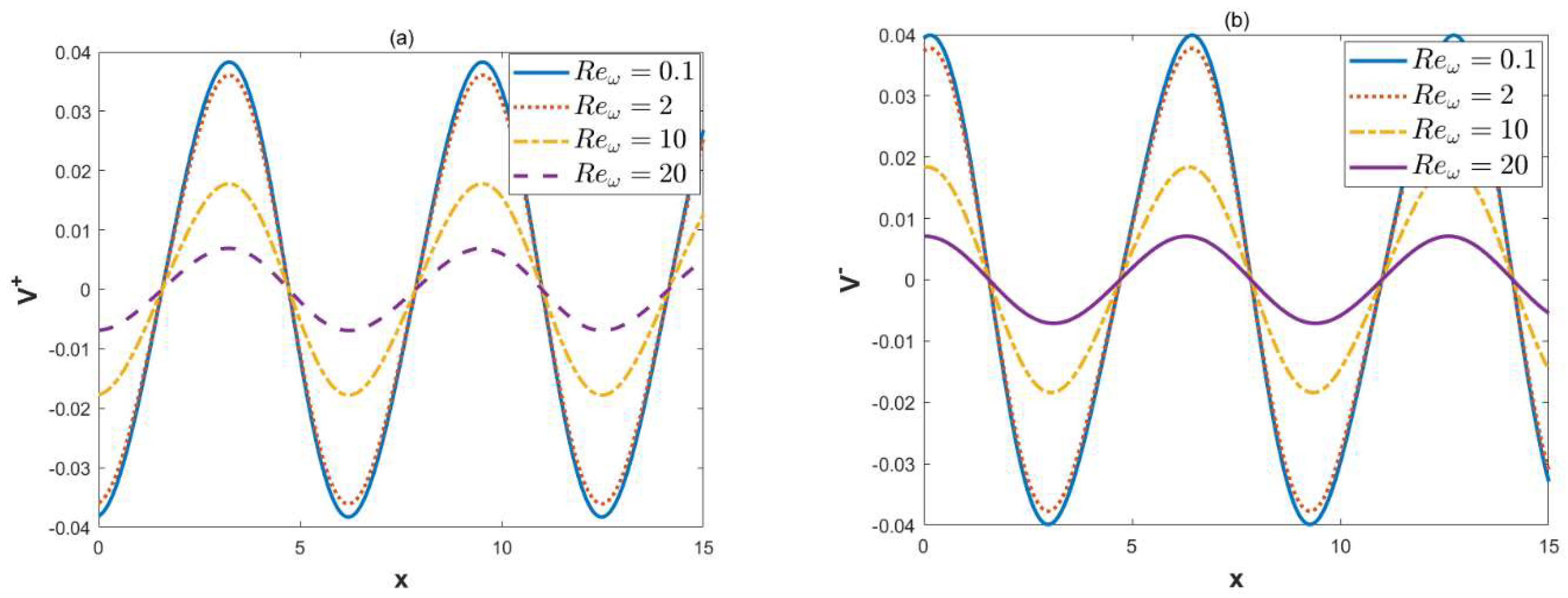
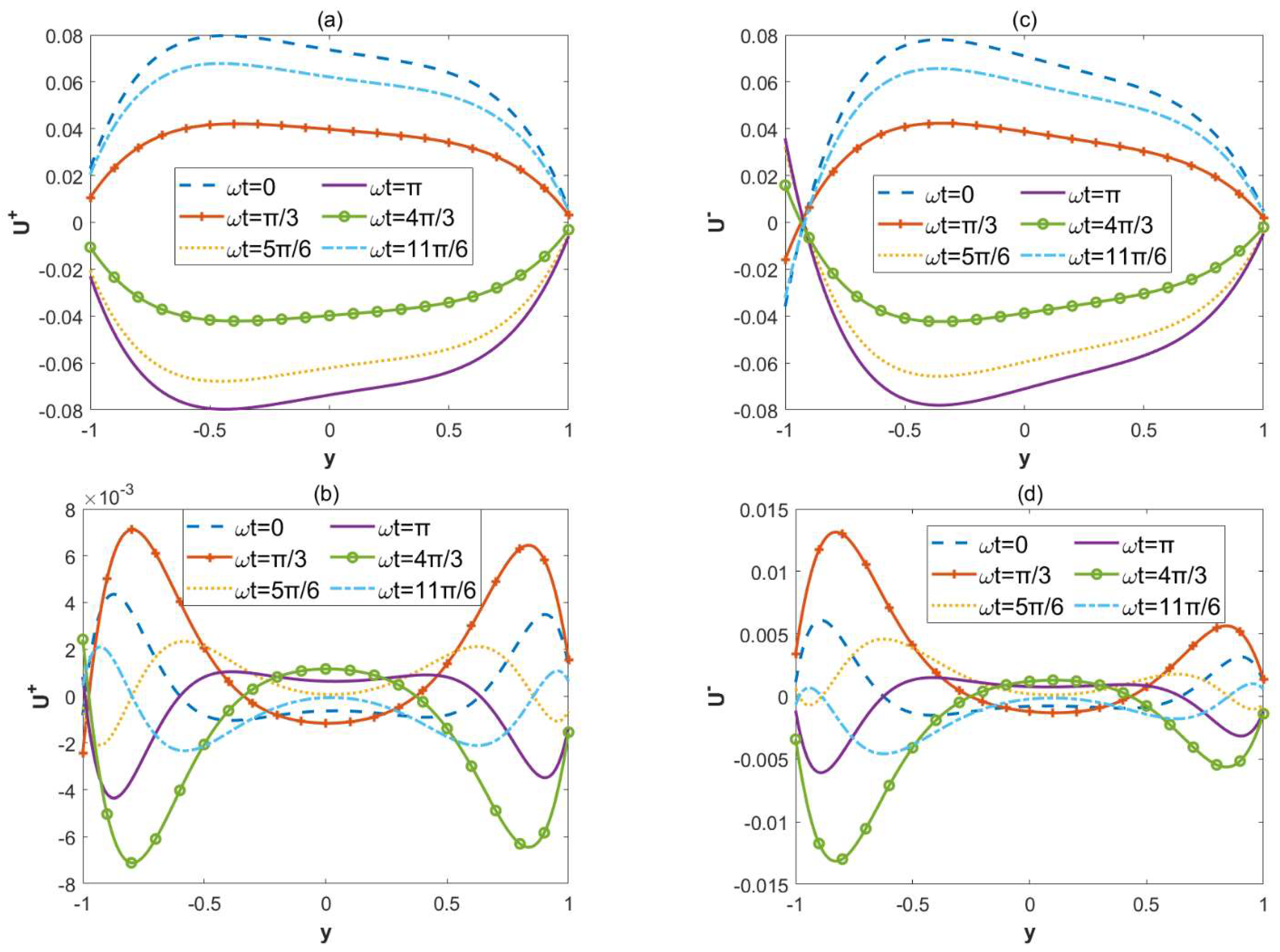
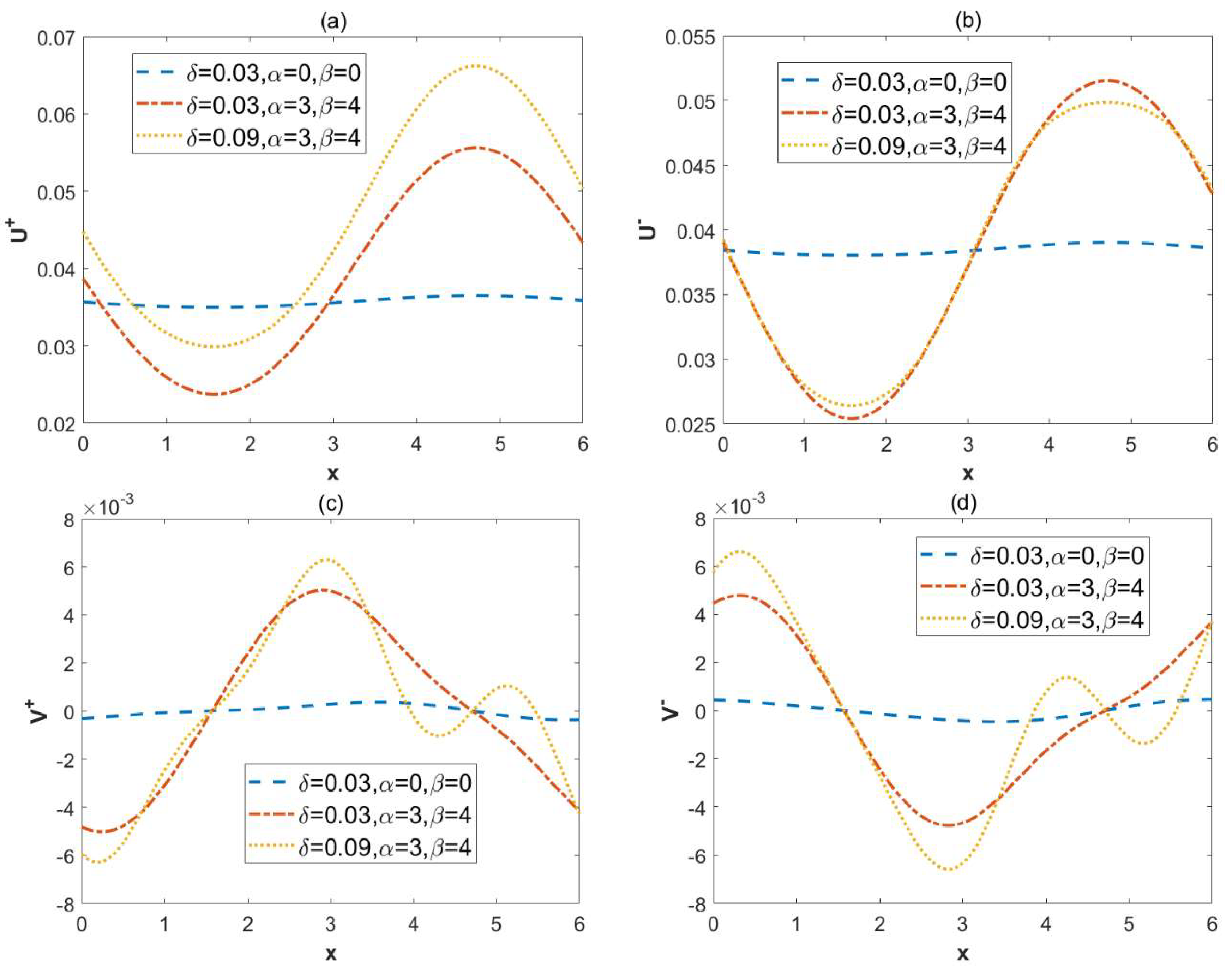
- When the modulated charge surface parameters (α, β) increases, the vertical velocity and the circulation flow are generated; the amplitudes of velocities also increase. In these cases, the local concentration of in-phase walls also increase.
- As the roughness parameter δ amplifies, the oscillation of the vertical velocity is enhanced. The in-phase walls are conducive to the diffusion of solutes.
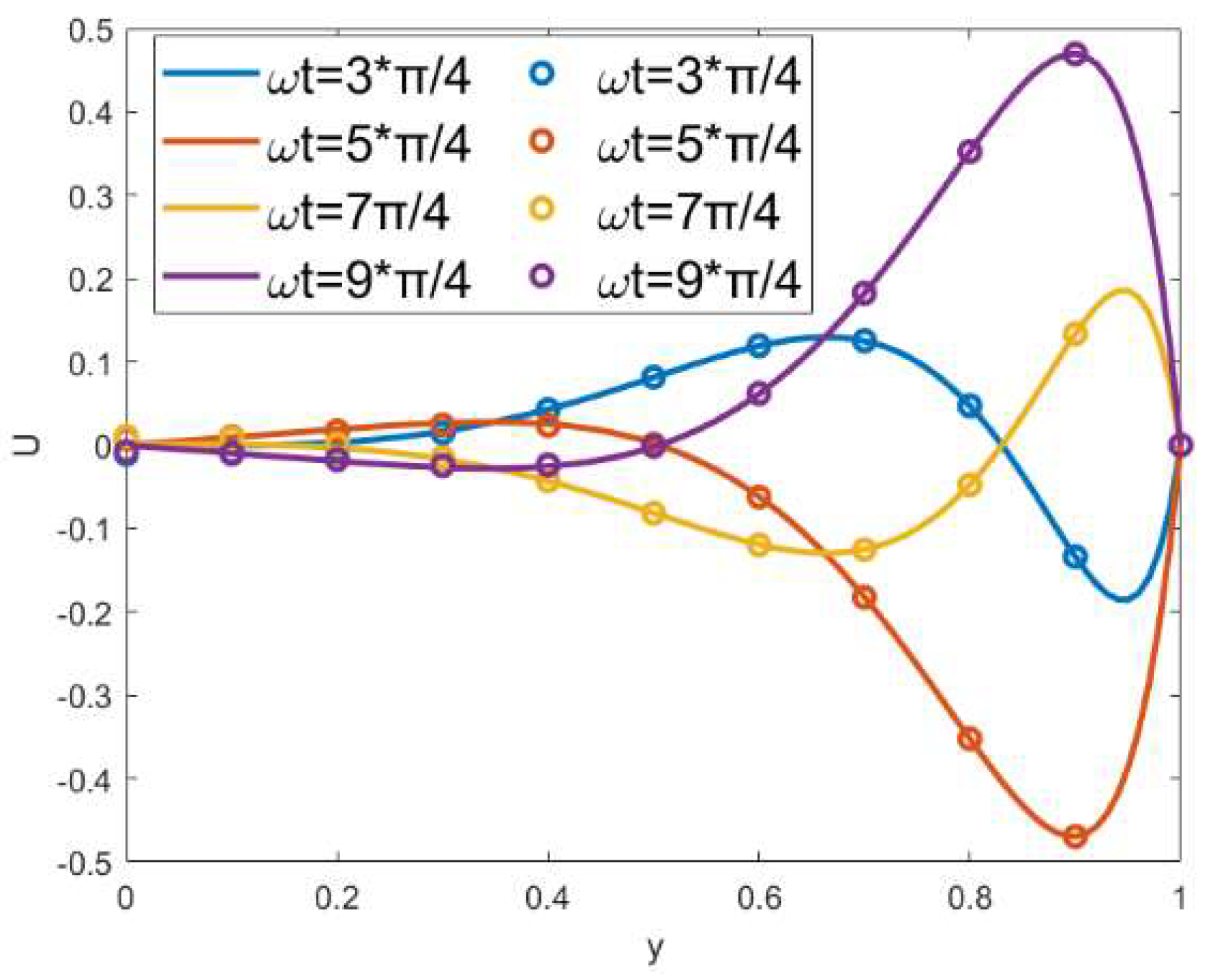
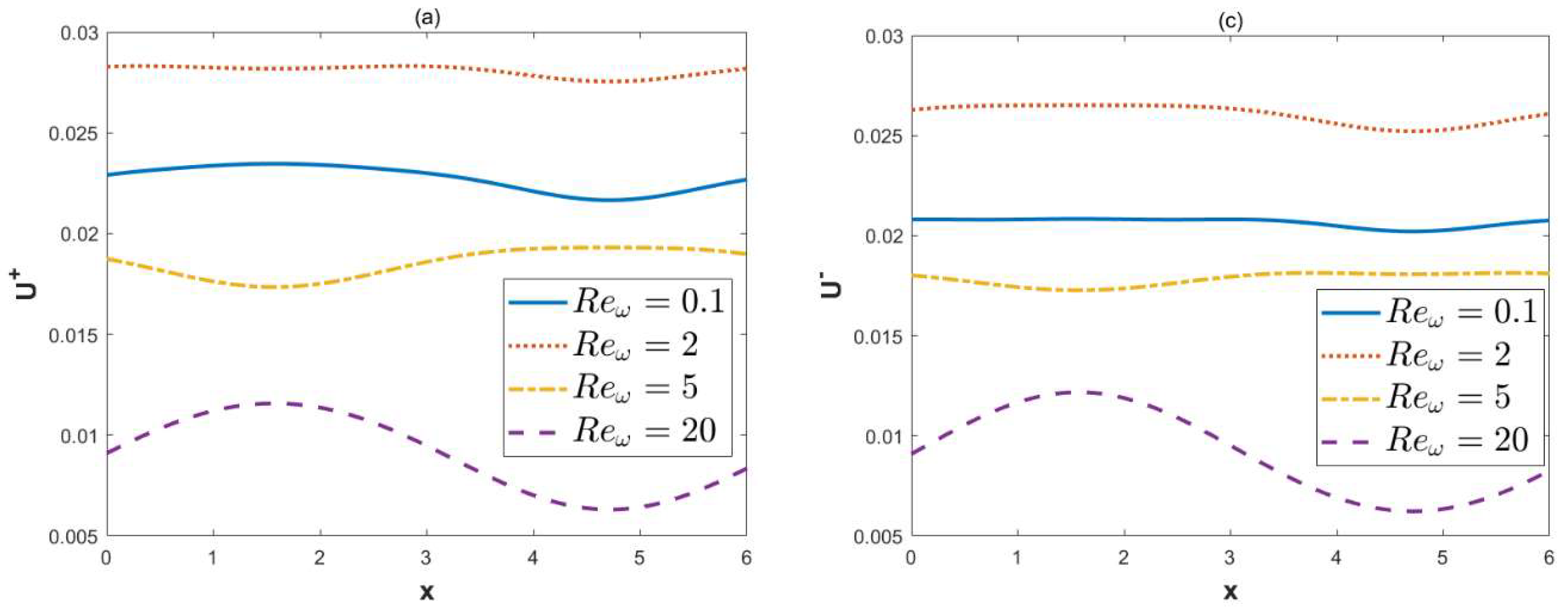
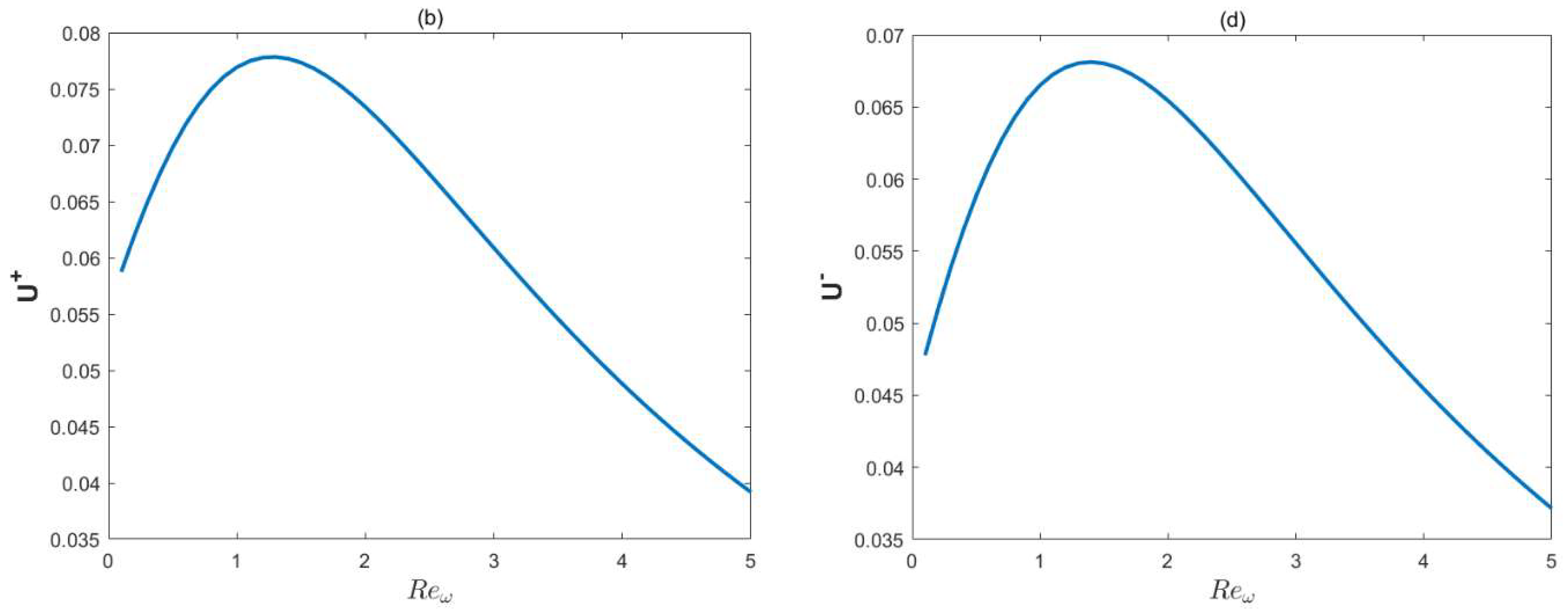
- With the increment in the oscillation Reynolds number, the oscillations of the transverse velocity also increase. It can be found that the local concentrations will increase when the oscillation Reynolds number is below a certain critical value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Formulas
Appendix B. Numerical Algorithm
References
- Wang, X.; Hong, X.Z.; Li, Y.W.; Li, Y.; Wang, J.; Chen, P.; Liu, B.F. Microfluidics-based strategies for molecular diagnostics of infectious diseases. Mil. Med. Res. 2022, 9, 727–753. [Google Scholar] [CrossRef] [PubMed]
- Battat, S.; Weitz, D.A.; Whitesides, G.M. An outlook on microfluidics: The promise and the challenge. LOC 2022, 22, 530–536. [Google Scholar] [CrossRef]
- Fiore, L.; Mazzaracchio, V.; Serani, A.; Fabiani, G.; Fabiani, L.; Volpe, G.; Arduini, F. Microfluidic paper-based wearable electrochemical biosensor for reliable cortisol detection in sweat. Sens. Actuators B Chem. 2023, 379, 133258. [Google Scholar] [CrossRef]
- Zhuang, J.; Zhao, Z.; Lian, K.; Yin, L.; Wang, J.; Man, S.; Ma, L. SERS-based CRISPR/Cas assay on microfluidic paper analytical devices for supersensitive detection of pathogenic bacteria in foods. Biosens. Bioelectron. 2022, 207, 114167. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ding, X.; Yin, K.; Avery, L.; Ballesteros, E.; Liu, C. Instrument-free, CRISPR-based diagnostics of SARS-CoV-2 using self-contained microfluidic system. Biosens. Bioelectron. 2022, 199, 113865. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.X.; Jia, L.; Dang, C.; Qi, Z.L. The mass transfer characteristics of R134a/R245fa during stratified flow condensation in rectangular channel. Int. J. Heat Mass Transf. 2022, 195, 123189. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Tahta, M.A.; Tuasikal, J.; She, Y.; Hu, Y.; Suekane, T. Dissolution mass transfer of trapped gases in porous media: A correlation of Sherwood, Reynolds, and Schmidt numbers. Int. J. Heat Mass Transf. 2023, 205, 123860. [Google Scholar] [CrossRef]
- Ye, M.; Zhang, N.; Zhou, T.; Wei, Z.; Jiang, F.; Ke, Y. Recent research on vanadium redox batteries: A review on electrolyte preparation, mass transfer, and charge transfer for electrolyte performance enhancement. J. Energy Storage 2024, 6, e610. [Google Scholar] [CrossRef]
- Piasecka, M.; Maciejewska, B.; Michalski, D.; Dadas, N.; Piasecki, A. Investigations of Flow Boiling in Mini-Channels: Heat Transfer Calculations with Temperature Uncertainty Analyses. Energies 2024, 17, 791. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, W.; Zhu, X.; Ding, Y.; Liao, Q. Experimental research on non-azeotropic immiscible binary mixed vapors condensation mode and heat mass transfer characteristics under natural convection. Int. J. Heat Mass Transf. 2024, 223, 125222. [Google Scholar] [CrossRef]
- Jian, Y. Transient MHD heat transfer and entropy generation in a microparallel channel combined with pressure and electroosmotic effects. Int. J. Heat Mass Transf. 2015, 89, 193–205. [Google Scholar] [CrossRef]
- An, S.; Tian, K.; Ding, Z.; Jian, Y. Electroosmotic and pressure-driven slip flow of fractional viscoelastic fluids in microchannels. Appl. Math. Comput. 2022, 425, 127073. [Google Scholar] [CrossRef]
- Wu, J. Understanding the electric double-layer structure, capacitance, and charging dynamics. Chem. Rev. 2022, 122, 10821–10859. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Zhou, M.; Liu, X.; Jiang, B. Effect of pressure-driven flow on electroosmotic flow and electrokinetic mass transport in microchannels. Int. J. Heat Mass Transf. 2023, 206, 123925. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, M.; Yue, X.; Wang, S. Exact solution of electroosmotic flow of the second grade fluid in a circular microchannel driving by an AC electric field. Chin. J. Phys. 2024, 88, 1–9. [Google Scholar]
- Deng, S.; Tan, X.; Liang, C. Analytical study of unsteady two-layer combined electroosmotic and pressure-driven flow through a cylindrical microchannel with slip-dependent zeta potential. Chem. Eng. Sci. 2024, 283, 119327. [Google Scholar] [CrossRef]
- Chakraborty, S.; Srivastava, A.K. Generalized model for time periodic electroosmotic flows with overlapping electrical double layers. Langmuir 2007, 23, 12421–12428. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.; Ganguly, S.; Dutta, P. Electrokinetically induced thermofluidic transport of power-law fluids under the influence of superimposed magnetic field. Chem. Eng. Sci. 2017, 171, 391–403. [Google Scholar] [CrossRef]
- Sadeghi, A. Theoretical modeling of electroosmotic flow in soft microchannels: A variational approach applied to the rectangular geometry. Phys. Fluids. 2018, 30, 032004. [Google Scholar] [CrossRef]
- Sadeghi, A.; Azari, M.; Hardt, S. Electroosmotic flow in soft microchannels at high grafting densities. Phys. Rev. Fluids 2019, 4, 063701. [Google Scholar] [CrossRef]
- Chang, L.; Sun, Y.; Buren, M.; Jian, Y. Thermal and Flow Analysis of Fully Developed Electroosmotic Flow in Parallel-Plate Micro- and Nanochannels with Surface Charge-Dependent Slip. Micromachines 2022, 13, 2166. [Google Scholar] [CrossRef]
- Hernández, A.; Arcos, J.; Martínez-Trinidad, J.; Bautista, O.; Sánchez, S.; Méndez, F. Thermodiffusive effect on the local Debye-length in an electroosmotic flow of a viscoelastic fluid in a slit microchannel. Int. J. Heat Mass Transf. 2022, 187, 122522. [Google Scholar] [CrossRef]
- Ng, C.O.; Qi, C. Electroosmotic flow of a power-law fluid in a non-uniform microchannel. J. Nonnewton. Fluid. Mech. 2014, 208, 118–125. [Google Scholar] [CrossRef]
- Qi, C.; Ng, C.O. Electroosmotic flow of a two-layer fluid in a slit channel with gradually varying wall shape and zeta potential. Int. J. Heat Mass Transf. 2018, 119, 52–64. [Google Scholar] [CrossRef]
- Mandal, S.; Ghosh, U.; Bandopadhyay, A.; Chakraborty, S. Electro-osmosis of superimposed fluids in the presence of modulated charged surfaces in narrow confinements. J. Fluid. Mech. 2015, 776, 390–429. [Google Scholar] [CrossRef]
- Bian, X.; Li, F.; Jian, Y. The Streaming Potential of Fluid through a Microchannel with Modulated Charged Surfaces. Micromachines 2021, 13, 66. [Google Scholar] [CrossRef] [PubMed]
- Akhtar, S.; Jamil, S.; Shah, N.; Chung, J.; Tufail, R. Effect of zeta potential in fractional pulsatile electroosmotic flow of Maxwell fluid. Chin. J. Phys. 2022, 76, 59–67. [Google Scholar] [CrossRef]
- Wang, J.; Li, F. Electroosmotic flow and heat transfer through a polyelectrolyte-grafted microchannel with modulated charged surfaces. Int. J. Heat Mass Transf. 2023, 216, 124545. [Google Scholar] [CrossRef]
- Siddiqa, S.; Mahfooz, M.; Hossain, M.A. Transient Analysis of Heat Transfer by Natural Convection Along a Vertical Wavy Surface. Int. J. Nonlin. Sci. Num. 2017, 18, 175–185. [Google Scholar] [CrossRef]
- Buren, M.; Jian, Y.; Chang, L. Electromagnetohydrodynamic flow through a microparallel channel with corrugated walls. J. Phys. D Appl. Phys. 2014, 47, 425501-1–425501-8. [Google Scholar] [CrossRef]
- Li, F.; Jian, Y.; Buren, M.; Chang, L. Effects of three-dimensional surface corrugations on electromagnetohydrodynamic flow through microchannel. Chin. J. Phys. 2019, 60, 345–361. [Google Scholar] [CrossRef]
- Chang, L.; Zhao, G.; Buren, M.; Sun, Y.; Jian, Y. Alternating Current Electroosmotic Flow of Maxwell Fluid in a Parallel Plate Microchannel with Sinusoidal Roughness. Micromachines 2023, 15, 4. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.H.; Lim, S.; Kwak, S.S.; Kim, J.; Delivery, A.I.S.-M.D. Techniques, and Applications. Adv. Healthc. Mater. 2024, 13, 2302375. [Google Scholar] [CrossRef] [PubMed]
- Matin, M.H.; Ohshima, H. Combined electroosmotically and pressure driven flow in soft nanofluidics. J. Colloid. Interface Sci. 2015, 460, 361–369. [Google Scholar] [CrossRef]
- Hossan, M.R.; Dutta, D.; Islam, N.; Dutta, P. Electric field driven pumping in microfluidic device. Electrophoresis 2018, 39, 702–731. [Google Scholar] [CrossRef] [PubMed]
- Medina, I.; Toledo, M.; Méndez, F.; Bautista, O. Pulsatile electroosmotic flow in a microchannel with asymmetric wall zeta potentials and its effect on mass transport enhancement and mixing. Chem. Eng. Sci. 2018, 184, 259–272. [Google Scholar] [CrossRef]
- Li, F.; Jian, Y. Solute dispersion generated by alternating current electric field through polyelectrolyte-grafted nanochannel with interfacial slip. Int. J. Heat. Mass. Tran. 2019, 141, 1066–1077. [Google Scholar] [CrossRef]
- Liu, Y.; Jian, Y. Electromagnetohydrodynamic flows and mass transport in curved rectangular microchannels. Appl. Math. Mech. 2020, 41, 1431–1446. [Google Scholar] [CrossRef]
- Leal, G.L. Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes; Cambridge University Press: Cambridge, UK, 2007; Volume 7, pp. 232–237. [Google Scholar]
- Li, Z.; Qiao, Z.; Tang, T. Numerical Solution of Differential equations: Introduction to Finite Difference and Finite Element Methods; Cambridge University Press: Cambridge, UK, 2017; pp. 108–131. [Google Scholar]
- Huang, H.F.; Lai, C.L. Enhancement of mass transport and separation of species by oscillatory electroosmotic flows. Proc. Math. Phys. Eng. Sci. 2006, 462, 2017–2038. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qing, Y.; Wang, J.; Li, F. Electro-Osmotic Flow and Mass Transfer through a Rough Microchannel with a Modulated Charged Surface. Micromachines 2024, 15, 882. https://doi.org/10.3390/mi15070882
Qing Y, Wang J, Li F. Electro-Osmotic Flow and Mass Transfer through a Rough Microchannel with a Modulated Charged Surface. Micromachines. 2024; 15(7):882. https://doi.org/10.3390/mi15070882
Chicago/Turabian StyleQing, Yun, Jiaqi Wang, and Fengqin Li. 2024. "Electro-Osmotic Flow and Mass Transfer through a Rough Microchannel with a Modulated Charged Surface" Micromachines 15, no. 7: 882. https://doi.org/10.3390/mi15070882
APA StyleQing, Y., Wang, J., & Li, F. (2024). Electro-Osmotic Flow and Mass Transfer through a Rough Microchannel with a Modulated Charged Surface. Micromachines, 15(7), 882. https://doi.org/10.3390/mi15070882




