Domain-Specific Acceleration of Gravity Forward Modeling via Hardware–Software Co-Design
Abstract
1. Introduction
- We propose a custom instruction set extension for a RISC-V CPU to support an FPGA-based gravity forward modeling accelerator. To the best of our knowledge, this is the first FPGA-based accelerator design specifically targeting gravity forward modeling.
- We introduce a piecewise linear approximation method optimized using stochastic gradient descent (SGD), which significantly reduces resource utilization and computational latency. Similar approximation techniques are applied to other nonlinear operations to improve efficiency while maintaining numerical accuracy.
- We implement and evaluate our design on an AMD UltraScale+ ZCU102 FPGA.At a clock frequency of 250 MHz, the proposed system achieves up to 179× speedup and 2040× improvement in energy efficiency compared to an Intel Xeon 5218R processor.
2. Background
| Algorithm 1: Core Algorithm for Forward Gravity Calculation on CPU |
 |
3. Methods
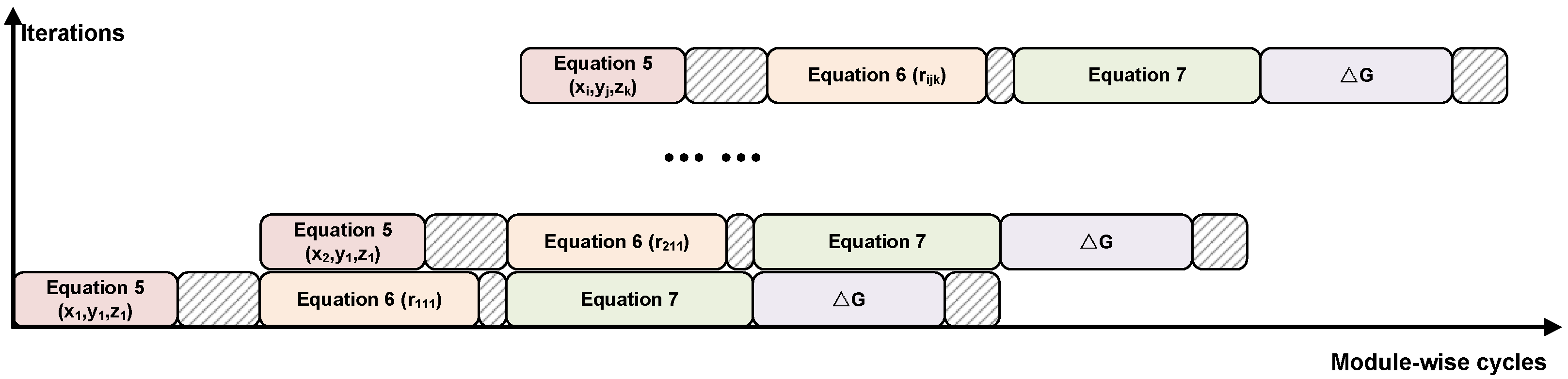
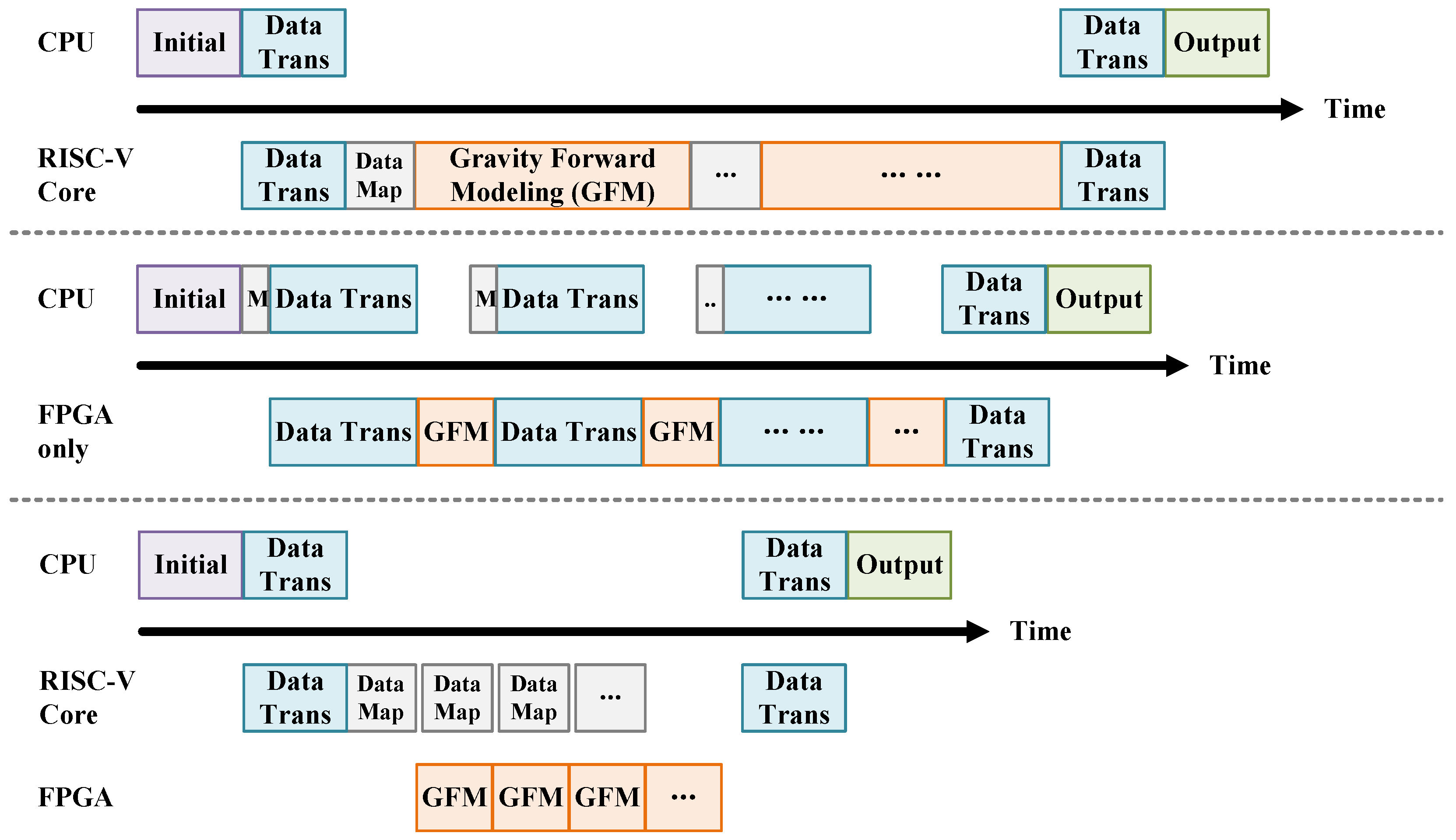
3.1. Parallelization Strategy
3.2. Customize RISC-V Extended Instruction Design
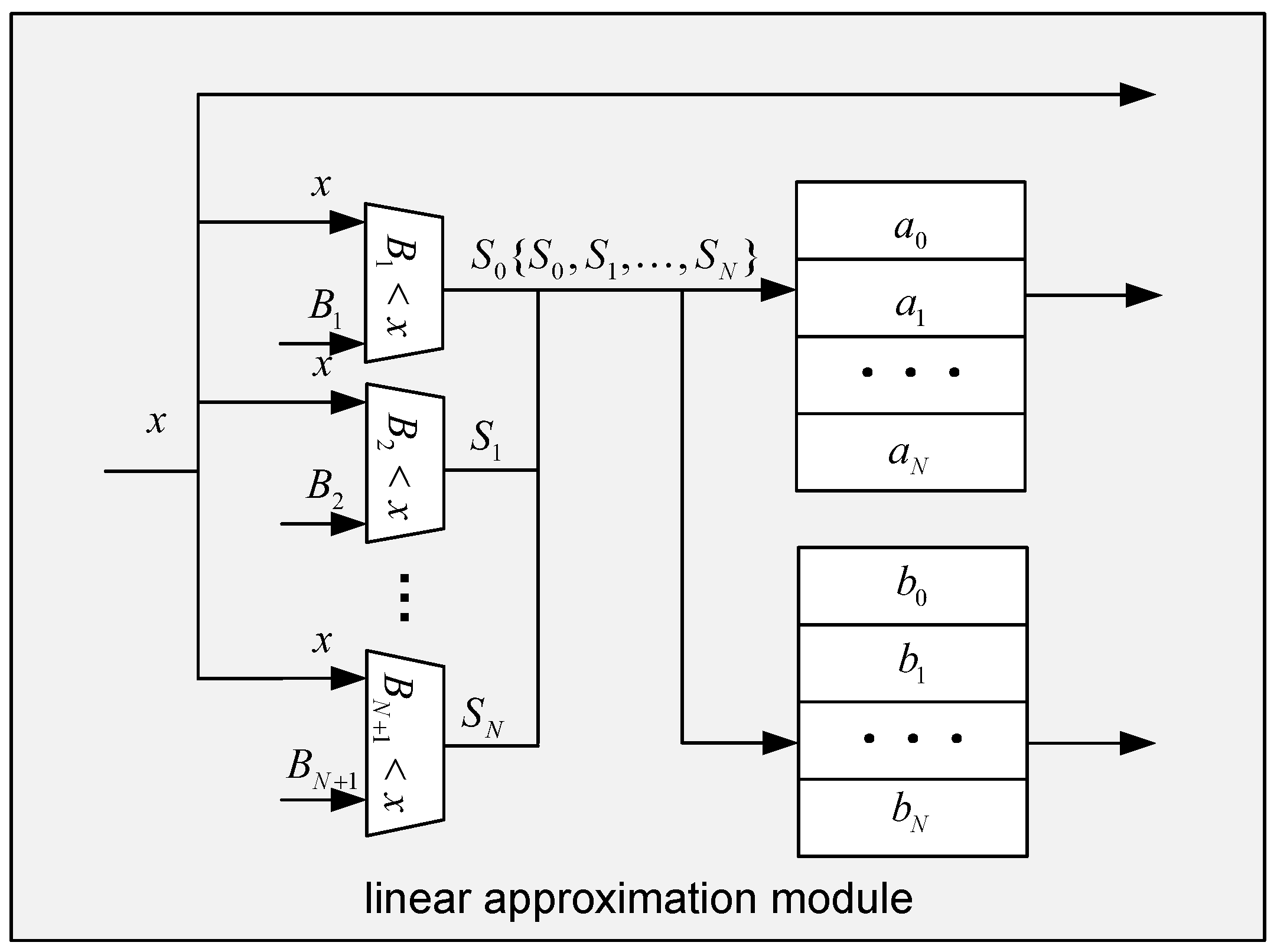
3.3. Hardware-Friendly Approximate Design
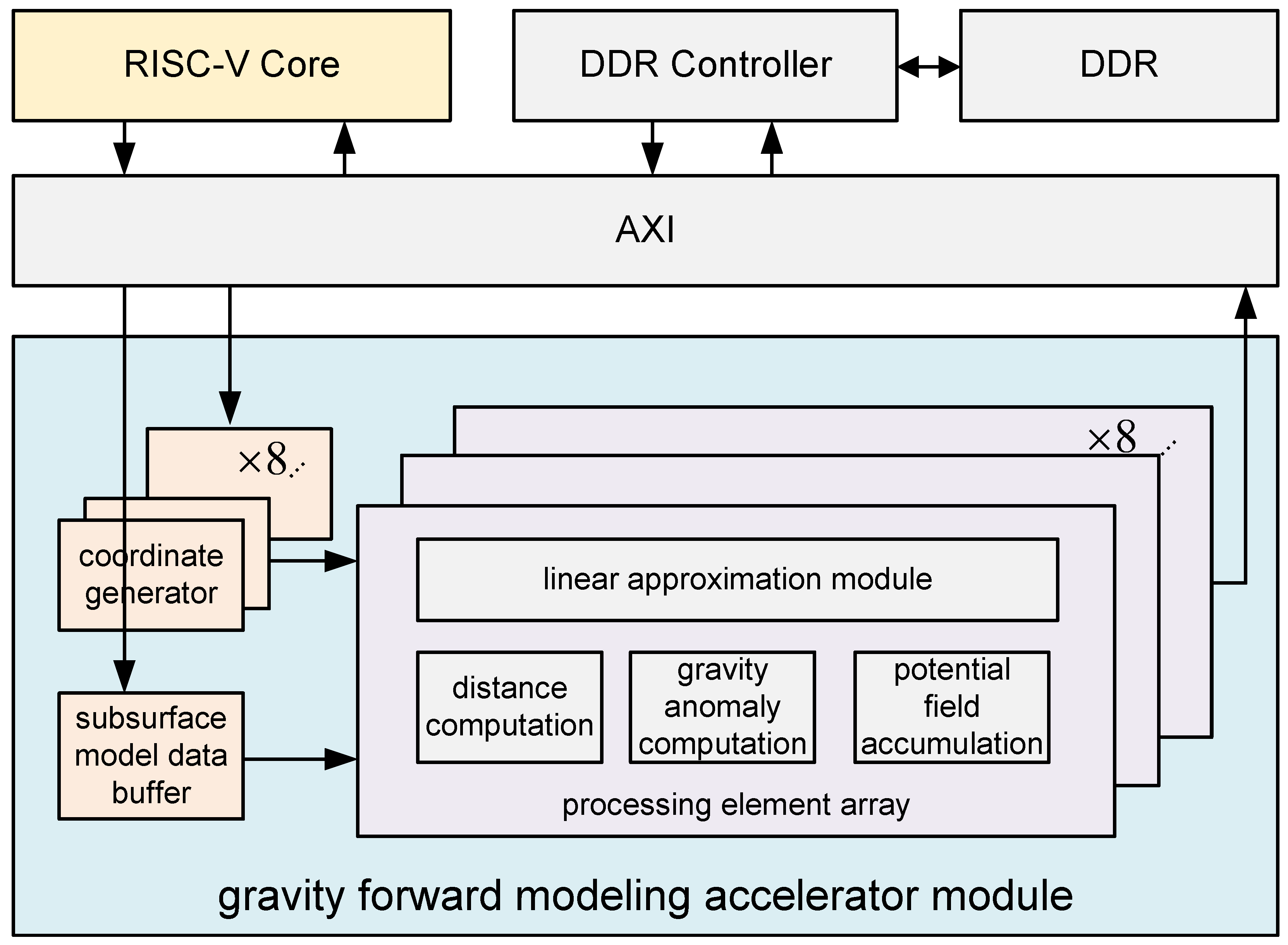
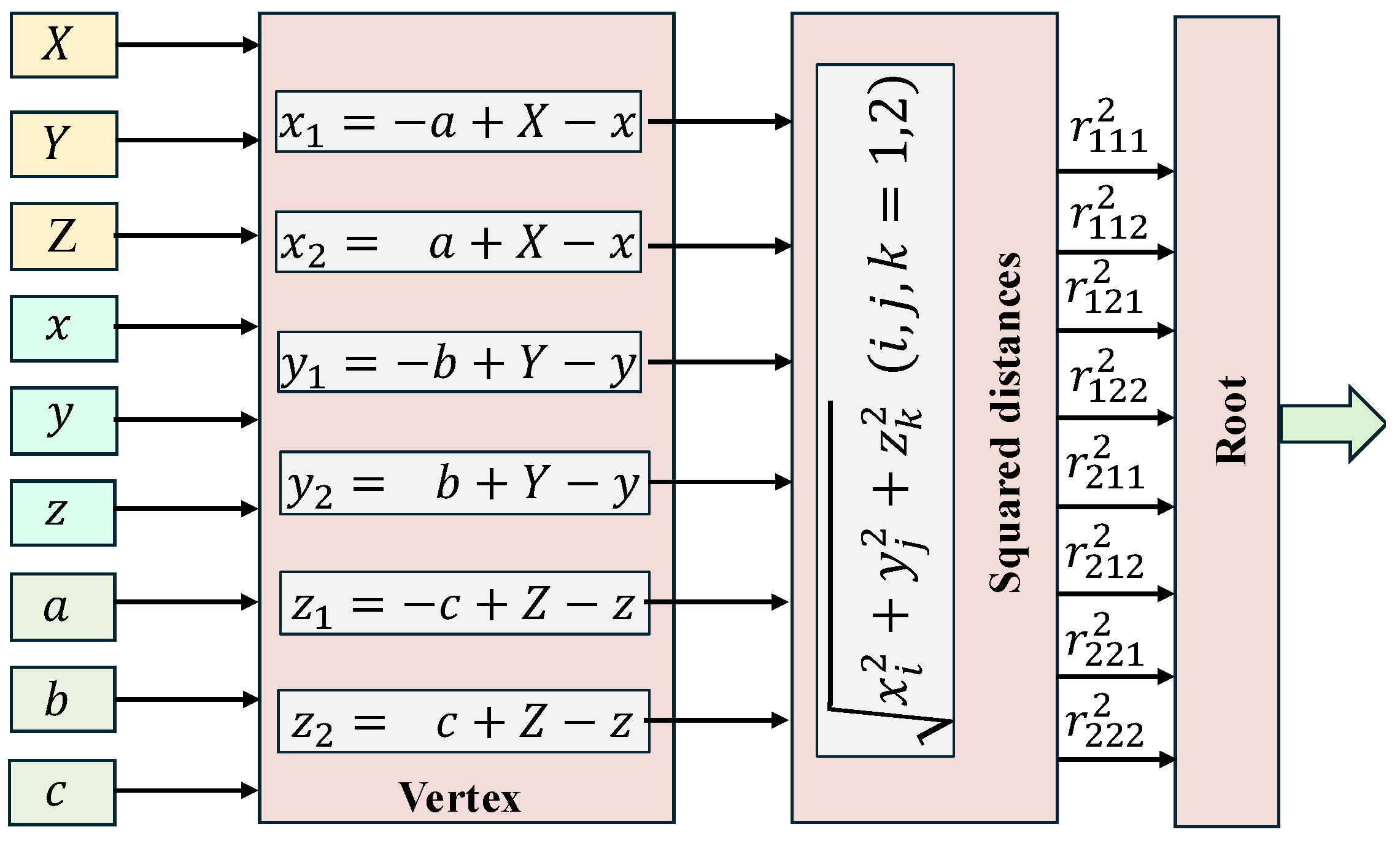
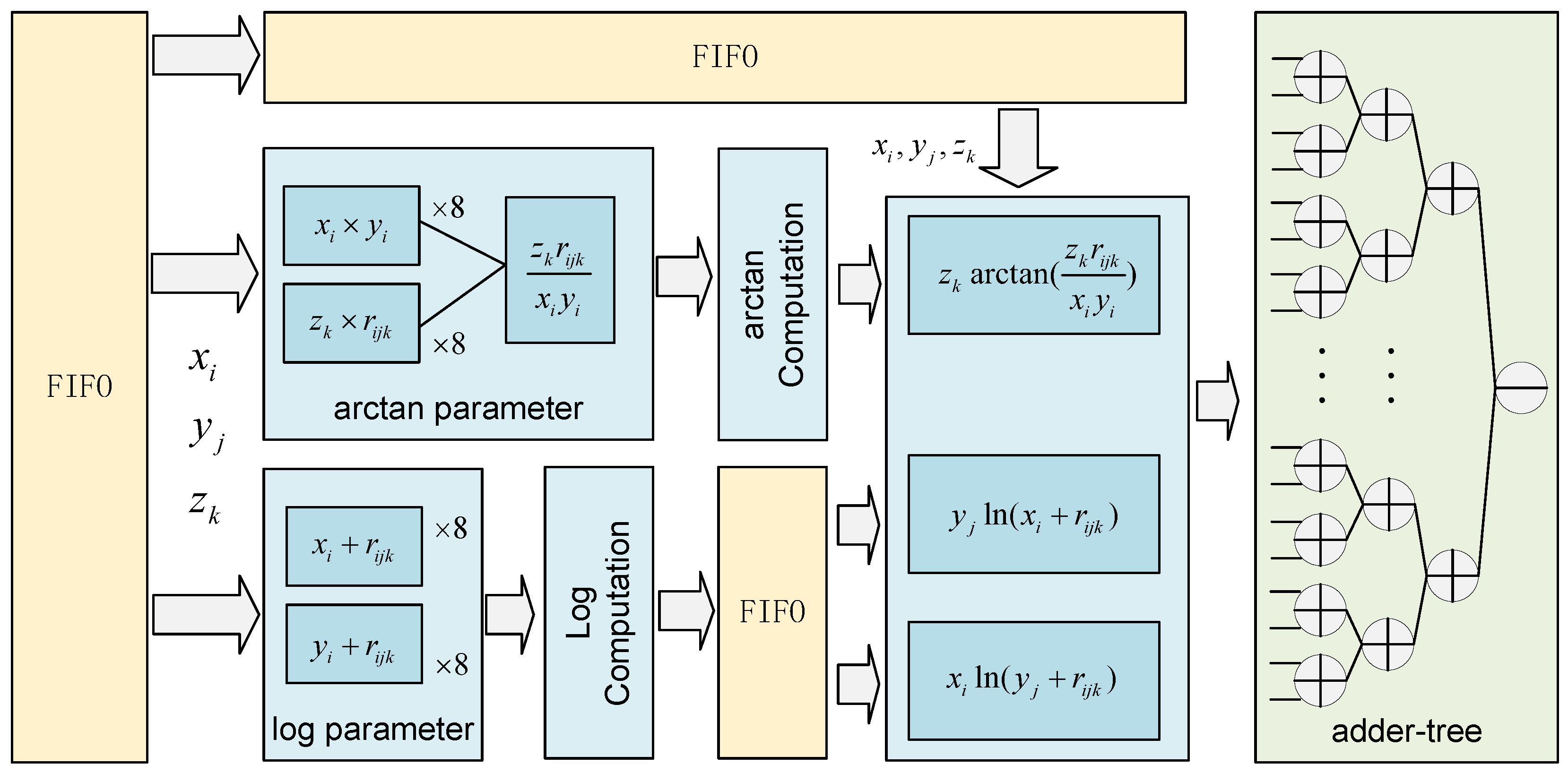
3.4. System Architecture
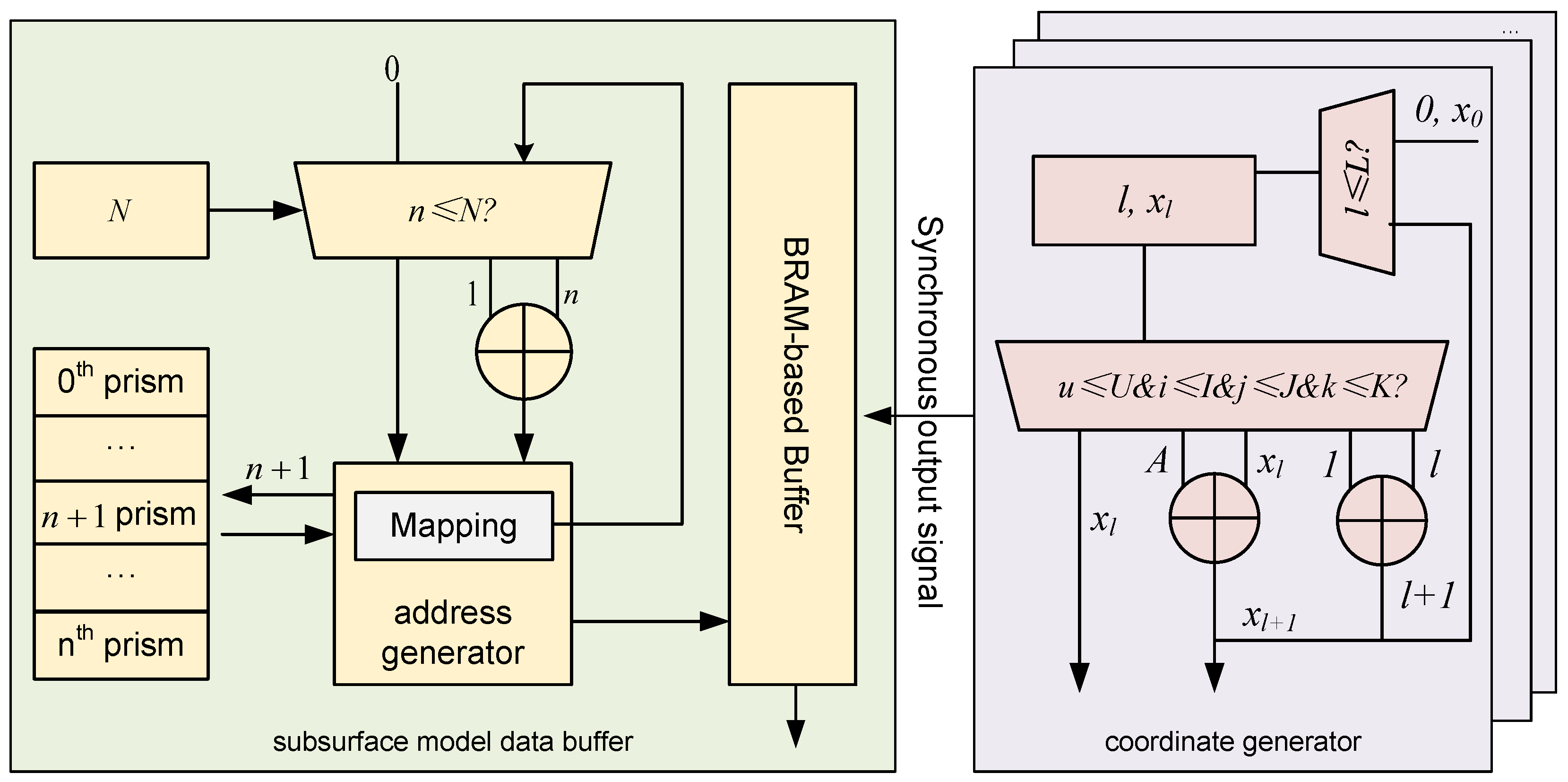
3.4.1. Microarchitecture of Subsurface Model Data Buffer & Coordinate Generator
3.4.2. Microarchitecture of PE Array
4. Results
4.1. Implementation Details
4.2. Experimental Setup
4.2.1. Benchmarks
4.2.2. Comparison Platforms
4.2.3. Evaluation Index
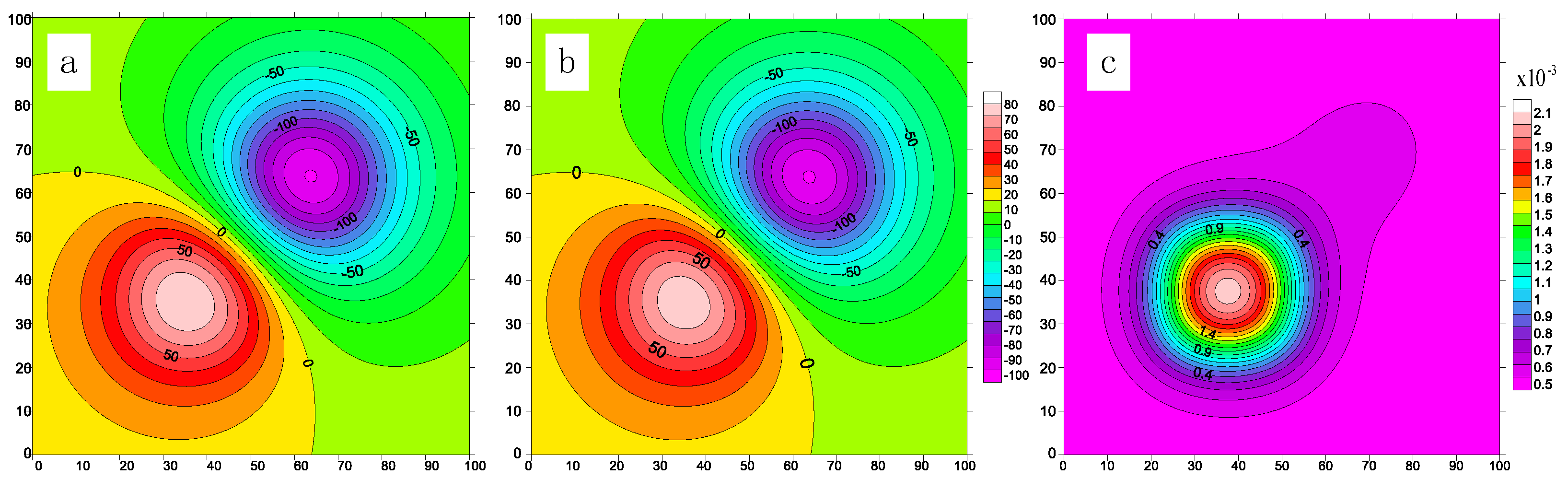
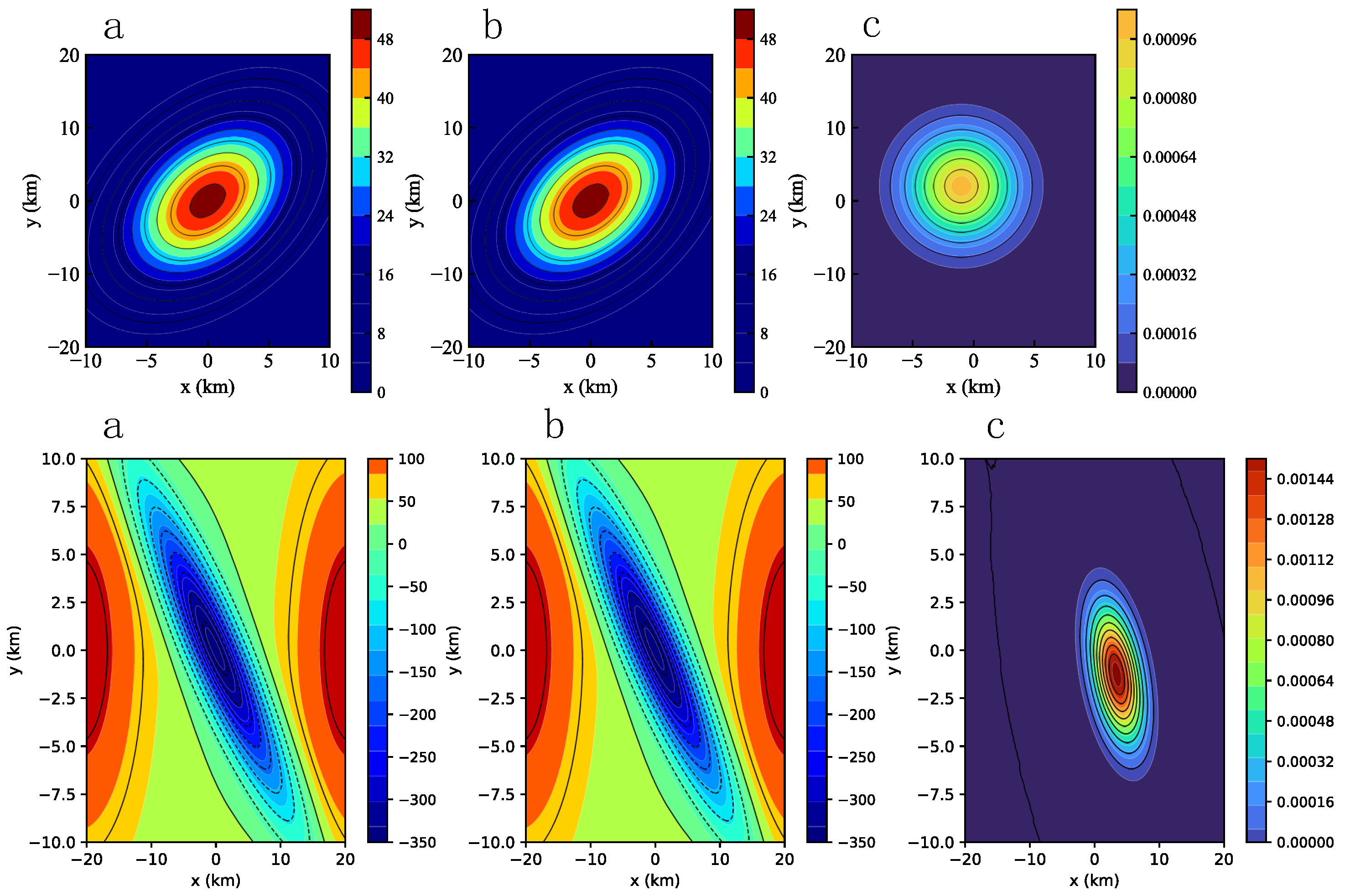
4.3. Accuracy Evaluation
4.4. Performance Evaluation
4.5. Ablation Study
5. Related Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AXI | Advanced eXtensible Interface |
| BRAM | Block RAM |
| CGS | Centimeter–Gram–Second (unit system) |
| CPU | Central Processing Unit |
| DDR | Double Data Rate (memory) |
| DSP | Digital Signal Processing slice |
| DSP48 | Xilinx DSP48 slice |
| FF | Flip-Flop |
| FIFO | First-In, First-Out (buffer) |
| FPGA | Field-Programmable Gate Array |
| GHz | Gigahertz |
| GOPS/W | Giga Operations Per Second per Watt |
| GPU | Graphics Processing Unit |
| HDL | Hardware Description Language |
| HPC | High-Performance Computing |
| ISA | Instruction Set Architecture |
| LUT | Look-Up Table |
| LUTRAM | Look-Up Table RAM |
| MHz | Megahertz |
| OpenMP | Open Multi-Processing |
| PE | Processing Element |
| RISC-V | Reduced Instruction Set Computer–Five |
| URAM | UltraRAM |
References
- Hinze, W.J.; Von Frese, R.; Saad, A.H. Gravity and Magnetic Exploration: Principles, Practices, and Applications; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Chaffaut, Q.; Lesparre, N.; Masson, F.; Hinderer, J.; Viville, D.; Bernard, J.D.; Ferhat, G.; Cotel, S. Hybrid gravimetry to map water storage dynamics in a mountain catchment. Front. Water 2022, 3, 715298. [Google Scholar] [CrossRef]
- Zhou, S.; Wei, Y.; Lu, P.; Yu, G.; Wang, S.; Jiao, J.; Yu, P.; Zhao, J. A deep learning gravity inversion method based on a self-constrained network and its application. Remote Sens. 2024, 16, 995. [Google Scholar] [CrossRef]
- Cui, Y.; Guo, L.; Li, J.; Zhao, S.; Shen, X. Spherical-Coordinate Algorithms for Gravity Forward Modeling and Iterative Inversion of Variable-density Interface: Application to Chinese Mainland Lithosphere. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5915719. [Google Scholar] [CrossRef]
- Prasetyo, N.; Firdaus, R.; Ekawati, G.M. 3D gravity forward modelling software in preparation. AIP Conf. Proc. 2023, 2623, 060002. [Google Scholar] [CrossRef]
- Zhu, D.X.; Dai, S.K.; Tian, H.J.; Chen, Q.R.; Zhao, W.X. Holographic approach for three-dimensional magnetotelluric modeling and CPU-GPU Parallel Architecture. Appl. Geophys. 2025, 1–18. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, G. Forward modeling of gravity anomalies based on cell mergence and parallel computing. Comput. Geosci. 2018, 120, 1–9. [Google Scholar] [CrossRef]
- Tan, X.; Wang, Q.; Feng, J.; Huang, Y.; Huang, Z. Fast modeling of gravity gradients from topographic surface data using GPU parallel algorithm. Geod. Geodyn. 2021, 12, 288–297. [Google Scholar] [CrossRef]
- Gunawan, I.; Alawiyah, S. Optimizing Gravity Forward Modeling through OpenMP Parallel Approach: A Case Study in Bawean Island. Indones. J. Comput. 2025, 10, 13–23. [Google Scholar]
- Liu, X.; Xu, W.; Wang, Q.; Zhang, M. Energy-efficient computing acceleration of unmanned aerial vehicles based on a cpu/fpga/npu heterogeneous system. IEEE Internet Things J. 2024, 11, 27126–27138. [Google Scholar] [CrossRef]
- Haan, S.; Ramos, F.; Dietmar Müller, R. Multiobjective Bayesian optimization and joint inversion for active sensor fusion. Geophysics 2020, 86, ID1–ID17. [Google Scholar] [CrossRef]
- Khan, U.; Khan, F.; Rabemaharitra, T.P.; Arsalan, M.; Abdulrahim, O.; Rahman, I.U. Surface and crustal study based on digital elevation modeling and 2-D gravity forward modeling in Thandiani to Boi areas of Hazara region, Pakistan. Earth 2020, 9, 130–142. [Google Scholar] [CrossRef]
- Cirstea, M.; Benkrid, K.; Dinu, A.; Ghiriti, R.; Petreus, D. Digital electronic system-on-chip design: Methodologies, tools, evolution, and trends. Micromachines 2024, 15, 247. [Google Scholar] [CrossRef]
- Zeng, S.; Liu, J.; Dai, G.; Yang, X.; Fu, T.; Wang, H.; Ma, W.; Sun, H.; Li, S.; Huang, Z.; et al. Flightllm: Efficient large language model inference with a complete mapping flow on fpgas. In Proceedings of the 2024 ACM/SIGDA International Symposium on Field Programmable Gate Arrays, Monterey, CA, USA, 3–5 March 2024; pp. 223–234. [Google Scholar]
- Chen, R.; Liu, J.; Tang, S.; Liu, Y.; Zhu, Y.; Ling, M.; Da Silva, B. ATE-GCN: An FPGA-Based Graph Convolutional Network Accelerator with Asymmetrical Ternary Quantization. In Proceedings of the 2025 Design, Automation & Test in Europe Conference (DATE), Lyon, France, 31 March–2 April 2025; pp. 1–6. [Google Scholar]
- Li, H.; Pang, Y. FPGA-accelerated quantum computing emulation and quantum key distillation. IEEE Micro 2021, 41, 49–57. [Google Scholar] [CrossRef]
- Lin, W.H.; Tan, B.; Niu, M.Y.; Kimko, J.; Cong, J. Domain-specific quantum architecture optimization. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 624–637. [Google Scholar] [CrossRef]
- Li, H.; Tang, Y.; Que, Z.; Zhang, J. FPGA accelerated post-quantum cryptography. IEEE Trans. Nanotechnol. 2022, 21, 685–691. [Google Scholar] [CrossRef]
- Song, L.; Chi, Y.; Sohrabizadeh, A.; Choi, Y.K.; Lau, J.; Cong, J. Sextans: A streaming accelerator for general-purpose sparse-matrix dense-matrix multiplication. In Proceedings of the 2022 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 3–5 March 2022; pp. 65–77. [Google Scholar]
- Liu, Y.; Chen, R.; Li, S.; Yang, J.; Li, S.; da Silva, B. FPGA-based sparse matrix multiplication accelerators: From state-of-the-art to future opportunities. ACM Trans. Reconfigurable Technol. Syst. 2024, 17, 1–37. [Google Scholar] [CrossRef]
- Ling, M.; Lin, Q.; Chen, R.; Qi, H.; Lin, M.; Zhu, Y.; Wu, J. Vina-FPGA: A hardware-accelerated molecular docking tool with fixed-point quantization and low-level parallelism. IEEE Trans. Very Large Scale Integr. Syst. 2022, 31, 484–497. [Google Scholar] [CrossRef]
- Wu, C.; Yang, C.; Bandara, S.; Geng, T.; Guo, A.; Haghi, P.; Li, A.; Herbordt, M. FPGA-accelerated range-limited molecular dynamics. IEEE Trans. Comput. 2024, 73, 1544–1558. [Google Scholar] [CrossRef]
- Li, X.; Chouteau, M. Three-dimensional gravity modeling in all space. Surv. Geophys. 1998, 19, 339–368. [Google Scholar] [CrossRef]
- Haáz, I.B. Relations between the potential of the attraction of the mass contained in a finite rectangular prism and its first and second derivatives. Geophys. Trans. II 1953, 7, 57–66. [Google Scholar]
- Chen, R.; Lyu, Y.; Bao, H.; Liu, J.; Zhu, Y.; Tang, S.; Ling, M.; Da Silva, B. FPGA-based Approximate Multiplier for FP8. In Proceedings of the 2025 IEEE 33rd Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Fayetteville, AR, USA, 4–7 May 2025; pp. 1–9. [Google Scholar]
- Tommiska, M.T. Efficient digital implementation of the sigmoid function for reprogrammable logic. IEE Proc. Comput. Digit. Tech. 2003, 150, 403–411. [Google Scholar] [CrossRef]
- Jokar, E.; Abolfathi, H.; Ahmadi, A. A novel nonlinear function evaluation approach for efficient FPGA mapping of neuron and synaptic plasticity models. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 454–469. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Li, Y.; Chen, R.; Li, S.; Yu, J.; Wang, K. DIF-LUT Pro: An Automated Tool for Simple yet Scalable Approximation of Nonlinear Activation on FPGA. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2025. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Liu, X.; Wilson, G.A.; Wan, L. Potential field migration for rapid imaging of gravity gradiometry data. Geophys. Prospect. 2011, 59, 1052–1071. [Google Scholar] [CrossRef]
- Cao, S.; Deng, Y.; Yang, B.; Lu, G.; Hu, X.; Mao, Y.; Hu, S.; Zhu, Z. Kernel density derivative estimation of Euler solutions. Appl. Sci. 2023, 13, 1784. [Google Scholar] [CrossRef]
- Wu, L. Modified Parker’s method for gravitational forward and inverse modeling using general polyhedral models. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022553. [Google Scholar] [CrossRef]
- Götze, H.J.; Lahmeyer, B. Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 1988, 53, 1096–1108. [Google Scholar] [CrossRef]
- NVIDIA. GeForce RTX 40 Series Laptops. Available online: https://www.nvidia.com/en-us/geforce/laptops/40-series/ (accessed on 30 August 2025).
- Ling, M.; Feng, Z.; Chen, R.; Shao, Y.; Tang, S.; Zhu, Y. Vina-FPGA-cluster: Multi-FPGA based molecular docking tool with high-accuracy and multi-level parallelism. IEEE Trans. Biomed. Circuits Syst. 2024, 18, 1321–1337. [Google Scholar] [CrossRef]
- Irfan, M.; Vipin, K.; Qureshi, R. Accelerating DNA sequence analysis using content-addressable memory in fpgas. In Proceedings of the 2023 IEEE 8th International Conference on Smart Cloud (SmartCloud), Tokyo, Japan, 16–18 September 2023; pp. 69–72. [Google Scholar]
- Pham-Quoc, C.; Kieu-Do, B.; Thinh, T.N. A high-performance fpga-based bwa-mem dna sequence alignment. Concurr. Comput. Pract. Exp. 2021, 33, e5328. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Chen, R.; da Silva, B.; Borca-Tasciuc, G.; Yu, D.; Hao, C. TrackGNN: A Highly Parallelized and Self-Adaptive GNN Accelerator for Track Reconstruction on FPGAs. In Proceedings of the 2025 IEEE 33rd Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Fayetteville, AR, USA, 4–7 May 2025; p. 269. [Google Scholar]
- Yuan, M.; Liu, Q.; Gan, L. An FPGA-based efficient accelerator for fault interaction of rupture dynamics. J. Supercomput. 2025, 81, 1323. [Google Scholar] [CrossRef]
- Chen, Y.; Zou, J.; Chen, X. April: Accuracy-Improved Floating-Point Approximation For Neural Network Accelerators. In Proceedings of the 2025 62nd ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 22–25 June 2025; pp. 1–7. [Google Scholar]
- Lyu, F.; Xia, Y.; Mao, Z.; Wang, Y.; Wang, Y.; Luo, Y. ML-PLAC: Multiplierless piecewise linear approximation for nonlinear function evaluation. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 1546–1559. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, X.; Xu, W.; Han, C.; Lyu, F.; Luo, Y.; Li, Y. An efficient hardware implementation for complex square root calculation using a pwl method. Electronics 2023, 12, 3012. [Google Scholar] [CrossRef]
- Yang, S.; Min, F.; Yang, X.; Ying, J. FPGA implementation of Hopfield neural network with transcendental nonlinearity. Nonlinear Dyn. 2024, 112, 20537–20548. [Google Scholar] [CrossRef]
- Xu, Z.; Yu, J.; Yu, C.; Shen, H.; Wang, Y.; Yang, H. CNN-based Feature-point Extraction for Real-time Visual SLAM on Embedded FPGA. In Proceedings of the 28th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Fayetteville, AR, USA, 3–6 May 2020; pp. 33–37. [Google Scholar]

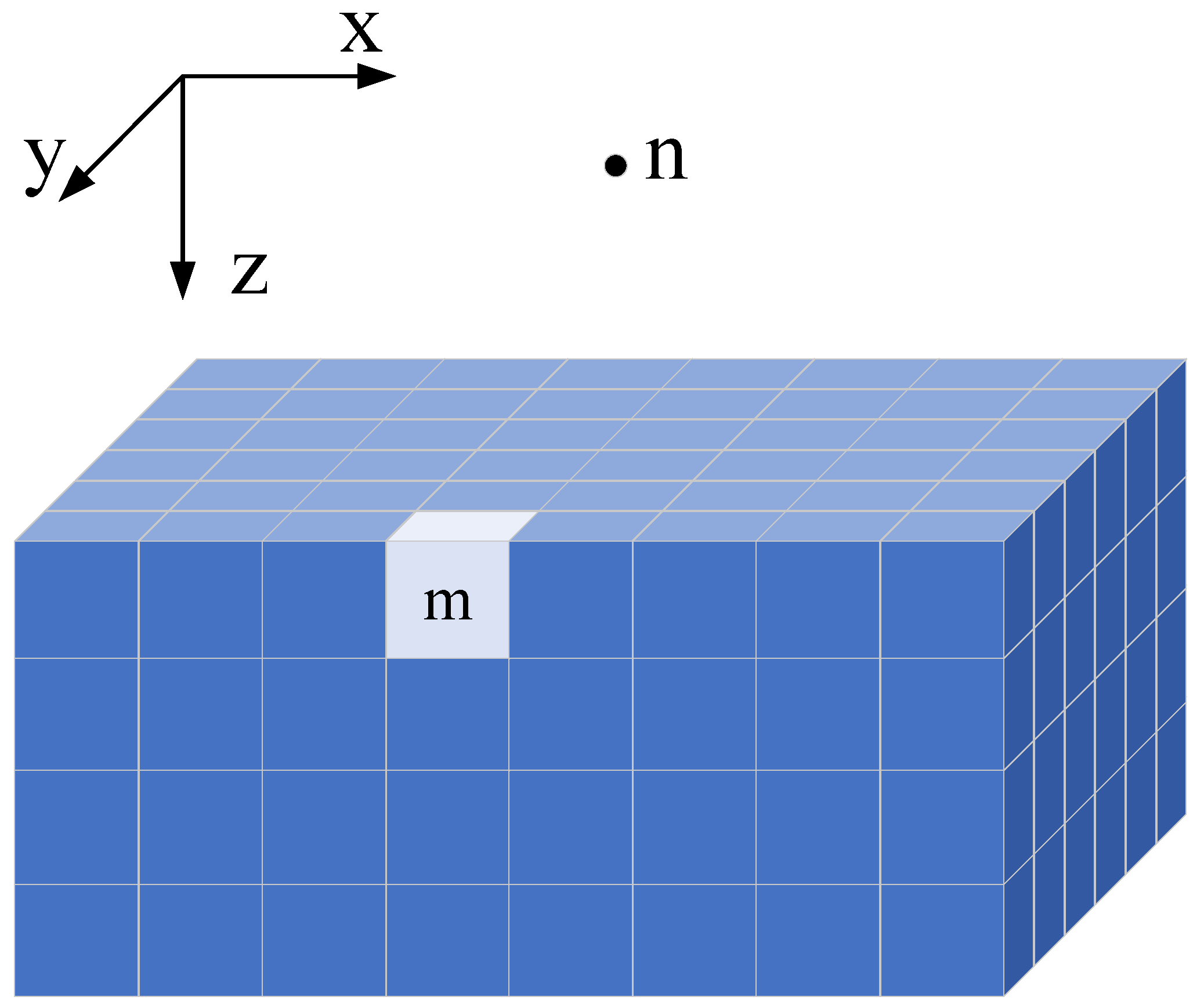



| funct7 (7 Bits) | RISC-V Register Mapping | Semantic Meaning (Original 4-Bit Opcode) |
|---|---|---|
| 0 × 0F (1111) | rs1 = a, rs2 = b, rd = c | Prism edge lengths (a, b, c) |
| 0 × 0E (1110) | rs1 = I, rs2 = J, rd = K | Grid dimensions along x, y, z (I, J, K) |
| 0 × 0C (1100) | rs1 = x0, rs2 = y0, rd = z0 | Grid starting coordinates (, , ) |
| 0 × 08 (1000) | rs1 = n, rd = | Prism ID (n) and density () |
| 0 × 00 (0000) | rs1 = N | Total number of model cells (N) |
| 0 × 01 (0001) | rs1 = X0, rs2 = Y0, rd = Z | Initial observation point (, , Z) |
| 0 × 02 (0010) | rs1 = A, rd = B | Grid spacing along x and y (A, B) |
| 0 × 04 (0100) | rs1 = L, rd = U | Number of observation points (L, U) |
| 0 × 7F (extended) | no operand | Start computation (START) |
| 0 × 7E (extended) | rd = status | Poll accelerator status (POLL) |
| 0 | |||
| 0 | |||
| 0 | 0 | ||
| 0 | 0 | ||
| 0 | 0 | ||
| 0 | 0 | ||
| 1 | 0 | 0 | |
| 0 | 0 | 1 |
| RISC-V | Coordinate Generator | Subsurface Data Buffer | PE Array | Others | Total | |
|---|---|---|---|---|---|---|
| LUT | 15,010 | 5126 | 2813 | 14,417 | 8332 | 45,698 (16.67%) |
| LUTRAM | 34 | 15 | 20 | 0 | 189 | 258 (0.18%) |
| FF | 5763 | 4842 | 4817 | 16,975 | 9913 | 42,310 (7.72%) |
| BRAM | 14.5 | 13.5 | 50.5 | 66 | 25.5 | 170 (18.64%) |
| DSP | 3 | 4 | 0 | 576 | 3 | 586 (23.25%) |
| Model | x Range | y Range | z Range | Density Contrast |
|---|---|---|---|---|
| Cube 1 | 25∼50 km | 25∼50 km | 12.6∼25.1 km | |
| Cube 2 | 50∼75 km | 5∼75 km | 12.6∼37.6 km |
| Platforms | Processor | Frequency | On-Chip Memory |
|---|---|---|---|
| HPC (CPU) | Xeon Gold 5218R | 4.0 GHz | 27.5 MB L3 cache |
| HP OMEN laptop (GPU) | GeForce RTX4070 Laptop GPU [33] | 1.39 GHz | 32 MB L2 cache |
| Zynq UltraScale+ ZCU102 | XCZU9EG | 250 MHz | 4.75 MB (BRAM + URAM) |
| Evaluation Index | HPC CPU (Baseline) | HP OMEN Laptop (GPU) | Ours | Improvement Over CPU | Improvement Over GPU | |
|---|---|---|---|---|---|---|
| Latency under different computational loads | 732 ms | 88.7 ms | 4.08 ms | 179.41× | 21.74× | |
| 63.96 s | 2.56 s | 0.42 s | 152.29× | 6.10× | ||
| 6436 s | 264.6 s | 40 s | 160.90× | 6.62× | ||
| Power (W) | 55.34 | 77.4 | 4.36 | 12.69× | 17.75× | |
| Energy efficiency (GOPS/W) | 28.09 | 488.56 | 57,304.60 | 2040.22× | 117.30× | |
| RISC-V Core Only | FPGA Only | RISC-V Core + FPGA | |
|---|---|---|---|
| Latency of communication (computational loads , , and ) | 16 ms, 82 ms, 205 ms | 1.67 s, 46.7 s, 5.4 min | 16 ms, 82 ms, 205 ms |
| Latency of computation (computational loads , , and ) | 56.6 s, 1.8 h, >5 days | 3.59 ms, 407.7 ms, 38.8 s | 4.08 ms, 420 ms, 40 s |
| End-to-end latency (computational loads , , and ) | 56.6 s, 1.8 h, >5 days | 1.67 s, 47.1 s, 6 min | 20.08 ms, 502 ms, 40.21 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Sun, D.; Ma, Z.; Gu, W. Domain-Specific Acceleration of Gravity Forward Modeling via Hardware–Software Co-Design. Micromachines 2025, 16, 1215. https://doi.org/10.3390/mi16111215
Yang Y, Sun D, Ma Z, Gu W. Domain-Specific Acceleration of Gravity Forward Modeling via Hardware–Software Co-Design. Micromachines. 2025; 16(11):1215. https://doi.org/10.3390/mi16111215
Chicago/Turabian StyleYang, Yong, Daying Sun, Zhiyuan Ma, and Wenhua Gu. 2025. "Domain-Specific Acceleration of Gravity Forward Modeling via Hardware–Software Co-Design" Micromachines 16, no. 11: 1215. https://doi.org/10.3390/mi16111215
APA StyleYang, Y., Sun, D., Ma, Z., & Gu, W. (2025). Domain-Specific Acceleration of Gravity Forward Modeling via Hardware–Software Co-Design. Micromachines, 16(11), 1215. https://doi.org/10.3390/mi16111215







