Reversibly Alterable Hot-Electron Photodetection Without Altering Working Wavelengths Through Phase-Change Material Sb2S3
Abstract
1. Introduction
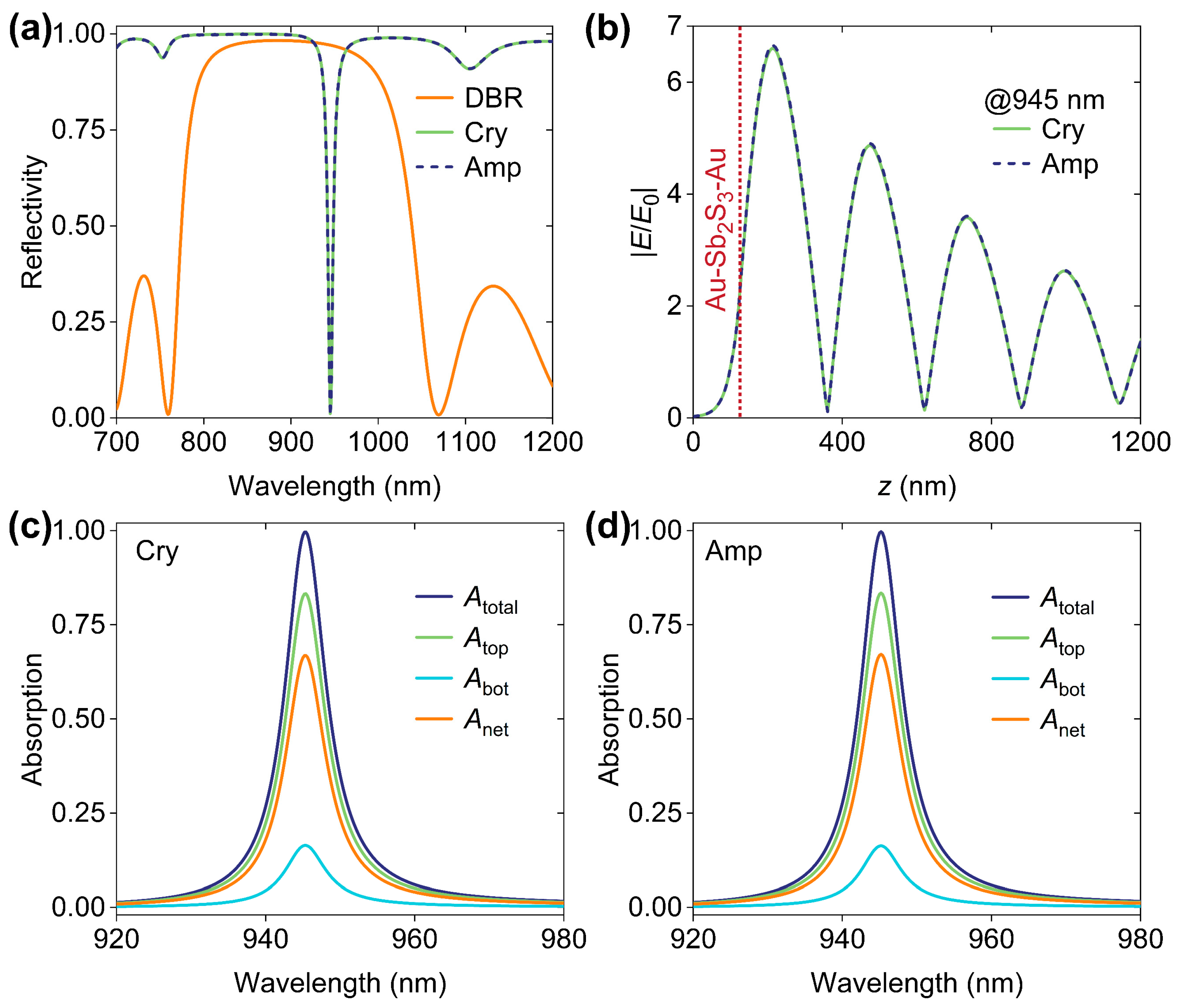
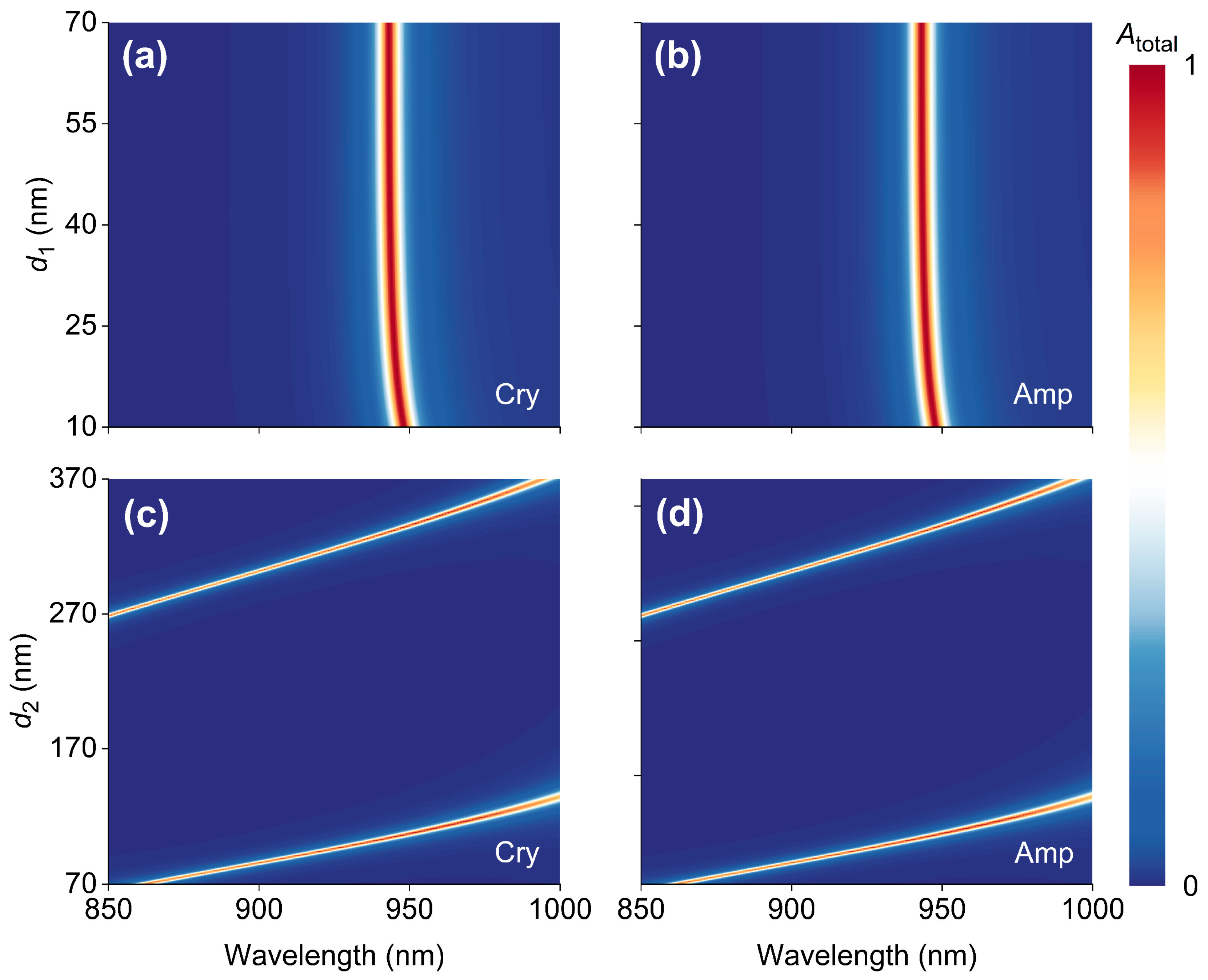
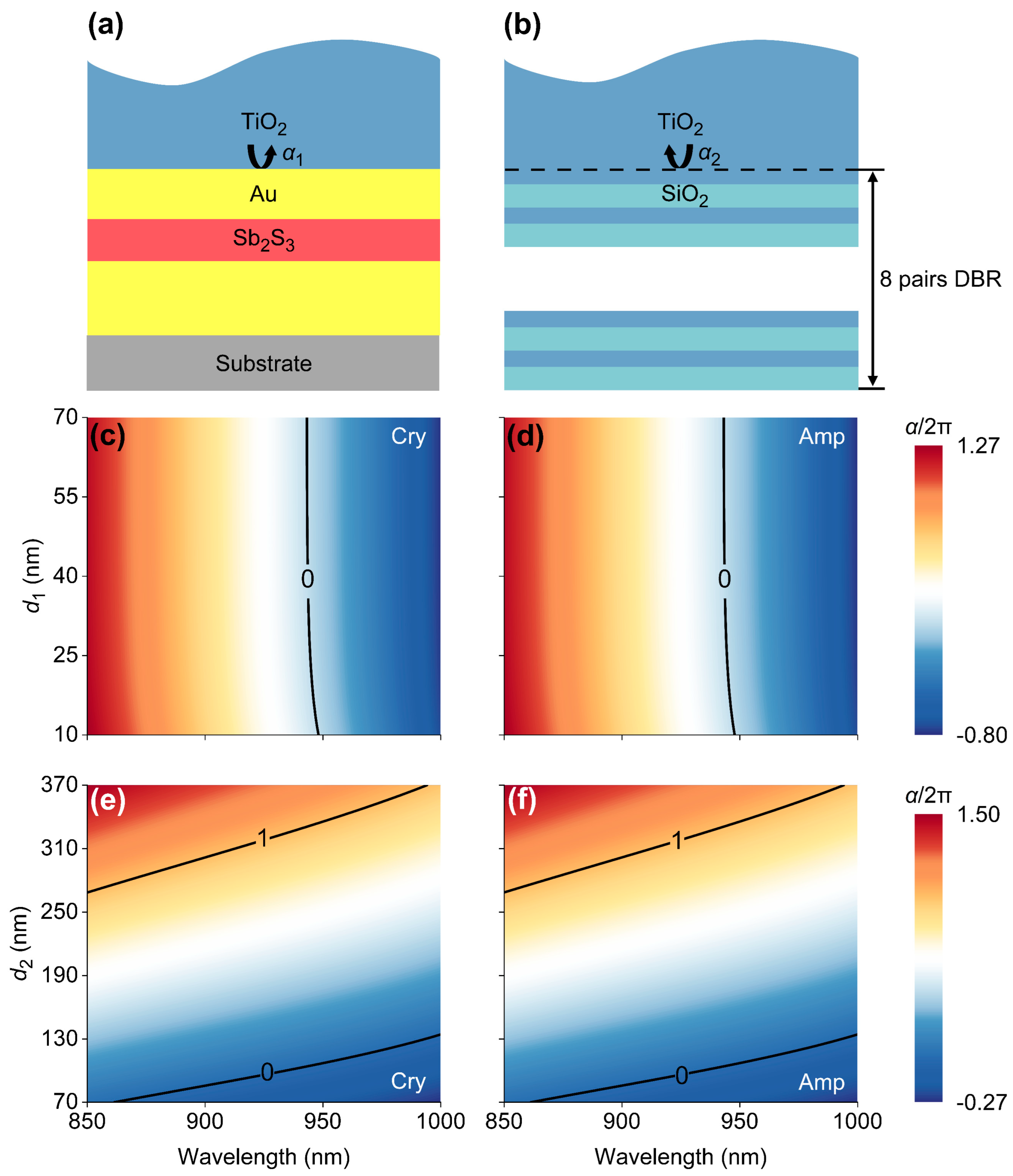
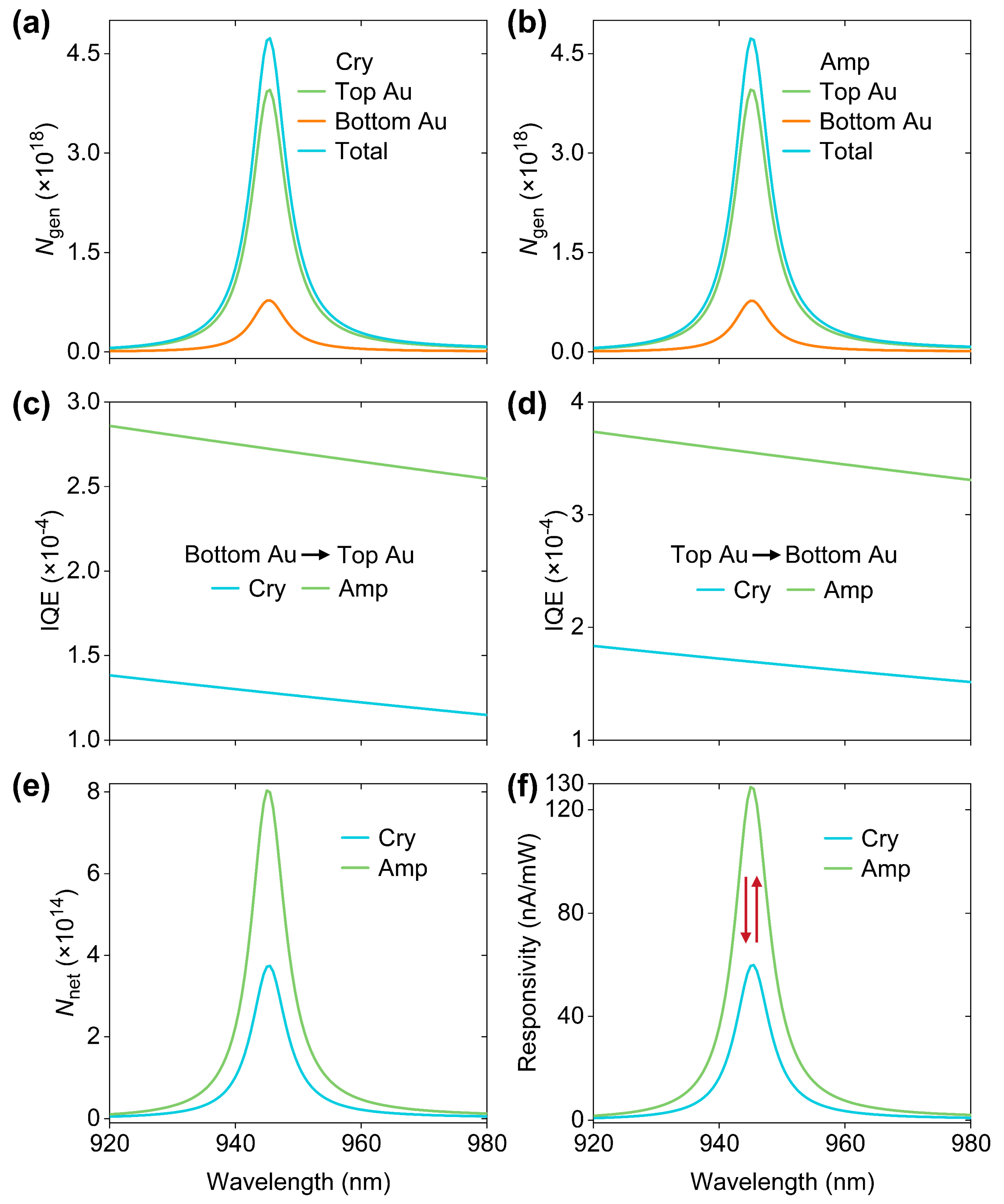
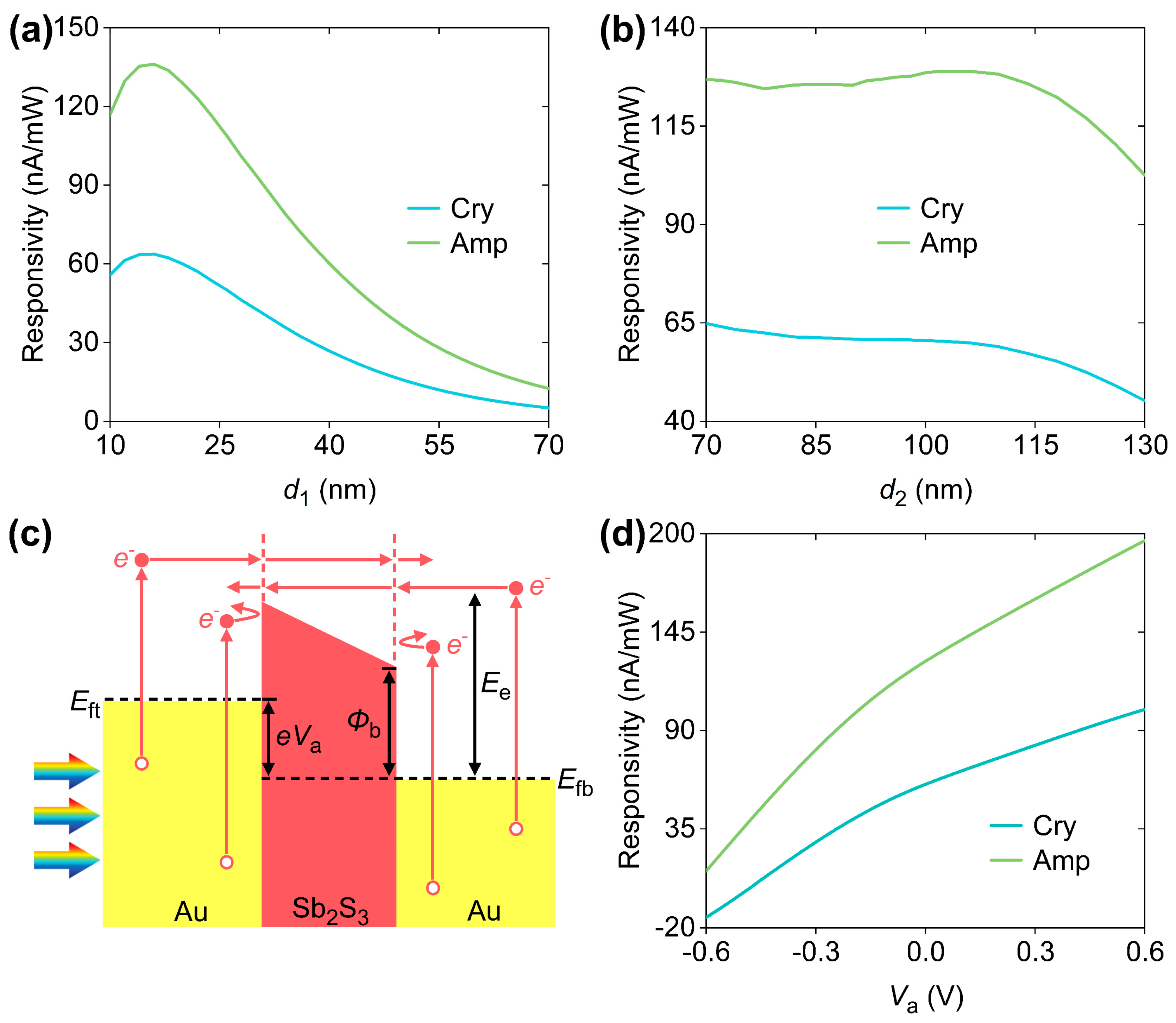
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leenheer, A.J.; Narang, P.; Lewis, N.S.; Atwater, H.A. Solar energy conversion via hot electron internal photoemission in metallic nanostructures: Efficiency estimates. J. Appl. Phys. 2014, 115, 134301. [Google Scholar] [CrossRef]
- Zhang, Y.; Yam, C.; Schatz, G.C. Fundamental limitations to plasmonic hot-carrier solar cells. J. Appl. Phys. 2016, 7, 1852–1858. [Google Scholar] [CrossRef] [PubMed]
- Mubeen, S.; Lee, J.; Singh, N.; Krämer, S.; Stucky, G.D.; Moskovits, M. An autonomous photosynthetic device in which all charge carriers derive from surface plasmons. Nat. Nanotechnol. 2013, 8, 247–251. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Kim, J.M.; Park, W.; Lee, H.; Lee, G.R.; Jung, Y.; Jung, Y.S.; Park, J.Y. Controlling hot electron flux and catalytic selectivity with nanoscale metal-oxide interfaces. Nat. Commun. 2021, 12, 40. [Google Scholar] [CrossRef]
- Tagliabue, G.; Jermyn, A.S.; Sundararaman, R.; Welch, A.J.; DuChene, J.S.; Pala, R.; Davoyan, A.R.; Narang, P.; Atwater, H.A. Quantifying the role of surface plasmon excitation and hot carrier transport in plasmonic devices. Nat. Commun. 2018, 9, 3394. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Besteiro, L.V.; Yu, P.; Lin, F.; Govorov, A.O.; Xu, H.; Wang, Z. Plasmonic hot-electron photodetection with quasi-bound states in the continuum and guided resonances. Nanophotonics 2021, 10, 1911–1921. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, K.; Giannini, V.; Li, X. Planar hot-electron photodetection with Tamm plasmons. ACS Nano 2017, 11, 1719–1727. [Google Scholar] [CrossRef]
- Reddy, H.; Wang, K.; Kudyshev, Z.; Zhu, L.; Yan, S.; Vezzoli, A.; Higgins, S.J.; Gavini, V.; Boltasseva, A.; Reddy, P.; et al. Determining plasmonic hot-carrier energy distributions via single-molecule transport measurements. Science. 2020, 369, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Schirato, A.; Maiuri, M.; Cerullo, G.; Della Valle, G. Ultrafast hot electron dynamics in plasmonic nanostructures: Experiments, modelling, design. Nanophotonics 2023, 12, 1–28. [Google Scholar] [CrossRef]
- Knight, M.W.; Wang, Y.; Urban, A.S.; Sobhani, A.; Zheng, B.Y.; Nordlander, P.; Halas, N.J. Embedding plasmonic nanostructure diodes enhances hot electron emission. Nano Lett. 2013, 13, 1687–1692. [Google Scholar] [CrossRef]
- Chalabi, H.; Schoen, D.; Brongersma, M.L. Hot-electron photodetection with a plasmonic nanostripe antenna. Nano Lett. 2014, 14, 1374–1380. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Valentine, J. Metamaterial perfect absorber based hot electron photodetection. Nano Lett. 2014, 14, 3510–3514. [Google Scholar] [CrossRef] [PubMed]
- Ratchford, D.C.; Dunkelberger, A.D.; Vurgaftman, I.; Owrutsky, J.C.; Pehrsson, P.E. Quantification of efficient plasmonic hot-electron injection in gold nanoparticle−TiO2 films. Nano Lett. 2017, 17, 6047–6055. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Li, F.; Wu, H.; Liu, W. Suppression of gap plasmon resonance for high-responsivity metal–insulator–metal near-infrared hot-electron photodetectors. Opt. Lett. 2022, 47, 42–45. [Google Scholar] [CrossRef]
- Hu, X.-L.; Wu, H.-L.; Tang, L.-Y.; Zhang, J.; Liu, W.-J. High-responsivity dual-frequency hot-electron photodetectors with magnetic polaritons beneath metal grating strips. J. Phys. D Appl. Phys. 2023, 56, 125101. [Google Scholar] [CrossRef]
- Hu, X.-L.; Li, F.; Xu, S.-H.; Liu, W.-J. Design of a binary metal micron grating and its application in near-infrared hot-electron photodetectors. Opt. Lett. 2023, 48, 4033–4036. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Wu, K.; Zhang, C.; Wu, S.; Li, X. Infrared hot-carrier photodetection based on planar perfect absorber. Opt. Lett. 2015, 40, 4261–4264. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wu, K.; Zhan, Y.; Giannini, V.; Li, X. Planar microcavity-integrated hot-electron photodetector. Nanoscale 2016, 8, 10323–10329. [Google Scholar] [CrossRef]
- Shao, W.; Yang, Q.; Zhang, C.; Wu, S.; Li, X. Planar dual-cavity hot-electron photodetectors. Nanoscale 2019, 11, 1396–1402. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, C.; Liu, H.; Liu, J.; Li, K.; Qin, L.; Wu, S.; Li, X. Planar, narrowband, and tunable photodetection in the near-infrared with Au/TiO2 nanodiodes based on Tamm plasmons. Nanoscale 2020, 11, 23182–23187. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Yu, P.; Liu, T.; Xu, H.; Govorov, A.O.; Wang, Z. Nanolayered Tamm plasmon-based multicolor hot electron photodetection for O- and C-band telecommunication. ACS Appl. Electron. Mater. 2021, 3, 639–650. [Google Scholar] [CrossRef]
- Shao, W.; Cui, W.; Hu, J.; Wang, Y.; Tang, J.; Li, X. Planar hot-electron photodetection with polarity-switchable photocurrents controlled by the working wavelength. Opt. Express 2023, 31, 25220–25229. [Google Scholar] [CrossRef] [PubMed]
- Krayer, L.J.; Tennyson, E.M.; Leite, M.S.; Munday, J.N. Near-IR imaging based on hot carrier generation in nanometer-scale optical coatings. ACS Photonics 2018, 5, 306–311. [Google Scholar] [CrossRef]
- Krayer, L.J.; Kim, J.; Garrett, J.L.; Munday, J.N. Optoelectronic devices on index-near-zero substrates. ACS Photonics 2019, 6, 2238–2244. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.; Li, L.; Wu, S.; Wang, C.; Li, X. Planar dual-layer system for ultra-broadband absorption and hot-carrier photodetection in longwave near-Infrared band. IEEE J. Sel. Top. Quant. Electron. 2022, 28, 3800109. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Y.; Wang, W.; Li, Y.; Gao, R.; Yu, P.; Xu, H.; Wang, Z. Broadband Tamm plasmon-enhanced planar hot-electron photodetector. Nanoscale 2020, 12, 23945–23952. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Xiao, Z.; Xu, H.; Deng, H.; Li, H.; Chen, W.; Liu, Z.; Long, Y. Ultranarrow-bandwidth planar hot electron photodetector based on coupled dual Tamm plasmons. Opt. Express 2020, 28, 31330–31344. [Google Scholar] [CrossRef]
- Gong, T.; Munday, J.N. Materials for hot carrier plasmonics. Opt. Mater. Express 2015, 5, 2501–2512. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, G.; Wu, S.; Shao, W.; Giannini, V.; Maier, S.A.; Li, X. Thermodynamic loss mechanisms and strategies for efficient hot-electron photoconversion. Nano Energy 2019, 55, 164–172. [Google Scholar] [CrossRef]
- Jin, Y.; Seok, J.; Yu, K. Highly efficient silicon-based thin-film Schottky barrier photodetectors. ACS Photonics 2023, 10, 1302–1309. [Google Scholar] [CrossRef]
- Zheng, J.-R.; You, E.-M.; Hu, Y.-F.; Yi, J.; Tian, Z.-Q. Ultrabroadband hot-hole photodetector based on ultrathin gold film. Nanoscale 2023, 15, 8863–8869. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Yu, P.; Ashalley, E.; Liu, T.; Lin, F.; Ji, H.; Takahara, J.; Govorov, A.; Wang, Z. Planar hot-electron photodetector utilizing high refractive index MoS2 in Fabry–Pérot perfect absorber. Nanotechnology 2020, 31, 274001. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wang, Y.; Li, Y.; Cui, W.; Hu, J.; Zhou, Q.; Shao, W. High-performance planar broadband hot-electron photodetection through platinum–dielectric triple junctions. Nanomaterials 2024, 14, 1552. [Google Scholar] [CrossRef]
- Chamoli, S.K.; Verma, G.; Singh, S.C.; Guo, C. Phase change material based hot electron photodetection. Nanoscale 2021, 13, 1311–1317. [Google Scholar] [CrossRef] [PubMed]
- Santos, G.; Georghe, M.; Cobianu, C.; Modreanu, M.; Losurdo, M.; Gutiérrez, Y.; Moreno, F. Plasmonic hot-electron reconfigurable photodetector based on phase-change material Sb2S3. Opt. Express 2022, 30, 38953–38965. [Google Scholar] [CrossRef]
- Narang, P.; Sundararaman, R.; Atwater, H.A. Plasmonic hot carrier dynamics in solid-state and chemical systems for energy conversion. Nanophotonics 2016, 5, 96–111. [Google Scholar] [CrossRef]
- Rao, C.; Zhong, L.; Guo, Y.; Li, M.; Zhang, L.; Wei, K. Astronomical adaptive optics: A review. PhotoniX 2024, 5, 16. [Google Scholar] [CrossRef]
- Sun, J.; Kuschmierz, R.; Katz, O.; Koukourakis, N.; Czarske, J.W. Lensless fiber endomicroscopy in biomedicine. PhotoniX 2024, 5, 18. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, X.; Hao, J.; Hu, J.; Zhou, Q.; Shao, W. Reversibly Alterable Hot-Electron Photodetection Without Altering Working Wavelengths Through Phase-Change Material Sb2S3. Micromachines 2025, 16, 146. https://doi.org/10.3390/mi16020146
Li Y, Yang X, Hao J, Hu J, Zhou Q, Shao W. Reversibly Alterable Hot-Electron Photodetection Without Altering Working Wavelengths Through Phase-Change Material Sb2S3. Micromachines. 2025; 16(2):146. https://doi.org/10.3390/mi16020146
Chicago/Turabian StyleLi, Yaoyao, Xiaoyan Yang, Jia Hao, Junhui Hu, Qingjia Zhou, and Weijia Shao. 2025. "Reversibly Alterable Hot-Electron Photodetection Without Altering Working Wavelengths Through Phase-Change Material Sb2S3" Micromachines 16, no. 2: 146. https://doi.org/10.3390/mi16020146
APA StyleLi, Y., Yang, X., Hao, J., Hu, J., Zhou, Q., & Shao, W. (2025). Reversibly Alterable Hot-Electron Photodetection Without Altering Working Wavelengths Through Phase-Change Material Sb2S3. Micromachines, 16(2), 146. https://doi.org/10.3390/mi16020146






