Predicting Thermal Resistance of Packaging Design by Machine Learning Models
Abstract
:1. Introduction
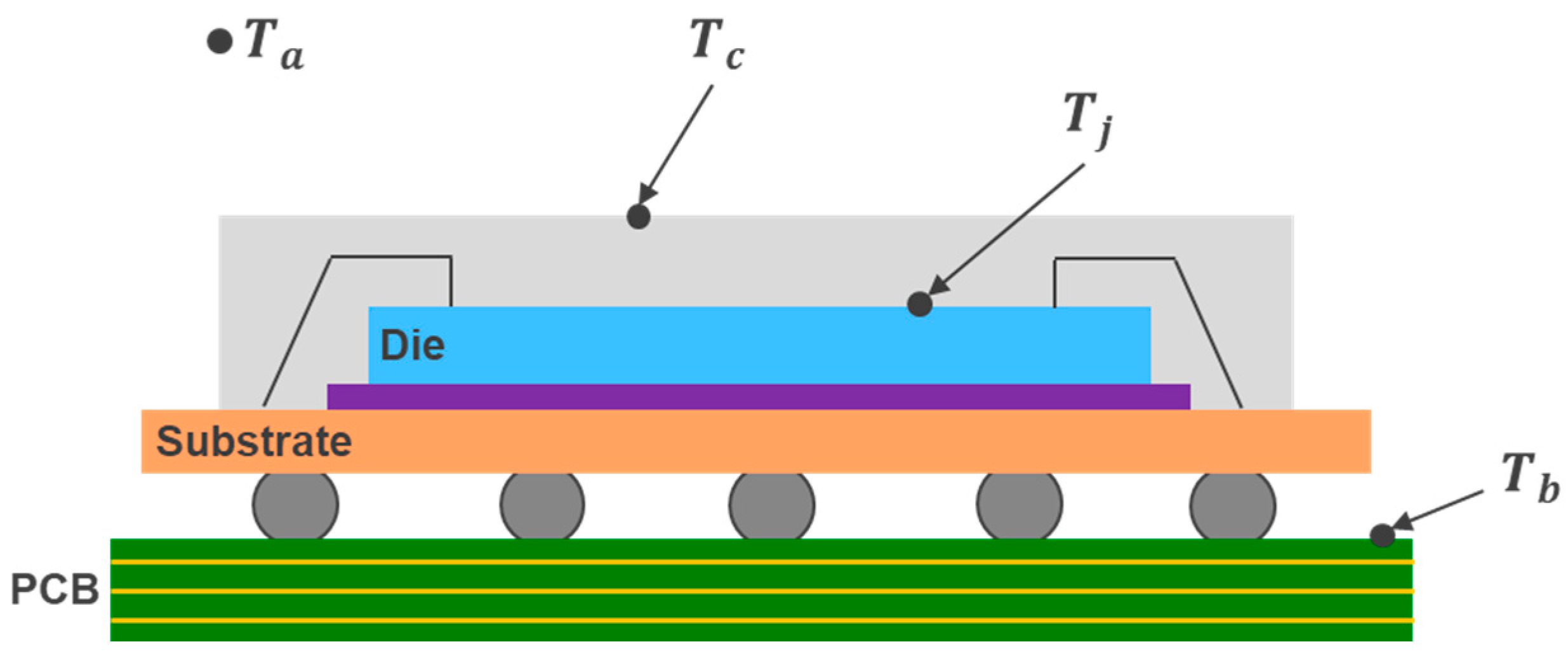
2. Thermal Resistance of IC Package
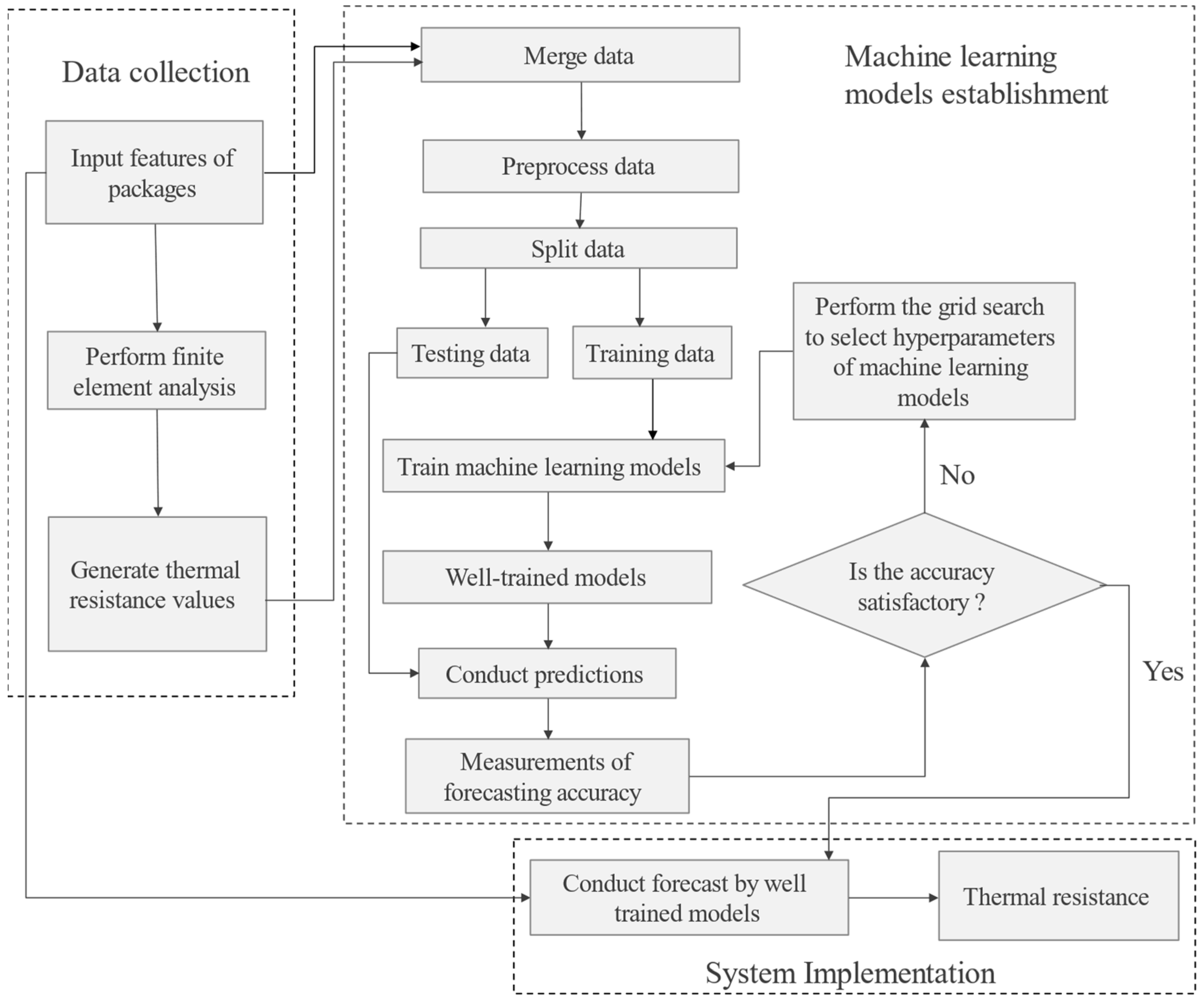
3. Machine Learning in Predicting Thermal Resistance (MLPTR) Model
3.1. Machine Learning Models for Regression
3.2. Machine Learning Architecture for Thermal Resistance Prediction
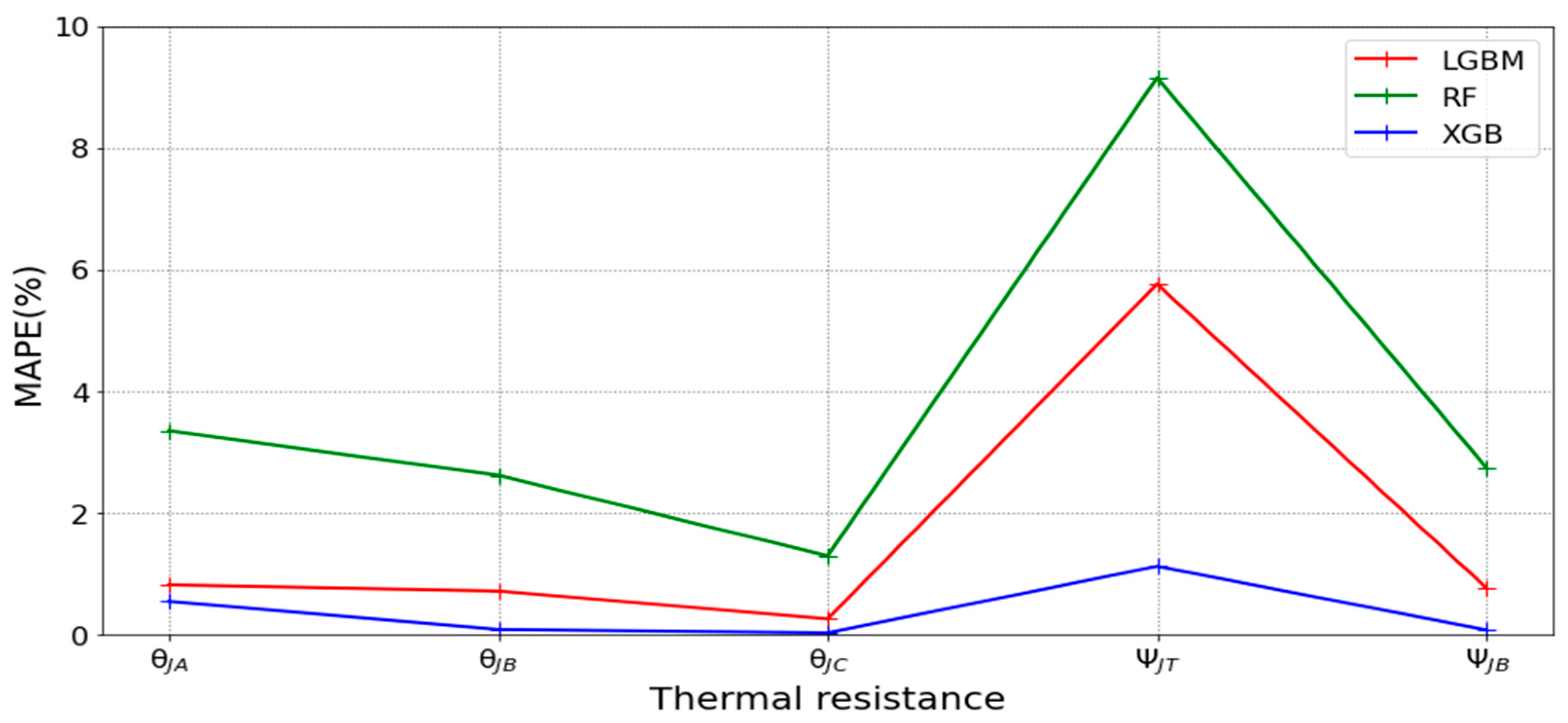
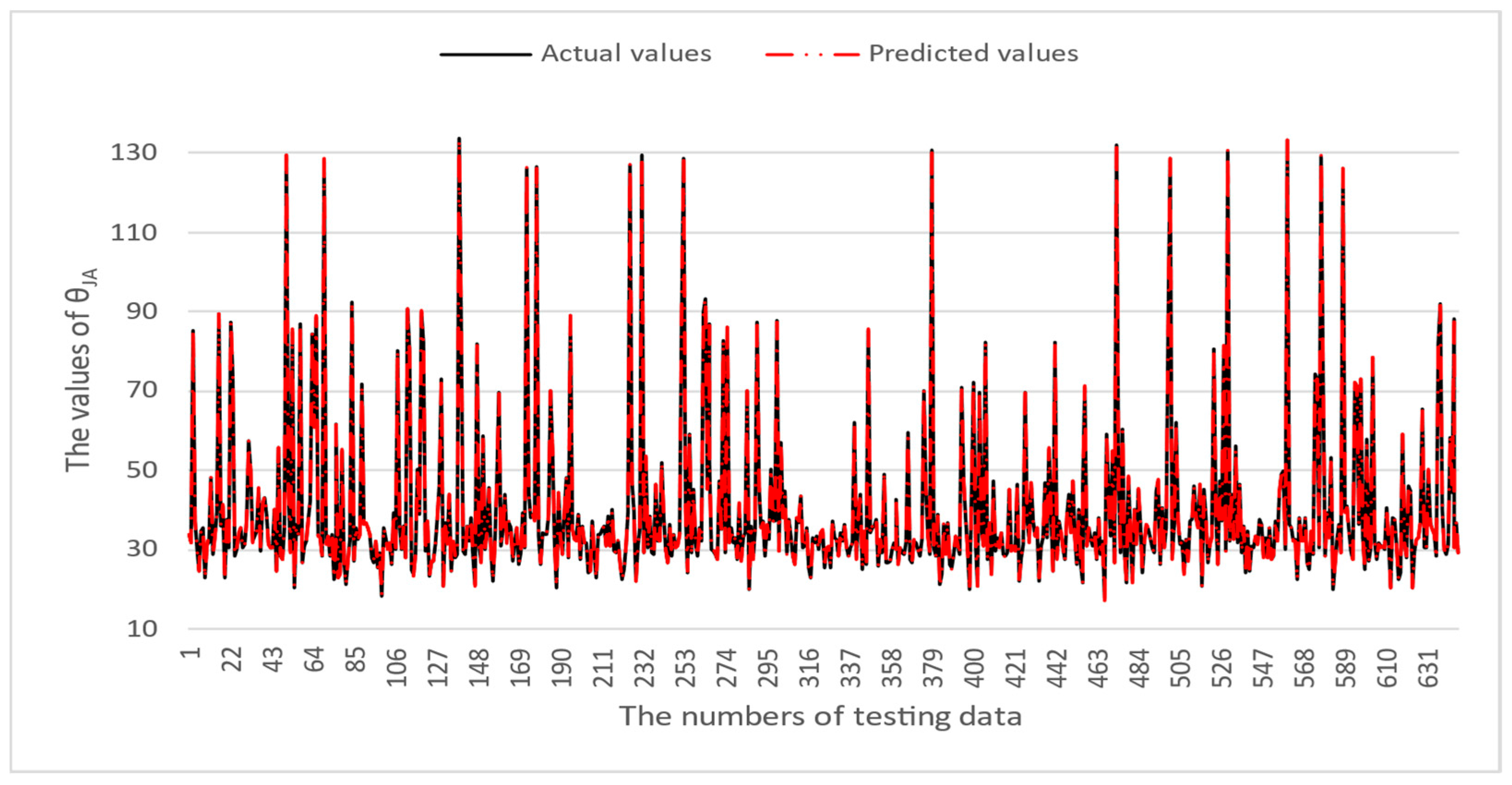
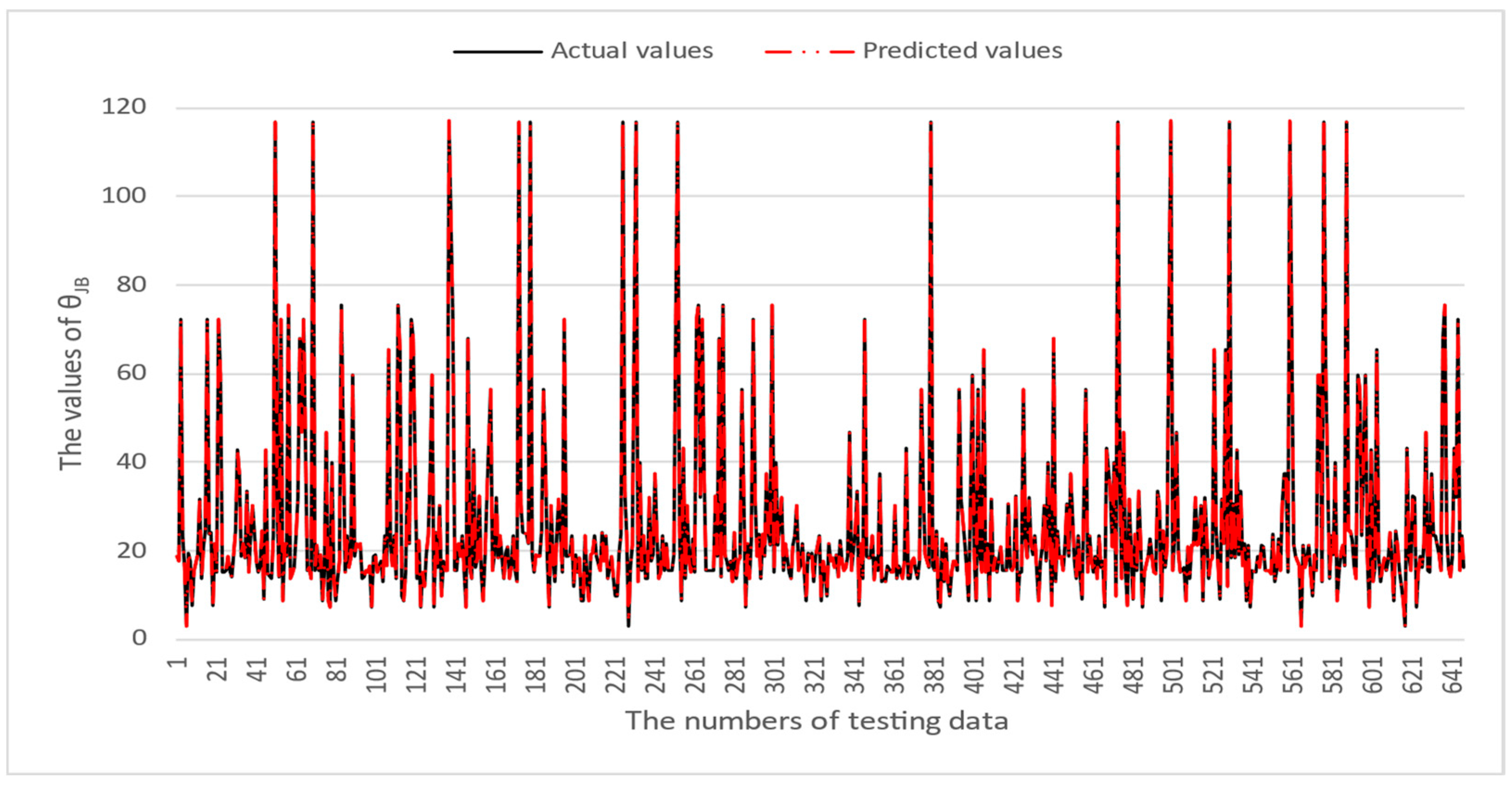
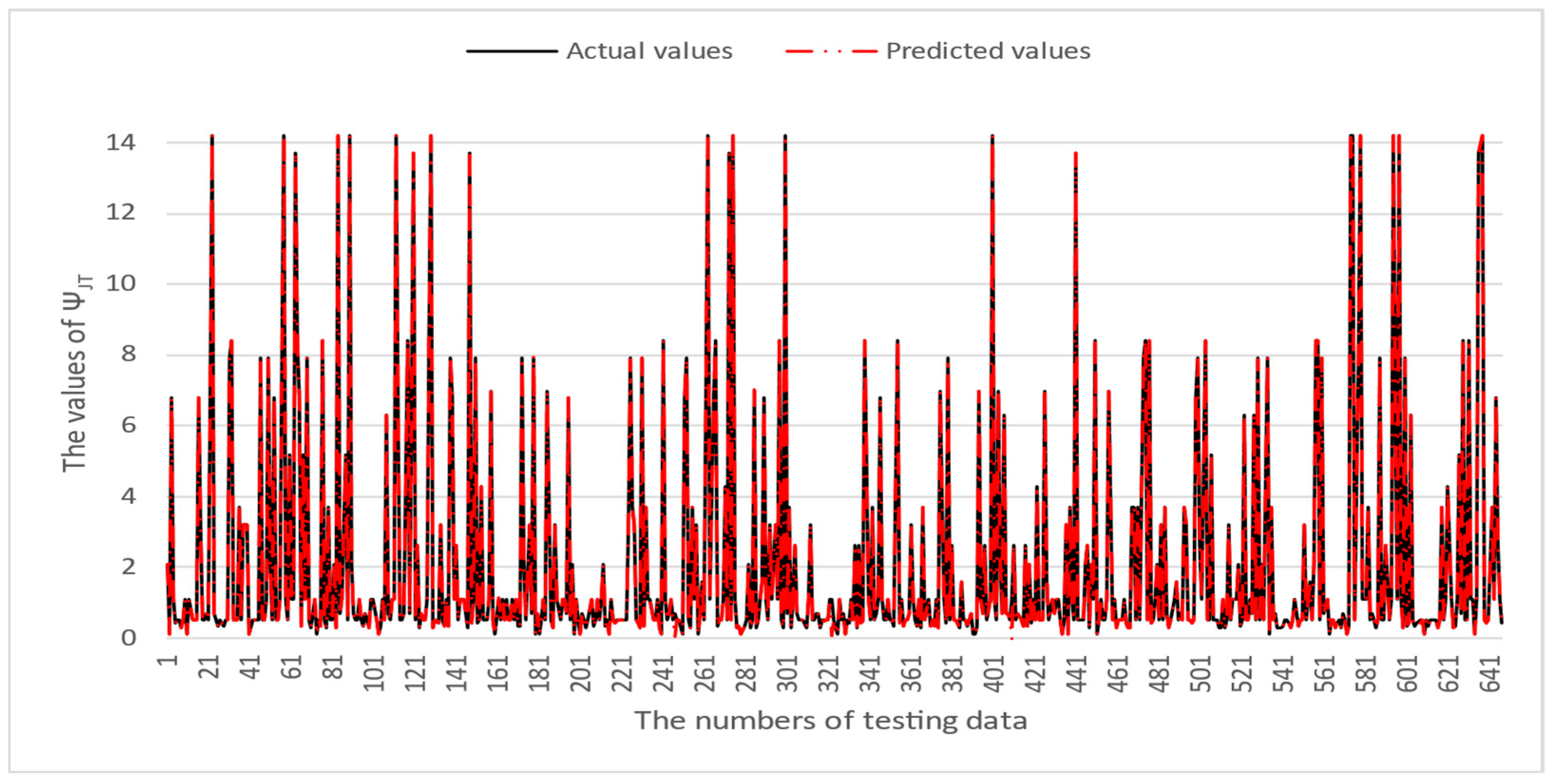
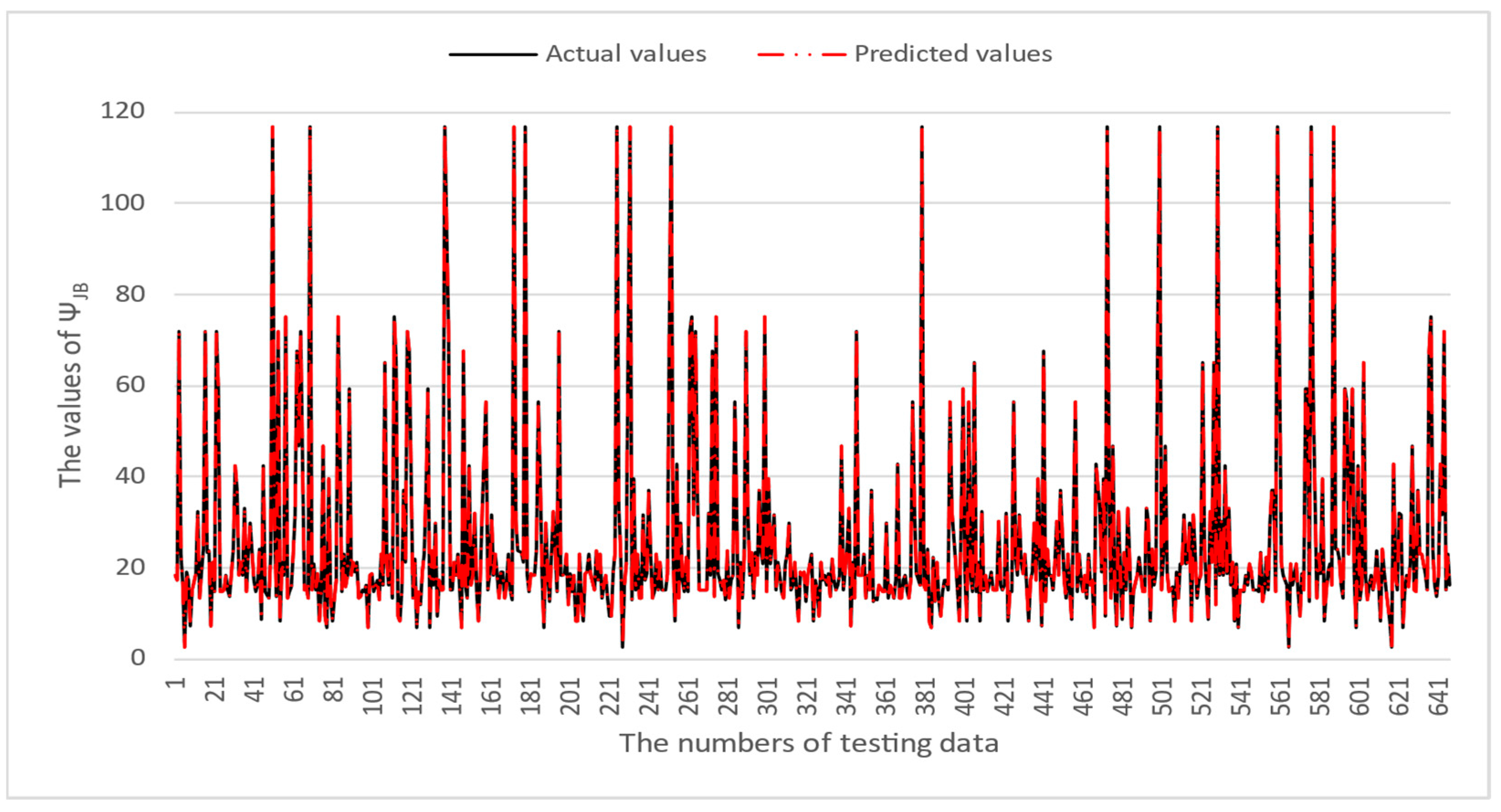
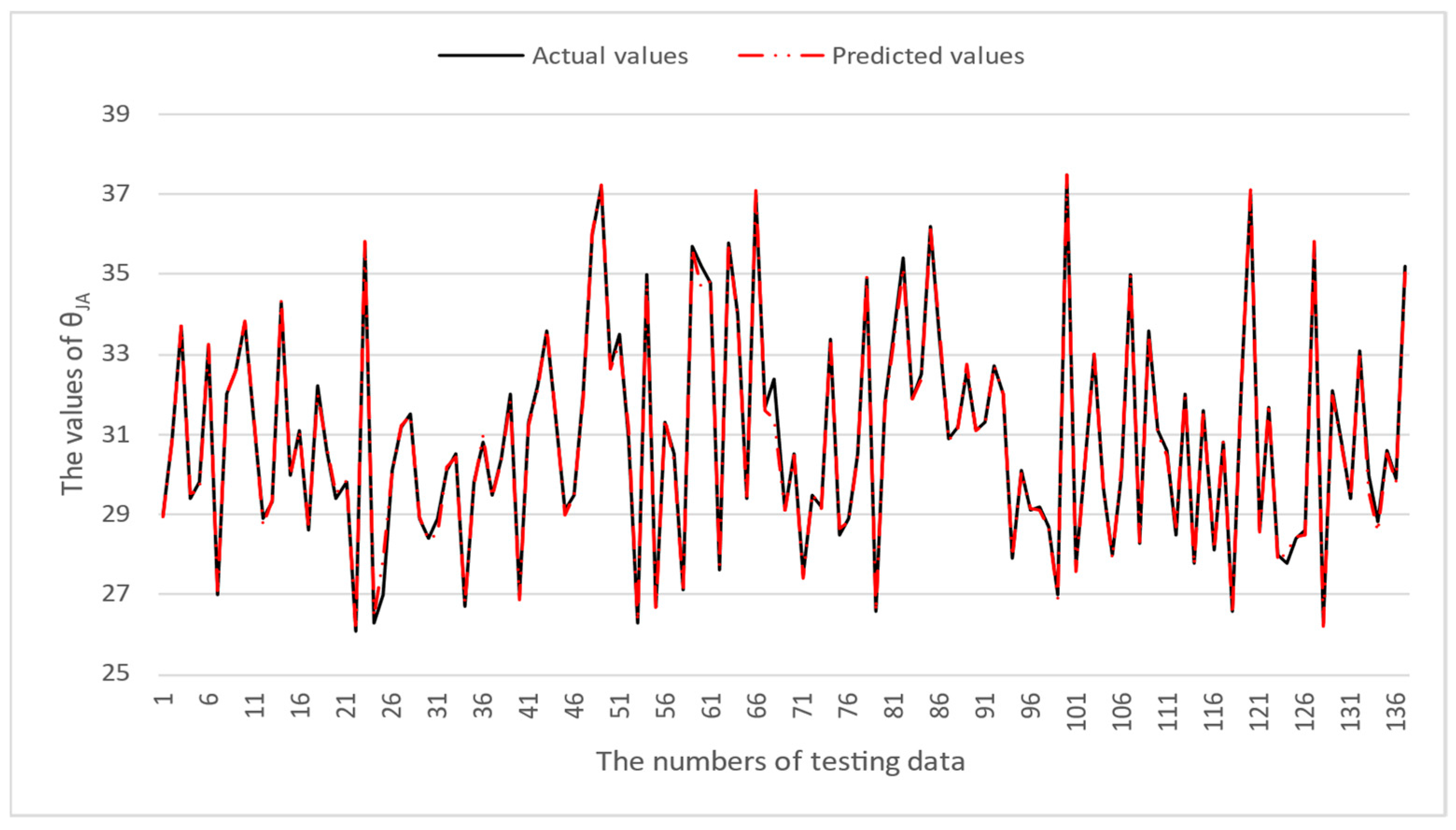
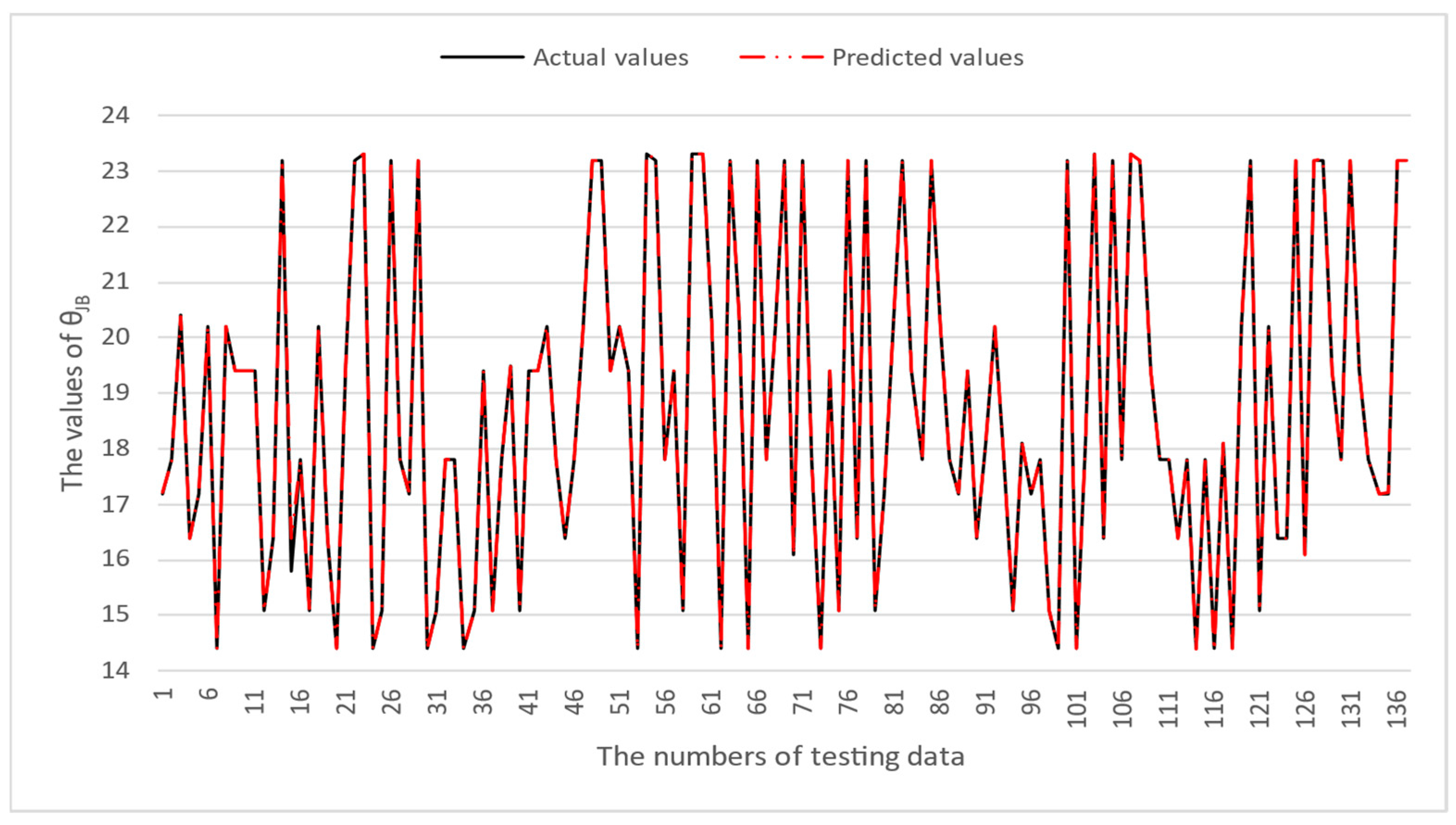
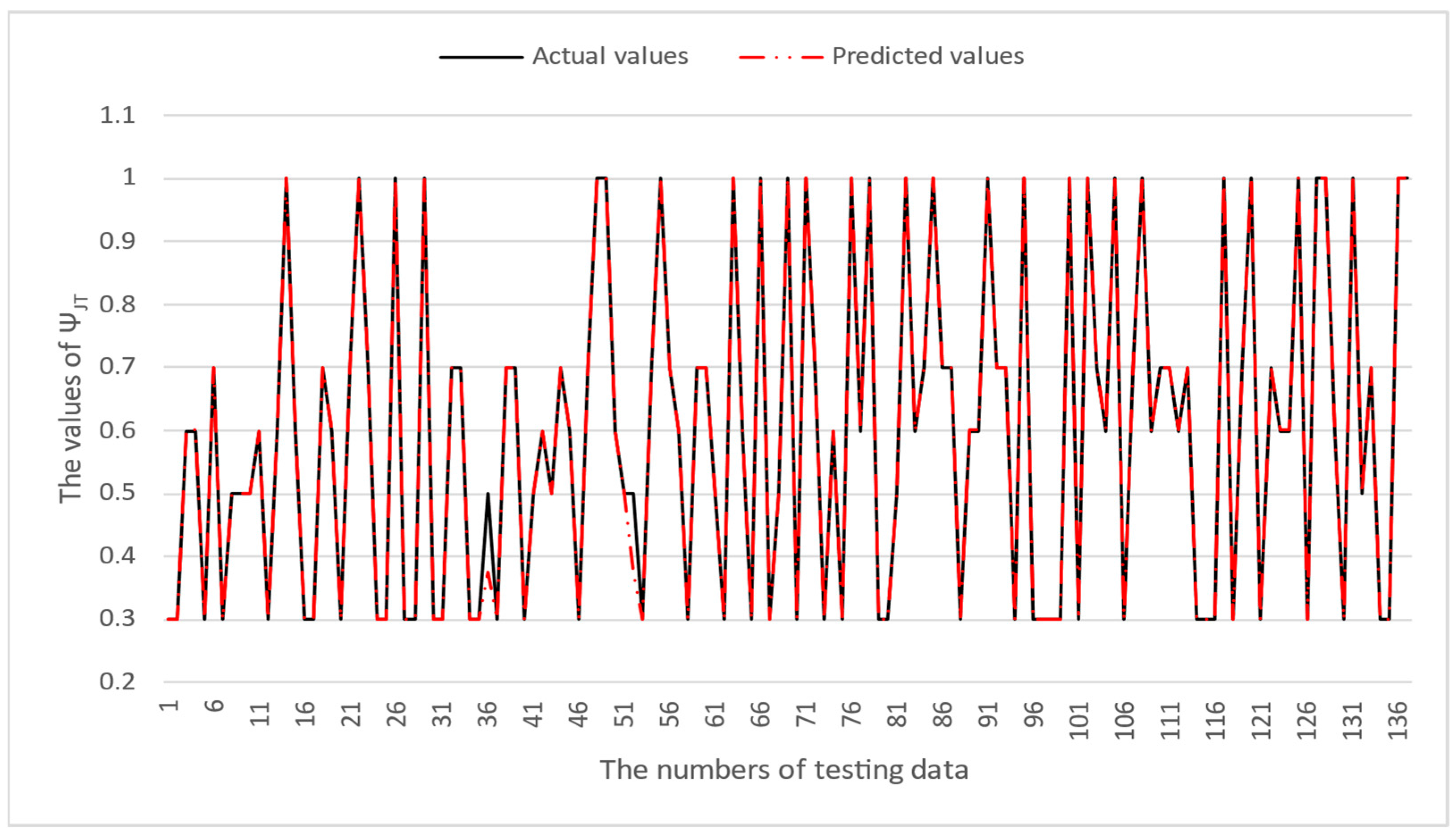
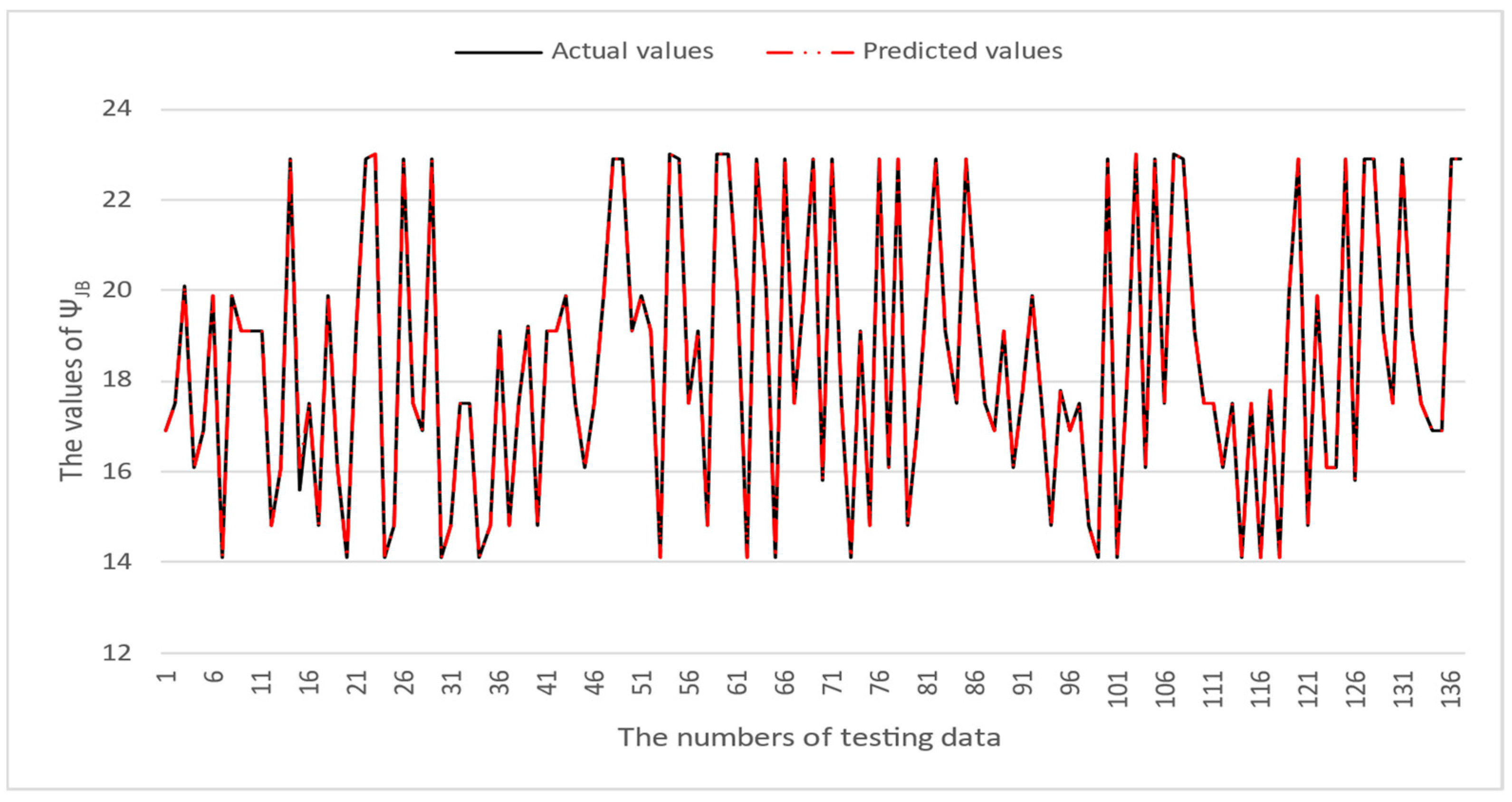
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hollstein, K.; Yang, X.; Weide-Zaage, K. Thermal analysis of the design parameters of a QFN package soldered on a PCB using a simulation approach. Microelectron. Reliab. 2021, 120, 114118. [Google Scholar] [CrossRef]
- Qiu, B.; Xiong, J.; Wang, H.; Zhou, S.; Yang, X.; Lin, Z.; Liu, M.; Cai, N. Survey on fatigue life prediction of BGA solder joints. Electronics 2022, 11, 542. [Google Scholar] [CrossRef]
- Shang, R.; Yao, Y.; Bi, A.; Wang, Y.; Wang, S. Exploring modeling and testing approaches for three-dimensional integrated thermal resistance of chiplets. J. Therm. Anal. Calorim. 2024, 149, 7689–7703. [Google Scholar] [CrossRef]
- Chen, G.-W.; Lin, Y.-C.; Hsu, C.-H.; Chen, T.-Y.; Wang, C.-C.; Hung, C.-P.; Wang, H.-K. Thermal resistance prediction model for IC packaging optimization and design cycle reduction. In Proceedings of the 2024 IEEE 74th Electronic Components and Technology Conference (ECTC), Denver, CO, USA, 28–31 May 2024; pp. 1593–1598. [Google Scholar]
- Wang, N.; Jieensi, J.; Zhen, Z.; Zhou, Y.; Ju, S. Predicting the interfacial thermal resistance of electronic packaging materials via machine learning. In Proceedings of the 2022 23rd International Conference on Electronic Packaging Technology (ICEPT), Dalian, China, 10–13 August 2022; pp. 1–4. [Google Scholar]
- Wang, C.; Vafai, K. Heat transfer enhancement for 3D chip thermal simulation and prediction. Appl. Therm. Eng. 2024, 236, 121499. [Google Scholar] [CrossRef]
- Park, J.-H.; Park, H.; Kim, T.; Kim, J.; Lee, E.-H. Numerical analysis of thermal and mechanical characteristics with property maps in complex semiconductor package designs. Appl. Math. Model. 2024, 130, 140–159. [Google Scholar] [CrossRef]
- Stoyanov, S.; Tilford, T.; Zhang, X.; Hu, Y.; Yang, X.; Shen, Y. Physics-informed Machine Learning for predicting fatigue damage of wire bonds in power electronic modules. In Proceedings of the 2024 25th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Catania, Italy, 7–10 April 2024; pp. 1–8. [Google Scholar]
- Kim, M.; Moon, J.H. Deep neural network prediction for effective thermal conductivity and spreading thermal resistance for flat heat pipe. Int. J. Numer. Methods Heat Fluid Flow 2022, 33, 437–455. [Google Scholar] [CrossRef]
- Lai, Y.; Kataoka, J.; Pan, K.; Ha, J.; Yang, J.; Deo, K.A.; Xu, J.; Yin, P.; Cai, C.; Park, S.; et al. A deep learning approach for reflow profile prediction. In Proceedings of the 2022 IEEE 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May–3 June 2022; pp. 2269–2274. [Google Scholar]
- Wang, Z.-Q.; Hua, Y.; Aubry, N.; Zhou, Z.-F.; Feng, F.; Wu, W.-T. Fast optimization of multichip modules using deep learning coupled with Bayesian method. Int. Commun. Heat Mass Transf. 2023, 141, 106592. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, X.; Zhang, G.; Hu, Z.; Zhao, Z.; Wang, L. Analytical thermal resistance model for calculating mean die temperature of eccentric quad flat no-leads packaging on printed circuit board. AIP Adv. 2021, 11, 035039. [Google Scholar] [CrossRef]
- Rao, X.; Liu, H.; Song, J.; Jin, C.; Xiao, C. Optimizing Heat Source Arrangement for 3D ICs with irregular structures using machine learning methods. In Proceedings of the 2023 24th International Conference on Electronic Packaging Technology (ICEPT), Shihezi, China, 8–11 August 2023; pp. 1–6. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LGBM: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 1–9. [Google Scholar]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression. 2004. Available online: https://escholarship.org/uc/item/35x3v9t4 (accessed on 6 December 2024).
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. Adv. Neural Inf. Process. Syst. 1996, 9, 281–287. [Google Scholar]
- da Silva Santos, C.E.; Sampaio, R.C.; dos Santos Coelho, L.; Bestard, G.A.; Llanos, C.H. Multi-objective adaptive differential evolution for SVM/SVR hyperparameters selection. Pattern Recognit. 2021, 110, 107649. [Google Scholar] [CrossRef]
- Yu, H.; Kim, S. SVM Tutorial-Classification, Regression and Ranking. Handb. Nat. Comput. 2012, 1, 479–506. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Chen, C.-H.; Lai, J.-P.; Chang, Y.-M.; Lai, C.-J.; Pai, P.-F. A study of optimization in deep neural networks for regression. Electronics 2023, 12, 3071. [Google Scholar] [CrossRef]
- Bhandari, U.; Chen, Y.; Ding, H.; Zeng, C.; Emanet, S.; Gradl, P.R.; Guo, S. Machine-Learning-Based Thermal Conductivity Prediction for Additively Manufactured Alloys. J. Manuf. Mater. Process. 2023, 7, 160. [Google Scholar] [CrossRef]
- Kıyak, B.; Öztop, H.F.; Ertam, F.; Aksoy, İ.G. An Intelligent Approach to Investigate the Effects of Container Orientation for PCM Melting Based on an XGBoost Regression Model. Eng. Anal. Bound. Elem. 2024, 161, 202–213. [Google Scholar] [CrossRef]
- Reddad, H.; Zemzami, M.; El Hami, N.; Hmina, N.; Nguyen, N.Q. Reliability Assessment of Solder Ball Joints Using Finite Element Analysis and Machine Learning Techniques. In Proceedings of the 2024 10th International Conference on Control, Decision and Information Technologies (CoDIT), Valletta, Malta, 1–4 July 2024; pp. 2750–2755. [Google Scholar]





| Literature | Years | Applications | Methods |
|---|---|---|---|
| Chen et al. [4] | 2024 | Thermal resistance prediction of IC packages | ANN |
| Wang and Vafai [6] | 2024 | Predicting changes in hot-spot temperature on 3D wafers | SVR |
| Park et al. [7] | 2024 | Predicting thermal and mechanical flux in packages | SVR, GPR, ANN |
| Stoyanov et al. [8] | 2024 | Predicting thermal fatigue damage due to the temperature of power electronic modules | ANN |
| Kim and Moon [9] | 2022 | Estimating the effective thermal conductivity of a flat heat pipe | CNNs |
| Lai et al. [10] | 2022 | Predicting the reflow profile of a bulky ball grid array package | LSTM |
| Wang et al. [11] | 2022 | Optimizing the thermal layout of multi-die modules | CNN |
| Symbols | Descriptions |
|---|---|
| θJA | Junction-to-Ambient Thermal Resistance |
| θJC | Junction-to-Case Thermal Resistance |
| θJB | Junction-to-Board Thermal Resistance |
| ΨJB | Junction-to-Board Characterization Parameter |
| ΨJT | Junction-to-Top Characterization Parameter |
| MAPE (%) | |||||
|---|---|---|---|---|---|
| θJA | θJB | θJC | ΨJT | ΨJB | |
| LGBM | 0.81910 | 0.71812 | 0.25985 | 5.76161 | 0.76677 |
| RF | 3.35084 | 2.61994 | 1.29613 | 9.15216 | 2.74191 |
| XGB | 0.54722 | 0.08679 | 0.03156 | 1.12312 | 0.07795 |
| SVR | 21.56125 | 38.94282 | 51.83620 | 74.77261 | 39.93139 |
| MLP | 9.44791 | 27.44147 | 54.38130 | 219.77778 | 28.19956 |
| RMSE | |||||
| θJA | θJB | θJC | ΨJT | ΨJB | |
| LGBM | 0.42701 | 0.18187 | 0.03496 | 0.08284 | 0.17618 |
| RF | 1.41133 | 0.59374 | 0.28861 | 0.31519 | 0.59424 |
| XGB | 0.29024 | 0.05605 | 0.00981 | 0.06757 | 0.02962 |
| SVR | 21.26226 | 21.61219 | 14.7613 | 3.34606 | 21.62768 |
| MLP | 5.87797 | 7.98745 | 7.08441 | 2.15471 | 7.84077 |
| MAPE (%) | |||||
|---|---|---|---|---|---|
| θJA | θJB | θJC | ΨJT | ΨJB | |
| LGBM | 0.54050 | 0.45001 | 0.52274 | 2.27755 | 0.50401 |
| RF | 0.83332 | 0.25039 | 0.16172 | 1.47055 | 0.19218 |
| XGB | 0.32796 | 0.05541 | 0.16484 | 0.44334 | 0.02457 |
| SVR | 6.67386 | 14.03057 | 36.35358 | 46.45564 | 14.26818 |
| MLP | 3.83322 | 14.02184 | 24.36788 | 52.48518 | 12.89667 |
| RMSE | |||||
| θJA | θJB | θJC | ΨJT | ΨJB | |
| LGBM | 0.23402 | 0.10868 | 0.05360 | 0.01964 | 0.10976 |
| RF | 0.32222 | 0.10872 | 0.05480 | 0.02109 | 0.08745 |
| XGB | 0.16306 | 0.05172 | 0.05822 | 0.01496 | 0.04275 |
| SVR | 2.64245 | 3.03563 | 2.40439 | 0.25818 | 3.03495 |
| MLP | 1.39098 | 2.96866 | 1.40718 | 0.27544 | 2.68824 |
| QFN | TFBGA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Models | Hyperparameters | θJA | θJB | θJC | ΨJT | ΨJB | θJA | θJB | θJC | ΨJT | ΨJB |
| SVR | C | 128 | 128 | 128 | 8 | 128 | 32 | 1 | 2 | 1 | 1 |
| 0.01 | 0.01 | 0.01 | 0.1 | 0.01 | 0.1 | 1.5 | 0.01 | 0.5 | 1.5 | ||
| gamma | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| MLP | Number of hidden nodes | 150 | 150 | 50 | 100 | 50 | 100 | 150 | 100 | 50 | 100 |
| Activation functions | tanh | tanh | tanh | tanh | tanh | relu | relu | relu | relu | tanh | |
| Optimizers | adam | adam | adam | adam | adam | adam | adam | adam | adam | adam | |
| Learning rate | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.05 | 0.1 | 0.001 | |
| QFN | MAPE (%) | ||||
|---|---|---|---|---|---|
| θJA | θJB | θJC | ΨJT | ΨJB | |
| SVR | 3.55823 | 5.93015 | 9.70486 | 50.39072 | 6.77025 |
| MLP | 1.96832 | 3.48456 | 10.19002 | 41.61330 | 4.48553 |
| RMSE | |||||
| SVR | 3.46385 | 3.35152 | 3.11810 | 1.98187 | 3.52001 |
| MLP | 0.89157 | 0.73737 | 1.25865 | 0.69823 | 0.88693 |
| TFBGA | MAPE (%) | ||||
| θJA | θJB | θJC | ΨJT | ΨJB | |
| SVR | 1.34762 | 13.62841 | 27.65896 | 52.00729 | 13.86218 |
| MLP | 1.62015 | 8.07679 | 21.61422 | 48.88836 | 8.21445 |
| RMSE | |||||
| SVR | 0.58975 | 2.91447 | 1.80322 | 0.26447 | 2.91400 |
| MLP | 0.64419 | 2.24097 | 1.36479 | 0.26156 | 2.24396 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, J.-P.; Lin, S.; Lin, V.; Kang, A.; Wang, Y.-P.; Pai, P.-F. Predicting Thermal Resistance of Packaging Design by Machine Learning Models. Micromachines 2025, 16, 350. https://doi.org/10.3390/mi16030350
Lai J-P, Lin S, Lin V, Kang A, Wang Y-P, Pai P-F. Predicting Thermal Resistance of Packaging Design by Machine Learning Models. Micromachines. 2025; 16(3):350. https://doi.org/10.3390/mi16030350
Chicago/Turabian StyleLai, Jung-Pin, Shane Lin, Vito Lin, Andrew Kang, Yu-Po Wang, and Ping-Feng Pai. 2025. "Predicting Thermal Resistance of Packaging Design by Machine Learning Models" Micromachines 16, no. 3: 350. https://doi.org/10.3390/mi16030350
APA StyleLai, J.-P., Lin, S., Lin, V., Kang, A., Wang, Y.-P., & Pai, P.-F. (2025). Predicting Thermal Resistance of Packaging Design by Machine Learning Models. Micromachines, 16(3), 350. https://doi.org/10.3390/mi16030350








