Research on the Trajectory and Relative Speed of a Single-Sided Chemical Mechanical Polishing Machine
Abstract
1. Introduction
- (1)
- The literature only has a one-way abrasive grain trajectory or lacks a detailed mathematical derivation process, which makes it difficult to systematically understand the characteristics of the whole motion in research and engineering applications. Therefore, in this work, motion trajectory parameter equations for silicon wafers to polishing pads and abrasives to silicon wafers of a single-sided polishing machine are constructed and simulated via the rotation and translation coordinate system method.
- (2)
- The literature lacks an intuitive graphical representation of the relative velocity, so this work uses the method of subtracting the velocity vector of the polishing plate and the carrier to derive a mathematical expression of the relative velocity; on this basis, the relative velocity is calculated and graphically simulated.
- (3)
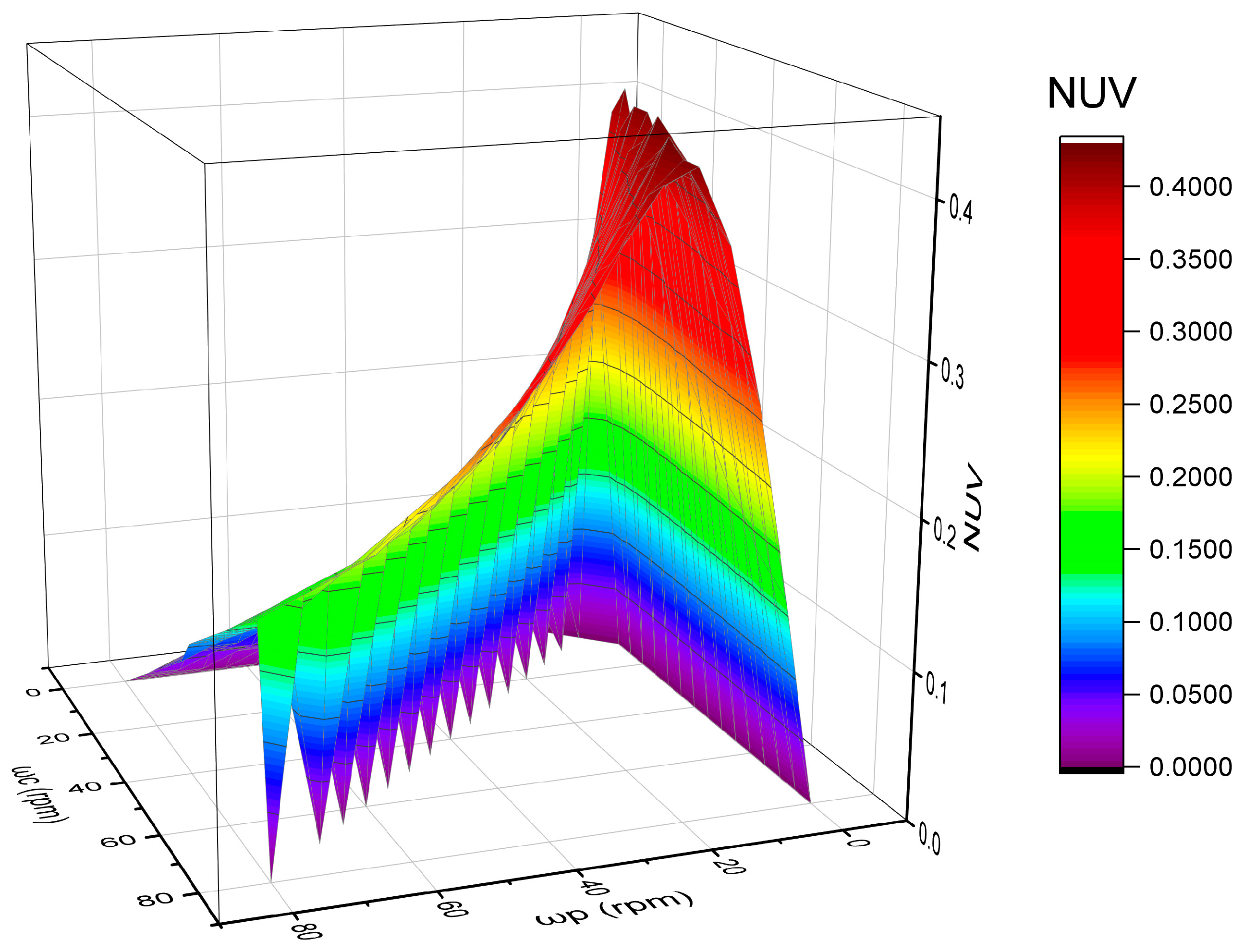
- The literature lacks a complete visual representation of the nonuniformity velocity (NUV) of the whole motion velocity range, so the relative velocity of the polishing plate and the carrier in the speed range of 0–80 rpm is plotted in 3D in a 17 × 17 matrix.
- (1)
- The bidirectional motion trajectory equation is established through the synergistic application of rotational and translational coordinate transformations, systematically resolving the multibody interaction dynamics within the tribological interface (wafer–pad–abrasive particle system).
- (2)
- A research method combining relative velocity analysis and silicon wafer polishing experiments is established, which can provide a reference for the relative velocity study of different single-sided polishing machines.
- (3)
- Speed nonuniformity was parameterized via high-resolution parametric 3D mapping (17 × 17 grid configuration), revealing novel distribution patterns across the full operational regime (0–80 rpm).
2. Methodology
2.1. Introduction of the Chemical Mechanical Polishing Working Image
2.2. Total Thickness Variation Inspection of the Silicon Wafer
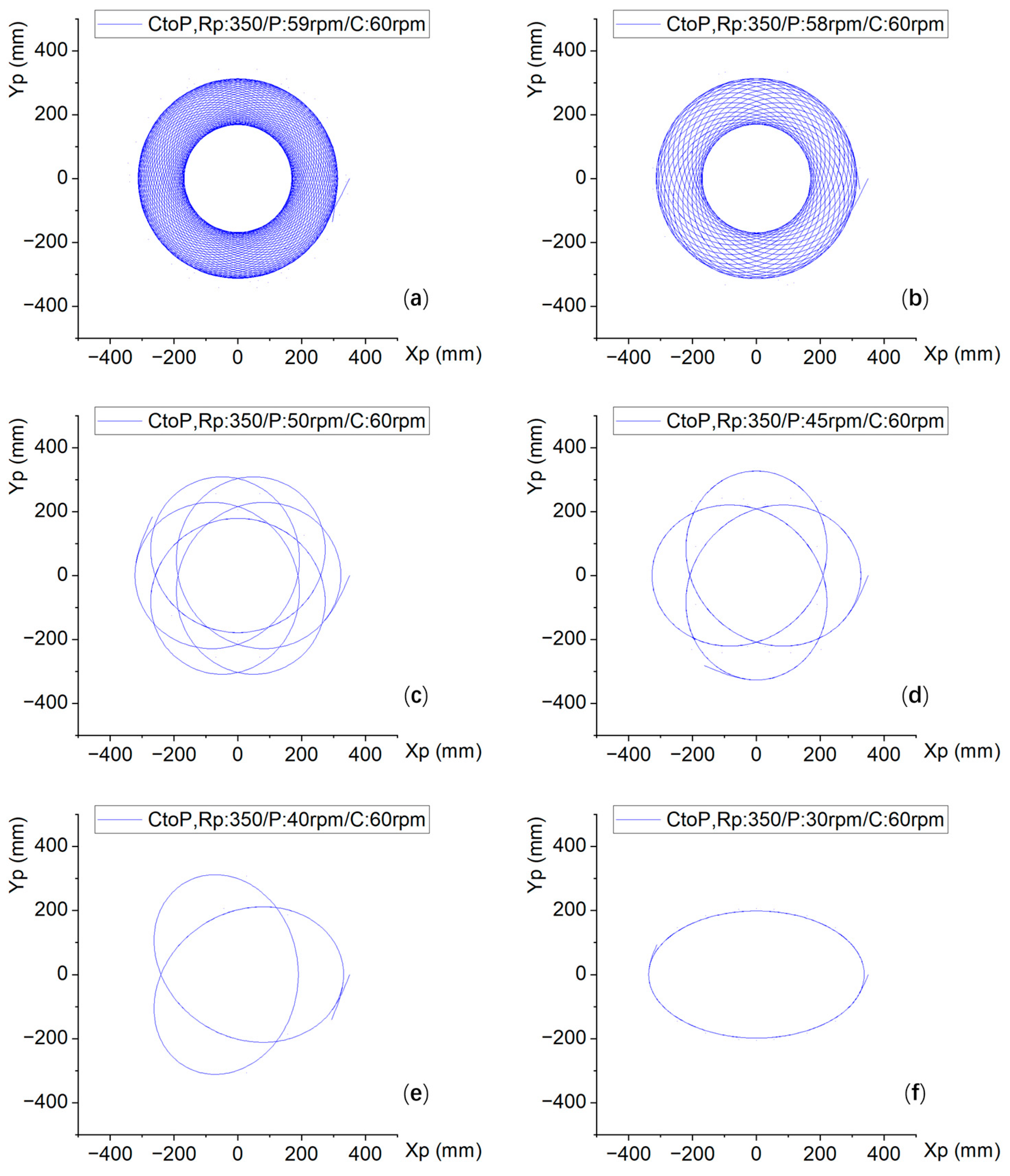
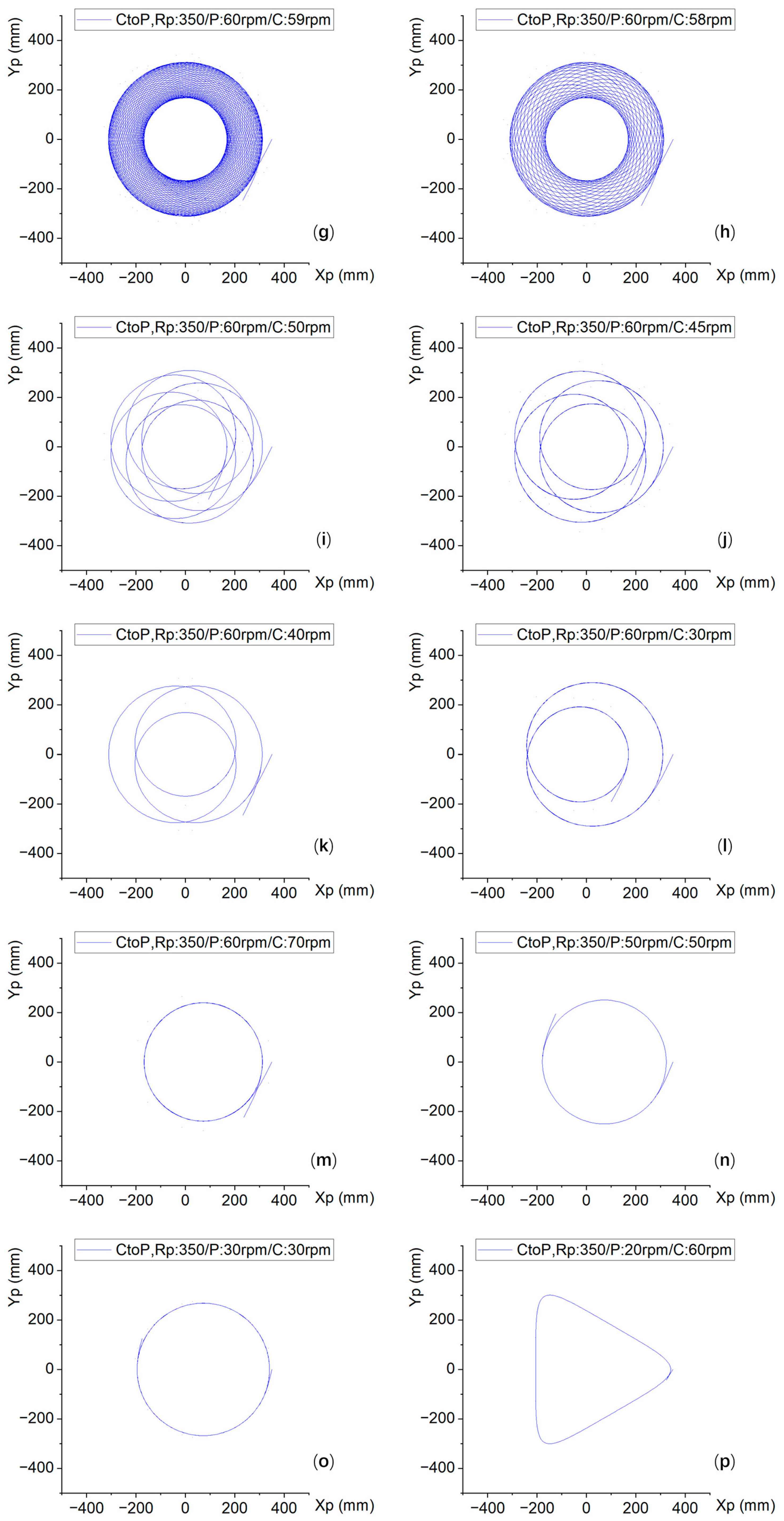
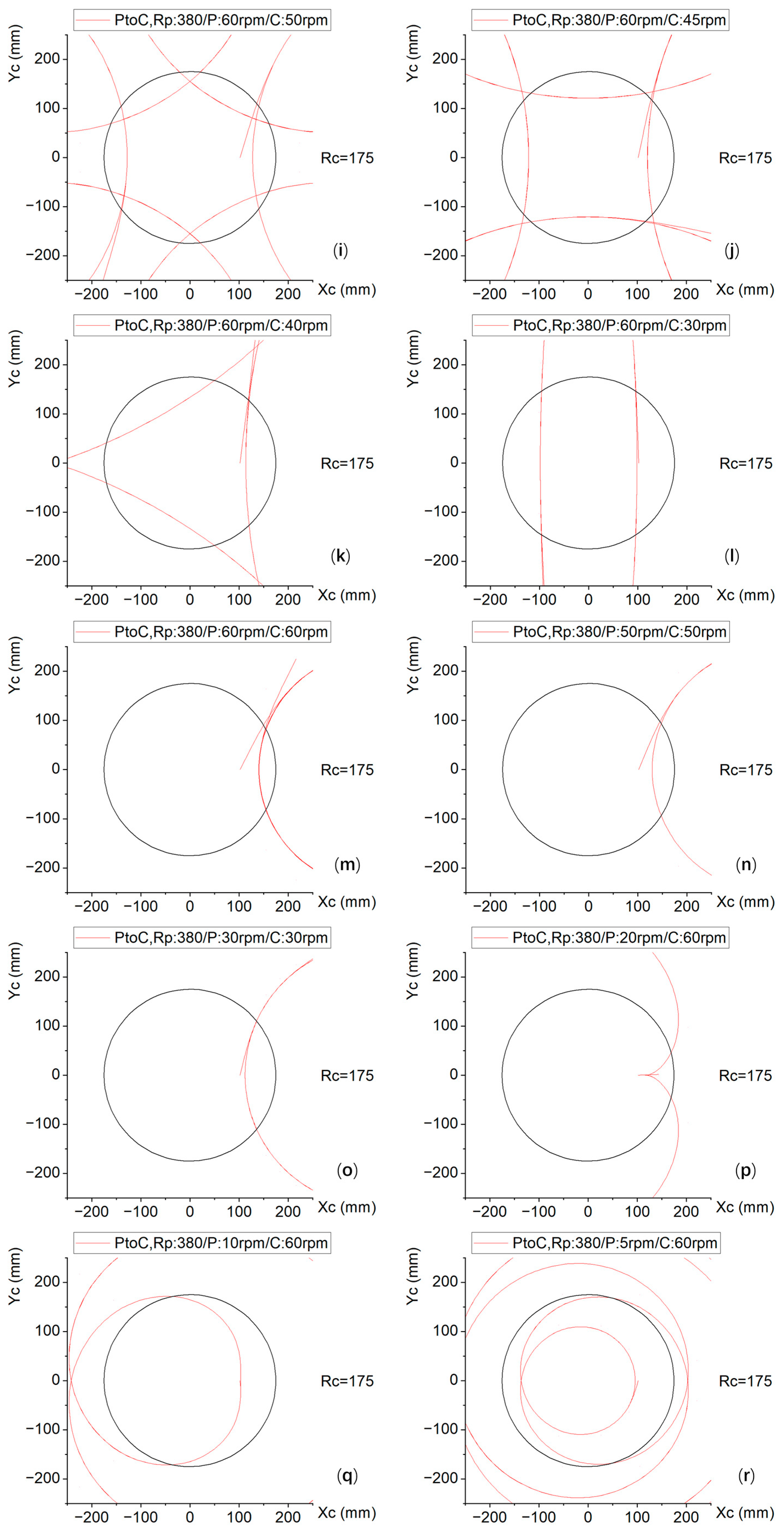
2.3. Motion Trajectory of Any Point on the Silicon Wafer Relative to the Polishing Plate (Pad)
2.4. Motion Trajectory at Any Point on the Polishing Plate (Pad) Relative to the Silicon Wafer
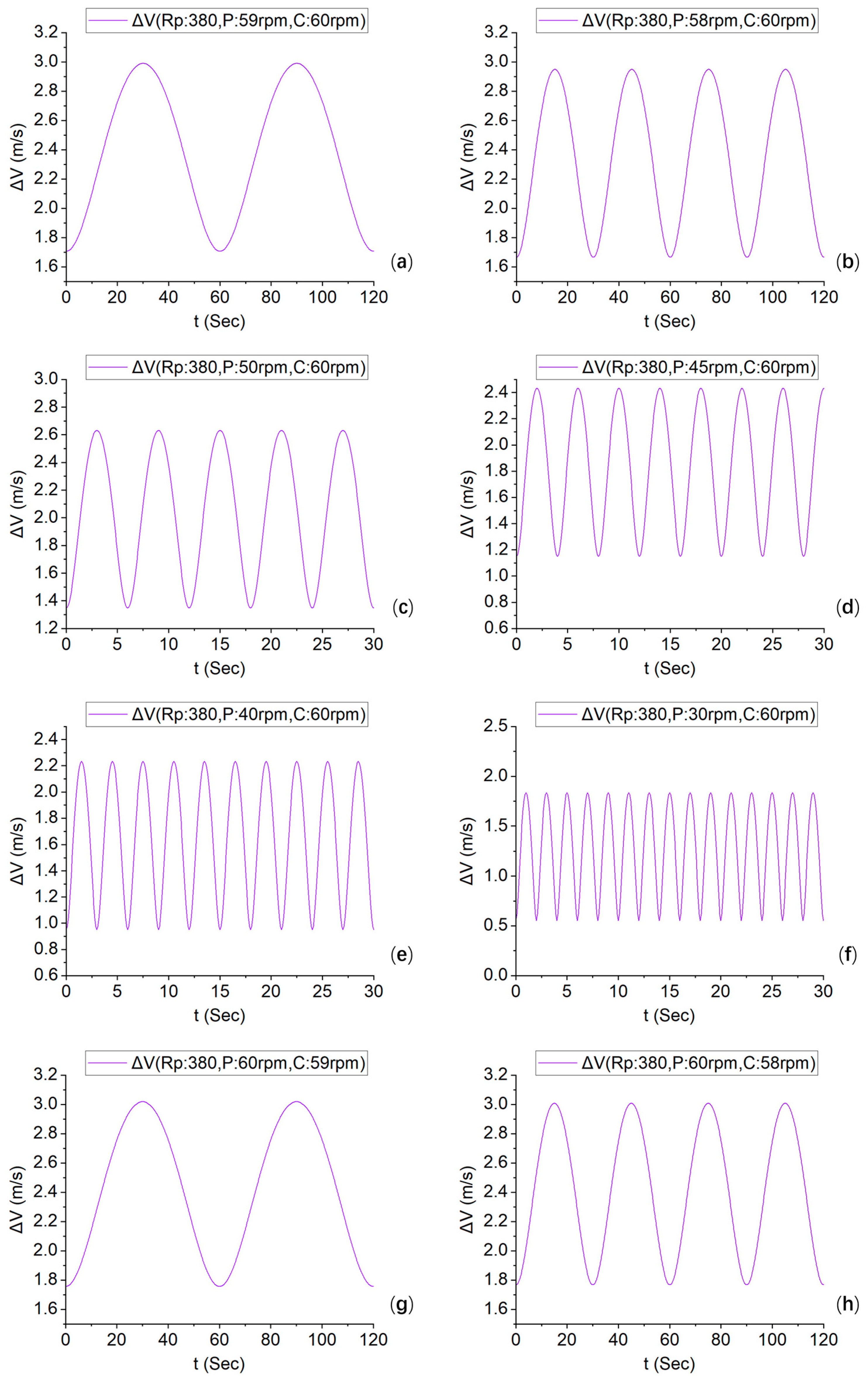
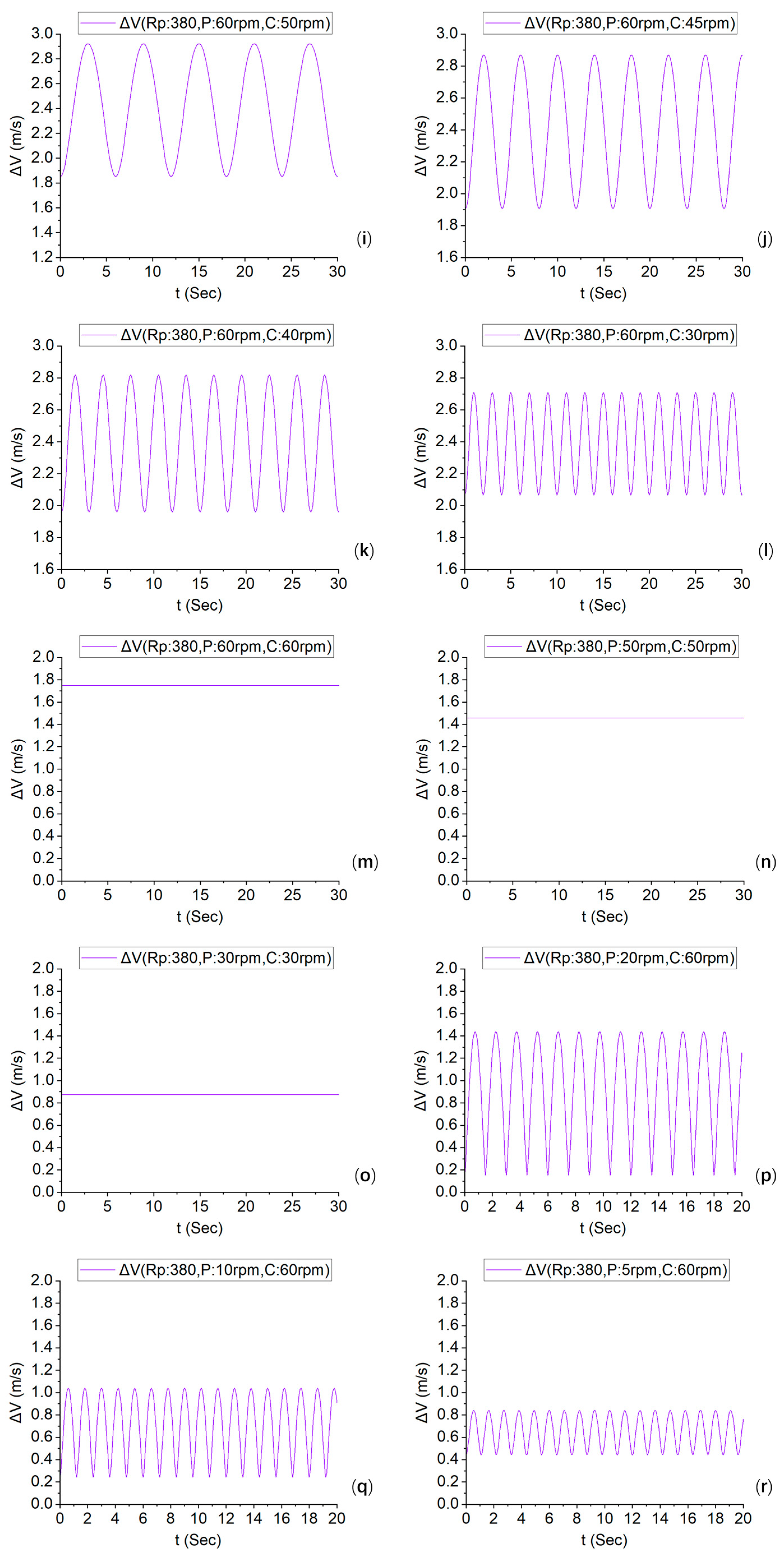
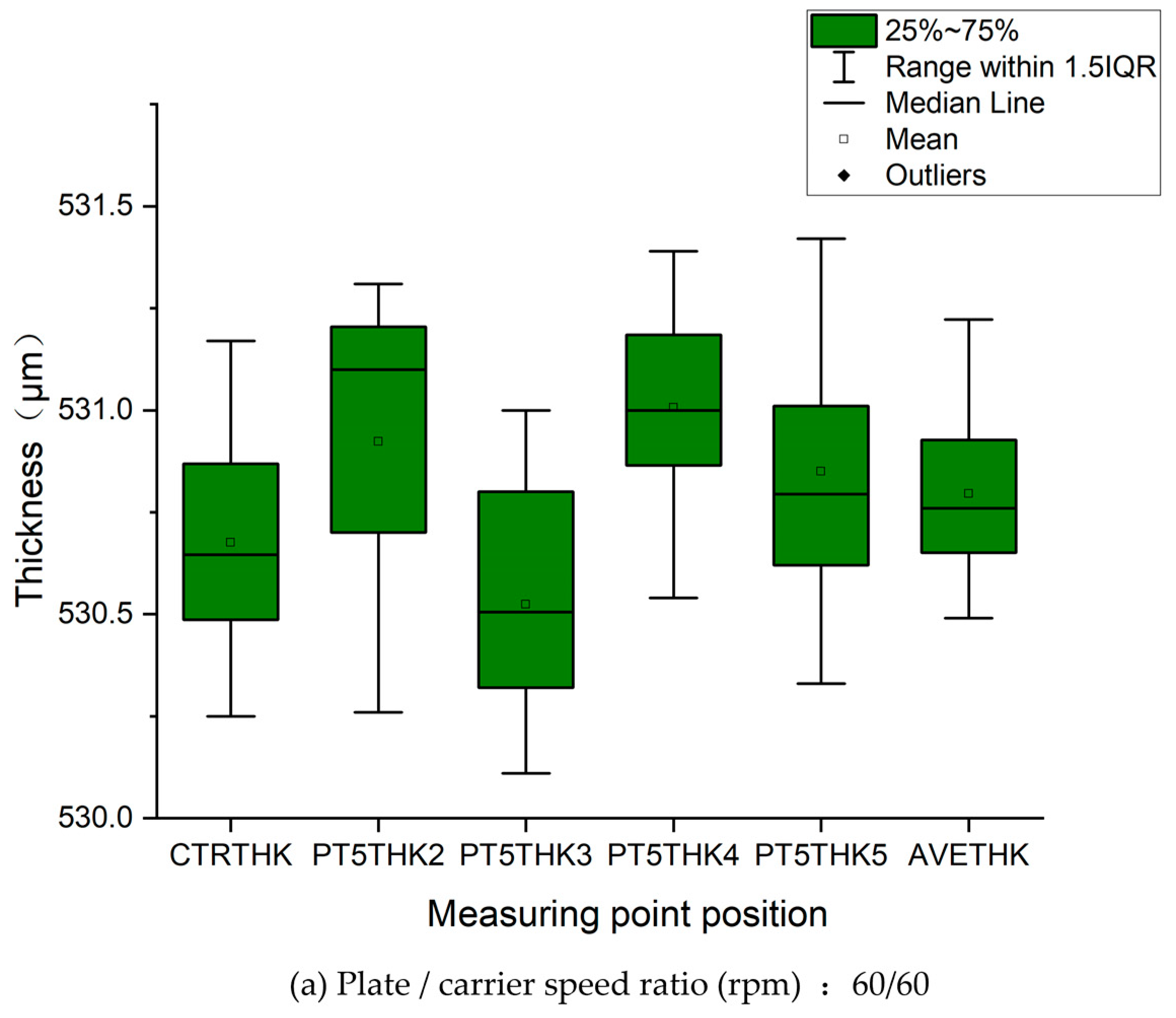
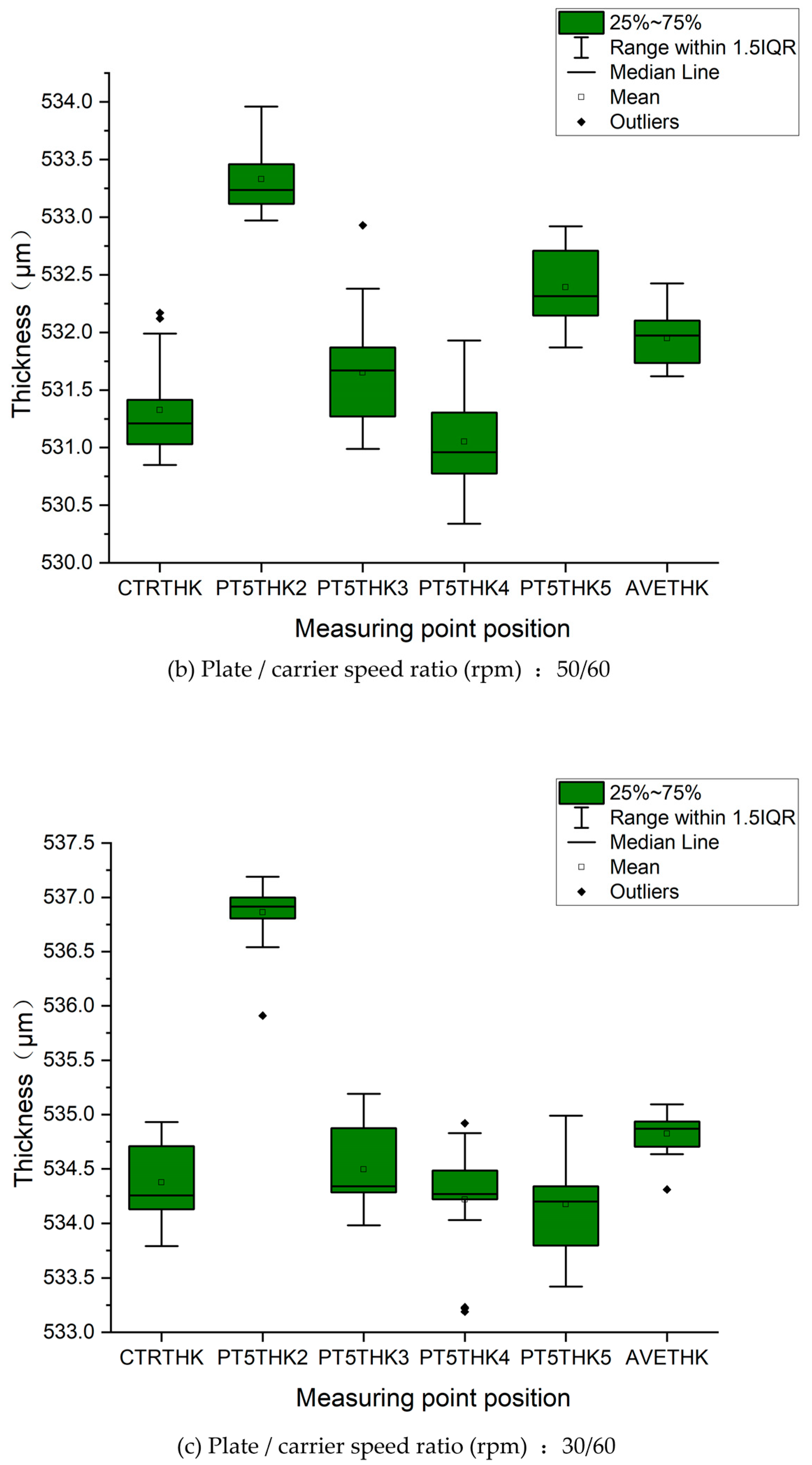
2.5. Relative Speeds of the Plate and Carrier at Different Speed Ratios
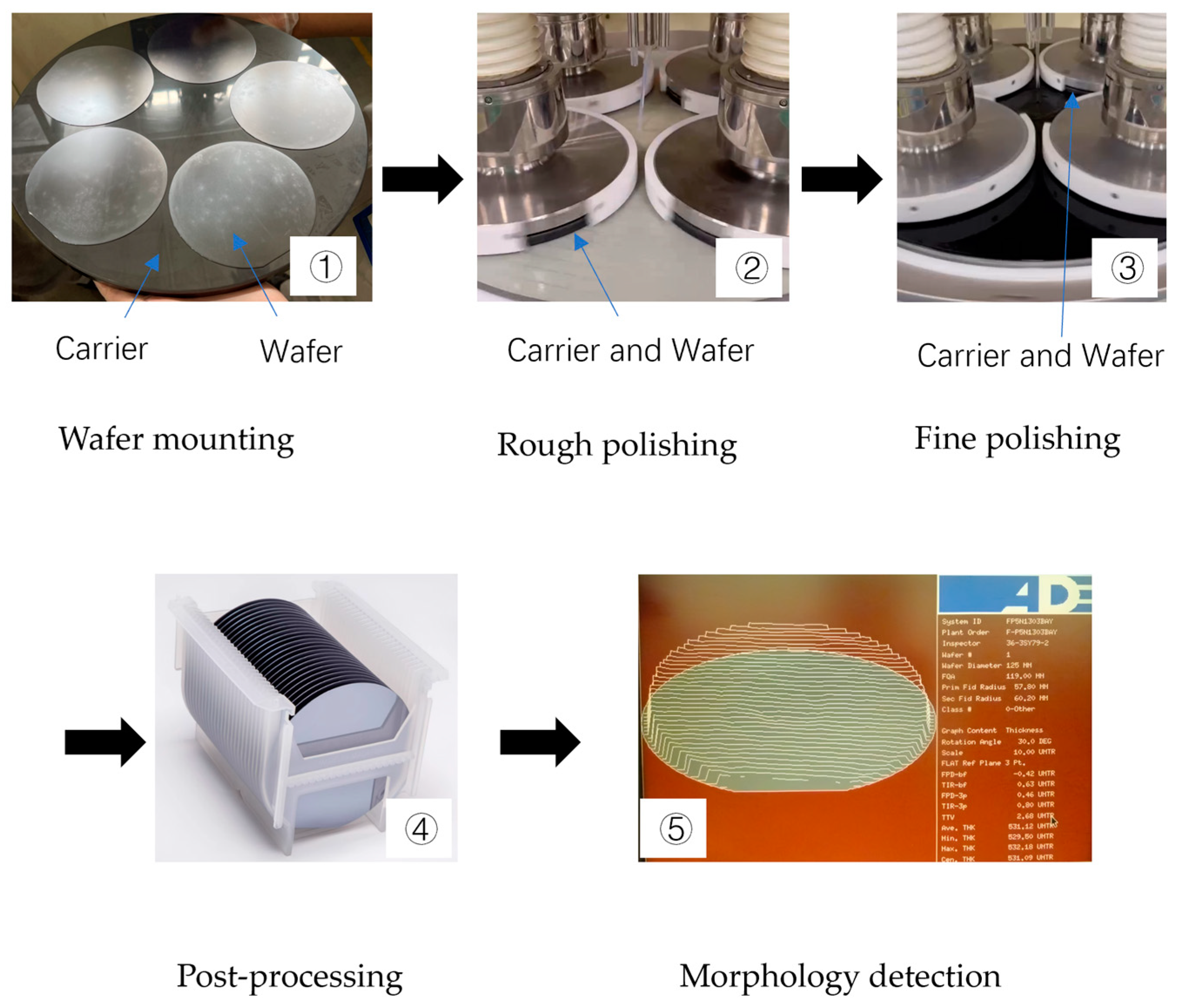
2.6. Experimental Procedures
- (1)
- Wafer mounting: Initial bonding of the silicon wafer to the carrier substrate is achieved through thermal wax deposition.
- (2)
- Rough polishing: A 30 min primary polishing phase is conducted to regulate the total thickness variation (TTV), constituting the critical thickness control stage.
- (3)
- Fine polishing: Subsequent precision processing over approximately 30 min primarily enhances the surface roughness (Ra < 0.2 nm).
- (4)
- Post-processing: Post-polished wafers undergo systematic cleaning in dedicated cassettes through ultrasonic agitation followed by drying with a nitrogen knife.
- (5)
- Morphology detection: Final thickness characterization was performed via noncontact capacitive measurement systems (WaferCheck-8300, ADE Corporation, Westwood, MA, USA) with 0.01 μm resolution, ensuring precise quantification of single-crystal silicon morphology parameters.
3. Results and Discussions
- (1)
- The trajectory equation derived on the basis of rotational coordinates, trajectory simulation, and relative velocity simulation can provide a theoretical basis for selecting different speed formulas for single-sided polishing machines. The shapes of different polishing machines at different points are different, and different parameters can be input. Numerical simulations reveal two fundamental regimes; those with near-unity rotational speed ratios (ωP/ωC = [0.95, 1) and (1, 1.05]) generate optimal spiral trajectories, achieving 95% surface coverage.
- (2)
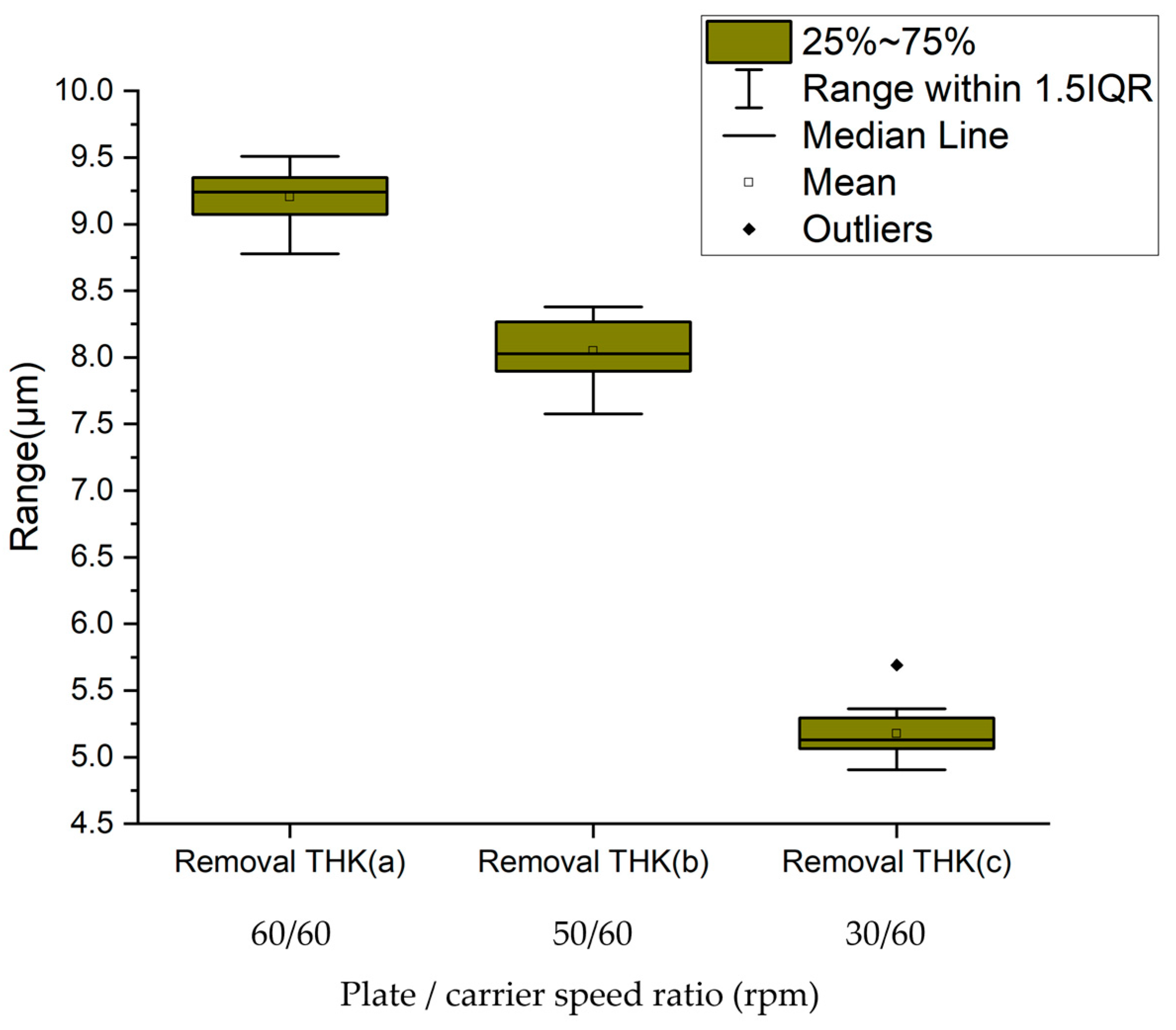
- When the speed of the polishing plate and the carrier is an integer multiple, the relative speed is constant, and a relatively uniform removal rate and removal uniformity can be obtained. The higher the relative speed, the faster the removal rate.
- (3)
- Equations for trajectory and relative velocity uniformity can also be applied as a reference for single-sided polishing of other materials, such as SiC. The basic principles are the same.
- (4)
- Due to the sensitivity of the ratio of the polishing plate and speed to the trajectory and relative speed, it is necessary to choose a reasonable speed ratio. Moreover, the accuracy of the deviation between the set speed and the true speed of the polishing machine is also quite important.
- (5)
- Due to the relative velocity fluctuations caused by the different rotational speeds of the polishing plate and the carrier, as well as the limitations of the carrier coverage range, traditional steady-state models have difficulty describing this state. Therefore, an effective velocity integration model can be considered, i.e., the MRR = K P description, where ΔV is the relative velocity, as shown in Equation (14) and Figure 8, which exhibits dynamic variability.
4. Conclusions
- (1)
- Trajectory parameterization and derivation
- (2)
- Relative velocity analysis
- (3)
- Parametric nonuniformity mapping
- (4)
- Methodological extensibility
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moon, Y. 1-Chemical and Physical Mechanisms of Dielectric Chemical Mechanical Polishing (CMP). In Advances in Chemical Mechanical Planarization (CMP), 2nd ed.; Babu, S., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: New Delhi, India, 2022; pp. 3–28. ISBN 978-0-12-821791-7. [Google Scholar]
- Lu, S.; Xia, J.; Yu, J.; Wang, Z. Investigating the Partial Plastic Formation Mechanism of Typical Scratches on Silicon Wafers Induced by Rogue Particles During Chemical Mechanical Polishing. Mater. Sci. Semicond. Process. 2024, 181, 108666. [Google Scholar] [CrossRef]
- Srivastava, M.; Singh, J.; Mishra, D.K.; Singh, R.P. Review on the Various Strategies Adopted for the Polishing of Silicon Wafer—A Chemical Perspective. Mater. Today Proc. 2022, 63, 62–68. [Google Scholar] [CrossRef]
- Datta, D.; Rai, H.; Singh, S.; Srivastava, M.; Sharma, R.K.; Gosvami, N.N. Nanoscale Tribological Aspects of Chemical Mechanical Polishing: A Review. Appl. Surf. Sci. Adv. 2022, 11, 100286. [Google Scholar] [CrossRef]
- Pandey, K.; Sharma, A.; Singh, A.K. Silicon Wafers; Its Manufacturing Processes and Finishing Techniques: An Overview. Silicon 2022, 14, 12031–12047. [Google Scholar] [CrossRef]
- Seo, J. A Review on Chemical and Mechanical Phenomena at the Wafer Interface During Chemical Mechanical Planarization. J. Mater. Res. 2021, 36, 235–257. [Google Scholar] [CrossRef]
- Cook, L. 21-CMP Pads and Their Performance. In Advances in Chemical Mechanical Planarization (CMP), 2nd ed.; Babu, S., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: New Delhi, India, 2022; pp. 567–590. ISBN 978-0-12-821791-7. [Google Scholar]
- Uneda, M.; Maeda, Y.; Ishikawa, K.; Ichikawa, K.; Doi, T.; Yamazaki, T.; Aida, H. Relationships between Contact Image Analysis Results for Pad Surface Texture and Removal Rate in CMP. J. Electrochem. Soc. 2011, 159, H90. [Google Scholar] [CrossRef]
- Jeong, J.; Shin, Y.; Jeong, S.; Jeong, H. Characterizing the Contact Evolution through the Combination of Surface Roughness Parameters in Chemical Mechanical Polishing Using a Polyurethane Polishing Pad. Wear 2025, 566–567, 205802. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, X. Chemical Mechanical Polishing: Theory and Experiment. Friction 2013, 1, 306–326. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Zhao, F.; Fan, C.; Feng, J.; Zhou, H.; Meng, F.; Zhuang, X.; Wang, J. Advanced Polishing Methods for Atomic-Scale Surfaces: A Review. Mater. Today Sustain. 2024, 27, 100841. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Luo, H.; Yin, S. Prediction of Material Removal Rate in Chemical Mechanical Polishing via Residual Convolutional Neural Network. Control Eng. Pract. 2021, 107, 104673. [Google Scholar] [CrossRef]
- Cheng, Z.; Gao, H.; Liu, Z.; Guo, D. Investigation of the Trajectory Uniformity in Water Dissolution Ultraprecision Continuous Polishing of Large-Sized KDP Crystal. Int. J. Extreme Manuf. 2020, 2, 045101. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, S.; Zhang, N.; Hao, Q.; Shi, F. High Steepness Aspheric Polishing Trajectory Planning Based on Equal Arc Length Sampling. In Proceedings of the AOPC 2023: Optical Design and Manufacturing, Beijing, China, 25–27 July 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12964, pp. 14–23. [Google Scholar]
- Hocheng, H.; Tsai, H.Y.; Tsai, M.S. Effects of Kinematic Variables on Nonuniformity in Chemical Mechanical Planarization. Int. J. Mach. Tools Manuf. 2000, 40, 1651–1669. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, T.; He, Y.; Lu, X. Kinematic Optimization for Chemical Mechanical Polishing Based on Statistical Analysis of Particle Trajectories. IEEE Trans. Semicond. Manuf. 2013, 26, 556–563. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Y.; Lai, Z.; Xu, Z.; Huang, H. Design and Experimental Validation of Non-Trimming Polishing Plate for High Wear-Resistant Workpieces Based on Optimized Motion Trajectory Distribution. Precis. Eng. 2025, 93, 551–558. [Google Scholar] [CrossRef]
- Yang, K.; Huang, N.; Di, H.; Zhou, P. Modeling of Surface Microtopography Evolution in Chemical Mechanical Polishing Considering Chemical-Mechanical Synergy. Tribol. Int. 2025, 201, 110206. [Google Scholar] [CrossRef]
- Jiang, B.; Guan, J.; Zhao, P.; Chen, Y.; Zhang, Z. Effect of Polyoxyethylene-Based Nonionic Surfactants on Chemical–Mechanical Polishing Performance of Monocrystalline Silicon Wafers. Crystals 2024, 14, 460. [Google Scholar] [CrossRef]
- Yoshitomi, K.; Shimada, Y.; Une, A. Development of High-Speed Rotation Polishing System with Slurry Confinement and Friction-State Control. Int. J. Autom. Technol. 2023, 17, 55–63. [Google Scholar] [CrossRef]
- Zheng, P.; Zhao, D.; Lu, X. Prediction of Pad Wear Profile and Simulation of Its Influence on Wafer Polishing. Micromachines 2023, 14, 1683. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wan, H.; Peng, F.; Chen, H.; Chen, C.; Chen, P.; Beri, T.H.; Chen, H.; Ren, K.; Lyu, B. Study on Grain Removal Characteristics and Influencing Factors of Polycrystalline Tungsten during Polishing Process. Precis. Eng. 2024, 91, 499–506. [Google Scholar] [CrossRef]
- Irfan, H.M.; Lee, C.-Y.; Mazumdar, D.; Aryanfar, Y.; Wu, W. Improvement of Material Removal Rate and Within Wafer Non-Uniformity in Chemical Mechanical Polishing Using Computational Fluid Dynamic Modeling. J. Manuf. Mater. Process. 2025, 9, 95. [Google Scholar] [CrossRef]
- Hwang, S.; Park, J.; Kim, W. The Stability Evaluation of Ceria Slurry Using Polymer Dispersants with Varying Contents for Chemical Mechanical Polishing Process. Polymers 2024, 16, 3593. [Google Scholar] [CrossRef]
- Jeon, S.; Hong, J.; Hong, S.; Kanade, C.; Park, K.; Seok, H.; Kim, H.; Lee, S.; Kim, T. Investigation of Abrasive-Free Slurry for Polysilicon Buffing Chemical Mechanical Planarization. Mater. Sci. Semicond. Process. 2021, 128, 105755. [Google Scholar] [CrossRef]
- Huo, Y.; Niu, Y.; Sun, Z.; Li, Y.; Niu, J. Surface/Subsurface Damage Mechanisms and Inhibition Strategies in Machining of Hard and Brittle Materials: A Systematic Review. Surf. Interfaces 2024, 54, 105088. [Google Scholar] [CrossRef]
- Bae, J.-Y.; Han, M.-H.; Lee, S.-J.; Kim, E.-S.; Lee, K.; Lee, G.-S.; Park, J.-H.; Park, J.-G. Silicon Wafer CMP Slurry Using a Hydrolysis Reaction Accelerator with an Amine Functional Group Remarkably Enhances Polishing Rate. Nanomaterials 2022, 12, 3893. [Google Scholar] [CrossRef] [PubMed]
- Leo, J.; Tan, H.; Ma, Y.; Parab, S.M.; Huang, Y.; Wang, D.; Zhu, L.; Lam, J.; Mai, Z. Key Issues for Implementing Smart Polishing in Semiconductor Failure Analysis. J. Appl. Math. Phys. 2017, 5, 1668–1677. [Google Scholar] [CrossRef][Green Version]
- Li, S.; Fu, J.; He, Z.; Luo, Y.; Wu, S. Nanomaterials and Equipment for Chemical–Mechanical Polishing of Single-Crystal Sapphire Wafers. Coatings 2023, 13, 2081. [Google Scholar] [CrossRef]
- Ye, G.; Yao, Z. Research on Deflection and Stress Analyses and the Improvement of the Removal Uniformity of Silicon in a Single-Sided Polishing Machine Under Pressure. Micromachines 2025, 16, 198. [Google Scholar] [CrossRef]
- Liu, Y.; Tao, H.; Zhao, D.; Lu, X. An Investigation on the Total Thickness Variation Control and Optimization in the Wafer Backside Grinding Process. Materials 2022, 15, 4230. [Google Scholar] [CrossRef]
- Tseng, W.T.; Chin, J.H.; Kang, L.C. A Comparative Study on the Roles of Velocity in the Material Removal Rate During Chemical Mechanical Polishing. J. Electrochem. Soc. 1999, 146, 1952–1959. [Google Scholar] [CrossRef]
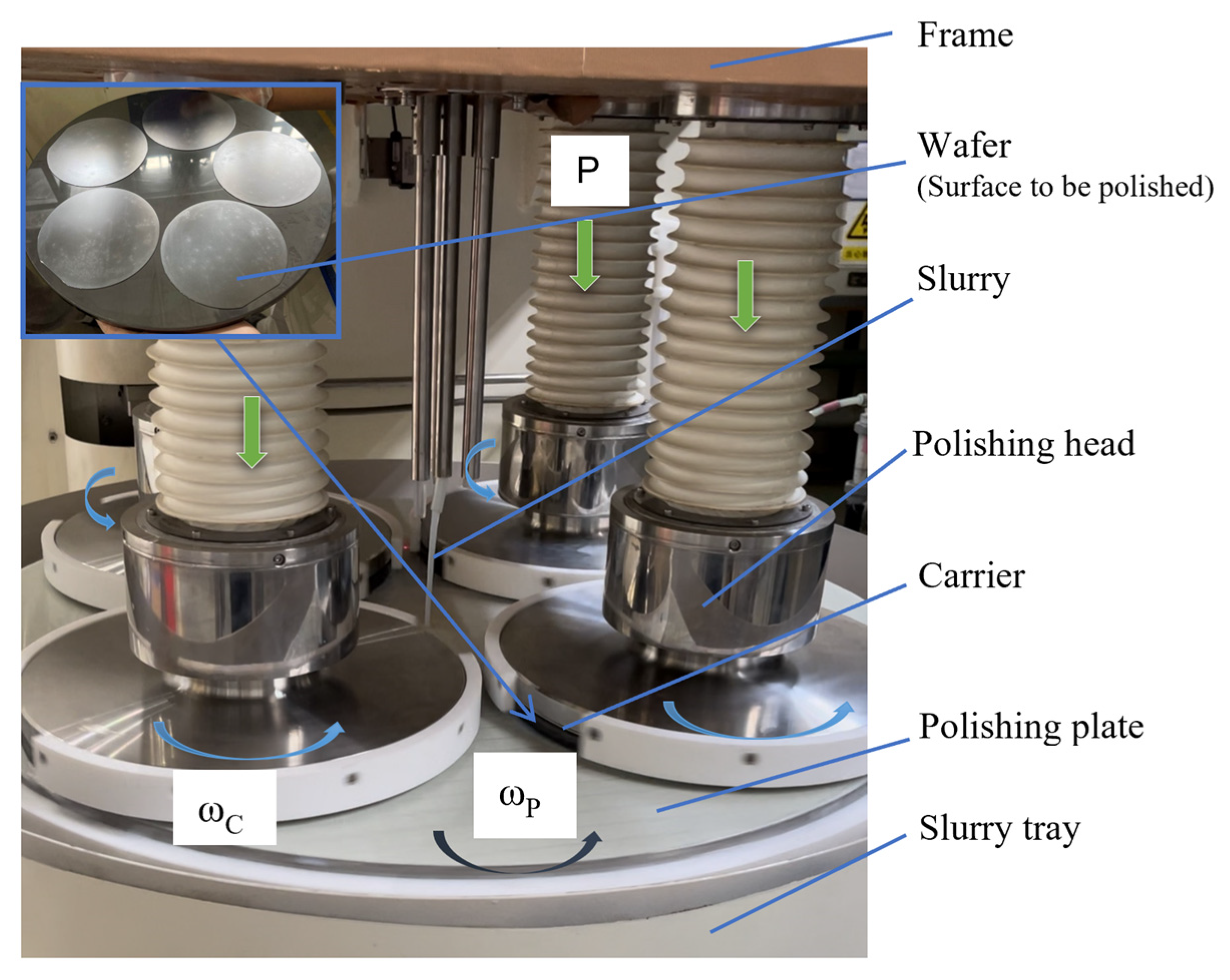
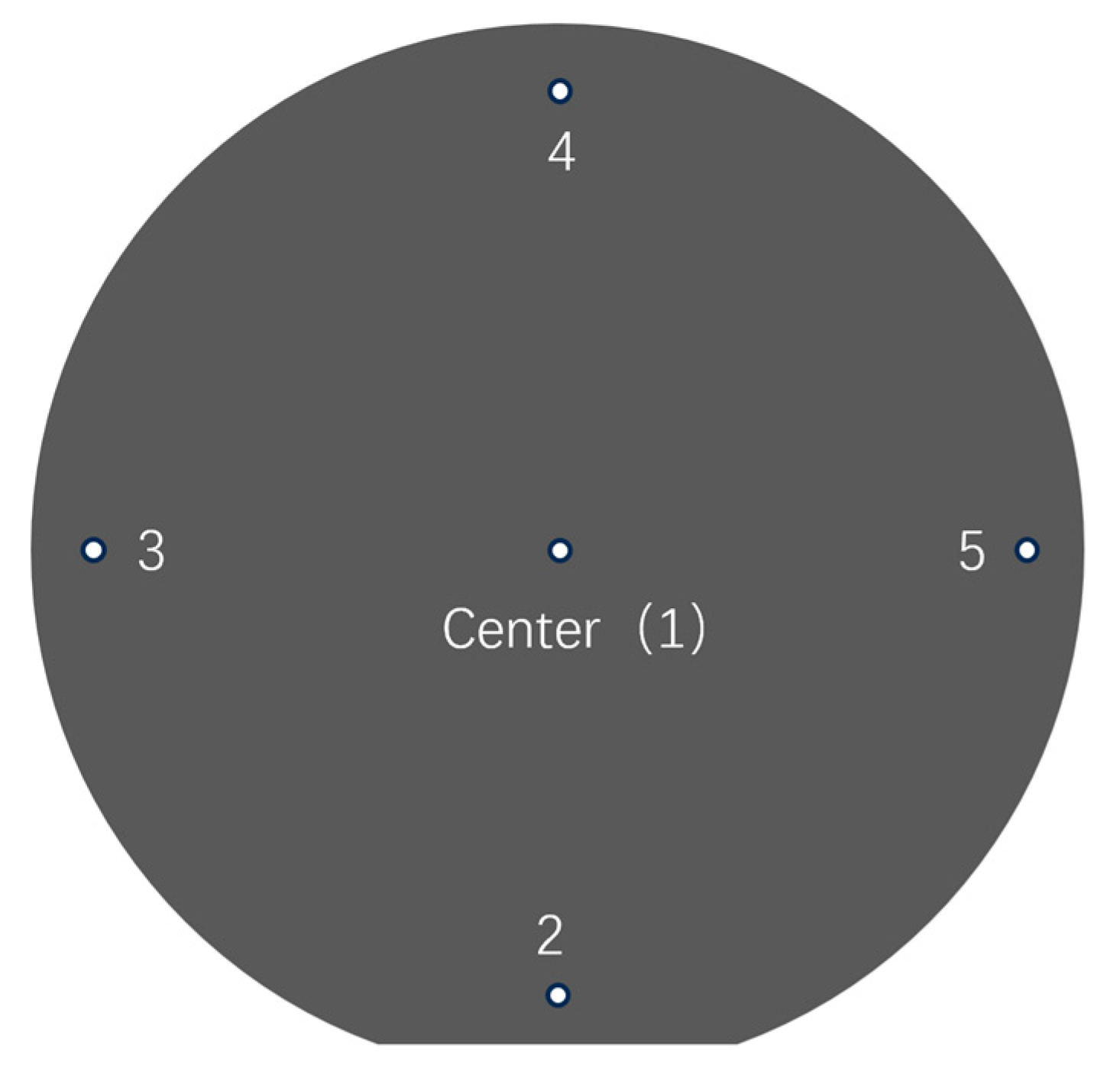
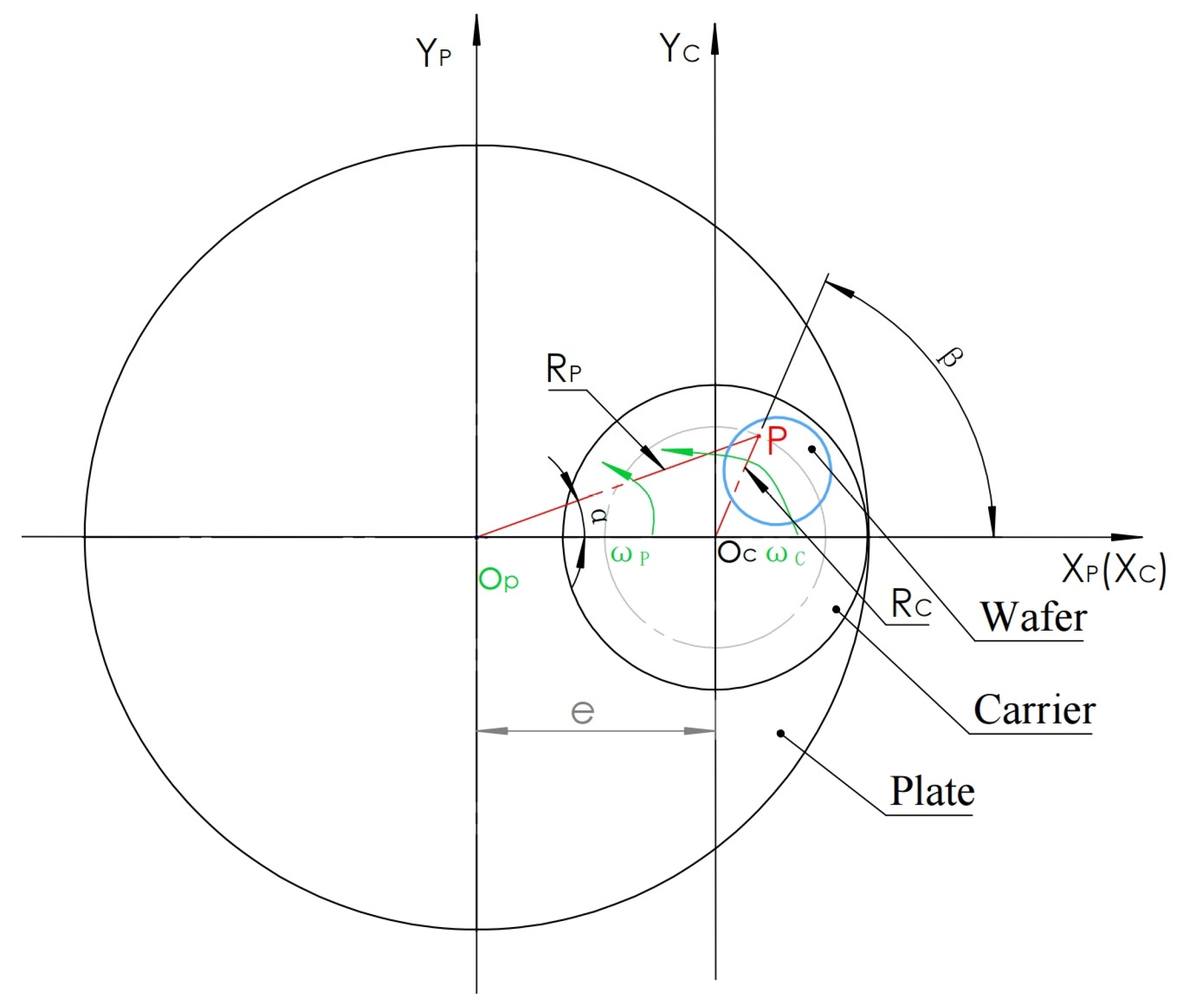
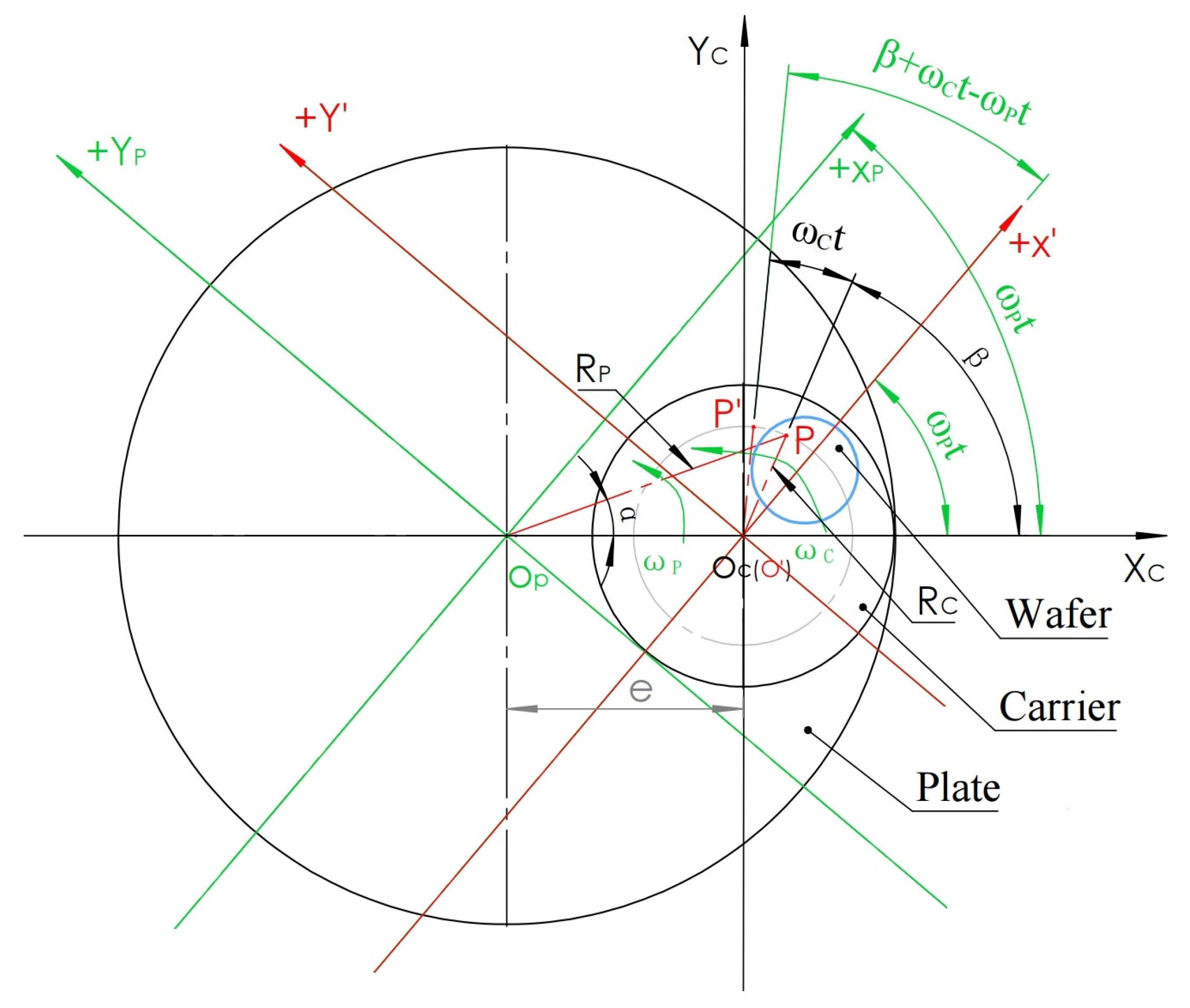

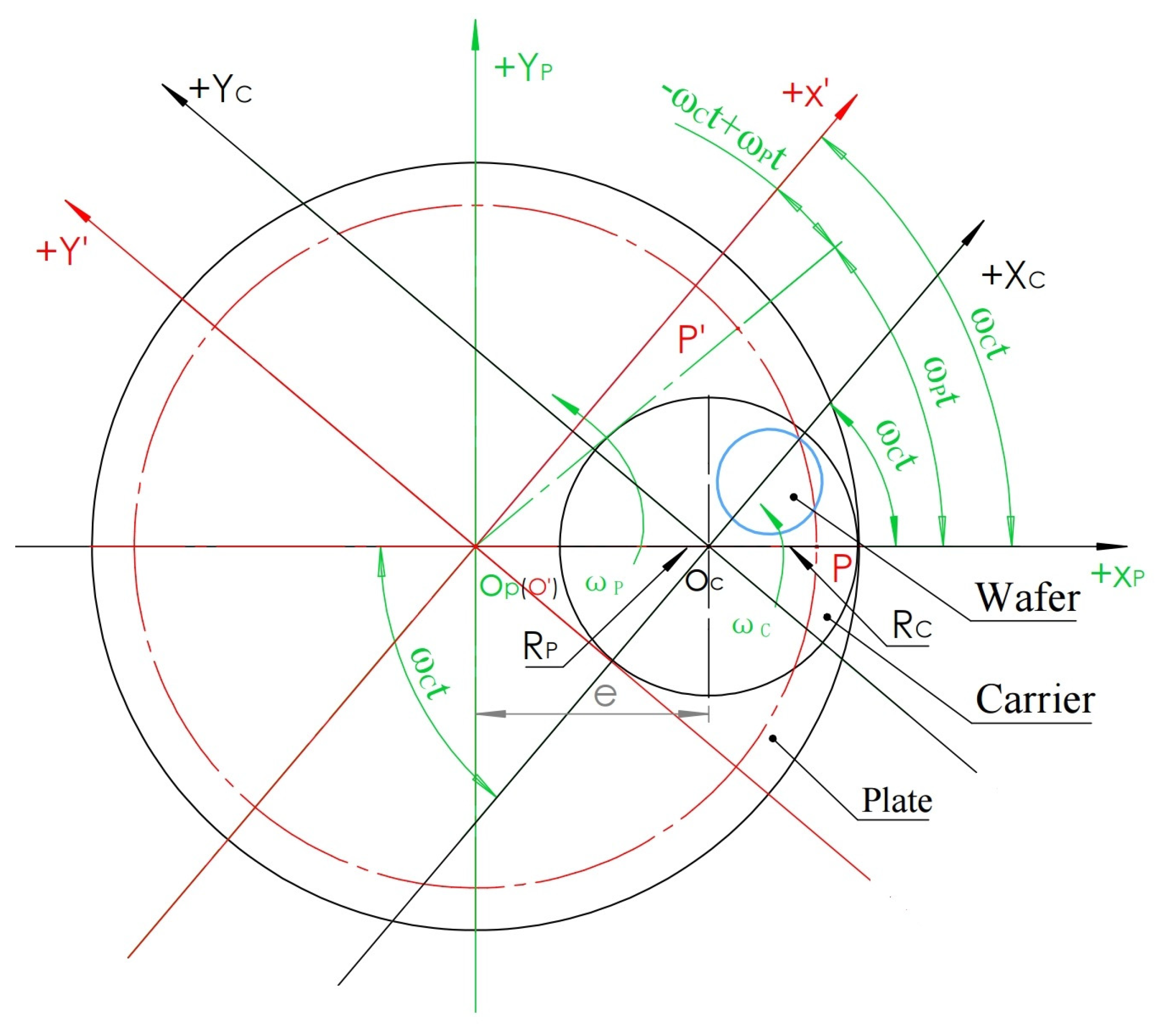
| Dimension | Radius (mm) |
|---|---|
| Carrier | 175 |
| Plate (Pad) | 457 |
| Wafer | 62.5 |
| e | 277.89 |
| Number | Rotation Speed of Plate (rpm) | Rotation Speed of Carrier (rpm) |
|---|---|---|
| (a) | 59 | 60 |
| (b) | 58 | 60 |
| (c) | 50 | 60 |
| (d) | 45 | 60 |
| (e) | 40 | 60 |
| (f) | 30 | 60 |
| (g) | 60 | 59 |
| (h) | 60 | 58 |
| (i) | 60 | 50 |
| (j) | 60 | 45 |
| (k) | 60 | 40 |
| (l) | 60 | 30 |
| (m) | 60 | 60 |
| (n) | 50 | 50 |
| (o) | 30 | 30 |
| (p) | 20 | 60 |
| (q) | 10 | 60 |
| (r) | 5 | 60 |
| Component | Configuration |
|---|---|
| Pad | MHTM-S15S (NITTA DuPont INCORPORATE, Osaka, Japan) Diameter: 914 mm |
| Polishing slurry | AJ-7120 colloided silica, Fujimi Corporation, Kiyosu, Aichi Prefecture, Japan Chemical additive: KOH, PH value of polishing solution: PH11 Flow rate: 2 L/min |
| Carrier | SiC ceramic (waxing with silicon wafers), 4pcs |
| workpiece | Material: Silicon wafer Diameter:125 mm, Thickness:540 μm Quantity: 4 × 5 = 20 |
| Applied load | 250 N (15 s) → 1050 N (29 min) → 250 N (75 s) |
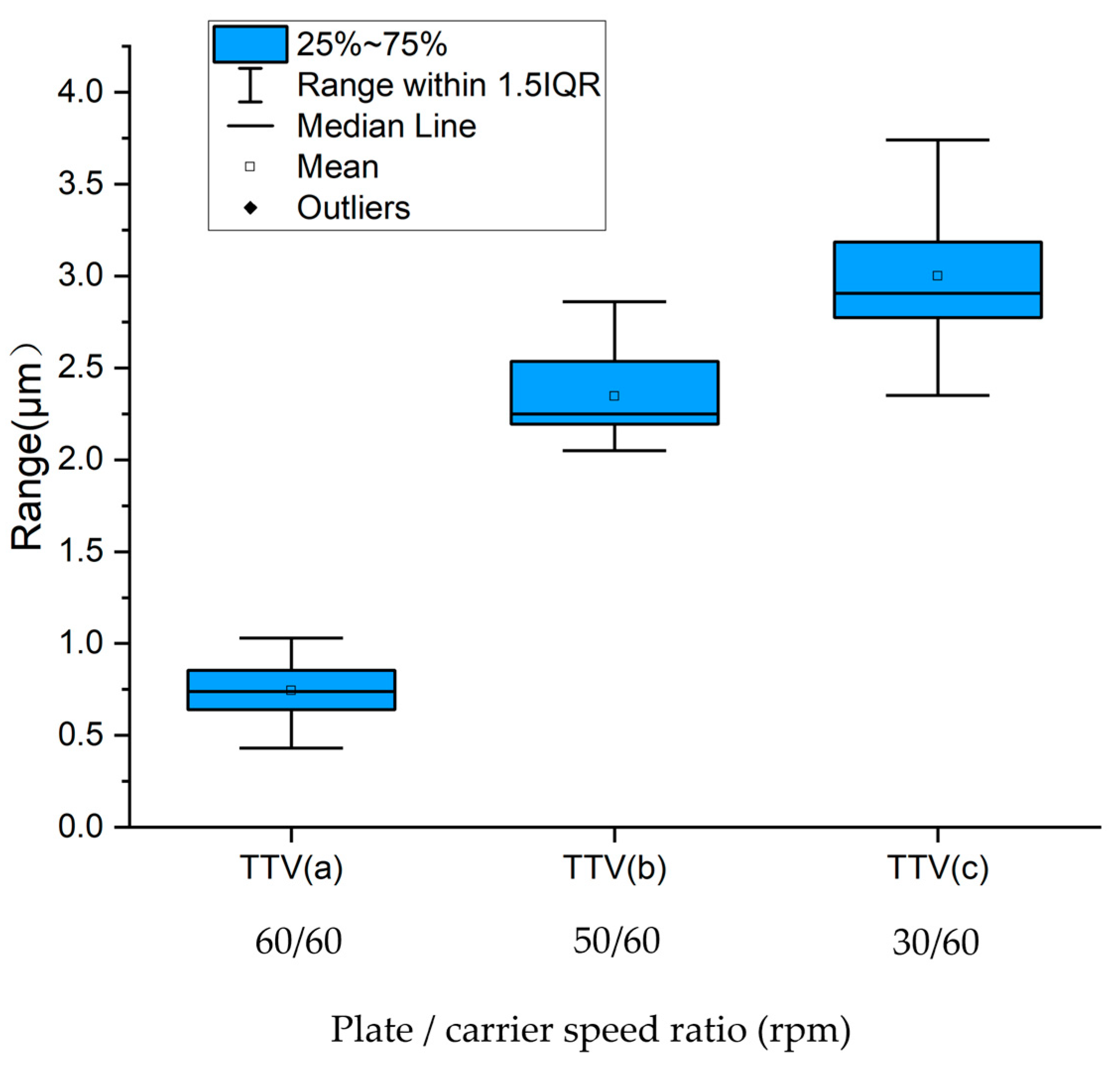
| Rotational speed of polishing plate/carrier | (a) 60 rpm/60 rpm (b) 50 rpm/60 rpm (c) 30 rpm/60 rpm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, G.; Yao, Z. Research on the Trajectory and Relative Speed of a Single-Sided Chemical Mechanical Polishing Machine. Micromachines 2025, 16, 450. https://doi.org/10.3390/mi16040450
Ye G, Yao Z. Research on the Trajectory and Relative Speed of a Single-Sided Chemical Mechanical Polishing Machine. Micromachines. 2025; 16(4):450. https://doi.org/10.3390/mi16040450
Chicago/Turabian StyleYe, Guoqing, and Zhenqiang Yao. 2025. "Research on the Trajectory and Relative Speed of a Single-Sided Chemical Mechanical Polishing Machine" Micromachines 16, no. 4: 450. https://doi.org/10.3390/mi16040450
APA StyleYe, G., & Yao, Z. (2025). Research on the Trajectory and Relative Speed of a Single-Sided Chemical Mechanical Polishing Machine. Micromachines, 16(4), 450. https://doi.org/10.3390/mi16040450






