Accelerated Electro-Optic Switching in Liquid Crystal Devices via Ion Trapping by Dispersed Helical Carbon Nanotubes
Abstract
1. Introduction
2. Materials
3. Experiments, Results, and Discussion
3.1. Ion Concentration
3.2. Rotational Viscosity
3.3. Dielectric Anisotropy
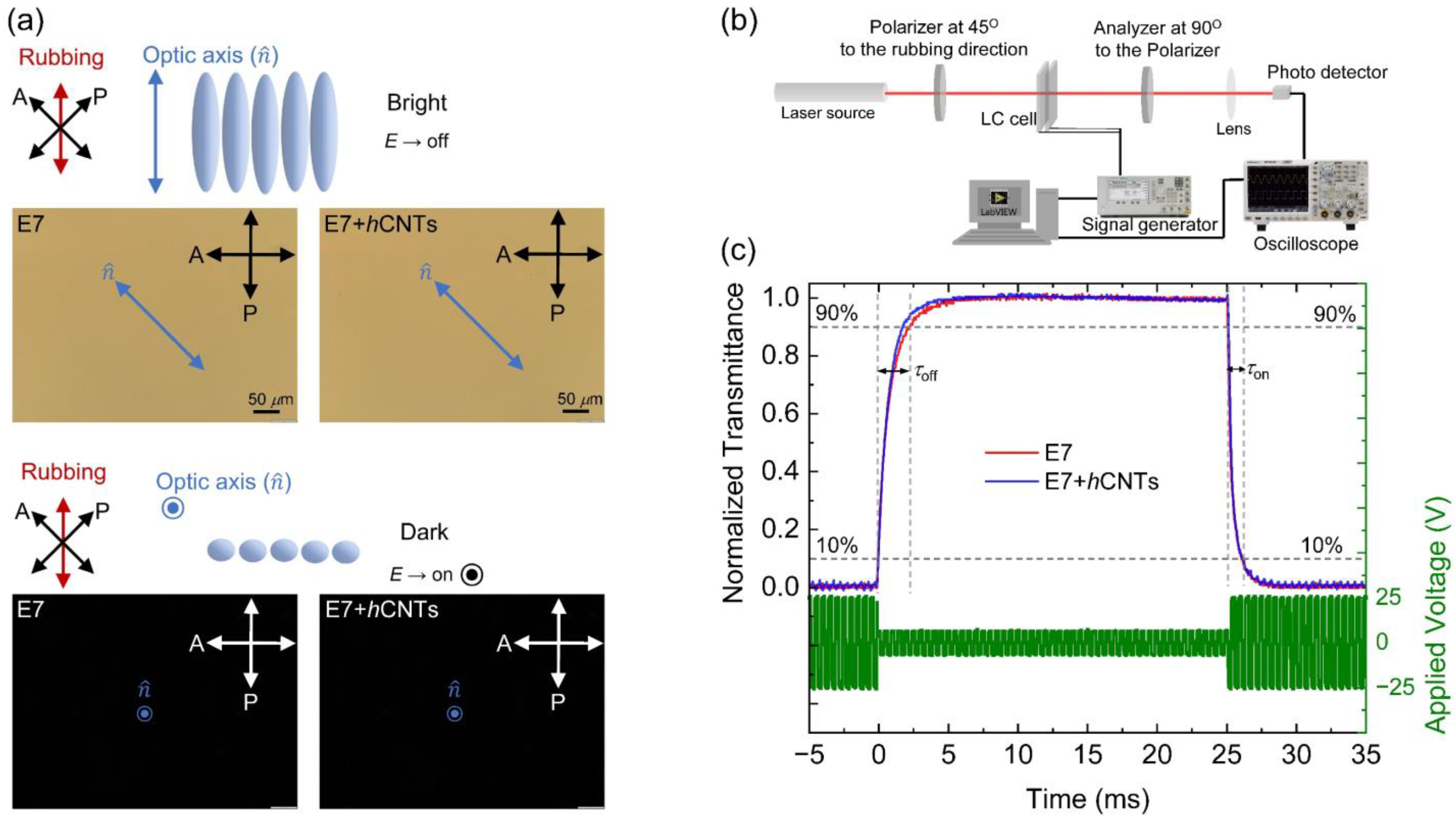
3.4. Electro-Optic Effect
3.5. The Effect of a Higher hCNTs Concentration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heilmeier, G.H.; Heyman, P.M. Note on Transient Current Measurements in Liquid Crystals and Related Systems. Phys. Rev. Lett. 1967, 18, 583–585. [Google Scholar] [CrossRef]
- Briere, G.; Gaspard, F.; Herino, R. Ionic residual conduction in the isotropic phase of a nematic liquid crystal. Chem. Phys. Lett. 1971, 9, 285–288. [Google Scholar] [CrossRef]
- Takahashi, S. The investigation of a dc induced transient optical 30-Hz element in twisted nematic liquid-crystal displays. J. Appl. Phys. 1991, 70, 5346–5350. [Google Scholar] [CrossRef]
- De Vleeschouwer, H.; Verweire, B.; D’Have, K.; Zhang, H. Electrical and Optical Measurements of the Image Sticking Effect in Nematic LCD’S. Mol. Cryst. Liq. Cryst. 1999, 331, 567–574. [Google Scholar] [CrossRef]
- De Vleeschouwer, H.; Bougrioua, F.; Pauwels, H. Importance of Ion Transport in Industrial LCD Applications. Mol. Cryst. Liq. Cryst. 2001, 360, 29–39. [Google Scholar] [CrossRef]
- Xu, D.; Peng, F.; Chen, H.; Yuan, J.; Wu, S.-T.; Li, M.-C.; Lee, S.-L.; Tsai, W.-C. Image sticking in liquid crystal displays with lateral electric fields. J. Appl. Phys. 2014, 116, 193102. [Google Scholar] [CrossRef]
- De Vleeschouwer, H.; Verschueren, A.; Bougrioua, F.; van Asselt, R.; Alexander, E.; Vermael, S.; Neyts, K.; Pauwels, H. Long-term Ion Transport in Nematic Liquid Crystal Displays. Jpn. J. Appl. Phys. 2001, 40, 3272–3276. [Google Scholar] [CrossRef]
- Yang, K.H. Charge retention of twisted nematic liquid-crystal displays. J. Appl. Phys. 1990, 67, 36–39. [Google Scholar] [CrossRef]
- Sasaki, N.A. New Measurement Method for Ion Density in TFT-LCD Panels. Mol. Cryst. Liq. Cryst. 2001, 367, 671–679. [Google Scholar] [CrossRef]
- Murakami, S.; Naito, H. Charge Injection and Generation in Nematic Liquid Crystal Cells. Jpn. J. Appl. Phys. 1997, 36, 773–776. [Google Scholar] [CrossRef]
- Naemura, S.; Sawada, A. Ion Generation in Liquid Crystals under Electric Field. Mol. Cryst. Liq. Cryst. 2000, 346, 155–168. [Google Scholar] [CrossRef]
- Van Aerle, N.A.J.M. Influence of Polyimide Orientation Layer Material on the Liquid Crystal Resistivity in LCDs. Mol. Cryst. Liq. Cryst. 1994, 257, 193–208. [Google Scholar] [CrossRef]
- Sierakowski, M. Ionic interface-effects in electro-optical LC-cells. Mol. Cryst. Liquid Cryst. 2002, 375, 659–677. [Google Scholar] [CrossRef]
- Hird, M. Fluorinated liquid crystals—Properties and applications. Chem. Soc. Rev. 2007, 36, 2070–2095. [Google Scholar] [CrossRef]
- Yang, D.-K.; Wu, S.-T. Fundamentals of Liquid Crystal Devices, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2014. [Google Scholar]
- Neyts, K.; Vermael, S.; Desimpel, C.; Stojmenovik, G.; van Asselt, R.; Verschueren, A.R.M.; de Boer, D.K.G.; Snijkers, R.; Machiels, P.; van Brandenburg, A. Lateral ion transport in nematic liquid-crystal devices. J. Appl. Phys. 2003, 94, 3891–3896. [Google Scholar] [CrossRef]
- Yamashita, M.; Amemiya, Y. Drift Mobility of Positive Ions in Nematic MBBA at Low Electric Field. Jpn. J. Appl. Phys. 1978, 17, 1513–1517. [Google Scholar] [CrossRef]
- Novotny, V. Measurement of mobilities of particles in liquids by optical and electrical transients. J. Appl. Phys. 1979, 50, 2787–2794. [Google Scholar] [CrossRef]
- Sugimura, A.; Matsui, N.; Takahashi, Y.; Sonomura, H.; Naito, H.; Okuda, M. Transient currents in nematic liquid crystals. Phys. Rev. B 1991, 43, 8272–8276. [Google Scholar] [CrossRef]
- Naito, H.; Okuda, M.; Sugimura, A. Transient discharging processes in nematic liquid crystals. Phys. Rev. A 1991, 44, R3434–R3497. [Google Scholar] [CrossRef]
- Naito, H.; Yoshida, K.; Okuda, M. Transient charging current in nematic liquid crystals. J. Appl. Phys. 1993, 73, 1119–1125. [Google Scholar] [CrossRef]
- Colpaert, C.; Maximus, B.; Meyere, A.D. Adequate measuring techniques for ions in liquid crystal layers. Liq. Cryst. 1996, 21, 133–142. [Google Scholar] [CrossRef]
- Sawada, A.; Manabe, A.; Nameura, S. A Comparative Study on the Attributes of Ions in Nematic and Isotropic Phases. Jpn. J. Appl. Phys. 2001, 40, 220–224. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Glushchenko, I. Nano-Objects and Ions in Liquid Crystals: Ion Trapping Effect and Related Phenomena. Crystals 2015, 5, 501–533. [Google Scholar] [CrossRef]
- Kumar, S. Liquid Crystals: Experimental Studies of Physical Properties and Phase Transitions, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Keller, P.; Liebert, L. Liquid crystal synthesis for physicists. In Liquid Crystals; Supplement, 14; Liebert, L., Ed.; Academic Press: New York, NY, USA, 1978; pp. 20–75. [Google Scholar]
- Haberfeld, J.L.; Hsu, E.C.; Johnson, J.F. Liquid crystal purification by zone refining. Mol. Cryst. Liquid Cryst. 1973, 24, 1–5. [Google Scholar] [CrossRef]
- Gaspard, F.; Herino, R.; Mondon, F. Low Field Conduction of Nematic Liquid Crystals Studied by Means of Electrodialysis. Mol. Cryst. Liquid Cryst. 1973, 24, 145–161. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Glushchenko, I. Ion trapping by means of ferroelectric nanoparticles, and the quantification of this process in liquid crystals. Appl. Phys. Lett. 2015, 107, 041106. [Google Scholar] [CrossRef]
- Basu, R.; Garvey, A. Effects of ferroelectric nanoparticles on ion transport in a liquid crystal. Appl. Phys. Lett. 2014, 105, 151905. [Google Scholar] [CrossRef]
- Ha, Y.-S.; Kim, H.-J.; Park, H.-G.; Seo, D.-S. Enhancement of electro-optic properties in liquid crystal devices via titanium nanoparticle doping. Opt. Express 2012, 20, 6448–6455. [Google Scholar] [CrossRef]
- Lee, C.-W.; Shih, W.-P. Quantification of ion trapping effect of carbon nanomaterials in liquid crystals. Mater. Lett. 2010, 64, 466–668. [Google Scholar] [CrossRef]
- Chen, H.Y.; Lee, W.; Clark, N.A. Faster electro-optical response characteristics of a carbon-nanotube-nematic suspension. Appl. Phys. Lett. 2007, 90, 033510. [Google Scholar] [CrossRef]
- Basu, R. Effects of graphene on electro-optic switching and spontaneous polarization of a ferroelectric liquid crystal. Appl. Phys. Lett. 2014, 105, 112905. [Google Scholar] [CrossRef]
- Basu, R.; Garvey, A.; Kinnamon, D. Effects of graphene on electro-optic response and ion-transport in a nematic liquid crystal. J. Appl. Phys. 2015, 117, 074301. [Google Scholar] [CrossRef]
- Wu, P.-W.; Lee, W. Phase and dielectric behaviors of a polymorphic liquid crystal doped with graphene nanoplatelets. Appl. Phys. Lett. 2013, 102, 162904. [Google Scholar] [CrossRef]
- Wu, P.-C.; Lisetski, L.N.; Lee, W. Suppressed ionic effect and low-frequency texture transitions in a cholesteric liquid crystal doped with graphene nanoplatelets. Opt. Express 2015, 23, 11195–11204. [Google Scholar] [CrossRef]
- Singh, D.P.; Gupta, S.K.; Vimal, T.; Manohar, R. Dielectric, electro-optical, and photoluminescence characteristics of ferroelectric liquid crystals on a graphene-coated indium tin oxide substrate. Phys. Rev. E 2014, 90, 022501. [Google Scholar] [CrossRef]
- Lee, W.; Wang, C.-Y.; Shih, Y.-C. Effects of carbon nanosolids on the electro-optical properties of a twisted nematic liquid-crystal host. Appl. Phys. Lett. 2004, 85, 513. [Google Scholar] [CrossRef]
- Shukla, R.K.; Raina, K.K.; Haase, W. Fast switching response and dielectric behaviour of fullerene/ferroelectric liquid crystal nanocolloids. Liq. Cryst. 2014, 41, 1726–1732. [Google Scholar] [CrossRef]
- Basu, R.; Gess, D. Ion trapping, reduced rotational viscosity, and accelerated electro-optic response characteristics in gold nano-urchin-nematic suspensions. Phys. Rev. E 2023, 107, 024705. [Google Scholar]
- Basu, R.; Lee, A. Ion trapping by the graphene electrode in a graphene-ITO hybrid liquid crystal cell. Appl. Phys. Lett. 2017, 111, 161905. [Google Scholar] [CrossRef]
- Basu, R.; Atwood, L. Reduced ionic effect and accelerated electro-optic response in a 2D hexagonal boron nitride planar-alignment agent based liquid crystal device. Opt. Mater. Express. 2019, 9, 1441–1449. [Google Scholar] [CrossRef]
- Basu, R. Reduced ionic effects and enhanced spontaneous polarization in a ferroelectric liquid crystal device employing a two-dimensional hexagonal boron nitride planar-alignment agent. Phys. Rev. E 2025, 111, 025402. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, Z.; Jia, A.; Yang, X.; Feng, W.; Wang, P.; Li, K.; Lei, W.; He, H.; Tian, Y.; et al. Controllable modification of helical carbon nanotubes for high-performance microwave absorption. Nanotechnol. Rev. 2021, 10, 671–679. [Google Scholar] [CrossRef]
- Vijayan, R.; Ghazinezami, A.; Taklimi, S.R.; Khan, M.Y.; Askari, D. The geometrical advantages of helical carbon nanotubes for high-performance multifunctional polymeric nanocomposites. Compos. Part B Eng. 2019, 156, 28–42. [Google Scholar] [CrossRef]
- Liu, M.; Cowley, J.M. Structures of the helical carbon nanotubes. Carbon 1994, 32, 393–403. [Google Scholar] [CrossRef]
- Park, K.A.; Lee, S.M.; Lee, S.H.; Lee, Y.H. Anchoring a Liquid Crystal Molecule on a Single-Walled Carbon Nanotube. J. Phys. Chem. C 2007, 111, 1620–1624. [Google Scholar] [CrossRef]
- Lynch, M.D.; Patrick, D.L. Organizing Carbon Nanotubes with Liquid Crystals. Nano Lett. 2002, 2, 1197–1201. [Google Scholar] [CrossRef]
- Dierking, I.; Scalia, G.; Morales, P. Liquid crystal–carbon nanotube dispersions. J. Appl. Phys. 2005, 97, 044309. [Google Scholar] [CrossRef]
- Basu, R.; Iannacchione, G.S. Orientational coupling enhancement in a carbon nanotube dispersed liquid crystal. Phys. Rev. E. 2010, 81, 051705. [Google Scholar] [CrossRef]
- Basu, R.; Garvey, A. Insulator-to-conductor transition in liquid crystal-carbon nanotube nanocomposites. J. Appl. Phys. 2016, 120, 164309. [Google Scholar] [CrossRef]
- Basu, R.; Boccuzzi, K.; Ferjani, S.; Rosenblatt, C. Carbon nanotube induced chirality in an achiral liquid crystal. Appl. Phys. Lett. 2010, 97, 121908. [Google Scholar] [CrossRef]
- Kalakonda, P.; Basu, R.; Nemitz, I.R.; Rosenblatt, C.; Iannacchione, G.S. Studies of nanocomposites of carbon nanotubes and a negative dielectric anisotropy liquid crystal. J. Chem. Phys. 2014, 140, 104908. [Google Scholar] [CrossRef] [PubMed]
- Basu, R.; Chen, C.-L.; Rosenblatt, C. Carbon nanotube-induced macroscopic helical twist in an achiral nematic liquid crystal. J. Appl. Phys. 2011, 109, 083518. [Google Scholar] [CrossRef]
- Lu, Y.; Chien, L.C. Carbon nanotube doped liquid crystal OCB cells: Physical and electro-optical properties. Opt. Express 2008, 16, 12777–12785. [Google Scholar] [CrossRef] [PubMed]
- Basu, R.; Atwood, L. Homeotropic liquid crystal device employing vertically aligned carbon nanotube arrays as the alignment agent. Phys. Rev. E 2020, 102, 022701. [Google Scholar] [CrossRef]
- Basu, R.; Gess, D. Electro-optic hybrid aligned nematic device utilizing carbon nanotube arrays and two-dimensional hexagonal boron nitride nanosheet as alignment substrates. Phys. Rev. E 2021, 104, 054702. [Google Scholar] [CrossRef]
- Zou, Z.; Clark, N.A.; Handschy, M.A. Ionic transport effects in SSFLC cells. Ferroelectrics 1991, 121, 147–158. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 1st ed.; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Liu, H.-H.; Lee, W. Ionic properties of liquid crystals dispersed with carbon nanotubes and montmorillonite nanoplatelets. Appl. Phys. Lett. 2010, 97, 173501. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Wen, H.; Cao, L.; Xiao, W.; Zhao, J.; Nan, Z.; Zhang, S.; Qiu, S.; Li, Q. Length-controlled sorting and length-dependent properties of short semiconducting single-walled carbon nanotubes. Carbon 2023, 215, 118468. [Google Scholar] [CrossRef]
- Imai, M.; Naito, H.; Okuda, M.; Okuda, M.; Sugimura, A. Determination of rotational viscosity of nematic liquid crystals from transient current numerical analysis and experiment. Jpn. J. Appl. Phys. 1994, 33, 3482–3487. [Google Scholar] [CrossRef]
- Imai, M.; Naito, H.; Okuda, M.; Sugimura, A. Determination of rotational viscosity and pretilt angle in nematic liquid crystals from transient current influence of ionic conduction. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A 1995, 259, 37–46. [Google Scholar] [CrossRef]
- Imai, M.; Naito, H.; Okuda, M.; Sugimura, A. A method for determination of rotational viscosity and pretilt angle from transient current in twisted nematic liquid crystal cells. Jpn. J. Appl. Phys. 1995, 34, 3170–3176. [Google Scholar] [CrossRef]
- Rastogi, A.; Pandey, F.; Manohar, R.; Singh, S. Effect of Doping of Cd1_xZnxS/ZnS Core/Shell Quantum Dots in Negative Dielectric Anisotropy Nematic Liquid Crystal p-Methoxybenzylidene p-Decylaniline. Crystals 2021, 11, 605. [Google Scholar] [CrossRef]
- Basu, R.; Atwood, L.J.; Sterling, G.W. Dielectric and electro-optic effects in a nematic liquid crystal doped with h-BN flakes. Crystals 2020, 10, 123. [Google Scholar] [CrossRef]
- Demus, D.; Goodby, J.; Gary, G.W.; Spiess, H.-W.; Vill, V. Physical Properties of Liquid Crystals, 1st ed.; Wiley VCH: Weinheim, Germany, 1999. [Google Scholar]
- Yadav, G.; Katiyar, R.; Pathak, G.; Manohar, R. Effect of ion trapping behavior of TiO2 nanoparticles on different parameters of weakly polar nematic liquid crystal. J. Theor. Appl. Phys. 2018, 12, 191–198. [Google Scholar] [CrossRef]
- Nie, X.; Lu, R.; Xianyu, H.; Wu, T.X.; Wu, S.T. Anchoring energy and cell gap effects on liquid crystal response time. J. Appl. Phys. 2007, 101, 103110. [Google Scholar] [CrossRef]
- Wu, S.T.; Wu, C.S. High-speed liquid-crystal modulators using transient nematic effect. J. Appl. Phys. 1989, 65, 527–532. [Google Scholar] [CrossRef]
- Wu, S.T.; Wu, C.S. Small angle relaxation of highly deformed nematic liquid crystals. Appl. Phys. Lett. 1988, 53, 1794–1796. [Google Scholar] [CrossRef]
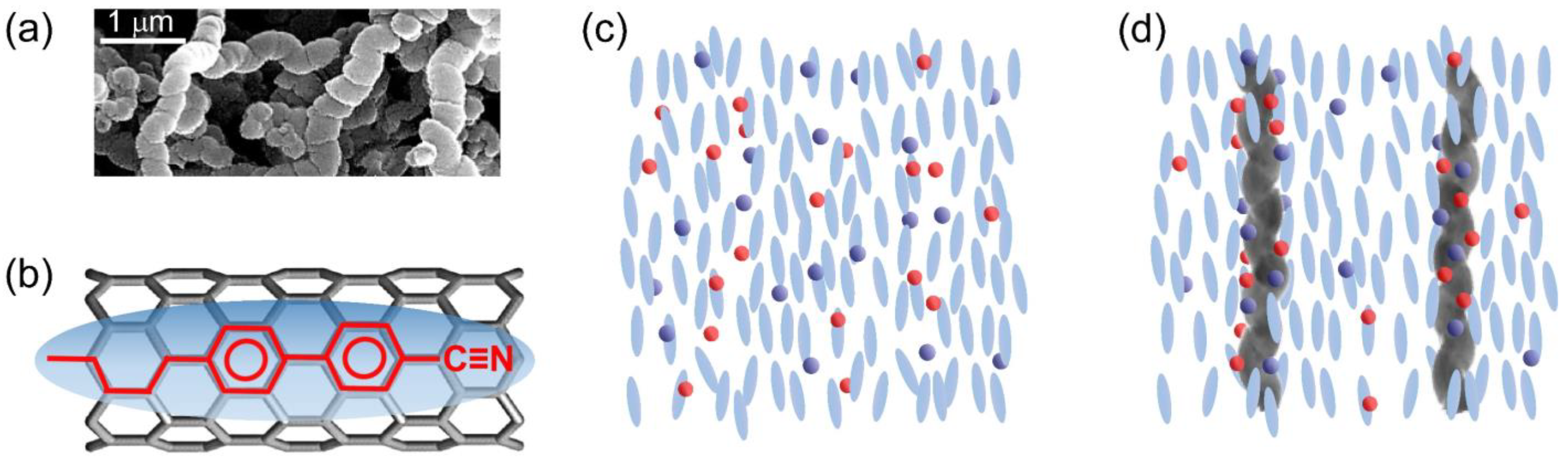
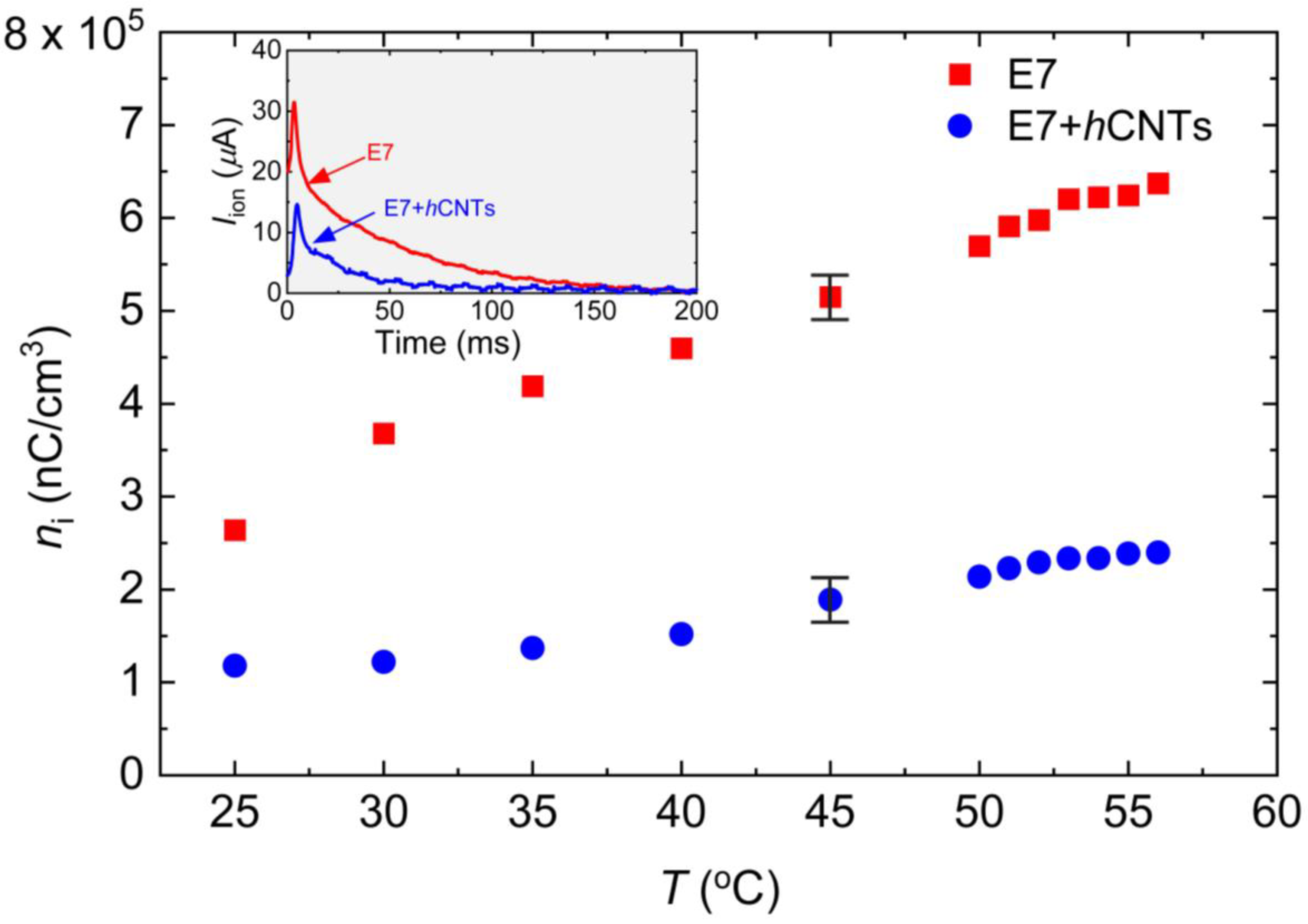
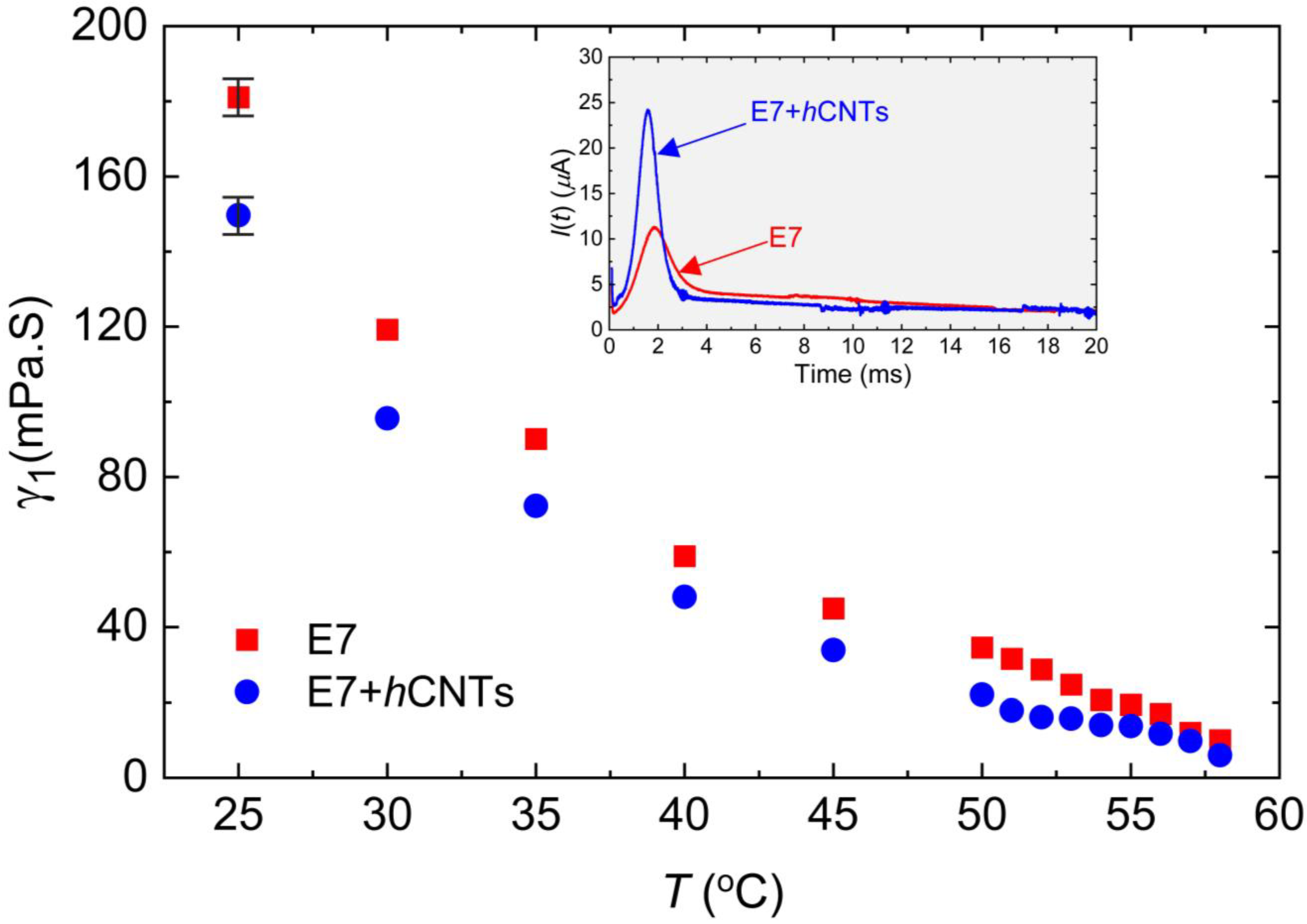
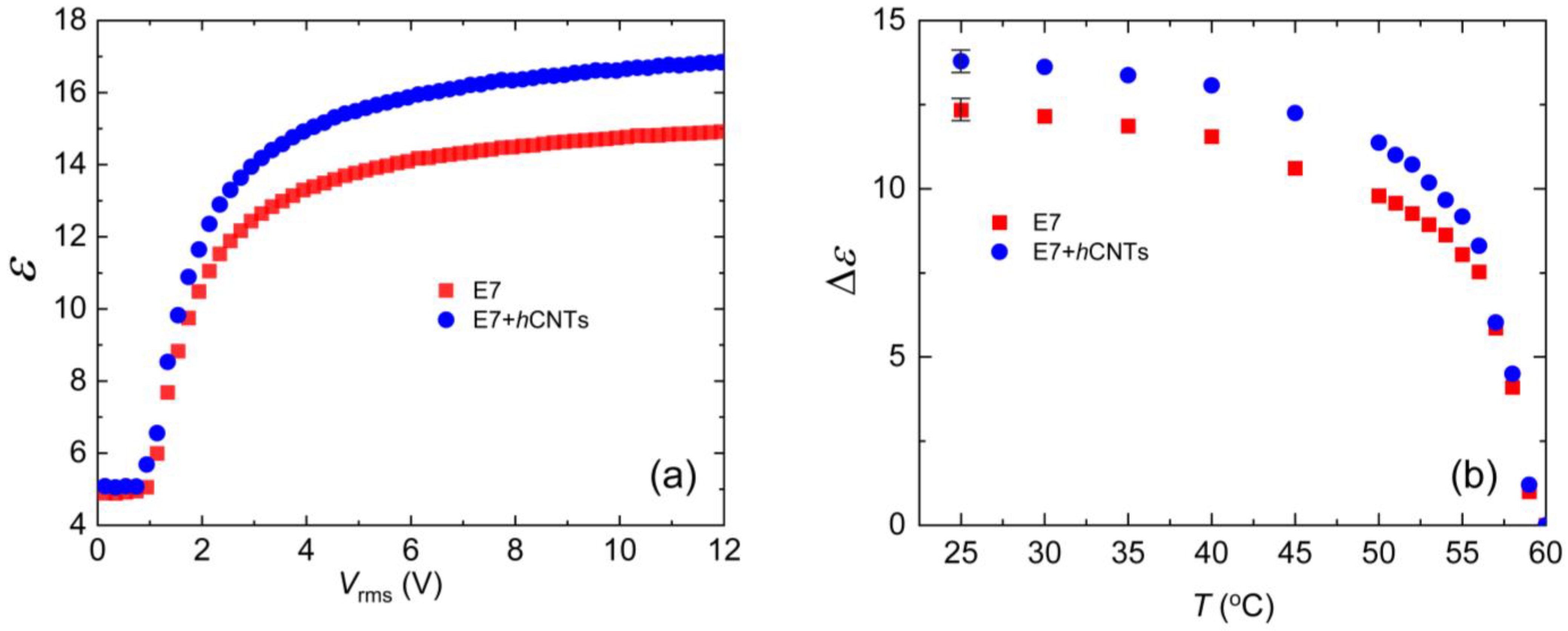

| Samples | τon (μs) | τoff (ms) |
|---|---|---|
| E7 | 970 | 2.40 |
| E7 + hCNTs | 930 | 1.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basu, R.; Kehr, C.C. Accelerated Electro-Optic Switching in Liquid Crystal Devices via Ion Trapping by Dispersed Helical Carbon Nanotubes. Micromachines 2025, 16, 457. https://doi.org/10.3390/mi16040457
Basu R, Kehr CC. Accelerated Electro-Optic Switching in Liquid Crystal Devices via Ion Trapping by Dispersed Helical Carbon Nanotubes. Micromachines. 2025; 16(4):457. https://doi.org/10.3390/mi16040457
Chicago/Turabian StyleBasu, Rajratan, and Christian C. Kehr. 2025. "Accelerated Electro-Optic Switching in Liquid Crystal Devices via Ion Trapping by Dispersed Helical Carbon Nanotubes" Micromachines 16, no. 4: 457. https://doi.org/10.3390/mi16040457
APA StyleBasu, R., & Kehr, C. C. (2025). Accelerated Electro-Optic Switching in Liquid Crystal Devices via Ion Trapping by Dispersed Helical Carbon Nanotubes. Micromachines, 16(4), 457. https://doi.org/10.3390/mi16040457






