A 3D DC Electric Field Meter Based on Sensor Chips Packaged Using a Highly Sensitive Scheme
Abstract
1. Introduction
- A moistureproof packaging structure has been incorporated into the design of the new 3D field meter to counter the effects of ambient humidity on the measurement’s accuracy.
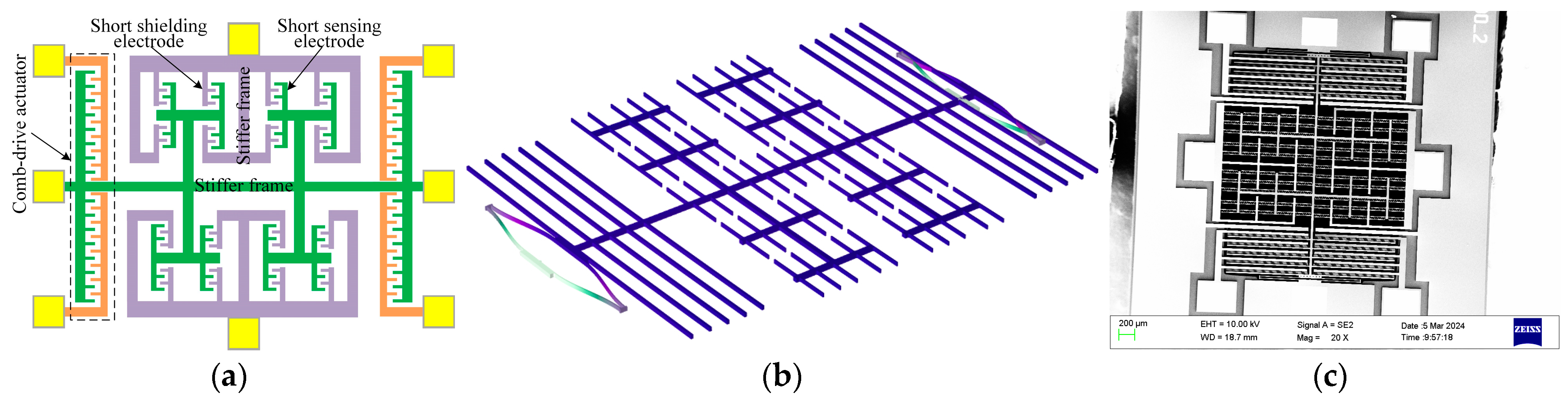
- The sensing units of the EFSCs use a combination of hard frames and short strip-type beams to improve vibration stability.
- Contrary to the flat packaging covers on EFSCs reported previously, the EFSCs in the proposed structure use inward-convex packaging covers, further improving the sensitivity of the 3D field meter.
- The proposed solution necessitates only the detecting electrodes to be assembled orthogonally, with no restrictions on the arrangement of EFSCs—a welcome flexibility for the EFM’s implementation.
- Unlike 3D EFMs in previous papers which contained probes separated from their signal conditioning circuit, and conveyed signals through wires, the proposed 3D field meter has been designed as an integrated structure. Here the data are transmitted wirelessly, eradicating potential issues of detection results being affected by the ground potential due to changes in the installation location of the signal conditioning circuit.
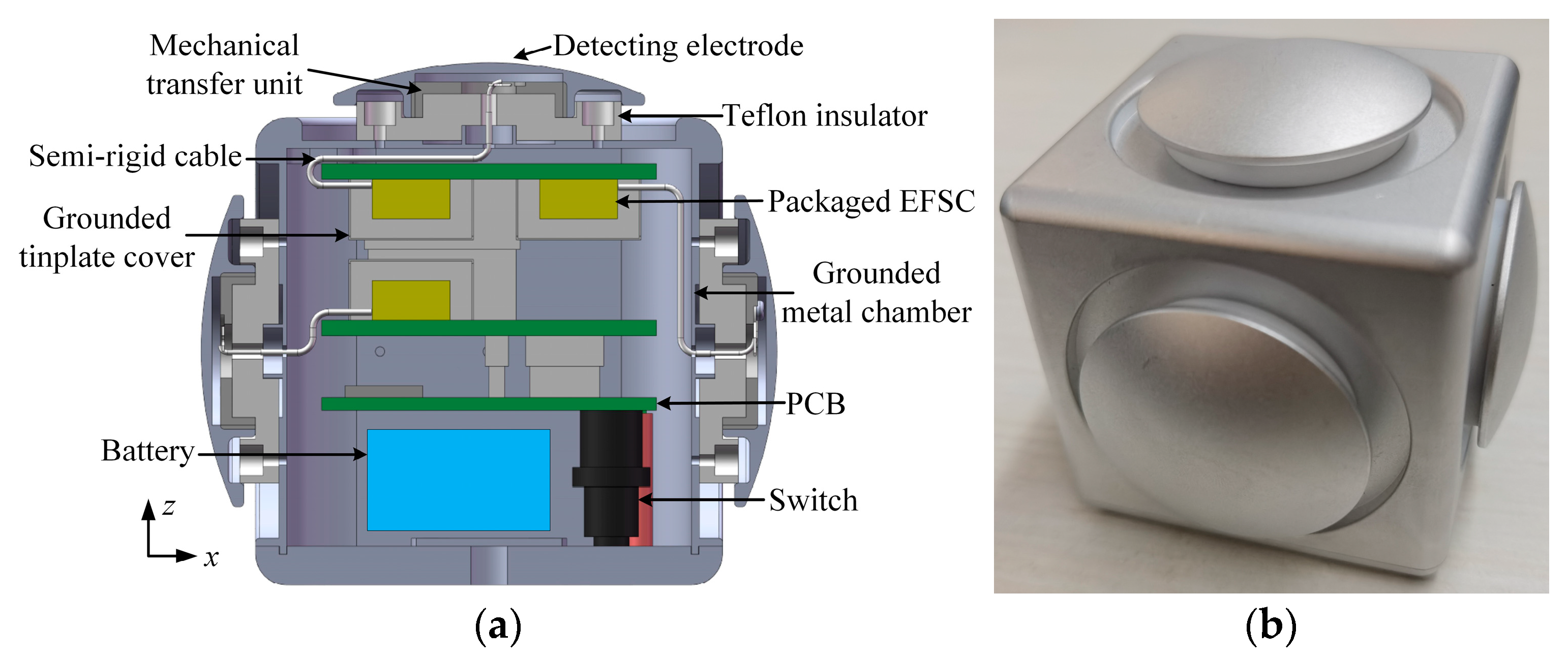
2. Microsensor and Its Package
3. Vector Fieldmeter
3.1. Anti-Humidity Scheme and Structural Arrangement
3.2. Measurement Principle
4. Numerical Simulation
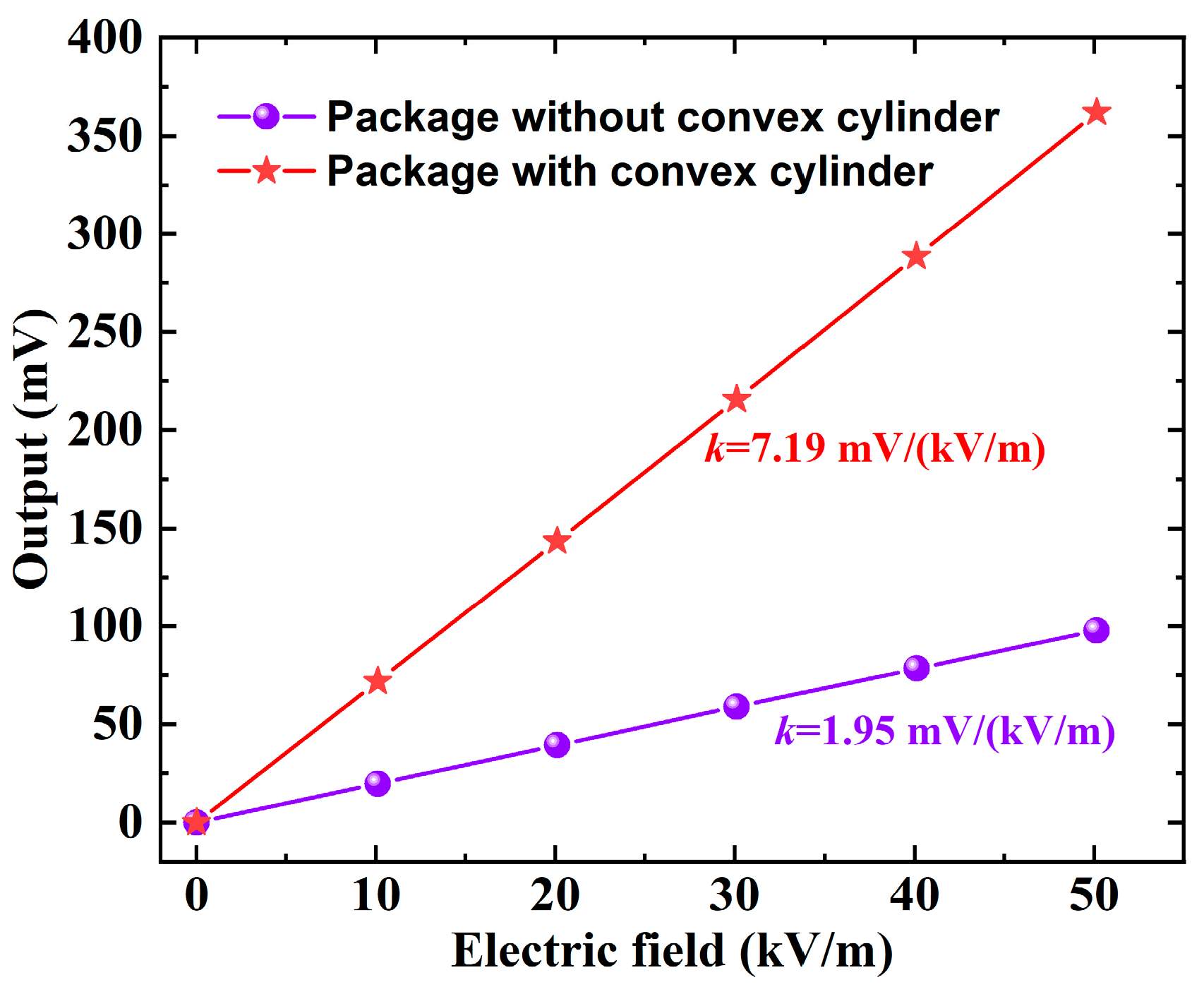
4.1. Simulation of Highly Sensitive Package
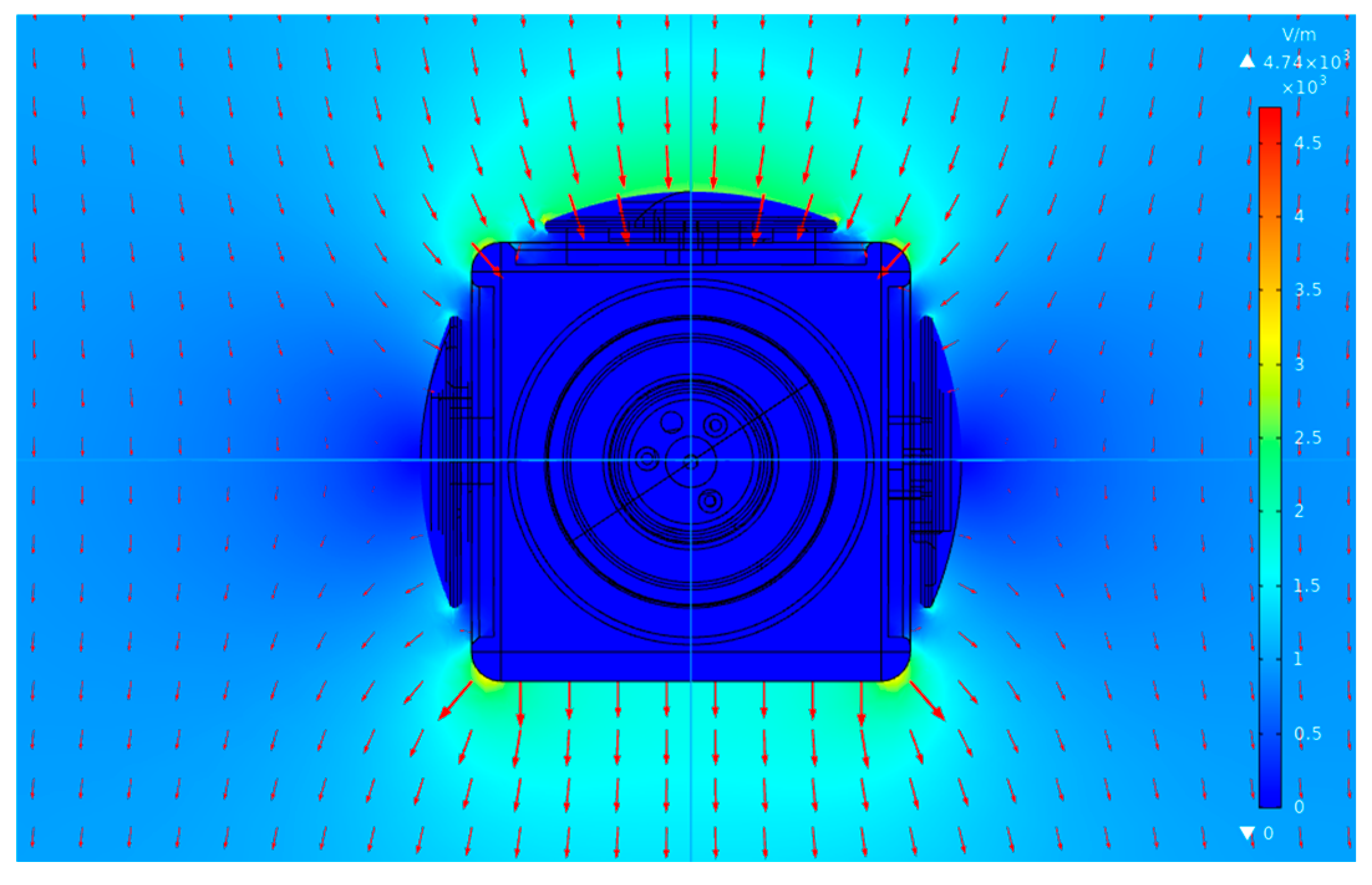
4.2. Simulation of 3D EFM Structure
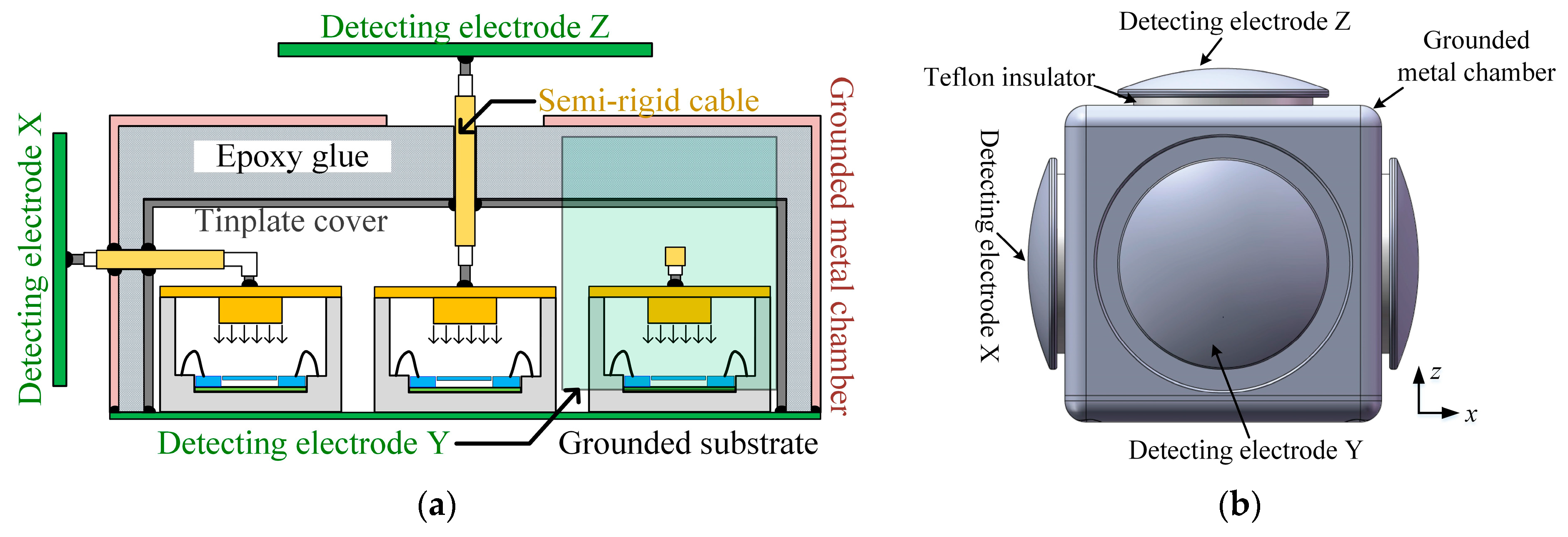
5. Implementation
5.1. Proposed Structure
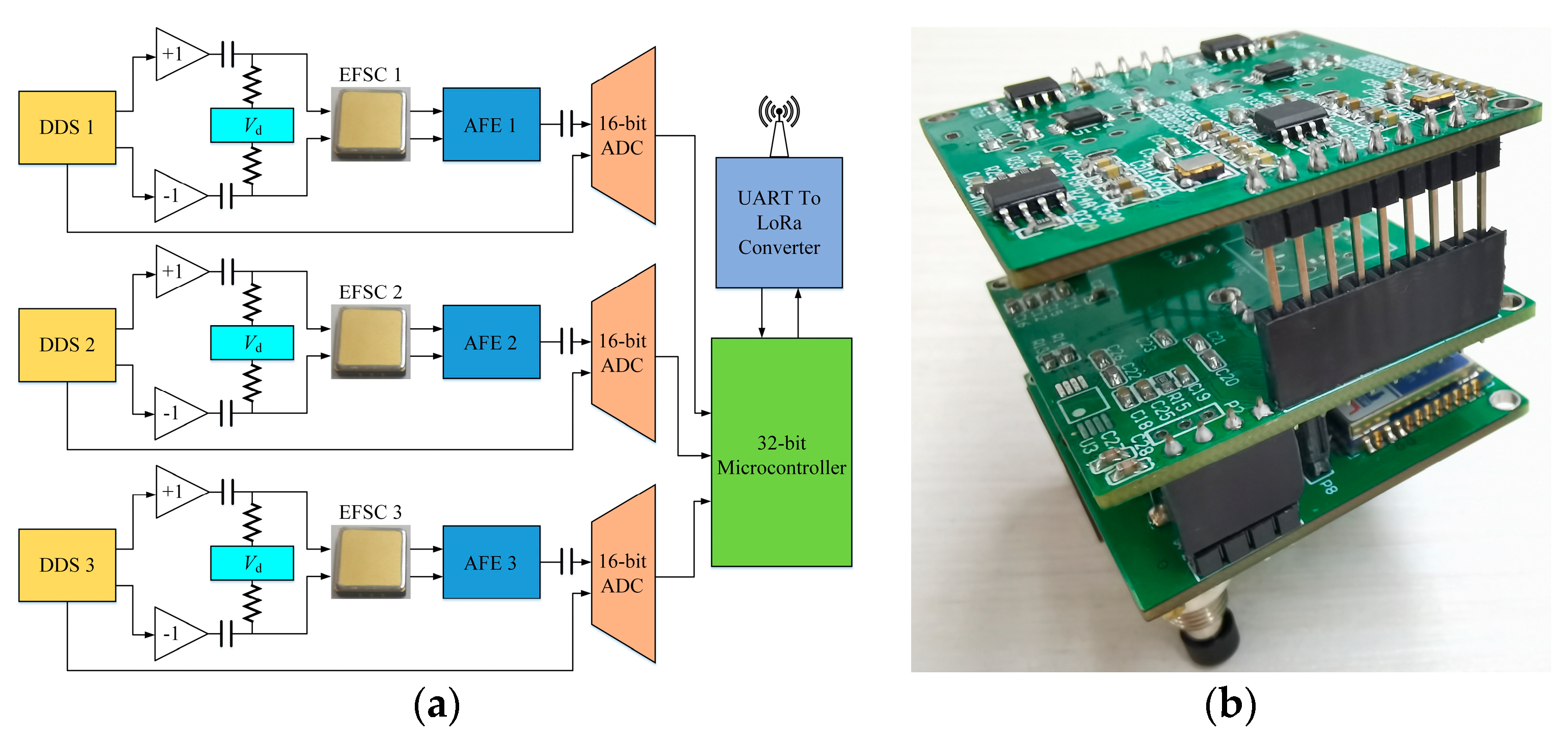
5.2. Interface Circuit
6. Experimental Results
6.1. Experiment Setup
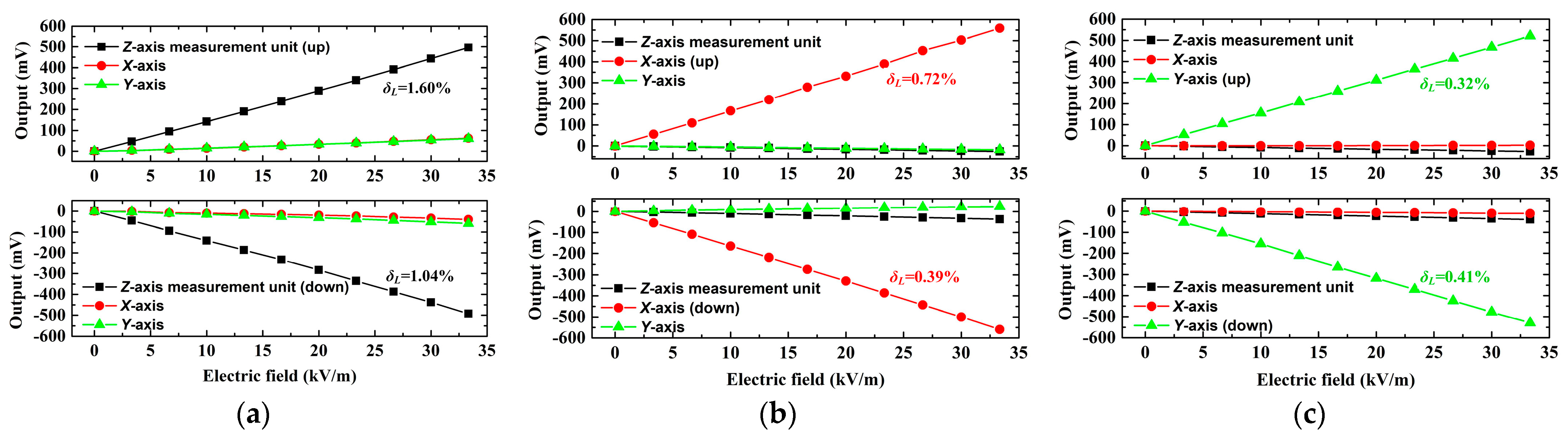
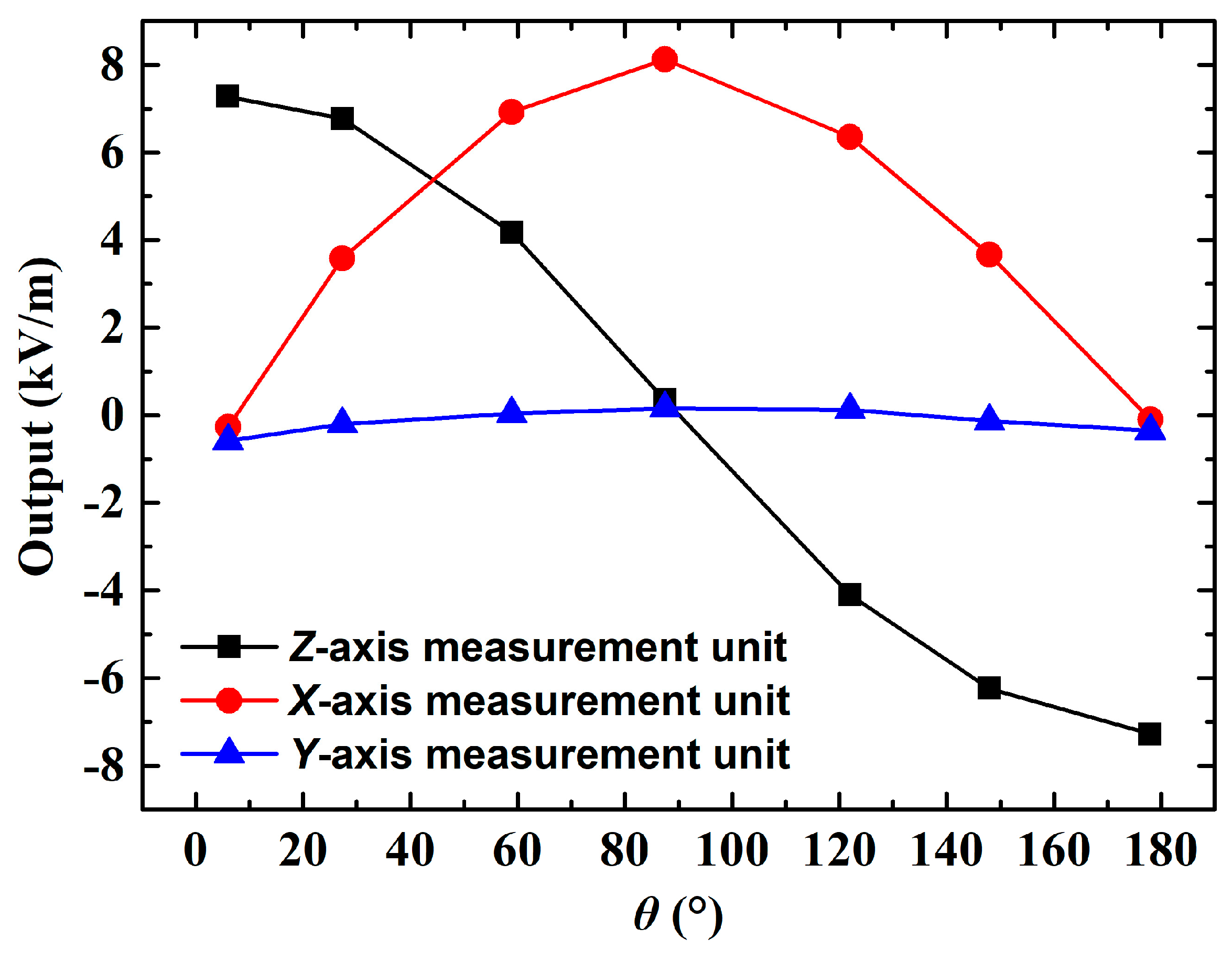
6.2. Sensitivity Matrix
6.3. Vector Electric Field Verification Tests
6.4. Moistureproof Verification Tests
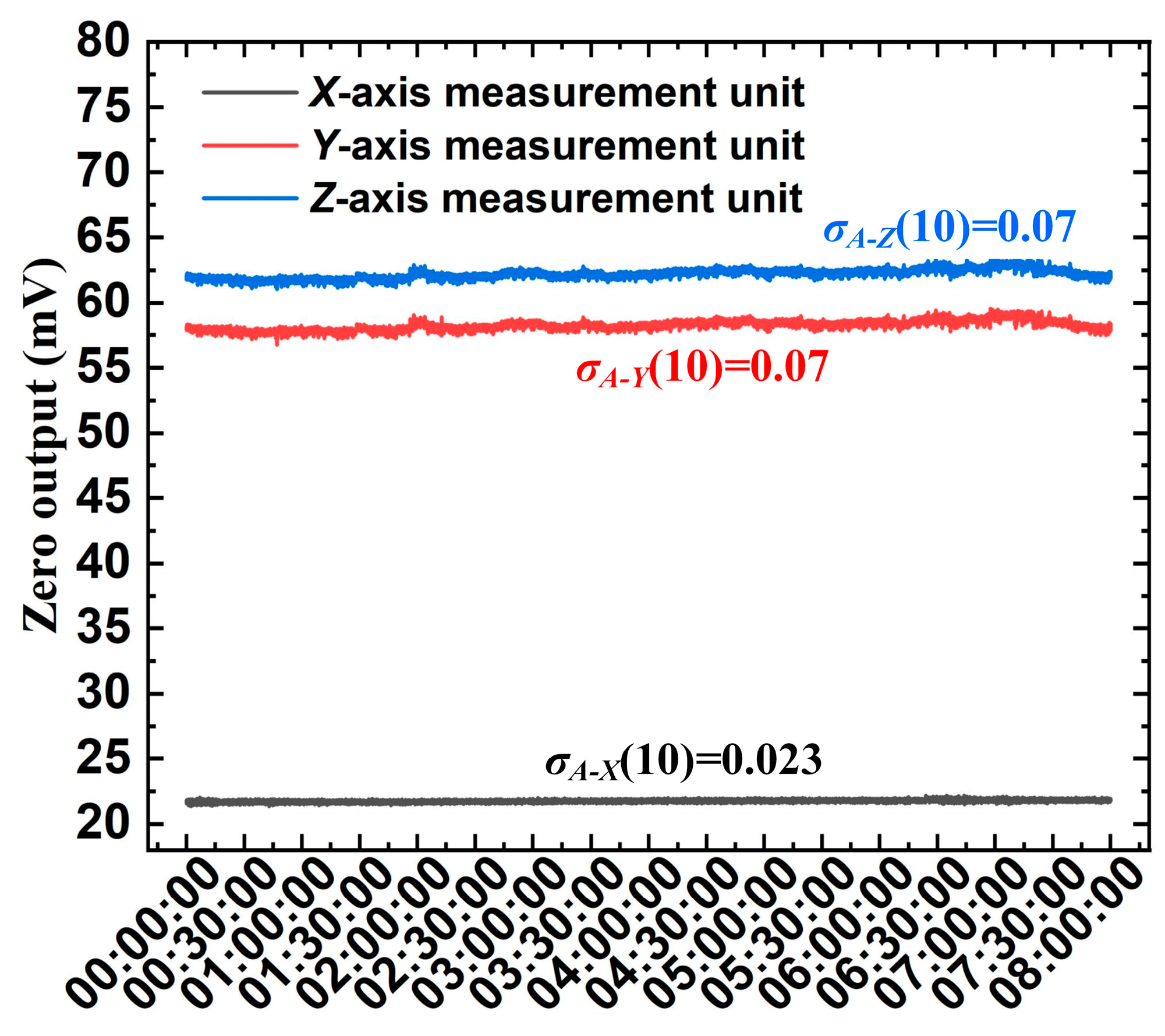
6.5. Zero Output Tests and Resolution Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, P.; Wen, X.; Lv, Y.; Chu, Z.; Peng, C.; Liu, Y.; Wu, S. Improved microsensor-based fieldmeter for ground-level atmospheric electric field Measurements. IEEE Trans. Instrum. Meas. 2022, 71, 2001510. [Google Scholar] [CrossRef]
- Fort, A.; Mugnaini, M.; Vignoli, V.; Rocchi, S.; Perini, F.; Monari, J. Design, modeling, and test of a system for atmospheric electric field measurement. IEEE Trans. Instrum. Meas. 2011, 60, 2778–2785. [Google Scholar] [CrossRef]
- Wijeweera, G.; Bahreyni, B.; Shafai, C.; Rajapakse, A.; Swatek, D. Micromachined electric-field sensor to measure AC and DC fields in power systems. IEEE Trans. Power Delivery. 2009, 24, 988–995. [Google Scholar] [CrossRef]
- Williams, K.R.; De Bruyker, D.P.H.; Limb, S.J.; Amendt, E.M.; Overland, D.A. Vacuum steered-electron electric-field sensor. J. Microelectromech. Syst. 2014, 23, 157–167. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, R.; Zhuang, C.; Lyu, G.; Yu, J.; Niu, B.; Li, C. Measuring AC/DC hybrid electric field using an integrated optical electric field sensor. Electr. Power Syst. Res. 2020, 179, 106087. [Google Scholar] [CrossRef]
- Song, B.; Zhou, R.; Yang, X.; Zhang, S.; Yang, N.; Fang, J.; Song, F.; Zhang, G. Surface electrostatic discharge of charged typical space materials induced by strong electromagnetic interference. J. Phys. D Appl. Phys. 2021, 54, 275002. [Google Scholar] [CrossRef]
- Cui, Y.; Yuan, H.; Song, X.; Zhao, L.; Liu, Y.; Lin, L. Model, design, and testing of field mill sensors for measuring electric fields under high-voltage direct-current power lines. IEEE Trans. Ind. Electron. 2018, 65, 608–615. [Google Scholar] [CrossRef]
- Harrison, R.G.; Marlton, G.J. Fair weather electric field meter for atmospheric science platforms. J. Electrost. 2020, 107, 103489. [Google Scholar] [CrossRef]
- Tantisattayakul, T.; Masugata, K.; Kitamura, I.; Kontani, K. Development of the hybrid electric field meter for simultaneous measuring of vertical and horizontal electric fields of the thundercloud. IEEE Trans. Electromagn. Compat. 2006, 48, 435–438. [Google Scholar] [CrossRef]
- Xing, H.; Yang, X.; Zhang, J. Thunderstorm cloud localization algorithm and performance analysis of a three-dimensional atmospheric electric field apparatus. J. Electr. Eng. Technol. 2019, 14, 2487–2495. [Google Scholar] [CrossRef]
- Liu, C.; Yuan, H.; Lv, J.; Zhao, P.; Li, J.; Xu, H. A sensor for 3-D component measurement of synthetic electric field vector in HVDC transmission lines using unidirectional motion. IEEE Trans. Instrum. Meas. 2022, 72, 1500110. [Google Scholar] [CrossRef]
- Ravichandran, M.; Kamra, A.K. Spherical field meter to measure the electric field vector—Measurements in fair weather and inside a dust devil. Rev. Sci. Instrum. 1999, 70, 2140–2149. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, L.; Xie, X.; Xiao, D.; He, W. Optimization design and research character of the passive electric field sensor. IEEE Sens. J. 2014, 14, 508–513. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, F.; Sun, B.; Chen, K.; Li, C. 3D Integrated optical e-field sensor for lightning electromagnetic impulse measurement. IEEE Photonics Technol. Lett. 2014, 26, 2353–2356. [Google Scholar] [CrossRef]
- Wen, X.; Fang, D.; Peng, C.; Yang, P.; Zheng, F.; Xia, S. Three dimensional electric field measurement method based on coplanar decoupling structure. In Proceedings of the 2014 IEEE SENSORS, Valencia, Spain, 2–5 November 2014; pp. 582–585. [Google Scholar]
- Li, B.; Peng, C.; Zheng, F.; Ling, B.; Chen, B.; Xia, S. A decoupling calibration method based on genetic algorithm for three dimensional electric field sensor. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Ling, B.; Wang, Y.; Peng, C.; Li, B.; Chu, Z.; Li, B.; Xia, S. Single-chip 3D electric field microsensor. Front. Mech. Eng. 2017, 12, 581–590. [Google Scholar] [CrossRef]
- Ling, B.; Peng, C.; Ren, R.; Chu, Z.; Zhang, Z.; Lei, H.; Xia, S. Design, fabrication and characterization of a MEMS-based three-dimensional electric field sensor with low cross-axis coupling interference. Sensors 2018, 18, 870. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Zhang, Z.; Liu, X.; Gao, Y.; Zhang, W.; Xing, X.; Liu, Y.; Peng, C.; Xia, S. A single-chip 3-D electric field microsensor with piezoelectric excitation. IEEE Trans. Electron Devices 2023, 70, 4359–4365. [Google Scholar] [CrossRef]
- Yang, P.; Wen, X.; Chu, Z.; Ni, X.; Peng, C. AC/DC fields demodulation methods of resonant electric field microsensor. Micromachines 2020, 11, 511. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Wen, X.; Chu, Z.; Ni, X.; Peng, C. Non-intrusive DC voltage measurement based on resonant electric field microsensors. J. Micromech. Microeng. 2021, 31, 064001. [Google Scholar] [CrossRef]
- IEEE Standard 644; IEEE Standard Procedures for Measurement of Power Frequency Electric and Magnetic Fields from AC Power Lines. IEEE: Piscataway, NY, USA, 2019.
- Ling, B.; Peng, C.; Ren, R.; Zheng, F.; Chu, Z.; Zhang, Z.; Lei, H.; Xia, S. A microassembled triangular-prism-shape three-dimensional electric field sensor. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 222–225. [Google Scholar]
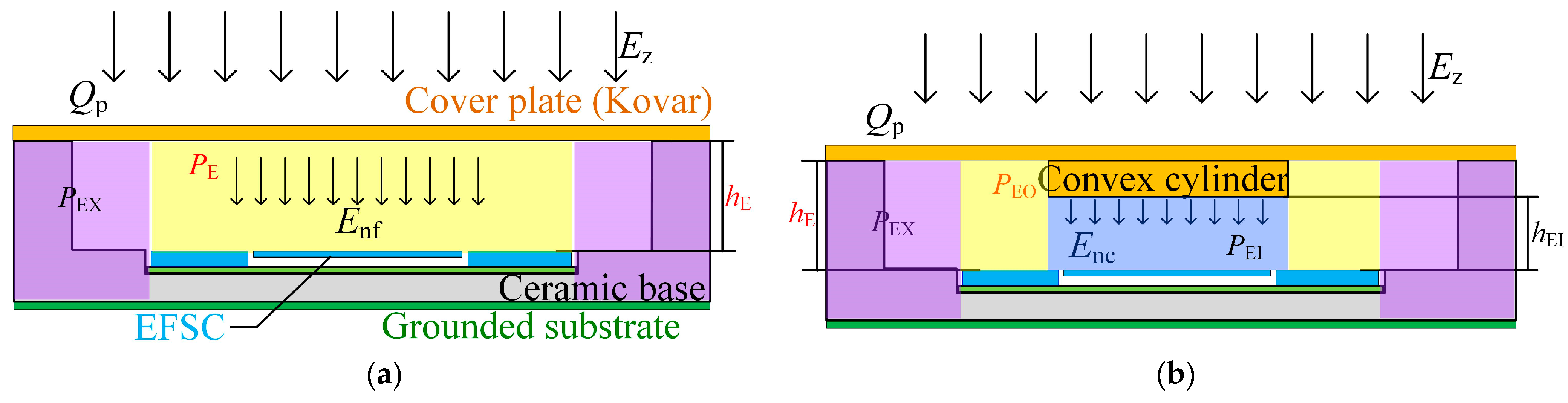


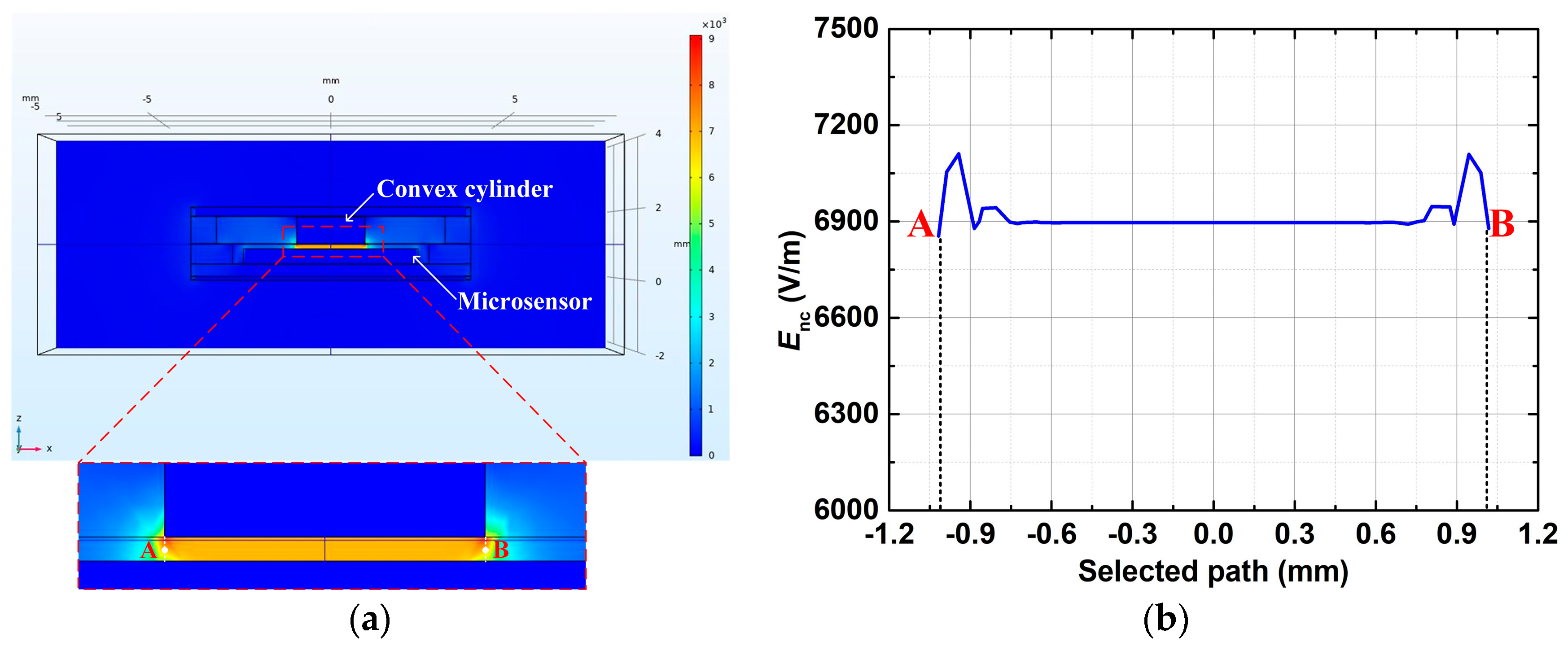



| Capacitance | Packaging Region |
|---|---|
| The whole package | |
| , yellow-colored region in Figure 2a | |
| , purple-colored region in Figure 2a | |
| , yellow-colored region in Figure 2b | |
| , light blue-colored region in Figure 2b |
| MEMS-Based 3D EFM | Year | ||
|---|---|---|---|
| Assembled 3D EFM with three 1D EFSCs [16] | 2016 | 3.18 | 3.53 |
| Single-chip 3D EFM based on in-plane rotary mechanism [17] | 2017 | 0.10 | 0.14 |
| Assembled 3D EFM with low cross-axis interference [18] | 2018 | 0.33 | 0.46 |
| Microassembled 3D EFM [23] | 2019 | 0.33 | 1.48 |
| Single-chip 3D EFM with piezoelectric excitation [19] | 2023 | 0.23 | 2.19 |
| This work | 2024 | 14.78 | 16.77 |
| (°) | (°) | Estimated Electric Field (kV/m) | RD (%) |
|---|---|---|---|
| 174 | 10 | 10.03 | 0.3 |
| 135 | 86 | 9.85 | −1.5 |
| 32 | 88 | 10.01 | 0.1 |
| 4 | 51 | 10.10 | 1.0 |
| 34 | 277 | 9.93 | −0.7 |
| 71 | 277 | 9.80 | −2.0 |
| 122 | 275 | 10.22 | 2.2 |
| 165 | 301 | 10.01 | 0.1 |
| Type | Duration (min) | (%) | |
|---|---|---|---|
| Non-moistureproof | 10 | 1.77 | 12.32 |
| 20 | 1.16 | 19.55 | |
| 30 | 1.04 | 29.63 | |
| Moistureproof | 30 | 15.04 | 0.32 |
| 60 | 15.05 | 0.18 | |
| 120 | 15.04 | 0.26 | |
| 180 | 14.95 | 0.77 | |
| 240 | 15.03 | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Wen, X.; Li, X.; Chu, Z.; Peng, C.; Wu, S. A 3D DC Electric Field Meter Based on Sensor Chips Packaged Using a Highly Sensitive Scheme. Micromachines 2025, 16, 484. https://doi.org/10.3390/mi16040484
Yang P, Wen X, Li X, Chu Z, Peng C, Wu S. A 3D DC Electric Field Meter Based on Sensor Chips Packaged Using a Highly Sensitive Scheme. Micromachines. 2025; 16(4):484. https://doi.org/10.3390/mi16040484
Chicago/Turabian StyleYang, Pengfei, Xiaolong Wen, Xiaonan Li, Zhaozhi Chu, Chunrong Peng, and Shuang Wu. 2025. "A 3D DC Electric Field Meter Based on Sensor Chips Packaged Using a Highly Sensitive Scheme" Micromachines 16, no. 4: 484. https://doi.org/10.3390/mi16040484
APA StyleYang, P., Wen, X., Li, X., Chu, Z., Peng, C., & Wu, S. (2025). A 3D DC Electric Field Meter Based on Sensor Chips Packaged Using a Highly Sensitive Scheme. Micromachines, 16(4), 484. https://doi.org/10.3390/mi16040484






