Predicting Thermal Conductivity of Nanoparticle-Doped Cutting Fluid Oils Using Feedforward Artificial Neural Networks (FFANN)
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivation and Contributions
1.3. Organization of the Study
2. Nanofluid Material Preparation, Thermal Conductivity, and Dataset
2.1. Nanofluid Preparation
2.2. Thermal Conductivity and Its Measurements
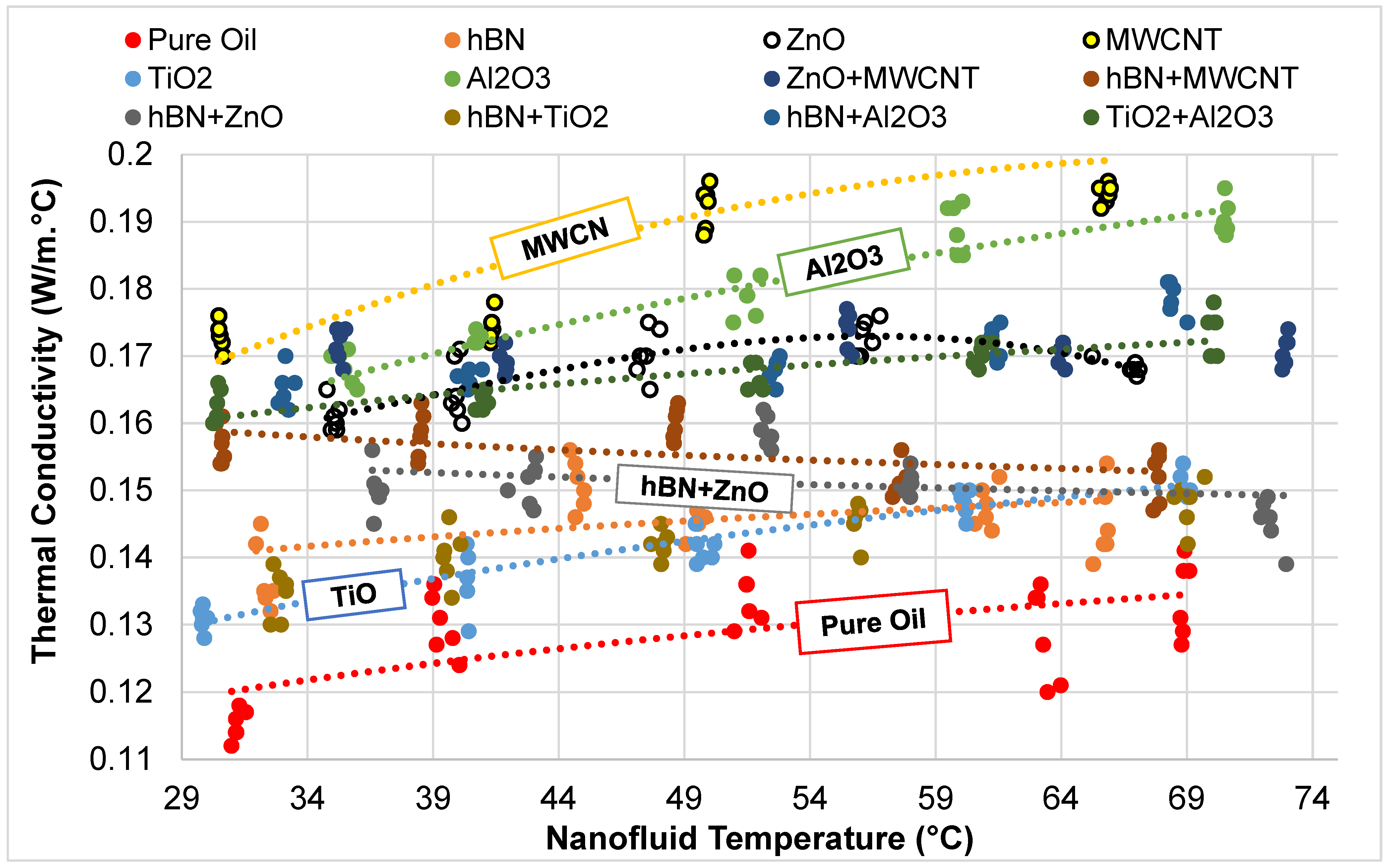
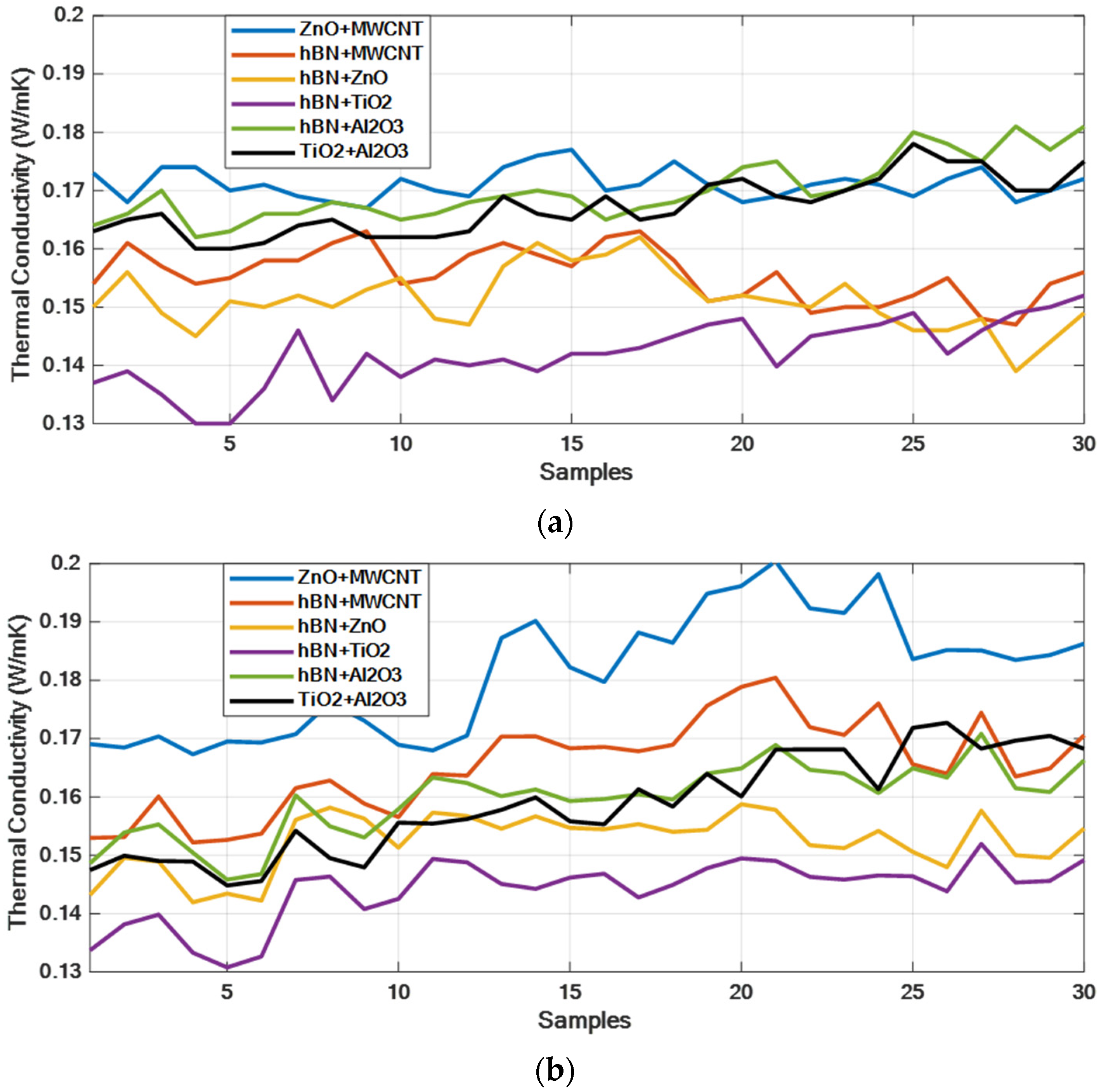
2.3. Dataset
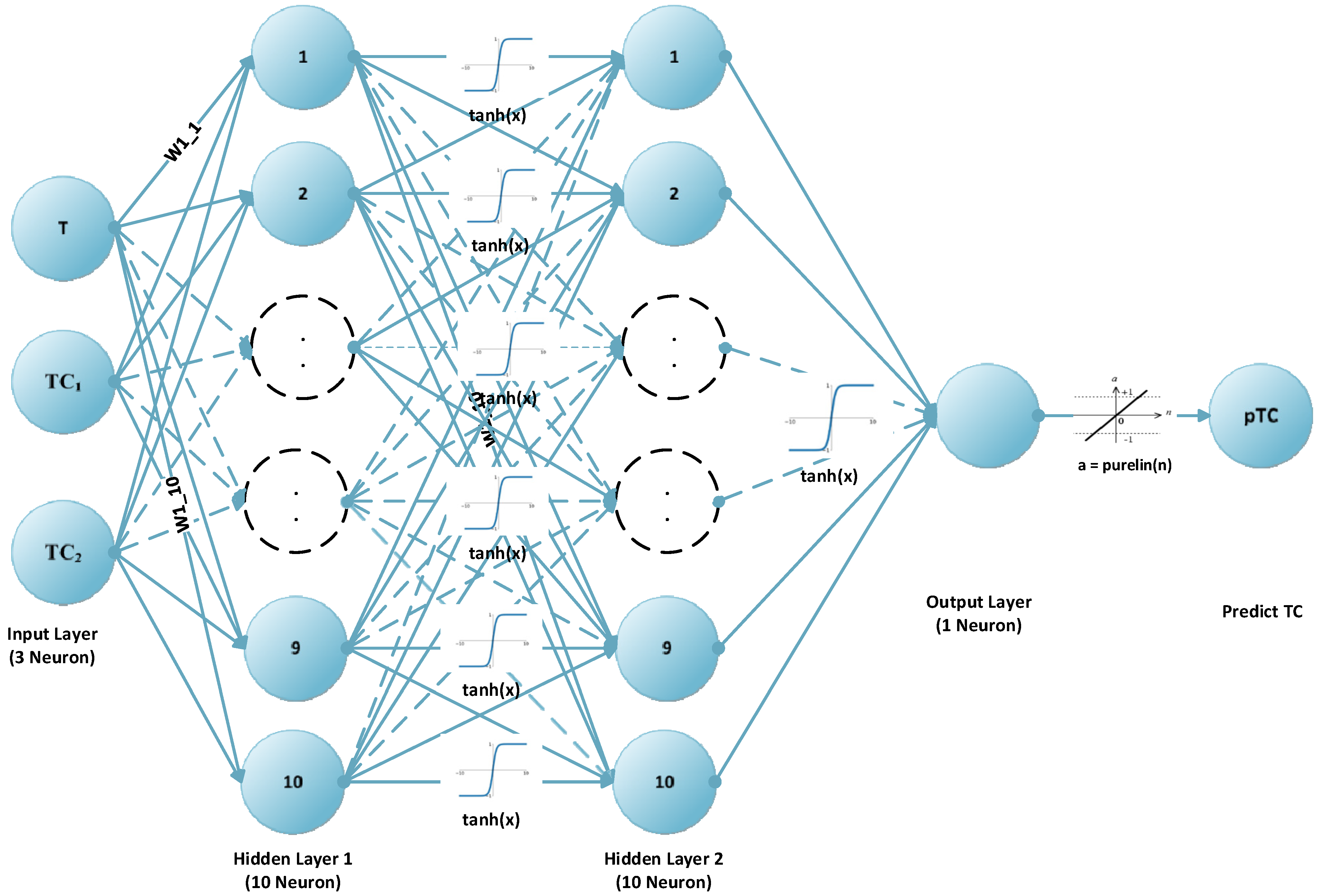
3. Methodology and Proposed Method
| Algorithm 1. Proposed method’s algorithm for thermal conductivity estimation (for each hybrid nanofluid) | |
| Input: T, TC1, TC2, ρ, and hybrid1_datas Output: pTC, MAE, MSE, MAPE, R2 | |
| 1 | size ← Load(hybrid1_datas) |
| 2 | i ← 0 |
| 3 | if i < 30 then |
| 3.1 | , wi2, hTCi = |
| 3.2 | inputDatas(Ti, TCi1, TCi2) |
| 3.3 | outputDatas(hTCi) |
| 3.4 | i = i + 1, go to step 3 |
| 4 | trainRatio = 0.8 trainIndex = randperm(size, round(trainRatio * size)) XTrain = inputDatas(trainIndex, :)’, YTrain = outputDatas(trainIndex, :)’ testIndex = setdiff(1:size, trainIndex) XTest = inputDatas(testIndex, :)’, YTest = outputDatas(testIndex, :)’ net = feedforwardnet([10 10]) net.trainFcn = ‘trainbr’ net.layers{1}.transferFcn = ‘tansig’ net.layers{2}.transferFcn = ‘tansig’ net.layers{3}.transferFcn = ‘purelin’ net.trainParam.epochs = 1000 net.trainParam.goal = 10−1000 |
| 5 | net = train(net, XTrain, YTrain) |
| 6 | pTC = net(XTest) |
| 7 | MAE = mean(abs(pTC − YTest)) MSE = mean((pTC − YTest).^2); MAPE = mean(abs((pTC − YTest)/YTest)) * 100 R2 = 1 − mean(((pTC-YTest).^2)/(YTest.^2)) |
| 8 | returnpTC, MAE, MSE, MAPE, R2 |
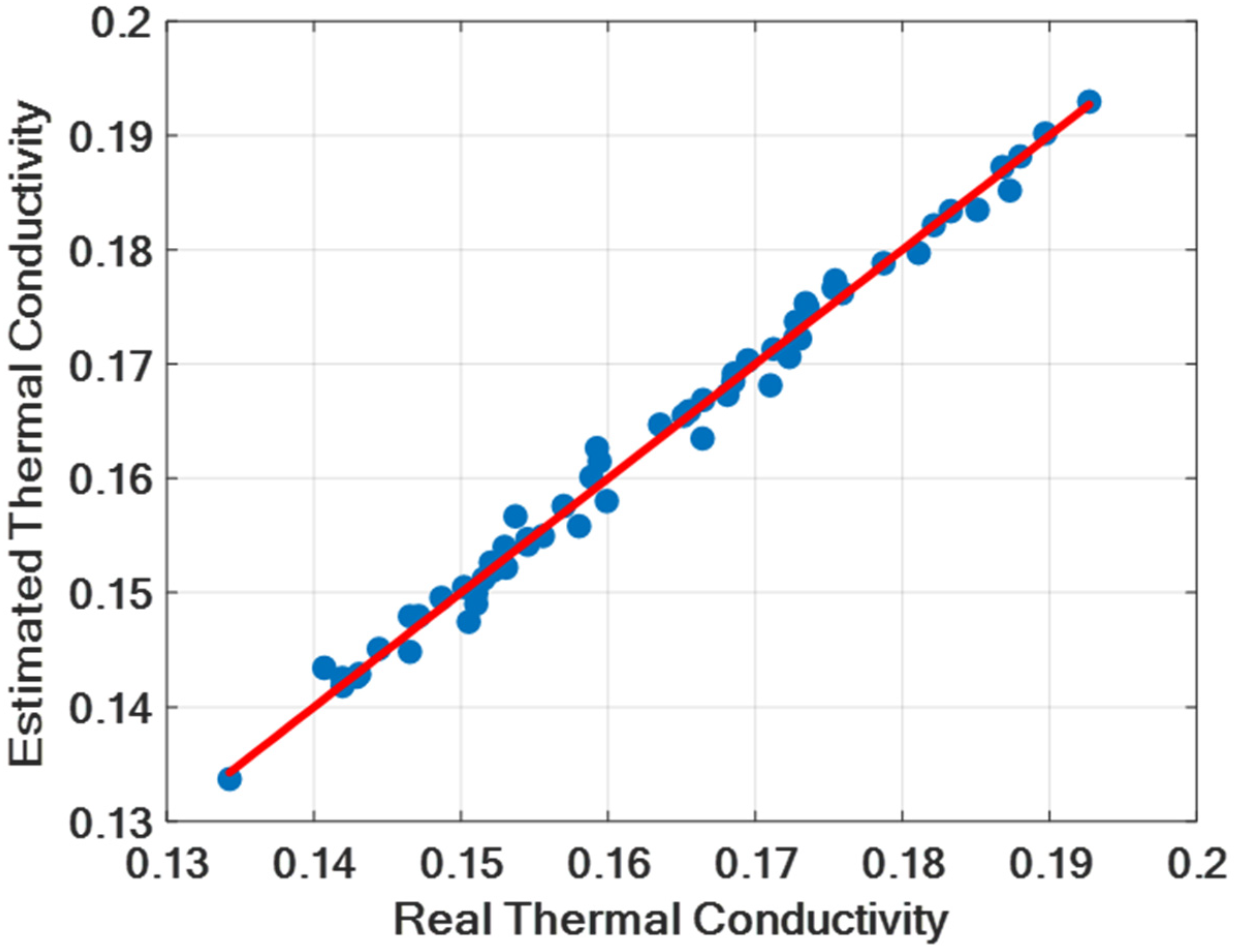
4. Experimental Results
5. Discussion and Comparison with Other Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Öndin, O.; Kıvak, T.; Sarıkaya, M.; Yıldırım, Ç.V. Investigation of the influence of MWCNTs mixed nanofluid on the machinability characteristics of PH 13-8 Mo stainless steel. Tribol. Int. 2020, 148, 106323. [Google Scholar] [CrossRef]
- Rodríguez, A.; Calleja, A.; de Lacalle, L.N.L.; Pereira, O.; Rubio-Mateos, A.; Rodríguez, G. Drilling of CFRP-Ti6Al4V stacks using CO2-cryogenic cooling. J. Manuf. Process. 2021, 64, 58–66. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.; de Lacalle, L.L.; Khanna, S.; Patel, V.K.; Ayesta, I. Parametric Optimization and effect of nano-graphene mixed dielectric fluid on performance of wire electrical discharge machining process of Ni55.8Ti shape memory alloy. Materials 2021, 14, 2533. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Mei, X.; Zhang, J.; Li, C. Prediction of Thermal Conductivity of EG–Al2O3 Nanofluids Using Six Supervised Machine Learning Models. Appl. Sci. 2024, 14, 6264. [Google Scholar] [CrossRef]
- Çolak, A.B.; Bayrak, M. Comparison of experimental thermal conductivity of water-based Al2O3–Cu hybrid nanofluid with theoretical models and artificial neural network output. J. Therm. Anal. Calorim. 2024, 149, 1–16. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Nazari, M.A.; Ghasempour, R.; Madah, H.; Shafii, M.B.; Ahmadi, M.A. Thermal conductivity ratio prediction of Al2O3/water nanofluid by applying connectionist methods. Colloids Surf. A Physicochem. Eng. Asp. 2018, 541, 154–164. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Nazari, M.A.; Mahian, O.; Ghasempour, R. A proposed model to predict thermal conductivity ratio of Al2O3/EG nanofluid by applying least squares support vector machine (LSSVM) and genetic algorithm as a connectionist approach. J. Therm. Anal. Calorim. 2019, 135, 271–281. [Google Scholar] [CrossRef]
- Esfe, M.H.; Ahangar, M.R.H.; Toghraie, D.; Hajmohammad, M.H.; Rostamian, H.; Tourang, H. Designing artificial neural network on thermal conductivity of Al2O3–water–EG (60–40%) nanofluid using experimental data. J. Therm. Anal. Calorim. 2016, 126, 837–843. [Google Scholar] [CrossRef]
- Esfe, M.H.; Amoozad, F.; Hatami, H.; Toghraie, D. Comprehensive study and scientific process to increase the accuracy in estimating the thermal conductivity of nanofluids containing SWCNTs and CuO nanoparticles using an artificial neural network. Micro Nano Syst. Lett. 2024, 12, 1–14. [Google Scholar] [CrossRef]
- Lee, J.-H.; Hwang, K.S.; Jang, S.P.; Lee, B.H.; Kim, J.H.; Choi, S.U.; Choi, C.J. Effective viscosities and thermal conductivities of aqueous nanofluids containing low volume concentrations of Al2O3 nanoparticles. Int. J. Heat Mass Transf. 2008, 51, 2651–2656. [Google Scholar] [CrossRef]
- Bag, R.; Panda, A.; Sahoo, A.K.; Kumar, R. A brief study on effects of nano cutting fluids in hard turning of AISI 4340 steel. Mater. Today Proc. 2019, 26, 3094–3099. [Google Scholar] [CrossRef]
- Ravi, S.; Gurusamy, P. Review of nanofluids as coolant in metal cutting operations. Mater. Today Proc. 2020, 37, 2387–2390. [Google Scholar] [CrossRef]
- Gajrani, K.K.; Suvin, P.; Kailas, S.V.; Mamilla, R.S. Thermal, rheological, wettability and hard machining performance of MoS2 and CaF2 based minimum quantity hybrid nano-green cutting fluids. J. Mech. Work. Technol. 2019, 266, 125–139. [Google Scholar] [CrossRef]
- Selvarajoo, K.; Wanatasanappan, V.V.; Luon, N.Y. Experimental measurement of thermal conductivity and viscosity of Al2O3-GO (80:20) hybrid and mono nanofluids: A new correlation. Diam. Relat. Mater. 2024, 144, 111018. [Google Scholar] [CrossRef]
- Khanna, N.; Shah, P.; de Lacalle, L.N.L.; Rodríguez, A.; Pereira, O. In pursuit of sustainable cutting fluid strategy for machining Ti-6Al-4V using life cycle analysis. Sustain. Mater. Technol. 2021, 29, e00301. [Google Scholar] [CrossRef]
- Sharma, A.K.; Singh, R.K.; Dixit, A.R.; Tiwari, A.K. Novel uses of alumina-MoS2 hybrid nanoparticle enriched cutting fluid in hard turning of AISI 304 steel. J. Manuf. Process. 2017, 30, 467–482. [Google Scholar] [CrossRef]
- Yadav, R.; Dubey, V.; Sharma, A.K. Investigation of cutting forces in MQL turning using mono and hybrid nano cutting fluid. Mater. Today Proc. 2023, 12, 657–689. [Google Scholar] [CrossRef]
- Hirudayanathan, H.P.; Debnath, S.; Anwar, M.; Johar, M.B.; Elumalai, N.K.; Iqbal, U.M. A review on influence of nanoparticle parameters on viscosity of nanofluids and machining performance in minimum quantity lubrication. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2023, 239, 09544089231189668. [Google Scholar] [CrossRef]
- Manikanta, J.E.; Raju, B.N.; Phanisankar, B.S.S.; Rajesh, M.; Kotteda, T.K. Nanoparticle Enriched Cutting Fluids in Metal Cutting Operation: A Review. In Recent Advances in Mechanical Engineering; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2023; pp. 147–156. [Google Scholar]
- Duc, T.M.; Long, T.T.; Van Thanh, D. Evaluation of minimum quantity lubrication and minimum quantity cooling lubrication performance in hard drilling of Hardox 500 steel using Al2O3 nanofluid. Adv. Mech. Eng. 2020, 12, 1687814019888404. [Google Scholar] [CrossRef]
- Arifuddin, A.; Redhwan, A.A.M.; Azmi, W.H.; Zawawi, N.N.M. Performance of Al2O3/TiO2 Hybrid Nano-Cutting Fluid in MQL Turning Operation via RSM Approach. Lubricants 2022, 10, 366. [Google Scholar] [CrossRef]
- Singh, R.K.; Dixit, A.R.; Mandal, A.; Sharma, A.K. Emerging application of nanoparticle-enriched cutting fluid in metal removal processes: A review. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4677–4717. [Google Scholar] [CrossRef]
- Prabhu, S.; Uma, M.; Vinayagam, B.K. Surface roughness prediction using Taguchi-fuzzy logic-neural network analysis for CNT nanofluids based grinding process. Neural Comput. Appl. 2015, 26, 41–55. [Google Scholar] [CrossRef]
- Vignesh, S.; Iqbal, U.M. Effect of tri-hybridized metallic nano cutting fluids in end milling of AA7075 in minimum quantity lubrication environment. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 235, 1458–1468. [Google Scholar] [CrossRef]
- Sharma, V.K.; Singh, T.; Singh, K.; Rana, M.; Gehlot, A. Optimization of surface qualities in face milling of EN-31 employing hBN nanoparticles-based minimum quantity lubrication. Mater. Today Proc. 2022, 69, 303–308. [Google Scholar] [CrossRef]
- De Lacalle, L.L.; Lamikiz, A.; Sánchez, J.A.; Salgado, M.A. Effects of tool deflection in the high-speed milling of inclined surfaces. Int. J. Adv. Manuf. Technol. 2004, 24, 621–631. [Google Scholar] [CrossRef]
- Arnaiz-González, Á.; Fernández-Valdivielso, A.; Bustillo, A.; de Lacalle, L.N.L. Using artificial neural networks for the prediction of dimensional error on inclined surfaces manufactured by ball-end milling. Int. J. Adv. Manuf. Technol. 2016, 83, 847–859. [Google Scholar] [CrossRef]
- Şahin, F.; Ulamiş, F. Makine Öğrenmesi İle Ataletsel Navigasyon Sistemlerinde Doğruluğun Geliştirilmesi. Int. J. Eng. Res. Dev. 2023, 15, 285–295. [Google Scholar] [CrossRef]
- Pereira, O.; Martin-Alfonso, J.E.; Rodríguez, A.; Calleja-Ochoa, A.; Fernández-Valdivielso, A.; Lopez de Lacalle, L.N. Sustainability analysis of lubricant oils for minimum quantity lubrication based on their tribo-rheological performance. J. Clean. Prod. 2017, 164, 1419–1429. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J. Enhancing Thermal Conductivity of Fluids with Nanoparticles, Developments and Applications of Non-Newtonian Flows; ASME: New York, NY, USA, 1995. [Google Scholar]
- Erdoğan, B.; Güneş, A.; Çakmak, G. Experimental Investigation of the Effect of Nanofluid Utilization on Heat Transfer Performance in Unmanned Aircraft Radiators with Various Spring-Type Fins. Nanomaterials 2025, 15, 489. [Google Scholar] [CrossRef]
- Taghizadehfard, M.; Hosseini, S.M.; Pierantozzi, M.; Alavianmehr, M.M. Densities and isothermal compressibilities from perturbed hard-dimer-chain equation of state: Application to nanofluids. J. Non Equilibrium Thermodyn. 2023, 48, 55–73. [Google Scholar] [CrossRef]
- Topuz, A.; Engin, T.; Özalp, A.A.; Erdoğan, B.; Mert, S.; Yeter, A. Experimental investigation of optimum thermal performance and pressure drop of water-based Al2O3, TiO2 and ZnO nanofluids flowing inside a circular microchannel. J. Therm. Anal. Calorim. 2018, 131, 2843–2863. [Google Scholar] [CrossRef]
- Yüksel, N. The Review of Some Commonly Used Methods and Techniques to Measure the Thermal Conductivity of Insulation Materials. In Insulation Materials in Context of Sustainability; Almusaed, A., Almssad, A., Eds.; IntechOpen: Rijeka, Croatia, 2016. [Google Scholar]
- Sánchez-Calderón, I.; Merillas, B.; Bernardo, V.; Rodríguez-Pérez, M.Á. Methodology for measuring the thermal conductivity of insulating samples with small dimensions by heat flow meter technique. J. Therm. Anal. Calorim. 2022, 147, 12523–12533. [Google Scholar] [CrossRef]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement techniques for thermal conductivity and interfacial thermal conductance of bulk and thin film materials. J. Electron. Packag. 2016, 138, 40802. [Google Scholar] [CrossRef]
- Faúndez, C.A.; Campusano, R.A.; Valderrama, J.O. Misleading results on the use of artificial neural networks for correlating and predicting properties of fluids. A case on the solubility of refrigerant R-32 in ionic liquids. J. Mol. Liq. 2020, 298, 112009. [Google Scholar] [CrossRef]
- Shang, Y.; Hammoodi, K.A.; Alizadeh, A.; Sharma, K.; Jasim, D.J.; Rajab, H.; Ahmed, M.; Kassim, M.; Maleki, H.; Salahshour, S. Artificial neural network hyperparameters optimization for predicting the thermal conductivity of MXene/graphene nanofluids. J. Taiwan Inst. Chem. Eng. 2024, 164, 105673. [Google Scholar] [CrossRef]
- Sahin, F.; Genc, O.; Gökcek, M.; Çolak, A.B. From experimental data to predictions: Artificial intelligence supported new mathematical approaches for estimating thermal conductivity, viscosity and zeta potential in Fe3O4-water magnetic nanofluids. Powder Technol. 2023, 430, 118974. [Google Scholar] [CrossRef]
- Kanti, P.K.; Paramasivam, P.; Wanatasanappan, V.V.; Dhanasekaran, S.; Sharma, P. Experimental and explainable machine learning approach on thermal conductivity and viscosity of water based graphene oxide based mono and hybrid nanofluids. Sci. Rep. 2024, 14, 30967. [Google Scholar] [CrossRef]
- Babu, M.N.; Devarajan, Y. Study on the prediction of thermal conductivity for Al-CuO/water nanofluids using artificial neural networks. Multiscale Multidiscip. Model. Exp. Des. 2024, 8, 90. [Google Scholar] [CrossRef]
- Shekhar; Sambyo, K.; Sharma, R.P.; Mishra, S.R. Predicting nanofluid density in ethylene glycol-based oxide nanoparticles using machine learning approach: GBR–GSO models. J. Therm. Anal. Calorim. 2025, 150, 1–18. [Google Scholar] [CrossRef]
- Sahin, F. Stability Optimization of Al2O3/SiO2 Hybrid Nanofluids and a New Correlation for Thermal Conductivity: An AI-Supported Approach. Int. J. Thermophys. 2024, 46, 9. [Google Scholar] [CrossRef]






| Oil Type | Density (15 °C, g/mL) | Viscosity (40 °C, mm2/s) | Flash Point (°C) | Appearance | Additions (%) |
|---|---|---|---|---|---|
| Sunflower oil | 0.888 | 34.25 | 130 | Clear, light yellow | Stabilizer: 0.3 Antifoam: 0.0015 |
| Nanoparticle Type | Density (g/cm3) | Particle Size (nm) | Purity (%) | Color |
|---|---|---|---|---|
| Hexagonal boron nitride (hBN) | 2.29 | 65–75 | 99.8 | White |
| Çinko Oksit (ZnO) | 5.61 | 18 | 99.9 | White |
| Multi-walled carbon nanotube (MWCNT) | 2.40 | 48–78 | 96.0 | Black |
| Titanium dioxide (TiO2) | 3.90 | 10–25 | 99.5 | White |
| Aluminum oxide (Al2O3) | 3.89 | 13 | 99.5 | White |
| Nanoparticle Volumetric Additive Rate ϕ (%) | Nanofluid Volume ∀n (mL) | Base Fluid Density b (kg/m3) | Nanoparticle Density p (kg/m3) | Total Nanofluid Mass (For Verification) mnf = mnp + mbf + mSDS (g) |
|---|---|---|---|---|
| Nanoparticle volume | Base fluid volume | Nanoparticle mass | Base fluid mass | Mass contribution rate |
| ∀p = ϕ∀n (mL) | ∀b = ∀n − ∀p (mL) | p∀p (g) | b∀b (g) | ϕw = mp/(mp + mb) (%) |
| Measurement No. | Pure Oil | hBN | ZnO | MWCNT | TiO2 | Al2O3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | |
| 1 | 31.16 | 0.116 | 32.28 | 0.135 | 35.06 | 0.161 | 30.53 | 0.173 | 29.84 | 0.133 | 35.48 | 0.168 |
| 2 | 31.29 | 0.118 | 31.96 | 0.142 | 34.78 | 0.165 | 30.65 | 0.170 | 30.02 | 0.131 | 35.62 | 0.171 |
| 3 | 30.98 | 0.112 | 32.15 | 0.145 | 34.95 | 0.159 | 30.48 | 0.176 | 29.75 | 0.132 | 34.95 | 0.170 |
| 4 | 31.18 | 0.114 | 32.65 | 0.135 | 35.16 | 0.159 | 30.61 | 0.172 | 29.80 | 0.130 | 35.27 | 0.170 |
| 5 | 31.56 | 0.117 | 32.54 | 0.132 | 35.26 | 0.162 | 30.50 | 0.173 | 29.90 | 0.128 | 35.98 | 0.165 |
| 6 | 31.15 | 0.114 | 32.33 | 0.134 | 35.14 | 0.160 | 30.48 | 0.174 | 29.84 | 0.131 | 35.79 | 0.166 |
| 7 | 39.28 | 0.131 | 44.75 | 0.152 | 39.92 | 0.164 | 41.36 | 0.174 | 40.36 | 0.137 | 40.75 | 0.172 |
| 8 | 40.05 | 0.124 | 45.01 | 0.150 | 40.07 | 0.171 | 41.45 | 0.178 | 40.40 | 0.140 | 41.02 | 0.165 |
| 9 | 39.05 | 0.136 | 45.00 | 0.148 | 39.86 | 0.170 | 41.38 | 0.174 | 40.42 | 0.129 | 41.02 | 0.164 |
| 10 | 38.97 | 0.134 | 44.67 | 0.146 | 39.74 | 0.163 | 41.30 | 0.172 | 40.36 | 0.135 | 40.72 | 0.174 |
| 11 | 39.14 | 0.127 | 44.45 | 0.156 | 40.15 | 0.160 | 41.29 | 0.173 | 40.20 | 0.142 | 40.65 | 0.172 |
| 12 | 39.78 | 0.128 | 44.66 | 0.154 | 39.97 | 0.162 | 41.34 | 0.175 | 40.34 | 0.142 | 40.90 | 0.173 |
| 13 | 51.59 | 0.132 | 49.51 | 0.147 | 47.48 | 0.170 | 49.89 | 0.194 | 49.75 | 0.140 | 51.51 | 0.179 |
| 14 | 51.56 | 0.141 | 49.56 | 0.145 | 47.58 | 0.175 | 50.01 | 0.196 | 50.20 | 0.142 | 52.03 | 0.182 |
| 15 | 50.99 | 0.129 | 49.15 | 0.149 | 47.12 | 0.168 | 49.85 | 0.189 | 50.10 | 0.140 | 51.85 | 0.176 |
| 16 | 52.07 | 0.131 | 49.83 | 0.151 | 47.63 | 0.165 | 49.78 | 0.188 | 49.50 | 0.139 | 50.95 | 0.175 |
| 17 | 51.58 | 0.132 | 49.06 | 0.142 | 48.02 | 0.174 | 49.79 | 0.194 | 49.45 | 0.145 | 50.99 | 0.182 |
| 18 | 51.48 | 0.136 | 49.82 | 0.146 | 47.25 | 0.170 | 49.95 | 0.193 | 49.50 | 0.142 | 51.49 | 0.179 |
| 19 | 63.28 | 0.127 | 61.03 | 0.148 | 56.49 | 0.172 | 57.59 | 0.205 | 60.15 | 0.148 | 59.85 | 0.188 |
| 20 | 63.18 | 0.136 | 61.54 | 0.152 | 56.19 | 0.175 | 57.84 | 0.205 | 60.22 | 0.145 | 60.09 | 0.185 |
| 21 | 63.45 | 0.120 | 60.85 | 0.150 | 56.78 | 0.176 | 57.48 | 0.210 | 60.02 | 0.149 | 60.07 | 0.193 |
| 22 | 63.98 | 0.121 | 60.56 | 0.145 | 55.87 | 0.170 | 57.62 | 0.203 | 59.95 | 0.150 | 59.48 | 0.192 |
| 23 | 62.98 | 0.134 | 61.24 | 0.144 | 56.01 | 0.170 | 57.60 | 0.202 | 60.35 | 0.150 | 59.71 | 0.192 |
| 24 | 63.06 | 0.134 | 61.00 | 0.146 | 56.09 | 0.174 | 57.61 | 0.208 | 60.20 | 0.147 | 59.87 | 0.185 |
| 25 | 68.87 | 0.138 | 65.85 | 0.144 | 66.85 | 0.168 | 65.79 | 0.193 | 68.75 | 0.152 | 70.63 | 0.192 |
| 26 | 68.91 | 0.141 | 65.27 | 0.139 | 67.01 | 0.167 | 65.87 | 0.196 | 69.13 | 0.150 | 70.51 | 0.195 |
| 27 | 68.84 | 0.129 | 65.81 | 0.154 | 67.09 | 0.168 | 65.52 | 0.195 | 69.02 | 0.149 | 70.48 | 0.190 |
| 28 | 68.79 | 0.127 | 65.69 | 0.142 | 66.95 | 0.169 | 65.58 | 0.192 | 68.75 | 0.152 | 70.60 | 0.189 |
| 29 | 68.74 | 0.131 | 65.80 | 0.142 | 66.75 | 0.168 | 65.90 | 0.194 | 68.85 | 0.154 | 70.55 | 0.188 |
| 30 | 69.10 | 0.138 | 65.75 | 0.149 | 65.23 | 0.170 | 65.95 | 0.195 | 68.92 | 0.150 | 70.40 | 0.189 |
| Measurement No. | ZnO + MWCNT | hBN + MWCNT | hBN + ZnO | hBN + TiO2 | hBN + Al2O3 | TiO2 + Al2O3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | K (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | T (°C) | k (W/mK) | |
| 1 | 35.31 | 0.173 | 30.60 | 0.154 | 36.75 | 0.150 | 32.91 | 0.137 | 33.05 | 0.164 | 30.41 | 0.163 |
| 2 | 35.42 | 0.168 | 30.62 | 0.161 | 36.58 | 0.156 | 32.65 | 0.139 | 33.50 | 0.166 | 30.55 | 0.165 |
| 3 | 35.51 | 0.174 | 30.59 | 0.157 | 36.85 | 0.149 | 33.15 | 0.135 | 33.13 | 0.170 | 30.45 | 0.166 |
| 4 | 35.18 | 0.174 | 30.54 | 0.154 | 36.65 | 0.145 | 32.95 | 0.130 | 33.25 | 0.162 | 30.36 | 0.160 |
| 5 | 35.24 | 0.170 | 30.69 | 0.155 | 36.66 | 0.151 | 32.54 | 0.130 | 32.85 | 0.163 | 30.25 | 0.160 |
| 6 | 35.15 | 0.171 | 30.62 | 0.158 | 36.95 | 0.150 | 33.15 | 0.136 | 33.01 | 0.166 | 30.40 | 0.161 |
| 7 | 41.89 | 0.169 | 38.49 | 0.158 | 42.79 | 0.152 | 39.64 | 0.146 | 40.46 | 0.166 | 40.97 | 0.164 |
| 8 | 41.92 | 0.168 | 38.62 | 0.161 | 41.98 | 0.150 | 39.75 | 0.134 | 40.95 | 0.168 | 41.08 | 0.165 |
| 9 | 41.86 | 0.167 | 38.54 | 0.163 | 43.05 | 0.153 | 40.10 | 0.142 | 39.98 | 0.167 | 40.78 | 0.162 |
| 10 | 41.87 | 0.172 | 38.41 | 0.154 | 43.10 | 0.155 | 39.55 | 0.138 | 40.39 | 0.165 | 40.69 | 0.162 |
| 11 | 41.66 | 0.170 | 38.42 | 0.155 | 42.85 | 0.148 | 39.45 | 0.141 | 40.45 | 0.166 | 40.98 | 0.162 |
| 12 | 41.94 | 0.169 | 38.53 | 0.159 | 43.00 | 0.147 | 39.41 | 0.140 | 40.44 | 0.168 | 41.19 | 0.163 |
| 13 | 55.54 | 0.174 | 48.66 | 0.161 | 52.29 | 0.157 | 48.18 | 0.141 | 52.67 | 0.169 | 51.85 | 0.169 |
| 14 | 55.56 | 0.176 | 48.63 | 0.159 | 52.31 | 0.161 | 48.08 | 0.139 | 52.80 | 0.170 | 52.00 | 0.166 |
| 15 | 55.47 | 0.177 | 48.59 | 0.157 | 52.46 | 0.158 | 47.68 | 0.142 | 52.74 | 0.169 | 52.13 | 0.165 |
| 16 | 55.68 | 0.170 | 48.71 | 0.162 | 52.06 | 0.159 | 48.15 | 0.142 | 52.64 | 0.165 | 51.65 | 0.169 |
| 17 | 55.49 | 0.171 | 48.75 | 0.163 | 52.15 | 0.162 | 48.32 | 0.143 | 52.39 | 0.167 | 51.54 | 0.165 |
| 18 | 55.44 | 0.175 | 48.56 | 0.158 | 52.46 | 0.156 | 48.07 | 0.145 | 52.61 | 0.168 | 51.99 | 0.166 |
| 19 | 64.04 | 0.171 | 57.57 | 0.151 | 57.96 | 0.151 | 56.01 | 0.147 | 61.41 | 0.170 | 60.82 | 0.171 |
| 20 | 64.15 | 0.168 | 57.84 | 0.152 | 58.03 | 0.152 | 55.92 | 0.148 | 61.25 | 0.174 | 60.85 | 0.172 |
| 21 | 63.89 | 0.169 | 57.64 | 0.156 | 58.04 | 0.151 | 56.03 | 0.140 | 61.58 | 0.175 | 60.51 | 0.169 |
| 22 | 63.98 | 0.171 | 57.29 | 0.149 | 57.80 | 0.150 | 55.75 | 0.145 | 61.45 | 0.169 | 60.72 | 0.168 |
| 23 | 64.07 | 0.172 | 57.41 | 0.150 | 58.00 | 0.154 | 55.80 | 0.146 | 61.56 | 0.170 | 60.86 | 0.170 |
| 24 | 64.10 | 0.171 | 57.69 | 0.150 | 57.99 | 0.149 | 55.98 | 0.147 | 61.23 | 0.173 | 61.26 | 0.172 |
| 25 | 72.92 | 0.169 | 67.88 | 0.152 | 72.30 | 0.146 | 69.12 | 0.149 | 68.46 | 0.180 | 70.07 | 0.178 |
| 26 | 73.01 | 0.172 | 67.89 | 0.155 | 71.95 | 0.146 | 69.03 | 0.142 | 68.37 | 0.178 | 70.15 | 0.175 |
| 27 | 73.03 | 0.174 | 67.91 | 0.148 | 72.05 | 0.148 | 69.00 | 0.146 | 69.02 | 0.175 | 69.85 | 0.175 |
| 28 | 72.80 | 0.168 | 67.67 | 0.147 | 72.95 | 0.139 | 68.50 | 0.149 | 68.24 | 0.181 | 69.95 | 0.170 |
| 29 | 72.81 | 0.170 | 67.73 | 0.154 | 72.35 | 0.144 | 68.75 | 0.150 | 68.34 | 0.177 | 70.20 | 0.170 |
| 30 | 72.95 | 0.172 | 67.89 | 0.156 | 72.22 | 0.149 | 69.71 | 0.152 | 68.32 | 0.181 | 70.10 | 0.175 |
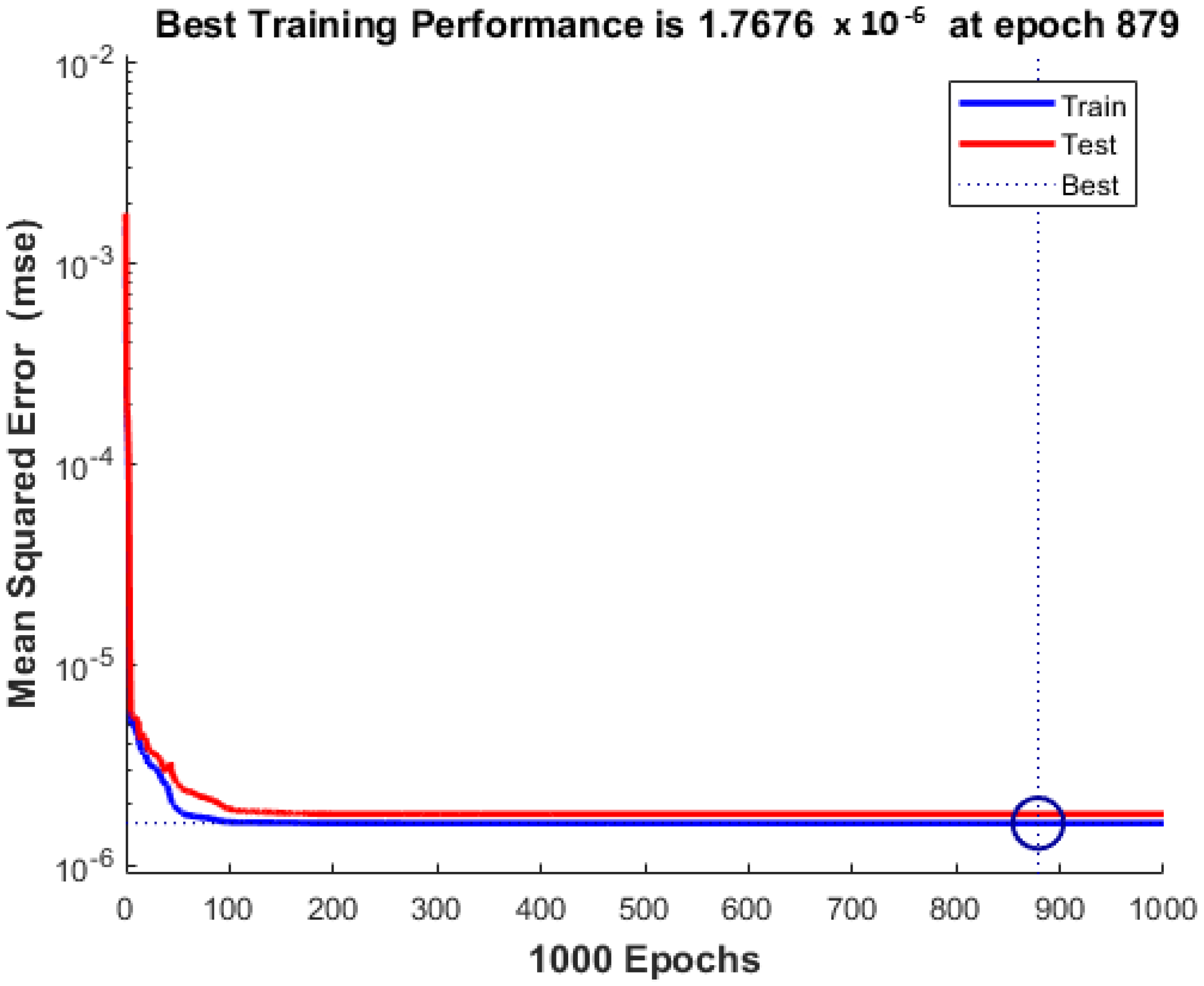
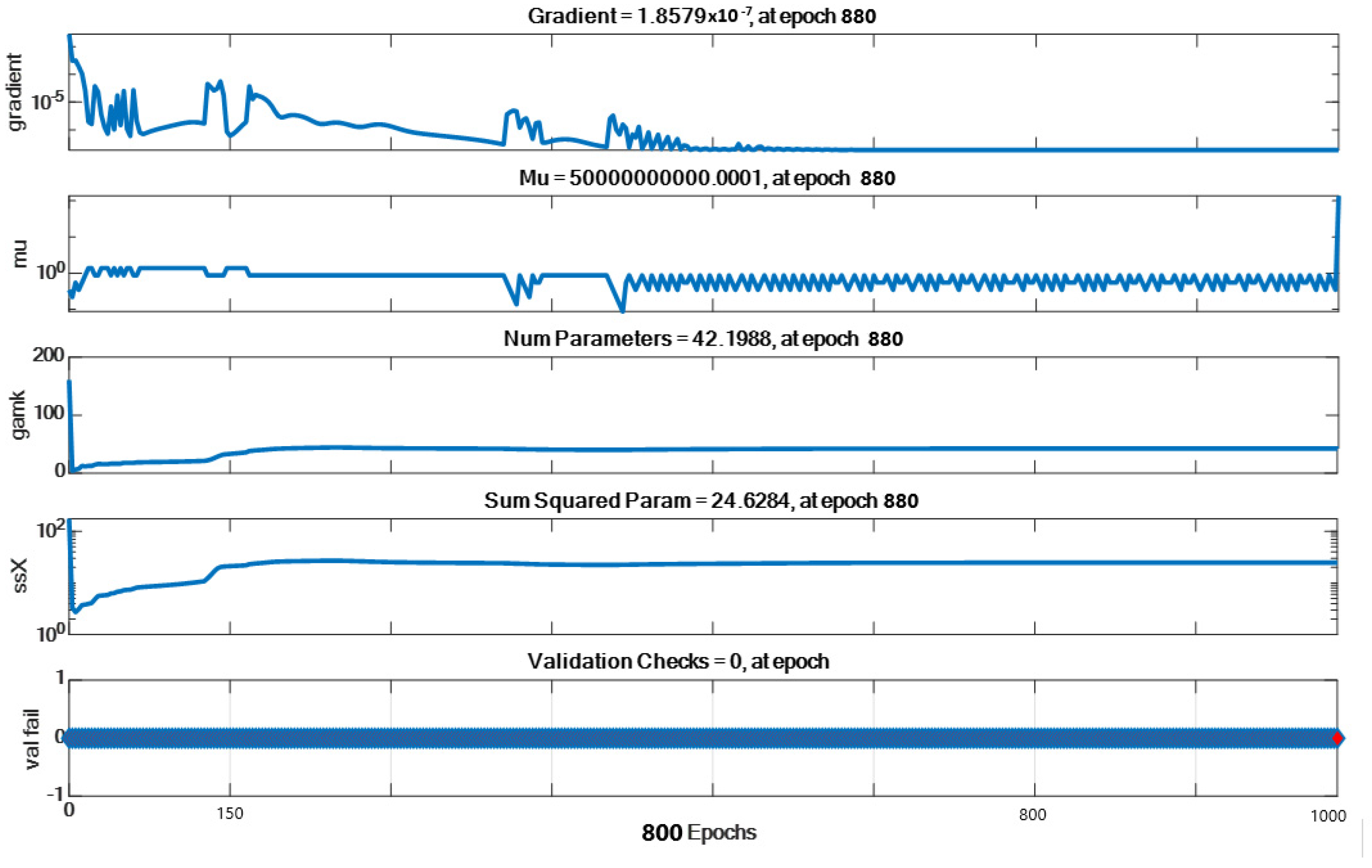
| Parameter | Initial Value | Stopped Value | Target Value |
|---|---|---|---|
| Epoch | 0 | 1000 | 1000 |
| Elapsed time | - | 00:00:10 | - |
| Performance | 0.00494 | 1.53 × 10−6 | 0 |
| Gradient | 0.016 | 1.75 × 10−7 | 10−7 |
| Mu | 0.005 | 0.05 | 1010 |
| Effective # Param | 161 | 43.6 | 0 |
| Sum Squared Param | 175 | 22.6 | 0 |
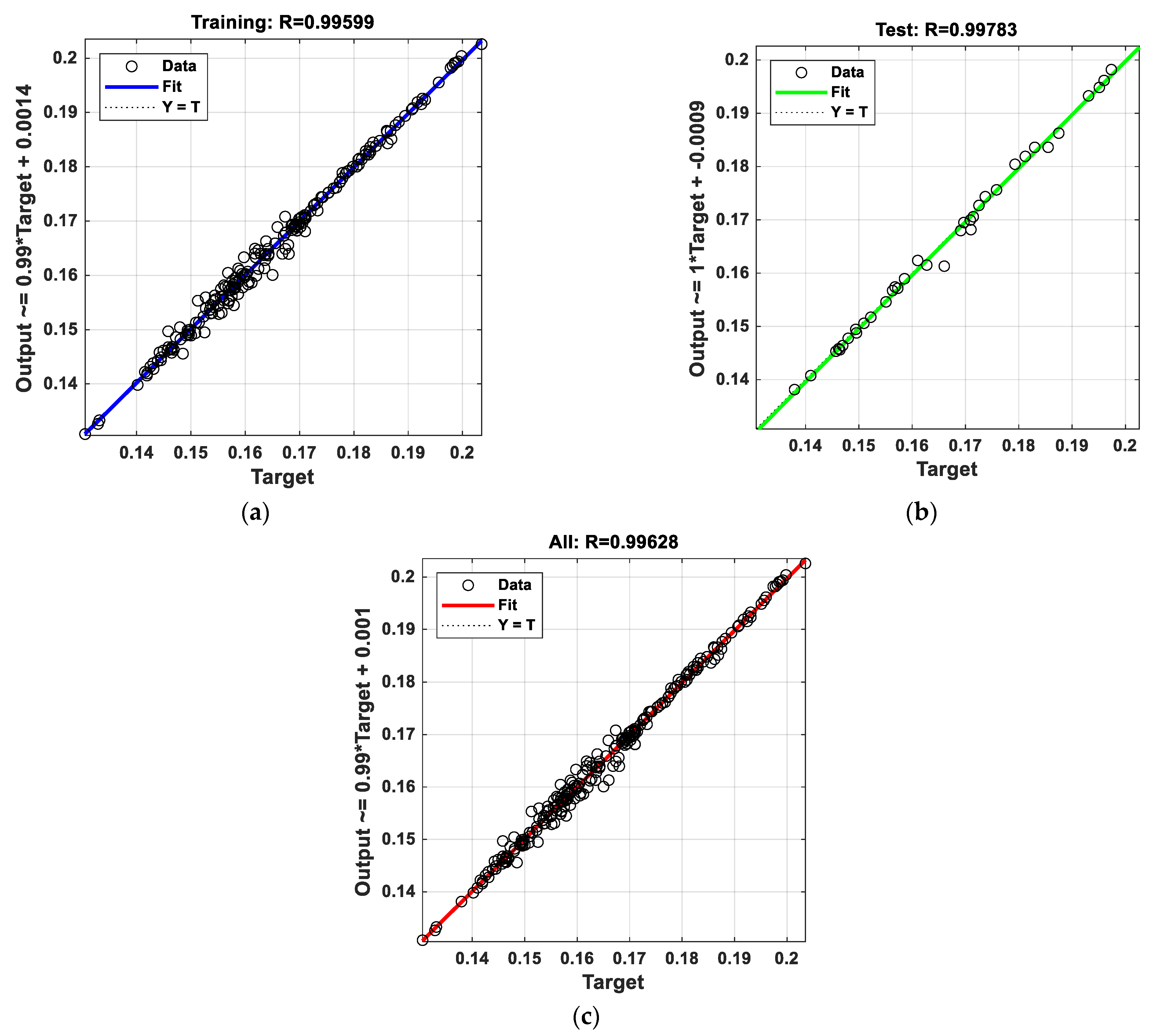
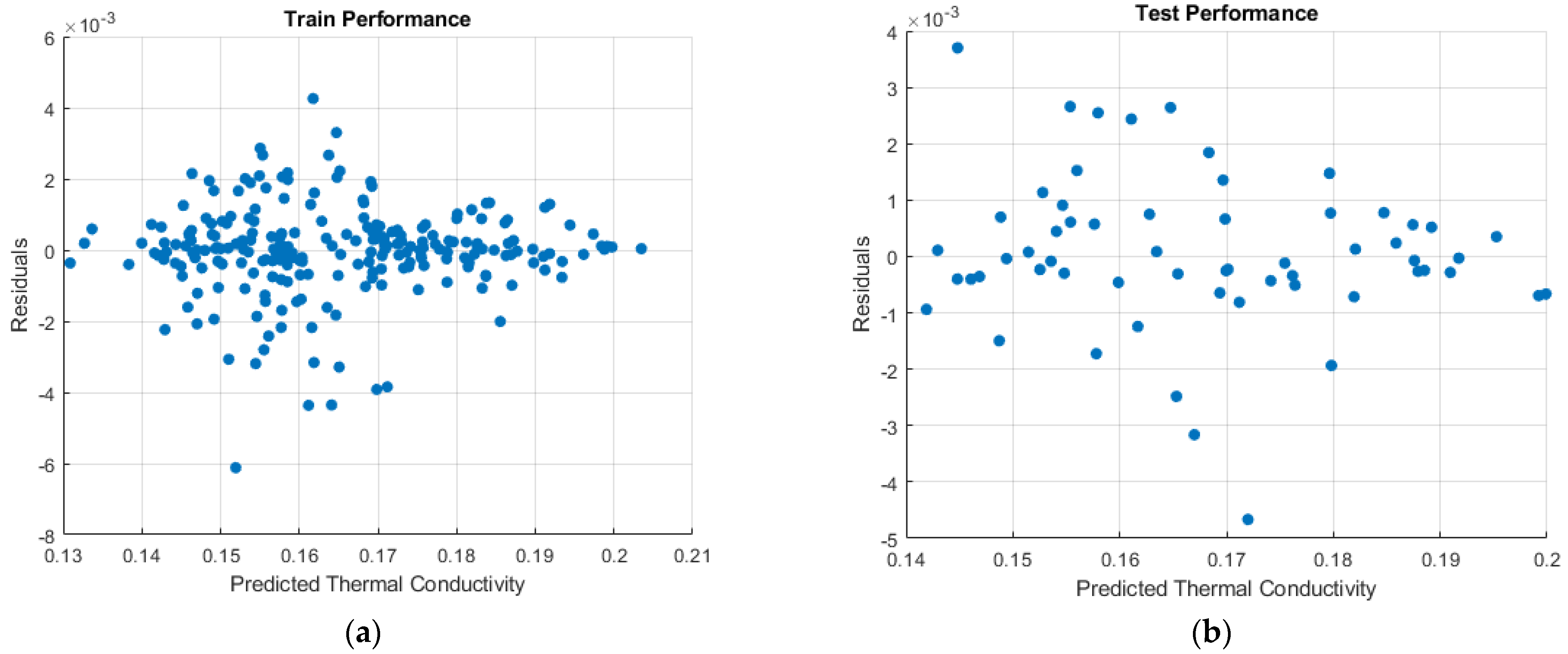
| MAE | MSE | MAPE | R2 | ||
|---|---|---|---|---|---|
| Random | Test (20%) | 0.0010 | 1.76 × 10−6 | 0.1490 | 0.9999 |
| Train (80%) | 0.0005 | 8.55 × 10−7 | 0.0077 | 1 | |
| Fold-1 | Test | 0.0010 | 2.00 × 10−6 | 0.6448 | 0.9909 |
| Train | 0.0010 | 2.00 × 10−6 | 0.5223 | 0.9926 | |
| Fold-2 | Test | 0.0009 | 2.00 × 10−6 | 0.5596 | 0.9907 |
| Train | 0.0008 | 1.00 × 10−6 | 0.4815 | 0.9940 | |
| Fold-3 | Test | 0.0010 | 2.00 × 10−6 | 0.6488 | 0.9907 |
| Train | 0.0009 | 2.00 × 10−6 | 0.5375 | 0.9925 | |
| Fold-4 | Test | 0.0012 | 3.00 × 10−6 | 0.7657 | 0.9845 |
| Train | 0.0009 | 1.00 × 10−6 | 0.5042 | 0.9937 | |
| Fold-5 | Test | 0.0012 | 3.00 × 10−6 | 0.7462 | 0.9885 |
| Train | 0.0008 | 1.00 × 10−6 | 0.4763 | 0.9941 | |
| Average 5-fold | All | 0.0011 | 2.52 × 10−6 | 0.6677 | 0.9883 |
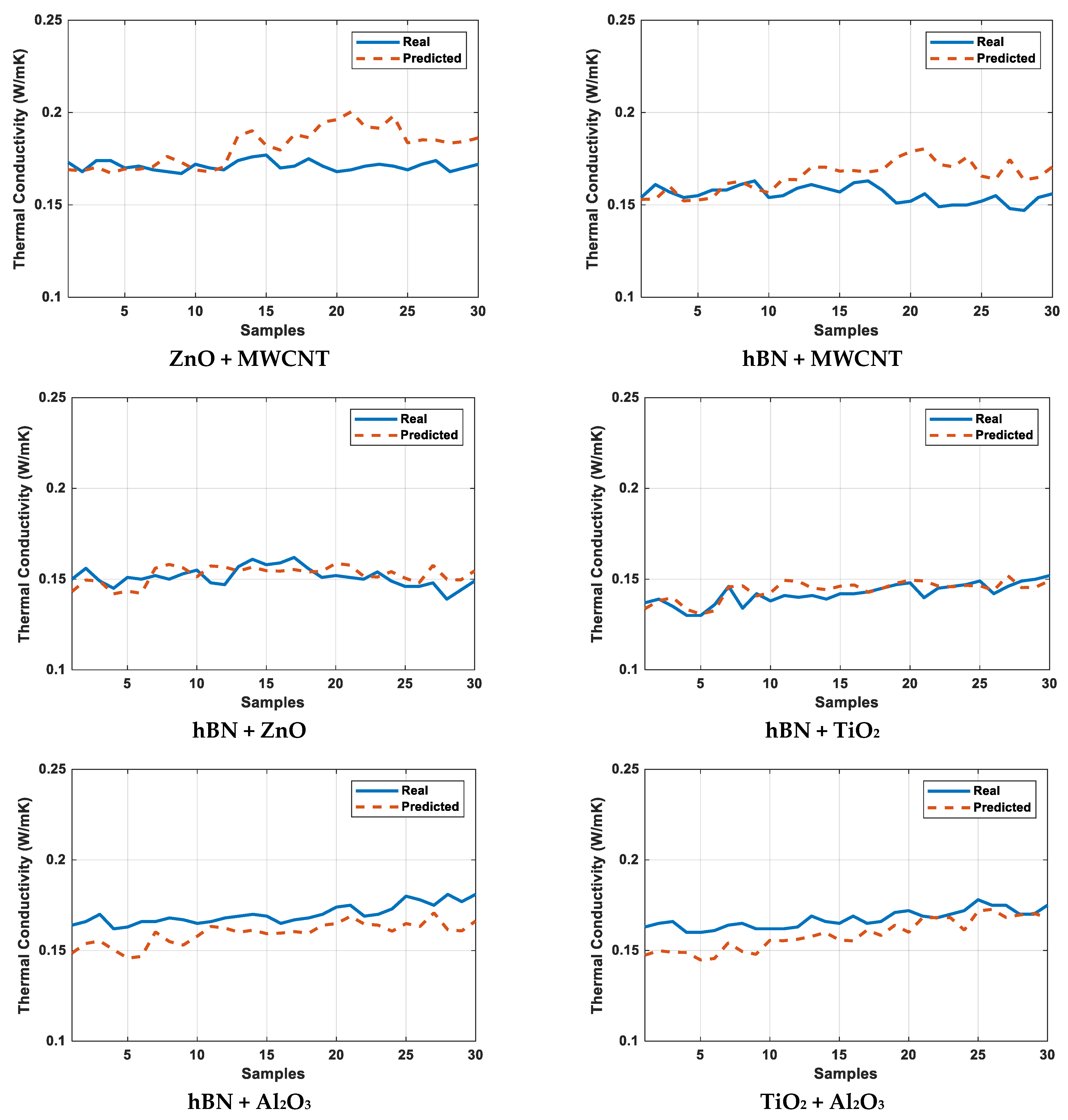
| ZnO + MWCNT | hBN + MWCNT | hBN + ZnO | hBN + TiO2 | hBN + Al2O3 | TiO2 + Al2O3 | |
|---|---|---|---|---|---|---|
| MAE | 0.0246 | 0.0113 | 0.0061 | 0.00117 | 0.0088 | 0.0085 |
| MSE | 0.0008 | 0.0002 | 0.0001 | 0.0002 | 0.0001 | 0.0001 |
| MAPE | 15.64 | 6.13 | 2.05 | 7.44 | 0.52 | 2.28 |
| R2 | 0.9693 | 0.9925 | 0.9977 | 0.9919 | 0.9963 | 0.9932 |
| ZnO + MWCNT | hBN + MWCNT | hBN + ZnO | hBN + TiO2 | hBN + Al2O3 | TiO2 + Al2O3 | |
|---|---|---|---|---|---|---|
| Max | 18.5711 | 17.8538 | 7.9092 | 9.2131 | 11.577 | 10.2272 |
| Mean | 6.7254 | 7.3220 | 3.5107 | 2.4979 | 6.1420 | 5.12931 |
| Min | 0.2788 | 0.6692 | 0.0439 | 0.0586 | 1.6121 | 0.08751 |
| Std | 5.1752 | 5.7071 | 1.8855 | 2.2245 | 2.7797 | 3.20273 |
| Number of Hidden Layers | FeedForwardNet | MAE | MSE | MAPE | R2 | |
|---|---|---|---|---|---|---|
| 2 | [5 10] | Train | 0.000996 | 2.17 × 10−6 | 0.15876012 | 0.9999 |
| Test | 0.000721 | 1.17 × 10−6 | 0.00235251 | 1 | ||
| [10 5] | Train | 0.000945 | 1.67 × 10−6 | 0.00244054 | 0.9999 | |
| Test | 0.000700 | 1.0 × 10−6 | 0.00602084 | 1.0000 | ||
| [10 10] | Train | 0.0010 | 1.76 × 10−6 | 0.1490 | 0.9999 | |
| Test | 0.0005 | 8.55 × 10−7 | 0.0077 | 1 | ||
| [20 20] | Train | 0.001188 | 3.62 × 10−6 | 0.08861923 | 0.9999 | |
| Test | 0.000480 | 9.4 × 10−7 | 0.02950661 | 1.0000 | ||
| 3 | [5 5 5] | Train | 0.000900 | 3.18 × 10−6 | 0.04344342 | 0.9999 |
| Test | 0.000716 | 1.74 × 10−6 | 0.04261764 | 0.9999 | ||
| [10 5 10] | Train | 0.000954 | 2.10 × 10−6 | 0.07332192 | 0.9999 | |
| Test | 0.000636 | 9.7 × 10−7 | 0.00020328 | 1 | ||
| [10 10 10] | Train | 0.013284 | 2.5 × 10−4 | 2.38267938 | 0.9899 | |
| Test | 0.012206 | 2.18 × 10−4 | 0.72491018 | 0.9916 | ||
| [20 20 20] | Train | 0.013867 | 2.6 × 10−4 | 1.74978362 | 0.9899 | |
| Test | 0.012032 | 2.1 × 10−4 | 1.21135047 | 0.9915 |
| Study, Year | Material/Method | MAE/MAD | MAPE | MSE/RMSE | R2 | R | |
|---|---|---|---|---|---|---|---|
| Yunyan Shang et al. [38], 2024 | MXene/graphene | GS-MLPNN | - | 0.5261 | 0.000027 | 0.99882 | 0.99941 |
| RS-MLPNN | - | 0.6046 | 0.000055 | 0.99774 | 0.99887 | ||
| Bayesian-MLPNN | - | 3.1981 | 0.00087 | 0.96234 | 0.98099 | ||
| Sahin et al. [39], 2024 | Fe3O4-MWCN/water | GMDH + NSGA II | 0.0009/- | 0.125 | 7.8 × 10−6 | 1 | 0.9954 |
| GMDH + MOWOA | 0.000915/- | 0.1285 | 7.89 × 10−6 | 0.999998 | 0.99537 | ||
| GMDH + MOMFO | 0.00093/- | 0.1292 | 8.2 × 10−6 | 0.999997 | 0.99511 | ||
| Praveen Kumar Kanti et al. [40], 2024 | GO + TiO2/GO + SiO2 (Test data) | Random Forest | - | 3.93 | 0.0052 | 0.9405 | - |
| Gradient Boost | - | 4.17 | 0.0056 | 0.9366 | - | ||
| Decision Tree | - | 4.54 | 0.0069 | 0.9217 | - | ||
| M. Dinesh Babu et al. [41], 2025 | Al2O3-CuO/water | Levenberg–Marquardt + ANN | 0.0023 | 0.9999 | |||
| Shekhar et al. [42], 2025 | Al2O3, CeO2, and CuO | GBR-GSO | -/0.0480 | - | -/0.00157 | - | 0.9995 |
| Fevzi Sahin [43], 2025 | Al2O3/ SiO2 | Levenberg–Marquardt + MLP | - | - | 8.2175 × 10−5 | - | 0.99958 |
| Our proposed method | ZnO + MWCNT, hBN + MWCNT, hBN + ZnO, hBN + TiO2, hBN + Al2O3 ve TiO2 + Al2O3 | Bayesian + FFANN | 0.0010 | 0.1490 | 1.76 × 10−6 | 0.9999 | 0.9962 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erdoğan, B.; Güneş, A.; Kılıç, İ.; Yaman, O. Predicting Thermal Conductivity of Nanoparticle-Doped Cutting Fluid Oils Using Feedforward Artificial Neural Networks (FFANN). Micromachines 2025, 16, 504. https://doi.org/10.3390/mi16050504
Erdoğan B, Güneş A, Kılıç İ, Yaman O. Predicting Thermal Conductivity of Nanoparticle-Doped Cutting Fluid Oils Using Feedforward Artificial Neural Networks (FFANN). Micromachines. 2025; 16(5):504. https://doi.org/10.3390/mi16050504
Chicago/Turabian StyleErdoğan, Beytullah, Abdulsamed Güneş, İrfan Kılıç, and Orhan Yaman. 2025. "Predicting Thermal Conductivity of Nanoparticle-Doped Cutting Fluid Oils Using Feedforward Artificial Neural Networks (FFANN)" Micromachines 16, no. 5: 504. https://doi.org/10.3390/mi16050504
APA StyleErdoğan, B., Güneş, A., Kılıç, İ., & Yaman, O. (2025). Predicting Thermal Conductivity of Nanoparticle-Doped Cutting Fluid Oils Using Feedforward Artificial Neural Networks (FFANN). Micromachines, 16(5), 504. https://doi.org/10.3390/mi16050504







