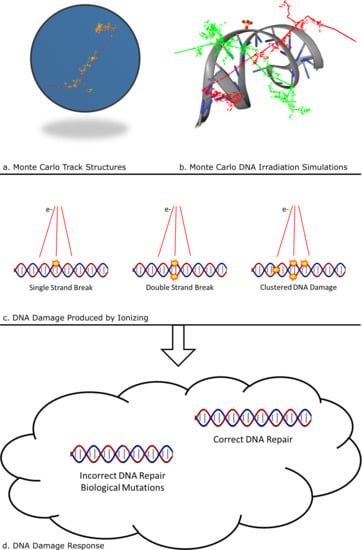
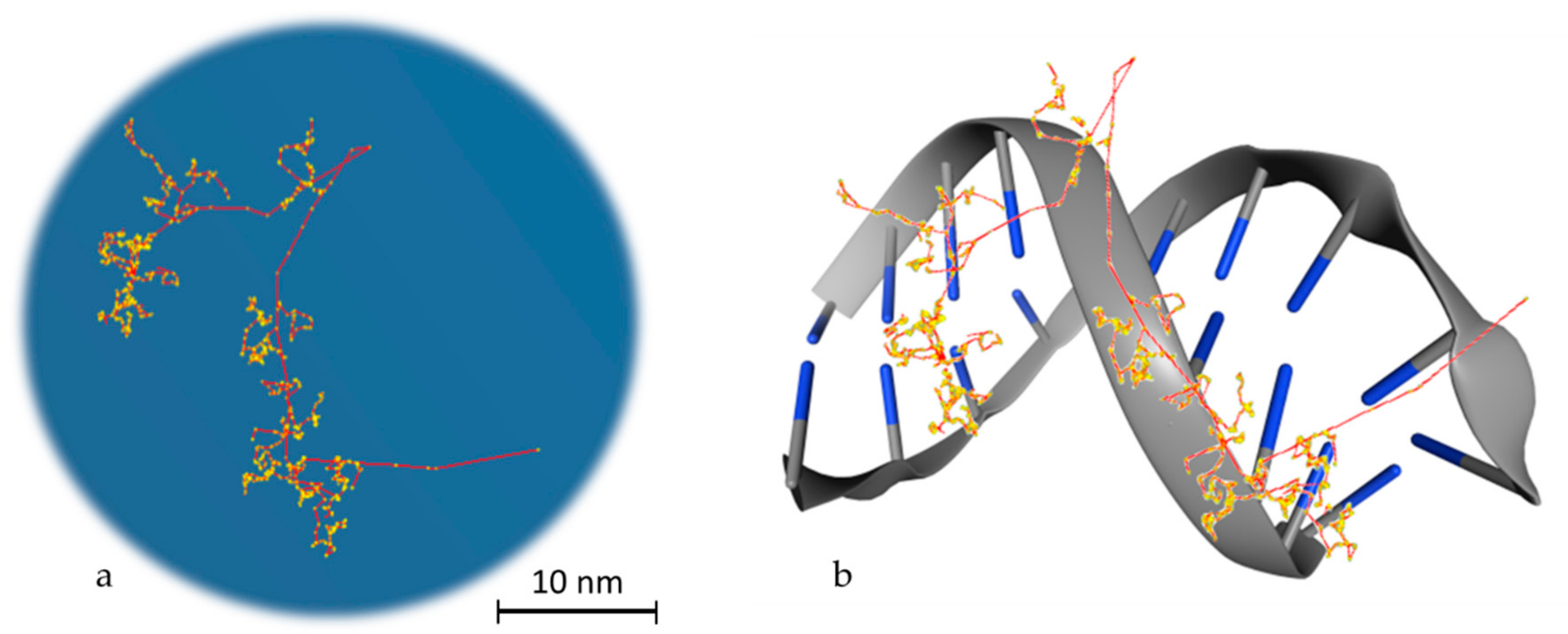
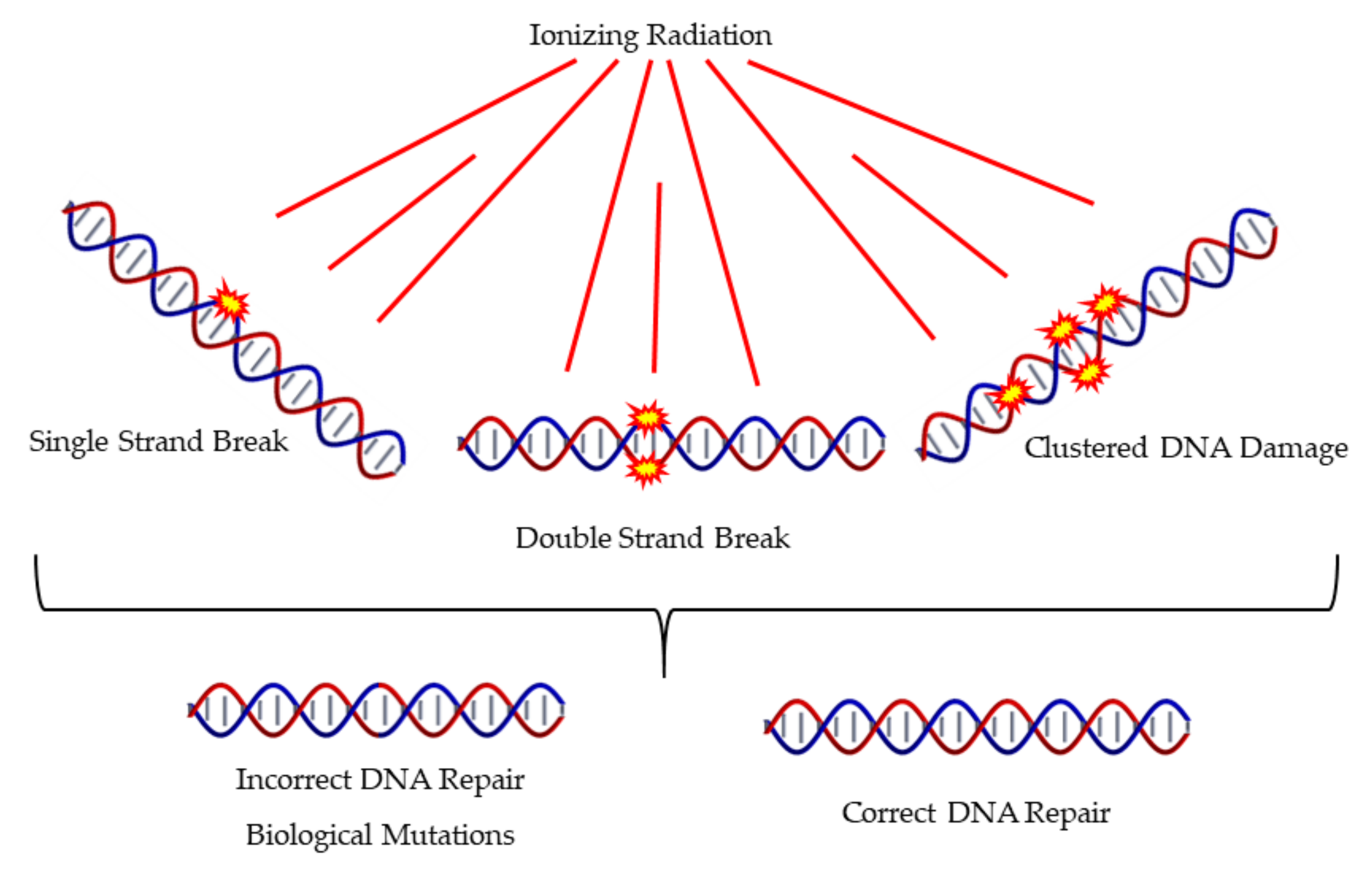
Ionizing Radiation and Complex DNA Damage: Quantifying the Radiobiological Damage Using Monte Carlo Simulations
Abstract
:1. Introduction
2. An Overview of the Methods Used in Nanoscale Simulations
2.1. Particle Track Structure Codes
2.2. Monte Carlo Techniques for Radiobiological Modelling
2.3. DNA Modelling
3. Monte Carlo Applications for Assessing Biological Damage
3.1. Types of Irradiation techniques and Applications
3.2. Direct Damage Studies
3.3. Water Radiolysis: Indirect Damage Studies
3.4. DNA Damage Repair Simulation Techniques
3.5. DNA Damage Quantification Techniques Other Than Monte Carlo
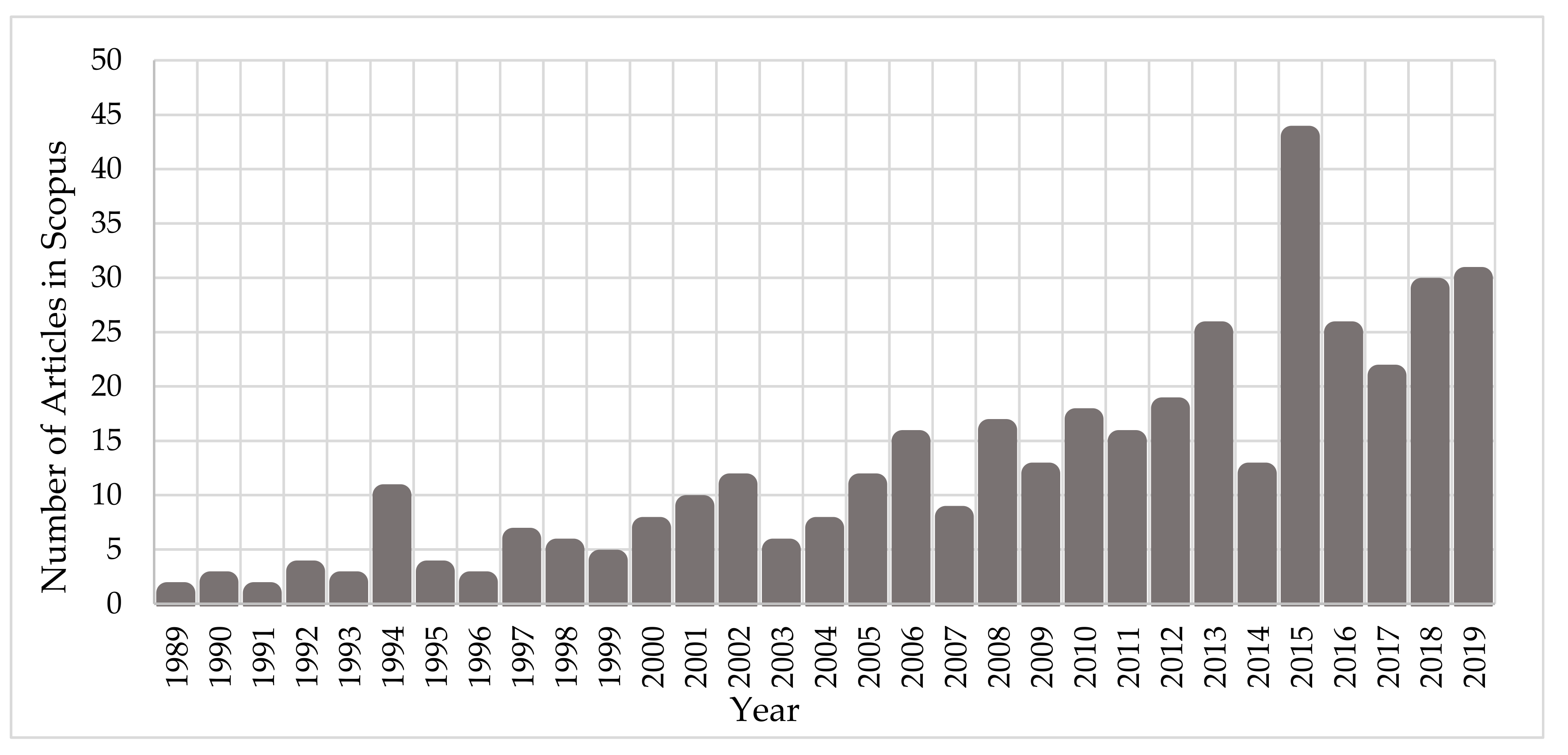
4. Conclusions and Future Prospects
Funding
Acknowledgments
Conflicts of Interest
References
- Cornforth, M.; Bedford, J. A quantitative comparison of potentially lethal damage repair and the rejoining of interphase chromosome breaks in low passage normal human fibroblasts. Radiat. Res. 1987, 111, 385–405. [Google Scholar] [CrossRef] [PubMed]
- Bedford, J. Sublethal damage, potentially lethal damage, and chromosomal aberrations in mammalian cells exposed to ionizing radiations. Int. J. Radiat. Oncol. Biol. Phys. 1991, 21, 1457–1469. [Google Scholar] [CrossRef]
- Hlatky, L.; Sachs, R.; Vazquez, M.; Cornforth, M. Radiation-induced chromosome aberrations: Insights gained from biophysical modeling. Bioessays 2002, 24, 714–723. [Google Scholar] [CrossRef] [PubMed]
- Hall, E.J.; Giaccia, A.J. Radiobiology for the Radiobiologist; Lippincott Williams & Wilkins: Philadelfia, PA, USA, 2006. [Google Scholar]
- Georgakilas, A.G.; O’Neill, P.; Stewart, R.D. Induction and Repair of Clustered DNA Lesions: What Do We Know So Far? Radiat. Res. 2013, 180, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Nikitaki, Z.; Hellweg, C.E.; Georgakilas, A.G.; Ravanat, J.-L. Stress-induced DNA damage biomarkers: Applications and limitations. Front. Chem. 2015, 3, 35. [Google Scholar] [CrossRef] [Green Version]
- Vitti, E.T.; Parsons, J.L. The Radiobiological Effects of Proton Beam Therapy: Impact on DNA Damage and Repair. Cancers (Basel) 2019, 11, 946. [Google Scholar] [CrossRef] [Green Version]
- Obe, G.; Pfeiffer, P.; Savage, J.R.K.; Johannes, C.; Goedecke, W.; Jeppesen, P.; Natarajan, A.T.; Martı́nez-López, W.; Folle, G.A.; Drets, M.E. Chromosomal aberrations: Formation, identification and distribution. Mutat. Res. /Fundam. Mol. Mech. Mutagenesis 2002, 504, 17–36. [Google Scholar] [CrossRef]
- Rothkamm, K.; Lobrich, M. Misrepair of radiation-induced DNA double-strand breaks and its relevance for tumorigenesis and cancer treatment (review). Int. J. Oncol. 2002, 21, 433–440. [Google Scholar] [CrossRef]
- Worku, M.; Fersht, N.; Martindale, C.; Funes, J.M.; Short, S.C. Sequential Transformation of Mesenchymal Stem Cells is Associated with Increased Radiosensitivity and Reduced DNA Repair Capacity. Radiat. Res. 2013, 179, 698–706. [Google Scholar] [CrossRef]
- Byrne, M.; Wray, J.; Reinert, B.; Wu, Y.; Nickoloff, J.; Lee, S.-H.; Hromas, R.; Williamson, E. Mechanisms of oncogenic chromosomal translocations. Ann. N. Y. Acad. Sci. 2014, 1310, 89–97. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1091. [Google Scholar] [CrossRef] [Green Version]
- Andrieu, C.; de Freitas, N.; Doucet, A.; Jordan, M.I. An Introduction to MCMC for Machine Learning. Mach. Learn. 2003, 50, 5–43. [Google Scholar] [CrossRef] [Green Version]
- Eckhardt, R. Stan Ulam, John Von Neumann, and the Monte Carlo method. Los Alamos Sci. Spec. Issue 1987, 131–136. [Google Scholar]
- Bouzy, B.; Helmstetter, B. Advances in Computer Games 10: Many Games, Many Challenges; al, H.v.d.H.e., Ed.; Kluwer: Boston, MA, USA, 2003; pp. 159–174. [Google Scholar]
- El Naqa, I.; Pater, P.; Seuntjens, J. Monte Carlo role in radiobiological modelling of radiotherapy outcomes. Phys. Med. Biol. 2012, 57, R75–R97. [Google Scholar] [CrossRef]
- Li, W.B.; Belchior, A.; Beuve, M.; Chen, Y.Z.; Di Maria, S.; Friedland, W.; Gervais, B.; Heide, B.; Hocine, N.; Ipatov, A.; et al. Intercomparison of dose enhancement ratio and secondary electron spectra for gold nanoparticles irradiated by X-rays calculated using multiple Monte Carlo simulation codes. Phys. Med. 2020, 69, 147–163. [Google Scholar] [CrossRef] [Green Version]
- Nikjoo, H.; Goodhead, D.T.; Charlton, D.E.; Paretzke, H.G. Energy deposition in small cylindrical targets by ultrasoft X-rays. Phys. Med. Biol. 1989, 34, 691–705. [Google Scholar] [CrossRef]
- Paretzke, H. Ch 3: Radiation track structure theory. In Kinetics of Non-homogeneous Processes; Freeman, G.R., Ed.; Wiley: New York, NY, USA, 1987; pp. 89–170. [Google Scholar]
- Goodhead, D.T.; Nikjoo, H. Track Structure Analysis of Ultrasoft X-rays Compared to High- and Low-LET Radiations. Int. J. Radiat. Biol. 1989, 55, 513–529. [Google Scholar] [CrossRef]
- Tomita, H.; Kai, M.; Kusama, T.; Aoki, Y.; Ito, A. Monte Carlo simulation of DNA strand breaks induced by monoenergetic electrons using higher-order structure models of DNA. Int. J. Radiat. Biol. 1994, 66, 669–682. [Google Scholar]
- Nikjoo, H.; Uehara, S.; Emfietzoglou, D.; Cucinotta, F.A. Track-structure codes in radiation research. Radiat. Meas. 2006, 41, 1052–1074. [Google Scholar] [CrossRef]
- MCNP: A General Monte Carlo code for Neutron and Photon Transport Version 3A Revision 2; LA--7396-M-Rev2; Los Alamos National Lab, N. M.: New Mexico, NM, USA, 1986; p. 591.
- Kawrakow, I.; Mainegra-Hing, E.; Rogers, D.; Tessier, F.; Walters, P. The EGSnrc Code System: Monte Carlo Simulation of Electron and Photon Transport; NRCC PIRS-701: Ottawa, ON, Canada, 2006. [Google Scholar]
- Ferrari, A.; Sala, P.R.; Fasso, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code; SLAC-R-773; TRN: US0601448 United States 10.2172/877507. Available online: http://www.fluka.org/fluka.php?id=man_onl (accessed on 22 March 2020).
- Baró, J.; Sempau, J.; Fernández-Varea, J.M.; Salvat, F. PENELOPE: An algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl. Instrum. Methods Phys. Res. Sect. B: Beam Interact. Mater. At. 1995, 100, 31–46. [Google Scholar] [CrossRef]
- Sato, T.; Matsuda, N.; Hashimoto, S.; Iwamoto, Y.; Noda, S.; Nakashima, H.; Fukahori, T.; Chiba, S.; Niita, K.; Iwase, H.; et al. Overview of the PHITS code and its application to medical physics. Prog. Nucl. Sci. Technol. 2014, 4, 879–882. [Google Scholar] [CrossRef]
- Nahum, A.E. Condensed-history Monte-Carlo simulation for charged particles: What can it do for us? Radiat. Environ. Biophys. 1999, 38, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; Emfietzoglou, D.; Liamsuwan, T.; Taleei, R.; Liljequist, D.; Uehara, S. Radiation track, DNA damage and response—a review. Rep. Prog. Phys. 2016, 79, 116601. [Google Scholar] [CrossRef] [PubMed]
- Dingfelder, M. Track-structure simulations for charged particles. Health Phys 2012, 103, 590–595. [Google Scholar] [CrossRef] [Green Version]
- Booz, J.; Braby, L.; Coyne, J.; Kliauga, P.; Lindborg, L.; Menzel, H.-G.; Parmentier, N. Parmentier, Report 36, Journal of the International Commission on Radiation Units and Measurements, Volume os19, Issue 1, December 31, 1983. Available online: https://doi.org/10.1093/jicru/os19.1.Report36 (accessed on 26 March 2020).
- Report 40, Journal of the International Commission on Radiation Units and Measurements, Volume os21, Issue 1, April 4, 1986, Page NP. Available online: https://doi.org/10.1093/jicru/os21.1.Report40 (accessed on 26 March 2020).
- Lazarakis, P.; Incerti, S.; Ivanchenko, V.; Kyriakou, I.; Emfietzoglou, D.; Corde, S.; Rosenfeld, A.B.; Lerch, M.; Tehei, M.; Guatelli, S. Investigation of track structure and condensed history physics models for applications in radiation dosimetry on a micro and nano scale in Geant4. Biomed. Phys. Eng. Express 2018, 4, 024001. [Google Scholar] [CrossRef] [Green Version]
- Kyriakou, I.; Emfietzoglou, D.; Ivanchenko, V.; Bordage, M.C.; Guatelli, S.; Lazarakis, P.; Tran, H.N.; Incerti, S. Microdosimetry of electrons in liquid water using the low-energy models of Geant4. J. Appl. Phys. 2017, 122, 024303. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Papamichael, G.; Nikjoo, H. Monte Carlo Electron Track Structure Calculations in Liquid Water Using a New Model Dielectric Response Function. Radiat. Res. 2017, 188, 355–368. [Google Scholar] [CrossRef]
- Famulari, G.; Pater, P.; Enger, S.A. Microdosimetry calculations for monoenergetic electrons using Geant4-DNA combined with a weighted track sampling algorithm. Phys. Med. Biol. 2017, 62, 5495–5508. [Google Scholar] [CrossRef]
- Incerti, S.; Kyriakou, I.; Bordage, M.C.; Guatelli, S.; Ivanchenko, V.; Emfietzoglou, D. Track structure simulations of proximity functions in liquid water using the Geant4-DNA toolkit. J. Appl. Phys. 2019, 125, 104301. [Google Scholar] [CrossRef] [Green Version]
- Kyriakou, I.; Ivanchenko, V.; Sakata, D.; Bordage, M.C.; Guatelli, S.; Incerti, S.; Emfietzoglou, D. Influence of track structure and condensed history physics models of Geant4 to nanoscale electron transport in liquid water. Phys. Med. Eur. J. Med. Phys. 2019, 58, 149–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedland, W.; Schmitt, E.; Kundrát, P.; Dingfelder, M.; Baiocco, G.; Barbieri, S.; Ottolenghi, A. Comprehensive track-structure based evaluation of DNA damage by light ions from radiotherapy-relevant energies down to stopping. Sci. Rep. 2017, 7, 45161. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, R.; Rahmanian, S.; Nikjoo, H. Spectrum of Radiation-Induced Clustered Non-DSB Damage—A Monte Carlo Track Structure Modeling and Calculations. Radiat. Res. 2015, 183, 525–540. [Google Scholar] [CrossRef]
- Chatzipapas, K.P.; Papadimitroulas, P.; Obeidat, M.; McConnell, K.A.; Kirby, N.; Loudos, G.; Papanikolaou, N.; Kagadis, G.C. Quantification of DNA double-strand breaks using Geant4-DNA. Med. Phys. 2019, 46, 405–413. [Google Scholar] [PubMed] [Green Version]
- Schuemann, J.; McNamara, A.L.; Warmenhoven, J.W.; Henthorn, N.T.; Kirkby, K.J.; Merchant, M.J.; Ingram, S.; Paganetti, H.; Held, K.D.; Ramos-Mendez, J.; et al. A New Standard DNA Damage (SDD) Data Format. Radiat. Res. 2019, 191, 76–92. [Google Scholar] [CrossRef] [PubMed]
- Pater, P.; Seuntjens, J.; El Naqa, I.; Bernal, M.A. On the consistency of Monte Carlo track structure DNA damage simulations. Med. Phys. 2014, 41, 121708. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Tan, Z.; Zhang, L.; Champion, C. Investigation on the correlation between energy deposition and clustered DNA damage induced by low-energy electrons. Radiat. Environ. Biophys. 2018, 57, 179–187. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Nikjoo, H. Accurate Electron Inelastic Cross Sections and Stopping Powers for Liquid Water over the 0.1-10 keV Range Based on an Improved Dielectric Description of the Bethe Surface. Radiat. Res. 2007, 167, 110–120. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Nikjoo, H. The Effect of Model Approximations on Single-Collision Distributions of Low-Energy Electrons in Liquid Water. Radiat. Res. 2005, 163, 98–111. [Google Scholar] [CrossRef]
- Semenenko, V.A.; Turner, J.E.; Borak, T.B. NOREC, a Monte Carlo code for simulating electron tracks in liquid water. Radiat. Environ. Biophys. 2003, 42, 213–217. [Google Scholar] [CrossRef]
- Liamsuwan, T.; Emfietzoglou, D.; Uehara, S.; Nikjoo, H. Microdosimetry of low-energy electrons. Int. J. Radiat. Biol. 2012, 88, 899–907. [Google Scholar] [CrossRef] [PubMed]
- Plante, I.; Cucinotta, F.A. Ionization and excitation cross sections for the interaction of HZE particles in liquid water and application to Monte Carlo simulation of radiation tracks. New J. Phys. 2008, 10, 125020. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, R.H.; Hamm, R.N.; Turner, J.E.; Wright, H.A.; Bolch, W.E. Radiation Interactions and Energy Transport in the Condensed Phase. In Physical and Chemical Mechanisms in Molecular Radiation Biology; Glass, W.A., Varma, M.N., Eds.; Springer US: Boston, MA, USA, 1991; pp. 99–135. [Google Scholar]
- Dingfelder, M.; Ritchie, R.H.; Turner, J.E.; Friedland, W.; Paretzke, H.G.; Hamm, R.N. Comparisons of calculations with PARTRAC and NOREC: Transport of electrons in liquid water. Radiat. Res. 2008, 169, 584–594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aydogan, B.; Marshall, D.T.; Swarts, S.G.; Turner, J.E.; Boone, A.J.; Richards, N.G.; Bolch, W.E. Site-Specific OH Attack to the Sugar Moiety of DNA: A Comparison of Experimental Data and Computational Simulation. Radiat. Res. 2002, 157, 38–44. [Google Scholar] [CrossRef]
- Friedland, W.; Paretzke, H.G.; Ballarini, F.; Ottolenghi, A.; Kreth, G.; Cremer, C. First steps towards systems radiation biology studies concerned with DNA and chromosome structure within living cells. Radiat. Environ. Biophys. 2008, 47, 49–61. [Google Scholar] [CrossRef]
- Friedland, W.; Dingfelder, M.; Kundrát, P.; Jacob, P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat. Res. /Fundam. Mol. Mech. Mutagenesis 2011, 711, 28–40. [Google Scholar] [CrossRef]
- Schmitt, E.; Friedland, W.; Kundrát, P.; Dingfelder, M.; Ottolenghi, A. Cross-section scaling for track structure simulations of low-energy ions in liquid water. Radiat. Prot. Dosim. 2015, 166, 15–18. [Google Scholar] [CrossRef]
- Dingfelder, M.; Travia, A.; McLawhorn, R.A.; Shinpaugh, J.L.; Toburen, L.H. Electron Emission from Foils and Biological Materials after Proton Impact. Radiat Phys. Chem. Oxf. Engl. 1993 2008, 77, 1213–1217. [Google Scholar] [CrossRef] [Green Version]
- Friedland, W.; Jacob, P.; Kundrát, P. Stochastic Simulation of DNA Double-Strand Break Repair by Non-homologous End Joining Based on Track Structure Calculations. Radiat. Res. 2010, 173, 677–688. [Google Scholar] [CrossRef]
- Friedland, W.; Kundrát, P. Track structure based modelling of chromosome aberrations after photon and alpha-particle irradiation. Mutat. Res. /Genet. Toxicol. Environ. Mutagenesis 2013, 756, 213–223. [Google Scholar] [CrossRef]
- Uehara, S.; Nikjoo, H.; Goodhead, D.T. Cross-sections for water vapour for the Monte Carlo electron track structure code from 10 eV to the MeV region. Phys. Med. Biol. 1993, 38, 1841–1858. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Cucinotta, F.A.; Nikjoo, H. A Complete Dielectric Response Model for Liquid Water: A Solution of the Bethe Ridge Problem. Radiat. Res. 2005, 164, 202–211. [Google Scholar] [CrossRef] [PubMed]
- Taleei, R.; Nikjoo, H. Repair of the double-strand breaks induced by low energy electrons: A modelling approach. Int. J. Radiat. Biol. 2012, 88, 948–953. [Google Scholar] [CrossRef]
- Taleei, R.; Nikjoo, H. The Non-homologous End-Joining (NHEJ) Pathway for the Repair of DNA Double-Strand Breaks: I. A Mathematical Model. Radiat. Res. 2013, 179, 530–539. [Google Scholar] [CrossRef]
- Rahmanian, S.; Taleei, R.; Nikjoo, H. Radiation induced base excision repair (BER): A mechanistic mathematical approach. DNA Repair 2014, 22, 89–103. [Google Scholar] [CrossRef] [PubMed]
- Plante, I.; Ponomarev, A.L.; Cucinotta, F.A. Calculation of the energy deposition in nanovolumes by protons and HZE particles: Geometric patterns of initial distributions of DNA repair foci. Phys. Med. Biol. 2013, 58, 6393–6405. [Google Scholar] [CrossRef] [PubMed]
- Nikitaki, Z.; Nikolov, V.; Mavragani, I.V.; Plante, I.; Emfietzoglou, D.; Iliakis, G.; Georgakilas, A.G. Non-DSB clustered DNA lesions. Does theory colocalize with the experiment? Radiat. Phys. Chem. 2016, 128, 26–35. [Google Scholar] [CrossRef]
- Wälzlein, C.; Scifoni, E.; Krämer, M.; Durante, M. Simulations of dose enhancement for heavy atom nanoparticles irradiated by protons. Phys. Med. Biol. 2014, 59, 1441–1458. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Papamichael, G.; Kostarelos, K.; Moscovitch, M. A Monte Carlo track structure code for electrons (~10 eV-10 keV) and protons (~0.3-10 MeV) in water: Partitioning of energy and collision events. Phys. Med. Biol. 2000, 45, 3171–3194. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Papamichael, G.; Karava, K.; Androulidakis, I.; Pathak, A.; Phillips, G.W.; Moscovitch, M.; Kostarelos, K. A Monte-Carlo code for the detailed simulation of electron and light-ion tracks in condensed matter. Radiat. Prot. Dosim. 2006, 119, 491–496. [Google Scholar] [CrossRef] [Green Version]
- Matsuya, Y.; Kai, T.; Yoshii, Y.; Yachi, Y.; Naijo, S.; Date, H.; Sato, T. Modeling of yield estimation for DNA strand breaks based on Monte Carlo simulations of electron track structure in liquid water. J. Appl. Phys. 2019, 126, 124701. [Google Scholar] [CrossRef]
- Goorley, T.; James, M.; Booth, T.; Brown, F.; Bull, J.; Cox, L.J.; Durkee, J.; Elson, J.; Fensin, M.; Forster, R.A.; et al. Features of MCNP6. Ann. Nucl. Energy 2016, 87, 772–783. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Varea, J.M.; González-Muñoz, G.; Galassi, M.E.; Wiklund, K.; Lind, B.K.; Ahnesjö, A.; Tilly, N. Limitations (and merits) of PENELOPE as a track-structure code. Int. J. Radiat. Biol. 2012, 88, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Bäckström, G.; Galassi, M.E.; Tilly, N.; Ahnesjö, A.; Fernández-Varea, J.M. Track structure of protons and other light ions in liquid water: Applications of the LIonTrack code at the nanometer scale. Med. Phys. 2013, 40, 064101. [Google Scholar] [CrossRef]
- Villegas, F.; Tilly, N.; Ahnesjö, A. Monte Carlo calculated microdosimetric spread for cell nucleus-sized targets exposed to brachytherapy125I and192Ir sources and60Co cell irradiation. Phys. Med. Biol. 2013, 58, 6149–6162. [Google Scholar] [CrossRef]
- Bernal, M.A.; Bordage, M.C.; Brown, J.M.C.; Davídková, M.; Delage, E.; El Bitar, Z.; Enger, S.A.; Francis, Z.; Guatelli, S.; Ivanchenko, V.N.; et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys. Med. 2015, 31, 861–874. [Google Scholar] [CrossRef]
- Incerti, S.; Kyriakou, I.; Bernal, M.A.; Bordage, M.C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739. [Google Scholar] [CrossRef] [Green Version]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—a simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef] [Green Version]
- Bernal, M.A.; Liendo, J.A. An investigation on the capabilities of the PENELOPE MC code in nanodosimetry. Med. Phys. 2009, 36, 620–625. [Google Scholar] [CrossRef]
- Villegas, F.; Bäckström, G.; Tilly, N.; Ahnesjö, A. Energy deposition clustering as a functional radiation quality descriptor for modeling relative biological effectiveness. Med. Phys. 2016, 43, 6322–6335. [Google Scholar] [CrossRef]
- Incerti, S.; Ivanchenko, A.; Karamitros, M.; Mantero, A.; Moretto, P.; Tran, H.N.; Mascialino, B.; Champion, C.; Ivanchenko, V.N.; Bernal, M.A.; et al. Comparison of GEANT4 very low energy cross section models with experimental data in water. Med. Phys. 2010, 37, 4692–4708. [Google Scholar] [CrossRef] [PubMed]
- Kyriakou, I.; Sefl, M.; Nourry, V.; Incerti, S. The impact of new Geant4-DNA cross section models on electron track structure simulations in liquid water. J. Appl. Phys. 2016, 119, 194902. [Google Scholar] [CrossRef]
- Bordage, M.C.; Bordes, J.; Edel, S.; Terrissol, M.; Franceries, X.; Bardies, M.; Lampe, N. Implementation of new physics models for low energy electrons inImplementation of new physics models for low energy electrons in liquid water in Geant4-DNA. Phys. Med. 2016, 32, 1833–1840. [Google Scholar] [CrossRef] [PubMed]
- Sakata, D.; Kyriakou, I.; Okada, S.; Tran, H.N.; Lampe, N.; Guatelli, S.; Bordage, M.-C.; Ivanchenko, V.; Murakami, K.; Sasaki, T.; et al. Geant4-DNA track-structure simulations for gold nanoparticles: The importance of electron discrete models in nanometer volumes. Med. Phys. 2018, 45, 2230–2242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakata, D.; Incerti, S.; Bordage, M.C.; Lampe, N.; Okada, S.; Emfietzoglou, D.; Kyriakou, I.; Murakami, K.; Sasaki, T.; Tran, H.; et al. An implementation of discrete electron transport models for gold in the Geant4 simulation toolkit. J. Appl. Phys. 2016, 120, 244901. [Google Scholar] [CrossRef] [Green Version]
- Sakata, D.; Kyriakou, I.; Tran, H.N.; Bordage, M.-C.; Rosenfeld, A.; Ivanchenko, V.; Incerti, S.; Emfietzoglou, D.; Guatelli, S. Electron track structure simulations in a gold nanoparticle using Geant4-DNA. Phys. Med. 2019, 63, 98–104. [Google Scholar] [CrossRef]
- Shin, W.-G.; Ramos-Mendez, J.; Faddegon, B.; Tran, H.N.; Villagrasa, C.; Perrot, Y.; Okada, S.; Karamitros, M.; Emfietzoglou, D.; Kyriakou, I.; et al. Evaluation of the influence of physical and chemical parameters on water radiolysis simulations under MeV electron irradiation using Geant4-DNA. J. Appl. Phys. 2019, 126, 114301. [Google Scholar] [CrossRef]
- Meylan, S.; Incerti, S.; Karamitros, M.; Tang, N.; Bueno, M.; Clairand, I.; Villagrasa, C. Simulation of early DNA damage after the irradiation of a fibroblast cell nucleus using Geant4-DNA. Sci. Rep. 2017, 7, 11923. [Google Scholar] [CrossRef]
- Sakata, D.; Lampe, N.; Karamitros, M.; Kyriakou, I.; Belov, O.; Bernal, M.A.; Bolst, D.; Bordage, M.-C.; Breton, V.; Brown, J.M.C.; et al. Evaluation of early radiation DNA damage in a fractal cell nucleus model using Geant4-DNA. Phys. Med. 2019, 62, 152–157. [Google Scholar] [CrossRef] [Green Version]
- Tang, N.; Bueno, M.; Meylan, S.; Incerti, S.; Tran, H.N.; Vaurijoux, A.; Gruel, G.; Villagrasa, C. Influence of chromatin compaction on simulated early radiation-induced DNA damage using Geant4-DNA. Med. Phys. 2019, 46, 1501–1511. [Google Scholar] [CrossRef] [Green Version]
- Schuemann, J.; McNamara, A.L.; Ramos-Méndez, J.; Perl, J.; Held, K.D.; Paganetti, H.; Incerti, S.; Faddegon, B. TOPAS-nBio: An Extension to the TOPAS Simulation Toolkit for Cellular and Sub-cellular Radiobiology. Radiat. Res. 2019, 191, 125–138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perl, J.; Shin, J.; Schumann, J.; Faddegon, B.; Paganetti, H. TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Med. Phys. 2012, 39, 6818–6837. [Google Scholar] [CrossRef] [PubMed]
- McNamara, A.; Geng, C.; Turner, R.; Mendez, J.R.; Perl, J.; Held, K.; Faddegon, B.; Paganetti, H.; Schuemann, J. Validation of the radiobiology toolkit TOPAS-nBio in simple DNA geometries. Phys. Med. : Pm : Int. J. Devoted Appl. Phys. Med. Biol. Off. J. Ital. Assoc. Biomed. Phys. (Aifb) 2017, 33, 207–215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villagrasa, C.; Bordage, M.-C.; Bueno, M.; Bug, M.; Chiriotti, S.; Gargioni, E.; Heide, B.; Nettelbeck, H.; Parisi, A.; Rabus, H. assessing the contribution of cross-Sections to the uncertainty Of monte carlo calculations in micro- And nanodosimetry. Radiat. Prot. Dosim. 2018, 183, 11–16. [Google Scholar] [CrossRef]
- Zheng, Y.; Sanche, L. Clustered DNA Damages induced by 0.5 to 30 eV Electrons. Int. J. Mol. Sci. 2019, 20, 3749. [Google Scholar] [CrossRef] [Green Version]
- Rezaee, M.; Hunting, D.J.; Sanche, L. Correlation between energy deposition and molecular damage from Auger electrons: A case study of ultra-low energy (5–18 eV) electron interactions with DNA. Med. Phys. 2014, 41, 072502. [Google Scholar] [CrossRef] [Green Version]
- Elsässer, T.; Scholz, M. Cluster Effects within the Local Effect Model. Radiat. Res. 2007, 167, 319–329. [Google Scholar] [CrossRef]
- Abolfath, R.M.; Carlson, D.J.; Chen, Z.J.; Nath, R. A molecular dynamics simulation of DNA damage induction by ionizing radiation. Phys. Med. Biol. 2013, 58, 7143–7157. [Google Scholar] [CrossRef]
- Liang, Y.; Yang, G.; Liu, F.; Wang, Y. Monte Carlo simulation of ionizing radiation induced DNA strand breaks utilizing coarse grained high-order chromatin structures. Phys. Med. Biol. 2015, 61, 445–460. [Google Scholar] [CrossRef]
- Liu, R.; Zhao, T.; Zhao, X.; Reynoso, F.J. Modeling gold nanoparticle radiosensitization using a clustering algorithm to quantitate DNA double-strand breaks with mixed-physics Monte Carlo simulation. Med. Phys. 2019, 46, 5314–5325. [Google Scholar] [CrossRef]
- Francis, Z.; Villagrasa, C.; Clairand, I. Simulation of DNA damage clustering after proton irradiation using an adapted DBSCAN algorithm. Comput. Methods Programs Biomed. 2011, 101, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, M.; Villagrasa, C.; Clairand, I.; Incerti, S. Influence of the DNA density on the number of clustered damages created by protons of different energies. Nucl. Instrum. Methods Phys. Res. Sect. B: Beam Interact. Mater. At. 2013, 298, 47–54. [Google Scholar] [CrossRef]
- Semenenko, V.A.; Stewart, R.D. A Fast Monte Carlo Algorithm to Simulate the Spectrum of DNA Damages Formed by Ionizing Radiation. Radiat. Res. 2004, 161, 451–457. [Google Scholar] [CrossRef] [PubMed]
- Semenenko, V.A.; Stewart, R.D. Fast Monte Carlo simulation of DNA damage formed by electrons and light ions. Phys. Med. Biol. 2006, 51, 1693–1706. [Google Scholar] [CrossRef] [Green Version]
- Stewart, R.; Yu, V.; Georgakilas, A.; Koumenis, C.; Park, J.; Carlson, D. Effects of radiation quality and oxygen on clustered DNA lesions and cell death. Radiat. Res. 2011, 176, 587–602. [Google Scholar] [CrossRef]
- Liu, R.; Zhao, T.; Swat, M.H.; Reynoso, F.J.; Higley, K.A. Development of computational model for cell dose and DNA damage quantification of multicellular system. Int. J. Radiat. Biol. 2019, 95, 1484–1497. [Google Scholar] [CrossRef]
- Lampe, N.; Karamitros, M.; Breton, V.; Brown, J.M.C.; Kyriakou, I.; Sakata, D.; Sarramia, D.; Incerti, S. Mechanistic DNA damage simulations in Geant4-DNA part 1: A parameter study in a simplified geometry. Phys. Med. Eur. J. Med. Phys. 2018, 48, 135–145. [Google Scholar] [CrossRef]
- Lampe, N.; Karamitros, M.; Breton, V.; Brown, J.M.C.; Sakata, D.; Sarramia, D.; Incerti, S. Mechanistic DNA damage simulations in Geant4-DNA Part 2: Electron and proton damage in a bacterial cell. Phys. Med. Eur. J. Med. Phys. 2018, 48, 146–155. [Google Scholar] [CrossRef]
- Štepán, V.; Davídková, M. Impact of oxygen concentration on yields of DNA damages caused by ionizing radiation. J. Phys. Conf. Ser. 2008, 101, 012015. [Google Scholar]
- Štěpán, V.; Davídková, M. RADAMOL tool: Role of radiation quality and charge transfer in damage distribution along DNA oligomer. Eur. Phys. J. D 2014, 68, 240. [Google Scholar] [CrossRef]
- Alloni, D.; Campa, A.; Friedland, W.; Mariotti, L.; Ottolenghi, A. Track structure, radiation quality and initial radiobiological events: Considerations based on the PARTRAC code experience. Int. J. Radiat. Biol. 2012, 88, 77–86. [Google Scholar] [CrossRef] [PubMed]
- Kreipl, M.S.; Friedland, W.; Paretzke, H.G. Interaction of ion tracks in spatial and temporal proximity. Radiat. Environ. Biophys. 2009, 48, 349. [Google Scholar] [CrossRef] [PubMed]
- Incerti, S.; Champion, C.; Tran, H.N.; Karamitros, M.; Bernal, M.; Francis, Z.; Ivanchenko, V.; Mantero, A. Energy deposition in small-scale targets of liquid water using the very low energy electromagnetic physics processes of the Geant4 toolkit. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2013, 306, 158–164. [Google Scholar] [CrossRef]
- Karamitros, M.; Incerti, S.; Mantero, A. Modeling radiation chemistry in the Geant4 toolkit. Prog. Nucl. Sci. Technol. 2011, 2, 503–508. [Google Scholar] [CrossRef]
- Okada, S.; Murakami, K.; Incerti, S.; Amako, K.; Sasaki, T. MPEXS-DNA, a new GPU-based Monte Carlo simulator for track structures and radiation chemistry at subcellular scale. Med. Phys. 2019, 46, 1483–1500. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, Y.; Stewart, R.D. Monte Carlo simulation of DNA damage induction by x-rays and selected radioisotopes. Phys. Med. Biol. 2007, 53, 233–244. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Delage, E.; Pham, Q.T.; Karamitros, M.; Payno, H.; Stepan, V.; Incerti, S.; Maigne, L.; Perrot, Y. PDB4DNA: Implementation of DNA geometry from the Protein Data Bank (PDB) description for Geant4-DNA Monte-Carlo simulations. Comput. Phys. Commun. 2015, 192, 282–288. [Google Scholar] [CrossRef] [Green Version]
- Flores, S.C.; Sherman, M.A.; Bruns, C.M.; Eastman, P.; Altman, R.B. Fast flexible modeling of RNA structure using internal coordinates. Ieee/Acm Trans Comput Biol Bioinform 2011, 8, 1247–1257. [Google Scholar] [CrossRef] [Green Version]
- Sherman, M. Simbody Home Page. Available online: https://simtk.org/home/simbody (accessed on 22 March 2020).
- Leontis, N.B.; Stombaugh, J.; Westhof, E. The non-Watson-Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002, 30, 3497–3531. [Google Scholar] [CrossRef]
- Howell, S.C.; Qiu, X.; Curtis, J.E. Monte Carlo simulation algorithm for B-DNA. J. Comput. Chem. 2016, 37, 2553–2563. [Google Scholar] [CrossRef]
- Wang, Y.; Tree, D.R.; Dorfman, K.D. Simulation of DNA Extension in Nanochannels. Macromolecules 2011, 44, 6594–6604. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Gao, H. A generalized bead-rod model for Brownian dynamics simulations of wormlike chains under strong confinement. J. Chem. Phys. 2005, 123, 084906. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.P., 3rd; Maher, L.J. DNA curvature and flexibility in vitro and in vivo. Q. Rev. Biophys. 2010, 43, 23–63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cumberworth, A.; Reinhardt, A.; Frenkel, D. Lattice models and Monte Carlo methods for simulating DNA origami self-assembly. J. Chem. Phys. 2018, 149, 234905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meylan, S.; Vimont, U.; Incerti, S.; Clairand, I.; Villagrasa, C. Geant4-DNA simulations using complex DNA geometries generated by the DnaFabric tool. Comput. Phys. Commun. 2016, 204, 159–169. [Google Scholar] [CrossRef]
- Mavragani, I.V.; Nikitaki, Z.; Kalospyros, S.A.; Georgakilas, A.G. Ionizing Radiation and Complex DNA Damage: From Prediction to Detection Challenges and Biological Significance. Cancers (Basel) 2019, 11, 1789. [Google Scholar] [CrossRef] [Green Version]
- Jakob, B.; Dubiak-Szepietowska, M.; Janiel, E.; Schmidt, A.; Durante, M.; Taucher-Scholz, G. Differential Repair Protein Recruitment at Sites of Clustered and Isolated DNA Double-Strand Breaks Produced by High-Energy Heavy Ions. Sci. Rep. 2020, 10, 1443. [Google Scholar] [CrossRef]
- Grün, R.; Friedrich, T.; Traneus, E.; Scholz, M. Is the dose-averaged LET a reliable predictor for the relative biological effectiveness? Med. Phys. 2019, 46, 1064–1074. [Google Scholar] [CrossRef]
- Huang, Y.W.; Pan, C.Y.; Hsiao, Y.Y.; Chao, T.C.; Lee, C.C.; Tung, C.J. Monte Carlo simulations of the relative biological effectiveness for DNA double strand breaks from 300 MeV u−1 carbon-ion beams. Phys. Med. Biol. 2015, 60, 5995–6012. [Google Scholar] [CrossRef]
- Stewart, R.D.; Streitmatter, S.W.; Argento, D.C.; Kirkby, C.; Goorley, J.T.; Moffitt, G.; Jevremovic, T.; Sandison, G.A. Rapid MCNP simulation of DNA double strand break (DSB) relative biological effectiveness (RBE) for photons, neutrons, and light ions. Phys. Med. Biol. 2015, 60, 8249–8274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Charlton, D.E.; Nikjoo, H.; Humm, J.L. Calculation of Initial Yields of Single- and Double-strand Breaks in Cell Nuclei from Electrons, Protons and Alpha Particles. Int. J. Radiat. Biol. 1989, 56, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Obeidat, M.; McConnell, K.A.; Li, X.; Bui, B.; Stathakis, S.; Papanikolaou, N.; Rasmussen, K.; Ha, C.S.; Lee, S.E.; Shim, E.Y.; et al. DNA double-strand breaks as a method of radiation measurements for therapeutic beams. Med. Phys. 2018, 45, 3460–3465. [Google Scholar] [CrossRef] [PubMed]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A Whole-Cell Computational Model Predicts Phenotype from Genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef] [Green Version]
- Ohno, H.; Naito, Y.; Nakajima, H.; Tomita, M. Construction of a Biological Tissue Model Based on a Single-Cell Model: A Computer Simulation of Metabolic Heterogeneity in the Liver Lobule. Artif. Life 2008, 14, 3–28. [Google Scholar] [CrossRef]
- Ishii, N.; Robert, M.; Nakayama, Y.; Kanai, A.; Tomita, M. Toward large-scale modeling of the microbial cell for computer simulation. J. Biotechnol. 2004, 113, 281–294. [Google Scholar] [CrossRef]
- Sandersius, S.A.; Weijer, C.J.; Newman, T.J. Emergent cell and tissue dynamics from subcellular modeling of active biomechanical processes. Phys. Biol. 2011, 8, 045007. [Google Scholar] [CrossRef]
- Tomita, M. Whole-cell simulation: A grand challenge of the 21st century. Trends Biotechnol. 2001, 19, 205–210. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Wilson, W.E.; Goodhead, D.T. Computational Approach for Determining the Spectrum of DNA Damage Induced by Ionizing Radiation. Radiat. Res. 2001, 156, 577–583. [Google Scholar] [CrossRef]
- Nikjoo, P.O.N.D.T.G.; M. Terrissol, H. Computational modelling of low-energy electron-induced DNA damage by early physical and chemical events. Int. J. Radiat. Biol. 1997, 71, 467–483. [Google Scholar] [CrossRef]
- Wilson, W.E.; Nikjoo, H. A Monte Carlo code for positive ion track simulation. Radiat. Environ. Biophys. 1999, 38, 97–104. [Google Scholar] [CrossRef]
- Terrissol, M.; Beaudré, A. Simulation of Space and Time Evolution of Radiolytic Species Induced by Electrons in Water. Radiat. Prot. Dosim. 1990, 31, 175–177. [Google Scholar] [CrossRef]
- Bernhardt, P.; Friedland, W.; Jacob, P.; Paretzke, H.G. Modeling of ultrasoft X-ray induced DNA damage using structured higher order DNA targets. Int. J. Mass Spectrom. 2003, 223-224, 579–597. [Google Scholar] [CrossRef]
- Karamitros, M.; Luan, S.; Bernal, M.A.; Allison, J.; Baldacchino, G.; Davidkova, M.; Francis, Z.; Friedland, W.; Ivantchenko, V.; Ivantchenko, A.; et al. Diffusion-controlled reactions modelingin Geant4-DNA. J. Comput. Phys. 2014, 274, 841–882. [Google Scholar] [CrossRef]
- Michalik, V.; Begusová, M.; Bigildeev, E.A. Computer-Aided Stochastic Modeling of the Radiolysis of Liquid Water. Radiat. Res. 1998, 149, 224–236. [Google Scholar] [CrossRef]
- De Berg, M.; van Kreveld, M.; Overmars, M.; Schwarzkopf, O.C. Computational Geometry. In Computational Geometry; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Balasubramanian, B.; Pogozelski, W.K.; Tullius, T.D. DNA strand breaking by the hydroxyl radical is governed by the accessible surface areas of the hydrogen atoms of the DNA backbone. Proc. Natl. Acad. Sci. USA 1998, 95, 9738–9743. [Google Scholar] [CrossRef] [Green Version]
- Dizdaroglu, M.; Jaruga, P. Mechanisms of free radical-induced damage to DNA. Free Radic. Res. 2012, 46, 382–419. [Google Scholar] [CrossRef]
- Tang, N.; Bueno, M.; Meylan, S.; Perrot, Y.; Tran, H.N.; Freneau, A.; Dos Santos, M.; Vaurijoux, A.; Gruel, G.; Bernal, M.A.; et al. Assessment of Radio-Induced Damage in Endothelial Cells Irradiated with 40 kVp, 220 kVp, and 4 MV X-rays by Means of Micro and Nanodosimetric Calculations. Int. J. Mol. Sci. 2019, 20, 6204. [Google Scholar] [CrossRef] [Green Version]
- Cunha, M.; Monini, C.; Testa, E.; Beuve, M. NanOx, a new model to predict cell survival in the context of particle therapy. Phys. Med. Biol. 2017, 62, 1248–1268. [Google Scholar] [CrossRef]
- Monini, C.; Cunha, M.; Testa, E.; Beuve, M. Study of the Influence of NanOx Parameters. Cancers (Basel) 2018, 10, 87. [Google Scholar] [CrossRef] [Green Version]
- Tsai, M.-Y.; Tian, Z.; Qin, N.; Yan, C.; Lai, Y.; Hung, S.-H.; Chi, Y.; Jia, X. A new open-source GPU-based microscopic Monte Carlo simulation tool for the calculations of DNA damages caused by ionizing radiation—Part I: Core algorithm and validation. Med. Phys. n/a 2020. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.; Tsai, M.-Y.; Tian, Z.; Qin, N.; Yan, C.; Hung, S.-H.; Chi, Y.; Jia, X. A new open-source GPU-based microscopic Monte Carlo simulation tool for the calculations of DNA damages caused by ionizing radiation—Part II: Sensitivity and uncertainty analysis. Med. Phys. 2020, in press. [Google Scholar] [CrossRef] [PubMed]
- Barnard, S.; Bouffler, S.; Rothkamm, K. The shape of the radiation dose response for DNA double-strand break induction and repair. Genome Integr 2013, 4, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warmenhoven, J.W.; Henthorn, N.T.; Sotiropoulos, M.; Korabel, N.; Fedotov, S.; Mackay, R.I.; Kirkby, K.J.; Merchant, M.J. An In Silico Model of DNA Repair for Investigation of Mechanisms in Non-Homologous End Joining. bioRxiv 2018, 318139. [Google Scholar] [CrossRef] [Green Version]
- Warmenhoven, J.W.; Henthorn, N.T.; Ingram, S.P.; Chadwick, A.L.; Sotiropoulos, M.; Korabel, N.; Fedotov, S.; Mackay, R.I.; Kirkby, K.J.; Merchant, M.J. Insights into the non-homologous end joining pathway and double strand break end mobility provided by mechanistic in silico modelling. DNA Repair 2020, 85, 102743. [Google Scholar] [CrossRef] [PubMed]
- Cucinotta, F.A.; Kim, M.-H.Y.; Willingham, V.; George, K.A. Physical and Biological Organ Dosimetry Analysis for International Space Station Astronauts. Radiat. Res. 2008, 170, 127–138. [Google Scholar] [CrossRef]
- Taleei, R.; Nikjoo, H. Biochemical DSB-repair model for mammalian cells in G1 and early S phases of the cell cycle. Mutat. Res. /Genet. Toxicol. Environ. Mutagenesis 2013, 756, 206–212. [Google Scholar] [CrossRef]
- Woods, M.L.; Barnes, C.P. Mechanistic Modelling and Bayesian Inference Elucidates the Variable Dynamics of Double-Strand Break Repair. PLoS Comput. Biol. 2016, 12, e1005131. [Google Scholar] [CrossRef] [Green Version]
- Cleri, F.; Landuzzi, F.; Blossey, R. Mechanical evolution of DNA double-strand breaks in the nucleosome. PLoS Comput. Biol. 2018, 14, e1006224. [Google Scholar] [CrossRef]
- Tello Cajiao, J.J.; Carante, M.P.; Bernal Rodriguez, M.A.; Ballarini, F. Proximity effects in chromosome aberration induction: Dependence on radiation quality, cell type and dose. DNA Repair 2018, 64, 45–52. [Google Scholar] [CrossRef]
- Li, Y.; Cucinotta, F.A. Mathematical Model of ATM Activation and Chromatin Relaxation by Ionizing Radiation. Int. J. Mol. Sci. 2020, 21, 1214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chadwick, K.H.; Leenhouts, H.P. A molecular theory of cell survival. Phys. Med. Biol. 1973, 18, 78–87. [Google Scholar] [CrossRef] [PubMed]
- Unkel, S.; Belka, C.; Lauber, K. On the analysis of clonogenic survival data: Statistical alternatives to the linear-quadratic model. Radiat. Oncol. 2016, 11, 11. [Google Scholar] [CrossRef] [Green Version]
- Belkić, D.; Belkić, K. Padé–Froissart exact signal-noise separation in nuclear magnetic resonance spectroscopy. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 125003. [Google Scholar] [CrossRef] [Green Version]
- Park, C.; Papiez, L.; Zhang, S.; Story, M.; Timmerman, R.D. Universal Survival Curve and Single Fraction Equivalent Dose: Useful Tools in Understanding Potency of Ablative Radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2008, 70, 847–852. [Google Scholar] [CrossRef] [PubMed]
- Guerrero, M.; Carlone, M. Mechanistic formulation of a lineal-quadratic-linear (LQL) model: Split-dose experiments and exponentially decaying sources. Med. Phys. 2010, 37, 4173–4181. [Google Scholar] [CrossRef]
- Friedrich, T.; Scholz, U.; Elsässer, T.; Durante, M.; Scholz, M. Systematic analysis of RBE and related quantities using a database of cell survival experiments with ion beam irradiation. J. Radiat Res. 2013, 54, 494–514. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, R.B. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET. Med. Phys. 1998, 25, 1157–1170. [Google Scholar] [CrossRef]
- Verkhovtsev, A.; Surdutovich, E.; Solov’yov, A.V. Multiscale approach predictions for biological outcomes in ion-beam cancer therapy. Sci. Rep. 2016, 6, 27654. [Google Scholar] [CrossRef] [Green Version]
- Carante, M.P.; Aimè, C.; Cajiao, J.J.T.; Ballarini, F. BIANCA, a biophysical model of cell survival and chromosome damage by protons, C-ions and He-ions at energies and doses used in hadrontherapy. Phys. Med. Biol. 2018, 63, 075007. [Google Scholar] [CrossRef]
- Carlson, D.J.; Stewart, R.D.; Semenenko, V.A.; Sandison, G.A. Combined Use of Monte Carlo DNA Damage Simulations and Deterministic Repair Models to Examine Putative Mechanisms of Cell Killing. Radiat. Res. 2008, 169, 447–459. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Li, C.; Qiu, R.; Chen, Y.; Wu, Z.; Zhang, H.; Li, J. Modelling of Cellular Survival Following Radiation-Induced DNA Double-Strand Breaks. Sci. Rep. 2018, 8, 16202. [Google Scholar] [CrossRef] [PubMed]
- Rørvik, E.; Fjæra, L.F.; Dahle, T.J.; Dale, J.E.; Engeseth, G.M.; Stokkevåg, C.H.; Thörnqvist, S.; Ytre-Hauge, K.S. Exploration and application of phenomenological RBE models for proton therapy. Phys. Med. Biol. 2018, 63, 185013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Solov’yov, I.A.; Solov’yov, A.V. Simulation of nanofractal dynamics with MBN Explorer. J. Phys. Conf. Ser. 2013, 438, 012006. [Google Scholar] [CrossRef]
- Plante, I.; Ponomarev, A.; Patel, Z.; Slaba, T.; Hada, M. RITCARD: Radiation-Induced Tracks, Chromosome Aberrations, Repair and Damage. Radiat. Res. 2019, 192, 282–298. [Google Scholar] [CrossRef]
- Plante, I.; Slaba, T.; Shavers, Z.; Hada, M. A Bi-Exponential Repair Algorithm for Radiation-Induced Double-Strand Breaks: Application to Simulation of Chromosome Aberrations. Genes 2019, 10, 936. [Google Scholar] [CrossRef] [Green Version]
- Helleday, T. The underlying mechanism for the PARP and BRCA synthetic lethality: Clearing up the misunderstandings. Mol. Oncol. 2011, 5, 387–393. [Google Scholar] [CrossRef] [Green Version]
- Killock, D. DNA polymerase θ—a new target for synthetic lethality? Nat. Rev. Clin. Oncol. 2015, 12, 125. [Google Scholar] [CrossRef]
- Rehman, F.L.; Lord, C.J.; Ashworth, A. Synthetic lethal approaches to breast cancer therapy. Nat. Rev. Clin. Oncol. 2010, 7, 718–724. [Google Scholar] [CrossRef]
- Shaheen, M.; Allen, C.; Nickoloff, J.A.; Hromas, R. Synthetic lethality: Exploiting the addiction of cancer to DNA repair. Blood 2011, 117, 6074–6082. [Google Scholar] [CrossRef]
- Schmitt, M.W.; Loeb, L.A.; Salk, J.J. The influence of subclonal resistance mutations on targeted cancer therapy. Nat. Rev. Clin. Oncol. 2016, 13, 335–347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nickoloff, J.A.; Boss, M.-K.; Allen, C.P.; LaRue, S.M. Translational research in radiation-induced DNA damage signaling and repair. Transl. Cancer Res. 2017, 6 (Suppl 5), S875–S891. [Google Scholar] [CrossRef] [PubMed]
- Sedelnikova, O.A.; Redon, C.E.; Dickey, J.S.; Nakamura, A.J.; Georgakilas, A.G.; Bonner, W.M. Role of oxidatively induced DNA lesions in human pathogenesis. Mutat. Res. /Rev. Mutat. Res. 2010, 704, 152–159. [Google Scholar] [CrossRef] [PubMed] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzipapas, K.P.; Papadimitroulas, P.; Emfietzoglou, D.; Kalospyros, S.A.; Hada, M.; Georgakilas, A.G.; Kagadis, G.C. Ionizing Radiation and Complex DNA Damage: Quantifying the Radiobiological Damage Using Monte Carlo Simulations. Cancers 2020, 12, 799. https://doi.org/10.3390/cancers12040799
Chatzipapas KP, Papadimitroulas P, Emfietzoglou D, Kalospyros SA, Hada M, Georgakilas AG, Kagadis GC. Ionizing Radiation and Complex DNA Damage: Quantifying the Radiobiological Damage Using Monte Carlo Simulations. Cancers. 2020; 12(4):799. https://doi.org/10.3390/cancers12040799
Chicago/Turabian StyleChatzipapas, Konstantinos P., Panagiotis Papadimitroulas, Dimitris Emfietzoglou, Spyridon A. Kalospyros, Megumi Hada, Alexandros G. Georgakilas, and George C. Kagadis. 2020. "Ionizing Radiation and Complex DNA Damage: Quantifying the Radiobiological Damage Using Monte Carlo Simulations" Cancers 12, no. 4: 799. https://doi.org/10.3390/cancers12040799
APA StyleChatzipapas, K. P., Papadimitroulas, P., Emfietzoglou, D., Kalospyros, S. A., Hada, M., Georgakilas, A. G., & Kagadis, G. C. (2020). Ionizing Radiation and Complex DNA Damage: Quantifying the Radiobiological Damage Using Monte Carlo Simulations. Cancers, 12(4), 799. https://doi.org/10.3390/cancers12040799