Early Prediction of Breast Cancer Recurrence for Patients Treated with Neoadjuvant Chemotherapy: A Transfer Learning Approach on DCE-MRIs
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Selection and Description
2.2. Data Pre-Processing
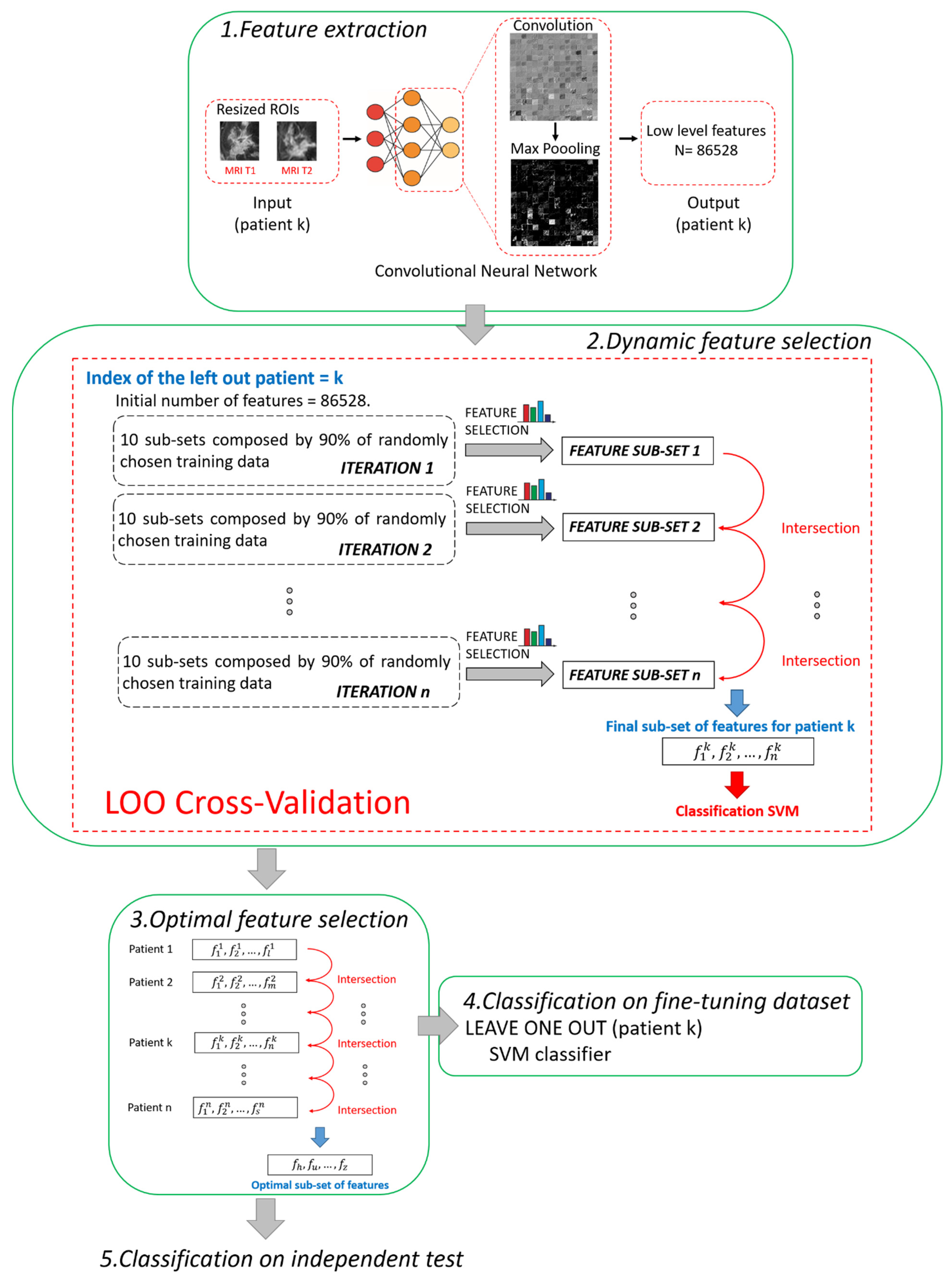
2.3. A Hybrid Machine Learning-Deep Learning Approach
2.3.1. Step 1. Feature Extraction
2.3.2. Step 2. Dynamic Feature Selection
2.3.3. Step 3. Optimal Feature Selection
2.3.4. Step 4. Classification on Fine-Tuning Dataset
2.3.5. Step 5. Classification on Independent Test
3. Results
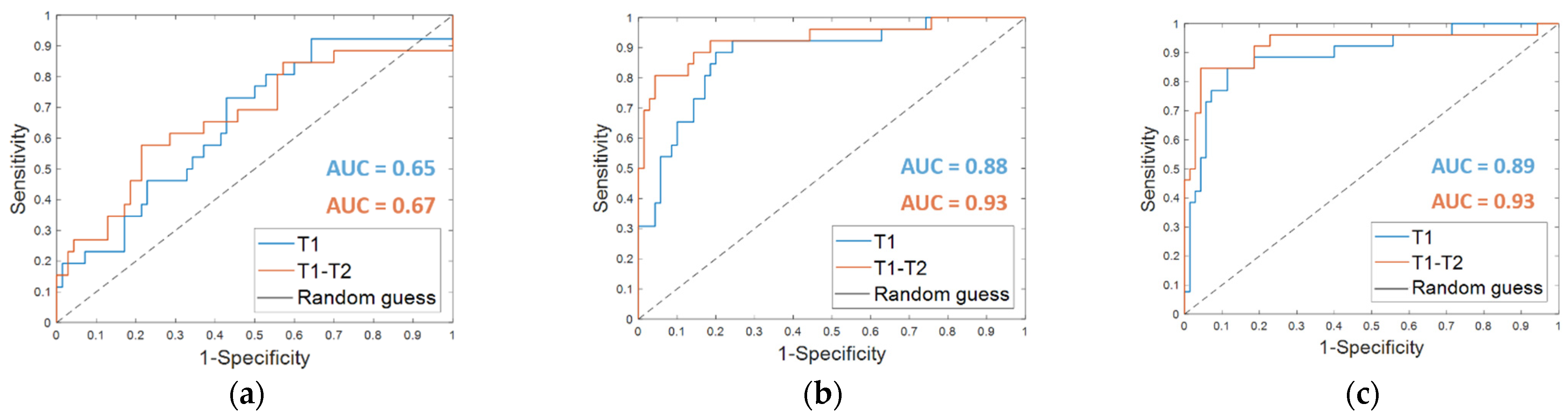
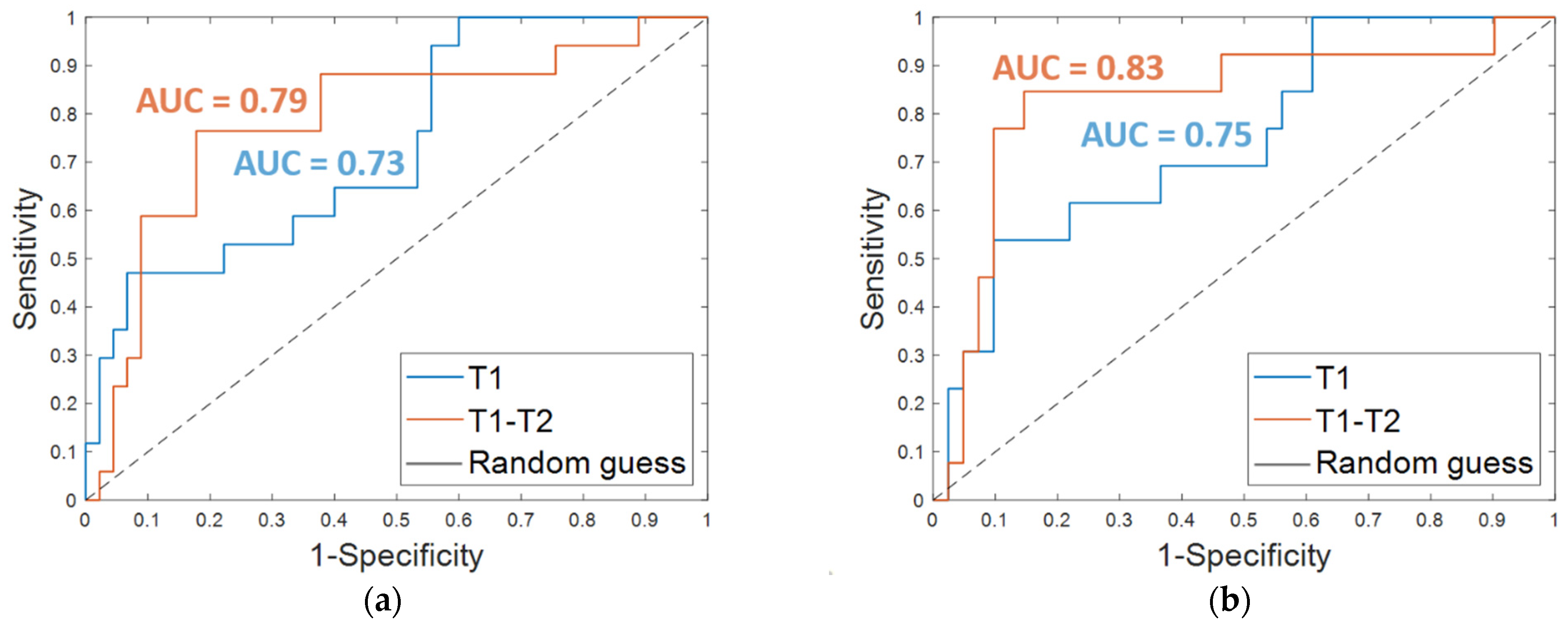
3.1. Predictive Contribution of the Features Extracted Solely from MRI T1 Exams
3.2. Breast Cancer Recurrence Prediction Using Features Extracted from MRI T1 and T2 Exams
3.3. Feature Visualization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hylton, N.M.; Blume, J.D.; Bernreuter, W.K.; Pisano, E.D.; Rosen, M.A.; Morris, E.A.; Weatherall, P.T.; Lehman, C.D.; Newstead, G.M.; Polin, S.; et al. Locally advanced breast cancer: MR imaging for prediction of response to neoadjuvant chemotherapy–Results from ACRIN 6657/I-SPY TRIAL. Radiology 2012, 263, 663–672. [Google Scholar] [CrossRef] [PubMed]
- Song, S.E.; Seo, B.K.; Cho, K.R.; Woo, O.H.; Son, G.S.; Kim, C.; Cho, S.B.; Kwon, S.-S. Computer-aided detection (CAD) system for breast MRI in assessment of local tumor extent, nodal status, and multifocality of invasive breast cancers: Preliminary study. Cancer Imaging 2015, 15, 1–9. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, M.C.; González, S.J.; Lin, H.; Zhao, X.; Kiluk, J.V.; Laronga, C.; Mooney, B. Prospective Trial of Breast MRI Versus 2D and 3D Ultrasound for Evaluation of Response to Neoadjuvant Chemotherapy. Ann. Surg. Oncol. 2015, 22, 2888–2894. [Google Scholar] [CrossRef]
- Krug, D.; Baumann, R.; Budach, W.; Dunst, J.; Feyer, P.; Fietkau, R.; Haase, W.; Harms, W.; Hehr, T.; Piroth, M.D.; et al. Neoadjuvant chemotherapy for breast cancer—background for the indication of locoregional treatment. Strahlenther. Onkol. 2018, 194, 797–805. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, C.; Devillers, A.; Sagan, C.; Ferrer, L.; Bridji, B.; Campion, L.; Ricaud, M.; Bourbouloux, E.; Doutriaux, I.; Clouet, M.; et al. Monitoring of early response to neoadjuvant chemotherapy in stage II and III breast cancer by [18F]fluorodeoxyglucose positron emission tomography. J. Clin. Oncol. 2006, 24, 5366–5372. [Google Scholar] [CrossRef] [PubMed]
- Marinovich, M.L.; Sardanelli, F.; Ciatto, S.; Mamounas, E.; Brennan, M.; Macaskill, P.; Irwig, L.; von Minckwitz, G.; Houssami, N. Early prediction of pathologic response to neoadjuvant therapy in breast cancer: Systematic review of the accuracy of MRI. Breast 2012, 21, 669–677. [Google Scholar] [CrossRef]
- Khairalseed, M.; Javed, K.; Jashkaran, G.; Kim, J.W.; Parker, K.J.; Hoyt, K. Monitoring early breast cancer response to neoadjuvant therapy using H-scan ultrasound imaging: Preliminary preclinical results. J. Ultrasound Med. 2019, 38, 1259–1268. [Google Scholar] [CrossRef]
- Tan, W.; Yang, M.; Yang, H.; Zhou, F.; Shen, W. Predicting the response to neoadjuvant therapy for early-stage breast cancer: Tumor-, blood-, and imaging-related biomarkers. Cancer Manag. Res. 2018, 10, 4333–4347. [Google Scholar] [CrossRef]
- Sharma, U.; Danishad, K.K.A.; Seenu, V.; Jagannathan, N.R. Longitudinal study of the assessment by MRI and diffusion-weighted imaging of tumor response in patients with locally advanced breast cancer undergoing neoadjuvant chemotherapy. NMR Biomed. 2009, 22, 104–113. [Google Scholar] [CrossRef]
- Drukker, K.; Li, H.; Antropova, N.; Edwards, A.; Papaioannou, J.; Giger, M.L. Most-enhancing tumor volume by MRI radiomics predicts recurrence-free survival ‘early on’ in neoadjuvant treatment of breast cancer. Cancer Imaging 2018, 18, 1–9. [Google Scholar] [CrossRef]
- Drukker, K.; Edwards, A.; Papaioannou, J.; Giger, M. Long short-term memory networks predict breast cancer recurrence in analysis of consecutive MRIs acquired during the course of neoadjuvant chemotherapy. In Proceedings of the Medical Imaging 2020: Computer-Aided Diagnosis, Houston, TX, USA, 15–20 February 2020; Volume 11314, p. 1131410. [Google Scholar] [CrossRef]
- Relapse-Free-Survival Definition. Available online: https://www.cancer.gov/publications/dictionaries/cancer-terms/def/relapse-free-survival (accessed on 1 February 2021).
- Hudis, C.A.; Barlow, W.E.; Costantino, J.P.; Gray, R.J.; Pritchard, K.I.; Chapman, J.-A.W.; Sparano, J.A.; Hunsberger, S.; Enos, R.A.; Gelber, R.D.; et al. Proposal for standardized definitions for efficacy end points in adjuvant breast cancer trials: The STEEP system. J. Clin. Oncol. 2007, 25, 2127–2132. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Ding, K.; Yang, H.; He, X.; Mo, W.; Ding, X. Does dose-dense neoadjuvant chemotherapy have clinically significant prognostic value in breast cancer?: A meta-analysis of 3724 patients. PLoS ONE 2020, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Korde, L.A.; Somerfield, M.R.; Carey, L.A.; Crews, J.R.; Denduluri, N.; Hwang, E.S.; Khan, S.A.; Loibl, S.; Morris, E.A.; Perez, A.; et al. Neoadjuvant Chemotherapy, Endocrine Therapy, and Targeted Therapy for Breast Cancer: ASCO Guideline. J. Clin. Oncol. 2021, 39, 1485–1505. [Google Scholar] [CrossRef]
- Hylton, N.M.; Gatsonis, C.A.; Rosen, M.A.; Lehman, C.D.; Newitt, D.C.; Partridge, S.C.; Bernreuter, W.K.; Pisano, E.D.; Morris, E.A.; Weatherall, P.T.; et al. Neoadjuvant chemotherapy for breast cancer: Functional tumor volume by MR imaging predicts recurrencefree survival-results from the ACRIN 6657/CALGB 150007 I-SPY 1 TRIAL. Radiology 2016, 279, 44–55. [Google Scholar] [CrossRef]
- Jahani, N.; Cohen, E.; Hsieh, M.K.; Weinstein, S.P.; Pantalone, L.; Davatzikos, C.; Kontos, D. Deformable image registration as a tool to improve survival prediction after neoadjuvant chemotherapy for breast cancer: Results from the ACRIN 6657/I-SPY-1 trial. In Proceedings of the Medical Imaging 2018: Computer-Aided Diagnosis, Houston, TX, USA, 10–15 February 2018; Volume 10575, p. 105752S. [Google Scholar]
- Jahani, N.; Cohen, E.; Hsieh, M.-K.; Weinstein, S.P.; Pantalone, L.; Hylton, N.; Newitt, D.; Davatzikos, C.; Kontos, D. Prediction of Treatment Response to Neoadjuvant Chemotherapy for Breast Cancer via Early Changes in Tumor Heterogeneity Captured by DCE-MRI Registration. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Olshen, A.; Wolf, D.; Jones, E.F.; Newitt, D.C.; Veer, L.V.; Yau, C.; Esserman, L.; Wulfkuhle, J.D.; Gallagher, R.I.; Singer, L.; et al. Features of MRI stromal enhancement with neoadjuvant chemotherapy: A subgroup analysis of the ACRIN 6657/I-SPY TRIAL. J. Med. Imaging 2017, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Panigrahi, S.; Nanda, A.; Swarnkar, T. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Wang, Z.; Li, M.; Wang, H.; Jiang, H.; Yao, Y.; Zhang, H.; Xin, J. Breast Cancer Detection Using Extreme Learning Machine Based on Feature Fusion with CNN Deep Features. IEEE Access 2019, 7, 105146–105158. [Google Scholar] [CrossRef]
- De Yu, S.; Liu, L.L.; Wang, Z.Y.; Dai, G.Z.; Xie, Y.Q. Transferring deep neural networks for the differentiation of mammographic breast lesions. Sci. China Technol. Sci. 2019, 62, 441–447. [Google Scholar] [CrossRef]
- Kumar, N.; Verma, R.; Arora, A.; Kumar, A.; Gupta, S.; Sethi, A.; Gann, P.H. Convolutional neural networks for prostate cancer recurrence prediction. In Proceedings of the Medical Imaging 2017: Digital Pathology, Orlando, FL, USA, 11–16 February 2017; Volume 10140, p. 101400H. [Google Scholar] [CrossRef]
- He, Y.; Guo, J.; Ding, X.; Van Ooijen, P.M.A.; Zhang, Y.; Chen, A.; Oudkerk, M.; Xie, X. Convolutional neural network to predict the local recurrence of giant cell tumor of bone after curettage based on pre-surgery magnetic resonance images. Eur. Radiol. 2019, 29, 5441–5451. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.Z.; Mutasa, S.; Chang, P.; Siddique, M.; Jambawalikar, S.; Ha, R. A novel CNN algorithm for pathological complete response prediction using an I-SPY TRIAL breast MRI database. Magn. Reson. Imaging 2020, 73, 148–151. [Google Scholar] [CrossRef] [PubMed]
- Ravichandran, K.; Braman, N.; Janowczyk, A.; Madabhushi, A. A deep learning classifier for prediction of pathological complete response to neoadjuvant chemotherapy from baseline breast DCE-MRI. In Proceedings of the Medical Imaging 2018: Computer-Aided Diagnosis, Houston, TX, USA, 10–15 February 2018; Volume 10575, p. 105750C. [Google Scholar] [CrossRef]
- Wu, J.; Cao, G.; Sun, X.; Lee, J.; Rubin, D.L.; Napel, S.; Kurian, A.W.; Daniel, B.L.; Li, R. Intratumoral spatial heterogeneity at perfusion MR imaging predicts recurrence-free survival in locally advanced breast cancer treated with neoadjuvant chemotherapy. Radiology 2018, 288, 26–35. [Google Scholar] [CrossRef] [PubMed]
- Esserman, L.J.; Berry, D.A.; Cheang, M.C.U.; Yau, C.; Perou, C.M.; Carey, L.; DeMichele, A.; Gray, J.W.; Conway-Dorsey, K.; Lenburg, M.E.; et al. Chemotherapy response and recurrence-free survival in Neoadjuvant breast cancer depends on biomarker profiles: Results from the I-SPY 1 TRIAL (CALGB 150007/150012; ACRIN 6657). Breast Cancer Res. Treat. 2012, 132, 1049–1062. [Google Scholar] [CrossRef]
- Newitt, N.; Hylton, D. Multi-center breast DCE-MRI data and segmentations from patients in the I-SPY 1/ACRIN 6657 trials. Cancer Imaging Arch. 2016. [Google Scholar] [CrossRef]
- Newitt, N.; Hylton, D. Single site breast DCE-MRI data and segmentations from patients undergoing neoadjuvant chemotherapy. Cancer Imaging Arch. 2016, 2. [Google Scholar] [CrossRef]
- Partridge, S.C.; Gibbs, J.E.; Lu, Y.; Esserman, L.J.; Tripathy, D.; Wolverton, D.S.; Rugo, H.S.; Hwang, E.S.; Ewing, C.A.; Hylton, N.M. MRI measurements of breast tumor volume predict response to neoadjuvant chemotherapy and recurrence-free survival. Am. J. Roentgenol. 2005, 184, 1774–1781. [Google Scholar] [CrossRef]
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; et al. The cancer imaging archive (TCIA): Maintaining and operating a public information repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef]
- Esserman, L.J.; Berry, D.A.; DeMichele, A.; Carey, L.; Davis, S.E.; Buxton, M.; Hudis, C.; Gray, J.W.; Perou, C.M.; Yau, C.; et al. Pathologic complete response predicts recurrence-free survival more effectively by cancer subset: Results from the I-SPY 1 TRIAL–CALGB 150007/150012, ACRIN 6657. J. Clin. Oncol. 2012, 30, 3242–3249. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Burges, C.J. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Mencattini, A.; Di Giuseppe, D.; Comes, M.C.; Casti, P.; Corsi, F.; Bertani, F.R.; Ghibelli, L.; Businaro, L.; Di Natale, C.; Parrini, M.C.; et al. Discovering the hidden messages within cell trajectories using a deep learning approach for in vitro evaluation of cancer drug treatments. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Casti, P.; Mencattini, A.; Comes, M.C.; Callari, G.; Di Giuseppe, D.; Natoli, S.; Dauri, M.; Daprati, E.; Martinelli, E. Calibration of Vision-Based Measurement of Pain Intensity with Multiple Expert Observers. IEEE Trans. Instrum. Meas. 2019, 68, 2442–2450. [Google Scholar] [CrossRef]
- Salakhutdinov, R.; Tenenbaum, J.B.; Torralba, A. Learning with Hierarchical-Deep Models. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1958–1971. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Zhao, Y.; Wang, S.; Wang, J.; Tian, Q. Good Practice in CNN Feature Transfer. arXiv 2016, arXiv:1604.00133. [Google Scholar]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Mann, D.R.; Whitney, B.H. On a Test of Whether one of Two Random Variables is Stochastically Larger Larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kalousis, A.; Prados, J.; Hilario, M. Stability of feature selection algorithms: A study on high-dimensional spaces. Knowl. Inf. Syst. 2007, 12, 95–116. [Google Scholar] [CrossRef]
- Křížek, P.; Kittler, J.; Hlaváč, V. Improving stability of feature selection methods. In Proceedings of the International Conference on Computer Analysis of Images and Patterns, Vienna, Austria, 27–29 August 2017; pp. 929–936. [Google Scholar] [CrossRef]
- Castelvecchi, D. Can we open the black box of AI? Nature News 2016, 538, 20–23. [Google Scholar] [CrossRef] [PubMed]
- Csáji, B.C. Approximation with Artificial Neural Networks. MsC Thesis, Faculty of Sciences, Etvs Lornd University, Budapest, Hungary, 2001. [Google Scholar]
- Alain, G.; Bengio, Y. Understanding intermediate layers using linear classifier probes. arXiv 2016, arXiv:1610.01644. [Google Scholar]
- Jacovi, A.; Hadash, G.; Kermany, E.; Carmeli, B.; Lavi, O.; Kour, G.; Berant, J. Neural network gradient-based learning of black-box function interfaces. arXiv 2019, arXiv:1901.03995. [Google Scholar]
- La Forgia, D.; Fanizzi, A.; Campobasso, F.; Bellotti, R.; Didonna, V.; Lorusso, V.; Moschetta, M.; Massafra, R.; Tamborra, P.; Tangaro, S.; et al. Radiomic analysis in contrast-enhanced spectral mammography for predicting breast cancer histological outcome. Diagnostics 2020, 10, 708. [Google Scholar] [CrossRef] [PubMed]
- Fanizzi, A.; Pomarico, D.; Paradiso, A.; Bove, S.; Diotiaiuti, S.; Didonna, V.; Giotta, F.; La Forgia, D.; Latorre, A.; Pastena, M.; et al. Predicting of sentinel lymph node status in breast cancer patients with clinically negative nodes: A validation study. Cancers 2021, 13, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Fanizzi, A.; Basile, T.M.; Losurdo, L.; Bellotti, R.; Bottigli, U.; Campobasso, F.; Didonna, V.; Fausto, A.; Massafra, R.; Tagliafico, A.; et al. Ensemble discretewavelet transform and gray-level co-occurrence matrix for microcalcification cluster classification in digital mammography. Appl. Sci. 2019, 9, 1–14. [Google Scholar] [CrossRef]
- Losurdo, L.; Basile, T.M.A.; Fanizzi, A.; Bellotti, R.; Bottigli, U.; Carbonara, R.; Dentamaro, R.; Diacono, D.; Didonna, V.; Lombardi, A.; et al. A Gradient-Based Approach for Breast DCE-MRI Analysis. Biomed Res. Int. 2018, 2018. [Google Scholar] [CrossRef]
- Bellotti, R.; Bagnasco, S.; Bottigli, U.; Castellano, M.; Cataldo, R.; Catanzariti, E.; Cerello, P.; Cheran, S.; De Carlo, F.; Delogu, P.; et al. The MAGIC-5 project: Medical applications on a grid infrastructure connection. IEEE Nucl. Sci. Symp. Conf. Rec. 2004, 3, 1902–1906. [Google Scholar] [CrossRef]
- Losurdo, L.; Fanizzi, A.; Basile, T.M.A.; Bellotti, R.; Bottigli, U.; Dentamaro, R.; Didonna, V.; Lorusso, V.; Massafra, R.; Tamborra, P.; et al. Radiomics analysis on contrast-enhanced spectral mammography images for breast cancer diagnosis: A pilot study. Entropy 2019, 21, 1110. [Google Scholar] [CrossRef]
- Fanizzi, A.; Basile, T.M.A.; Losurdo, L.; Bellotti, R.; Tangaro, S.; La Forgia, D.; Didonna, V.; Massafra, R.; Tamborra, P.; Moschetta, M.; et al. Hough transform for microcalcification detection in digital mammograms. Appl. Digit. Image Process. XL 2017, 10396, 41. [Google Scholar] [CrossRef]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Breslow, N.E. Analysis of Survival Data under the Proportional Hazards Model. Int. Stat. Rev. 1975, 43, 45. [Google Scholar] [CrossRef]
- Cook, N.R. Statistical evaluation of prognostic versus diagnostic models: Beyond the ROC curve. Clin. Chem. 2008, 54, 17–23. [Google Scholar] [CrossRef] [PubMed]


| Characteristic | Non-RFSi | RFSi |
|---|---|---|
| Number (n = 158) | 43 | 115 |
| Average Age (years) | 47.21 ± 8.67 | 48.86 ± 8.96 |
| Receptor Status | ||
| ER Positive | 12 | 66 |
| PgR Positive | 14 | 53 |
| HER2 Positive | 17 | 26 |
| Fine-Tuning Dataset | ||||||
|---|---|---|---|---|---|---|
| Performance Metric | DSF | OSF | OSF + Clinical | |||
| T1 | T1–T2 | T1 | T1–T2 | T1 | T1–T2 | |
| N. features | - | - | 15 | 13 + 5 | 15 + 4 | 13 + 5 + 4 |
| Accuracy | 67.7% | 72.9% | 82.3% | 87.5% | 87.5% | 91.7% |
| Sensitivity | 38.5% | 57.7% | 57.7% | 80.8% | 69.2% | 80.8% |
| Specificity | 78.6% | 78.6% | 91.4% | 90.0% | 94.3% | 95.7% |
| Independent Test | ||||
|---|---|---|---|---|
| Performance Metric | OSF | OSF + Clinical | ||
| T1 | T1–T2 | T1 | T1–T2 | |
| N. features | 15 | 13 + 5 | 15 + 4 | 13 + 5 + 4 |
| Accuracy | 80.7% | 80.7% | 80.3% | 85.2% |
| Sensitivity | 47.1% | 76.5% | 53.9% | 84.6% |
| Specificity | 93.3% | 82.2% | 90.2% | 85.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comes, M.C.; La Forgia, D.; Didonna, V.; Fanizzi, A.; Giotta, F.; Latorre, A.; Martinelli, E.; Mencattini, A.; Paradiso, A.V.; Tamborra, P.; et al. Early Prediction of Breast Cancer Recurrence for Patients Treated with Neoadjuvant Chemotherapy: A Transfer Learning Approach on DCE-MRIs. Cancers 2021, 13, 2298. https://doi.org/10.3390/cancers13102298
Comes MC, La Forgia D, Didonna V, Fanizzi A, Giotta F, Latorre A, Martinelli E, Mencattini A, Paradiso AV, Tamborra P, et al. Early Prediction of Breast Cancer Recurrence for Patients Treated with Neoadjuvant Chemotherapy: A Transfer Learning Approach on DCE-MRIs. Cancers. 2021; 13(10):2298. https://doi.org/10.3390/cancers13102298
Chicago/Turabian StyleComes, Maria Colomba, Daniele La Forgia, Vittorio Didonna, Annarita Fanizzi, Francesco Giotta, Agnese Latorre, Eugenio Martinelli, Arianna Mencattini, Angelo Virgilio Paradiso, Pasquale Tamborra, and et al. 2021. "Early Prediction of Breast Cancer Recurrence for Patients Treated with Neoadjuvant Chemotherapy: A Transfer Learning Approach on DCE-MRIs" Cancers 13, no. 10: 2298. https://doi.org/10.3390/cancers13102298
APA StyleComes, M. C., La Forgia, D., Didonna, V., Fanizzi, A., Giotta, F., Latorre, A., Martinelli, E., Mencattini, A., Paradiso, A. V., Tamborra, P., Terenzio, A., Zito, A., Lorusso, V., & Massafra, R. (2021). Early Prediction of Breast Cancer Recurrence for Patients Treated with Neoadjuvant Chemotherapy: A Transfer Learning Approach on DCE-MRIs. Cancers, 13(10), 2298. https://doi.org/10.3390/cancers13102298












