Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials & Methods
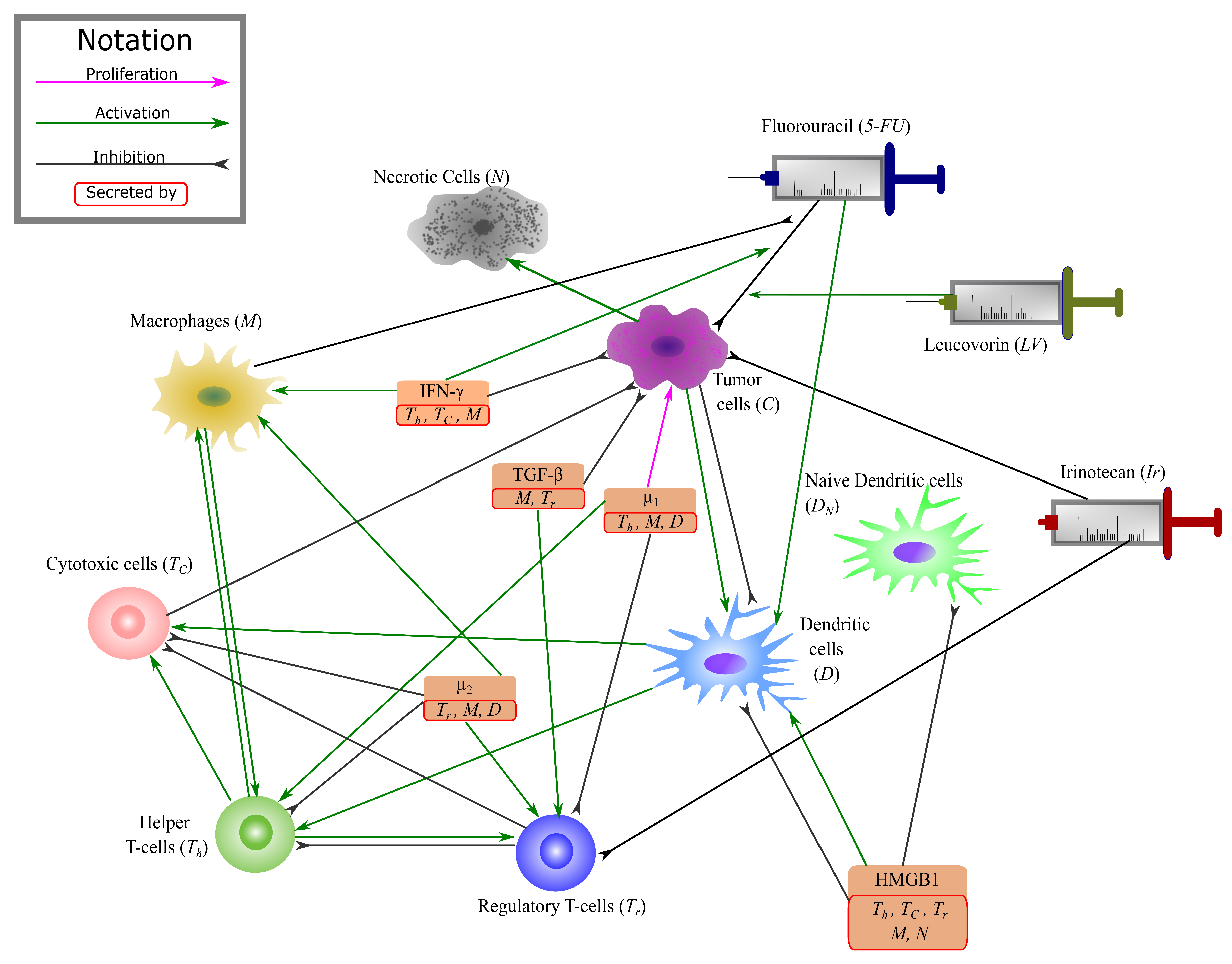
2.1. Mathematical Model
2.1.1. Cancer & Necrotic Cells
2.1.2. T-Cells
2.1.3. 5-FU & Leucovorin
2.1.4. Irinotecan
2.2. Non-Dimensionalization
2.3. Data of the Model
Treatment Data
2.4. Numerical Methods
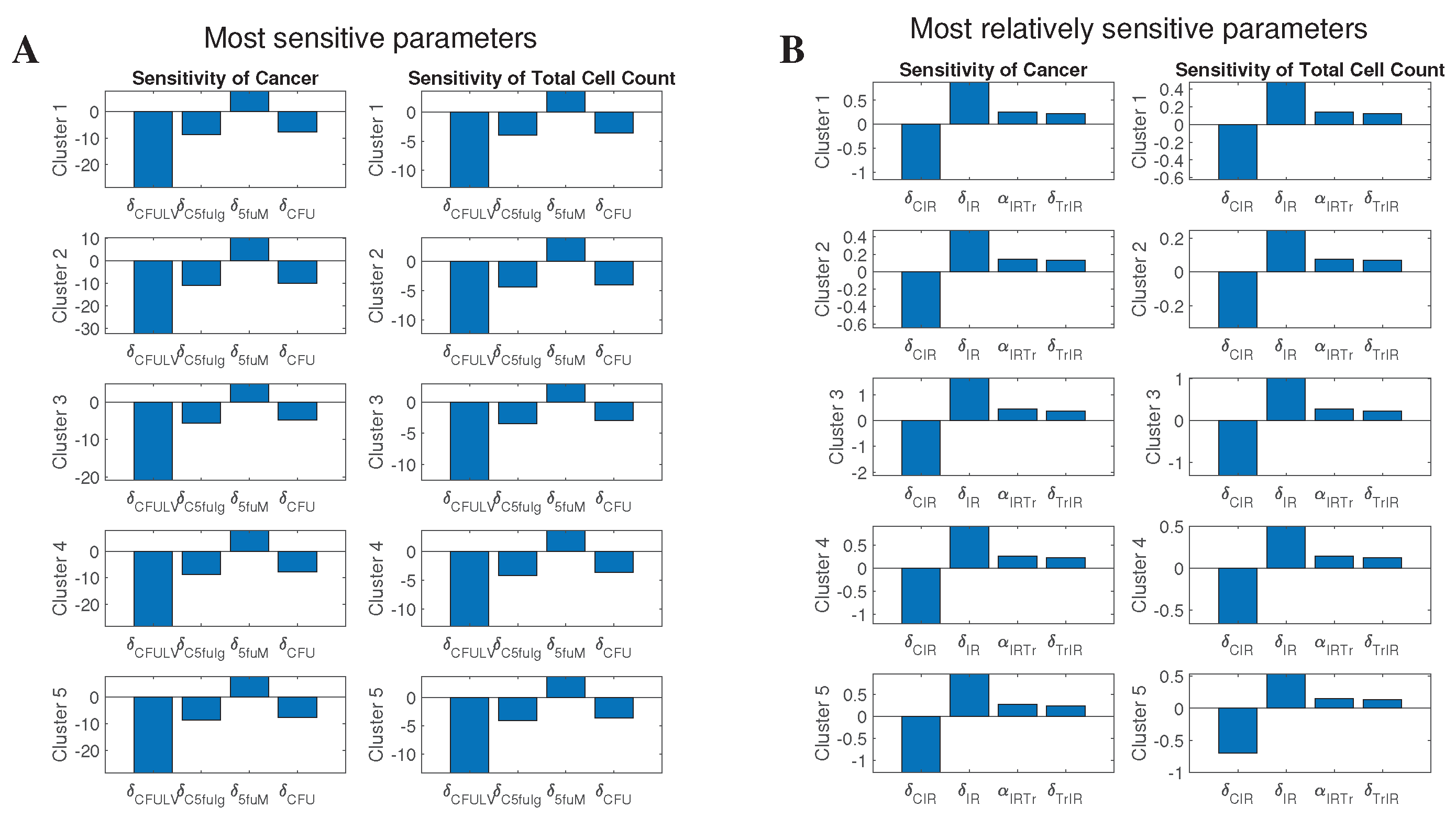
2.5. Sensitivity Analysis
3. Results
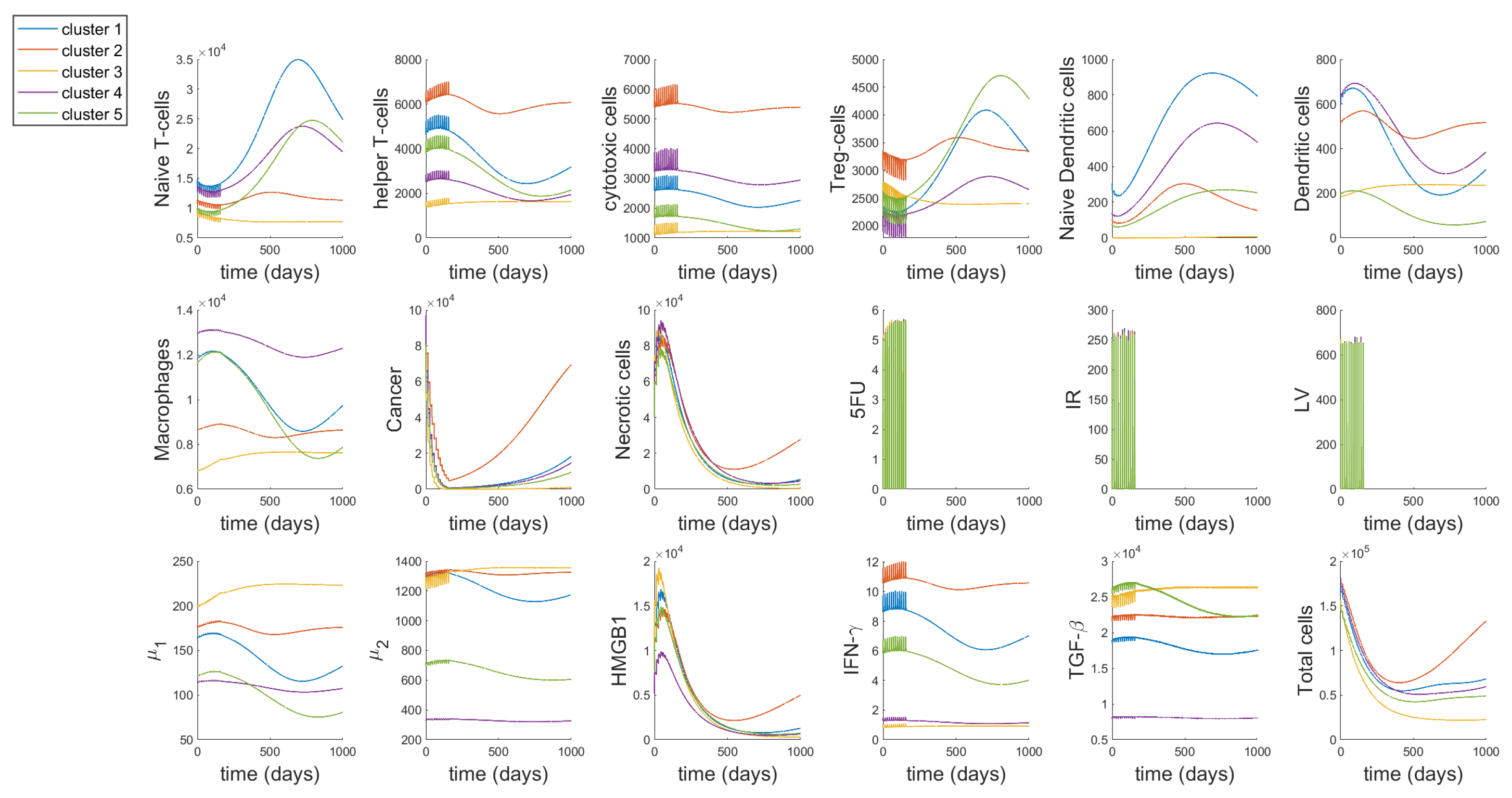
3.1. Dynamics
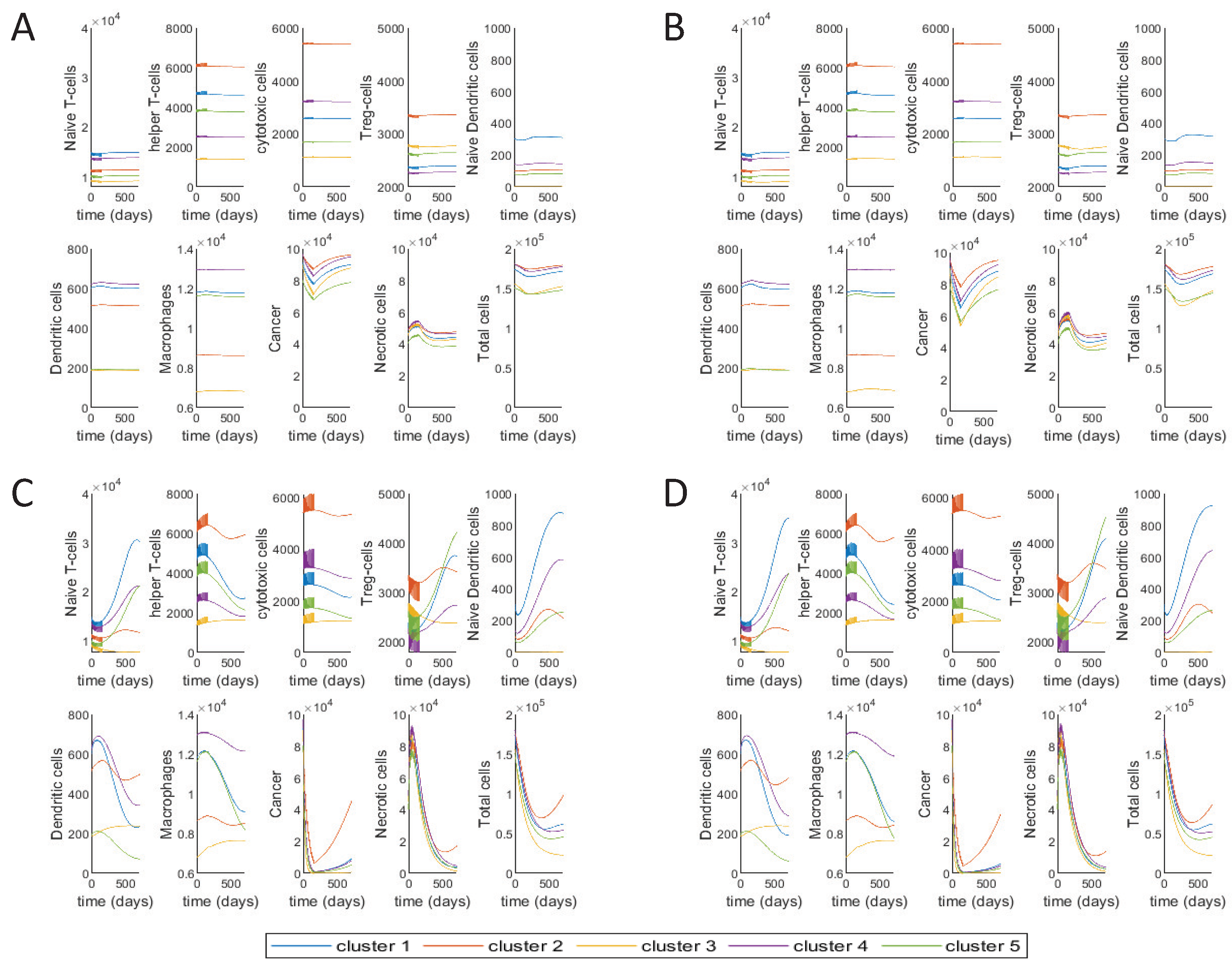
3.2. Different Treatment Options
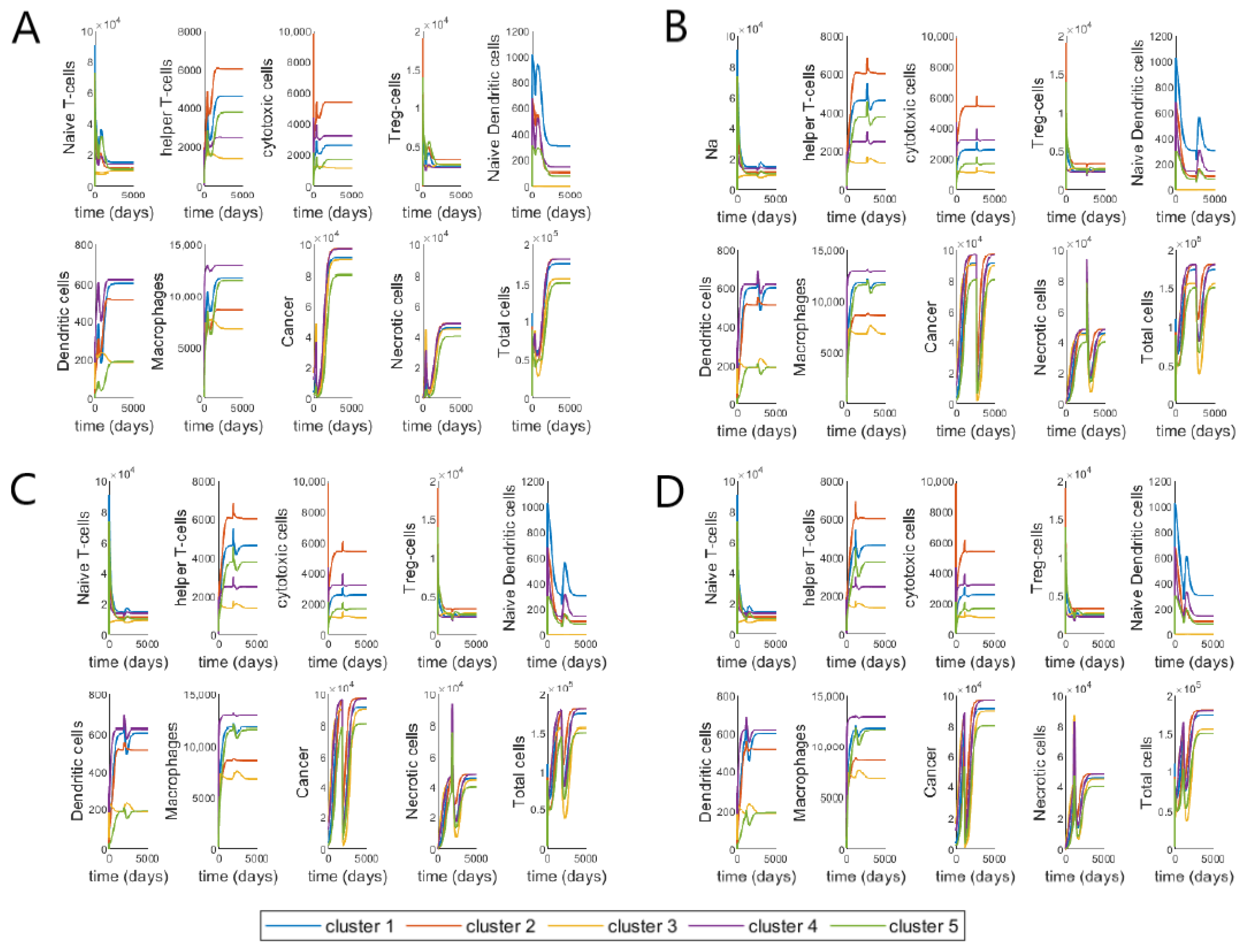
3.3. Varying Treatment Start Time
3.4. Validating Model Using Patient Data
3.4.1. Predicting Tumor Status—ROC Curve
3.4.2. Individual Patients
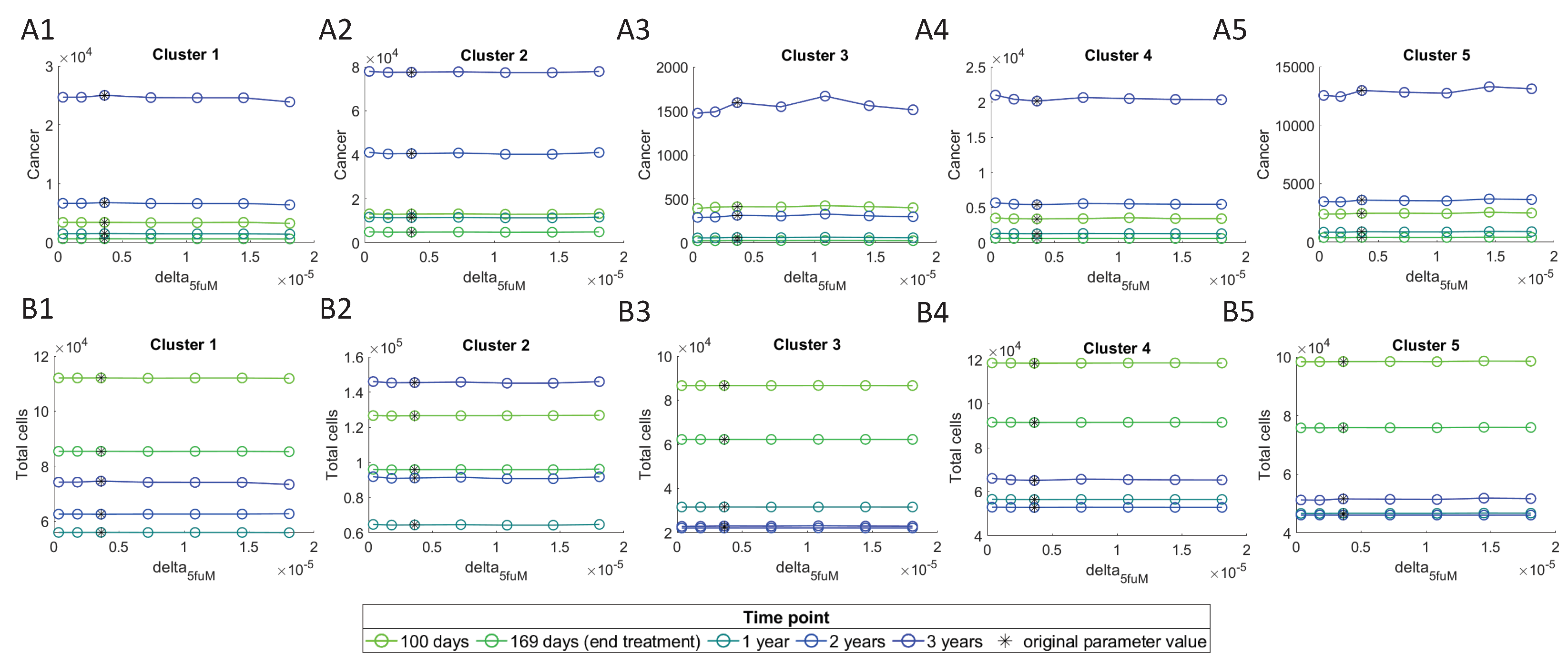
3.4.3. Effect of Sensitive Parameters
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| COAD | Colon adenocarcinoma |
| CRC | Colorectal cancer |
| HMGB1 | High mobility group box 1 |
| DAMP | damage-associated molecular pattern |
| TAM | Tumor-associated macrophages |
| ODE | Ordinary differential equation |
| TYMS | thymidylate synthase |
| TCD | Total cell density |
| TIC | Total immune cell |
Appendix A. ODE System & Non-Dimensionalization
References
- Key Statistics for Colorectal Cancer. Available online: https://www.cancer.org/cancer/colon-rectal-cancer/about/key-statistics.html (accessed on 30 March 2021).
- Guinney, J.; Dienstmann, R.; Wang, X.; de Reyniès, A.; Schlicker, A.; Soneson, C.; Marisa, L.; Roepman, P.; Nyamundanda, G.; Angelino, P.; et al. The consensus molecular subtypes of colorectal cancer. Nat. Med. 2015, 21, 1350–1356. [Google Scholar] [CrossRef]
- Van Cutsem, E.; Cervantes, A.; Adam, R.; Sobrero, A.; Van Krieken, J.; Aderka, D.; Aranda Aguilar, E.; Bardelli, A.; Benson, A.; Bodoky, G.; et al. ESMO consensus guidelines for the management of patients with metastatic colorectal cancer. Ann. Oncol. 2016, 27, 1386–1422. [Google Scholar] [CrossRef]
- Poston, G.J.; Tait, D.; O’Connell, S.; Bennett, A.; Berendse, S. Diagnosis and management of colorectal cancer: Summary of NICE guidance. BMJ 2011, 343, d6751. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2020. CA Cancer J. Clin. 2020, 70, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Morse, M.A.; Hochster, H.; Benson, A. Perspectives on Treatment of Metastatic Colorectal Cancer with Immune Checkpoint Inhibitor Therapy. Oncologist 2020, 25, 33–45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, T.; Dai, Y. Tumor microenvironment and therapeutic response. Cancer Lett. 2017, 387, 61–68. [Google Scholar] [CrossRef]
- Golden, E.B.; Frances, D.; Pellicciotta, I.; Demaria, S.; Helen Barcellos-Hoff, M.; Formenti, S.C. Radiation fosters dose-dependent and chemotherapy-induced immunogenic cell death. OncoImmunology 2014, 3, e28518. [Google Scholar] [CrossRef] [Green Version]
- Schildkopf, P.; Frey, B.; Mantel, F.; Ott, O.J.; Weiss, E.M.; Sieber, R.; Janko, C.; Sauer, R.; Fietkau, R.; Gaipl, U.S. Application of hyperthermia in addition to ionizing irradiation fosters necrotic cell death and HMGB1 release of colorectal tumor cells. Biochem. Biophys. Res. Commun. 2010, 391, 1014–1020. [Google Scholar] [CrossRef] [PubMed]
- Apetoh, L.; Ghiringhelli, F.; Tesniere, A.; Criollo, A.; Ortiz, C.; Lidereau, R.; Mariette, C.; Chaput, N.; Mira, J.P.P.; Delaloge, S.; et al. The interaction between HMGB1 and TLR4 dictates the outcome of anticancer chemotherapy and radiotherapy. Immunol. Rev. 2007, 220, 47–59. [Google Scholar] [CrossRef]
- Liu, L.; Yang, M.; Kang, R.; Wang, Z.; Zhao, Y.; Yu, Y.; Xie, M.; Yin, X.; Livesey, K.M.; Lotze, M.T.; et al. HMGB1-induced autophagy promotes chemotherapy resistance in leukemia cells. Leuk. Off. J. Leuk. Soc. Am. Leuk. Res. Fund UK 2011, 25, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Scaffidi, P.; Misteli, T.; Bianchi, M.E. Release of chromatin protein HMGB1 by necrotic cells triggers inflammation. Nature 2002, 418, 191–195. [Google Scholar] [CrossRef]
- Lotze, M.T.; Tracey, K.J. High-mobility group box 1 protein (HMGB1): Nuclear weapon in the immune arsenal. Nat. Rev. Immunol. 2005, 5, 331–342. [Google Scholar] [CrossRef]
- Xu, X.; Fu, X.Y.; Plate, J.; Chong, A.S. IFN-gamma induces cell growth inhibition by Fas-mediated apoptosis: Requirement of STAT1 protein for up-regulation of Fas and FasL expression. Cancer Res. 1998, 58, 2832–2837. [Google Scholar] [PubMed]
- Kroemer, G.; Galluzzi, L.; Kepp, O.; Zitvogel, L. Immunogenic Cell Death in Cancer Therapy. Annu. Rev. Immunol. 2013, 31, 51–72. [Google Scholar] [CrossRef] [PubMed]
- Nathan, C.F.; Murray, H.W.; Wiebe, M.E.; Rubin, B.Y. Identification of interferon-gamma as the lymphokine that activates human macrophage oxidative metabolism and antimicrobial activity. J. Exp. Med. 1983, 158, 670–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bogdan, C.; Stenger, S.; Röllinghoff, M.; Solbach, W. Cytokine interactions in experimental cutaneous leishmaniasis. Interleukin 4 synergizes with interferon-γ to activate murine macrophages for killing ofLeishmania major amastigotes. Eur. J. Immunol. 1991, 21, 327–333. [Google Scholar] [CrossRef] [PubMed]
- Popivanova, B.K.; Kitamura, K.; Wu, Y.; Kondo, T.; Kagaya, T.; Kaneko, S.; Oshima, M.; Fujii, C.; Mukaida, N. Blocking TNF-alpha in mice reduces colorectal carcinogenesis associated with chronic colitis. J. Clin. Investig. 2008, 118, 560–570. [Google Scholar] [CrossRef] [PubMed]
- Qian, B.Z.; Pollard, J.W. Macrophage Diversity Enhances Tumor Progression and Metastasis. Cell 2010, 141, 39–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ostuni, R.; Kratochvill, F.; Murray, P.J.; Natoli, G. Macrophages and cancer: From mechanisms to therapeutic implications. Trends Immunol. 2015, 36, 229–239. [Google Scholar] [CrossRef]
- Pagès, F.; Berger, A.; Camus, M.; Sanchez-Cabo, F.; Costes, A.; Molidor, R.; Mlecnik, B.; Kirilovsky, A.; Nilsson, M.; Damotte, D.; et al. Effector memory T cells, early metastasis, and survival in colorectal cancer. N. Engl. J. Med. 2005, 353, 2654–2666. [Google Scholar] [CrossRef]
- Dahlin, A.M.; Henriksson, M.L.; Van Guelpen, B.; Stenling, R.; Öberg, Å.; Rutegård, J.; Palmqvist, R. Colorectal cancer prognosis depends on T-cell infiltration and molecular characteristics of the tumor. Mod. Pathol. 2011, 24, 671–682. [Google Scholar] [CrossRef]
- Funada, Y.; Noguchi, T.; Kikuchi, R.; Takeno, S.; Uchida, Y.; Gabbert, H.E. Prognostic significance of CD8+ T cell and macrophage peritumoral infiltration in colorectal cancer. Oncol. Rep. 2003, 10, 309–313. [Google Scholar] [CrossRef]
- Lugade, A.A.; Sorensen, E.W.; Gerber, S.A.; Moran, J.P.; Frelinger, J.G.; Lord, E.M. Radiation-Induced IFN-γ Production within the Tumor Microenvironment Influences Antitumor Immunity. J. Immunol. 2008, 180, 3132–3139. [Google Scholar] [CrossRef]
- Burnette, B.C.; Liang, H.; Lee, Y.; Chlewicki, L.; Khodarev, N.N.; Weichselbaum, R.R.; Fu, Y.X.; Auh, S.L. The Efficacy of Radiotherapy Relies upon Induction of Type I Interferon–Dependent Innate and Adaptive Immunity. Cancer Res. 2011, 71, 2488–2496. [Google Scholar] [CrossRef] [Green Version]
- Tosolini, M.; Kirilovsky, A.; Mlecnik, B.; Fredriksen, T.; Mauger, S.; Bindea, G.; Berger, A.; Bruneval, P.; Fridman, W.H.; Pagès, F.; et al. Clinical impact of different classes of infiltrating T cytotoxic and helper cells (Th1, th2, treg, th17) in patients with colorectal cancer. Cancer Res. 2011, 71, 1263–1271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mantovani, A.; Allavena, P. The interaction of anticancer therapies with tumor-associated macrophages. J. Exp. Med. 2015, 212, 435–445. [Google Scholar] [CrossRef] [PubMed]
- Thorn, C.F.; Marsh, S.; Carrillo, M.W.; McLeod, H.L.; Klein, T.E.; Altman, R.B. PharmGKB summary: Fluoropyrimidine pathways. Pharmacogenet. Genom. 2010, 21, 237–242. [Google Scholar] [CrossRef] [Green Version]
- Longley, D.B.; Harkin, D.P.; Johnston, P.G. 5-Fluorouracil: Mechanisms of action and clinical strategies. Nat. Rev. Cancer 2003, 3, 330–338. [Google Scholar] [CrossRef]
- Johnston, P.G.; Kaye, S. Capecitabine: A novel agent for the treatment of solid tumors. Anti-Cancer Drugs 2001, 12, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Douillard, J.; Cunningham, D.; Roth, A.; Navarro, M.; James, R.; Karasek, P.; Jandik, P.; Iveson, T.; Carmichael, J.; Alakl, M.; et al. Irinotecan combined with fluorouracil compared with fluorouracil alone as first-line treatment for metastatic colorectal cancer: A multicentre randomised trial. Lancet 2000, 355, 1041–1047. [Google Scholar] [CrossRef]
- Shahriyari, L.; Komarova, N.L. Symmetric vs. asymmetric stem cell divisions: An adaptation against cancer? PLoS ONE 2013, 8, e76195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shahriyari, L.; Komarova, N.L. The role of the bi-compartmental stem cell niche in delaying cancer. Phys. Biol. 2015, 12, 055001. [Google Scholar] [CrossRef]
- Shahriyari, L.; Mahdipour-Shirayeh, A. Modeling dynamics of mutants in heterogeneous stem cell niche. Phys. Biol. 2017, 14. [Google Scholar] [CrossRef]
- Bollas, A.; Shahriyari, L. The role of backward cell migration in two-hit mutants’ production in the stem cell niche. PLoS ONE 2017, 12, e0184651. [Google Scholar] [CrossRef] [Green Version]
- Brady, R.; Enderling, H. Mathematical Models of Cancer: When to Predict Novel Therapies, and When Not to. Bull. Math. Biol. 2019, 81, 3722–3731. [Google Scholar] [CrossRef] [Green Version]
- Chamseddine, I.M.; Rejniak, K.A. Hybrid modeling frameworks of tumor development and treatment. Wiley Interdiscip. Rev. Syst. Biol. Med. 2019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreira, J.; Deutsch, A. Cellular Automaton Models of Tumor Development: A Critical Review. Adv. Complex Syst. 2002, 5, 247–267. [Google Scholar] [CrossRef]
- Lowengrub, J.S.; Frieboes, H.B.; Jin, F.; Chuang, Y.L.; Li, X.; Macklin, P.; Wise, S.M.; Cristini, V. Nonlinear modelling of cancer: Bridging the gap between cells and tumours. Nonlinearity 2010, 23, R1–R91. [Google Scholar] [CrossRef] [Green Version]
- Shahriyari, L. Cell dynamics in tumour environment after treatments. J. R. Soc. Interface 2017, 14, 20160977. [Google Scholar] [CrossRef]
- Lewin, T.D.; Maini, P.K.; Moros, E.G.; Enderling, H.; Byrne, H.M. The Evolution of Tumour Composition During Fractionated Radiotherapy: Implications for Outcome. Bull. Math. Biol. 2018, 80, 1207–1235. [Google Scholar] [CrossRef] [Green Version]
- Enderling, H.; Chaplain, M.A.; Anderson, A.R.; Vaidya, J.S. A mathematical model of breast cancer development, local treatment and recurrence. J. Theor. Biol. 2007, 246, 245–259. [Google Scholar] [CrossRef] [PubMed]
- Pérez-García, V.M.; Bogdanska, M.; Martínez-González, A.; Belmonte-Beitia, J.; Schucht, P.; Pérez-Romasanta, L.A. Delay effects in the response of low-grade gliomas to radiotherapy: A mathematical model and its therapeutical implications. Math. Med. Biol. 2015, 32, 307–329. [Google Scholar] [CrossRef] [Green Version]
- Kather, J.N.; Poleszczuk, J.; Suarez-Carmona, M.; Krisam, J.; Charoentong, P.; Valous, N.A.; Weis, C.A.; Tavernar, L.; Leiss, F.; Herpel, E.; et al. In Silico Modeling of Immunotherapy and Stroma-Targeting Therapies in Human Colorectal Cancer. Cancer Res. 2017, 77, 6442–6452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alharbi, S.A.; Rambely, A.S. A New ODE-Based Model for Tumor Cells and Immune System Competition. Mathematics 2020, 8, 1285. [Google Scholar] [CrossRef]
- DePillis, L.; Savage, H.; Radunskaya, A. Mathematical model of colorectal cancer with monoclonal antibody treatments. arXiv 2013, arXiv:1312.3023. [Google Scholar] [CrossRef]
- Sameen, S.; Barbuti, R.; Milazzo, P.; Cerone, A.; Del Re, M.; Danesi, R. Mathematical modeling of drug resistance due to KRAS mutation in colorectal cancer. J. Theor. Biol. 2016, 389, 263–273. [Google Scholar] [CrossRef]
- Kirshtein, A.; Akbarinejad, S.; Hao, W.; Le, T.; Su, S.; Aronow, R.A.; Shahriyari, L. Data Driven Mathematical Model of Colon Cancer Progression. J. Clin. Med. 2020, 9, 3947. [Google Scholar] [CrossRef]
- Beutler, B.; Greenwald, D.; Hulmes, J.D.; Chang, M.; Pan, Y.C.E.; Mathison, J.; Ulevitch, R.; Cerami, A. Identity of tumour necrosis factor and the macrophage-secreted factor cachectin. Nature 1985, 316, 552–554. [Google Scholar] [CrossRef]
- Grivennikov, S.I.; Greten, F.R.; Karin, M. Immunity, Inflammation, and Cancer. Cell 2010, 140, 883–899. [Google Scholar] [CrossRef] [Green Version]
- Mudter, J.; Neurath, M.F. IL-6 signaling in inflammatory bowel disease: Pathophysiological role and clinical relevance. Inflamm. Bowel Dis. 2007, 13, 1016–1023. [Google Scholar] [CrossRef]
- Waldner, M.J.; Neurath, M.F. Colitis-associated cancer: The role of T cells in tumor development. Semin. Immunopathol. 2009, 31, 249–256. [Google Scholar] [CrossRef]
- Terzić, J.; Grivennikov, S.; Karin, E.; Karin, M. Inflammation and Colon Cancer. Gastroenterology 2010, 138, 2101–2114. [Google Scholar] [CrossRef]
- Waldner, M.J.; Foersch, S.; Neurath, M.F. Interleukin-6—A key regulator of colorectal cancer development. Int. J. Biol. Sci. 2012, 8, 1248–1253. [Google Scholar] [CrossRef]
- Hart, A.L.; Al-Hassi, H.O.; Rigby, R.J.; Bell, S.J.; Emmanuel, A.V.; Knight, S.C.; Kamm, M.A.; Stagg, A.J. Characteristics of intestinal dendritic cells in inflammatory bowel diseases. Gastroenterology 2005, 129, 50–65. [Google Scholar] [CrossRef]
- Pasare, C.; Medzhitov, R. Toll pathway-dependent blockade of CD4+CD25+ T cell-mediated suppression by dendritic cells. Science 2003, 299, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Aras, S.; Zaidi, M.R. TAMeless traitors: Macrophages in cancer progression and metastasis. Br. J. Cancer 2017, 117, 1583–1591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, X.; Zhang, H.; Cheng, Y.; Jiang, X.; Zhu, J.; Jin, T. Double roles of macrophages in human neuroimmune diseases and their animal models. Mediat. Inflamm. 2016, 2016, 8489251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, G. Tumor-infiltrating regulatory T cells: Origins and features. Am. J. Clin. Exp. Immunol. 2018, 7, 81–87. [Google Scholar]
- Iwasaki, A.; Kelsall, B.L. Freshly isolated Peyer’s patch, but not spleen, dendritic cells produce interleukin 10 and induce the differentiation of T helper type 2 cells. J. Exp. Med. 1999, 190, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Vella, A.T. Regulatory T Cells and Cancer: A Two-Sided Story. Immunol. Investig. 2016, 45, 797–812. [Google Scholar] [CrossRef]
- Leman, J.K.H.; Sandford, S.K.; Rhodes, J.L.; Kemp, R.A. Multiparametric analysis of colorectal cancer immune responses. World J. Gastroenterol. 2018, 24, 2995–3005. [Google Scholar] [CrossRef]
- Cheng, K.J.; Alshawsh, M.A.; Mejia Mohamed, E.H.; Thavagnanam, S.; Sinniah, A.; Ibrahim, Z.A. HMGB1: An overview of its versatile roles in the pathogenesis of colorectal cancer. Cell. Oncol. 2020, 43, 177–193. [Google Scholar] [CrossRef] [PubMed]
- Süren, D.; Yıldırım, M.; Demirpençe, Ö.; Kaya, V.; Alikanoğlu, A.S.; Bülbüller, N.; Yıldız, M.; Sezer, C. The role of high mobility group box 1 (HMGB1) in colorectal cancer. Med. Sci. Monit. Int. Med J. Exp. Clin. Res. 2014, 20, 530–537. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.S.; Liu, Z.; Bartlett, D.L.; Tang, D.; Lotze, M.T. Life after death: Targeting high mobility group box 1 in emergent cancer therapies. Am. J. Cancer Res. 2013, 3, 1–20. [Google Scholar]
- Wang, H.; Bloom, O.; Zhang, M.; Vishnubhakat, J.M.; Ombrellino, M.; Che, J.; Frazier, A.; Yang, H.; Ivanova, S.; Borovikova, L.; et al. HMG-1 as a late mediator of endotoxin lethality in mice. Science 1999, 285, 248–251. [Google Scholar] [CrossRef]
- Ong, S.M.; Tan, Y.C.; Beretta, O.; Jiang, D.; Yeap, W.H.; Tai, J.J.Y.; Wong, W.C.; Yang, H.; Schwarz, H.; Lim, K.H.; et al. Macrophages in human colorectal cancer are pro-inflammatory and prime T cells towards an anti-tumour type-1 inflammatory response. Eur. J. Immunol. 2012, 42, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Darwich, L.; Coma, G.; Peña, R.; Bellido, R.; Blanco, E.J.J.; Este, J.A.; Borras, F.E.; Clotet, B.; Ruiz, L.; Rosell, A.; et al. Secretion of interferon-γ by human macrophages demonstrated at the single-cell level after costimulation with interleukin (IL)-12 plus IL-18. Immunology 2009, 126, 386–393. [Google Scholar] [CrossRef] [PubMed]
- Robinson, C.M.; O’Dee, D.; Hamilton, T.; Nau, G.J. Cytokines involved in interferon-gamma production by human macrophages. J. Innate Immun. 2010, 2, 56–65. [Google Scholar] [CrossRef]
- Zaidi, M.R.; Davis, S.; Noonan, F.P.; Graff-Cherry, C.; Hawley, T.S.; Walker, R.L.; Feigenbaum, L.; Fuchs, E.; Lyakh, L.; Young, H.A.; et al. Interferon-γ links ultraviolet radiation to melanomagenesis in mice. Nature 2011, 469, 548–553. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhang, P.; Li, J.; Kulkarni, A.B.; Perruche, S.; Chen, W. A critical function for TGF-beta signaling in the development of natural CD4+CD25+Foxp3+ regulatory T cells. Nat. Immunol. 2008, 9, 632–640. [Google Scholar] [CrossRef]
- Boyman, O.; Sprent, J. The role of interleukin-2 during homeostasis and activation of the immune system. Nat. Rev. Immunol. 2012, 12, 180–190. [Google Scholar] [CrossRef]
- West, N.R.; McCuaig, S.; Franchini, F.; Powrie, F. Emerging cytokine networks in colorectal cancer. Nat. Rev. Immunol. 2015, 15, 615–629. [Google Scholar] [CrossRef]
- Fontenot, J.D.; Rasmussen, J.P.; Gavin, M.A.; Rudensky, A.Y. A function for interleukin 2 in Foxp3-expressing regulatory T cells. Nat. Immunol. 2005, 6, 1142–1151. [Google Scholar] [CrossRef] [PubMed]
- Vang, K.B.; Yang, J.; Mahmud, S.A.; Burchill, M.A.; Vegoe, A.L.; Farrar, M.A. IL-2, -7, and -15, but not thymic stromal lymphopoeitin, redundantly govern CD4+Foxp3+ regulatory T cell development. J. Immunol. 2008, 181, 3285–3290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kusume, A.; Sasahira, T.; Luo, Y.; Isobe, M.; Nakagawa, N.; Tatsumoto, N.; Fujii, K.; Ohmori, H.; Kuniyasu, H. Suppression of dendritic cells by HMGB1 is associated with lymph node metastasis of human colon cancer. Pathobiology 2009, 76, 155–162. [Google Scholar] [CrossRef]
- Erdman, S.E.; Poutahidis, T. Roles for Inflammation and Regulatory T Cells in Colon Cancer. Toxicol. Pathol. 2010, 38, 76–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Y.; Shurin, G.V.; Peiyuan, Z.; Shurin, M.R. Dendritic cells in the cancer microenvironment. J. Cancer 2013, 4, 36–44. [Google Scholar] [CrossRef] [Green Version]
- Menetrier-Caux, C.; Montmain, G.; Dieu, M.C.; Bain, C.; Favrot, M.C.; Caux, C.; Blay, J.Y. Inhibition of the differentiation of dendritic cells from CD34+ progenitors by tumor cells: Role of interleukin-6 and macrophage colony-stimulating factor. Blood J. Am. Soc. Hematol. 1998, 92, 4778–4791. [Google Scholar]
- Esche, C.; Lokshin, A.; Shurin, G.V.; Gastman, B.R.; Rabinowich, H.; Watkins, S.C.; Lotze, M.T.; Shurin, M.R. Tumor’s other immune targets: Dendritic cells. J. Leukoc. Biol. 1999, 66, 336–344. [Google Scholar] [CrossRef]
- Sica, A.; Saccani, A.; Mantovani, A. Tumor-associated macrophages: A molecular perspective. Int. Immunopharmacol. 2002, 2, 1045–1054. [Google Scholar] [CrossRef]
- Sakai, Y.; Honda, M.; Fujinaga, H.; Tatsumi, I.; Mizukoshi, E.; Nakamoto, Y.; Kaneko, S. Common transcriptional signature of tumor-infiltrating mononuclear inflammatory cells and peripheral blood mononuclear cells in hepatocellular carcinoma patients. Cancer Res. 2008, 68, 10267–10279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Folkman, J.; Hochberg, M. Self-regulation of growth in three dimensions. J. Exp. Med. 1973, 138, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Enderling, H.; Sunassee, E.; Caudell, J.J. Predicting patient-specific radiotherapy responses in head and neck cancer to personalize radiation dose fractionation. bioRxiv 2019, 630806. [Google Scholar] [CrossRef]
- Yu, H.; Kortylewski, M.; Pardoll, D. Crosstalk between cancer and immune cells: Role of STAT3 in the tumour microenvironment. Nat. Rev. Immunol. 2007, 7, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Badache, A.; Hynes, N.E. Interleukin 6 inhibits proliferation and, in cooperation with an epidermal growth factor receptor autocrine loop, increases migration of T47D breast cancer cells. Cancer Res. 2001, 61, 383–391. [Google Scholar] [PubMed]
- Lin, M.T.; Juan, C.Y.; Chang, K.J.; Chen, W.J.; Kuo, M.L. IL-6 inhibits apoptosis and retains oxidative DNA lesions in human gastric cancer AGS cells through up-regulation of anti-apoptotic gene mcl-1. Carcinogenesis 2001, 22, 1947–1953. [Google Scholar] [CrossRef] [Green Version]
- Moses, H.L.; Yang, E.Y.; Pietenpol, J.A. TGF-beta stimulation and inhibition of cell proliferation: New mechanistic insights. Cell 1990, 63, 245–247. [Google Scholar] [CrossRef]
- Markowitz, S.D.; Roberts, A.B. Tumor suppressor activity of the TGF-beta pathway in human cancers. Cytokine Growth Factor Rev. 1996, 7, 93–102. [Google Scholar] [CrossRef]
- Wang, C.Y.; Eshleman, J.R.; Willson, J.K.; Markowitz, S. Both transforming growth factor-beta and substrate release are inducers of apoptosis in a human colon adenoma cell line. Cancer Res. 1995, 55, 5101–5105. [Google Scholar]
- Engel, M.A.; Neurath, M.F. Anticancer properties of the IL-12 family-focus on colorectal cancer. Curr. Med. Chem. 2010, 17, 3303–3308. [Google Scholar] [CrossRef]
- Voit, E.O.; Martens, H.A.; Omholt, S.W. 150 years of the mass action law. PLoS Comput. Biol. 2015, 11, e1004012. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, C.; Liu, P.; Eisenberg, B. Field theory of reaction-diffusion: Mass action with an energetic variational approach. arXiv 2020, arXiv:2001.10149. [Google Scholar]
- Zoetemelk, M.; Ramzy, G.M.; Rausch, M.; Nowak-Sliwinska, P. Drug-Drug Interactions of Irinotecan, 5-Fluorouracil, Folinic Acid and Oxaliplatin and Its Activity in Colorectal Carcinoma Treatment. Molecules 2020, 25, 2614. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.; Yang, C.; Wang, S.; Shi, D.; Zhang, C.; Lin, X.; Xiong, B. M2 macrophages confer resistance to 5-fluorouracil in colorectal cancer through the activation of CCL22/PI3K/AKT signaling. OncoTargets Ther. 2019, 12, 3051–3063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Chen, Y.; Hao, L.; Hou, A.; Chen, X.; Li, Y.; Wang, R.; Luo, P.; Ruan, Z.; Ou, J.; et al. Macrophages induce resistance to 5-fluorouracil chemotherapy in colorectal cancer through the release of putrescine. Cancer Lett. 2016, 381, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Malesci, A.; Bianchi, P.; Celesti, G.; Basso, G.; Marchesi, F.; Grizzi, F.; Di Caro, G.; Cavalleri, T.; Rimassa, L.; Palmqvist, R.; et al. Tumor-associated macrophages and response to 5-fluorouracil adjuvant therapy in stage III colorectal cancer. OncoImmunology 2017, 6, e1342918. [Google Scholar] [CrossRef]
- Machover, D.; Goldschmidt, E.; Chollet, P.; Metzger, G.; Zittoun, J.; Marquet, J.; Vandenbulcke, J.M.; Misset, J.L.; Schwarzenberg, L.; Fourtillan, J.B. Treatment of advanced colorectal and gastric adenocarcinomas with 5-fluorouracil and high-dose folinic acid. J. Clin. Oncol. 1986, 4, 685–696. [Google Scholar] [CrossRef]
- Mini, E.; Trave, F.; Rustum, Y.M.; Bertino, J.R. Enhancement of the antitumor effects of 5-fluorouracil by folinic acid. Pharmacol. Ther. 1990, 47, 1–19. [Google Scholar] [CrossRef]
- Danenberg, P.V.; Gustavsson, B.; Johnston, P.; Lindberg, P.; Moser, R.; Odin, E.; Peters, G.J.; Petrelli, N. Folates as adjuvants to anticancer agents: Chemical rationale and mechanism of action. Crit. Rev. Oncol. 2016, 106, 118–131. [Google Scholar] [CrossRef] [Green Version]
- Kciuk, M.; Marciniak, B.; Kontek, R. Irinotecan—Still an Important Player in Cancer Chemotherapy: A Comprehensive Overview. Int. J. Mol. Sci. 2020, 21, 4919. [Google Scholar] [CrossRef]
- Rosner, G.; Panetta, J.; Innocenti, F.; Ratain, M. Pharmacogenetic Pathway Analysis of Irinotecan. Clin. Pharmacol. Ther. 2008, 84, 393–402. [Google Scholar] [CrossRef]
- de Man, F.M.; Goey, A.K.L.; van Schaik, R.H.N.; Mathijssen, R.H.J.; Bins, S. Individualization of Irinotecan Treatment: A Review of Pharmacokinetics, Pharmacodynamics, and Pharmacogenetics. Clin. Pharmacokinet. 2018, 57, 1229–1254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Almeida, C.V.; Zamame, J.A.; Romagnoli, G.G.; Rodrigues, C.P.; Magalhães, M.B.; Amedei, A.; Kaneno, R. Treatment of colon cancer cells with 5-fluorouracil can improve the effectiveness of RNA-transfected antitumor dendritic cell vaccine. Oncol. Rep. 2017, 38, 561–568. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bailly, C.; Thuru, X.; Quesnel, B. Combined cytotoxic chemotherapy and immunotherapy of cancer: Modern times. NAR Cancer 2020, 2. [Google Scholar] [CrossRef] [Green Version]
- Maeda, K.; Hazama, S.; Tokuno, K.; Kan, S.; Maeda, Y.; Watanabe, Y.; Kamei, R.; Shindo, Y.; Maeda, N.; Yoshimura, K.; et al. Impact of chemotherapy for colorectal cancer on regulatory T-cells and tumor immunity. Anticancer. Res. 2011, 31, 4569–4574. [Google Scholar]
- Focaccetti, C.; Bruno, A.; Magnani, E.; Bartolini, D.; Principi, E.; Dallaglio, K.; Bucci, E.O.; Finzi, G.; Sessa, F.; Noonan, D.M.; et al. Effects of 5-Fluorouracil on Morphology, Cell Cycle, Proliferation, Apoptosis, Autophagy and ROS Production in Endothelial Cells and Cardiomyocytes. PLoS ONE 2015, 10, e0115686. [Google Scholar] [CrossRef]
- Zhang, N.; Yin, Y.; Xu, S.J.; Chen, W.S. 5-Fluorouracil: Mechanisms of Resistance and Reversal Strategies. Molecules 2008, 13, 1551–1569. [Google Scholar] [CrossRef] [Green Version]
- Newman, A.; Steen, C.; Liu, C.; Gentles, A.; Chaudhuri, A.; Scherer, F.; Khodadoust, M.; Esfahani, M.; Luca, B.; Steiner, D.; et al. Determining cell type abundance and expression from bulk tissues with digital cytometry. Nat. Biotechnol. 2019, 37, 773–782. [Google Scholar] [CrossRef]
- Le, T.; Aronow, R.A.; Kirshtein, A.; Shahriyari, L. A review of digital cytometry methods: Estimating the relative abundance of cell types in a bulk of cells. Briefings Bioinform. 2020. [Google Scholar] [CrossRef]
- Su, S.; Akbarinejad, S.; Shahriyari, L. Immune classification of clear cell renal cell carcinoma. Sci. Rep. 2021, 11, 4338. [Google Scholar] [CrossRef]
- Le, T.; Su, S.; Shahriyari, L. Immune classification of osteosarcoma. Math. Biosci. Eng. 2021, 18, 1879–1897. [Google Scholar] [CrossRef] [PubMed]
- Goldman, M.J.; Craft, B.; Hastie, M.; Repečka, K.; McDade, F.; Kamath, A.; Banerjee, A.; Luo, Y.; Rogers, D.; Brooks, A.N.; et al. Visualizing and interpreting cancer genomics data via the Xena platform. Nat. Biotechnol. 2020, 38, 675–678. [Google Scholar] [CrossRef]
- Kim, Y.; Friedman, A. Interaction of Tumor with Its Micro-environment: A Mathematical Model. Bull. Math. Biol. 2010, 72, 1029–1068. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- FOLFIRI Chemotherapy. Available online: https://www.cancerresearchuk.org/about-cancer/cancer-in-general/treatment/cancer-drugs/drugs/folfiri (accessed on 27 March 2021).
- Karagiannis, G.; Hao, W.; Lin, G. Calibrations and validations of biological models with an application on the renal fibrosis. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3329. [Google Scholar] [CrossRef]
- Seefeld, S.; Stockwell, W.R. First-order sensitivity analysis of models with time-dependent parameters: An application to PAN and ozone. Atmos. Environ. 1999, 33, 2941–2953. [Google Scholar] [CrossRef]
- Yang, I.H. Uncertainty and sensitivity analysis of time-dependent effects in concrete structures. Eng. Struct. 2007, 29, 1366–1374. [Google Scholar] [CrossRef]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef]
- Dagogo-Jack, I.; Shaw, A.T. Tumour heterogeneity and resistance to cancer therapies. Nat. Rev. Clin. Oncol. 2018, 15, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Tian, X.; Ji, L.; Zhang, X.; Cao, Y.; Shen, C.; Hu, Y.; Wong, J.W.H.; Fang, J.Y.; Hong, J.; et al. A tumor microenvironment-specific gene expression signature predicts chemotherapy resistance in colorectal cancer patients. NPJ Precis. Oncol. 2021, 5, 7. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.M.J.; Mills, G.B.; Ram, P.T. Cancer Systems Biology: A peek into the future of patient care? Nat. Rev. Clin. Oncol. 2014, 11, 167–176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bekisz, S.; Geris, L. Cancer modeling: From mechanistic to data-driven approaches, and from fundamental insights to clinical applications. J. Comput. Sci. 2020, 46, 101198. [Google Scholar] [CrossRef]
- Galon, J.; Costes, A.; Sanchez-Cabo, F.; Kirilovsky, A.; Mlecnik, B.; Lagorce-Pagès, C.; Tosolini, M.; Camus, M.; Berger, A.; Wind, P.; et al. Type, density, and location of immune cells within human colorectal tumors predict clinical outcome. Science 2006, 313, 1960–1964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taube, J.M.; Klein, A.; Brahmer, J.R.; Xu, H.; Pan, X.; Kim, J.H.; Chen, L.; Pardoll, D.M.; Topalian, S.L.; Anders, R.A. Association of PD-1, PD-1 Ligands, and Other Features of the Tumor Immune Microenvironment with Response to Anti–PD-1 Therapy. Clin. Cancer Res. 2014, 20, 5064–5074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tredan, O.; Galmarini, C.M.; Patel, K.; Tannock, I.F. Drug Resistance and the Solid Tumor Microenvironment. JNCI J. Natl. Cancer Inst. 2007, 99, 1441–1454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saltz, L.B.; Cox, J.V.; Blanke, C.; Rosen, L.S.; Fehrenbacher, L.; Moore, M.J.; Maroun, J.A.; Ackland, S.P.; Locker, P.K.; Pirotta, N.; et al. Irinotecan plus Fluorouracil and Leucovorin for Metastatic Colorectal Cancer. N. Engl. J. Med. 2000, 343, 905–914. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Lu, J.; An, H. The relative change in regulatory T cells/T helper lymphocytes ratio as parameter for prediction of therapy efficacy in metastatic colorectal cancer patients. Oncotarget 2017, 8, 109079–109093. [Google Scholar] [CrossRef] [Green Version]
- Roselli, M.; Formica, V.; Cereda, V.; Jochems, C.; Richards, J.; Grenga, I.; Orlandi, A.; Ferroni, P.; Guadagni, F.; Schlom, J. The association of clinical outcome and peripheral T-cell subsets in metastatic colorectal cancer patients receiving first-line FOLFIRI plus bevacizumab therapy. OncoImmunology 2016, 5, e1188243. [Google Scholar] [CrossRef] [Green Version]
- Voss, A.; Voss, J. A fast numerical algorithm for the estimation of diffusion model parameters. J. Math. Psychol. 2008, 52, 1–9. [Google Scholar] [CrossRef]
- Parra-Rojas, C.; Hernandez-Vargas, E.A. PDEparams: Parameter fitting toolbox for partial differential equations in python. Bioinformatics 2019, 1–2. [Google Scholar] [CrossRef]
- Vyshemirsky, V.; Girolami, M. BioBayes: A software package for Bayesian inference in systems biology. Bioinformatics 2008, 24, 1933–1934. [Google Scholar] [CrossRef] [Green Version]
- Xun, X.; Cao, J.; Mallick, B.; Maity, A.; Carroll, R.J. Parameter Estimation of Partial Differential Equation Models. J. Am. Stat. Assoc. 2013, 108, 1009–1020. [Google Scholar] [CrossRef] [Green Version]
- Diasio, R.B.; Harris, B.E. Clinical Pharmacology of 5-Fluorouracil. Clin. Pharmacokinet. 1989, 16, 215–237. [Google Scholar] [CrossRef] [PubMed]
- Leucovorin Calcium Injection Label. Available online: https://www.accessdata.fda.gov/drugsatfda_docs/label/2012/040347s010lbl.pdf (accessed on 29 March 2021).
- Greiner, P.; Zittoun, J.; Marquet, J.; Cheron, J. Pharmacokinetics of (−)−folinic acid after oral and intravenous administration of the racemate. Br. J. Clin. Pharmacol. 1989, 28, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Macarulla, T.; Cervantes, A.; Tabernero, J.; Roselló, S.; Van Cutsem, E.; Tejpar, S.; Prenen, H.; Martinelli, E.; Troiani, T.; Laffranchi, B.; et al. Phase I study of FOLFIRI plus pimasertib as second-line treatment for KRAS-mutated metastatic colorectal cancer. Br. J. Cancer 2015, 112, 1874–1881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mathijssen, R.H.; van Alphen, R.J.; Verweij, J.; Loos, W.J.; Nooter, K.; Stoter, G.; Sparreboom, A. Clinical Pharmacokinetics and Metabolism of Irinotecan (CPT-11). Clin. Cancer Res. 2001, 7, 2182–2194. [Google Scholar] [PubMed]




| Variable | Name | Description |
|---|---|---|
| Naive T-cells | ||
| Helper T-cells | ||
| Cytotoxic cells | includes CD8+ T-cells and NK cells | |
| Regulatory T-cells | ||
| Naive dendritic cells | ||
| D | Activated dendritic cells | antigen presenting cells |
| M | Macrophages | |
| C | Cancer cells | |
| N | Nectrotic cells | |
| H | HMGB1 | |
| Carcinogenic cytokines | includes effects of IL-6, IL-17, IL-21 and IL-22 | |
| Immunosuppresive agents | includes effects of IL-10 and CCL20 | |
| IFN- | ||
| TGF- | ||
| 5-FU | Fluorouracil | |
| Ir | Irinotecan | |
| LV | Leucovorin |
| Cluster | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 3.66 × 10 | 4.90 × 10 | 9.67 × 10 | 2.70 × 10 | 6.41 × 10 | 1.23 × 10 | 2.64 × 10 |
| 2 | 2.63 × 10 | 2.81 × 10 | 3.25 × 10 | 1.09 × 10 | 4.37 × 10 | 5.95 × 10 | 2.76 × 10 |
| 3 | 1.38 × 10 | 2.20 × 10 | 8.59 × 10 | 6.26 × 10 | 1.53 × 10 | 2.61 × 10 | 1.56 × 10 |
| 4 | 1.58 × 10 | 1.71 × 10 | 6.35 × 10 | 9.72 × 10 | 6.20 × 10 | 4.68 × 10 | 1.01 × 10 |
| 5 | 1.36 × 10 | 5.24 × 10 | 3.27 × 10 | 3.78 × 10 | 4.72 × 10 | 9.11 × 10 | 1.55 × 10 |
| 1 | 4.64 × 10 | 1.55 × 10 | 4.97 × 10 | 5.12 × 10 | 1.47 | 3.89 | 2.55 × 10 |
| 2 | 2.38 × 10 | 1.46 × 10 | 7.58 × 10 | 1.79 × 10 | 6.04 × 10 | 9.38 × 10 | 5.57 × 10 |
| 3 | 1.83 × 10 | 0 | 7.51 × 10 | 7.14 × 10 | 1.03 | 4.90 × 10 | 3.87 |
| 4 | 1.22 × 10 | 0 | 4.14 × 10 | 5.77 × 10 | 1.46 × 10 | 0 | 2.56 × 10 |
| 5 | 2.69 × 10 | 7.03 × 10 | 4.59 × 10 | 2.30 | 1.18 | 4.08 × 10 | 3.46 × 10 |
| Fluorouracil | Leucovorin | Irinotecan | |
|---|---|---|---|
| median | 770 | 725 | 300 |
| min | 598 | 75 | 208 |
| number of cycles | 12 | 12 | 12 |
| cycle length | 14 | 14 | 14 |
| Tumor Free | With Tumor | |
|---|---|---|
| Early follow up day | 23 | 8 |
| Last follow up day | 24 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Budithi, A.; Su, S.; Kirshtein, A.; Shahriyari, L. Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer. Cancers 2021, 13, 2632. https://doi.org/10.3390/cancers13112632
Budithi A, Su S, Kirshtein A, Shahriyari L. Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer. Cancers. 2021; 13(11):2632. https://doi.org/10.3390/cancers13112632
Chicago/Turabian StyleBudithi, Aparajita, Sumeyye Su, Arkadz Kirshtein, and Leili Shahriyari. 2021. "Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer" Cancers 13, no. 11: 2632. https://doi.org/10.3390/cancers13112632
APA StyleBudithi, A., Su, S., Kirshtein, A., & Shahriyari, L. (2021). Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer. Cancers, 13(11), 2632. https://doi.org/10.3390/cancers13112632







