Genome Scale Modeling to Study the Metabolic Competition between Cells in the Tumor Microenvironment
Abstract
:Simple Summary
Abstract
1. Introduction
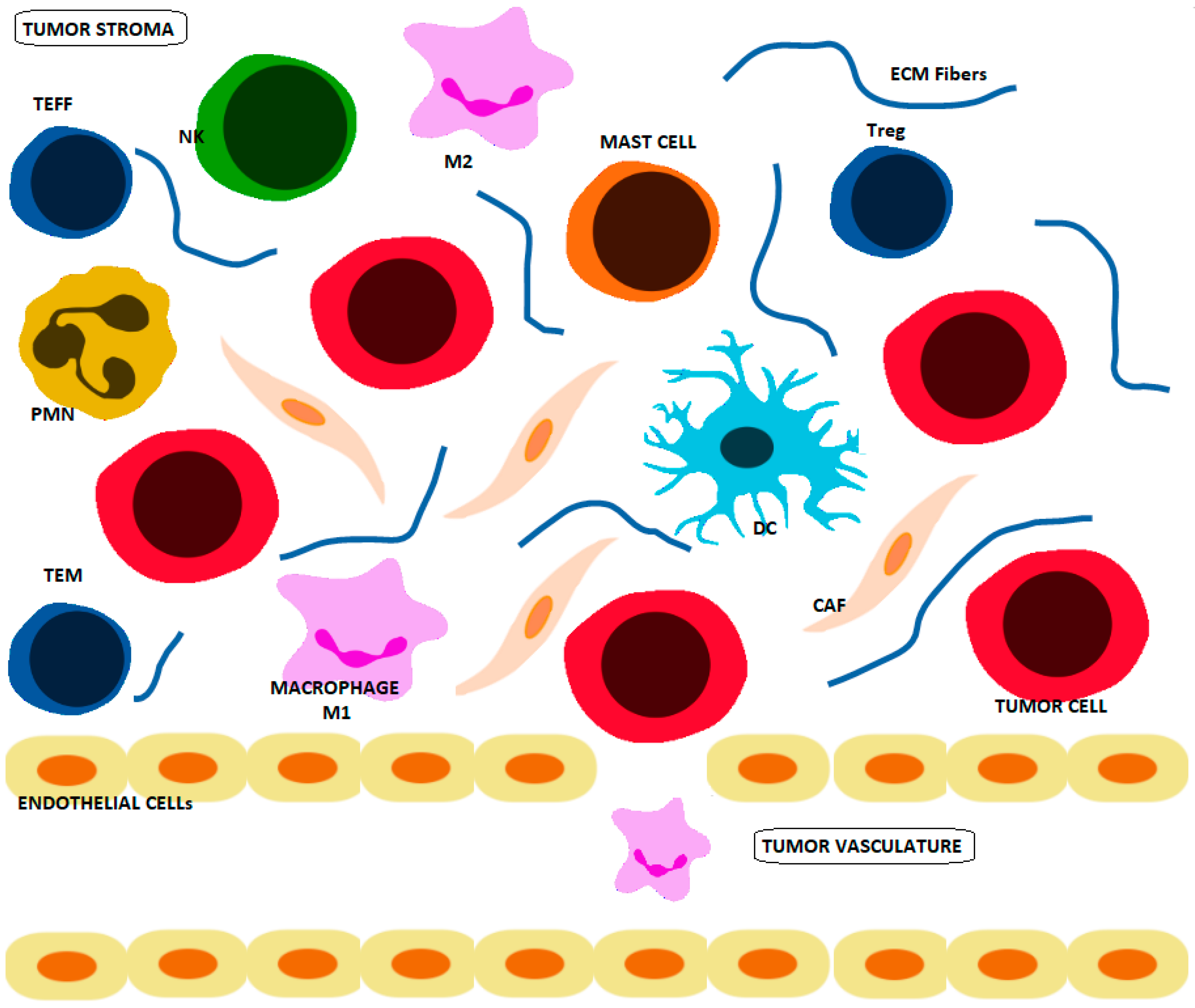
1.1. Crosstalk between Cancer and Immune Cells
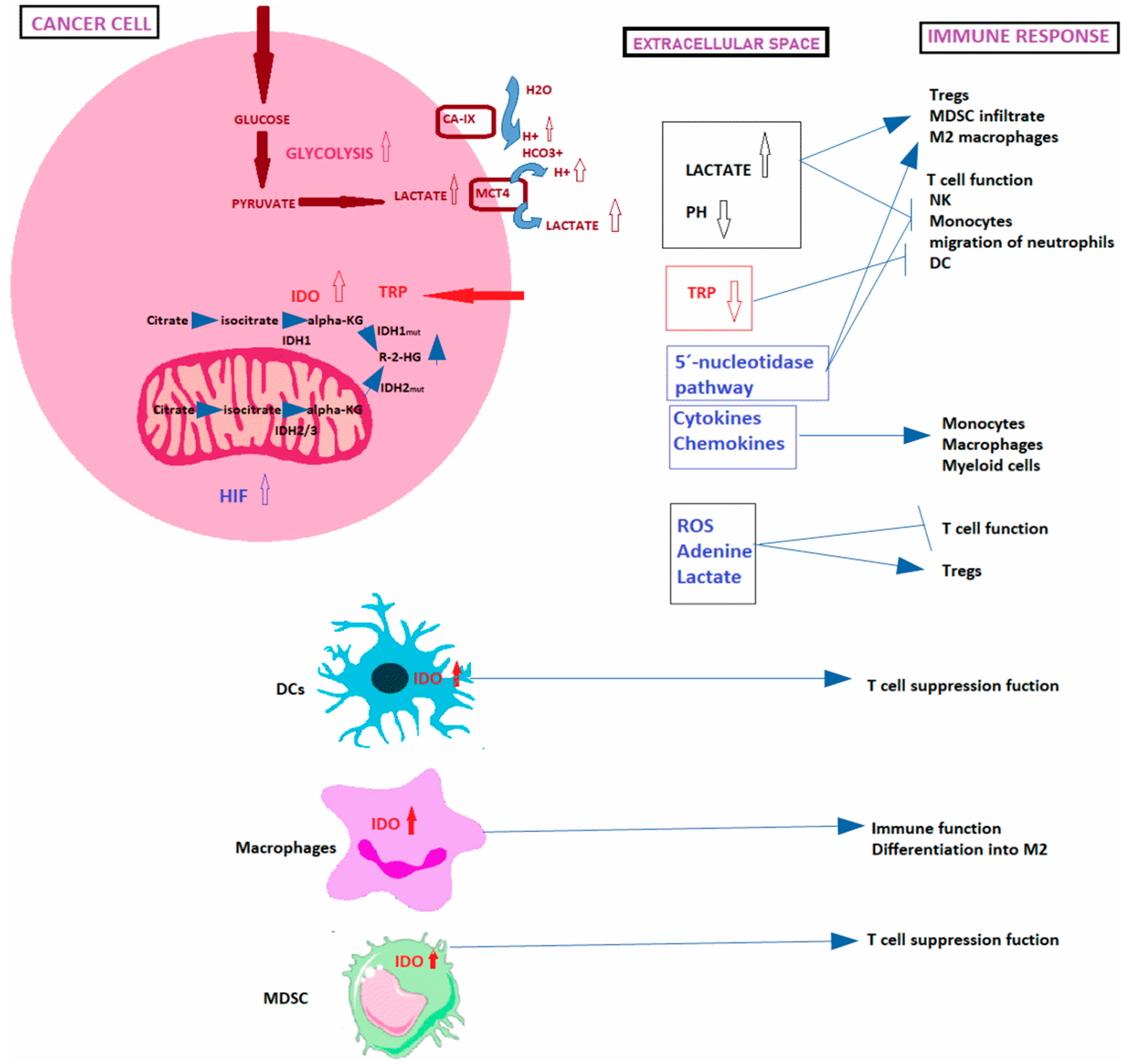
1.1.1. Warburg Effect
1.1.2. Acidification of the TME
1.1.3. Role of Amino Acids in Battle between Immune and Cancer Cells
1.1.4. Hypoxia
1.1.5. Signaling Events Induced by Metabolite-Sensing
1.1.6. Macromolecules and Organelles Released in the TME
1.1.7. Reverse Warburg Effect
1.2. Crosstalk between the TME, Extracellular Matrix and Cell Metabolism in Cancer
2. Genome Scale Metabolic Modeling in Cancer
2.1. GEMs
2.2. Constraint-Based Modeling
2.3. Context-Specific GEMs
2.4. Kinetic Models
2.5. Application of Metabolic Analysis Tools in Cancer Research
2.5.1. Software for Constraint-Based Modeling Tools
2.5.2. Application of GEMs in Metabolic Cancer Research
2.5.3. Modeling the Metabolic Crosstalk between Cell Populations
PopFBA
Single-Cell FBA (scFBA)
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lyssiotis, C.A.; Kimmelman, A.C. Metabolic Interactions in the Tumor Microenvironment. Trends Cell Biol. 2017, 27, 863–875. [Google Scholar] [CrossRef] [Green Version]
- Seager, R.J.; Hajal, C.; Spill, F.; Kamm, R.D.; Zaman, M.H. Dynamic interplay between tumour, stroma and immune system can drive or prevent tumour progression. Converg. Sci. Phys. Oncol. 2017, 3, 034002. [Google Scholar] [CrossRef] [PubMed]
- Muenst, S.; Läubli, H.; Soysal, S.; Zippelius, A.; Tzankov, A.; Hoeller, S. The immune system and cancer evasion strategies: Therapeutic concepts. J. Intern. Med. 2016, 279, 541–562. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, D.; Cang, H.; Guo, B. Crosstalk between cancer and immune cells: Role of tumor-associated macrophages in the tumor microenvironment. Cancer Med. 2019, 8, 4709–4721. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, G. Cancer and innate immune system interactions: Translational potentials for cancer immunotherapy. J. Im-munother. 2012, 35, 299–308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cassim, S.; Pouyssegur, J. Tumor Microenvironment: A Metabolic Player that Shapes the Immune Response. Int. J. Mol. Sci. 2019, 21, 157. [Google Scholar] [CrossRef] [Green Version]
- Kishton, R.J.; Sukumar, M.; Restifo, N.P. Metabolic Regulation of T Cell Longevity and Function in Tumor Immunotherapy. Cell Metab. 2017, 26, 94–109. [Google Scholar] [CrossRef] [Green Version]
- Unanue, E.R.; Turk, V.; Neefjes, J. Variations in MHC Class II Antigen Processing and Presentation in Health and Disease. Annu. Rev. Immunol. 2016, 34, 265–297. [Google Scholar] [CrossRef] [PubMed]
- Hivroz, C.; Chemin, K.; Tourret, M.; Bohineust, A. Crosstalk between T Lymphocytes and Dendritic Cells. Crit. Rev. Immunol. 2012, 32, 139–155. [Google Scholar] [CrossRef]
- Valenzuela, J.; Schmidt, C.; Mescher, M. The Roles of IL-12 in Providing a Third Signal for Clonal Expansion of Naive CD8 T Cells. J. Immunol. 2002, 169, 6842–6849. [Google Scholar] [CrossRef]
- Tian, Y.; Babor, M.; Lane, J.; Schulten, V.; Patil, V.S.; Seumois, G.; Rosales, S.L.; Fu, Z.; Picarda, G.; Burel, J.; et al. Unique phenotypes and clonal expansions of human CD4 effector memory T cells re-expressing CD45RA. Nat. Commun. 2017, 8, 1–13. [Google Scholar] [CrossRef]
- Akbar, A.N.; Terry, L.; Timms, A.; Beverley, P.; Janossy, G. Loss of CD45R and gain of UCHL1 reactivity is a feature of primed T cells. J. Immunol. 1988, 140, 2171–2178. [Google Scholar]
- Koch, S.; Larbi, A.; Derhovanessian, E.; Özcelik, D.; Naumova, E.; Pawelec, G. Multiparameter flow cytometric analysis of CD4 and CD8 T cell subsets in young and old people. Immun. Ageing 2008, 5, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, A.R.; Rathmell, W.K.; Rathmell, J.C. The tumor microenvironment as a metabolic barrier to effector T cells and immuno-therapy. Elife 2020, 9, e55185. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Bai, L.; Li, W.; Zeng, T.; Tian, H.; Cui, J. Targeting T cell metabolism in the tumor microenvironment: An anti-cancer thera-peutic strategy. J. Exp. Clin. Cancer Res. 2019, 38, 403. [Google Scholar] [CrossRef]
- Han, Y.; Liu, D.; Li, L. PD-1/PD-L1 pathway: Current researches in cancer. Am. J. Cancer Res. 2020, 10, 727–742. [Google Scholar]
- Ohaegbulam, K.C.; Assal, A.; Lazar-Molnar, E.; Yao, Y.; Zang, X. Human cancer immunotherapy with antibodies to the PD-1 and PD-L1 pathway. Trends Mol. Med. 2015, 21, 24–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pardoll, D.M. The blockade of immune checkpoints in cancer immunotherapy. Nat. Rev. Cancer 2012, 12, 252–264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Le Bourgeois, T.; Strauss, L.; Aksoylar, H.I.; Daneshmandi, S.; Seth, P.; Patsoukis, N.; Boussiotis, V.A. Targeting T Cell Metabolism for improvement of cancer immunotherapy. Front. Oncol. 2018, 8, 237. [Google Scholar] [CrossRef]
- Patsoukis, N.; Bardhan, K.; Chatterjee, P.; Sari, D.; Liu, B.; Bell, L.N.; Karoly, E.D.; Freeman, G.J.; Petkova, V.; Seth, P.; et al. PD-1 alters T-cell metabolic reprogramming by inhibiting glycolysis and promoting lipolysis and fatty acid oxidation. Nat. Commun. 2015, 6, 6692. [Google Scholar] [CrossRef] [Green Version]
- Andrejeva, G.; Rathmell, J.C. Similarities and Distinctions of Cancer and Immune Metabolism in Inflammation and Tumors. Cell Metab. 2017, 26, 49–70. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ma, S.; Ruzzo, W.L. Spatial modeling of prostate cancer metabolism reveals extensive heterogeneity and selective vulnerabilities. BioRxiv 2019, 719294. [Google Scholar] [CrossRef] [Green Version]
- Motamedian, E.; Ghavami, G.; Sardari, S. Investigation on metabolism of cisplatin resistant ovarian cancer using a genome scale metabolic model and microarray data. Iran. J. Basic Med. Sci. 2015, 18, 267–276. [Google Scholar] [PubMed]
- Kim, H.U.; Kim, T.Y.; Lee, S.Y. Genome-scale metabolic network analysis and drug targeting of multi-drug resistant pathogen Acinetobacter baumannii AYE. Mol. BioSyst. 2009, 6, 339–348. [Google Scholar] [CrossRef] [PubMed]
- Renner, K.; Singer, K.; Koehl, G.E.; Geissler, E.K.; Peter, K.; Siska, P.J.; Kreutz, M. Metabolic Hallmarks of Tumor and Immune Cells in the Tumor Microenvironment. Front. Immunol. 2017, 8, 248. [Google Scholar] [CrossRef] [Green Version]
- Xia, L.; Oyang, L.; Lin, J.; Tan, S.; Han, Y.; Wu, N.; Yi, P.; Tang, L.; Pan, Q.; Rao, S.; et al. The cancer metabolic reprogramming and immune response. Mol. Cancer 2021, 20, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Domblides, C.; Lartigue, L.; Faustin, B. Control of the Antitumor Immune Response by Cancer Metabolism. Cells 2019, 8, 104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singer, K.; Cheng, W.-C.; Kreutz, M.; Ho, P.-C.; Siska, P.J. Immunometabolism in cancer at a glance. Dis. Model. Mech. 2018, 11, 034272. [Google Scholar] [CrossRef] [Green Version]
- Schulze, A.; Yuneva, M. The big picture: Exploring the metabolic cross-talk in cancer. Dis. Model. Mech. 2018, 11, dmm036673. [Google Scholar] [CrossRef] [Green Version]
- Rabinovich, G.A.; Gabrilovich, D.; Sotomayor, E.M. Immunosuppressive Strategies that are Mediated by Tumor Cells. Annu. Rev. Immunol. 2007, 25, 267–296. [Google Scholar] [CrossRef] [Green Version]
- Warburg, O. On the Origin of Cancer Cells. Science 1956, 123, 309–314. [Google Scholar] [CrossRef] [PubMed]
- Marbaniang, C.; Kma, L. Dysregulation of Glucose Metabolism by Oncogenes and Tumor Suppressors in Cancer Cells. Asian Pac. J. Cancer Prev. 2018, 19, 2377–2390. [Google Scholar] [CrossRef]
- Tarrado-Castellarnau, M.; de Atauri, P.; Cascante, M. Oncogenic regulation of tumor metabolic reprogramming. Oncotarget 2016, 7, 62726–62753. [Google Scholar] [CrossRef] [Green Version]
- Gillies, R.J.; Gatenby, R.A. Metabolism and Its Sequelae in Cancer Evolution and Therapy. Cancer J. 2015, 21, 88–96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagao, A.; Kobayashi, M.; Koyasu, S.; Chow, C.C.T.; Harada, H. HIF-1-Dependent Reprogramming of Glucose Metabolic Pathway of Cancer Cells and Its Therapeutic Significance. Int. J. Mol. Sci. 2019, 20, 238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harris, A.L. Hypoxia—A key regulatory factor in tumour growth. Nat. Rev. Cancer 2002, 2, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Pastorekova, S.; Gillies, R.J. The role of carbonic anhydrase IX in cancer development: Links to hypoxia, acidosis, and beyond. Cancer Metastasis Rev. 2019, 38, 65–77. [Google Scholar] [CrossRef]
- Ames, S.; Pastorekova, S.; Becker, H.M. The proteoglycan-like domain of carbonic anhydrase IX mediates non-catalytic facilitation of lactate transport in cancer cells. Oncotarget 2018, 9, 27940–27957. [Google Scholar] [CrossRef] [Green Version]
- Siska, P.J.; Kim, B.; Ji, X.; Hoeksema, M.D.; Massion, P.P.; Beckermann, K.E.; Wu, J.; Chi, J.-T.; Hong, J.; Rathmell, J.C. Fluorescence-based measurement of cystine uptake through xCT shows requirement for ROS detoxification in activated lymphocytes. J. Immunol. Methods 2016, 438, 51–58. [Google Scholar] [CrossRef] [Green Version]
- Jun, J.C.; Rathore, A.; Younas, H.; Gilkes, D.; Polotsky, V.Y. Hypoxia-Inducible Factors and Cancer. Curr. Sleep Med. Rep. 2017, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Masoud, G.N.; Li, W. HIF-1α pathway: Role, regulation and intervention for cancer therapy. Acta Pharm. Sin. B 2015, 5, 378–389. [Google Scholar] [CrossRef] [Green Version]
- Laukka, T.; Mariani, C.J.; Ihantola, T.; Cao, J.Z.; Hokkanen, J.; Kaelin, W.G., Jr.; Godley, L.A.; Koivunen, P. Fumarate and Succinate Regulate Expression of Hypoxia-inducible Genes via TET Enzymes. J. Biol. Chem. 2016, 291, 4256–4265. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, C.; Giannoudis, A.; Lewis, C.E. Mechanisms regulating the recruitment of macrophages into hypoxic areas of tumors and other ischemic tissues. Blood 2004, 104, 2224–2234. [Google Scholar] [CrossRef]
- Lewis, C.; Murdoch, C. Macrophage Responses to Hypoxia: Implications for Tumor Progression and Anti-Cancer Therapies. Am. J. Pathol. 2005, 167, 627–635. [Google Scholar] [CrossRef]
- Mandl, M.; Depping, R. ARNT is a potential direct HIF-1 target gene in human Hep3B hepatocellular carcinoma cells. Cancer Cell Int. 2017, 17, 77. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Geng, Y.; Wang, P.; Zhou, Y.; Yang, H.; Huo, Y.; Zhang, H.; Li, Y.; He, H.; Tian, X.; et al. Extracellular ATP promotes breast cancer invasion and epithelial-mesenchymal transition via hypoxia-inducible factor 2α signaling. Cancer Sci. 2019, 110, 2456–2470. [Google Scholar] [CrossRef]
- Jia, Y.; Hao, S.; Jin, G.; Li, H.; Ma, X.; Zheng, Y.; Xiao, D.; Wang, Y. Overexpression of ARNT2 is associated with decreased cell pro-liferation and better prognosis in gastric cancer. Mol. Cell Biochem. 2019, 450, 97–103. [Google Scholar] [CrossRef] [PubMed]
- Yazdani, B.; Sirous, H. HIF3A: A Potent Prognostic Biomarker in Different Kinds of Cancer. Preprints 2021, 2021040265. [Google Scholar] [CrossRef]
- Saravia, J.; Raynor, J.L.; Chapman, N.M.; Lim, S.A.; Chi, H. Signaling networks in immunometabolism. Cell Res. 2020, 30, 328–342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.-P.; Lei, Q.-Y. Metabolite sensing and signaling in cell metabolism. Signal Transduct. Target. Ther. 2018, 3, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Robles-Flores, M.; Moreno-Londoño, A.P.; Castañeda-Patlán, M.C. Signaling Pathways Involved in Nutrient Sensing Control in Cancer Stem Cells: An Overview. Front. Endocrinol. 2021, 12, 627745. [Google Scholar] [CrossRef] [PubMed]
- Eniafe, J.; Jiang, S. The functional roles of TCA cycle metabolites in cancer. Oncogene 2021, 40, 3351–3363. [Google Scholar] [CrossRef] [PubMed]
- Kedia-Mehta, N.; Finlay, D.K. Competition for nutrients and its role in controlling immune responses. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef]
- Wei, J.; Raynor, J.; Nguyen, T.-L.M.; Chi, H. Nutrient and Metabolic Sensing in T Cell Responses. Front. Immunol. 2017, 8, 247. [Google Scholar] [CrossRef] [Green Version]
- Blagih, J.; Coulombe, F.; Vincent, E.; Dupuy, F.; Vazquez, G.G.; Yurchenko, E.; Raissi, T.C.; van der Windt, G.J.; Viollet, B.; Pearce, E.L.; et al. The Energy Sensor AMPK Regulates T Cell Metabolic Adaptation and Effector Responses In Vivo. Immunity 2015, 42, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Dembitz, V.; Lalic, H. The Role of AMPK/mTOR Modulators in the Therapy of Acute Myeloid Leukemia. Curr. Med. Chem. 2019, 26, 2208–2229. [Google Scholar] [CrossRef]
- Zhao, W.; Peng, F.; Shu, M.; Liu, H.; Hou, X.; Wang, X.; Ye, J.; Zhao, B.; Wang, K.; Zhong, C.; et al. Isogambogenic Acid Inhibits the Growth of Glioma Through Activation of the AMPK-mTOR Pathway. Cell. Physiol. Biochem. 2017, 44, 1381–1395. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chhipa, R.R.; Nakano, I.; Dasgupta, B. The AMPK Inhibitor Compound C Is a Potent AMPK-Independent Antiglioma Agent. Mol. Cancer Ther. 2014, 13, 596–605. [Google Scholar] [CrossRef] [Green Version]
- Yue, W.; Yang, C.S.; DiPaola, R.S.; Tan, X.L. Repurposing of metformin and aspirin by targeting AMPK-mTOR and inflammation for pancreatic cancer prevention and treatment. Cancer Prev. Res. (Phila) 2014, 7, 388–397. [Google Scholar] [CrossRef] [Green Version]
- Roudsari, N.M.; Lashgari, N.A.; Momtaz, S.; Abaft, S.; Jamali, F.; Safaiepour, P.; Narimisa, K.; Jackson, G.; Bishayee, A.; Rezaei, N.; et al. Inhibitors of the PI3K/Akt/mTOR Pathway in Prostate Cancer Chemoprevention and Inter-vention. Pharmaceutics 2021, 13, 1195. [Google Scholar] [CrossRef]
- Zou, Y.-F.; Xie, C.-W.; Yang, S.-X.; Xiong, J.-P. AMPK activators suppress breast cancer cell growth by inhibiting DVL3-facilitated Wnt/β-catenin signaling pathway activity. Mol. Med. Rep. 2016, 15, 899–907. [Google Scholar] [CrossRef] [Green Version]
- Xie, W.-Y.; Zhou, X.-D.; Yang, J.; Chen, L.-X.; Ran, D.-H. Inhibition of autophagy enhances heat-induced apoptosis in human non-small cell lung cancer cells through ER stress pathways. Arch. Biochem. Biophys. 2016, 607, 55–66. [Google Scholar] [CrossRef] [PubMed]
- Rogers, R.S.; Bhattacharya, J. When Cells Become Organelle Donors. Physiology 2013, 28, 414–422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moschoi, R.; Imbert, V.; Nebout, M.; Chiche, J.; Mary, D.; Prebet, T.; Saland, E.; Castellano, R.; Pouyet, L.; Collette, Y.; et al. Protective mitochondrial transfer from bone marrow stromal cells to acute myeloid leukemic cells during chemotherapy. Blood 2016, 128, 253–264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Y.; Chen, X.; Wang, X.; Zhao, Z.; Hu, W.; Zeng, S.; Wei, J.; Yang, X.; Qian, L.; Zhou, S.; et al. The effects and the mechanisms of autophagy on the cancer-associated fibroblasts in cancer. J. Exp. Clin. Cancer Res. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- de la Cruz-López, K.G.; Castro-Muñoz, L.J.; Reyes-Hernández, D.O.; García-Carrancá, A.; Manzo-Merino, J. Lactate in the Regulation of Tumor Microenvironment and Therapeutic Approaches. Front. Oncol. 2019, 9, 1143. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Yang, L.; Baddour, J.; Achreja, A.; Bernard, V.; Moss, T.; Marini, J.C.; Tudawe, T.; Seviour, E.; Lucas, F.A.S.; et al. Tumor microenvironment derived exosomes pleiotropically modulate cancer cell metabolism. eLife 2016, 5, e10250. [Google Scholar] [CrossRef]
- Nallanthighal, S.; Heiserman, J.P.; Cheon, D.-J. The Role of the Extracellular Matrix in Cancer Stemness. Front. Cell Dev. Biol. 2019, 7, 86. [Google Scholar] [CrossRef]
- Sazeides, C.; Le, A. Metabolic relationship between cancer-associated fibroblasts and cancer cells. In the heterogeneity of cancer metabolism. Adv. Exp. Med. Biol. 2018, 1063, 149–165. [Google Scholar]
- Nazemi, M.; Rainero, E. Cross-Talk between the Tumor Microenvironment, Extracellular Matrix, and Cell Metabolism in Cancer. Front. Oncol. 2020, 10, 239. [Google Scholar] [CrossRef] [Green Version]
- Mardinoglu, A.; Agren, R.; Kampf, C.; Asplund, A.; Nookaew, I.; Jacobson, P.; Walley, A.J.; Froguel, P.; Carlsson, L.M.; Uhlen, M.; et al. Integration of clinical data with a genome-scale metabolic model of the human adipocyte. Mol. Syst. Biol. 2013, 9, 649. [Google Scholar] [CrossRef]
- Mardinoglu, A.; Agren, R.; Kampf, C.; Asplund, A.; Uhlen, M.; Nielsen, J. Genome-scale metabolic modelling of hepatocytes reveals serine deficiency in patients with non-alcoholic fatty liver disease. Nat. Commun. 2014, 5, 3083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duarte, N.C.; Becker, S.A.; Jamshidi, N.; Thiele, I.; Mo, M.L.; Vo, T.D.; Srivas, R.; Palsson, B.Ø. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc. Natl. Acad. Sci. USA 2007, 104, 1777–1782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thiele, I.; Swainston, N.; Fleming, R.M.; Hoppe, A.; Sahoo, S.; Aurich, M.K.; Haraldsdottir, H.; Mo, M.L.; Rolfsson, Ó.; Stobbe, M.D.; et al. A community-driven global reconstruction of human metabolism. Nat. Biotechnol. 2013, 31, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Sahoo, S.; Zielinski, D.C.; Altunkaya, A.; Dräger, A.; Mih, N.; Gatto, F.; Nilsson, A.; Gonzalez, G.A.P.; Aurich, M.K.; et al. Recon3D enables a three-dimensional view of gene variation in human metabolism. Nat. Biotechnol. 2018, 36, 272–281. [Google Scholar] [CrossRef]
- Ma, H.; Sorokin, A.; Mazein, A.; Selkov, A.; Selkov, E.; Demin, O.; Goryanin, I. The Edinburgh human metabolic network reconstruc-tion and its functional analysis. Mol. Syst. Biol. 2007, 3, 135. [Google Scholar] [CrossRef]
- Nilsson, A.; Nielsen, J. Genome scale metabolic modeling of cancer. Metab. Eng. 2017, 43, 103–112. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Monk, J.M.; Palsson, B.O. Using Genome-scale Models to Predict Biological Capabilities. Cell 2015, 161, 971–987. [Google Scholar] [CrossRef] [Green Version]
- Yizhak, K.; Chaneton, B.; Gottlieb, E.; Ruppin, E. Modeling cancer metabolism on a genome scale. Mol. Syst. Biol. 2015, 11, 817. [Google Scholar] [CrossRef]
- Wang, F.-S.; Wu, W.-H.; Hsiu, W.-S.; Liu, Y.-J.; Chuang, K.-W. Genome-Scale Metabolic Modeling with Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference. Metabolites 2019, 10, 16. [Google Scholar] [CrossRef] [Green Version]
- Gatto, F.; Nookaew, I.; Nielsen, J. Chromosome 3p loss of heterozygosity is associated with a unique metabolic network in clear cell renal carcinoma. Proc. Natl. Acad. Sci. USA 2014, 111, E866–E875. [Google Scholar] [CrossRef] [Green Version]
- Agren, R.; Bordel, S.; Mardinoglu, A.; Pornputtapong, N.; Nookaew, I.; Nielsen, J. Reconstruction of Genome-Scale Active Metabolic Networks for 69 Human Cell Types and 16 Cancer Types Using INIT. PLoS Comput. Biol. 2012, 8, e1002518. [Google Scholar] [CrossRef]
- Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501. [Google Scholar] [CrossRef]
- Shlomi, T.; Benyamini, T.; Gottlieb, E.; Sharan, R.; Ruppin, E. Genome-Scale Metabolic Modeling Elucidates the Role of Proliferative Adaptation in Causing the Warburg Effect. PLoS Comput. Biol. 2011, 7, e1002018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, J.; Ye, J.; Kamphorst, J.J.; Shlomi, T.; Thompson, C.B.; Rabinowitz, J.D. Quantitative flux analysis reveals folate-dependent NADPH production. Nature 2014, 510, 298–302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Marcišauskas, S.; Sánchez, B.J.; Domenzain, I.; Hermansson, D.; Agren, R.; Nielsen, J.; Kerkhoven, E.J. RAVEN 2.0: A versatile toolbox for metabolic network reconstruction and a case study on Streptomyces coelicolor. PLoS Comput. Biol. 2018, 14, e1006541. [Google Scholar] [CrossRef] [Green Version]
- Yizhak, K.; Le Dévédec, S.E.; Rogkoti, V.M.; Baenke, F.; Boer, V.C.; Frezza, C.; Schulze, A.; Water, B.; Ruppin, E. A computational study of the Warburg effect identifies metabolic targets inhibiting cancer migration. Mol. Syst. Biol. 2014, 10, 744. [Google Scholar] [CrossRef] [PubMed]
- Nam, H.; Campodonico, M.; Bordbar, A.; Hyduke, D.R.; Kim, S.; Zielinski, D.C.; Palsson, B.O. A systems approach to predict on-cometabolites via context-specific genome-scale metabolic networks. PLoS Comput. Biol. 2014, 10, 9. [Google Scholar] [CrossRef] [Green Version]
- Reimers, A.M.; Reimers, A.C. The steady-state assumption in oscillating and growing systems. J. Theor. Biol. 2016, 406, 176–186. [Google Scholar] [CrossRef] [Green Version]
- Marín De Mas, I.; Torrents, L.; Bedia, C.; Nielsen, L.K.; Cascante, M.; Tauler, R. Stoichiometric gene-to-reaction associations enhance model-driven analysis performance: Metabolic response to chronic exposure to aldrin in prostate cancer. BMC Genom. 2019, 20, 1–12. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Mahadevan, R.; Schilling, C.H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003, 5, 264–276. [Google Scholar] [CrossRef]
- Lovász, L. Hit-and-run mixes fast. Math. Program. 1999, 86, 443–461. [Google Scholar] [CrossRef]
- Price, N.; Schellenberger, J.; Palsson, B.O. Uniform Sampling of Steady-State Flux Spaces: Means to Design Experiments and to Interpret Enzymopathies. Biophys. J. 2004, 87, 2172–2186. [Google Scholar] [CrossRef] [Green Version]
- Haraldsdóttir, H.S.; Cousins, B.; Thiele, I.; Fleming, R.M.T.; Vempala, S. CHRR: Coordinate hit-and-run with rounding for uniform sampling of constraint-based models. Bioinformatics 2017, 33, 1741–1743. [Google Scholar] [CrossRef]
- Lovász, L.; Vempala, S. Hit-and-run from a corner. SIAM J. Comput. 2004, 35, 985–1005. [Google Scholar] [CrossRef]
- Smith, R.L. Efficient Monte Carlo Procedures for Generating Points Uniformly Distributed over Bounded Regions. Oper. Res. 1984, 32, 1296–1308. [Google Scholar] [CrossRef]
- Zamboni, N.; Kümmel, A.; Heinemann, M. anNET: A tool for network-embedded thermodynamic analysis of quantitative metabolome data. BMC Bioinform. 2008, 9, 199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flamholz, A.; Noor, E.; Bar-Even, A.; Milo, R. eQuilibrator--the biochemical thermodynamics calculator. Nucleic Acids Res. 2011, 40, D770–D775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Thermodynamics-Based Metabolic Flux Analysis. Biophys. J. 2007, 92, 1792–1805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salvy, P.; Fengos, G.; Ataman, M.; Pathier, T.; Soh, K.C.; Hatzimanikatis, V. pyTFA and matTFA: A Python package and a Matlab toolbox for Thermodynamics-based Flux Analysis. Bioinformatics 2018, 35, 167–169. [Google Scholar] [CrossRef] [Green Version]
- Tomi-Andrino, C.; Norman, R.; Millat, T.; Soucaille, P.; Winzer, K.; Barrett, D.A.; King, J.; Kim, D.-H. Physicochemical and metabolic constraints for thermodynamics-based stoichiometric modelling under mesophilic growth conditions. PLoS Comput. Biol. 2021, 17, e1007694. [Google Scholar] [CrossRef] [PubMed]
- Pries, C.; Razaghi-Moghadam, Z.; Kopka, J.; Nikoloski, Z. Integration of relative metabolomics and transcriptomics time-course data in a metabolic model pinpoints effects of ribosome biogenesis defects on Arabidopsis thaliana metabolism. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Tian, M.; Reed, J.L. Integrating Proteomic or Transcriptomic Data into Metabolic Models Using Linear Bound Flux Balance Analysis. Bioinformatics 2018, 34, 3882–3888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandey, V.; Hadadi, N.; Hatzimanikatis, V. Enhanced flux prediction by integrating relative expression and relative metabolite abundance into thermodynamically consistent metabolic models. PLoS Comput. Biol. 2019, 15, e1007036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jamialahmadi, O.; Hashemi-Najafabadi, S.; Motamedian, E.; Romeo, S.; Bagheri, F. A benchmark-driven approach to reconstruct metabolic networks for studying cancer metabolism. PLoS Comput. Biol. 2019, 15, e1006936. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, B.J.; Ebrahim, A.; Metz, T.O.; Adkins, J.N.; Palsson, B.Ø.; Hyduke, D.R. GIM3E: Condition-specific models of cellular metab-olism developed from metabolomics and expression data. Bioinformatics 2013, 29, 2900–2908. [Google Scholar] [CrossRef] [Green Version]
- Zur, H.; Ruppin, E.; Shlomi, T. iMAT: An integrative metabolic analysis tool. Bioinformatics 2010, 26, 3140–3142. [Google Scholar] [CrossRef] [PubMed]
- Shlomi, T.; Ruppin, E. Computational reconstruction of tissue-specific metabolic models: Application to human liver metabo-lism. Mol. Syst. Biol. 2010, 6, 1–9. [Google Scholar]
- Wang, Y.; A Eddy, J.; Price, N.D. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE. BMC Syst. Biol. 2012, 6, 153. [Google Scholar] [CrossRef] [Green Version]
- Schultz, A.; Qutub, A.A. Reconstruction of Tissue-Specific Metabolic Networks Using CORDA. PLoS Comput. Biol. 2016, 12, e1004808. [Google Scholar] [CrossRef]
- Vlassis, N.; Pacheco, M.P.; Sauter, T. Fast Reconstruction of Compact Context-Specific Metabolic Network Models. PLoS Comput. Biol. 2014, 10, e1003424. [Google Scholar] [CrossRef]
- Pacheco, M.P.; John, E.; Kaoma, T.; Heinäniemi, M.; Nicot, N.; Vallar, L.; Bueb, J.L.; Sinkkonen, L.; Sauter, T. Integrated metabolic mod-elling reveals cell-type specific epigenetic control points of the macrophage metabolic network. BMC Genom. 2015, 16, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Mienda, B.S.; Salihu, R.; Adamu, A.; Idris, S. Genome-scale metabolic models as platforms for identification of novel genes as antimicrobial drug targets. Futur. Microbiol. 2018, 13, 455–467. [Google Scholar] [CrossRef] [PubMed]
- Sadhukhan, P.P.; Raghunathan, A. Investigating Host–Pathogen Behavior and Their Interaction Using Genome-Scale Metabolic Network Models. Methods Mol. Biol. 2014, 1184, 523–562. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, A.; Reed, J.; Shin, S.; Palsson, B.; Daefler, S. Constraint-based analysis of metabolic capacity of salmonella typhi-murium during host-pathogen interaction. BMC Syst. Biol. 2009, 3, 38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hur, W.; Ryu, J.Y.; Kim, H.U.; Hong, S.W.; Lee, E.B.; Lee, S.Y.; Yoon, S.K. Systems approach to characterize the metabolism of liver cancer stem cells expressing CD133. Sci. Rep. 2017, 7, 45557. [Google Scholar] [CrossRef] [Green Version]
- Chelliah, V.; Juty, N.; Ajmera, I.; Ali, R.; Dumousseau, M.; Glonț, M.; Hucka, M.; Jalowicki, G.; Keating, S.; Knight-Schrijver, V.; et al. BioModels: Ten-year anniversary. Nucleic Acids Res. 2015, 43, D542–D548. [Google Scholar] [CrossRef]
- Robinson, J.L.; Kocabaş, P.; Wang, H.; Cholley, P.-E.; Cook, D.; Nilsson, A.; Anton, M.; Ferreira, R.; Domenzain, I.; Billa, V.; et al. An atlas of human metabolism. Sci. Signal. 2020, 13, eaaz1482. [Google Scholar] [CrossRef] [PubMed]
- King, Z.A.; Lu, J.; Dräger, A.; Miller, P.; Federowicz, S.; Lerman, J.A.; Ebrahim, A.; Palsson, B.O.; Lewis, N.E. BiGG Models: A platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016, 44, D515–D522. [Google Scholar] [CrossRef]
- Kim, O.D.; Rocha, M.; Maia, P.A. Review of dynamic modeling approaches and their application in computational strain optimi-zation for metabolic engineering. Front. Microbiol. 2018, 9, 1690. [Google Scholar] [CrossRef] [PubMed]
- Marin-Hernandez, A.; Gallardo-Perez, J.C.; Rodriguez-Enriquez, S.; Encalada, R.; Moreno-Sanchez, R.; Saavedra, E. Modeling cancer glycolysis. Biochim. Et Biophys. Acta 2011, 1807, 755–767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shestov, A.A.; Liu, X.; Ser, Z.; Cluntun, A.A.; Hung, Y.P.; Huang, L.; Kim, D.; Le, A.; Yellen, G.; Albeck, J.G.; et al. Quantitative determinants of aerobic glycolysis identify flux through the enzyme GAPDH as a limiting step. eLife 2014, 3, e03342. [Google Scholar] [CrossRef] [PubMed]
- Khazaei, T.; McGuigan, A.P.; Mahadevan, R. Ensemble Modeling of Cancer Metabolism. Front. Physiol. 2012, 3, 135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schomburg, I.; Chang, A.; Schomburg, D. BRENDA, enzyme data and metabolic information. Nucleic Acids Res. 2002, 30, 47–49. [Google Scholar] [CrossRef]
- Wittig, U.; Golebiewski, M.; Kania, R.; Krebs, O.; Mir, S.; Weidemann, A.; Anstein, S.; Saric, J.; Rojas, I. SABIO-RK: Integration and cu-ration of reaction kinetics data. Lect. Notes Bioinformat. 2006, 4075, 94–103. [Google Scholar]
- Jia, G.; Stephanopoulos, G.N.; Gunawan, R. Parameter estimation of kinetic models from metabolic profiles: Two-phase dynamic decoupling method. Bioinformatics 2011, 27, 1964–1970. [Google Scholar] [CrossRef] [Green Version]
- Jia, G.; Stephanopoulos, G.; Gunawan, R. Incremental parameter estimation of kinetic metabolic network models. BMC Syst. Biol. 2012, 6, 142. [Google Scholar] [CrossRef] [Green Version]
- Murabito, E.; Verma, M.; Bekker, M.; Bellomo, D.; Westerhoff, H.; Teusink, B.; Steuer, R. Monte-Carlo Modeling of the Central Carbon Metabolism of Lactococcus lactis: Insights into Metabolic Regulation. PLoS ONE 2014, 9, e106453. [Google Scholar] [CrossRef] [Green Version]
- Miskovic, L.; Béal, J.; Moret, M.; Hatzimanikatis, V. Uncertainty reduction in biochemical kinetic models: Enforcing desired model properties. PLoS Comput. Biol. 2019, 15, e1007242. [Google Scholar] [CrossRef] [Green Version]
- Mišković, L.; Hatzimanikatis, V. Modeling of uncertainties in biochemical reactions. Biotechnol. Bioeng. 2010, 108, 413–423. [Google Scholar] [CrossRef] [Green Version]
- Stanford, N.J.; Lubitz, T.; Smallbone, K.; Klipp, E.; Mendes, P.; Liebermeister, W. Systematic Construction of Kinetic Models from Genome-Scale Metabolic Networks. PLoS ONE 2013, 8, e79195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soh, K.C.; Miskovic, L.; Hatzimanikatis, V. From network models to network responses: Integration of thermodynamic and kinetic properties of yeast genome-scale metabolic networks. FEMS Yeast Res. 2011, 12, 129–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khodayari, A.; Zomorrodi, A.R.; Liao, J.; Maranas, C.D. A kinetic model of Escherichia coli core metabolism satisfying multiple sets of mutant flux data. Metab. Eng. 2014, 25, 50–62. [Google Scholar] [CrossRef]
- Chowdhury, A.; Zomorrodi, A.R.; Maranas, C.D. k-OptForce: Integrating Kinetics with Flux Balance Analysis for Strain Design. PLoS Comput. Biol. 2014, 10, e1003487. [Google Scholar] [CrossRef] [Green Version]
- Volkova, S.; Matos, M.R.A.; Mattanovich, M.; Marín de Mas, I. Metabolic modelling as a framework for metabolomics data inte-gration and analysis. Metabolites 2020, 10, 303. [Google Scholar] [CrossRef]
- Tran, L.M.; Rizk, M.L.; Liao, J.C. Ensemble Modeling of Metabolic Networks. Biophys. J. 2008, 95, 5606–5617. [Google Scholar] [CrossRef] [Green Version]
- Miskovic, L.; Hatzimanikatis, V. Production of biofuels and biochemicals: In need of an ORACLE. Trends Biotechnol. 2010, 28, 391–397. [Google Scholar] [CrossRef]
- Saa, P.; Nielsen, L.K. A general framework for thermodynamically consistent parameterization and efficient sampling of enzy-matic reactions. PLoS Comput. Biol. 2015, 11, e1004195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gopalakrishnan, S.; Dash, S.; Maranas, C. K-FIT: An accelerated kinetic parameterization algorithm using steady-state fluxomic data. Metab. Eng. 2020, 61, 197–205. [Google Scholar] [CrossRef] [PubMed]
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdóttir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V.; et al. Creation and analysis of bio-chemical constraint-based models using the COBRA toolbox v.3.0. Nat. Protoc. 2019, 14, 639–702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ebrahim, A.; Lerman, J.A.; Palsson, B.O.; Hyduke, D.R. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst. Biol. 2013, 7, 74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heirendt, L.; Thiele, I.; Fleming, R.M.T. DistributedFBA.jl: High-level, high-performance flux balance analysis in Julia. Bioinformatics 2017, 33, 1421–1423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mendoza, S.N.; Olivier, B.G.; Molenaar, D.; Teusink, B. A systematic assessment of current genome-scale metabolic reconstruction tools. Genome Biol. 2019, 20, 1–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kotze, H.L.; Armitage, E.G.; Sharkey, K.J.; Allwood, J.W.; Dunn, W.B.; Williams, K.J.; Goodacre, R. A novel untargeted metabolomics correlation-based network analysis incorporating human metabolic reconstructions. BMC Syst. Biol. 2013, 7, 107. [Google Scholar] [CrossRef] [Green Version]
- Klamt, S.; Saez-Rodriguez, J.; Gilles, E.D. Structural and functional analysis of cellular networks with CellNetAnalyzer. BMC Syst. Biol. 2007, 1, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grafahrend-Belau, E.; Klukas, C.; Junker, B.H.; Schreiber, F. FBA-SimVis: Interactive visualization of constraint-based metabolic models. Bioinformatics 2009, 25, 2755–2757. [Google Scholar] [CrossRef] [Green Version]
- Rocha, I.; Maia, P.; Evangelista, P.; Vilaça, P.; Soares, S.; Pinto, J.P.; Nielsen, J.; Patil, K.R.; Ferreira, E.C.; Rocha, M. OptFlux: An open-source software platform for in silico metabolic engineering. BMC Syst. Biol. 2010, 4, 45. [Google Scholar] [CrossRef] [Green Version]
- Gelius-Dietrich, G.; Desouki, A.A.; Fritzemeier, C.J.; Lercher, M.J. sybil—Efficient constraint-based modelling in R. BMC Syst. Biol. 2013, 7, 125. [Google Scholar] [CrossRef] [Green Version]
- Olivier, B.G.; Rohwer, J.; Hofmeyr, J.-H.S. Modelling cellular systems with PySCeS. Bioinformatics 2004, 21, 560–561. [Google Scholar] [CrossRef] [Green Version]
- Gevorgyan, A.; Bushell, M.E.; Avignone-Rossa, C.; Kierzek, A.M. SurreyFBA: A command line tool and graphics user interface for constraint-based modeling of genome-scale metabolic reaction networks. Bioinformatics 2010, 27, 433–434. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, A.; Hoffmann, S.; Gerasch, A.; Gille, C.; Holzhütter, H.-G. FASIMU: Flexible software for flux-balance computation series in large metabolic networks. BMC Bioinform. 2011, 12, 28. [Google Scholar] [CrossRef] [Green Version]
- Boele, J.; Olivier, B.G.; Teusink, B. FAME, the Flux Analysis and Modeling Environment. BMC Syst. Biol. 2012, 6, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Latendresse, M.; Karp, P.D. Web-based metabolic network visualization with a zooming user interface. BMC Bioinform. 2011, 12, 176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arkin, A.P.; Cottingham, R.; Henry, C.S.; Harris, N.L.; Stevens, R.L.; Maslov, S.; Dehal, P.; Ware, D.; Perez, F.; Canon, S.; et al. KBase: The United States Department of Energy Systems Biology Knowledgebase. Nat. Biotechnol. 2018, 36, 566–569. [Google Scholar] [CrossRef] [Green Version]
- Karlsen, E.; Schulz, C.; Almaas, E. Automated generation of genome-scale metabolic draft reconstructions based on KEGG. BMC Bioinform. 2018, 19, 1–11. [Google Scholar] [CrossRef]
- Aite, M.; Chevallier, M.; Frioux, C.; Trottier, C.; Got, J.; Cortés, M.P.; Mendoza, S.N.; Carrier, G.; Dameron, O.; Guillaudeux, N.; et al. Traceability, reproducibility and wiki-exploration for ‘à-La-Carte’ reconstructions of genome-scale metabolic models. PLoS Comput. Biol. 2018, 14, 1–25. [Google Scholar] [CrossRef]
- Machado, D.; Andrejev, S.; Tramontano, M.; Patil, K.R. Fast automated reconstruction of genome-scale metabolic models for mi-crobial species and communities. Nucleic Acids Res. 2018, 46, 7542–7553. [Google Scholar] [CrossRef]
- Hanemaaijer, M.; Olivier, B.G.; Röling, W.F.M.; Bruggeman, F.; Teusink, B. Model-based quantification of metabolic interactions from dynamic microbial-community data. PLoS ONE 2017, 12, e0173183. [Google Scholar] [CrossRef] [PubMed]
- Henry, C.S.; DeJongh, M.; A Best, A.; Frybarger, P.M.; Linsay, B.; Stevens, R.L. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 2010, 28, 977–982. [Google Scholar] [CrossRef] [PubMed]
- Karp, P.D.; Latendresse, M.; Paley, S.M.; Krummenacker, M.; Ong, Q.D.; Billington, R.; Kothari, A.; Weaver, D.; Lee, T.; Subhraveti, P.; et al. Pathway tools version 19.0 update: Software for pathway/genome informatics and systems biology. Brief Bioinform. 2016, 17, 877–890. [Google Scholar] [CrossRef]
- Dias, O.; Rocha, M.; Ferreira, E.C.; Rocha, I. Reconstructing genome-scale metabolic models with merlin. Nucleic Acids Res. 2015, 43, 3899–3910. [Google Scholar] [CrossRef] [PubMed]
- Pitkänen, E.; Jouhten, P.; Hou, J.; Syed, M.F.; Blomberg, P.; Kludas, J.; Oja, M.; Holm, L.; Penttilä, M.; Rousu, J.; et al. Comparative Genome-Scale Reconstruction of Gapless Metabolic Networks for Present and Ancestral Species. PLoS Comput. Biol. 2014, 10, e1003465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pabinger, S.; Snajder, R.; Hardiman, T.; Willi, M.; Dander, A.; Trajanoski, Z. MEMOSys 2.0: An update of the bioinformatics database for genome-scale models and genomic data. Database 2014, 2014, bau004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liao, Y.-C.; Tsai, M.-H.; Chen, F.-C.; Hsiung, C.A. GEMSiRV: A software platform for GEnome-scale metabolic model simulation, reconstruction and visualization. Bioinformatics 2012, 28, 1752–1758. [Google Scholar] [CrossRef]
- Cottret, L.; Frainay, C.; Chazalviel, M.; Cabanettes, F.; Gloaguen, Y.; Camenen, E.; Jourdan FMerlet, B.; Heux, S.; Portais, J.C.; Poupin, N.; et al. MetExplore: Collaborative edition and exploration of metabolic networks. Nucleic Acids Res. 2018, 46, 495–502. [Google Scholar] [CrossRef] [Green Version]
- Thorleifsson, S.G.; Thiele, I. rBioNet: A COBRA toolbox extension for reconstructing high-quality biochemical networks. Bioinformatics 2011, 27, 2009–2010. [Google Scholar] [CrossRef]
- Latendresse, M.; Krummenacker, M.; Trupp, M.; Karp, P.D. Construction and completion of flux balance models from pathway databases. Bioinformatics 2012, 28, 388–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Apaolaza, I.; San José-Eneriz, E.; Agirre, X.; Prósper, F.; Planes, F.J. COBRA methods and metabolic drug targets in cancer. Mol. Cell. Oncol. 2018, 5, 10–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Turanli, B.; Zhang, C.; Kim, W.; Benfeitas, R.; Uhlen, M.; Arga, K.Y.; Mardinoglu, A. Discovery of therapeutic agents for prostate cancer using genome-scale metabolic modeling and drug repositioning. EBioMedicine 2019, 42, 386–396. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Ji, B.; Mardinoglu, A.; Nielsen, J.; Hua, Q. Logical transformation of genome-scale metabolic models for gene level ap-plications and analysis. Bioinformatics 2015, 31, 2324–2331. [Google Scholar] [CrossRef] [Green Version]
- Ortmayr, K.; Dubuis, S.; Zampieri, M. Metabolic profiling of cancer cells reveals genome-wide crosstalk between transcriptional regulators and metabolism. Nat. Commun. 2019, 10, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raškevičius, V.; Mikalayeva, V.; Antanavičiūtė, I.; Ceslevičienė, I.; Skeberdis, V.A.; Kairys, V.; Bordel, S. Genome scale metabolic models as tools for drug design and personalized medicine. PLoS ONE. 2018, 13, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A Major Update to the DrugBank Database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef] [PubMed]
- O’Boyle, N.M.; Banck, M.; James CAMorley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldman, A.; Khiste, S.; Freinkman, E.; Dhawan, A.; Majumder, B.; Mondal, J.; Pinkerton, A.B.; Eton, E.; Medhi, R.; Chandrasekar, V.; et al. Targeting tumor phenotypic plasticity and metabolic remodeling in adaptive cross-drug tolerance. Sci. Signal. 2019, 12, eaas8779. [Google Scholar] [CrossRef] [PubMed]
- Mazat, J.-P.; Ransac, S. The Fate of Glutamine in Human Metabolism. The Interplay with Glucose in Proliferating Cells. Metab. 2019, 9, 81. [Google Scholar] [CrossRef] [Green Version]
- Uhlén, M.; Zhang, C.; Lee, S.; Sjöstedt, E.; Fagerberg, L.; Bidkhori, G.; Benfeitas, R.; Arif, M.; Liu, Z.; Edfors, F.; et al. A pathology atlas of the human cancer transcriptome. Science 2017, 357, eaan2507. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Aldrees, M.; Arif, M.; Li, X.; Mardinoglu, A.; Aziz, M.A. Elucidating the Reprograming of Colorectal Cancer Metabolism Using Genome-Scale Metabolic Modeling. Front. Oncol. 2019, 9, 681. [Google Scholar] [CrossRef] [Green Version]
- Resendis-Antonio, O.; Gonzalez-Torres, C.; Jaime-Muñoz, G.; Hernandez-Patiño, C.E.; Salgado-Muñoz, C.F. Modeling metabolism: A window toward a comprehensive interpretation of networks in cancer. Semin. Cancer Biol. 2015, 30, 79–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vazquez, A.; Liu, J.; Zhou, Y.; Oltvai, Z.N. Catabolic efficiency of aerobic glycolysis: The Warburg effect revisited. BMC Syst. Biol. 2010, 4, 58. [Google Scholar] [CrossRef] [Green Version]
- Asgari, Y.; Zabihinpour, Z.; Salehzadeh-Yazdi, A.; Schreiber, F.; Masoudi-Nejad, A. Alterations in cancer cell metabolism: The Warburg effect and metabolic adaptation. Genomics 2015, 105, 275–281. [Google Scholar] [CrossRef]
- Magnusdottir, S.; Heinken, A.; Kutt, L.; Ravcheev, D.; Bauer, E.; Noronha, A.; Greenhalgh, K.; Jäger, C.; Baginska, J.; Wilmes, P.; et al. Generation of genome-scale metabolic reconstructions for 773 members of the human gut microbiota. Nat. Biotechnol. 2017, 35, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Bauer, E.; Thiele, I. From metagenomic data to personalized in silico microbiotas: Predicting dietary supplements for Crohn’s disease. NPJ Syst. Biol. Appl. 2018, 4, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Diener, C.; Gibbons, S.M.; Resendis-Antonio, O. MICOM: Metagenome-Scale Modeling To Infer Metabolic Interactions in the Gut Microbiota. mSystems 2020, 5, 00606-19. [Google Scholar] [CrossRef] [Green Version]
- Thiele, I.; Sahoo, S.; Heinken, A.; Hertel, J.; Heirendt, L.; Aurich, M.K.; Fleming, R.M. Personalized whole-body models integrate me-tabolism, physiology, and the gut microbiome. Mol. Syst. Biol. 2020, 16, e8982. [Google Scholar] [CrossRef]
- Wu, F.; Fan, J.; He, Y.; Xiong, A.; Yu, J.; Li, Y.; Zhang, Y.; Zhao, W.; Zhou, F.; Li, W.; et al. Single-cell profiling of tumor heterogeneity and the microenvironment in advanced non-small cell lung cancer. Nat. Commun. 2021, 12, 1–11. [Google Scholar] [CrossRef]
- Lin, W.; Noel, P.; Borazanci, E.H.; Lee, J.; Amini, A.; Han, I.W.; Heo, J.S.; Jameson, G.S.; Fraser, C.; Steinbach, M.; et al. Single-cell transcriptome analysis of tumor and stromal compartments of pancreatic ductal adenocarcinoma primary tumors and metastatic lesions. Genome Med. 2020, 12, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, C.X.; Müller, S.; Keerthivasan, S.; Koeppen, H.; Hung, J.; Gierke, S.; Breart, B.; Foreman, O.; Bainbridge, T.W.; Castiglioni, A.; et al. Single-Cell RNA Sequencing Reveals Stromal Evolution into LRRC15+ Myofibroblasts as a Determinant of Patient Response to Cancer Immunotherapy. Cancer Discov. 2020, 10, 232–253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Damiani, C.; Di Filippo, M.; Pescini, D.; Maspero, D.; Colombo, R.; Mauri, G. popFBA: Tackling intratumour heterogeneity with Flux Balance Analysis. Bioinformatics 2017, 33, i311–i318. [Google Scholar] [CrossRef] [Green Version]
- Damiani, C.; Maspero, D.; Di Filippo, M.; Colombo, R.; Pescini, D.; Graudenzi, A.; Westerhoff, H.V.; Alberghina, L.; Vanoni, M.; Mauri, G. Integration of single-cell RNA-seq data into population models to characterize cancer metabolism. PLoS Comput. Biol. 2019, 15, e1006733. [Google Scholar] [CrossRef]
- Kang, Y.P.; Ward, N.; DeNicola, G.M. Recent advances in cancer metabolism: A technological perspective. Exp. Mol. Med. 2018, 50, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Durinikova, E.; Buzo, K.; Arena, S. Preclinical models as patients’ avatars for precision medicine in colorectal cancer: Past and future challenges. J. Exp. Clin. Cancer Res. 2021, 40, 1–17. [Google Scholar] [CrossRef]
- Karta, J.; Bossicard, Y.; Kotzamanis, K.; Dolznig, H.; Letellier, E. Mapping the metabolic networks of tumor cells and can-cer-associated fibroblasts. Cells 2021, 10, 304. [Google Scholar] [CrossRef] [PubMed]
- Capuani, F.; De Martino, D.; Marinari, E.; De Martino, A. Quantitative constraint-based computational model of tumor-to-stroma coupling via lactate shuttle. Sci. Rep. 2015, 5, 11880. [Google Scholar] [CrossRef] [Green Version]
- Shan, M.; Dai, D.; Vudem, A.; Varner, J.D.; Stroock, A. Multi-scale computational study of the Warburg effect, reverse Warburg effect and glutamine addiction in solid tumors. PLoS Comput. Biol. 2018, 14, e1006584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Goede, K.; Driessen, A.; Bossche, J.V.D. Metabolic Cancer-Macrophage Crosstalk in the Tumor Microenvironment. Biology 2020, 9, 380. [Google Scholar] [CrossRef] [PubMed]
- Rath, M.; Mã¼Ller, I.; Kropf, P.; Closs, E.I.; Munder, M. Metabolism via Arginase or Nitric Oxide Synthase: Two Competing Arginine Pathways in Macrophages. Front. Immunol. 2014, 5, 532. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Jolly, M.K.; George, J.; Pienta, K.J.; Levine, H. Computational Modeling of the Crosstalk Between Macrophage Polarization and Tumor Cell Plasticity in the Tumor Microenvironment. Front. Oncol. 2019, 9, 10. [Google Scholar] [CrossRef]
- Puniya, B.L.; Amin, R.; Lichter, B.; Moore, R.; Ciurej, A.; Bennett, S.J.; Shah, A.R.; Barberis, M.; Helikar, T. Integrative computational approach identifies drug targets in CD4+ T-cell-mediated immune disorders. NPJ Syst. Biol. Appl. 2021, 7, 4. [Google Scholar] [CrossRef]



| Human Generic Model | No. of Genes | No. of Reactions | No. of Metabolites | Cancer-Type Application | Application References |
|---|---|---|---|---|---|
| Human Metabolic Reaction (HMR) [71] | 3668 | 8100 | 6000 | Renal carcinoma | [81] |
| Human Metabolic Reaction (HMR2) [72] | 3765 | 8181 | 6007 | Hepatocellular carcinoma | [82] |
| Recon 1 [73] | 1496 | 3311 | 2766 | Generic cancer | [83,84,85] |
| 16 cancer types | [82] | ||||
| NCI-60 CCLs | [86] | ||||
| Recon 2 [74] | 1789 | 7440 | 2626 | 9 cancer types from TCGA | [87] |
| Recon 3D [75] | 3288 | 13,543 | 4140 | Prostate cancer | [80] |
| Edinburgh model [76] | 2322 | 2823 | 2671 | Colon and breast CCLs | [88] |
| Name (and Reference) | Language | Interface | Development | OS |
|---|---|---|---|---|
| COBRA Toolbox [141] | MATLAB COBRA.py, COBRA.jl (Python and Julia) | Script | Open source | AllM |
| RAVEN [145] | MATLAB | Script | Open source | AllM |
| CellNetAnalyzer [146] | MATLAB | Script/GUI | Closed source | AllM |
| FBA-SimVis [147] | MATLAB/Java | GUI | Closed source | Windows |
| OptFlux [148] | Java | Script | Open source | All |
| Sybil [149] | R | Script | Open source | All |
| CBMPy [150] | Python | Script | Open source | All |
| SurreyFBA [151] | C++ | Script/GUI | Open source | All |
| FASIMU [152] | C | Script | Open source | Linux |
| FAME [153] | Web-based | GUI | Open source | All |
| PathwayTools [154] | Web-based | GUI/script | Closed source | All |
| Kbase [155] | Web-based | Script | Open source | All |
| AutoKEEGRec [156] | MATLAB | Script | Open source | AllM |
| AuReMe [157] | Python | GUI | Open source | All |
| CarveMe [158] | Python | Script | ||
| MetaDraft [159] | Python | Script | Open source | All |
| ModelSEED [160] | Web-based | GUI | Open source | All |
| PathwayTools [161] | Common Lisp | GUI (API) | Open source | All |
| Merlin [162] | Java | GUI | Open source | All |
| CoReCO [163] | Python | Script | Open source | All |
| MEMOSys [164] | Java | GUI | Proprietary source | All |
| GEMSiRV [165] | Java | GUI | Open source | All |
| MetExplore [166] | Web-based | GUI | Open source | All |
| RbioNet [167] | Part of the COBRA ToolBox | Script | Open source | All |
| MetaFlux [168] | Web-based | GUI | Open source (distributed as part of Pathways tools) | All |
| Reference | Category | Concept | Tools Used | Databases | Type of Validation |
|---|---|---|---|---|---|
| [170] | CSGEMs to generate metabolic signatures for drug repositioning | PC GEM to explore PC metabolism and repurpose new drugs. Reconstruction performed combining personalized GEMs from individual patient’s transcriptome and PC-specific proteomics data from the HCA. | RAVEN, FastGeneSL [171], DIRAC, TCGAbiolinks, DESeq, gcrma | HPA, HMA, ConnectivityMap2 | In silico cell viability assay and in vitro cell assay. |
| [172] | CSGEMs to predict biomarkers and drug targets | GEM of transcriptional regulator-metabolite associations with mixed computational and wet lab experiments integrating intracellular metabolic profiles of NCI-60 (4) 54 CCLs with transcriptomic and proteomic data. Perform metabolic profiling of CCLs and resolve signaling across multiple regulatory layers. | fitlm (Matlab) sparseNCA | Gene Expression Omnibus NCI-60, HMD, TRRUST, KEGG | In vivo metabolite fold-changes between normal and cancer tissues. |
| [83] | CSGEMs to predict biomarkers and drug targets | CSGEM to study the role of metabolic alterations for novel therapy targets. Predicts 52 cytostatic drug targets (40% by known drugs). Analyze synthetic lethal drug targets to identify drug synergies. | NCI-60 | shRNA data, cytostatic scores for single and double drug target predictions, synergistic drug targets via yeast orthologs. | |
| [173] | GEMs to identify antimetabolites for drug design | Assess anticancer effects of drugs structurally similar to DrugBank [174]. Uses Tanimoto scores from OpenBabel [175] to assess structural similarity between DrugBank drugs and metabolites CSGEM predicted to be essential for maximal growth rate. Developed pyTARG to constrain the HMR, using 34 CCLs and 26 healthy tissue RNA-Seqs. Implemented FBA within PyTARG to quantify the original drug affecting reactions rates decrease. Model the impact of a relative inhibition on global cell metabolism. | OpenBabel [175], pyTARG, COBRApy | DrugBank [174], KEGG, BioProject, HPA, GEO, BioModels | Differential effects of a lipoamide analog on MCF7 and ASM cells. Proof of concept of identification of therapeutic windows. |
| [109] | GEMs to identify antimetabolites for drug design | Proteomics samples from 27 HCC patients and 83 healthy individuals from HPA to reconstruct cancer and healthy GEMs with the tINIT from the HMR 2.0 generic GEM. CSGEMs to identify antimetabolites used as anticancer drugs. Healthy GEMs to explore candidate antimetabolites toxicity on healthy samples. | RAVEN (gap-filling, tINIT, checkTasks) | HPA | Usage of antimetabolites for treatment of HCC demonstrated by the inhibitory effect of the l-carnitine analog, one of the predicted antimetabolites, on the proliferation of the HepG2 CCL. |
| [176] | GEMs to identify metabolic inhibitors to administrate with drug combinations in adaptive therapies | Found that taxane-treated breast cancer cells undergo a metastable transition in which they depend more on oxidative and non-oxidative glucose metabolism conferring them resistance to doxorubicin. Predict that these rewired cancer cells can be effectively targeted when a glucose metabolism inhibitor is co-administered with doxorubicin. | Prism (GraphPad) | In vivo experiments with mouse models, patient explant system. | |
| [177] | GEMs to explore cancer metabolism biology | Central C and N RMGEM to study the interplay between glucose and glutamine for biomass formation in ammonia microenvironment. Perform Warburg effect quantitative. Used the RMGEM to do FBA to study all possible glutamine fates. Found that glutamine can supply C sources for cell energy production and can be used as a C and N source to synthesize essential metabolites. | FAME | ||
| [178] | GEMs to explore cancer metabolism biology | HPaA to explore the prognosis of each protein in 17 major cancers. Uses CSGEMs to identify tumor growth involved genes. Based on transcriptomics of ~ 8000 patients with clinical metadata. Revealed that survival is associated with upregulation mitosis and cell growth genes while downregulated genes are mostly involved in cellular differentiation. | Kaplan–Meier plots, PCA | HPaA [178], BioModels, TCGA, GO, GDC | Immunohistochemistry. |
| [179] | CSGEMs to explore cancer metabolism biology | Merged 374 CSGEMs from the HPaA to reconstruct a generic CRC GEM. Identified the mayor differences between tumor and normal samples in terms of highly perturbed metabolites by applying modules reporter metabolite and reporter subnetworks algorithms. Mayor differences were related to the glutathione, arginine and proline metabolic reprogramming. | PIANO (R) (KEGG and GO enrichment analysis), CRC (Bioprofiler analysis), RAVEN, Kaplan-Meier survival analysis, log-rank p-value | HpaA, BioModels, TCGA, GO, GDC | ODC1, SMOX, SRM and SAT validated in vivo and in vitro, using 15 patients and 4 CRC CCLs. |
| [71] | GEMs to explore cancer metabolism biology | HMR 2.0 and proteomics data in HPA to construct consensus hepatocytes GEM (iHepatocytes2322) that improves previous GEMs including an extensive description of lipid metabolism. GEM used to analyze transcriptomics data from non-alcoholic fatty liver disease patients. | INIT, Reporter Subnetwork analysis checkTasks (RAVEN), RAVEN | HPA, Uniprot, GEO | Hepatocytes biological functions of hepatocyte-specific GEM demonstrated by simulating 256 metabolic functions of HepatoNet, using checkTasks/fitTasks (RAVEN). |
| [90] | GEMs to explore cancer metabolism biology | GPR called S-GPR considering transcripts stoichiometry. Investigate PC cells metabolic effects chronic exposure to an endocrine disruptor. | Mann-Whitney test, FASIMU, Gimme, Mat, pFBA MADE | HMD, Lipid Maps, HMA, GEO | Qualitative comparison between predicted metabolic consumption/productions and the metabolomic and lipidomic experimental measurements. |
| [180] | Warburg effect computer metabolic modeling | Study common and robust metabolic pathways supporting cancer cells (glycolysis, TCA cycle, pentose phosphate, glutaminolysis and oxidative phosphorylation). Propose metabolic targets for anticancer treatments by a constraint-based modeling on integrated data. | COBRA toolbox | GEO | Verified that the in silico kinetic growth curve exhibit a comparable behavior with the experimentally obtained from Hela CCLs. |
| [84] | Warburg effect computer metabolic modeling | GEM human metabolic network accounting stoichiometry and enzyme solvent capacity. Demonstrate that Warburg effect happens since the metabolic adaptation of cancer cells to increase biomass production rate. | BRENDA, SABIO-RK | Correlation between enzyme concentration predictions and expression of 1269 metabolic genes from 60 NCI CCLs. Validated against 1000 flux distributions of two models by ACHR sampling. | |
| [181] | Warburg effect computer metabolic modeling | Expand metabolic efficiency notion by ATP production FBM constrained by glucose uptake and solvent capacities in the cell’s cytoplasm. Found that at low glucose uptake rates mitochondrial respiration is the most efficient pathway for ATP generation while when increasing glucose uptake rates a gradual switch to aerobic glycolysis achieves ATP highest rate since it is more efficient for the required solvent capacity. | Agreement between the experimentally determined fluxes and the model predictions. | ||
| [182] | Warburg effect computer metabolic modeling | Constraint-based modeling with E-Flux integrating 13 different cancer cell transcriptomics with Recon1 generic model. Found that metabolic changes distributions are similar in different cancer types, supporting that Warburg effect is a general metabolic adaptation. | E-Flux, GeWorkbench 2.4.0, COBRA | GEO |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frades, I.; Foguet, C.; Cascante, M.; Araúzo-Bravo, M.J. Genome Scale Modeling to Study the Metabolic Competition between Cells in the Tumor Microenvironment. Cancers 2021, 13, 4609. https://doi.org/10.3390/cancers13184609
Frades I, Foguet C, Cascante M, Araúzo-Bravo MJ. Genome Scale Modeling to Study the Metabolic Competition between Cells in the Tumor Microenvironment. Cancers. 2021; 13(18):4609. https://doi.org/10.3390/cancers13184609
Chicago/Turabian StyleFrades, Itziar, Carles Foguet, Marta Cascante, and Marcos J. Araúzo-Bravo. 2021. "Genome Scale Modeling to Study the Metabolic Competition between Cells in the Tumor Microenvironment" Cancers 13, no. 18: 4609. https://doi.org/10.3390/cancers13184609
APA StyleFrades, I., Foguet, C., Cascante, M., & Araúzo-Bravo, M. J. (2021). Genome Scale Modeling to Study the Metabolic Competition between Cells in the Tumor Microenvironment. Cancers, 13(18), 4609. https://doi.org/10.3390/cancers13184609







