Conceptual Design of a Novel Nozzle Combined with a Clinical Proton Linac for Magnetically Focussed Minibeams
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
- (1)
- Minibeam generation: The first part considered the generation of proton minibeams. For this, first the minimum beam size achievable at a specified target position was determined for different beam parametrisations at the nozzle entrance. The aim of this was to identify the conditions for which minibeams (i.e., beams with a mm) can be obtained. Moreover, simulations evaluating the robustness were performed which considered the effect of errors in magnet alignment and magnetic fields.
- (2)
- Delivery of conventional PBS irradiations: The second part considered the delivery of conventional PBS with the new minibeam nozzle in combination with the LIGHT accelerator. For this, an example irradiation field in a water phantom was simulated.
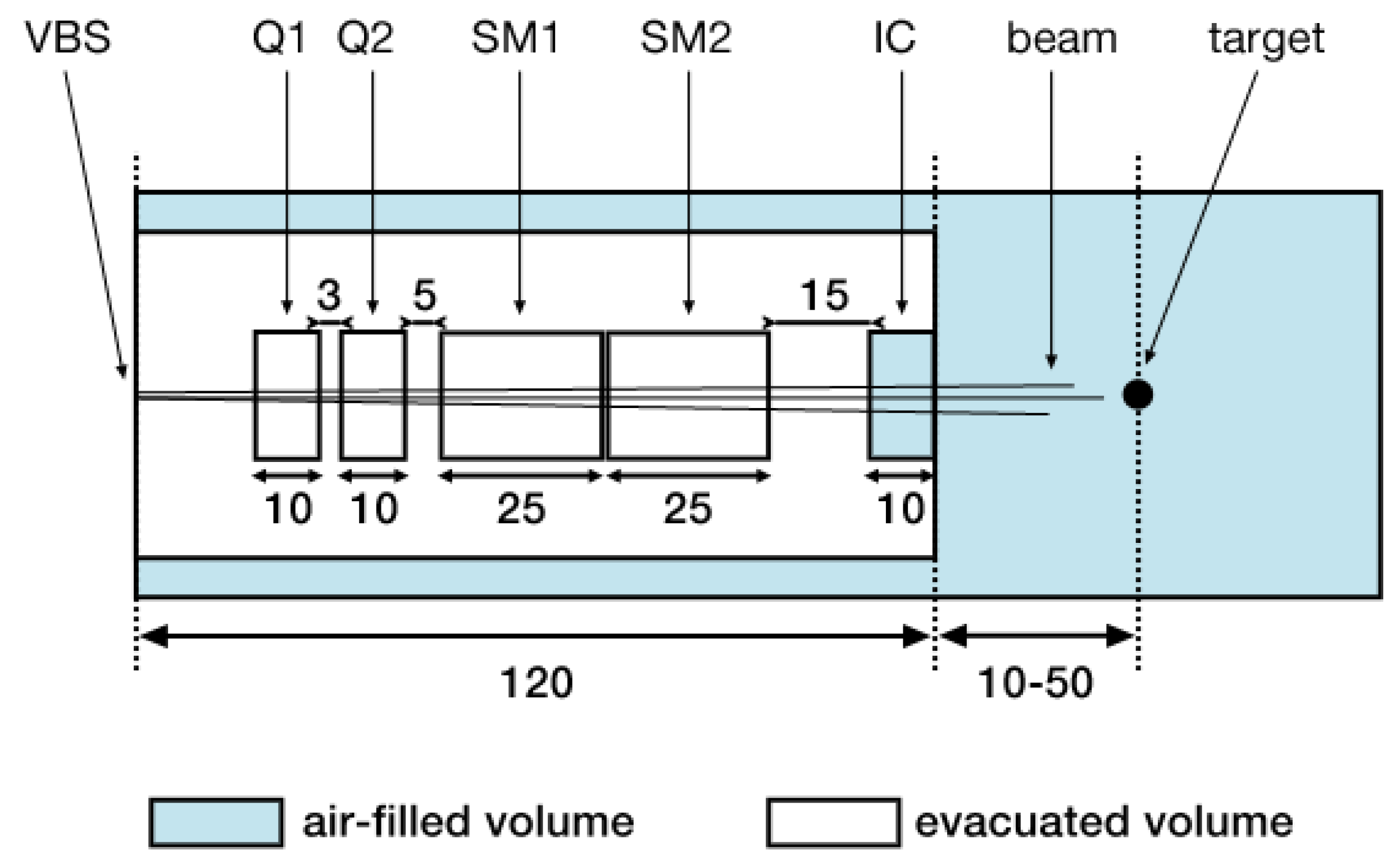
2.1. Nozzle Geometry and Beam Model
- The beam size parameters and which correspond to the widths of the Gaussians describing the horizontal and vertical spatial particle distributions, respectively.
- The beam divergence parameters and which correspond to the widths of the Gaussians describing the horizontal and vertical angular particle distributions, respectively.
- The correlation parameters and which correspond to the correlation coefficients in - and -phase space (or rather trace space), respectively.
- Var 1: The size parameters were increased by a factor of 2.
- Var 2: The divergence parameters were increased by a factor of 2.
- Var 3: The modulus of the correlation coefficients was decreased such that the factors and were increased by a factor of 2. Note that the correlation coefficients reach a minimum at 0 so that the factors cannot be arbitrarily increased.
- Var 4: A combined variation where each of the parameters , , was increased by a factor of , resulting also in an emittance increase by a factor of 2.
2.2. Minibeam Generation
- Translational and rotational misalignment: For the first part, the quadrupoles Q1 and Q2 were translated laterally by an offset from the beam axis. Both, and were randomly and independently sampled from a Gaussian distribution with mm and mm. Additionally, the quadrupoles were also misaligned by a horizontal tilt and vertical tilt where both angles were randomly and independently sampled from a Gaussian distribution with deg and deg.
- Field gradient errors: For the second part, the quadrupoles were considered to be perfectly aligned but the field gradients deviated from their nominal values by an amount (i.e., and where and are the gradients of Q1 and Q2, respctively), representing field variations caused by possible pulse-to-pulse fluctuations in the power supplies. Both, and were randomly and independently sampled from a Gaussian distribution with T/cm and T/cm.
2.3. Delivery of Conventional PBS Irradiations
3. Results
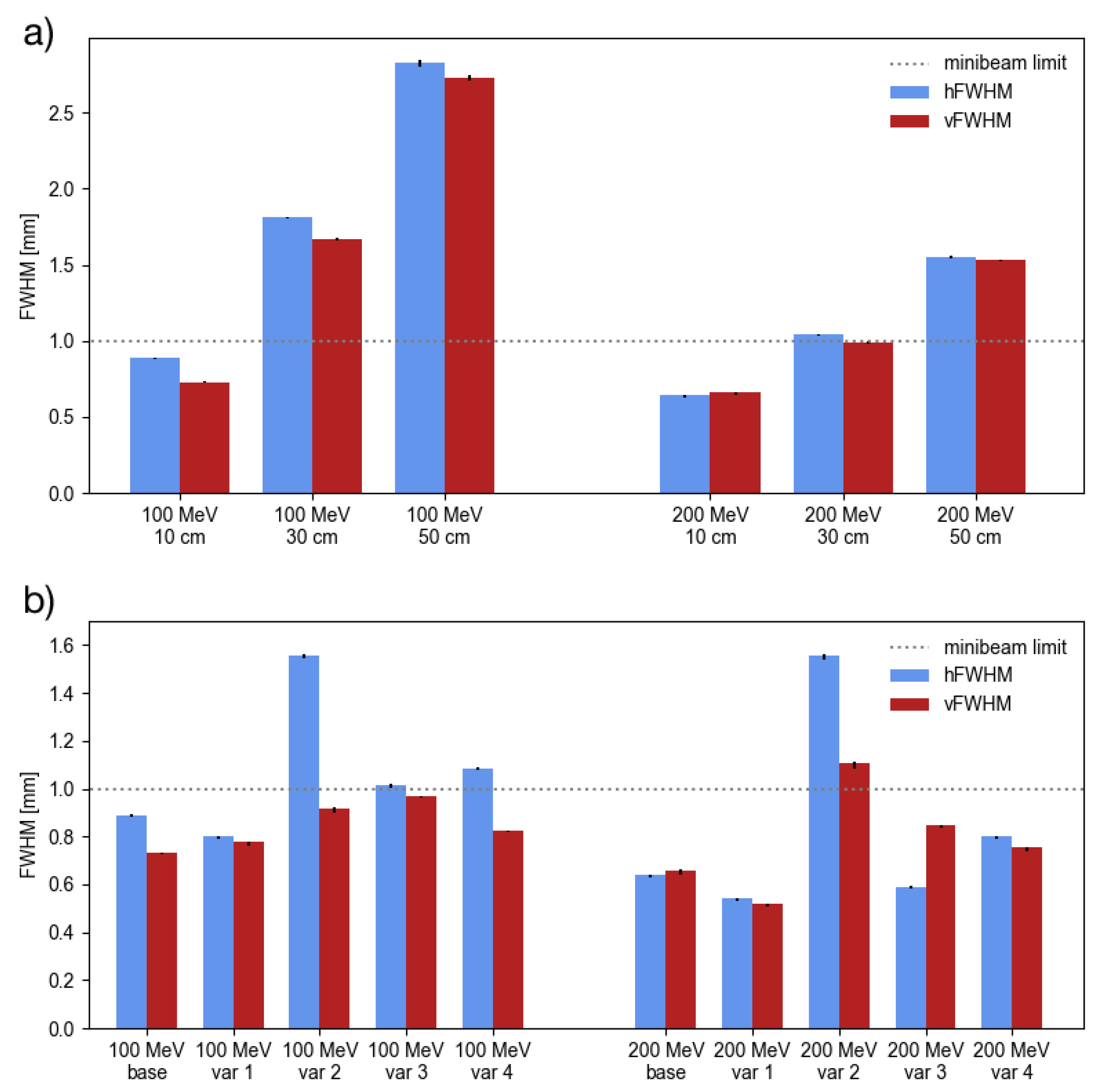
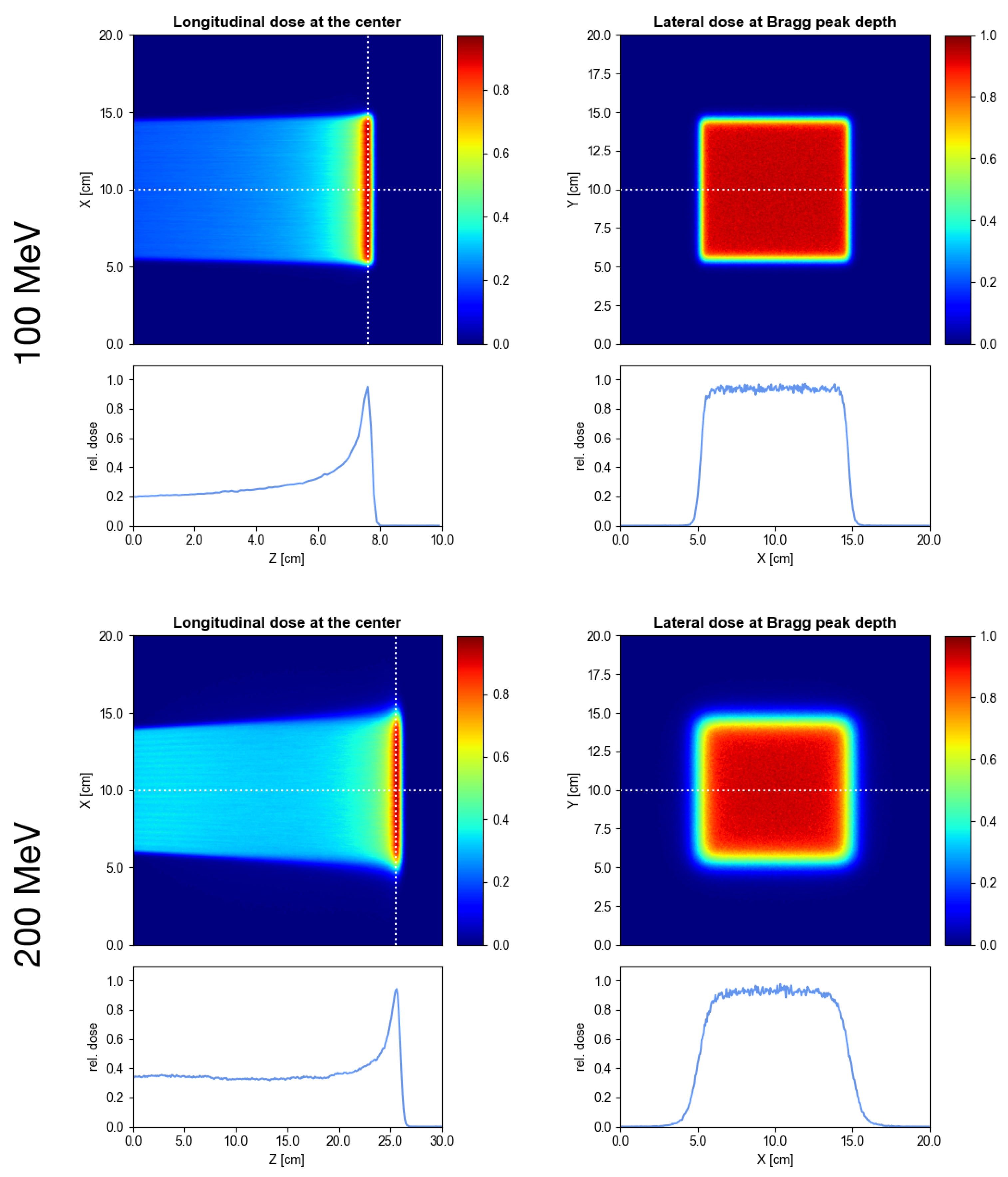
3.1. Minibeam Generation
3.2. Delivery of Conventional PBS
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCL | cell coupled linac |
| FWHM | full width at half maximum |
| hFWHM | horizontal full width at half maximum |
| LIGHT | Linac For Image Guided Hadron Therapy |
| linac | linear accelerator |
| PBS | pencil beam scanning |
| pMBRT | proton minibeam radiation therapy |
| RFQ | radio frequency quadrupole |
| SAD | source-to-axis distance |
| SCDTL | side coupled drift tube linac |
| vFWHM | vertical full width at half maximum |
References
- Prezado, Y.; Fois, G.R. Proton-minibeam radiation therapy: A proof of concept. Med. Phys. 2013, 40, 031712. [Google Scholar] [CrossRef] [PubMed]
- Prezado, Y.; Dos Santos, M.; Gonzalez, W.; Jouvion, G.; Guardiola, C.; Heinrich, S.; Labiod, D.; Juchaux, M.; Jourdain, L.; Sebrie, C.; et al. Transfer of Minibeam Radiation Therapy into a cost-effective equipment for radiobiological studies: A proof of concept. Sci. Rep. 2017, 7, 17295. [Google Scholar] [CrossRef] [PubMed]
- Prezado, Y.; Jouvion, G.; Guardiola, C.; Gonzalez, W.; Juchaux, M.; Bergs, J.; Nauraye, C.; Labiod, D.; De Marzi, L.; Pouzoulet, F.; et al. Tumor Control in RG2 Glioma-Bearing Rats: A Comparison Between Proton Minibeam Therapy and Standard Proton Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2019, 104, 266–271. [Google Scholar] [CrossRef]
- Peucelle, C.; Nauraye, C.; Patriarca, A.; Hierso, E.; Fournier-Bidoz, N.; Martínez-Rovira, I.; Prezado, Y. Proton minibeam radiation therapy: Experimental dosimetry evaluation. Med. Phys. 2015, 42, 7108–7113. [Google Scholar] [CrossRef] [PubMed]
- De Marzi, L.; Patriarca, A.; Nauraye, C.; Hierso, E.; Dendale, R.; Guardiola, C.; Prezado, Y. Implementation of planar proton minibeam radiation therapy using a pencil beam scanning system: A proof of concept study. Med. Phys. 2018, 45, 5305–5316. [Google Scholar] [CrossRef]
- Tobola-Galus, A.; Swakon, J.; Olko, P. Dosimetric characterization of collimators for spatially fractionated proton therapy of the eye. Radiat. Prot. Dosim. 2018, 180, 351–354. [Google Scholar] [CrossRef] [PubMed]
- Charyyev, S.; Artz, M.; Szalkowski, G.; Chang, C.W.; Stanforth, A.; Lin, L.; Zhang, R.; Wang, C.K.C. Optimization of hexagonal-pattern minibeams for spatially fractionated radiotherapy using proton beam scanning. Med. Phys. 2020, 47, 3485–3495. [Google Scholar] [CrossRef] [PubMed]
- Datzmann, G.; Sammer, M.; Girst, S.; Mayerhofer, M.; Dollinger, G.; Reindl, J. Preclinical Challenges in Proton Minibeam Radiotherapy: Physics and Biomedical Aspects. Front. Phys. 2020, 8, 471. [Google Scholar] [CrossRef]
- Schneider, T.; De Marzi, L.; Patriarca, A.; Prezado, Y. Monte Carlo Comparison of Proton and Helium-ion Minibeam Generation Techniques. Front. Phys. 2021, 9, 35. [Google Scholar] [CrossRef]
- Pedroni, E.; Meer, D.; Bula, C.; Safai, S.; Zenklusen, S. Pencil beam characteristics of the next-generation proton scanning gantry of PSI: Design issues and initial commissioning results. Eur. Phys. J. Plus 2011, 126, 66. [Google Scholar] [CrossRef]
- Saini, J.; Cao, N.; Bowen, S.R.; Herrera, M.; Nicewonger, D.; Wong, T.; Bloch, C.D. Clinical Commissioning of a Pencil Beam Scanning Treatment Planning System for Proton Therapy. Int. J. Part. Ther. 2016, 3, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Kang, M.; Souris, K.; Ainsley, C.; Solberg, T.D.; McDonough, J.E.; Simone, C.B., 2nd; Lin, L. Validation and clinical implementation of an accurate Monte Carlo code for pencil beam scanning proton therapy. J. Appl. Clin. Med. Phys. 2018, 19, 558–572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, T.; De Marzi, L.; Patriarca, A.; Prezado, Y. Advancing proton minibeam radiation therapy: Magnetically focussed proton minibeams at a clinical centre. Sci. Rep. 2020, 10, 1384. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T. Advancing the Generation of Proton Minibeams for Radiation Therapy. 2020UPASP069. Ph.D. Thesis, Université Paris-Saclay, Orsay, France, 2020. [Google Scholar]
- Degiovanni, A.; Adam, J.; Aguilera Murciano, D.; Ballestrero, S.; Benot-Morell, A.; Bonomi, R.; Cabaleiro Magallanes, F.; Caldara, M.; Cerv, M.; D’Auria, G.; et al. Status of the Commissioning of the LIGHT Prototype. In Proceedings of the 9th International Particle Accelerator Conference (IPAC2018), Vancouver, BC, Canada, April 29–May 4 2018; JACoW Publishing: Geneva, Switzerland, 2018; p. MOPML014. [Google Scholar] [CrossRef]
- Ungaro, D.; Degiovanni, A.; Stabile, P. LIGHT: A Linear Accelerator for Proton Therapy. In Proceedings of the NAPAC2016, Chicago, IL, USA, 9–14 October 2016; p. FRB1IO02. [Google Scholar] [CrossRef]
- Perl, J.; Shin, J.; Schumann, J.; Faddegon, B.; Paganetti, H. TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Med. Phys. 2012, 39, 6818–6837. [Google Scholar] [CrossRef]
- Faddegon, B.; Ramos-Méndez, J.; Schuemann, J.; McNamara, A.; Shin, J.; Perl, J.; Paganetti, H. The TOPAS tool for particle simulation, a Monte Carlo simulation tool for physics, biology and clinical research. Phys. Med. 2020, 72, 114–121. [Google Scholar] [CrossRef]
- Chung, K.; Kim, J.; Kim, D.H.; Ahn, S.; Han, Y. The proton therapy nozzles at Samsung Medical Center: A Monte Carlo simulation study using TOPAS. J. Korean Phys. Soc. 2015, 67, 170–174. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.; Kang, M.; Solberg, T.D.; Ainsley, C.G.; McDonough, J.E. Experimentally validated pencil beam scanning source model in TOPAS. Phys. Med. Biol. 2014, 59, 6859–6873. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z.; Slopsema, R.; Hong, L.; Pei, X.; Xu, X.G. TOPAS Monte Carlo simulation for double scattering proton therapy and dosimetric evaluation. Phys. Med. 2019, 62, 53–62. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Li, Z.; Liang, X.; Park, J.; Song, Y.; Feng, H. Commissioning and validation of TOPAS beam model for IBA Proteus-ONE at UFHPTI. Radiat. Phys. Chem. 2021, 180, 109256. [Google Scholar] [CrossRef]
- Perl, J. Formal quality control for a proton Monte Carlo system in radiation therapy. J. Phys. Conf. Ser. 2014, 489, 012021. [Google Scholar] [CrossRef] [Green Version]
- Testa, M.; Schümann, J.; Lu, H.M.; Shin, J.; Faddegon, B.; Perl, J.; Paganetti, H. Experimental validation of the TOPAS Monte Carlo system for passive scattering proton therapy. Med. Phys. 2013, 40, 121719. [Google Scholar] [CrossRef] [Green Version]
- Arce, P.; Bolst, D.; Bordage, M.C.; Brown, J.M.C.; Cirrone, P.; Cortés-Giraldo, M.A.; Cutajar, D.; Cuttone, G.; Desorgher, L.; Dondero, P.; et al. Report on G4-Med, a Geant4 benchmarking system for medical physics applications developed by the Geant4 Medical Simulation Benchmarking Group. Med. Phys. 2020, 48, 19–56. [Google Scholar] [CrossRef] [PubMed]
- Zacharatou Jarlskog, C.; Paganetti, H. Physics Settings for Using the Geant4 Physics Settings for Using the Geant4 Toolkit in Proton Therapy. IEEE Trans. Nucl. Sci. 2008, 55, 1018–1025. [Google Scholar] [CrossRef]
- Chetty, I.J.; Rosu, M.; Kessler, M.L.; Fraass, B.A.; Ten Haken, R.K.; Kong, F.M.S.; McShan, D.L. Reporting and analyzing statistical uncertainties in Monte Carlo-based treatment planning. Int. J. Radiat. Oncol. Biol. Phys. 2006, 65, 1249–1259. [Google Scholar] [CrossRef] [PubMed]
- Humphries, S. Chapter 3—Introduction to beam emittance. In Charged Particle Beams; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- De Marzi, L.; Da Fonseca, A.; Moignier, C.; Patriarca, A.; Goudjil, F.; Mazal, A.; Buvat, I.; Hérault, J. Experimental characterisation of a proton kernel model for pencil beam scanning techniques. Phys. Med. 2019, 64, 195–203. [Google Scholar] [CrossRef]
- Kang, M.; Pang, D. Commissioning and beam characterization of the first gantry-mounted accelerator pencil beam scanning proton system. Med. Phys. 2020, 47, 3496–3510. [Google Scholar] [CrossRef]
- Pidikiti, R.; Patel, B.C.; Maynard, M.R.; Dugas, J.P.; Syh, J.; Sahoo, N.; Wu, H.T.; Rosen, L.R. Commissioning of the world’s first compact pencil-beam scanning proton therapy system. J. Appl. Clin. Med. Phys. 2018, 19, 94–105. [Google Scholar] [CrossRef]
- Vilches-Freixas, G.; Unipan, M.; Rinaldi, I.; Martens, J.; Roijen, E.; Almeida, I.P.; Decabooter, E.; Bosmans, G. Beam commissioning of the first compact proton therapy system with spot scanning and dynamic field collimation. Br. J. Radiol. 2020, 93, 20190598. [Google Scholar] [CrossRef]
- Charlwood, F.C.; Aitkenhead, A.H.; Mackay, R.I. A Monte Carlo study on the collimation of pencil beam scanning proton therapy beams. Med. Phys. 2016, 43, 1462–1472. [Google Scholar] [CrossRef]
- Maes, D.; Regmi, R.; Taddei, P.; Bloch, C.; Bowen, S.; Nevitt, A.; Leuro, E.; Wong, T.; Rosenfeld, A.; Saini, J. Parametric characterization of penumbra reduction for aperture-collimated pencil beam scanning (PBS) proton therapy. Biomed. Phys. Eng. Express 2019, 5, 035002. [Google Scholar] [CrossRef] [Green Version]
- Winterhalter, C.; Lomax, A.; Oxley, D.; Weber, D.C.; Safai, S. A study of lateral fall-off (penumbra) optimisation for pencil beam scanning (PBS) proton therapy. Phys. Med. Biol. 2018, 63, 025022. [Google Scholar] [CrossRef]
- Girst, S.; Greubel, C.; Reindl, J.; Siebenwirth, C.; Zlobinskaya, O.; Walsh, D.W.M.; Ilicic, K.; Aichler, M.; Walch, A.; Wilkens, J.J.; et al. Proton Minibeam Radiation Therapy Reduces Side Effects in an In Vivo Mouse Ear Model. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 234–241. [Google Scholar] [CrossRef] [Green Version]
- Sammer, M.; Zahnbrecher, E.; Dobiasch, S.; Girst, S.; Greubel, C.; Ilicic, K.; Reindl, J.; Schwarz, B.; Siebenwirth, C.; Walsh, D.W.M.; et al. Proton pencil minibeam irradiation of an in-vivo mouse ear model spares healthy tissue dependent on beam size. PLoS ONE 2019, 14, e0224873. [Google Scholar] [CrossRef] [Green Version]
- Zlobinskaya, O.; Girst, S.; Greubel, C.; Hable, V.; Siebenwirth, C.; Walsh, D.W.M.; Multhoff, G.; Wilkens, J.J.; Schmid, T.E.; Dollinger, G. Reduced side effects by proton microchannel radiotherapy: Study in a human skin model. Radiat. Environ. Biophys. 2013, 52, 123–133. [Google Scholar] [CrossRef]
- Mayerhofer, M.; Datzmann, G.; Degiovanni, A.; Dimov, V.; Dollinger, G. Magnetically focused 70 MeV proton minibeams for preclinical experiments combining a tandem accelerator and a 3 GHz linear post-accelerator. Med. Phys. 2021, 48, 2733–2749. [Google Scholar] [CrossRef]
- Grevillot, L.; Osorio Moreno, J.; Letellier, V.; Dreindl, R.; Elia, A.; Fuchs, H.; Carlino, A.; Kragl, G.; Palmans, H.; Vatnitsky, S.; et al. Clinical implementation and commissioning of the MedAustron Particle Therapy Accelerator for non-isocentric scanned proton beam treatments. Med. Phys. 2020, 47, 380–392. [Google Scholar] [CrossRef]
- Schippers, J.M.; Lomax, A.; Garonna, A.; Parodi, K. Can Technological Improvements Reduce the Cost of Proton Radiation Therapy? Semin. Radiat. Oncol. 2018, 28, 150–159. [Google Scholar] [CrossRef] [PubMed]
- Younkin, J.E.; Shen, J.; Bues, M.; Robertson, D.G.; Mundy, D.W.; Clouser, E.; Liu, W.; Ding, X.; Stoker, J.B. Technical Note: An efficient daily QA procedure for proton pencil beam scanning. Med. Phys. 2018, 45, 1040–1049. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Clasie, B.; Lu, H.M.; Flanz, J.; Shen, T.; Jee, K.W. Impacts of gantry angle dependent scanning beam properties on proton PBS treatment. Phys. Med. Biol. 2017, 62, 344–357. [Google Scholar] [CrossRef] [PubMed]
- McAuley, G.A.; Teran, A.V.; McGee, P.Q.; Nguyen, T.T.; Slater, J.M.; Slater, J.D.; Wroe, A.J. Experimental validation of magnetically focused proton beams for radiosurgery. Phys. Med. Biol. 2019, 64, 115024. [Google Scholar] [CrossRef]
| E | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [MeV] | [%] | [mm] | [mm] | [mrad] | [mrad] | [mm mrad] | [mm mrad] | |||
| Base model | 100.5 | 0.22 | 0.30 | 0.45 | 0.54 | 0.53 | −0.91 | 0.98 | 0.21 | 0.15 |
| 199.7 | 0.15 | 0.24 | 0.47 | 0.20 | 0.45 | 0.19 | 0.97 | 0.15 | 0.16 | |
| Var 1 | 100.5 | 0.22 | 0.60 | 0.90 | 0.54 | 0.53 | −0.91 | 0.98 | 0.42 | 0.30 |
| (increased beam size) | 199.7 | 0.15 | 0.48 | 0.94 | 0.20 | 0.45 | 0.19 | 0.97 | 0.30 | 0.32 |
| Var 2 | 100.5 | 0.22 | 0.30 | 0.45 | 1.08 | 1.06 | −0.91 | 0.98 | 0.42 | 0.30 |
| (increased divergence) | 199.7 | 0.15 | 0.24 | 0.47 | 0.40 | 0.90 | 0.19 | 0.97 | 0.30 | 0.32 |
| Var 3 | 100.5 | 0.22 | 0.30 | 0.45 | 0.54 | 0.53 | −0.56 | 0.92 | 0.42 | 0.29 |
| (decreased correlation) | 199.7 | 0.15 | 0.24 | 0.47 | 0.20 | 0.45 | 0.00 | 0.87 | 0.15 | 0.33 |
| Var 4 | 100.5 | 0.22 | 0.38 | 0.57 | 0.68 | 0.67 | −0.85 | 0.97 | 0.43 | 0.29 |
| (combined variation) | 199.7 | 0.15 | 0.30 | 0.59 | 0.25 | 0.57 | 0.00 | 0.95 | 0.24 | 0.33 |
| Beam size minimisation with unvaried base model | |||||
|---|---|---|---|---|---|
| E [MeV] | Air gap [cm] | hFWHM [mm] | vFWHM [mm] | [T/cm] | [T/cm] |
| 100 | 10 | 0.608 | 0.496 | ||
| 30 | 0.544 | 0.400 | |||
| 50 | 0.432 | 0.256 | |||
| 200 | 10 | 0.800 | 0.752 | ||
| 30 | 0.800 | 0.736 | |||
| 50 | 0.800 | 0.736 | |||
| Beam size minimisation with model variations (air gap 10 cm) | |||||
| E [MeV] | Beam model | hFWHM [mm] | vFWHM [mm] | [T/cm] | [T/cm] |
| 100 | var 1 | 0.544 | 0.496 | ||
| var 2 | 0.800 | 0.720 | |||
| var 3 | 0.672 | 0.640 | |||
| var 4 | 0.608 | 0.496 | |||
| 200 | var 1 | 0.784 | 0.800 | ||
| var 2 | 0.800 | 0.576 | |||
| var 3 | 0.800 | 0.752 | |||
| var 4 | 0.800 | 0.720 | |||
| E [MeV] | Spot | X [mm] | Y [mm] | hFWHM [mm] | vFWHM [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Translational and rotational alignment errors | |||||||||
| 100 | center | (0.4%) | (0.4%) | ||||||
| scan y | (6.9%) | (0.3%) | (1.7%) | ||||||
| scan x | (3.5%) | (0.4%) | (0.4%) | ||||||
| scan xy | (3.5%) | (6.9%) | (0.4%) | (0.5%) | |||||
| 200 | center | (0.3%) | (0.3%) | ||||||
| scan y | (4.6%) | (0.4%) | (0.4%) | ||||||
| scan x | (2.3%) | (0.4%) | (0.4%) | ||||||
| scan xy | (2.3%) | (4.6%) | (0.4%) | (0.5%) | |||||
| Field gradient errors | |||||||||
| 100 | center | (1.0%) | (2.8%) | ||||||
| scan y | (1.0%) | (2.8%) | |||||||
| scan x | (1.0%) | (2.8%) | |||||||
| scan xy | (1.0%) | (2.8%) | |||||||
| 200 | center | (4.7%) | (10.2%) | ||||||
| scan y | (4.7%) | (9.7%) | |||||||
| scan x | (4.4%) | (10.1%) | |||||||
| scan xy | (4.4%) | (9.6%) | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schneider, T.; Patriarca, A.; Degiovanni, A.; Gallas, M.; Prezado, Y. Conceptual Design of a Novel Nozzle Combined with a Clinical Proton Linac for Magnetically Focussed Minibeams. Cancers 2021, 13, 4657. https://doi.org/10.3390/cancers13184657
Schneider T, Patriarca A, Degiovanni A, Gallas M, Prezado Y. Conceptual Design of a Novel Nozzle Combined with a Clinical Proton Linac for Magnetically Focussed Minibeams. Cancers. 2021; 13(18):4657. https://doi.org/10.3390/cancers13184657
Chicago/Turabian StyleSchneider, Tim, Annalisa Patriarca, Alberto Degiovanni, Manuel Gallas, and Yolanda Prezado. 2021. "Conceptual Design of a Novel Nozzle Combined with a Clinical Proton Linac for Magnetically Focussed Minibeams" Cancers 13, no. 18: 4657. https://doi.org/10.3390/cancers13184657
APA StyleSchneider, T., Patriarca, A., Degiovanni, A., Gallas, M., & Prezado, Y. (2021). Conceptual Design of a Novel Nozzle Combined with a Clinical Proton Linac for Magnetically Focussed Minibeams. Cancers, 13(18), 4657. https://doi.org/10.3390/cancers13184657







