Performance Evaluation for Repair of HSGc-C5 Carcinoma Cell Using Geant4-DNA
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
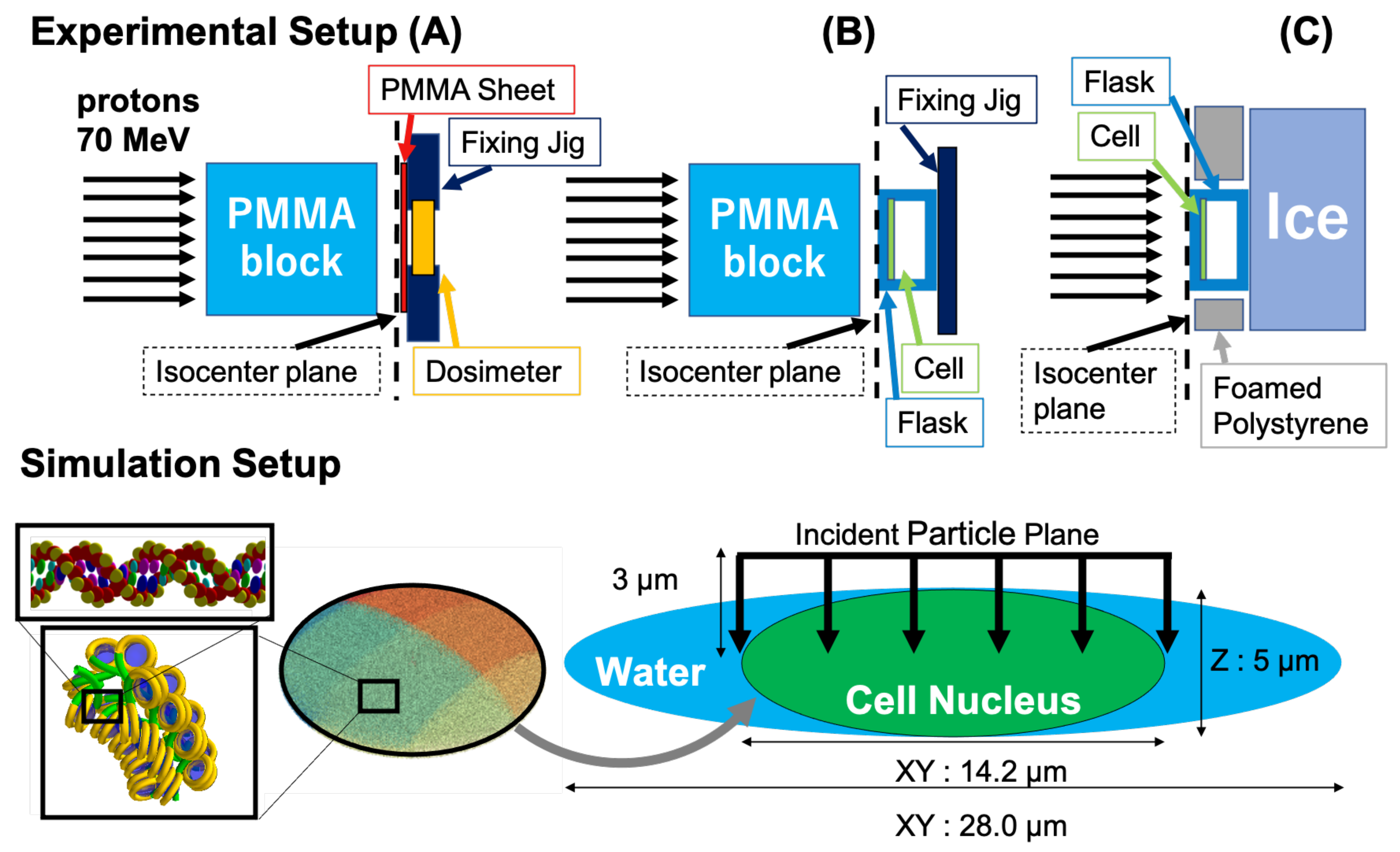
2.1. Experimental Condition
2.1.1. Irradiation Condition
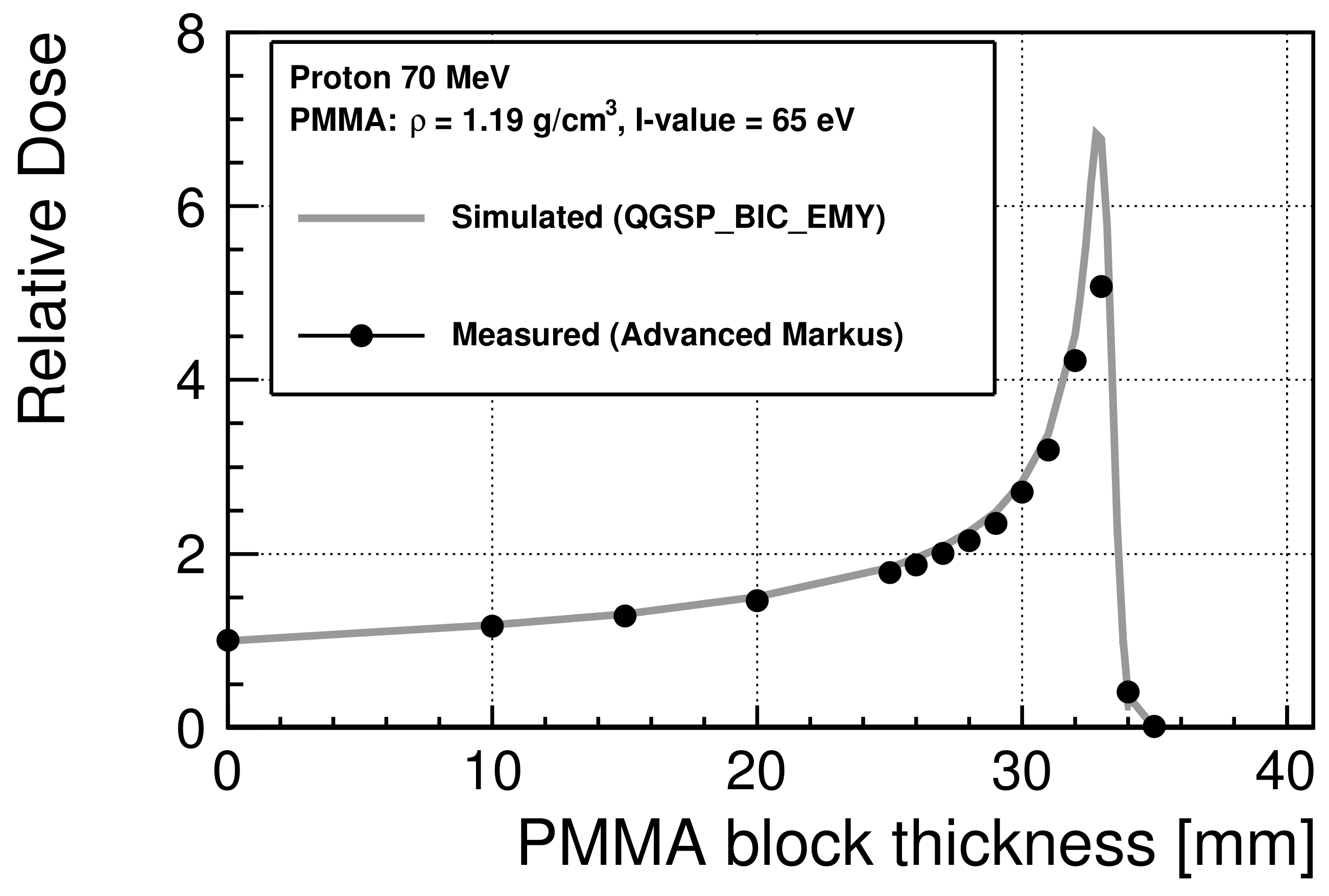
Dosimetry
Colony Assay
Gel Electrophoresis Assay
2.1.2. Cell Culture and Biological Processing before Irradiation
2.1.3. Cell Survival Measurement
2.1.4. DNA Rejoining Kinetics Measurement
2.2. Simulation Conditions and Model Calculation
2.2.1. Calculation of the Incident Proton Energy Spectra at the Cell Entrance
2.2.2. Initial DNA Damage
Simulation Using Geant4-DNA
DNA Damage Classification
2.2.3. Evaluation of Repair Performance
TLK Model
Random-Breakage Model
Parameter Optimization
3. Results
3.1. Incident Energy Spectra at the Cell Entrance
3.2. Initial DNA Damage
3.3. Optimized Repair Performance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| bp | base pair |
| DSB | double-strand break |
| MC | Monte Carlo |
| TLK | two-lesion kinetics |
| RBE | relative biological effectiveness |
| PMMA | poly methyl methacrylate |
| SF | surviving fraction |
| FAR | fraction of activity released |
| LET | linear energy transfer |
| NHEJ | non-homologous end-joining |
| HR | homologous recombination |
Appendix A. Limitation of the Application

| (h) | (h) | (h) | |||
|---|---|---|---|---|---|
| 33,062.9 | 0. | 0.19 |
References
- Baskar, R.; Lee, K.A.; Yeo, R.; Yeoh, K.-W. Cancer and Radiation Therapy: Current Advances and Future Directions. Int. J. Med. Sci. 2012, 9, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Rich, T.; Allen, R.L.; Wyllie, A.H. Defying death after DNA damage. Nature 2000, 408, 777–783. [Google Scholar] [CrossRef] [PubMed]
- Aaij, C.; Borst, P. The gel electrophoresis of DNA. Biochim. Biophys. Acta (BBA) Nucleic Acids Protein Synth. 1972, 269, 192–200. [Google Scholar] [CrossRef]
- Iliakis, G.E.; Cicilioni, O.; Metzger, L. Measurement of DNA double strand breaks in CHO cells at various stages of the cell cycle using pulse field gel electrophoresis: Calibrations by means of 125I decay. Int. J. Radiat. Biol. 1972, 59, 343–357. [Google Scholar] [CrossRef] [PubMed]
- Munne, S. Chromosome abnormalities and their relationship to morphology and development of human embryos. Reprod. Biomed. Online. 2006, 12, 234–253. [Google Scholar] [CrossRef]
- Paul, T.T.; Rogakou, E.P.; Yamazaki, V.; Kirchgessner, C.U.; Gellert, M.; Bonner, W.M. A critical role for histone H2AX in recruitment of repair factors to nuclear foci after DNA damage. Curr. Biol. 2000, 10, 886–895. [Google Scholar] [CrossRef]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA double-stranded breaks induce histone H2AX phosphorylation on serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef]
- Rogakou, E.P.; Boon, C.; Redon, C.; Bonner, W.M. Megabase chromatin domains involved in DNA double-strand breaks in vivo. J. Cell Biol. 1999, 146, 905–916. [Google Scholar] [CrossRef]
- Nikjoo, H.; Uehara, S.; Wilson, W.E.; Hoshi, M.; Goodhead, D.T. Track structure in radiation biology: Theory and applications. Int. J. Radiat. Biol. 1998, 73, 355–364. [Google Scholar] [CrossRef]
- Nikjoo, H.; Taleei, R.; Liamsuwan, T.; Liljequist, D.; Emfietzoglou, D. Perspectives in radiation biophysics: From radiation track structure simulation to mechanistic models of DNA damage and repair. Rad. Phys. Chem. 2016, 128, 3–10. [Google Scholar] [CrossRef]
- Nikjoo, H.; Emfietzoglou, D.; Liamsuwan, T.; Taleei, R.; Liljequist, D.; Uehara, S. Radiation track, DNA damage and response—A review. Rep. Prog. Phys. 2016, 79, 116601. [Google Scholar] [CrossRef]
- Uehara, S.; Nikjoo, H.; Goodhead, D.T. Cross-section of water vapour for the Monte Carlo electrons track structure code from 10 eV to the MeV region. Phys. Med. Biol. 1993, 38, 1841–1858. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Goodhead, D.T.; Terrissol, M. Computational modeling of low-energy electron-induced DNA damage by early physical and chemical events. Int. J. Radiat. Biol. 1997, 71, 467–483. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Wilson, W.E.; Goodhead, D.T. Computational approach for determining the spectrum of DNA damage induced by ionizing radiation. Radiat. Res. 2001, 156, 577–583. [Google Scholar] [CrossRef]
- Nikjoo, H.; Uehara, S.; Emfietzoglou, D.; Cucinotta, F.A. Track-structure codes in radiation research. Radiat. Meas. 2006, 41, 1052–1074. [Google Scholar] [CrossRef]
- Friedland, W.; Jacob, P.; Paretzke, H.G.; Stork, T. Monte Carlo simulation of the production of short DNA fragments by low-linear energy transfer radiation using higher-order DNA models. Radiat. Res. 1998, 150, 170–182. [Google Scholar] [CrossRef]
- Friedland, W.; Jacob, P.; Bernhardt, P.; Paretzke, H.G.; Dingfelder, M. Simulation of DNA Damage after Proton Irradiation. Radiat. Res. 2003, 159, 401–410. [Google Scholar] [CrossRef]
- Friedl, W.; Dingfelder, M.; Kundrát, P.; Jacob, P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat. Res. 2011, 711, 28–40. [Google Scholar] [CrossRef]
- Friedland, W.; Schmitt, E.; Kundrát, P.; Dingfelder, M.; Baiocco, G.; Barbieri, S.; Ottolenghi, A. Comprehensive track-structure based evaluation of DNA damage by light ions from radiotherapy-relevant energies down to stopping. Sci. Rep. 2017, 7, 45161. [Google Scholar] [CrossRef]
- Plante, I.; Francis, A. Applications of Monte Carlo Methods in Biology, Medicine and Other Fields of Science; Monte-Carlo Simulation of Ionizing Radiation Tracks; IntechOpen Limited: London, UK, 2011; pp. 315–356. [Google Scholar]
- Plante, I.; Devroye, L. Considerations for the Independent Reaction Times and Step-by-Step Methods for Radiation Chemistry Simulations. Radiat. Phys. Chem. 2016, 139, 157–172. [Google Scholar] [CrossRef]
- Meylan, S.; Incerti, S.; Karamitros, M.; Tang, N.; Bueno, M.; Clairand, I.; Villagrasa, C. Simulation of early DNA damage after the irradiation of a fibroblast cell nucleus using Geant4-DNA. Sci. Rep. 2017, 7, 11923. [Google Scholar] [CrossRef] [PubMed]
- Sakata, D.; Lampe, N.; Karamitros, M.; Kyriakou, I.; Belov, O.; Bernal, M.A.; Bolst, D.; Bordage, M.-C.; Breton, V.; Brown, J.M.C.; et al. Evaluation of early radiation DNA damage in a fractal cell nucleus model using Geant4-DNA. Phys. Med. 2019, 62, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Sakata, D.; Belov, O.; Bordage, M.-C.; Emfietzoglou, D.; Guatelli, S.; Inaniwa, T.; Ivanchenko, V.; Karamitros, M.; Kyriakou, I.; Lampe, N.; et al. Fully integrated Monte Carlo simulation for evaluating radiation induced DNA damage and subsequent repair using Geant4-DNA. Sci. Rep. 2020, 10, 20788. [Google Scholar] [CrossRef] [PubMed]
- Schuemann, J.; McNamara, A.L.; Ramos-Méndez, J.; Perl, J.; Held, K.D.; Paganetti, H.; Incerti, S.; Faddegon, F. TOPAS-nBio: An Extension to the TOPAS Simulation Toolkit for Cellular and Sub-cellular Radiobiology. Radiat. Res. 2018, 191, 125–138. [Google Scholar] [CrossRef]
- McNamara, A.L.; Ramos-Méndez, J.; Perl, J.; Held, K.; Dominguez, N.; Moreno, E.; Henthorn, N.T.; Kirkby, K.J.; Meylan, S.; Villagrasa, C.; et al. Geometrical Structures for Radiation Biology Research as Implemented in the TOPAS-nBio Toolkit. Phys. Med. Biol. 2018, 63, 175018. [Google Scholar] [CrossRef]
- Chatzipapas, K.P.; Papadimitroulas, P.; Obeidat, M.; McConnell, K.A.; Kirby, N.; Loudos, G.; Papanikolaou, N.; Kagadis, G.C. Quantification of DNA double-strand breaks using Geant4-DNA. Med. Phys. 2019, 48, 405–413. [Google Scholar] [CrossRef]
- Chatzipapas, K.P.; Papadimitroulas, P.; Emfietzoglou, D.; Kalospyros, S.K.; Hada, M.; Georgakilas, A.G.; Kagadis, G.C. Ionizing Radiation and Complex DNA Damage: Quantifying the Radiobiological Damage Using Monte Carlo Simulations. Cancers 2020, 12, 799. [Google Scholar] [CrossRef]
- Chatzipapas, K.P.; Papadimitroulas, P.; Loudos, G.; Papanikolaou, N.; Kagadis, G.C. IDDRRA: A novel platform, based on Geant4-DNA to quantify DNA damage by ionizing radiation. Med. Phys. 2019, 48, 2624–2636. [Google Scholar] [CrossRef]
- Sakata, D. Prediction of DNA rejoining kinetics and cell survival after proton irradiation for V79 cells using Geant4-DNA. Phys. Med. 2021. submitted. [Google Scholar]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guatelli, S.; Guèye, P.; Mantero, A.; Mascialino, B.; et al. The Geant4-DNA project. Int. J. Model. Simul. Sci. Comput. 2009, 1, 157–178. [Google Scholar] [CrossRef]
- Incerti, S.; Ivanchenko, A.; Karamitros, M.; Mantero, A.; Moretto, P.; Tran, H.N.; Mascialino, B.; Champion, C.; Ivanchenko, V.N.; Bernal, M.A.; et al. Comparison of Geant4 very low energy cross section models with experimental data in water. Med. Phys. 2010, 37, 4692–4708. [Google Scholar] [CrossRef]
- Bernal, M.A.; Bordage, M.-C.; Brown, J.M.C.; Davídková, M.; Delage, E.; El Bitar, Z.; Enger, S.A.; Francis, Z.; Guatelli, S.; Ivanchenko, V.N.; et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys. Med. 2015, 31, 157–178. [Google Scholar] [CrossRef]
- Incerti, S.; Kyriakou, I.; Bernal, M.A.; Bordage, M.-C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A Simulation Toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Ado, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent Developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Stewart, R.D. Two-Lesion Kinetic Model of Double-Strand Break Rejoining and Cell Killing. Radiat. Res. 2001, 156, 365–378. [Google Scholar] [CrossRef]
- Guerrero, M.; Stewart, R.D.; Wang, J.Z.; Li, X.A. Equivalence of the linear-quadratic and two-lesion kinetic models. Phys. Med. Biol. 2002, 47, 3197–3209. [Google Scholar] [CrossRef]
- Inaniwa, T.; Kanematsu, N.; Matsufuji, N.; Kanai, T.; Shirai, T.; Noda, K.; Tsuji, H.; Kamada, T.; Tsujii, H. Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the National Institute of Radiological Sciences, Japan. Phys. Med. Biol. 2015, 60, 3271. [Google Scholar] [CrossRef]
- Inaniwa, T.; Kanematsu, N.; Noda, N.; Kamada, T. Treatment planning of intensity modulated composite particle therapy with dose and linear energy transfer optimization. Phys. Med. Biol. 2017, 62, 5180. [Google Scholar] [CrossRef]
- Scholz, M.; Kraft, G. Track structure and the calculation of biological effects of heavy charged particles. Adv. Space Res. 1996, 18, 5–14. [Google Scholar] [CrossRef]
- Stewart, R.D.; Carlson, D.J.; Butkus, M.P.; Hawkins, R.; Friedrich, T.; Scholz, M.A. A comparison of mechanism-inspired models for particle relative biological effectiveness (RBE). Med. Phys. 2018, 45, e925–e952. [Google Scholar] [CrossRef]
- Furusawa, Y.; Fukutsu, K.; Aoki, M.; Itsukaichi, H.; Eguchi-Kasai, K.; Ohara, H.; Yatagai, F.; Kanai, T.; Ando, K. Inactivation of Aerobic and Hypoxic Cells from Three Different Cell Lines by Accelerated 3He-, 12C- and 20Ne-Ion Beams. Radiat. Res. 2000, 154, 485–496. [Google Scholar] [CrossRef]
- Ando, K.; Furusawa, Y.; Suzuki, M.; Nojima, K.; Majima, H.; Koike, S.; Aoki, M.; Shimizu, W.; Futami, Y.; Ogino, T.; et al. Relative biological effectiveness of the 235 MeV proton beams at the National Cancer Center Hospital East. J. Radiat. Res. 2001, 42, 79–89. [Google Scholar] [CrossRef][Green Version]
- Kase, Y.; Kanai, T.; Matsumoto, Y.; Furusawa, Y.; Okamoto, H.; Asaba, T.; Sakama, M.; Shinoda, H. Microdosimetric measurements and estimation of human cell survival for heavy-ion beams. Radiat. Res. 2006, 166, 629–638. [Google Scholar] [CrossRef]
- Uzawa, A.; Ando, K.; Koike, S.; Furusawa, Y.; Matsumoto, Y.; Takai, N.; Hirayama, R.; Watanabe, M.; Scholz, M.; Elsässer, T.; et al. Comparison of biological effectiveness of carbon-ion beams in Japan and Germany. Int. J. Radiat. Oncol. Biol. Phys. 2009, 73, 1545–1551. [Google Scholar] [CrossRef]
- Matsuura, T.; Egashira, Y.; Nishio, T.; Matsumoto, Y.; Wada, M.; Koike, S.; Furusawa, Y.; Kohno, K.; Nishioka, S.; Kameoka, S.; et al. Apparent absence of a proton beam dose rate effect and possible differences in RBE between Bragg peak and plateau. Med. Phys. 2010, 37, 5376–5381. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, H.; Kanai, T.; Kase, Y.; Matsumoto, Y.; Furusawa, Y.; Fujita, Y.; Saitoh, H.; Itami, J.; Kohno, T. Relation between lineal energy distribution and relative biological effectiveness for photon beams according to the microdosimetric kinetic model. J. Radiat. Res. 2010, 52, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Koehler, A.M.; Schneider, R.J.; Sisterson, J.M. Range modulators for protons and heavy ions. Nucl. Instrum. Methods 1975, 131, 437–440. [Google Scholar] [CrossRef]
- Suzuki, M.; Kase, Y.; Yamaguchi, H.; Kanai, T.; Ando, K. Relative biological effectiveness for cell-killing effect on various human cell lines irradiated with heavy-ion medical accelerator in Chiba (HIMAC) carbon-ion beams. Int. J. Radiat. Oncol. Biol. Phys. 2000, 48, 241–250. [Google Scholar] [CrossRef]
- Suzuki, M.; Yasuda, N.; Kitamura, H. Lethal and mutagenic bystander effects in human fibroblast cell cultures subjected to low-energy- carbon ions. Int. J. Radiat. Biol. 2019, 96, 179–186. [Google Scholar] [CrossRef]
- Hirayama, R.; Furusawa, Y.; Fukawa, T.; Ando, K. Repair kinetics of DNA-DSB induced by X-rays or carbon ions under oxic and hypoxic conditions. J. Radiat. Res. 2005, 46, 325–332. [Google Scholar] [CrossRef]
- Resch, A.F.; Elia, A.; Fuchs, H.; Carlino, A.; Palmans, H.; Stock, M.; Georg, D.; Grevillot, L. Evaluation of electromagnetic and nuclear scattering models in GATE/Geant4 for proton therapy. Med. Phys. 2019, 46, 2444–2456. [Google Scholar] [CrossRef]
- Lazarakis, P.; Incerti, S.; Ivanchenko, V.; Kyriakou, I.; Emfietzoglou, D.; Corde, S.; Rosenfeld, A.B.; Lerch, M.; Tehei, M.; Guatelli, S. Investigation of track structure and condensed history physics models for applications in radiation dosimetry on a micro and nano scale in Geant4. Biomed. Phys. Eng. Express 2018, 4, 024001. [Google Scholar] [CrossRef]
- Lampe, N.; Karamitros, M.; Breton, V.; Brown, J.M.C.; Kyriakou, I.; Sakata, D.; Sarramia, D.; Incerti, S. Mechanistic DNA damage simulations in Geant4-DNA part 1: A parameter study in a simplified geometry. Phys. Med. 2018, 48, 135–145. [Google Scholar] [CrossRef]
- Lampe, N.; Karamitros, M.; Breton, V.; Brown, J.M.C.; Sakata, D.; Sarramia, D.; Incerti, S. Mechanistic DNA damage simulations in Geant4-DNA part 2: Electron and proton damage in a bacterial cell. Phys. Med. 2018, 48, 146–155. [Google Scholar] [CrossRef]
- ICRU. Report 90: Key Data for Ionizing-Radiation Dosimetry: Measurement Standards and Applications. J. Int. Com. Radiat. Units Meas. 2016, 14, 1. [Google Scholar]
- Emfietzoglou, D. Inelastic cross-sections for electron transport in liquid water: A comparison of dielectric models. Radiat. Phys. Chem. 2003, 66, 373–385. [Google Scholar] [CrossRef]
- Kyriakou, I.; Incerti, S.; Francis, Z. Technical Note: Improvements in geant4 energy-loss model and the effect on low-energy electron transport in liquid water. Med. Phys. 2015, 42, 3870–3876. [Google Scholar] [CrossRef]
- Kyriakou, I.; Šefl1, M.; Nourry, V.; Incerti, S. The impact of new Geant4-DNA cross section models on electron track structure simulations in liquid water. J. Appl. Phys. 2016, 119, 194902. [Google Scholar] [CrossRef]
- Green, N.J.B.; Pilling, M.J.; Pimblott, S.M.; Clifford, P. Stochastic modeling of fast kinetics in a radiation track. J. Phys. Chem. 1990, 94, 251–258. [Google Scholar] [CrossRef]
- Karamitros, M.; Brown, J.M.C.; Lampe, N.; Sakata, D.; Tran, H.N.; Shin, W.-G.; Ramos-Mendez, J.; Guatelli, S.; Incerti, S.; LaVerne, J.A. Implementing the Independent Reaction Time method in Geant4 for radiation chemistry simulations. arXiv 2020, arXiv:2006.14225. [Google Scholar]
- Tang, N. Évaluation, à Partir de Modélisations Nanodosimétriques, de L’influence de la Compaction de la Chromatine sur les Effets Radio-Induits Précoces et Extension aux Effets Tardifs (Réparation des Dommages à l’ADN et Mort Cellulaire). Ph.D. Thesis, University of Bordeaux, Bordeaux, France, 2019. [Google Scholar]
- Contopoulou, C.R.; Cook, V.E.; Mortimer, R.K. Analysis of DNA double strand breakage and repair using orthogonal field alternation gel electrophoresis. Yeast 1987, 3, 71–76. [Google Scholar] [CrossRef]
- Cook, V.E.; Mortimer, R.K. A quantitative model of DNA fragments generated by ionizing radiation, and possible experimental applications. Radiat. Res. 1991, 125, 102–106. [Google Scholar] [CrossRef]
- Belli, M.; Cherubini, R.; Vecchia, M.D.; Dini, V.; Moschini, G.; Signoretti, C.; Simone, G.; Tabocchini, M.A.; Tiveron, P. DNA DSB induction and rejoining in V79 cells irradiated with light ions: A constant field gel electrophoresis study. Int. J. Radiat. Biol. 2000, 76, 1095–1104. [Google Scholar]
- Ceres-Solver. Available online: http://ceres-solver.org (accessed on 19 September 2021).
- Mao, Z.; Bozzella, M.; Seluanov, A.; Gorbunova, V. Comparison of nonhomologous end joining and homologous recombination in human cells. DNA Repair 2008, 7, 1765–1771. [Google Scholar] [CrossRef]
- Hanscom, T.; McVey, M. Regulation of Error-Prone DNA Double-Strand Break Repair and Its Impact on Genome Evolution. Cells 2020, 9, 1657. [Google Scholar] [CrossRef]
- Belov, O.V.; Krasavin, E.A.; Lyashko, M.S.; Batmunkh, M.; Sweilam, N.H. A quantitative model of the major pathways for radiation-induced DNA double-strand break repair. J. Theor. Biol. 2015, 366, 115–130. [Google Scholar] [CrossRef]



| (h) | (h) | (h) | |||
|---|---|---|---|---|---|
| 3.36 | 0. | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakata, D.; Suzuki, M.; Hirayama, R.; Abe, Y.; Muramatsu, M.; Sato, S.; Belov, O.; Kyriakou, I.; Emfietzoglou, D.; Guatelli, S.; et al. Performance Evaluation for Repair of HSGc-C5 Carcinoma Cell Using Geant4-DNA. Cancers 2021, 13, 6046. https://doi.org/10.3390/cancers13236046
Sakata D, Suzuki M, Hirayama R, Abe Y, Muramatsu M, Sato S, Belov O, Kyriakou I, Emfietzoglou D, Guatelli S, et al. Performance Evaluation for Repair of HSGc-C5 Carcinoma Cell Using Geant4-DNA. Cancers. 2021; 13(23):6046. https://doi.org/10.3390/cancers13236046
Chicago/Turabian StyleSakata, Dousatsu, Masao Suzuki, Ryoichi Hirayama, Yasushi Abe, Masayuki Muramatsu, Shinji Sato, Oleg Belov, Ioanna Kyriakou, Dimitris Emfietzoglou, Susanna Guatelli, and et al. 2021. "Performance Evaluation for Repair of HSGc-C5 Carcinoma Cell Using Geant4-DNA" Cancers 13, no. 23: 6046. https://doi.org/10.3390/cancers13236046
APA StyleSakata, D., Suzuki, M., Hirayama, R., Abe, Y., Muramatsu, M., Sato, S., Belov, O., Kyriakou, I., Emfietzoglou, D., Guatelli, S., Incerti, S., & Inaniwa, T. (2021). Performance Evaluation for Repair of HSGc-C5 Carcinoma Cell Using Geant4-DNA. Cancers, 13(23), 6046. https://doi.org/10.3390/cancers13236046








