Can Systems Biology Advance Clinical Precision Oncology?
Abstract
:Simple Summary
Abstract
1. Introduction
2. Precision Oncology Challenges
3. Systems Biology
Cancers as Dynamical Systems
4. Statistical Methods
5. Network Analysis
6. Logic Models
7. Mechanistic Models
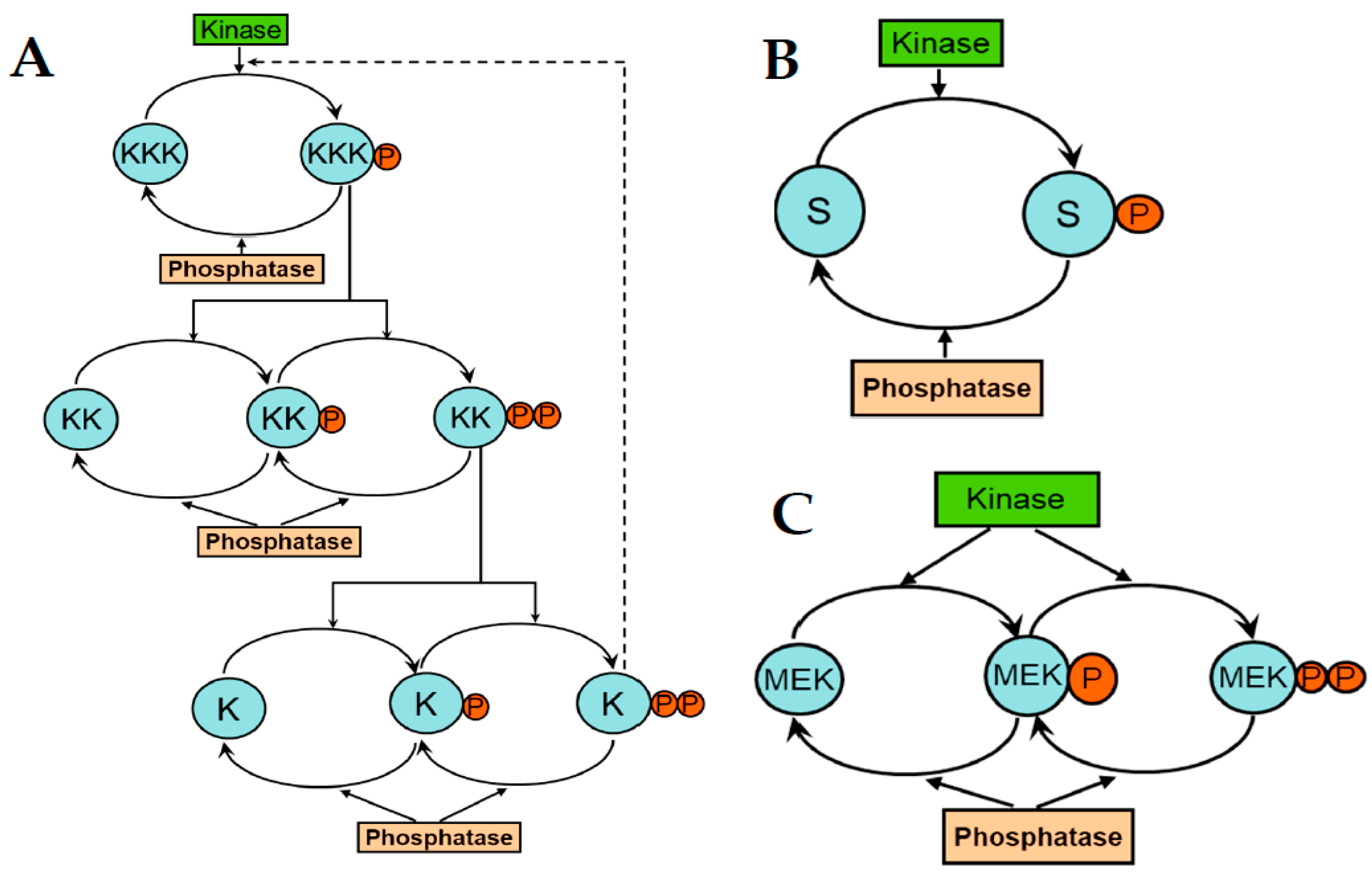
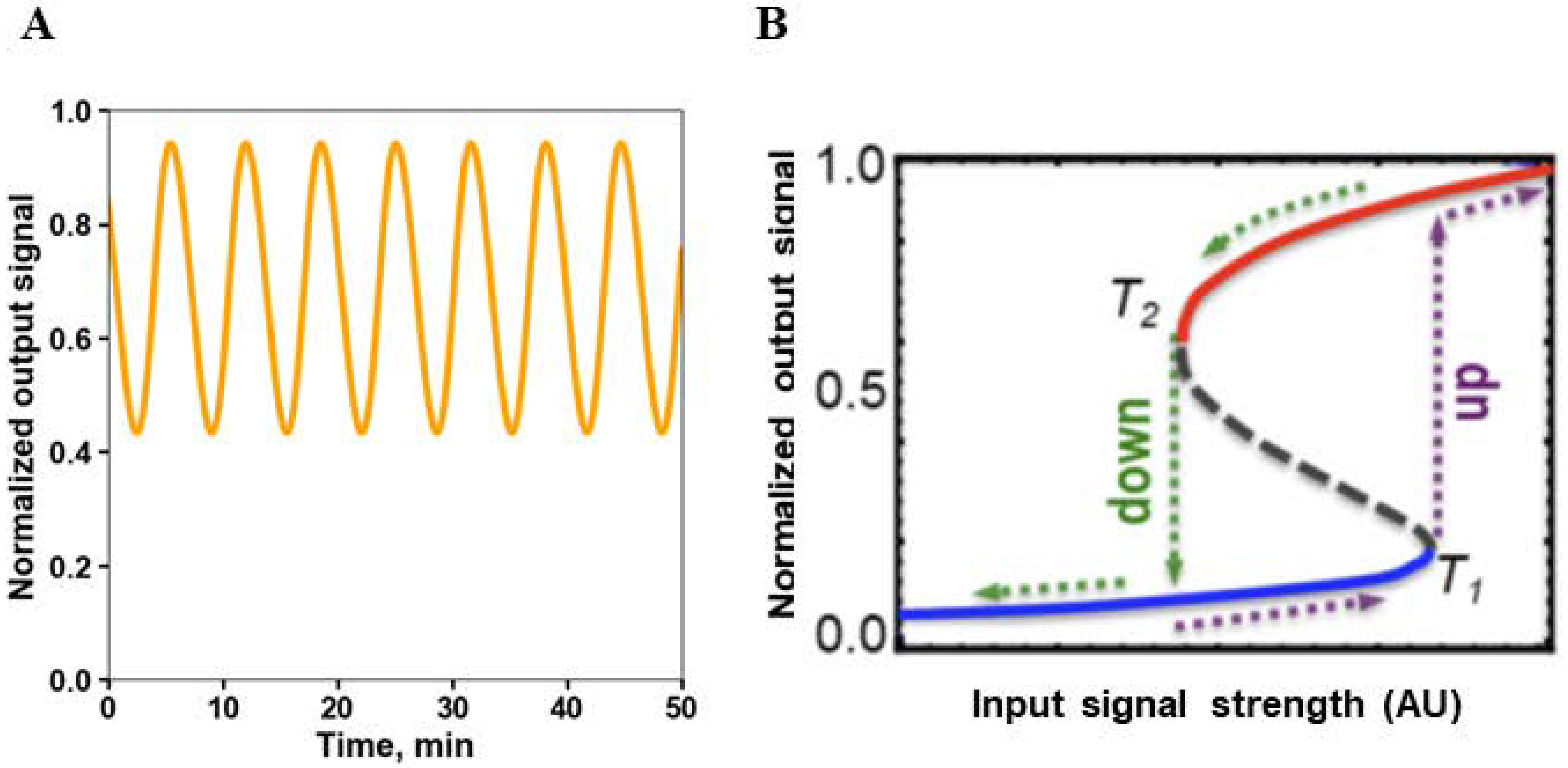
8. Emerging Network Properties Captured by Differential Equation Models
9. Modeling Spatiotemporal Network Behavior by Partial Differential Equations
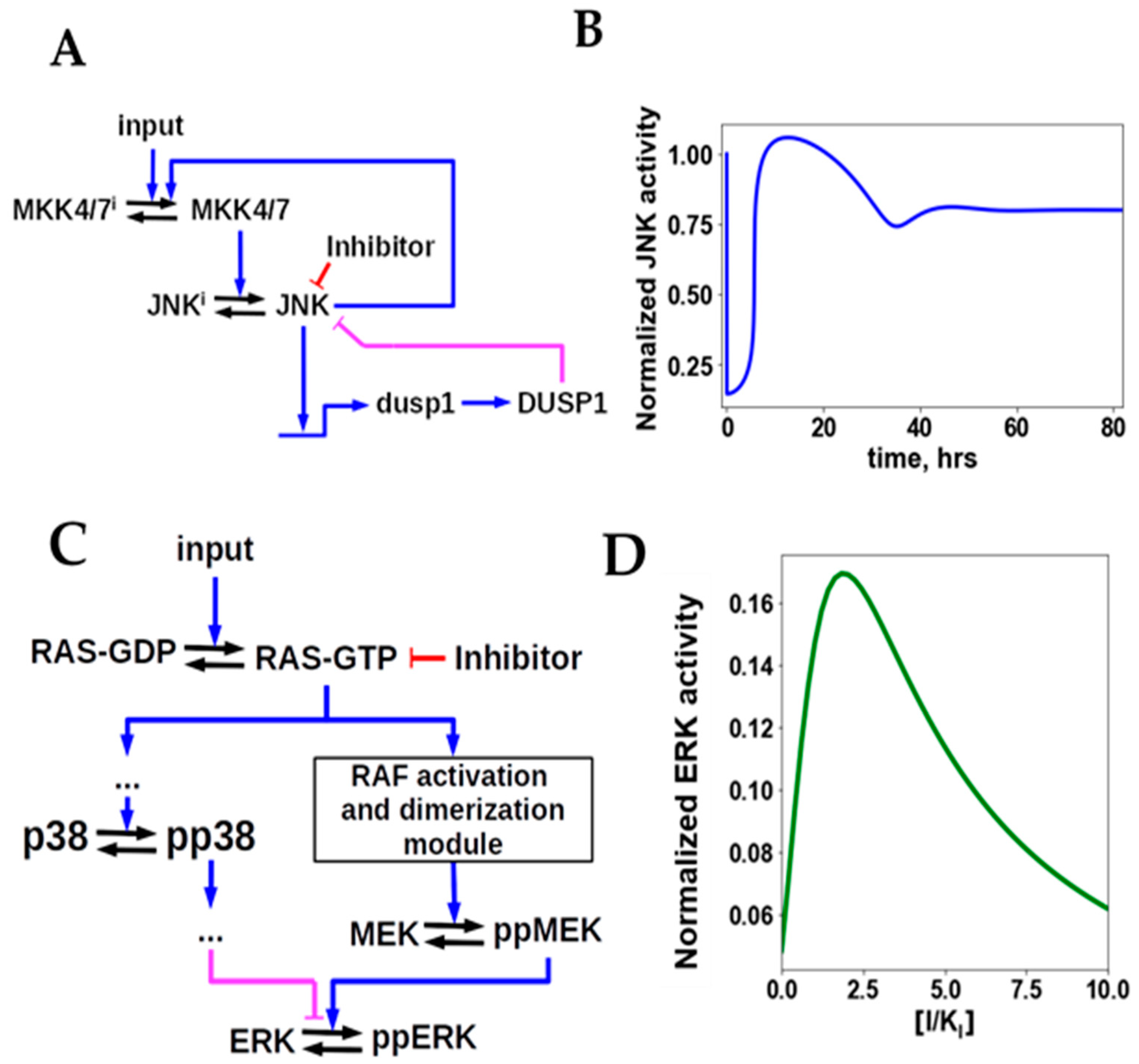
10. Mechanistic Models Help Us Understand Resistance to Targeted Therapies
11. Signaling Network Models Can Predict Drug Sensitivity
12. Patient-Specific Network Modeling
13. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yusuf, S.; Collins, R.; Peto, R. Why do we need some large, simple randomized trials? Stat. Med. 1984, 3, 409–420. [Google Scholar] [CrossRef]
- Greenhalgh, T.; Howick, J.; Maskrey, N.; Brassey, J.; Burch, D.; Burton, M.; Chang, H.; Glasziou, P.; Heath, I.; Heneghan, C.; et al. Evidence based medicine: A movement in crisis? BMJ 2014, 348, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campbell, P.J.; Getz, G.; Korbel, J.O.; Stuart, J.M.; Jennings, J.L.; Stein, L.D.; Perry, M.D.; Nahal-Bose, H.K.; Ouellette, B.F.F.; Li, C.H.; et al. Pan-cancer analysis of whole genomes. Nature 2020, 578, 82–93. [Google Scholar] [CrossRef] [Green Version]
- Bailey, M.H.; Tokheim, C.; Porta-Pardo, E.; Sengupta, S.; Bertrand, D.; Weerasinghe, A.; Colaprico, A.; Wendl, M.C.; Kim, J.; Reardon, B.; et al. Comprehensive Characterization of Cancer Driver Genes and Mutations. Cell 2018, 173, 371–385. [Google Scholar] [CrossRef] [Green Version]
- Tsimberidou, A.M.; Fountzilas, E.; Bleris, L.; Kurzrock, R. Transcriptomics and solid tumors: The next frontier in precision cancer medicine. Semin. Cancer Biol. 2020. [Google Scholar] [CrossRef]
- Kolch, W.; Pitt, A. Functional proteomics to dissect tyrosine kinase signalling pathways in cancer. Nat. Rev. Cancer 2010, 10, 618–629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, Y.T.; Tan, Y.J.; Oon, C.E. Molecular targeted therapy: Treating cancer with specificity. Eur. J. Pharmacol. 2018, 834, 188–196. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of Cancer: The Next Generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Vega, F.; Mina, M.; Armenia, J.; Chatila, W.K.; Luna, A.; La, K.C.; Dimitriadoy, S.; Liu, D.L.; Kantheti, H.S.; Saghafinia, S.; et al. Oncogenic Signaling Pathways in The Cancer Genome Atlas. Cell 2018, 173, 321–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawrence, M.S.; Stojanov, P.; Polak, P.; Kryukov, G.V.; Cibulskis, K.; Sivachenko, A.; Carter, S.L.; Stewart, C.; Mermel, C.H.; Roberts, S.A.; et al. Mutational heterogeneity in cancer and the search for new cancer-associated genes. Nat. Cell Biol. 2013, 499, 214–218. [Google Scholar] [CrossRef] [PubMed]
- Janiszewska, M. The microcosmos of intratumor heterogeneity: The space-time of cancer evolution. Oncogene 2020, 39, 2031–2039. [Google Scholar] [CrossRef]
- Yates, L.; Seoane, J.; Le Tourneau, C.; Siu, L.; Marais, R.; Michiels, S.; Soria, J.; Campbell, P.; Normanno, N.; Scarpa, A.; et al. The European Society for Medical Oncology (ESMO) Precision Medicine Glossary. Ann. Oncol. 2018, 29, 30–35. [Google Scholar] [CrossRef]
- Abrams, J.; Conley, B.; Mooney, M.; Zwiebel, J.; Chen, A.; Welch, J.J.; Takebe, N.; Malik, S.; McShane, L.; Korn, E.; et al. National Cancer Institute’s Precision Medicine Initiatives for the New National Clinical Trials Network. Am. Soc. Clin. Oncol. Educ. Book 2014, 34, 71–76. [Google Scholar] [CrossRef] [PubMed]
- Hood, L.; Friend, S.H. Predictive, personalized, preventive, participatory (P4) cancer medicine. Nat. Rev. Clin. Oncol. 2011, 8, 184–187. [Google Scholar] [CrossRef] [PubMed]
- Filipp, F.V. Precision medicine driven by cancer systems biology. Cancer Metastasis Rev. 2017, 36, 91–108. [Google Scholar] [CrossRef] [Green Version]
- Du, W.; Elemento, O. Cancer systems biology: Embracing complexity to develop better anticancer therapeutic strategies. Oncogene 2014, 34, 3215–3225. [Google Scholar] [CrossRef] [PubMed]
- Stéphanou, A.; Fanchon, E.; Innominato, P.F.; Ballesta, A. Systems Biology, Systems Medicine, Systems Pharmacology: The What and The Why. Acta Biotheor. 2018, 66, 345–365. [Google Scholar] [CrossRef]
- Kent, D.M.; Steyerberg, E.; van Klaveren, D. Personalized evidence based medicine: Predictive approaches to heterogeneous treatment effects. BMJ 2018, 363, k4245. [Google Scholar] [CrossRef]
- Kent, D.M.; Paulus, J.K.; van Klaveren, D.; Agostino, D.; Goodman, S.; Hayward, R.; John, P.A.; Patrick-lake, B.; Morton, S.; Pencina, M.; et al. The Predictive Approaches to Treatment effect Heterogeneity (PATH) Statement. Ann. Intern. Med. 2020, 172, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Kent, D.M.; van Klaveren, D.; Paulus, J.K.; Agostino, D.; Goodman, S.; Hayward, R.; John, P.A.; Patrick-lake, B.; Morton, S.; Pencina, M.; et al. The PATH Statement Explanation and Elaboration Document. Ann. Intern. Med. 2020, 172, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Lee, J.J.; Ford, J.M. Statistical Methods in Precision Oncology. J. Clin. Oncol. 2020, 38, 660–661. [Google Scholar] [CrossRef] [PubMed]
- Angus, D.C.; Alexander, B.M.; Berry, S.; Buxton, M.; Lewis, R.; Paoloni, M.; Woodcock, J. The Adaptive Platform Trials Coalition Adaptive platform trials: Definition, design, conduct and reporting considerations. Nat. Rev. Drug Discov. 2019, 18, 797–807. [Google Scholar]
- Woodcock, J.; LaVange, L.M. Master Protocols to Study Multiple Therapies, Multiple Diseases, or Both. N. Engl. J. Med. 2017, 377, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Adashek, J.J.; Subbiah, V.; Kurzrock, R. From Tissue-Agnostic to N-of-One Therapies: (R) Evolution of the Precision Paradigm. Trends Cancer 2021, 7, 15–28. [Google Scholar] [CrossRef] [PubMed]
- Ciardiello, F.; Arnold, D.; Casali, P.G.; Cervantes, A.; Douillard, J.-Y.; Eggermont, A.; Eniu, A.; McGregor, K.; Peters, S.; Piccart, M.; et al. Delivering precision medicine in oncology today and in future—the promise and challenges of personalised cancer medicine: A position paper by the European Society for Medical Oncology (ESMO). Ann. Oncol. 2014, 25, 1673–1678. [Google Scholar] [CrossRef]
- Tsimberidou, A.M.; Fountzilas, E.; Nikanjam, M.; Kurzrock, R. Review of precision cancer medicine: Evolution of the treatment paradigm. Cancer Treat. Rev. 2020, 86, 102019. [Google Scholar] [CrossRef] [PubMed]
- Perou, C.M.; Sørlie, T.; Eisen, M.B.; van de Rijn, M.; Jeffrey, S.S.; Rees, C.A.; Pollack, J.R.; Ross, D.T.; Johnsen, H.; Akslen, L.A.; et al. Molecular portraits of human breast tumours. Nature 2000, 406, 747–752. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, A.A.; Eisen, M.B.; Davis, R.E.; Ma, C.; Lossos, I.S.; Rosenwald, A.; Boldrick, J.C.; Sabet, H.; Tran, T.; Yu, X.; et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nat. Cell Biol. 2000, 403, 503–511. [Google Scholar] [CrossRef]
- The Cancer Genome Atlas Network. Comprehensive molecular portraits of human breast tumours. Nature 2012, 490, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Collisson, E.A.; Campbell, J.D.; Brooks, A.N.; Berger, A.H.; Lee, W.; Chmielecki, J.; Beer, D.G.; Cope, L.; Creighton, C.J.; Danilova, L.; et al. Comprehensive molecular profiling of lung adenocarcinoma: The cancer genome atlas research network. Nature 2014, 511, 543–550. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, J.; Wang, X.; Zhu, J.; Liu, Q.; Shi, Z.; Chambers, M.C.; Zimmerman, L.J.; Shaddox, K.F.; Kim, S.; et al. Proteogenomic characterization of human colon and rectal cancer. Nature 2014, 513, 382–387. [Google Scholar] [CrossRef] [Green Version]
- Curtis, C.; Shah, S.P.; Chin, S.-F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef]
- Ali, H.R.; Rueda, O.M.; Chin, S.-F.; Curtis, C.; Dunning, M.J.; Aparicio, S.A.; Caldas, C. Genome-driven integrated classification of breast cancer validated in over 7500 samples. Genome Biol. 2014, 15, 1–14. [Google Scholar] [CrossRef]
- Montor, W.R.; Salas, A.R.O.S.E.; de Melo, F.H.M. Receptor tyrosine kinases and downstream pathways as druggable targets for cancer treatment: The current arsenal of inhibitors. Mol. Cancer 2018, 17, 1–18. [Google Scholar] [CrossRef]
- Dupont, C.A.; Riegel, K.; Pompaiah, M.; Juhl, H.; Rajalingam, K. Druggable genome and precision medicine in cancer: Current challenges. FEBS J. 2021, 288, 6142–6158. [Google Scholar] [CrossRef] [PubMed]
- Kalemkerian, G.P.; Narula, N.; Kennedy, E.B.; Biermann, W.A.; Donington, J.; Leighl, N.B.; Lew, M.; Pantelas, J.; Ramalingam, S.S.; Reck, M.; et al. Molecular Testing Guideline for the Selection of Patients With Lung Cancer for Treatment With Targeted Tyrosine Kinase Inhibitors: American Society of Clinical Oncology Endorsement of the College of American Pathologists/International Association for the Study of Lung Cancer/Association for Molecular Pathology Clinical Practice Guideline Update. J. Clin. Oncol. 2018, 36, 911–919. [Google Scholar] [CrossRef]
- Wolff, A.C.; Hammond, M.E.H.; Allison, K.H.; Harvey, B.E.; Mangu, P.B.; Bartlett, J.M.S.; Bilous, M.; Ellis, I.O.; Fitzgibbons, P.; Hanna, W.; et al. Human Epidermal Growth Factor Receptor 2 Testing in Breast Cancer: American Society of Clinical Oncology/College of American Pathologists Clinical Practice Guideline Focused Update. J. Clin. Oncol. 2018, 36, 2105–2122. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, F.; van’t Veer, L.J.; Bogaerts, J.; Slaets, L.; Viale, G.; Delaloge, S.; Pierga, J.Y.; Brain, E.; Causeret, S.; Delorenzi, M.; et al. 70-Gene Signature as an Aid to Treatment Decisions in Early-Stage Breast Cancer. N. Engl. J. Med. 2016, 375, 717–729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sparano, J.A.; Gray, R.J.; Makower, D.F.; Pritchard, K.I.; Albain, K.S.; Hayes, D.F.; Geyer, C.E., Jr.; Dees, E.C.; Goetz, M.P.; Olson, J.A.; et al. Adjuvant Chemotherapy Guided by a 21-Gene Expression Assay in Breast Cancer. N. Engl. J. Med. 2018, 379, 111–121. [Google Scholar] [CrossRef] [Green Version]
- Andre, F.; Ismaila, N.; Henry, N.L.; Somerfield, M.R.; Bast, R.C.; Barlow, W.; Collyar, D.E.; Hammond, M.E.; Kuderer, N.M.; Liu, M.C.; et al. Use of Biomarkers to Guide Decisions on Adjuvant Systemic Therapy for Women With Early-Stage Invasive Breast Cancer: ASCO Clinical Practice Guideline Update—Integration of Results From TAILORx. J. Clin. Oncol. 2019, 37, 1956–1964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sjöström, M.; Chang, S.L.; Fishbane, N.; Davicioni, E.; Zhao, S.G.; Hartman, L.; Holmberg, E.; Feng, F.Y.; Speers, C.W.; Pierce, L.J.; et al. Clinicogenomic Radiotherapy Classifier Predicting the Need for Intensified Locoregional Treatment After Breast-Conserving Surgery for Early-Stage Breast Cancer. J. Clin. Oncol. 2019, 37, 3340–3349. [Google Scholar] [CrossRef] [PubMed]
- Llombart-Cussac, A.; Cortes, J.; Pare, L.; Galván, P.; Bermejo, B.; Martínez, N.; Vidal, M.; Pernas, S.; López, R.L.; Munoz, M.; et al. HER2-enriched subtype as a predictor of pathological complete response following trastuzumab and lapatinib without chemotherapy in early-stage HER2-positive breast cancer (PAMELA): An open-label, single-group, multicentre, phase 2 trial. Lancet Oncol. 2017, 18, 545–554. [Google Scholar] [CrossRef]
- Shi, W.; Jiang, T.; Nuciforo, P.; Hatzis, C.; Holmes, E.; Harbeck, N.; Sotiriou, C.; Peña, L.; Loi, S.; Rosa, D.D.; et al. Pathway level alterations rather than mutations in single genes predict response to HER2-targeted therapies in the neo-ALTTO trial. Ann. Oncol. 2017, 28, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Wulfkuhle, J.D.; Berg, D.; Wolff, C.; Langer, R.; Tran, K.; Illi, J.; Espina, V.; Pierobon, M.; Deng, J.; DeMichele, A.; et al. Molecular Analysis of HER2 Signaling in Human Breast Cancer by Functional Protein Pathway Activation Mapping. Clin. Cancer Res. 2012, 18, 6426–6435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wulfkuhle, J.D.; Yau, C.; Wolf, D.M.; Vis, D.J.; Gallagher, R.I.; Brown-Swigart, L.; Hirst, G.; Voest, E.E.; DeMichele, A.; Hylton, N.; et al. Evaluation of the HER/PI3K/AKT Family Signaling Network as a Predictive Biomarker of Pathologic Complete Response for Patients With Breast Cancer Treated With Neratinib in the I-SPY 2 TRIAL. JCO Precis. Oncol. 2018, 2, 1–20. [Google Scholar] [CrossRef]
- Mertins, P.; Cptac, N.; Mani, D.R.; Ruggles, K.V.; Gillette, M.A.; Clauser, K.R.; Wang, P.; Wang, X.; Qiao, J.W.; Cao, S.; et al. Proteogenomics connects somatic mutations to signalling in breast cancer. Nat. Cell Biol. 2016, 534, 55–62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sengupta, S.; Sun, S.Q.; Huang, K.-L.; Oh, C.; Bailey, M.H.; Varghese, R.; Wyczalkowski, M.A.; Ning, J.; Tripathi, P.; McMichael, J.F.; et al. Integrative omics analyses broaden treatment targets in human cancer. Genome Med. 2018, 10, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Hahn, W.C.; Bader, J.S.; Braun, T.P.; Califano, A.; Clemons, P.A.; Druker, B.J.; Ewald, A.J.; Fu, H.; Jagu, S.; Kemp, C.J.; et al. An expanded universe of cancer targets. Cell 2021, 184, 1142–1155. [Google Scholar] [CrossRef]
- Kim, H.; Chung, J.-H. PD-L1 Testing in Non-small Cell Lung Cancer: Past, Present, and Future. J. Pathol. Transl. Med. 2019, 53, 199–206. [Google Scholar] [CrossRef] [Green Version]
- Miglietta, F.; Griguolo, G.; Guarneri, V.; Dieci, M.V. Programmed Cell Death Ligand 1 in Breast Cancer: Technical Aspects, Prognostic Implications, and Predictive Value. Oncologist 2019, 24, 24. [Google Scholar] [CrossRef] [Green Version]
- Stein, M.; Oluoha, O.; Patel, K.; VanderWalde, A. Precision Medicine in Oncology: A Review of Multi-Tumor Actionable Molecular Targets with an Emphasis on Non-Small Cell Lung Cancer. J. Pers. Med. 2021, 11, 518. [Google Scholar] [CrossRef] [PubMed]
- Blank, C.U.; Haanen, J.B.; Ribas, A.; Schumacher, T.N. The “cancer immunogram”. Science 2016, 352, 658–660. [Google Scholar] [CrossRef]
- Grasso, C.S.; Tsoi, J.; Onyshchenko, M.; Abril-Rodriguez, G.; Ross-Macdonald, P.; Wind-Rotolo, M.; Champhekar, A.; Medina, E.; Torrejon, D.Y.; Shin, D.S.; et al. Conserved Interferon-γ Signaling Drives Clinical Response to Immune Checkpoint Blockade Therapy in Melanoma. Cancer Cell 2020, 38, 500–515. [Google Scholar] [CrossRef] [PubMed]
- Hugo, W.; Zaretsky, J.M.; Sun, L.; Song, C.; Moreno, B.H.; Hu-Lieskovan, S.; Berent-Maoz, B.; Pang, J.; Chmielowski, B.; Cherry, G.; et al. Genomic and Transcriptomic Features of Response to Anti-PD-1 Therapy in Metastatic Melanoma. Cell 2016, 165, 35–44. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y. The root cause of drug resistance in HER2-positive breast cancer and the therapeutic approaches to overcoming the resistance. Pharmacol. Ther. 2021, 218, 107677. [Google Scholar] [CrossRef] [PubMed]
- Murtuza, A.; Bulbul, A.; Shen, J.P.; Keshavarzian, P.; Woodward, B.D.; Lopez-Diaz, F.J.; Lippman, S.M.; Husain, H. Novel Third-Generation EGFR Tyrosine Kinase Inhibitors and Strategies to Overcome Therapeutic Resistance in Lung Cancer. Cancer Res. 2019, 79, 689–698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leonetti, A.; Sharma, S.; Minari, R.; Perego, P.; Giovannetti, E.; Tiseo, M. Resistance mechanisms to osimertinib in EGFR-mutated non-small cell lung cancer. Br. J. Cancer 2019, 121, 725–737. [Google Scholar] [CrossRef]
- Lake, D.; Corrêa, S.A.L.; Müller, J. Negative feedback regulation of the ERK1/2 MAPK pathway. Cell. Mol. Life Sci. 2016, 73, 4397–4413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arpino, G.; Wiechmann, L.; Osborne, C.K.; Schiff, R. Crosstalk between the Estrogen Receptor and the HER Tyrosine Kinase Receptor Family: Molecular Mechanism and Clinical Implications for Endocrine Therapy Resistance. Endocr. Rev. 2008, 29, 217–233. [Google Scholar] [CrossRef] [Green Version]
- Swain, S.M.; Baselga, J.; Kim, S.-B.; Ro, J.; Semiglazov, V.; Campone, M.; Ciruelos, E.; Ferrero, J.-M.; Schneeweiss, A.; Heeson, S.; et al. Pertuzumab, Trastuzumab, and Docetaxel in HER2-Positive Metastatic Breast Cancer. N. Engl. J. Med. 2015, 372, 724–734. [Google Scholar] [CrossRef] [Green Version]
- Blackwell, K.L.; Burstein, H.J.; Storniolo, A.M.; Rugo, H.S.; Sledge, G.; Aktan, G.; Ellis, C.; Florance, A.; Vukelja, S.; Bischoff, J.; et al. Overall Survival Benefit With Lapatinib in Combination With Trastuzumab for Patients With Human Epidermal Growth Factor Receptor 2–Positive Metastatic Breast Cancer: Final Results From the EGF104900 Study. J. Clin. Oncol. 2012, 30, 2585–2592. [Google Scholar] [CrossRef] [PubMed]
- Larkin, J.; Ascierto, P.A.; Dréno, B.; Atkinson, V.; Liszkay, G.; Maio, M.; Mandalà, M.; Demidov, L.; Stroyakovskiy, D.; Thomas, L.; et al. Combined Vemurafenib and Cobimetinib in BRAF-Mutated Melanoma. N. Engl. J. Med. 2014, 371, 1867–1876. [Google Scholar] [CrossRef] [Green Version]
- Robert, C.; Karaszewska, B.; Schachter, J.; Rutkowski, P.; Mackiewicz, A.; Stroiakovski, D.; Lichinitser, M.; Dummer, R.; Grange, F.; Mortier, L.; et al. Improved overall survival in melanoma with combined dabrafenib and trametinib. N. Engl. J. Med. 2015, 372, 30–39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dummer, R.; Ascierto, P.A.; Gogas, H.J.; Arance, A.; Mandala, M.; Liszkay, G.; Garbe, C.; Schadendorf, D.; Krajsova, I.; Gutzmer, R.; et al. Overall survival in patients with BRAF-mutant melanoma receiving encorafenib plus binimetinib versus vemurafenib or encorafenib (COLUMBUS): A multicentre, open-label, randomised, phase 3 trial. Lancet Oncol. 2018, 19, 1315–1327. [Google Scholar] [CrossRef]
- Kholodenko, B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006, 7, 165–176. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Hancock, J.; Kolch, W. Signalling ballet in space and time. Nat. Rev. Mol. Cell Biol. 2010, 11, 414–426. [Google Scholar] [CrossRef] [Green Version]
- Kolch, W.; Halasz, M.; Granovskaya, M.; Kholodenko, B. The dynamic control of signal transduction networks in cancer cells. Nat. Rev. Cancer 2015, 15, 515–527. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.; Hoek, J.; Westerhoff, H.; Brown, G.C. Quantification of information transfer via cellular signal transduction pathways. FEBS Lett. 1997, 414, 430–434. [Google Scholar] [CrossRef] [Green Version]
- Bhalla, U.S.; Iyengar, R. Emergent Properties of Networks of Biological Signaling Pathways. Science 1999, 283, 381–387. [Google Scholar] [CrossRef] [Green Version]
- Uthamacumaran, A. A review of dynamical systems approaches for the detection of chaotic attractors in cancer networks. Gene Expr. Patterns 2021, 2, 100226. [Google Scholar] [CrossRef]
- Citri, A.; Yarden, Y. EGF–ERBB signalling: Towards the systems level. Nat. Rev. Mol. Cell Biol. 2006, 7, 505–516. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H. Cancer as a robust system: Implications for anticancer therapy. Nat. Rev. Cancer 2004, 4, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Hastings, J.F.; O’Donnell, Y.E.; Fey, D.; Croucher, D.R. Applications of personalised signalling network models in precision oncology. Pharmacol. Ther. 2020, 212, 107555. [Google Scholar] [CrossRef] [PubMed]
- Tavassoly, I.; Goldfarb, J.; Iyengar, R. Systems biology primer: The basic methods and approaches. Essays Biochem. 2018, 62, 487–500. [Google Scholar] [CrossRef]
- Ebata, K.; Yamashiro, S.; Iida, K.; Okada, M. Building patient-specific models for receptor tyrosine kinase signaling networks. FEBS J. 2021. advance online publication. [Google Scholar] [CrossRef]
- Yurkovich, J.T.; Tian, Q.; Price, N.D.; Hood, L. A systems approach to clinical oncology uses deep phenotyping to deliver personalized care. Nat. Rev. Clin. Oncol. 2019, 17, 183–194. [Google Scholar] [CrossRef]
- Karlebach, G.; Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 2008, 9, 770–780. [Google Scholar] [CrossRef]
- Barbuti, R.; Gori, R.; Milazzo, P.; Nasti, L. A survey of gene regulatory networks modelling methods: From differential equations, to Boolean and qualitative bioinspired models. J. Membr. Comput. 2020, 2, 207–226. [Google Scholar] [CrossRef]
- Tyson, J.J.; Laomettachit, T.; Kraikivski, P. Modeling the dynamic behavior of biochemical regulatory networks. J. Theor. Biol. 2019, 462, 514–527. [Google Scholar] [CrossRef]
- Clarke, M.A.; Fisher, J. Executable cancer models: Successes and challenges. Nat. Rev. Cancer 2020, 20, 343–354. [Google Scholar] [CrossRef]
- Jaqaman, K.; Danuser, G. Linking data to models: Data regression. Nat. Rev. Mol. Cell Biol. 2006, 7, 813–819. [Google Scholar] [CrossRef]
- Kristensen, V.N.; Lingjærde, O.C.; Russnes, H.G.; Vollan, H.K.M.; Frigessi, A.; Børresen-Dale, A.-L. Principles and methods of integrative genomic analyses in cancer. Nat. Rev. Cancer 2014, 14, 299–313. [Google Scholar] [CrossRef]
- Clarke, R.; Ressom, H.W.; Wang, A.; Xuan, J.; Liu, M.C.; Gehan, E.A.; Wang, Y. The properties of high-dimensional data spaces: Implications for exploring gene and protein expression data. Nat. Rev. Cancer 2008, 8, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Janes, K.A.; Yaffe, M.B. Data-driven modelling of signal-transduction networks. Nat. Rev. Mol. Cell Biol. 2006, 7, 820–828. [Google Scholar] [CrossRef] [PubMed]
- Niepel, M.; Hafner, M.; Pace, E.A.; Chung, M.; Chai, D.H.; Zhou, L.; Schoeberl, B.; Sorger, P.K. Profiles of Basal and Stim-ulated Receptor Signaling Networks Predict Drug Response in Breast Cancer Lines. Sci. Signal. 2013, 6, ra84. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; McClain, C.J.; Rai, S.N. Fifteen Years of Gene Set Analysis for High-Throughput Genomic Data: A Review of Statistical Approaches and Future Challenges. Entropy 2020, 22, 427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toy, H.I.; Karakülah, G.; Kontou, P.I.; Alotaibi, H.; Georgakilas, A.G.; Pavlopoulou, A. Investigating Molecular Determinants of Cancer Cell Resistance to Ionizing Radiation Through an Integrative Bioinformatics Approach. Front. Cell Dev. Biol. 2021, 9, 620248. [Google Scholar] [CrossRef]
- Yeung, T.-L.; Sheng, J.; Leung, C.S.; Li, F.; Kim, J.; Ho, S.Y.; Matzuk, M.M.; Lu, K.H.; Wong, S.T.C.; Mok, S.C. Systematic Identification of Druggable Epithelial-Stromal Crosstalk Signaling Networks in Ovarian Cancer. J. Natl. Cancer Inst. 2019, 111, 272–282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saez-Rodriguez, J.; Blüthgen, N. Personalized signaling models for personalized treatments. Mol. Syst. Biol. 2020, 16, e9042. [Google Scholar] [CrossRef]
- Cook, D.P.; Vanderhyden, B.C. Context specificity of the EMT transcriptional response. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.S.; Zivanovic, N.; van Dijk, D.; Wolf, G.; Bodenmiller, B.; Krishnaswamy, S. Uncovering axes of variation among single-cell cancer specimens. Nat. Methods 2020, 17, 302–310. [Google Scholar] [CrossRef]
- Molinelli, E.J.; Korkut, A.; Wang, W.; Miller, M.L.; Gauthier, N.P.; Jing, X.; Kaushik, P.; He, Q.; Mills, G.; Solit, D.B.; et al. Perturbation Biology: Inferring Signaling Networks in Cellular Systems. PLoS Comput. Biol. 2013, 9, e1003290. [Google Scholar] [CrossRef]
- Nagy, M.; Radakovich, N.; Nazha, A. Machine Learning in Oncology: What Should Clinicians Know? JCO Clin. Cancer Inform. 2020, 4, 799–810. [Google Scholar] [CrossRef]
- Bhinder, B.; Gilvary, C.; Madhukar, N.S.; Elemento, O. Artificial Intelligence in Cancer Research and Precision Medicine. Cancer Discov. 2021, 11, 900–915. [Google Scholar] [CrossRef] [PubMed]
- Goecks, J.; Jalili, V.; Heiser, L.M.; Gray, J.W. How Machine Learning Will Transform Biomedicine. Cell 2020, 181, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Adam, G.; Rampášek, L.; Safikhani, Z.; Smirnov, P.; Haibe-Kains, B.; Goldenberg, A. Machine learning approaches to drug response prediction: Challenges and recent progress. NPJ Precis. Oncol. 2020, 4, 1–10. [Google Scholar] [CrossRef]
- De Silva, E.; Stumpf, M.P. Complex networks and simple models in biology. J. R. Soc. Interface 2005, 2, 419–430. [Google Scholar] [CrossRef] [Green Version]
- Pieroni, E.; Bentem, S.D.L.F.V.; Mancosu, G.; Capobianco, E.; Hirt, H.; de La Fuente, A. Protein networking: Insights into global functional organization of proteomes. Proteomics 2008, 8, 799–816. [Google Scholar] [CrossRef] [PubMed]
- Le Novère, N. Quantitative and logic modelling of molecular and gene networks. Nat. Rev. Genet. 2015, 16, 146–158. [Google Scholar] [CrossRef] [Green Version]
- Szklarczyk, D.; Gable, A.L.; Nastou, K.C.; Lyon, D.; Kirsch, R.; Pyysalo, S.; Doncheva, N.T.; Legeay, M.; Fang, T.; Bork, P.; et al. The STRING database in 2021: Customizable protein-protein networks, and functional characterization of user-uploaded gene/measurement sets. Nucleic Acids Res. 2021, 49, D605–D612. [Google Scholar] [CrossRef] [PubMed]
- Stolovitzky, G.; Monroe, D.; Califano, A. Dialogue on Reverse-Engineering Assessment and Methods: The DREAM of High-Throughput Pathway Inference. Ann. N. Y. Acad. Sci. 2007, 1115, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Villaverde, A.; Banga, J.R. Reverse engineering and identification in systems biology: Strategies, perspectives and challenges. J. R. Soc. Interface 2014, 11, 20130505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haury, A.-C.; Mordelet, F.; Vera-Licona, P.; Vert, J.-P. TIGRESS: Trustful Inference of Gene REgulation using Stability Selection. BMC Syst. Biol. 2012, 6, 145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedman, N. Inferring Cellular Networks Using Probabilistic Graphical Models. Science 2004, 303, 799–805. [Google Scholar] [CrossRef]
- Liepe, J.; Kirk, P.; Filippi, S.; Toni, T.; Barnes, C.; Stumpf, M.P. A framework for parameter estimation and model selection from experimental data in systems biology using approximate Bayesian computation. Nat. Protoc. 2014, 9, 439–456. [Google Scholar] [CrossRef] [Green Version]
- Dondelinger, F.; Mukherjee, S. Statistical Network Inference for Time-Varying Molecular Data with Dynamic Bayesian Networks. Adv. Struct. Saf. Stud. 2018, 1883, 25–48. [Google Scholar] [CrossRef]
- Kim, Y.; Han, S.; Choi, S.; Hwang, D. Inference of dynamic networks using time-course data. Brief. Bioinform. 2013, 15, 212–228. [Google Scholar] [CrossRef] [Green Version]
- Basso, K.; Margolin, A.A.; Stolovitzky, G.; Klein, U.; Dalla-Favera, R.; Califano, A. Reverse engineering of regulatory networks in human B cells. Nat. Genet. 2005, 37, 382–390. [Google Scholar] [CrossRef]
- Califano, A.; Butte, A.J.; Friend, S.; Ideker, T.; Schadt, E. Leveraging models of cell regulation and GWAS data in integrative network-based association studies. Nat. Genet. 2012, 44, 841–847. [Google Scholar] [CrossRef]
- Bruggeman, F.J.; Westerhoff, H.V.; Hoek, J.B.; Kholodenko, B.N. Modular Response Analysis of Cellular Regulatory Networks. J. Theor. Biol. 2002, 218, 507–520. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Kiyatkin, A.; Bruggeman, F.; Sontag, E.; Westerhoff, H.; Hoek, J. Untangling the wires: A strategy to trace functional interactions in signaling and gene networks. Proc. Natl. Acad. Sci. USA 2002, 99, 12841–12846. [Google Scholar] [CrossRef] [Green Version]
- Mekedem, M.; Ravel, P.; Colinge, J. Application of Modular Response Analysis to Medium- to Large-Size Biological Systems. bioRxiv 2021, 453942. [Google Scholar] [CrossRef]
- Santra, T.; Kolch, W.; Kholodenko, B.N. Integrating Bayesian variable selection with Modular Response Analysis to infer biochemical network topology. BMC Syst. Biol. 2013, 7, 57. [Google Scholar] [CrossRef] [Green Version]
- Halasz, M.; Kholodenko, B.N.; Kolch, W.; Santra, T. Integrating network reconstruction with mechanistic modeling to predict cancer therapies. Sci. Signal. 2016, 9, ra114. [Google Scholar] [CrossRef]
- Santra, T.; Rukhlenko, O.; Zhernovkov, V.; Kholodenko, B.N. Reconstructing static and dynamic models of signaling pathways using Modular Response Analysis. Curr. Opin. Syst. Biol. 2018, 9, 11–21. [Google Scholar] [CrossRef]
- Morris, M.K.; Saez-Rodriguez, J.; Sorger, P.; Lauffenburger, D.A. Logic-Based Models for the Analysis of Cell Signaling Networks. Biochemistry 2010, 49, 3216–3224. [Google Scholar] [CrossRef] [Green Version]
- Mishra, D.; Bepler, T.; Teague, B.; Berger, B.; Broach, J.; Weiss, R. An engineered protein-phosphorylation toggle network with implications for endogenous network discovery. Science 2021, 373, aav0780. [Google Scholar] [CrossRef] [PubMed]
- Saez-Rodriguez, J.; Alexopoulos, L.G.; Epperlein, J.; Samaga, R.; Lauffenburger, D.A.; Klamt, S.; Sorger, P.K. Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction. Mol. Syst. Biol. 2009, 5, 331. [Google Scholar] [CrossRef]
- Wynn, M.L.; Consul, N.; Merajver, S.D.; Schnell, S. Logic-based models in systems biology: A predictive and parameter-free network analysis method. Integr. Biol. 2012, 4, 1323–1337. [Google Scholar] [CrossRef] [PubMed]
- Priami, C.; Morine, M.J. Analysis of Biological Systems; Imperial College Press: London, UK, 2015. [Google Scholar]
- Fey, D.; Dobrzynski, M.; Kholodenko, B.N. Modeling with Ordinary Differential Equations. Available online: https://mitpress.mit.edu/books/quantitative-biology (accessed on 9 December 2021)2018.
- Munsky, B.; Hlavacek, W.S.; Tsimring, L.S. (Eds.) Quantitative Biology: Theory, Computational Methods, and Models; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Hurtado, P.J.; Richards, C. Building mean field ODE models using the generalized linear chain trick & Markov chain theory. J. Biol. Dyn. 2021, 15, S248–S272. [Google Scholar] [CrossRef]
- Chen, W.W.; Niepel, M.; Sorger, P.K. Classic and contemporary approaches to modeling biochemical reactions. Genes Dev. 2010, 24, 1861–1875. [Google Scholar] [CrossRef] [Green Version]
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics; Portland Press: London, UK, 1995. [Google Scholar]
- Wilkinson, D.J. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 2009, 10, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.; Grima, R. Spatial Stochastic Intracellular Kinetics: A Review of Modelling Approaches. Bull. Math. Biol. 2018, 81, 2960–3009. [Google Scholar] [CrossRef] [Green Version]
- Simoni, G.; Vo, H.T.; Priami, C.; Marchetti, L. A comparison of deterministic and stochastic approaches for sensitivity analysis in computational systems biology. Brief. Bioinform. 2019, 21, 527–540. [Google Scholar] [CrossRef]
- Hahl, S.K.; Kremling, A. A Comparison of Deterministic and Stochastic Modeling Approaches for Biochemical Reaction Systems: On Fixed Points, Means, and Modes. Front. Genet. 2016, 7, 7. [Google Scholar] [CrossRef] [Green Version]
- Gillespie, D.T. Stochastic Simulation of Chemical Kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35–55. [Google Scholar] [CrossRef]
- Simoni, G.; Reali, F.; Priami, C.; Marchetti, L. Stochastic simulation algorithms for computational systems biology: Exact, approximate, and hybrid methods. Wiley Interdiscip. Rev. Syst. Biol. Med. 2019, 11, e1459. [Google Scholar] [CrossRef] [PubMed]
- Rukhlenko, O.; Khorsand, F.; Krstic, A.; Rozanc, J.; Alexopoulos, L.G.; Rauch, N.; Erickson, K.E.; Hlavacek, W.S.; Posner, R.G.; Gómez-Coca, S.; et al. Dissecting RAF Inhibitor Resistance by Structure-based Modeling Reveals Ways to Overcome Oncogenic RAS Signaling. Cell Syst. 2018, 7, 161–179. [Google Scholar] [CrossRef] [Green Version]
- Blinov, M.; Faeder, J.; Goldstein, B.; Hlavacek, W.S. BioNetGen: Software for rule-based modeling of signal transduction based on the interactions of molecular domains. Bioinformatics 2004, 20, 3289–3291. [Google Scholar] [CrossRef] [PubMed]
- Borisov, N.; Kholodenko, B.; Faeder, J.; Chistopolsky, A. Domain-oriented reduction of rule-based network models. IET Syst. Biol. 2008, 2, 342–351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sneddon, M.W.; Faeder, J.R.; Emonet, T. Efficient modeling, simulation and coarse-graining of biological complexity with NFsim. Nat. Methods 2010, 8, 177–183. [Google Scholar] [CrossRef]
- Erickson, K.E.; Rukhlenko, O.S.; Shahinuzzaman, M.; Slavkova, K.P.; Lin, Y.T.; Suderman, R.; Stites, E.C.; Anghel, M.; Posner, R.G.; Barua, D.; et al. Modeling cell line-specific recruitment of signaling proteins to the insulin-like growth factor 1 receptor. PLoS Comput. Biol. 2019, 15, e1006706. [Google Scholar] [CrossRef] [PubMed]
- Rukhlenko, O.S.; Kholodenko, B.N. Modeling the Nonlinear Dynamics of Intracellular Signaling Networks. Bio Protoc. 2021, 11, e4089. [Google Scholar] [CrossRef] [PubMed]
- Yaffe, M.B. Why geneticists stole cancer research even though cancer is primarily a signaling disease. Sci. Signal. 2019, 12, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Nagashima, T.; Shimodaira, H.; Ide, K.; Nakakuki, T.; Tani, Y.; Takahashi, K.; Yumoto, N.; Hatakeyama, M. Quantitative Transcriptional Control of ErbB Receptor Signaling Undergoes Graded to Biphasic Response for Cell Differentiation. J. Biol. Chem. 2007, 282, 4045–4056. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldbeter, A.; Koshland, D.E., Jr. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA 1981, 78, 6840–6844. [Google Scholar] [CrossRef] [Green Version]
- Markevich, N.I.; Hoek, J.; Kholodenko, B.N. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 2004, 164, 353–359. [Google Scholar] [CrossRef]
- Stelling, J.; Sauer, U.; Szallasi, Z.; Doyle, F.J.; Doyle, J. Robustness of Cellular Functions. Cell 2004, 118, 675–685. [Google Scholar] [CrossRef] [Green Version]
- Kholodenko, B.N. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. JBIC J. Biol. Inorg. Chem. 2000, 267, 1583–1588. [Google Scholar] [CrossRef] [Green Version]
- Pomerening, J.R.; Sontag, E.; Ferrell, J.E. Building a cell cycle oscillator: Hysteresis and bistability in the activation of Cdc2. Nat. Cell Biol. 2003, 5, 346–351. [Google Scholar] [CrossRef] [PubMed]
- Sha, W.; Moore, J.; Chen, K.; Lassaletta, A.D.; Yi, C.-S.; Tyson, J.J.; Sible, J.C. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc. Natl. Acad. Sci. USA 2003, 100, 975–980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novak, B.; Tyson, J. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J. Cell Sci. 1993, 106, 1153–1168. [Google Scholar] [CrossRef] [PubMed]
- Xiong, W.; Ferrell, J.E. A positive-feedback-based bistable ‘memory module’ that governs a cell fate decision. Nat. Cell Biol. 2003, 426, 460–465. [Google Scholar] [CrossRef] [PubMed]
- Yao, G.; Lee, T.J.; Mori, S.; Nevins, J.R.; You, L. A bistable Rb-E2F switch underlies the restriction point. Nat. Cell Biol. 2008, 10, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Sevier, S.A.; Kessler, D.A.; Levine, H. Mechanical bounds to transcriptional noise. Proc. Natl. Acad. Sci. USA 2016, 113, 13983–13988. [Google Scholar] [CrossRef] [Green Version]
- Ham, L.; Brackston, R.D.; Stumpf, M.P.H. Extrinsic Noise and Heavy-Tailed Laws in Gene Expression. Phys. Rev. Lett. 2020, 124, 108101. [Google Scholar] [CrossRef]
- Lu, M.; Onuchic, J.; Ben-Jacob, E. Construction of an Effective Landscape for Multistate Genetic Switches. Phys. Rev. Lett. 2014, 113, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Waddington, C.H. Organisers and Genes; Cambridge University Press: Cambridge, UK, 1940. [Google Scholar]
- Brackston, R.D.; Lakatos, E.; Stumpf, M.P.H. Transition state characteristics during cell differentiation. PLoS Comput. Biol. 2018, 14, e1006405. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Yuan, R.; Wang, G.; Zhu, X.; Gaowei, W. Potential landscape of high dimensional nonlinear stochastic dynamics with large noise. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Brown, G.C.; Kholodenko, B.N. Spatial gradients of cellular phospho-proteins. FEBS Lett. 1999, 457, 452–454. [Google Scholar] [CrossRef] [Green Version]
- Kholodenko, B.N. Spatially distributed cell signalling. FEBS Lett. 2009, 583, 4006–4012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bolado-Carrancio, A.; Rukhlenko, O.S.; Nikonova, E.; Tsyganov, M.A.; Wheeler, A.; Garcia-Munoz, A.; Kolch, W.; von Kriegsheim, A.; Kholodenko, B.N. Periodic propagating waves coordinate RhoGTPase network dynamics at the leading and trailing edges during cell migration. eLife 2020, 9, 1–34. [Google Scholar] [CrossRef]
- Heasman, S.J.; Ridley, A.J. Mammalian Rho GTPases: New insights into their functions from in vivo studies. Nat. Rev. Mol. Cell Biol. 2008, 9, 690–701. [Google Scholar] [CrossRef]
- Edelstein-Keshet, L. Flipping the Rac-Rho Switch in Cell Motility. Cell Syst. 2016, 2, 10–12. [Google Scholar] [CrossRef]
- Machacek, M.; Hodgson, L.; Welch, C.; Elliott, H.; Pertz, O.; Nalbant, P.; Abell, A.; Johnson, G.L.; Hahn, K.M.; Danuser, G. Coordination of Rho GTPase activities during cell protrusion. Nat. Cell Biol. 2009, 461, 99–103. [Google Scholar] [CrossRef] [Green Version]
- Kholodenko, B.N.; Demin, O.V.; Moehren, G.; Hoek, J. Quantification of Short Term Signaling by the Epidermal Growth Factor Receptor. J. Biol. Chem. 1999, 274, 30169–30181. [Google Scholar] [CrossRef] [Green Version]
- Wiley, H.S.; Shvartsman, S.Y.; Lauffenburger, D.A. Computational modeling of the EGF-receptor system: A paradigm for systems biology. Trends Cell Biol. 2003, 13, 43–50. [Google Scholar] [CrossRef]
- Erickson, K.; Rukhlenko, O.; Posner, R.G.; Hlavacek, W.S.; Kholodenko, B.N. New insights into RAS biology reinvigorate interest in mathematical modeling of RAS signaling. Semin. Cancer Biol. 2019, 54, 162–173. [Google Scholar] [CrossRef] [PubMed]
- Kochańczyk, M.; Kocieniewski, P.; Kozlowska, E.; Jaruszewicz-Błońska, J.; Sparta, B.; Pargett, M.; Albeck, J.G.; Hlavacek, W.S.; Lipniacki, T. Relaxation oscillations and hierarchy of feedbacks in MAPK signaling. Sci. Rep. 2017, 7, 38244. [Google Scholar] [CrossRef] [Green Version]
- Hall-Jackson, C.A.; Goedert, M.; Hedge, P.; Cohen, P. Effect of SB 203580 on the activity of c-Raf in vitro and in vivo. Oncogene 1999, 18, 2047–2054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lito, P.; Rosen, N.; Solit, D.B. Tumor adaptation and resistance to RAF inhibitors. Nat. Med. 2013, 19, 1401–1409. [Google Scholar] [CrossRef]
- Rajakulendran, T.; Sahmi, M.; Lefrançois, M.; Sicheri, F.; Therrien, M. A dimerization-dependent mechanism drives RAF catalytic activation. Nat. Cell Biol. 2009, 461, 542–545. [Google Scholar] [CrossRef]
- Kholodenko, B.N. Drug Resistance Resulting from Kinase Dimerization Is Rationalized by Thermodynamic Factors Describing Allosteric Inhibitor Effects. Cell Rep. 2015, 12, 1939–1949. [Google Scholar] [CrossRef] [Green Version]
- Kholodenko, B.N.; Rauch, N.; Kolch, W.; Rukhlenko, O.S. A systematic analysis of signaling reactivation and drug resistance. Cell Rep. 2021, 35, 109157. [Google Scholar] [CrossRef] [PubMed]
- Lito, P.; Pratilas, C.A.; Joseph, E.W.; Tadi, M.; Halilovic, E.; Zubrowski, M.; Huang, A.; Wong, W.L.; Callahan, M.K.; Merghoub, T.; et al. Relief of Profound Feedback Inhibition of Mitogenic Signaling by RAF Inhibitors Attenuates Their Activity in BRAFV600E Melanomas. Cancer Cell 2012, 22, 668–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montero-Conde, C.; Ruiz-Llorente, S.; Dominguez, J.M.; Knauf, J.; Viale, A.; Sherman, E.J.; Ryder, M.; Ghossein, R.A.; Rosen, N.; Fagin, J.A. Relief of Feedback Inhibition of HER3 Transcription by RAF and MEK Inhibitors Attenuates Their Antitumor Effects in BRAF-Mutant Thyroid Carcinomas. Cancer Discov. 2013, 3, 520–533. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prahallad, A.; Sun, C.; Huang, S.; Di Nicolantonio, F.; Salazar, R.; Zecchin, D.; Beijersbergen, R.L.; Bardelli, A.; Bernards, R. Unresponsiveness of colon cancer to BRAF(V600E) inhibition through feedback activation of EGFR. Nat. Cell Biol. 2012, 483, 100–103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ryan, M.B.; de La Cruz, F.F.; Phat, S.; Myers, D.T.; Wong, E.; Shahzade, H.A.; Hong, C.; Corcoran, R.B. Vertical Pathway Inhibition Overcomes Adaptive Feedback Resistance to KRASG12C Inhibition. Clin. Cancer Res. 2019, 26, 1633–1643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, C.; Wang, L.; Huang, S.; Heynen, G.J.J.E.; Prahallad, A.; Robert, C.; Haanen, J.; Blank, C.; Wesseling, J.; Willems, S.M.; et al. Reversible and adaptive resistance to BRAF(V600E) inhibition in melanoma. Nature 2014, 508, 118–122. [Google Scholar] [CrossRef]
- Yaeger, R.; Corcoran, R.B. Targeting Alterations in the RAF-MEK Pathway. Cancer Discov. 2019, 9, 329–341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eduati, F.; Doldàn-Martelli, V.; Klinger, B.; Cokelaer, T.; Sieber, A.; Kogera, F.; Dorel, M.; Garnett, M.J.; Blüthgen, N.; Saez-Rodriguez, J. Drug Resistance Mechanisms in Colorectal Cancer Dissected with Cell Type-Specific Dynamic Logic Models. Cancer Res. 2017, 77, 3364–3375. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Demas, D.M.; Conde, I.P.; Shajahan-Haq, A.N.; Baumann, W.T. Mathematical modelling of breast cancer cells in response to endocrine therapy and Cdk4/6 inhibition. J. R. Soc. Interface 2020, 17, 20200339. [Google Scholar] [CrossRef]
- Chen, C.; Baumann, W.T.; Xing, J.; Xu, L.; Clarke, R.; Tyson, J.J. Mathematical models of the transitions between endocrine therapy responsive and resistant states in breast cancer. J. R. Soc. Interface 2014, 11, 20140206. [Google Scholar] [CrossRef] [PubMed]
- Kondratova, M.; Barillot, E.; Zinovyev, A.; Calzone, L. Modelling of Immune Checkpoint Network Explains Synergistic Effects of Combined Immune Checkpoint Inhibitor Therapy and the Impact of Cytokines in Patient Response. Cancers 2020, 12, 3600. [Google Scholar] [CrossRef] [PubMed]
- Rehm, M.; Huber, H.J.; Düssmann, H.; Prehn, J.H.M. Systems analysis of effector caspase activation and its control by X-linked inhibitor of apoptosis protein. EMBO J. 2006, 25, 4338–4349. [Google Scholar] [CrossRef] [Green Version]
- Hector, S.; Rehm, M.; Schmid, J.; Kehoe, J.; McCawley, N.; Dicker, P.; Murray, F.; McNamara, D.; Kay, E.W.; Concannon, C.G.; et al. Clinical application of a systems model of apoptosis execution for the prediction of colorectal cancer therapy responses and personalisation of therapy. Gut 2011, 61, 725–733. [Google Scholar] [CrossRef]
- Lindner, A.; Concannon, C.G.; Boukes, G.J.; Cannon, M.D.; Llambi, F.; Ryan, D.; Boland, K.; Kehoe, J.; McNamara, D.A.; Murray, F.; et al. Systems Analysis of BCL2 Protein Family Interactions Establishes a Model to Predict Responses to Chemotherapy. Cancer Res. 2013, 73, 519–528. [Google Scholar] [CrossRef] [Green Version]
- Huber, H.J.; McKiernan, R.G.; Prehn, J.H.M. Harnessing system models of cell death signalling for cytotoxic chemotherapy: Towards personalised medicine approaches? J. Mol. Med. 2014, 92, 227–237. [Google Scholar] [CrossRef] [PubMed]
- Béal, J.; Montagud, A.; Traynard, P.; Barillot, E.; Calzone, L. Personalization of Logical Models With Multi-Omics Data Allows Clinical Stratification of Patients. Front. Physiol. 2019, 9, 1965. [Google Scholar] [CrossRef]
- Eduati, F.; Jaaks, P.; Wappler, J.; Cramer, T.; Merten, C.A.; Garnett, M.J.; Saez-Rodriguez, J. Patient-specific logic models of signaling pathways from screenings on cancer biopsies to prioritize personalized combination therapies. Mol. Syst. Biol. 2020, 16, e8664. [Google Scholar] [CrossRef]
- Zañudo, J.G.T.; Steinway, S.; Albert, R. Discrete dynamic network modeling of oncogenic signaling: Mechanistic insights for personalized treatment of cancer. Curr. Opin. Syst. Biol. 2018, 9, 1–10. [Google Scholar] [CrossRef]
- Guo, W.-F.; Zhang, S.-W.; Zeng, T.; Akutsu, T.; Chen, L. Network control principles for identifying personalized driver genes in cancer. Brief. Bioinform. 2019, 21, 1641–1662. [Google Scholar] [CrossRef]
- Guo, W.-F.; Zhang, S.-W.; Feng, Y.-H.; Liang, J.; Zeng, T.; Chen, L. Network controllability-based algorithm to target personalized driver genes for discovering combinatorial drugs of individual patients. Nucleic Acids Res. 2021, 49, e37. [Google Scholar] [CrossRef]
- Maron, B.A.; Wang, R.-S.; Shevtsov, S.; Drakos, S.G.; Arons, E.; Wever-Pinzon, O.; Huggins, G.S.; Samokhin, A.O.; Oldham, W.M.; Aguib, Y.; et al. Individualized interactomes for network-based precision medicine in hypertrophic cardiomyopathy with implications for other clinical pathophenotypes. Nat. Commun. 2021, 12, 1–11. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Stanford, N.J.; Lubitz, T.; Smallbone, K.; Klipp, E.; Mendes, P.; Liebermeister, W. Systematic Construction of Kinetic Models from Genome-Scale Metabolic Networks. PLoS ONE 2013, 8, e79195. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, A.; Maranas, C.D. Personalized Kinetic Models for Predictive Healthcare. Cell Syst. 2015, 1, 250–251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bordbar, A.; McCloskey, D.; Zielinski, D.C.; Sonnenschein, N.; Jamshidi, N.; Palsson, B.O. Personalized Whole-Cell Kinetic Models of Metabolism for Discovery in Genomics and Pharmacodynamics. Cell Syst. 2015, 1, 283–292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, J.; Forshaw, T.E.; Boothman, D.A.; Furdui, C.M.; Kemp, M.L. Personalized Genome-Scale Metabolic Models Identify Targets of Redox Metabolism in Radiation-Resistant Tumors. Cell Syst. 2021, 12, 68–81. [Google Scholar] [CrossRef] [PubMed]
- Fey, D.; Halasz, M.; Dreidax, D.; Kennedy, S.P.; Hastings, J.F.; Rauch, N.; Munoz, A.G.; Pilkington, R.; Fischer, M.; Westermann, F.; et al. Signaling pathway models as biomarkers: Patient-specific simulations of JNK activity predict the survival of neuroblastoma patients. Sci. Signal. 2015, 8, ra130. [Google Scholar] [CrossRef] [Green Version]
- Flaherty, K.T.; Gray, R.J.; Chen, A.P.; Li, S.; McShane, L.M.; Patton, D.; Hamilton, S.R.; Williams, P.M.; Iafrate, A.J.; Sklar, J.; et al. Molecular Landscape and Actionable Alterations in a Genomically Guided Cancer Clinical Trial: National Cancer Institute Molecular Analysis for Therapy Choice (NCI-MATCH). J. Clin. Oncol. 2020, 38, 3883–3894. [Google Scholar] [CrossRef]
- André, F.; Bachelot, T.; Commo, F.; Campone, M.; Arnedos, M.; Dieras, V.; Lacroix-Triki, M.; Lacroix, L.; Cohen, P.; Gentien, D.; et al. Comparative genomic hybridisation array and DNA sequencing to direct treatment of metastatic breast cancer: A multicentre, prospective trial (SAFIR01/UNICANCER). Lancet Oncol. 2014, 15, 267–274. [Google Scholar] [CrossRef]
- Turner, N.C.; Kingston, B.; Kilburn, L.; Kernaghan, S.; Wardley, A.M.; Macpherson, I.R.; Baird, R.; Roylance, R.; Stephens, P.; Oikonomidou, O.; et al. Circulating tumour DNA analysis to direct therapy in advanced breast cancer (plasmaMATCH): A multicentre, multicohort, phase 2a, platform trial. Lancet Oncol. 2020, 21, 1296–1308. [Google Scholar] [CrossRef]
- Cobain, E.F.; Wu, Y.-M.; Vats, P.; Chugh, R.; Worden, F.; Smith, D.C.; Schuetze, S.M.; Zalupski, M.M.; Sahai, V.; Alva, A.; et al. Assessment of Clinical Benefit of Integrative Genomic Profiling in Advanced Solid Tumors. JAMA Oncol. 2021, 48109, 1–9. [Google Scholar] [CrossRef]
- Sicklick, J.K.; Kato, S.; Okamura, R.; Schwaederle, M.; Hahn, M.E.; Williams, C.B.; De, P.; Krie, A.; Piccioni, D.E.; Miller, V.A.; et al. Molecular profiling of cancer patients enables personalized combination therapy: The I-PREDICT study. Nat. Med. 2019, 25, 744–750. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Niepel, M.; Mitchison, T.K.; Sorger, P.K. Dissecting Variability in Responses to Cancer Chemotherapy Through Systems Pharmacology. Clin. Pharmacol. Ther. 2010, 88, 34–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niikura, N.; Shimomura, A.; Fukatsu, Y.; Sawaki, M.; Ogiya, R.; Yasojima, H.; Fujisawa, T.; Yamamoto, M.; Tsuneizumi, M.; Kitani, A.; et al. Durable complete response in HER2-positive breast cancer: A multicenter retrospective analysis. Breast Cancer Res. Treat. 2018, 167, 81–87. [Google Scholar] [CrossRef]
- Witzel, I.; Müller, V.; Abenhardt, W.; Kaufmann, M.; Schoenegg, W.; Schneeweiß, A.; Jänicke, F. Long-term tumor remission under trastuzumab treatment for HER2 positive metastatic breast cancer-results from the HER-OS patient registry. BMC Cancer 2014, 14, 806. [Google Scholar] [CrossRef] [Green Version]
- Spano, J.-P.; Beuzeboc, P.; Coeffic, D.; Arnould, L.; Lortholary, A.; Andre, F.; Ferrero, J.-M. Long term HER2+ metastatic breast cancer survivors treated by trastuzumab: Results from the French cohort study LHORA. Breast 2015, 24, 376–383. [Google Scholar] [CrossRef]
- Jabbour, E.; Kantarjian, H. Chronic myeloid leukemia: 2020 update on diagnosis, therapy and monitoring. Am. J. Hematol. 2020, 95, 691–709. [Google Scholar] [CrossRef] [PubMed]
- Schork, N.J. Personalized medicine: Time for one-person trials. Nat. Cell Biol. 2015, 520, 609–611. [Google Scholar] [CrossRef]
- Lillie, E.O.; Patay, B.; Diamant, J.; Issell, B.; Topol, E.J.; Schork, N.J. The n-of-1 clinical trial: The ultimate strategy for individualizing medicine? Pers. Med. 2011, 8, 161–173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antman, E.; Weiss, S.; Loscalzo, J. Systems pharmacology, pharmacogenetics, and clinical trial design in network medicine. Wiley Interdiscip. Rev. Syst. Biol. Med. 2012, 4, 367–383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C.; Dignam, J.J. Biomarker-Driven Oncology Clinical Trials: Key Design Elements, Types, Features, and Practical Considerations. JCO Precis. Oncol. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Simon, R. Review of Statistical Methods for Biomarker-Driven Clinical Trials. JCO Precis. Oncol. 2019, 1–9. [Google Scholar] [CrossRef]
- Antoniou, M.; Jorgensen, A.L.; Kolamunnage-Dona, R. Biomarker-Guided Adaptive Trial Designs in Phase II and Phase III: A Methodological Review. PLoS ONE 2016, 11, e0149803. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, M.; Kolamunnage-Dona, R.; Jorgensen, A.L. Biomarker-Guided Non-Adaptive Trial Designs in Phase II and Phase III: A Methodological Review. J. Pers. Med. 2017, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Kolch, W.; Fey, D. Personalized Computational Models as Biomarkers. J. Pers. Med. 2017, 7, 9. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocca, A.; Kholodenko, B.N. Can Systems Biology Advance Clinical Precision Oncology? Cancers 2021, 13, 6312. https://doi.org/10.3390/cancers13246312
Rocca A, Kholodenko BN. Can Systems Biology Advance Clinical Precision Oncology? Cancers. 2021; 13(24):6312. https://doi.org/10.3390/cancers13246312
Chicago/Turabian StyleRocca, Andrea, and Boris N. Kholodenko. 2021. "Can Systems Biology Advance Clinical Precision Oncology?" Cancers 13, no. 24: 6312. https://doi.org/10.3390/cancers13246312
APA StyleRocca, A., & Kholodenko, B. N. (2021). Can Systems Biology Advance Clinical Precision Oncology? Cancers, 13(24), 6312. https://doi.org/10.3390/cancers13246312






