Mechanistic Modelling of Slow and Fast NHEJ DNA Repair Pathways Following Radiation for G0/G1 Normal Tissue Cells
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. DNA Damage Model
2.2. DNA Repair Model; Workings, Assumptions, and Limitations
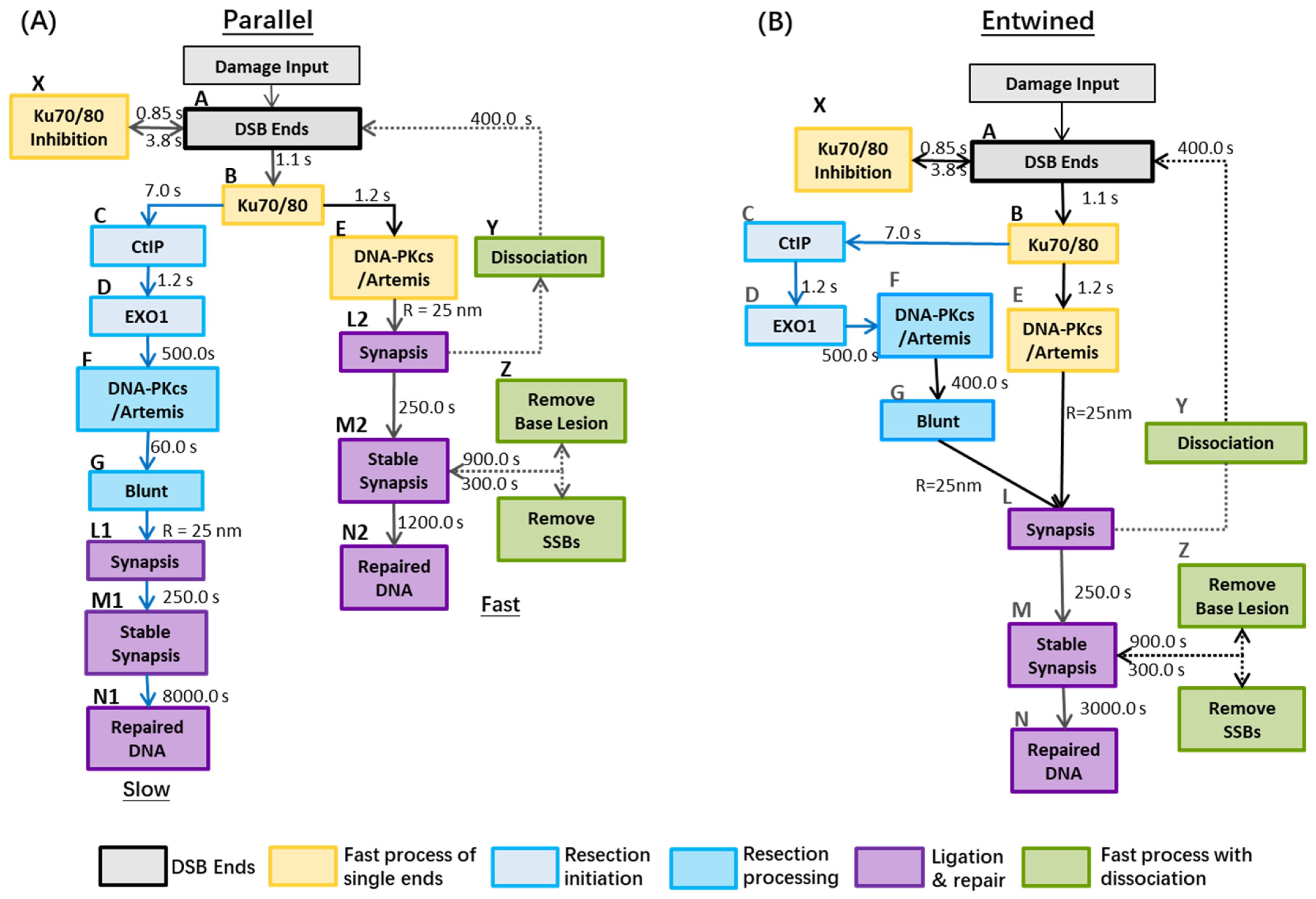
2.3. Potential Models in G0/G1 Cells for Combined Slow and Fast Processes
| Process | Model A | Model B | Fitted |
|---|---|---|---|
| Ku70/80 Inhibition | 0.85 | 0.85 | Ref. [18] |
| Release from Ku70/70 Inhibition | 3.8 | 3.8 | Ref. [18] |
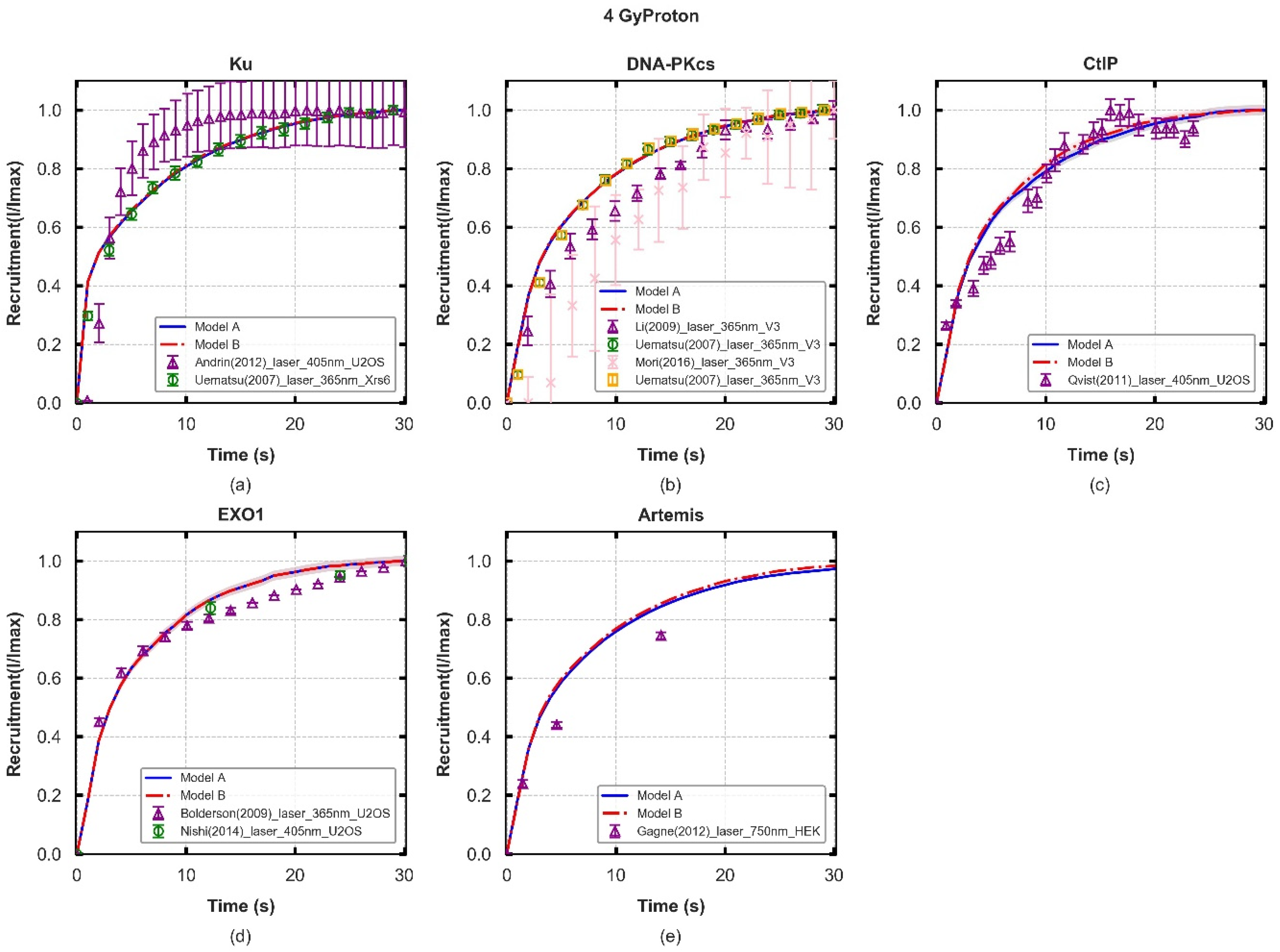
| Ku70/80 Recruitment | 1.1 | 1.1 | Figure 2a |
| DNA-PKcs Recruitment in fast process | 1.2 | 1.2 | Figure 2b |
| Artemis:DNA-PKcs Recruitment resection process | 500.0 | 500.0 | Figure 2b |
| CtIP Recruitment | 7.0 | 7.0 | Figure 2c |
| EXO1 Recruitment | 1.2 | 1.2 | Figure 2d |
| Become blunts | 60.0 | 400.0 | Figure 2e |
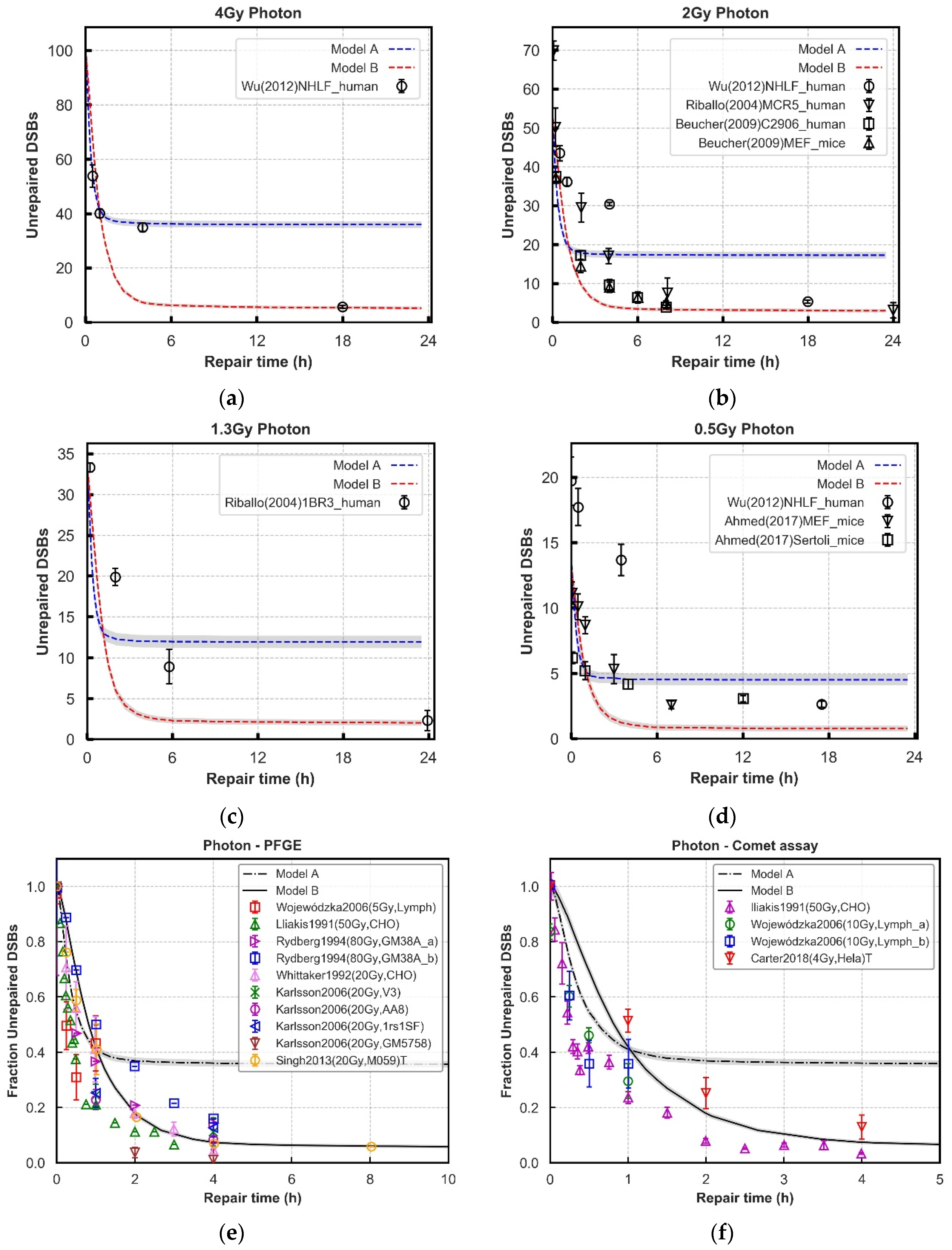
| Dissociation of synapsis | 400.0 | 400.0 | Figure 3 and Figure 4 |
| Remove Base lesion | 300.0 | 300.0 | Ref. [18] |
| Remove SSBs | 900.0 | 900.0 | Ref. [18] |
| Stabilisation of synapsis | 250.0 | 250.0 | Ref. [18] |
| Ligation of two ends | 1200.0/8000.0 | 3000.0 | Ref. [18] and Figure 3 and Figure 4 |
| Form synapsis (nm) | 25 | 25 | Ref. [18] |
| Jump diffusion coefficient (nm2·s−1) | 6.0 × e10 | 6.0 × e10 | Figure 5 |
| Synapsis can form between DSB ends from different pathways | No | Yes | |
| Artemis & DNA-PKcs co-recruitment | Yes | Yes | |
| All DSB ends require Artemis | No | No | |
| Dissociation in slow process | No | Yes | |
| Final fixed ligation stage | Long (slow brach) and Fast (fast branch) | Intermediate |

2.4. Model Evaluation; Fitting Data and Limitations
3. Results
3.1. Recruitment Kinetics of Repair Proteins
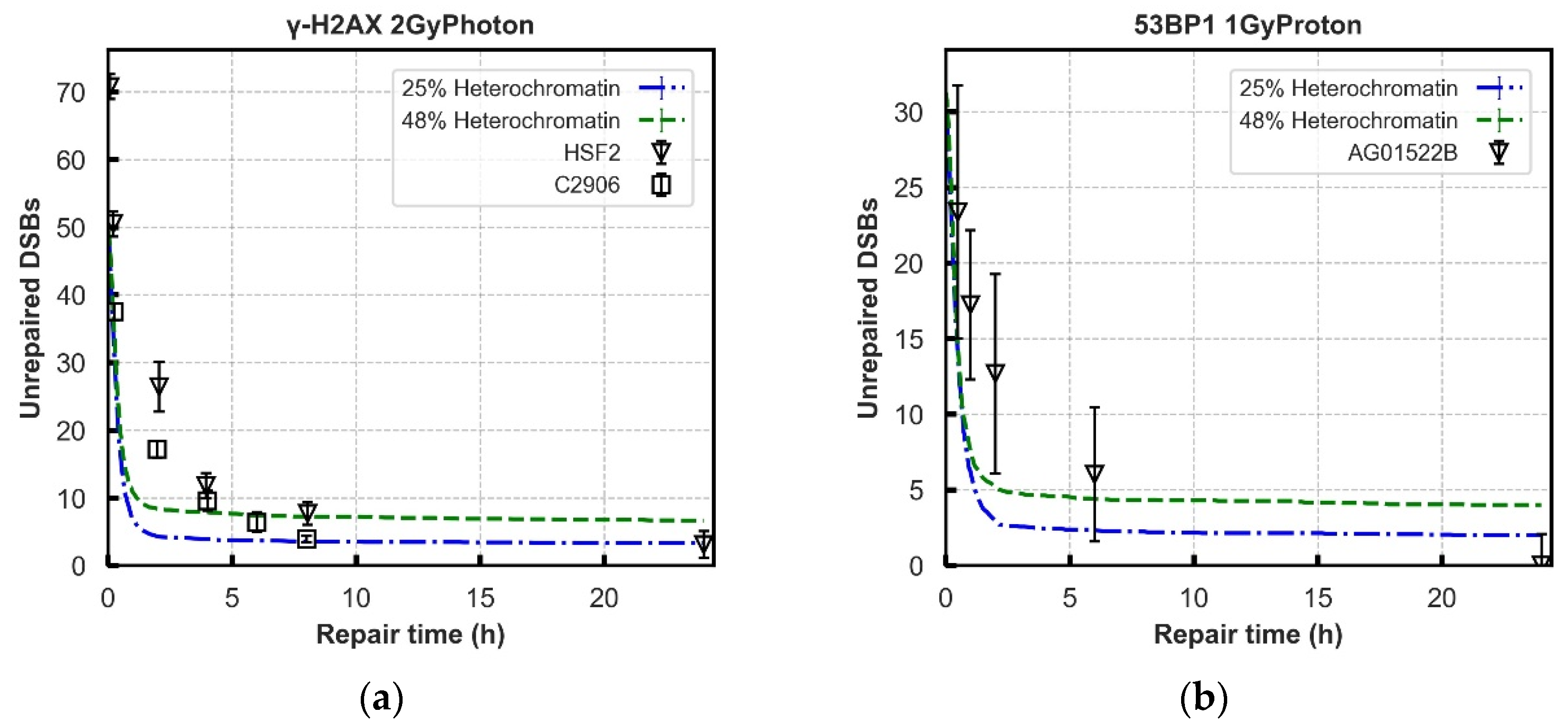
3.2. Repair Kinetics for Wild-Type Cells
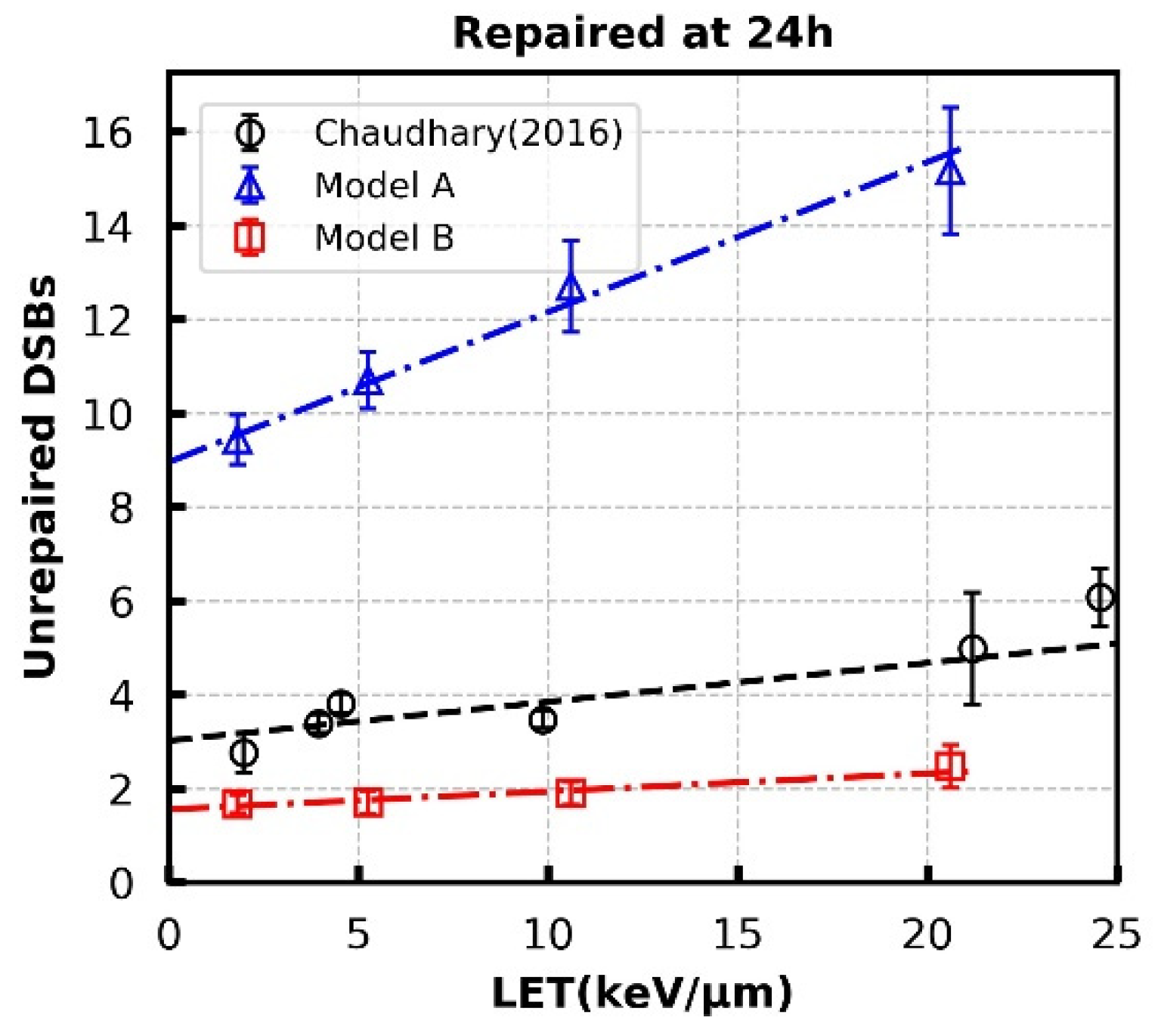
3.3. Repair Kinetics for Protein-Deficient Cells
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shibata, A.; Jeggo, P.A. Historical reflection on our understanding of radiation-induced DNA double strand break repair in somatic mammalian cells; interfacing the past with the present. Int. J. Radiat. Biol. 2019, 95, 945–956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rothkamm, K.; Kruger, I.; Thompson, L.H.; Lobrich, M. Pathways of DNA double-strand break repair during the mammalian cell cycle. Mol. Cell. Biol. 2003, 23, 5706–5715. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.H.Y.; Pannunzio, N.R.; Adachi, N.; Lieber, M.R. Non-homologous DNA end joining and alternative pathways to double-strand break repair. Nat. Rev. Mol. Cell Biol. 2017, 18, 495–506. [Google Scholar] [CrossRef] [PubMed]
- Jeggo, P. Artemis links ATM to Double Strand Break Rejoining. Cell Cycle 2005, 4, 359–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, P.; Gan, W.; Guo, C.; Xie, A.; Gao, D.; Guo, J.; Zhang, J.; Willis, N.; Su, A.; Asara, J. Akt-mediated phosphorylation of XLF impairs non-homologous end-joining DNA repair. Mol. Cell 2015, 57, 648–661. [Google Scholar] [CrossRef] [Green Version]
- Shibata, A.; Jeggo, P. Canonical DNA non-homologous end-joining; capacity versus fidelity. Br. J. Radiol. 2020, 93, 20190966. [Google Scholar] [CrossRef] [PubMed]
- Mcmahon, S.J.; Prise, K.M. Mechanistic Modelling of Radiation Responses. Cancers 2019, 11, 205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thames, H.D.; Withers, H.R.; Peters, L.J.; Fletcher, G.H. Changes in early and late radiation responses with altered dose fractionation: Implications for dose-survival relationships. Int. J. Radiat. Oncol. Biol. Phys. 1982, 8, 219–226. [Google Scholar] [CrossRef]
- Alper, T.; Gillies, N.E.; Elkind, M.M. The Sigmoid Survival Curve in Radiobiology. Nature 1960, 186, 1062–1063. [Google Scholar] [CrossRef] [PubMed]
- KraMer, M.; Scholz, M. Treatment planning for heavy-ion radiotherapy: Calculation and optimization of biologically effective dose. Phys. Med. Biol. 2000, 45, 3319–3330. [Google Scholar] [CrossRef]
- Mcnamara, A.L.; Schuemann, J.; Paganetti, H. A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data. Phys. Med. Biol. 2015, 60, 8399–8416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inaniwa, T.; Kanematsu, N.; Noda, K.; Kamada, T. Treatment planning of intensity modulated composite particle therapy with dose and linear energy transfer optimization. Phys. Med. Biol. 2017, 62, 5180–5197. [Google Scholar] [CrossRef] [PubMed]
- Stewart, R.D.; Streitmatter, S.W.; Argento, D.C.; Kirkby, C.; Goorley, J.T.; Moffitt, G.; Jevremovic, T.J.; Sandison, G.A. Rapid MCNP simulation of DNA double strand break (DSB) relative biological effectiveness (RBE) for photons, neutrons, and light ions. Phys. Med. Biol. 2015, 60, 8249–8274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedland, W.; Dingfelder, M.; Kundrat, P.; Jacob, P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat. Res. 2011, 711, 28–40. [Google Scholar] [CrossRef] [PubMed]
- Friedland, W.; Jacob, P.; Bernhardt, P.; Herwig, G.P.; Dingfelder, M. Simulation of DNA Damage after Proton Irradiation. Rad. Res. 2003, 159, 401–410. [Google Scholar] [CrossRef]
- Friedland, W.; Schmitt, E.; Kundrat, P.; Dingfelder, M.; Baiocco, G.; Barbieri, S.; Ottolenghi, A. Comprehensive track-structure based evaluation of DNA damage by light ions from radiotherapy-relevant energies down to stopping. Sci. Rep. 2017, 7, 45161. [Google Scholar] [CrossRef] [PubMed]
- Henthorn, N.T.; Warmenhoven, J.W.; Sotiropoulos, M.; Mackay, R.I.; Kirkby, N.F.; Kirkby, K.J.; Merchant, M.J. In Silico Non-Homologous End Joining Following Ion Induced DNA Double Strand Breaks Predicts That Repair Fidelity Depends on Break Density. Sci. Rep. 2018, 8, 2654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warmenhoven, J.W.; Henthorn, N.T.; Ingram, S.P.; Chadwick, A.L.; Sotiropoulos, M.; Korabel, N.; Fedotov, S.; Mackay, R.I.; Kirkby, N.F.; Kirkby, K.J.; et al. Insights into the non-homologous end joining pathway and double strand break end mobility provided by mechanistic in silico modelling. DNA Repair 2020, 85, 102743. [Google Scholar] [CrossRef] [PubMed]
- Ingram, S.P.; Warmenhoven, J.W.; Henthorn, N.T.; Smith, E.A.K.; Chadwick, A.L.; Burnet, N.G.; Mackay, R.I.; Kirkby, N.F.; Kirkby, K.J.; Merchant, M.J. Mechanistic modelling supports entwined rather than exclusively competitive DNA double-strand break repair pathway. Sci. Rep. 2019, 9, 6359. [Google Scholar] [CrossRef]
- Taleei, R.; Nikjoo, H. Biochemical DSB-repair model for mammalian cells in G1 and early S phases of the cell cycle. Mutat. Res. 2013, 756, 206–212. [Google Scholar] [CrossRef]
- Riballo, E.; Kuhne, M.; Rief, N.; Doherty, A.; Lobrich, M. A pathway of double-strand break rejoining dependent upon ATM, Artemis, and proteins locating to gamma-H2AX foci. Mol. Cell 2004, 16, 715–724. [Google Scholar] [CrossRef] [PubMed]
- Shibata, A.; Conrad, S.; Birraux, J.; Geuting, V.; Barton, O. Factors determining DNA double-strand break repair pathway choice in G2 phase. EMBO J. 2011, 30, 1079–1092. [Google Scholar] [CrossRef] [PubMed]
- Lobrich, M.; Jeggo, P.A. Process of Resection-Dependent Nonhomologous End Joining Involving the Goddess Artemis. Trends Biochem. Sci. 2017, 42, 690–701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biehs, R.; Steinlage, M.; Barton, O.; Juhász, S.; Künzel, J.; Spies, J.; Shibata, A.; Jeggo, P.A.; Lobrich, M. DNA Double-Strand Break Resection Occurs during Non-homologous End Joining in G1 but Is Distinct from Resection during Homologous Recombination. Mol. Cell 2017, 65, 671–684. [Google Scholar] [CrossRef] [Green Version]
- Yasuhara, T.; Kato, R.; Hagiwara, Y.; Shiotani, B.; Yamauchi, M.; Nakada, S.; Shibata, A.; Miyagawa, K. Human Rad52 Promotes XPG-Mediated R-loop Processing to Initiate Transcription-Associated Homologous Recombination Repair. Cell 2018, 175, 558–570. [Google Scholar] [CrossRef] [Green Version]
- Barton, O.; Naumann, S.C.; Diemer-Biehs, R.; Künzel, J.; Steinlage, M.; Conrad, S.; Makharashvili, N.; Wang, J.; Feng, L.; Lopez, B. Polo-like kinase 3 regulates CtIP during DNA double-strand break repair in G1. J. Cell Biol. 2014, 206, 877–894. [Google Scholar] [CrossRef]
- Zhu, Z.; Chung, W.H.; Shim, E.Y.; Sang, E.L.; Ira, G. Sgs1 helicase and two nucleases Dna2 and Exo1 resect DNA double-strand break ends. Cell 2008, 134, 981–994. [Google Scholar] [CrossRef] [Green Version]
- Carabe-Fernandez, A.; Dale, R.G.; Jones, B. The incorporation of the concept of minimum RBE (RbEmin) into the linear-quadratic model and the potential for improved radiobiological analysis of high-LET treatments. Int. J. Radiat. Biol. 2007, 83, 27–39. [Google Scholar] [CrossRef]
- Smith, E.K.; Henthorn, N.T.; Warmenhoven, J.W.; Ingram, S.P.; Mackay, R.I. In Silico Models of DNA Damage and Repair in Proton Treatment Planning: A Proof of Concept. Sci. Rep. 2019, 9, 19870. [Google Scholar] [CrossRef] [PubMed]
- Cornforth, M.N.; Bedford, J.S. A quantitative comparison of potentially lethal damage repair and the rejoining of interphase chromosome breaks in low passage normal human fibroblasts. Radiat. Res. 1987, 111, 385–405. [Google Scholar] [CrossRef] [PubMed]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guèye, P.; Mantero, A.; Mascielino, B.; Moretto, P. The Geant4-DNA Project. Int. J. Model. Simul. Sci. Comput. 2019, 1, 157–178. [Google Scholar] [CrossRef]
- Henthorn, N.T.; Warmenhoven, J.W.; Sotiropoulos, M.; Mackay, R.I.; Kirkby, K.J.; Merchant, M.J. Nanodosimetric Simulation of Direct Ion-Induced DNA Damage Using Different Chromatin Geometry Models. Radiat. Res. 2017, 188, 690–703. [Google Scholar] [CrossRef] [PubMed]
- Ingram, S.P.; Henthorn, N.T.; Warmenhoven, J.W.; Kirkby, N.F.; Mackay, R.I.; Kirkby, K.J.; Merchant, M.J. Hi-C implementation of genome structure for in silico models of radiation-induced DNA damage. PLoS Comput. Biol. 2020, 16, e1008476. [Google Scholar] [CrossRef] [PubMed]
- Schuemann, J.; Warmenhoven, J.W.; Henthorn, N.T.; Kirkby, K.J.; Merchant, M.J.; Ingram, S.P.; Paganetti, H.; Held, K.D.; Ramos-Mendez, J.; Faddegon, W.; et al. A New Standard DNA Damage (SDD) Data Format. Radiat. Res. 2019, 191, 76–92. [Google Scholar] [CrossRef] [PubMed]
- Tang, N.; Bueno, M.; Incerti, S.; Tran, N.H.; Vaurijoux, A.; Gruel, G.; Villagrasa, C. Influence of chromatin compaction on simulated early radiation-induced DNA damage using Geant4-DNA. Med. Phys. 2019, 46, 1501–1511. [Google Scholar] [CrossRef] [Green Version]
- Goodarzi, A.A.; Noon, A.T.; Deckbar, D.; Ziv, Y.; Jeggo, P.A. ATM signaling facilitates repair of DNA double-strand breaks associated with heterochromatin. Mol. Cell 2008, 31, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Lisa, W.; Brunton, H.; Goodarzi, A.A.; Shibata, P.A.; Jeggo, P.A. Endogenously induced DNA double strand breaks arise in heterochromatic DNA regions and require ataxia telangiectasia mutated and Artemis for their repair. Nucleic Acids Res. 2011, 16, 6986–6997. [Google Scholar]
- Burgess, R.C.; Burman, B.; Kruhlak, M.J.; Misteli, T. Activation of DNA Damage Response Signaling by Condensed Chromatin. Cell Rep. 2014, 9, 1703–1717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, K.J.; Saha, J.; Sun, J.; Fattah, K.R.; Wang, S.C.; Jakob, B.; Chi, L.; Wang, S.Y.; Taucher-Scholz, G.; Davis, A.J. Phosphorylation of Ku dictates DNA double-strand break (DSB) repair pathway choice in S phase. Nucleic Acids Res. 2016, 44, 1732–1745. [Google Scholar] [CrossRef] [Green Version]
- Uematsu, N.; Weterings, E.; Yano, K.; Morotomi-Yano, K.; Chen, D.J. Autophosphorylation of DNA-PKCS regulates its dynamics at DNA double-strand breaks. J. Cell Biol. 2007, 177, 219–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Graham, T.W.; Walter, J.C.; Loparo, J.J. Two-Stage Synapsis of DNA Ends during Non-homologous End Joining. Mol. Cell 2016, 61, 850–858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kishore, K.; Chiruvella, Z.L.; Thomas, E.W. Repair of Double-Strand Breaks by End Joining. Cold Spring Harb. Perspect. Biol. 2013, 5, a012757. [Google Scholar]
- Brown, J.S.; O′carrigan, B.; Jackson, S.P.; Yap, T.A. Targeting DNA Repair in Cancer: Beyond PARP Inhibitors. Cancer Discov. 2017, 7, 20–37. [Google Scholar] [CrossRef] [Green Version]
- Walker, J.R. Structure of the Ku heterodimer bound to DNA and its implications for double-strand break repair. Nature 2001, 412, 607–614. [Google Scholar] [CrossRef] [PubMed]
- Goodarzi, A.A.; Yu, Y.; Riballo, E.; Douglas, P.; Lees-Miller, S.P. DNA-PK autophosphorylation facilitates Artemis endonuclease activity. EMBO J. 2006, 25, 3880–3889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shibata, A.; Moiani, D.; Arvai, A.S.; Perry, J.; Harding, S.M.; Genois, M.M.; Maity, R.; Rossum-Fikkert, S.; Kertokalio, A.; Romoli, R.; et al. DNA double-strand break repair pathway choice is directed by distinct MRE11 nuclease activities. Mol. Cell 2014, 53, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Tomimatsu, N.; Mukherjee, B.; Deland, K.; Kurimasa, A.; Burma, S. Exo1 plays a major role in DNA end resection in humans and influences double-strand break repair and damage signaling decisions. DNA Repair 2012, 11, 441–448. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Pannicke, U.; Schwarz, K.; Lieber, M.R. Hairpin opening and overhang processing by an Artemis/DNA-dependent protein kinase complex in nonhomologous end joining and V(D)J recombination. Cell 2002, 108, 781–794. [Google Scholar] [CrossRef] [Green Version]
- Dynan, W.S.; Yoo, S. Interaction of Ku protein and DNA-dependent protein kinase catalytic subunit with nucleic acids. Nucleic Acids Res. 1998, 26, 1551–1559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, J.; Li, S.; Zhang, X.; LC Wang, L.C.; Niewolik, D.; Schwarz, K.K.; Legerski, R.J.; Zandi, E.; Lieber, M.R. DNA-PKcs regulates a single-stranded DNA endonuclease activity of Artemis. DNA Repair 2010, 9, 429–437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rydberg, B.; Lobrich, M.; Cooper, P.K. DNA double-strand breaks induced by high-energy neon and iron ions in human fibroblasts. I. Pulsed-field gel electrophoresis method. Radiat. Res. 1994, 139, 133–141. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, B. Role of Non-Homologous End-Joining in Repair of Radiation-Induced DNA Double-Strand Breaks; Acta Universitatis Upsaliensis: Uppsala, Sweden, 2006. [Google Scholar]
- Wojewodzka, M.; Buraczewska, I.; Szumiel, I.; Gradzka, I. DNA double-strand break rejoining in radioadapted human lymphocytes: Evaluation by neutral comet assay and pulse-field gel electrophoresis. Nukl. Orig. Ed. 2006, 51, 185–191. [Google Scholar]
- Singh, S.K.; Bencsik-Theilen, A.; Mladenov, E. Reduced contribution of thermally labile sugar lesions to DNA double strand break formation after exposure to heavy ions. Radiat. Oncol. 2013, 8, 77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lliakis, G. The role of DNA double strand breaks in lonizing radiation-induced killing of eukaryotic cells. Bioessays 1991, 13, 641–648. [Google Scholar] [CrossRef] [PubMed]
- Carter, R.J.; Nickson, C.M.; Thompson, J.M.; Kacperek, A.; Hill, M.A.; Parsons, J.L. Complex DNA Damage Induced by High Linear Energy Transfer Alpha-Particles and Protons Triggers a Specific Cellular DNA Damage Response. Int. J. Radiat. Oncol. Biol. Phys. 2018, 100, 776–784. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whitaker, S.J.; Mcmillan, T.J. Pulsed-field gel electrophoresis in the measurement of DNA double-strand break repair in xrs-6 and CHO cell lines: DNA degradation under some conditions interferes with the assessment of double-strand break rejoining. Radiat. Res. 1992, 130, 389–392. [Google Scholar] [CrossRef]
- Nishi, R.; Wijnhoven, P.; Sage, C.L.; Tjeertes, J.; Galanty, Y.; Forment, J.V.; Clague, M.J.; Urbé, S.; Jackson, S.P. Systematic characterization of deubiquitylating enzymes for roles in maintaining genome integrity. Nat. Cell Biol. 2014, 16, 1016–1026. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qvist, P.; Huertas, P.; Jimeno, S.; Nyegaard, M.; Børglum, A.D. CtIP Mutations Cause Seckel and Jawad Syndromes. PLoS Genet. 2011, 7, e1002310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gagné, J.P.; Pic, E.; Isabelle, M.; Krietsch, J.; Éthier, C.; Paquet, E.; Kelly, I.; Boutin, M.; Moon, K.M.; Foster, L.J.; et al. Quantitative proteomics profiling of the poly(ADP-ribose)-related response to genotoxic stress. Nucleic Acids Res. 2012, 40, 7788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrin, C.; Mcdonald, D.; Attwood, K.M.; Rodrigue, A.; Ghosh, S.; Mirzayans, R.; Masson, J.Y.; Dellaire, G.; Hendzel, M.J. A requirement for polymerized actin in DNA double-strand break repair. Nucleus 2012, 3, 384–395. [Google Scholar] [CrossRef] [Green Version]
- Li, A.Y.J.; Boo, L.M.; Wang, S.Y.; Lin, H.H.; Wang, C.C.C.; Yen, Y.; Chen, B.P.C.; Chen, D.J.; Ann, D.K. Suppression of nonhomologous end joining repair by overexpression of HMGA2. Cancer Res. 2009, 69, 5699–5706. [Google Scholar] [CrossRef] [Green Version]
- Mori, E.; Davis, A.J.; Hasegawa, M.; Chen, D.J. Lysines 3241 and 3260 of DNA-PKcs are important for genomic stability and radioresistance. Biophys. Res. Commun. 2016, 477, 235–240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emma, B.; Nozomi, T.; Richard, D.J.; Didier, B.; Rakesh, K.; Pandita, T.K.; Sandeep, B.; Kum, K.K. Phosphorylation of Exo1 modulates homologous recombination repair of DNA double-strand breaks. Nucleic Acids Res. 2019, 38, 1821–1831. [Google Scholar]
- Ahmed, E.A. DNA repair kinetics in SCID mice Sertoli cells and DNA-PKcs-deficient mouse embryonic fibroblasts. Chromosoma 2017, 126, 287–298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, J.; Fu, Q.; Quan, Y.; Wang, W.; Mei, T.; Li, J.; Yang, G.; Ren, X.; Xue, J.; Wang, Y. Repair rates of DNA double-strand breaks under different doses of proton and γ-ray irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B 2012, 276, 1–6. [Google Scholar] [CrossRef]
- Beucher, A.B.J.; Tchouandong, L.; Barton, O.; Shibata, A.; Conrad, S.; Goodarzi, A.A.; Krempler, A.; Jeggo, P.A.; Lobrich, M. ATM and Artemis promote homologous recombination of radiation-induced DNA double-strand breaks in G2. EMBO J. 2009, 28, 3413–3427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miszczyk, J.; Panek, A. DNA Repair Progress in Human Lymphocytes Irradiated With A 60-MeV Proton Radiotherapeutic Beam. In Proceedings of the RAD Conference Proceedings, Herceg Novi, Montenegro, 1 January 2019. [Google Scholar]
- Barbieri, S.; Babini, G.; Morini, J.; Friedland, W.; Buonanno, M.; Grilj, V.; Brenner, D.J.; Ottolenghi, A.; Baiocco, G. Predicting DNA damage foci and their experimental readout with 2D microscopy: A unified approach applied to photon and neutron exposures. Sci. Rep. 2019, 9, 14019. [Google Scholar] [CrossRef] [PubMed]
- Rabus, H.; Barbieri, S.; Baiocco, G.; Ottolenghi, A.; Giesen, U. Investigation into the Probability for Miscounting in Foci-Based Assays. Radiat. Prot. Dosim. 2018, 183, 126–130. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, P.; Marshall, T.I.; Frederick, J.C.; Kacperek, A.; Prise, K.M. Variations in the Processing of DNA Double-Strand Breaks Along 60-MeV Therapeutic Proton Beams. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 86–94. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henthorn, N.T.; Warmenhoven, J.W.; Sotiropoulos, M.; Aitkenhead, A.H.; Smith, E.A.K.; Ingram, S.P.; Kirkby, N.F.; Chadwick, A.L.; Burnet, N.G.; Mackay, R.I. Clinically relevant nanodosimetric simulation of DNA damage complexity from photons and protons. RSC Adv. 2019, 9, 6845–6858. [Google Scholar] [CrossRef] [Green Version]
- Oeck, S.; Szymonowicz, K.; Wiel, G.; Krysztofiak, A.; Lambert, J.; Koska, B.; Iliakis, G.; Timmermann, B.; Jendrossek, V. Relating Linear Energy Transfer to the Formation and Resolution of DNA Repair Foci after Irradiation with Equal Doses of X-ray Photons, Plateau, or Bragg-Peak Protons. Int. J. Mol. Sci. 2018, 19, 3779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girst, S.; Hable, V.; Drexler, G.A.; Greubel, C.; Dollinger, G. Subdiffusion Supports Joining of Correct Ends During Repair of DNA Double-Strand Breaks. Sci. Rep. 2013, 3, 2511. [Google Scholar] [CrossRef]
- Soutoglou, E.; Dorn, J.F.; Sengupta, K.; Jasin, M.; Nussenzweig, A.; Ried, T.; Danuser, G.; Misteli, T. Positional stability of single double-strand breaks in mammalian cells. Nat. Cell Biol. 2007, 9, 675–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joiner, M.C.; Marples, B.; Lambin, P.; Short, S.C.; Turesson, I. Low-dose hypersensitivity: Current status and possible mechanisms-ScienceDirect. Int. J. Radiat. Oncol. Biol. Phys. 2001, 49, 379–389. [Google Scholar] [CrossRef]
- Lucas, J.S.; Zhang, Y.; Dudko, O.K.; Murre, C. 3D Trajectories Adopted by Coding and Regulatory DNA Elements: First-Passage Times for Genomic Interactions. Cell 2014, 158, 339–352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Okada, R.R. Estimation of Life Times and Diffusion Distances of Radicals Involved in X-ray-Induced DNA Strand Breaks or Killing of Mammalian Cells. Rad. Res. 1975, 64, 306–320. [Google Scholar]
- Yaneva, M. Interaction of DNA-dependent protein kinase with DNA and with Ku: Biochemical and atomic-force microscopy studies. EMBO J. 1997, 16, 5098–5112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedland, W.; Jacob, P.; Kundrát, P. Mechanistic simulation of radiation damage to DNA and its repair: On the track towards systems radiation biology modelling. Radiat. Prot. Dosim. 2011, 2, 542. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Warmenhoven, J.W.; Henthorn, N.T.; Ingram, S.P.; Xu, X.G.; Kirkby, K.J.; Merchant, M.J. Mechanistic Modelling of Slow and Fast NHEJ DNA Repair Pathways Following Radiation for G0/G1 Normal Tissue Cells. Cancers 2021, 13, 2202. https://doi.org/10.3390/cancers13092202
Qi Y, Warmenhoven JW, Henthorn NT, Ingram SP, Xu XG, Kirkby KJ, Merchant MJ. Mechanistic Modelling of Slow and Fast NHEJ DNA Repair Pathways Following Radiation for G0/G1 Normal Tissue Cells. Cancers. 2021; 13(9):2202. https://doi.org/10.3390/cancers13092202
Chicago/Turabian StyleQi, Yaping, John William Warmenhoven, Nicholas Thomas Henthorn, Samuel Peter Ingram, Xie George Xu, Karen Joy Kirkby, and Michael John Merchant. 2021. "Mechanistic Modelling of Slow and Fast NHEJ DNA Repair Pathways Following Radiation for G0/G1 Normal Tissue Cells" Cancers 13, no. 9: 2202. https://doi.org/10.3390/cancers13092202
APA StyleQi, Y., Warmenhoven, J. W., Henthorn, N. T., Ingram, S. P., Xu, X. G., Kirkby, K. J., & Merchant, M. J. (2021). Mechanistic Modelling of Slow and Fast NHEJ DNA Repair Pathways Following Radiation for G0/G1 Normal Tissue Cells. Cancers, 13(9), 2202. https://doi.org/10.3390/cancers13092202






