Preclinical Three-Dimensional Vibrational Shear Wave Elastography for Mapping of Tumour Biomechanical Properties In Vivo
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Culture
2.2. Animals
2.3. Vibrational Shear Wave Elastography (VSWE) Imaging Using Ultrasound
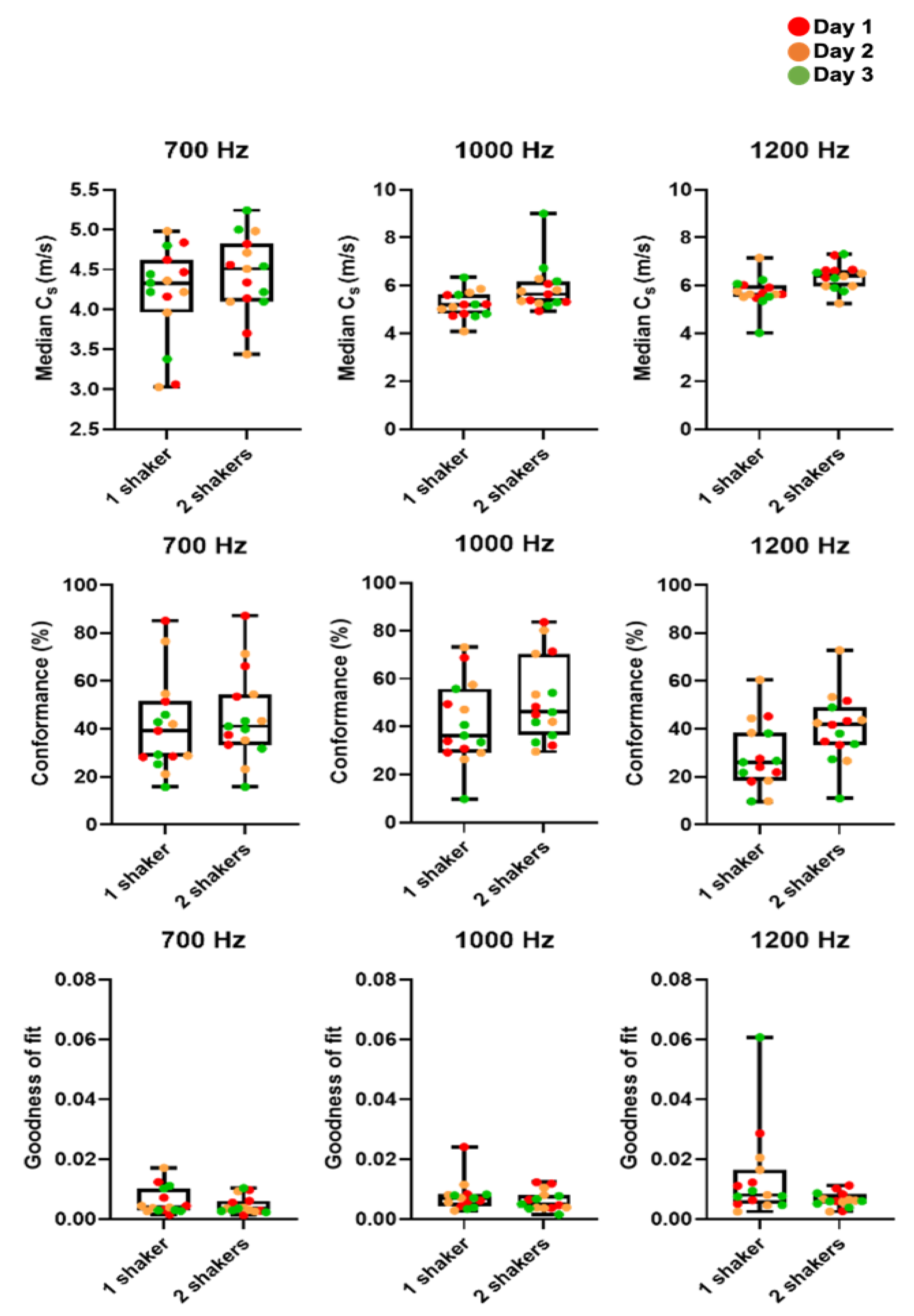
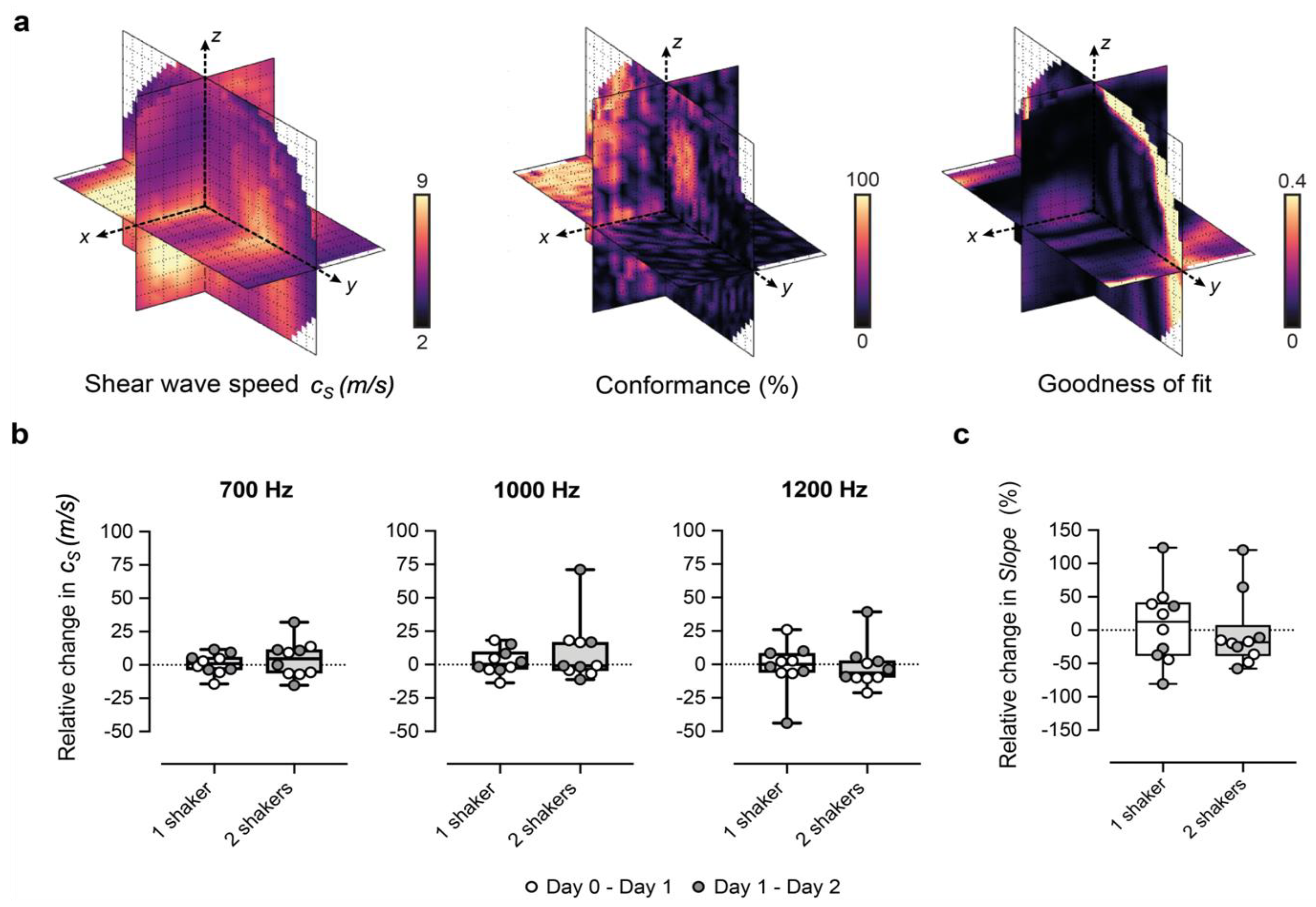
2.4. Shear Wave Speed Estimation
2.5. Data Quality Metrics
2.6. High-Frequency B-Mode Imaging
2.7. Analysis of Ultrasound Datasets
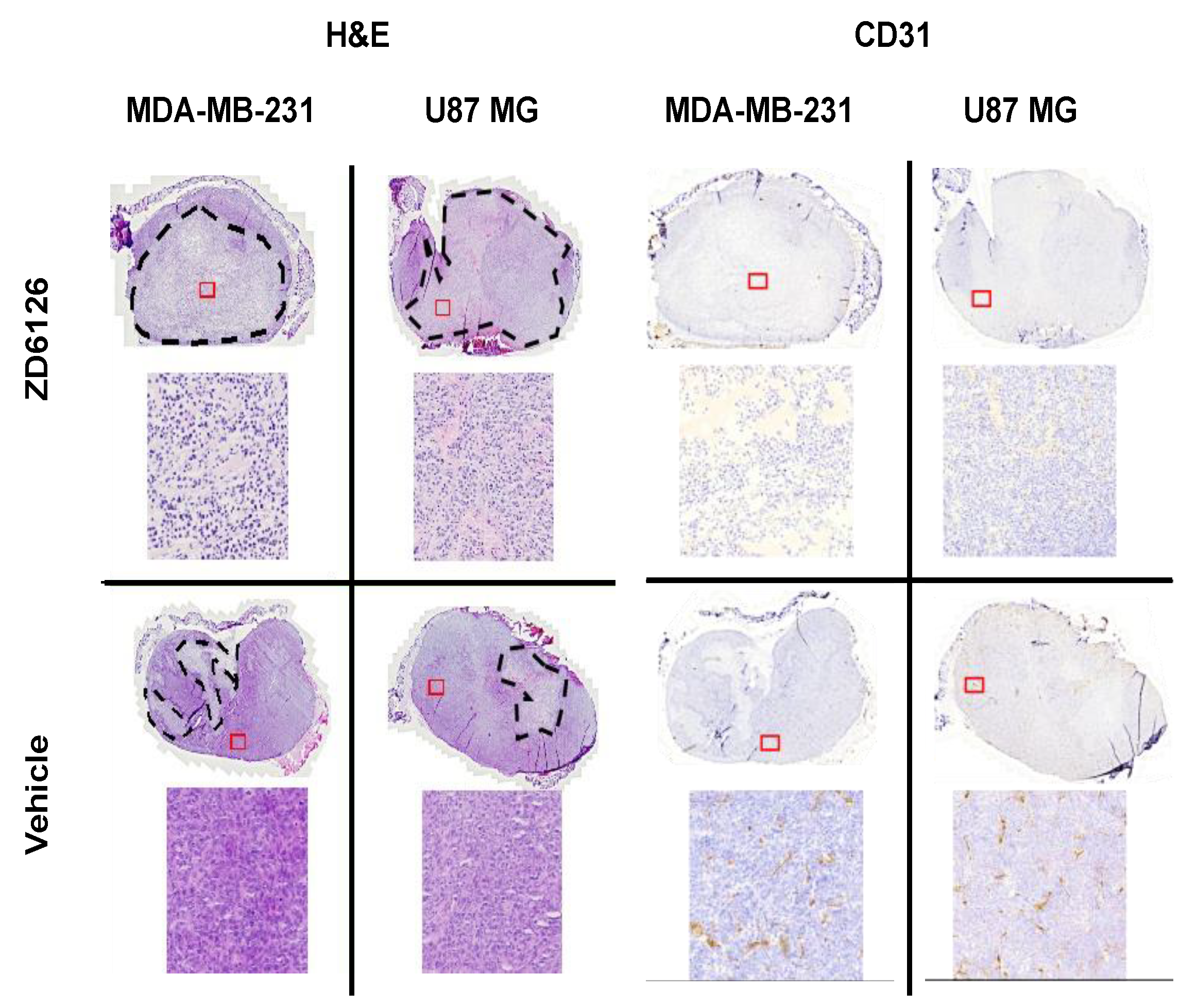
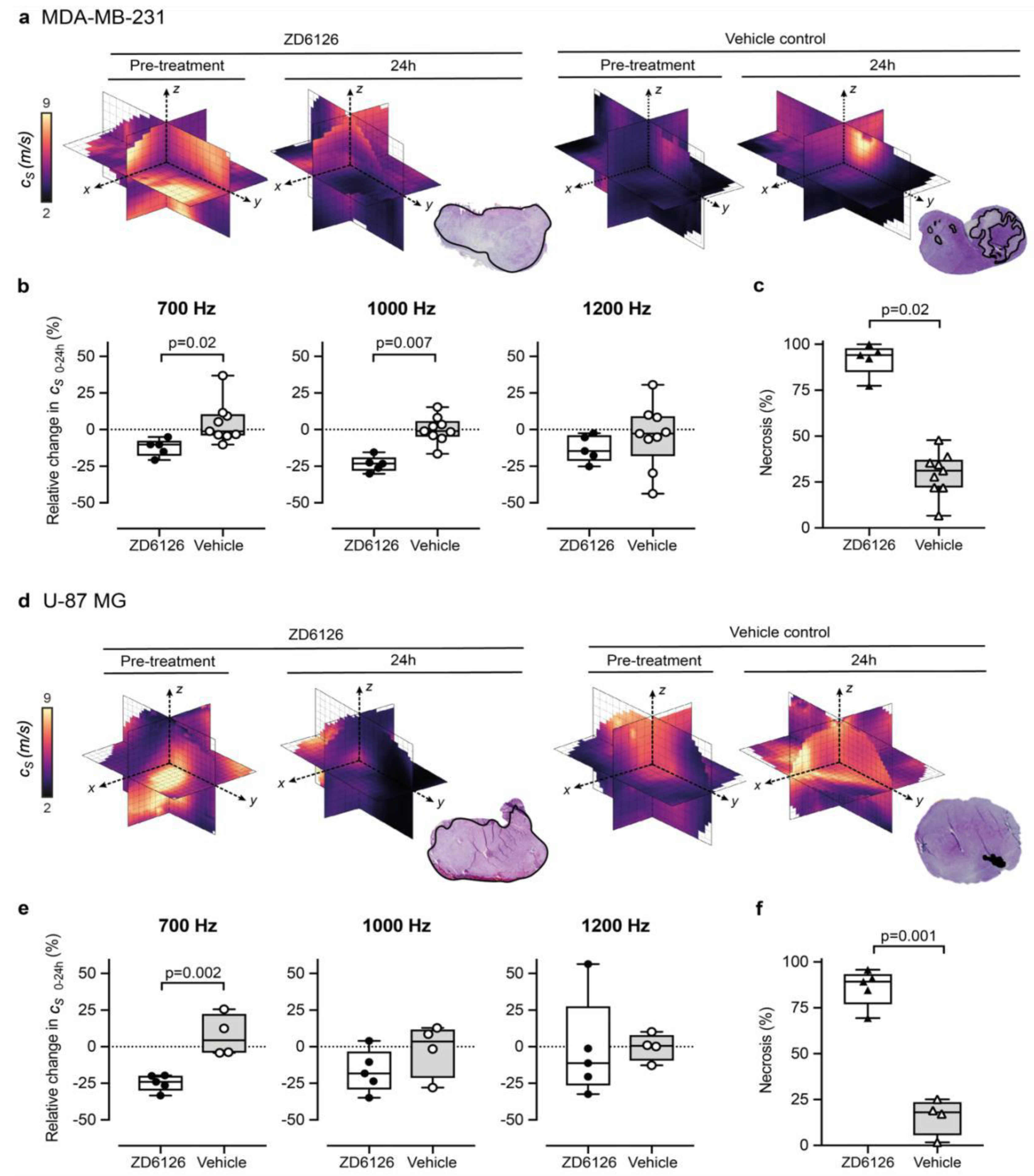
2.8. Histopathological Validation
2.9. Statistical Analysis
3. Results
3.1. Optimization and Repeatability of Preclinical VSWE
3.2. 3D-VSWE Can Detect Treatment-Induced Changes in Tumour Tissue Integrity
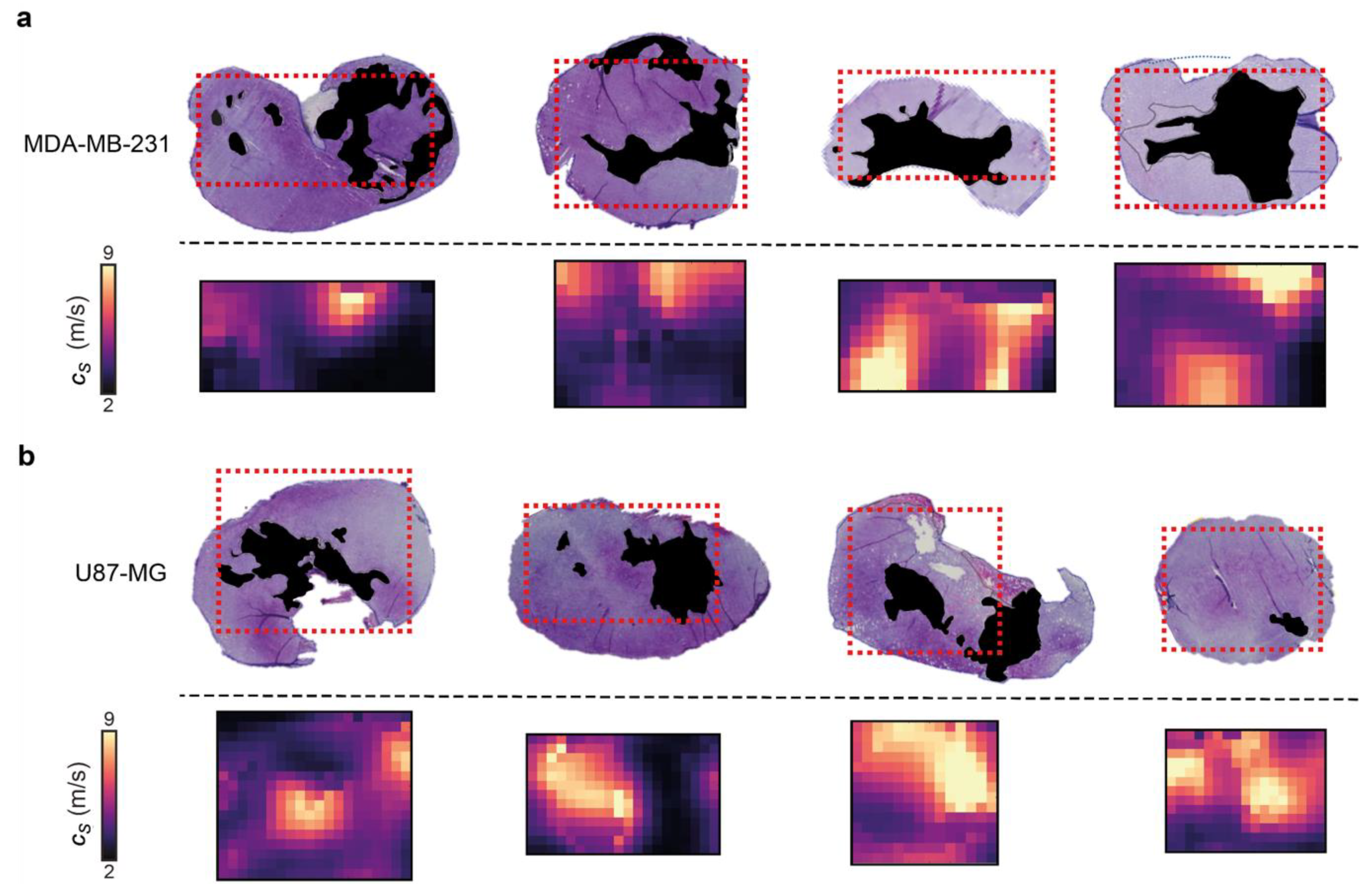
3.3. 3D-VSWE Can Provide a Map of Tumour Tissue Integrity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Northey, J.J.; Przybyla, L.; Weaver, V.M. Tissue force programs cell fate and tumor aggression. Cancer Discov. 2017, 7, 1224–1237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Northcott, J.M.; Dean, I.S.; Mouw, J.K.; Weaver, V.M. Feeling stress: The mechanics of cancer progression and aggression. Front. Cell Dev. Biol. 2018, 6, 17. [Google Scholar] [CrossRef] [PubMed]
- Nagelkerke, A.; Bussink, J.; Rowan, A.E.; Span, P.N. The mechanical microenvironment in cancer: How physics affects tumours. Semin. Cancer Biol. 2015, 35, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, H.; Sahai, E. Mechanisms and impact of altered tumour mechanics. Nat. Cell Biol. 2018, 20, 766–774. [Google Scholar] [CrossRef] [PubMed]
- Dewhirst, M.W.; Secomb, T.W. Transport of drugs from blood vessels to tumour tissue. Nat. Rev. Cancer 2017, 17, 738–750. [Google Scholar] [CrossRef] [PubMed]
- Jamin, Y.; Boult, J.K.R.; Li, J.; Popov, S.; Garteiser, P.; Ulloa, J.L.; Cummings, C.; Box, G.; Eccles, S.A.; Jones, C.; et al. Exploring the biomechanical properties of brain malignancies and their pathologic determinants in vivo with magnetic resonance elastography. Cancer Res. 2015, 75, 1216–1224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jugé, L.; Doan, B.-T.; Seguin, J.; Albuquerque, M.; Larrat, B.; Mignet, N.; Chabot, G.G.; Scherman, D.; Paradis, V.; Vilgrain, V.; et al. Colon tumor growth and antivascular treatment in mice: Complementary assessment with MR elastography and diffusion-weighted MR imaging. Radiology 2012, 264, 436–444. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Jamin, Y.; Boult, J.K.R.; Cummings, C.; Waterton, J.C.; Ulloa, J.; Sinkus, R.; Bamber, J.C.; Robinson, S.P. Tumour biomechanical response to the vascular disrupting agent ZD6126 in vivo assessed by magnetic resonance elastography. Br. J. Cancer 2014, 110, 1727–1732. [Google Scholar] [CrossRef] [Green Version]
- Pepin, K.M.; Chen, J.; Glaser, K.J.; Mariappan, Y.K.; Reuland, B.; Ziesmer, S.; Carter, R.; Ansell, S.M.; Ehman, R.L.; McGee, K.P. MR elastography derived shear stiffness—A new imaging biomarker for the assessment of early tumor response to chemotherapy. Magn. Reson. Med. 2014, 71, 1834–1840. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Clayton, E.H.; Okamoto, R.J.; Engelbach, J.; Bayly, P.V.; Garbow, J.R. A longitudinal magnetic resonance elastography study of murine brain tumors following radiation therapy. Phys. Med. Biol. 2016, 61, 6121. [Google Scholar] [CrossRef]
- Garteiser, P.; Doblas, S.; Daire, J.-L.; Wagner, M.; Leitao, H.; Vilgrain, V.; Sinkus, R.; Van Beers, B.E. MR elastography of liver tumours: Value of viscoelastic properties for tumour characterisation. Eur. Radiol. 2012, 22, 2169–2177. [Google Scholar] [CrossRef] [PubMed]
- Reiss-Zimmermann, M.; Streitberger, K.-J.; Sack, I.; Braun, J.; Arlt, F.; Fritzsch, D.; Hoffmann, K.-T. High resolution imaging of viscoelastic properties of intracranial tumours by multi-frequency magnetic resonance elastography. Clin. Neuroradiol. 2015, 25, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Bohte, A.E.; Nelissen, J.L.; Runge, J.H.; Holub, O.; Lambert, S.A.; de Graaf, L.; Kolkman, S.; van der Meij, S.; Stoker, J.; Strijkers, G.J.; et al. Breast magnetic resonance elastography: A review of clinical work and future perspectives. NMR Biomed. 2018, 31, e3932. [Google Scholar] [CrossRef]
- Riegler, J.; Labyed, Y.; Rosenzweig, S.; Javinal, V.; Castiglioni, A.; Dominguez, C.X.; Long, J.E.; Li, Q.; Sandoval, W.; Junttila, M.R.; et al. Tumor elastography and its association with collagen and the tumor microenvironment. Clin. Cancer Res. 2018, 24, 4455–4467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evans, A.; Armstrong, S.; Whelehan, P.; Thomson, K.; Rauchhaus, P.; Purdie, C.; Jordan, L.; Jones, L.; Thompson, A.; Vinnicombe, S. Can shear-wave elastography predict response to neoadjuvant chemotherapy in women with invasive breast cancer? Br. J. Cancer 2013, 109, 2798–2802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evans, A.; Whelehan, P.; Thomson, K.; McLean, D.; Brauer, K.; Purdie, C.; Baker, L.; Jordan, L.; Rauchhaus, P.; Thompson, A. Invasive breast cancer: Relationship between shear-wave elastographic findings and histologic prognostic factors. Radiology 2012, 263, 673–677. [Google Scholar] [CrossRef] [PubMed]
- Lampi, M.C.; Reinhart-King, C.A. Targeting extracellular matrix stiffness to attenuate disease: From molecular mechanisms to clinical trials. Sci. Translat. Med. 2018, 10, eaao0475. [Google Scholar] [CrossRef] [Green Version]
- Bamber, J.; Cosgrove, D.; Dietrich, C.F.; Fromageau, J.; Bojunga, J.; Calliada, F.; Cantisani, V.; Correas, J.-M.; D’onofrio, M.; Drakonaki, E. EFSUMB guidelines and recommendations on the clinical use of ultrasound elastography. Part 1: Basic principles and technology. Ultraschall Der Med. Eur. J. Ultrasound 2013, 34, 169–184. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Konstantatou, E.; Romanos, O.; Yusuf, G.T.; Quinlan, D.J.; Sidhu, P.S. Reproducibility of 2-Dimensional Shear Wave Elastography Assessment of the Liver: A Direct Comparison with Point Shear Wave Elastography in Healthy Volunteers. J. Ultrasound Med. 2017, 36, 1563–1569. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Song, P.; Urban, M.W.; Kinnick, R.R.; Yin, M.; Greenleaf, J.F.; Chen, S. Bias observed in time-of-flight shear wave speed measurements using radiation force of a focused ultrasound beam. Ultrasound Med. Biol. 2011, 37, 1884–1892. [Google Scholar] [CrossRef]
- Chang, S.; Kim, M.J.; Kim, J.; Lee, M.J. Variability of shear wave velocity using different frequencies in acoustic radiation force impulse (ARFI) elastography: A phantom and normal liver study. Ultraschall Med. 2013, 34, 260–265. [Google Scholar] [CrossRef] [PubMed]
- Piscaglia, F.; Salvatore, V.; Mulazzani, L.; Cantisani, V.; Colecchia, A.; Di Donato, R.; Felicani, C.; Ferrarini, A.; Gamal, N.; Grasso, V.; et al. Differences in liver stiffness values obtained with new ultrasound elastography machines and Fibroscan: A comparative study. Dig. Liver Dis. 2017, 49, 802–808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krouskop, T.A.; Dougherty, D.R.; Vinson, F.S. A pulsed Doppler ultrasonic system for making noninvasive measurements of the mechanical properties of soft tissue. J. Rehabil. Res. Dev. 1987, 24, 1–8. [Google Scholar] [PubMed]
- Muthupillai, R.; Lomas, D.J.; Rossman, P.J.; Greenleaf, J.F.; Manduca, A.; Ehman, R.L. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science 1995, 269, 1854–1857. [Google Scholar] [CrossRef]
- Bayly, P.V.; Garbow, J.R. Pre-clinical MR elastography: Principles, techniques, and applications. J. Magn. Reason. 2018, 291, 73–83. [Google Scholar] [CrossRef]
- Zeng, Q.; Honarvar, M.; Schneider, C.; Mohammad, S.K.; Lobo, J.; Pang, E.H.T.; Lau, K.T.; Hu, C.; Jago, J.; Erb, S.R.; et al. Three-Dimensional Multi-Frequency Shear Wave Absolute Vibro-Elastography (3D S-WAVE) With a Matrix Array Transducer: Implementation and Preliminary In Vivo Study of the Liver. IEEE Trans. Med. Imaging 2021, 40, 648–660. [Google Scholar] [CrossRef]
- Deffieux, T.; Gennisson, J.-L.; Bercoff, J.; Tanter, M. On the effects of reflected waves in transient shear wave elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2032–2035. [Google Scholar] [CrossRef]
- Blakey, D.C.; Westwood, F.R.; Walker, M.; Hughes, G.D.; Davis, P.D.; Ashton, S.E.; Ryan, A.J. Antitumor activity of the novel vascular targeting agent ZD6126 in a panel of tumor models. Clin. Cancer Res. 2002, 8, 1974–1983. [Google Scholar]
- Loupas, T.; Powers, J.; Gill, R.W. An axial velocity estimator for ultrasound blood flow imaging, based on a full evaluation of the Doppler equation by means of a two-dimensional autocorrelation approach. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 672–688. [Google Scholar] [CrossRef]
- Hoyt, K.; Castaneda, B.; Parker, K.J. Two-dimensional sonoelastographic shear velocity imaging. Ultrasound Med. Biol. 2008, 34, 276–288. [Google Scholar] [CrossRef]
- Belevich, I.; Joensuu, M.; Kumar, D.; Vihinen, H.; Jokitalo, E. Microscopy Image Browser: A Platform for Segmentation and Analysis of Multidimensional Datasets. PLoS Biol. 2016, 14, e1002340. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Quirk, J.D.; Engelbach, J.A.; Bretthorst, G.L.; Li, S.; Shoghi, K.I.; Garbow, J.R.; Ackerman, J.J. Test–retest performance of a 1-hour multiparametric MR image acquisition pipeline with orthotopic triple-negative breast cancer patient-derived tumor xenografts. Tomography 2019, 5, 320–331. [Google Scholar] [CrossRef] [PubMed]
- Shoukri, M.M.; Colak, D.; Kaya, N.; Donner, A. Comparison of two dependent within subject coefficients of variation to evaluate the reproducibility of measurement devices. BMC Med. Res. Methodol. 2008, 8, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bankhead, P.; Loughrey, M.B.; Fernandez, J.A.; Dombrowski, Y.; McArt, D.G.; Dunne, P.D.; McQuaid, S.; Gray, R.T.; Murray, L.J.; Coleman, H.G.; et al. QuPath: Open source software for digital pathology image analysis. Sci. Rep. 2017, 7, 16878. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zormpas-Petridis, K.; Boult, J.K.R.; Reeves, E.L.; Heindl, A.; Vinci, M.; Lopes, F.; Cummings, C.; Springer, C.J.; Chesler, L.; et al. Investigating the Contribution of Collagen to the Tumor Biomechanical Phenotype with Noninvasive Magnetic Resonance Elastography. Cancer Res. 2019, 79, 5874–5883. [Google Scholar] [CrossRef] [Green Version]
- Chamming’s, F.; Le-Frere-Belda, M.A.; Latorre-Ossa, H.; Fitoussi, V.; Redheuil, A.; Assayag, F.; Pidial, L.; Gennisson, J.L.; Tanter, M.; Cuenod, C.A.; et al. Supersonic Shear Wave Elastography of Response to Anti-cancer Therapy in a Xenograft Tumor Model. Ultrasound Med. Biol. 2016, 42, 924–930. [Google Scholar] [CrossRef]
- Wang, H.X.; Mills, B.; Mislati, R.; Ahmed, R.; Gerber, S.A.; Linehan, D.; Doyley, M.M. Shear Wave Elastography Can Differentiate between Radiation-Responsive and Non-responsive Pancreatic Tumors: An ex Vivo Study with Murine Models. Ultrasound Med. Biol. 2020, 46, 393–404. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, S.; Zang, L.; Li, J.; Li, J.; Kang, Y.; Ren, W. Combination of shear wave elastography and Ki-67 index as a novel predictive modality for the pathological response to neoadjuvant chemotherapy in patients with invasive breast cancer. Eur. J. Cancer 2016, 69, 86–101. [Google Scholar] [CrossRef]
- Choi, H.; Sohn, Y.-M.; Seo, M. Comparison of 3D and 2D shear-wave elastography for differentiating benign and malignant breast masses: Focus on the diagnostic performance. Clin. Radiol. 2017, 72, 878–886. [Google Scholar] [CrossRef] [Green Version]
- Shin, Y.; Huh, J.; Ham, S.J.; Cho, Y.C.; Choi, Y.; Woo, D.C.; Lee, J.; Kim, K.W. Test-retest repeatability of ultrasonographic shear wave elastography in a rat liver fibrosis model: Toward a quantitative biomarker for preclinical trials. Ultrasonography 2021, 40, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Weis, J.A.; Flint, K.M.; Sanchez, V.; Yankeelov, T.E.; Miga, M.I. Assessing the accuracy and reproducibility of modality independent elastography in a murine model of breast cancer. J. Med. Imaging 2015, 2, 036001. [Google Scholar] [CrossRef] [PubMed]
- Elyas, E.; Papaevangelou, E.; Alles, E.J.; Erler, J.T.; Cox, T.R.; Robinson, S.P.; Bamber, J.C. Correlation of Ultrasound Shear Wave Elastography with Pathological Analysis in a Xenografic Tumour Model. Sci. Rep. 2017, 7, 165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Mislati, R.; Ahmed, R.; Vincent, P.; Nwabunwanne, S.F.; Gunn, J.R.; Pogue, B.W.; Doyley, M.M. Elastography Can Map the Local Inverse Relationship between Shear Modulus and Drug Delivery within the Pancreatic Ductal Adenocarcinoma Microenvironment. Clin. Cancer Res. 2019, 25, 2136–2143. [Google Scholar] [CrossRef] [Green Version]
- Baek, J.; Ahmed, R.; Ye, J.; Gerber, S.A.; Parker, K.J.; Doyley, M.M. H-scan, Shear Wave and Bioluminescent Assessment of the Progression of Pancreatic Cancer Metastases in the Liver. Ultrasound Med. Biol. 2020, 46, 3369–3378. [Google Scholar] [CrossRef]
- Mieulet, V.; Garnier, C.; Kieffer, Y.; Guilbert, T.; Nemati, F.; Marangoni, E.; Renault, G.; Chamming’s, F.; Vincent-Salomon, A.; Mechta-Grigoriou, F. Stiffness increases with myofibroblast content and collagen density in mesenchymal high grade serous ovarian cancer. Sci. Rep. 2021, 11, 4219. [Google Scholar] [CrossRef]
- Nabavizadeh, A.; Payen, T.; Iuga, A.C.; Sagalovskiy, I.R.; Desrouilleres, D.; Saharkhiz, N.; Palermo, C.F.; Sastra, S.A.; Oberstein, P.E.; Rosario, V.; et al. Noninvasive Young’s modulus visualization of fibrosis progression and delineation of pancreatic ductal adenocarcinoma (PDAC) tumors using Harmonic Motion Elastography (HME) in vivo. Theranostics 2020, 10, 4614–4626. [Google Scholar] [CrossRef] [PubMed]
- Ormachea, J.; Castaneda, B.; Parker, K.J. Shear Wave Speed Estimation Using Reverberant Shear Wave Fields: Implementation and Feasibility Studies. Ultrasound Med. Biol. 2018, 44, 963–977. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Song, P.; Mellema, D.C.; Gong, P.; Lok, U.W.; Tang, S.; Ling, W.; Meixner, D.D.; Urban, M.W.; Manduca, A.; et al. Three-dimensional shear wave elastography on conventional ultrasound scanners with external vibration. Phys. Med. Biol. 2020, 65, 215009. [Google Scholar] [CrossRef]
- Garteiser, P.; Pagé, G.; d’Assignies, G.; Leitao, H.S.; Vilgrain, V.; Sinkus, R.; Van Beers, B.E. Necro-inflammatory activity grading in chronic viral hepatitis with three-dimensional multifrequency MR elastography. Sci. Rep. 2021, 11, 19386. [Google Scholar] [CrossRef]
- Jensen, J.A. Medical ultrasound imaging. Prog. Biophys. Mol. Biol. 2007, 93, 153–165. [Google Scholar] [CrossRef]
- Workman, P.; Aboagye, E.O.; Balkwill, F.; Balmain, A.; Bruder, G.; Chaplin, D.J.; Double, J.A.; Everitt, J.; Farningham, D.A.; Glennie, M.J.; et al. Guidelines for the welfare and use of animals in cancer research. Br. J. Cancer 2010, 102, 1555–1577. [Google Scholar] [CrossRef] [PubMed]
- Kilkenny, C.; Browne, W.J.; Cuthill, I.C.; Emerson, M.; Altman, D.G. Improving bioscience research reporting: The ARRIVE guidelines for reporting animal research. J. Pharm. Pharm. 2010, 1, 94–99. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parasaram, V.; Civale, J.; Bamber, J.C.; Robinson, S.P.; Jamin, Y.; Harris, E. Preclinical Three-Dimensional Vibrational Shear Wave Elastography for Mapping of Tumour Biomechanical Properties In Vivo. Cancers 2022, 14, 4832. https://doi.org/10.3390/cancers14194832
Parasaram V, Civale J, Bamber JC, Robinson SP, Jamin Y, Harris E. Preclinical Three-Dimensional Vibrational Shear Wave Elastography for Mapping of Tumour Biomechanical Properties In Vivo. Cancers. 2022; 14(19):4832. https://doi.org/10.3390/cancers14194832
Chicago/Turabian StyleParasaram, Vaideesh, John Civale, Jeffrey C. Bamber, Simon P. Robinson, Yann Jamin, and Emma Harris. 2022. "Preclinical Three-Dimensional Vibrational Shear Wave Elastography for Mapping of Tumour Biomechanical Properties In Vivo" Cancers 14, no. 19: 4832. https://doi.org/10.3390/cancers14194832
APA StyleParasaram, V., Civale, J., Bamber, J. C., Robinson, S. P., Jamin, Y., & Harris, E. (2022). Preclinical Three-Dimensional Vibrational Shear Wave Elastography for Mapping of Tumour Biomechanical Properties In Vivo. Cancers, 14(19), 4832. https://doi.org/10.3390/cancers14194832






