Alpha-Emitter Radiopharmaceuticals and External Beam Radiotherapy: A Radiobiological Model for the Combined Treatment
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Data Search
2.2. Radiobiological Model
2.2.1. Radiobiological Model for Low-LET EBRT
2.2.2. Generation of Virtual Cohort of Patients Treated with 223RaCl2
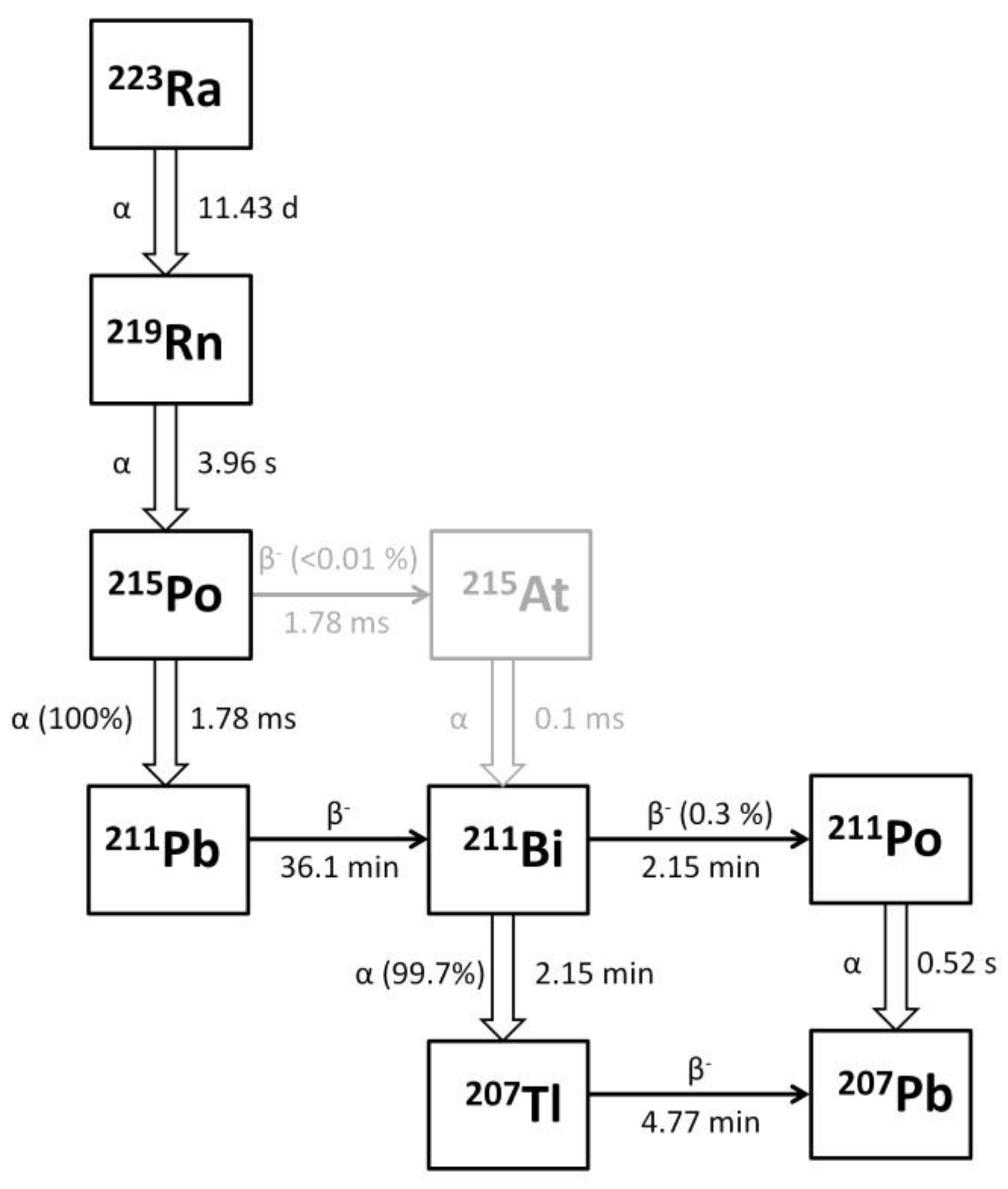
2.2.3. Radiobiological Model for High-LET α-Particle RN 223RaCl2
2.3. Radiobiological Model of Combined Therapy
2.4. Treatment Outcome Modeling and Model Comparison
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Roodman, G.D. Mechanisms of bone metastasis. Discov. Med. 2004, 4, 144–148. [Google Scholar] [CrossRef] [PubMed]
- Cornford, P.; Bellmunt, J.; Bolla, M.; Briers, E.; De Santis, M.; Gross, T.; Henry, A.M.; Joniau, S.; Lam, T.B.; Mason, M.D.; et al. EAU-ESTRO-SIOG Guidelines on Prostate Cancer. Part II: Treatment of Relapsing, Metastatic, and Castration-Resistant Prostate Cancer. Eur. Urol. 2017, 71, 630–642. [Google Scholar] [CrossRef]
- Saad, F.; Hotte, S.J. Guidelines for the management of castrate-resistant prostate cancer. Can. Urol. Assoc. J. 2010, 4, 380–384. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Amm, J.; Aragon-Ching, J.B. Radium-223 for the treatment of castration-resistant prostate cancer. OncoTargets Ther. 2015, 8, 1103–1109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sgouros, G.; Roeske, J.C.; McDevitt, M.R.; Palm, S.; Allen, B.J.; Fisher, D.R.; Brill, A.B.; Song, H.; Howell, R.W.; Akabani, G.; et al. MIRD Pamphlet No. 22 (abridged): Radiobiology and dosimetry of alpha-particle emitters for targeted radionuclide therapy. J. Nucl. Med. 2010, 51, 311–328. [Google Scholar] [CrossRef] [Green Version]
- Parker, C.C.; Pascoe, S.; Chodacki, A.; O’Sullivan, J.M.; Germa, J.R.; O’Bryan-Tear, C.G.; Haider, T.; Hoskin, P. A randomized, double-blind, dose-finding, multicenter, phase 2 study of radium chloride (Ra 223) in patients with bone metastases and castration-resistant prostate cancer. Eur. Urol. 2013, 63, 189–197. [Google Scholar] [CrossRef]
- Parker, C.; Nilsson, S.; Heinrich, D.; Helle, S.I.; O’Sullivan, J.M.; Fosså, S.D.; Chodacki, A.; Wiechno, P.; Logue, J.; Seke, M.; et al. Alpha emitter radium-223 and survival in metastatic prostate cancer. N. Engl. J. Med. 2013, 369, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, S.; Franzen, L.; Parker, C.; Tyrrell, C.; Blom, R.; Tennvall, J.; Lennernas, B.; Petersson, U.; Johannessen, D.C.; Sokal, M.; et al. Two-year survival follow-up of the randomized, double-blind, placebo-controlled phase II study of radium-223 chloride in patients with castration-resistant prostate cancer and bone metastases. Clin. Genitourin Cancer 2013, 11, 20–26. [Google Scholar] [CrossRef]
- Nilsson, S.; Franzén, L.; Parker, C.; Tyrrell, C.; Blom, R.; Tennvall, J.; Lennernäs, B.; Petersson, U.; Johannessen, D.C.; Sokal, M.; et al. Bone-targeted radium-223 in symptomatic, hormone-refractory prostate cancer: A randomised, multicentre, placebo-controlled phase II study. Lancet Oncol. 2007, 8, 587–594. [Google Scholar] [CrossRef]
- Uemura, H.; Uemura, H.; Nagamori, S.; Wakumoto, Y.; Kimura, G.; Kikukawa, H.; Yokomizo, A.; Mizokami, A.; Kosaka, T.; Masumori, N.; et al. Three-year follow-up of a phase II study of radium-223 dichloride in Japanese patients with symptomatic castration-resistant prostate cancer and bone metastases. Int. J. Clin. Oncol. 2019, 24, 557–566. [Google Scholar] [CrossRef] [Green Version]
- Belli, M.L.; Sarnelli, A.; Mezzenga, E.; Cesarini, F.; Caroli, P.; Di Iorio, V.; Strigari, L.; Cremonesi, M.; Romeo, A.; Nicolini, S.; et al. Targeted Alpha Therapy in mCRPC (Metastatic Castration-Resistant Prostate Cancer) Patients: Predictive Dosimetry and Toxicity Modeling of (225)Ac-PSMA (Prostate-Specific Membrane Antigen). Front. Oncol. 2020, 10, 531660. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, R.F.; Howell Rw Fau-Song, H.; Song, H.; Fau-Baechler, S.; Baechler, S.; Fau-Sgouros, G.; Sgouros, G. Redefining relative biological effectiveness in the context of the EQDX formalism: Implications for alpha-particle emitter therapy. Radiat. Res. 2014, 181, 90–98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McMahon, S.J. The linear quadratic model: Usage, interpretation and challenges. Phys. Med. Biol. 2018, 64, 01TR01. [Google Scholar] [CrossRef] [PubMed]
- Pacilio, M.; Ventroni, G.; De Vincentis, G.; Cassano, B.; Pellegrini, R.; Di Castro, E.; Frantellizzi, V.; Follacchio, G.A.; Garkavaya, T.; Lorenzon, L.; et al. Dosimetry of bone metastases in targeted radionuclide therapy with alpha-emitting (223)Ra-dichloride. Eur. J. Nucl. Med. Mol. Imaging 2016, 43, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Siegel, J.A.; Thomas, S.R.; Stubbs, J.B.; Stabin, M.G.; Hays, M.T.; Koral, K.F.; Robertson, J.S.; Howell, R.W.; Wessels, B.W.; Fisher, D.R.; et al. MIRD pamphlet no. 16: Techniques for quantitative radiopharmaceutical biodistribution data acquisition and analysis for use in human radiation dose estimates. J. Nucl. Med. 1999, 40, 37S–61S. [Google Scholar]
- Bolch, W.E.; Bouchet, L.G.; Robertson, J.S.; Wessels, B.W.; Siegel, J.A.; Howell, R.W.; Erdi, A.K.; Aydogan, B.; Costes, S.; Watson, E.E.; et al. MIRD pamphlet No. 17: The dosimetry of nonuniform activity distributions—Radionuclide S values at the voxel level. J. Nucl. Med. 1999, 40, 11S–36S. [Google Scholar]
- Snyder, W.; Ford; Warner, G.G.; Watson, S. (Eds.) MIRD Pamphlet #11: S, Absorbed Dose per Unit Cumulated Activity for Selected Radionuclides and Organs; 1975; Available online: https://s3.amazonaws.com/rdcms-snmmi/files/production/public/MIRD%20Pamphlet%2011.pdf (accessed on 16 February 2022).
- Stabin, M.G.; Sparks, R.B.; Crowe, E. OLINDA/EXM: The second-generation personal computer software for internal dose assessment in nuclear medicine. J. Nucl. Med. 2005, 46, 1023–1027. [Google Scholar]
- Dale, R.G.; Jones, B. The assessment of RBE effects using the concept of biologically effective dose. Int. J. Radiat. Oncol. Biol. Phys. 1999, 43, 639–645. [Google Scholar] [CrossRef]
- Bazan, J.G.; Luxton, G.; Mok, E.C.; Koong, A.C.; Chang, D.T. Normal tissue complication probability modeling of acute hematologic toxicity in patients treated with intensity-modulated radiation therapy for squamous cell carcinoma of the anal canal. Int. J. Radiat Oncol. Biol. Phys. 2012, 84, 700–706. [Google Scholar] [CrossRef]
- Yoshimura, T.; Kinoshita, R.; Onodera, S.; Toramatsu, C.; Suzuki, R.; Ito, Y.M.; Takao, S.; Matsuura, T.; Matsuzaki, Y.; Umegaki, K.; et al. NTCP modeling analysis of acute hematologic toxicity in whole pelvic radiation therapy for gynecologic malignancies—A dosimetric comparison of IMRT and spot-scanning proton therapy (SSPT). Phys. Med. 2016, 32, 1095–1102. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.; Ma, Y.; Zheng, J.; Deng, H.; Wang, X.; Li, Y.; Pang, X.; Chen, H.; He, F.; Wang, L.; et al. Impact of Chemotherapy Regimens on Normal Tissue Complication Probability Models of Acute Hematologic Toxicity in Rectal Cancer Patients Receiving Intensity Modulated Radiation Therapy With Concurrent Chemotherapy From a Prospective Phase III Clinical Trial. Front. Oncol. 2019, 9, 244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henriksen, G.; Fisher, D.R.; Roeske, J.C.; Bruland, Ø.S.; Larsen, R.H. Targeting of osseous sites with alpha-emitting 223Ra: Comparison with the beta-emitter 89Sr in mice. J. Nucl. Med. 2003, 44, 252–259. [Google Scholar] [PubMed]
- Sgouros, G. Dosimetry, Radiobiology and Synthetic Lethality: Radiopharmaceutical Therapy (RPT) With Alpha-Particle-Emitters. Semin. Nucl. Med. 2020, 50, 124–132. [Google Scholar] [CrossRef] [PubMed]
- Etchebehere, E.C.; Milton, D.R.; Araujo, J.C.; Swanston, N.M.; Macapinlac, H.A.; Rohren, E.M. Factors affecting (223)Ra therapy: Clinical experience after 532 cycles from a single institution. Eur. J. Nucl. Med. Mol. Imaging 2016, 43, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, S.E.; Michalski, J.M.; O’Sullivan, J.M.; Parker, C.; Garcia-Vargas, J.E.; Sartor, A.O. External beam radiation therapy (EBRT) use and safety with radium-223 dichloride (Ra-223) in patients (pts) with castration-resistant prostate cancer (CRPC) and symptomatic bone metastases (mets) from the ALSYMPCA trial. J. Clin. Oncol. 2015, 33, 182. [Google Scholar] [CrossRef]
- Sciuto, R.; Rea, S.; Ungania, S.; Testa, A.; Dini, V.; Tabocchini, M.A.; Patrono, C.; Soriani, A.; Palma, V.; Marconi, R.; et al. The role of dosimetry and biological effects in metastatic castration-resistant prostate cancer (mCRPC) patients treated with (223)Ra: First in human study. J. Exp. Clin. Cancer Res. 2021, 40, 1–12. [Google Scholar] [CrossRef]
- Zeng, K.L.; Tseng, C.L.; Soliman, H.; Weiss, Y.; Sahgal, A.; Myrehaug, S. Stereotactic Body Radiotherapy (SBRT) for Oligometastatic Spine Metastases: An Overview. Front. Oncol. 2019, 9, 337. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, Q.N.; Chun, S.G.; Chow, E.; Komaki, R.; Liao, Z.; Zacharia, R.; Szeto, B.K.; Welsh, J.W.; Hahn, S.M.; Fuller, C.D.; et al. Single-Fraction Stereotactic vs Conventional Multifraction Radiotherapy for Pain Relief in Patients With Predominantly Nonspine Bone Metastases: A Randomized Phase 2 Trial. JAMA Oncol. 2019, 5, 872–878. [Google Scholar] [CrossRef] [Green Version]
- Andersson, M.A.-O.; Johansson, L.; Eckerman, K.; Mattsson, S. IDAC-Dose 2.1, an internal dosimetry program for diagnostic nuclear medicine based on the ICRP adult reference voxel phantoms. EJNMMI Res. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Chiesa, C.; Strigari, L.; Pacilio, M.; Richetta, E.; Cannatà, V.; Stasi, M.; Marzola, M.C.; Schillaci, O.; Bagni, O.; Maccauro, M. Dosimetric optimization of nuclear medicine therapy based on the Council Directive 2013/59/EURATOM and the Italian law N. 101/2020. Position paper and recommendations by the Italian National Associations of Medical Physics (AIFM) and Nuclear Medicine (AIMN). Phys. Med. 2021, 89, 317–326. [Google Scholar] [CrossRef]
- Morgenstern, A.; Apostolidis, C.; Kratochwil, C.; Sathekge, M.; Krolicki, L.; Bruchertseifer, F. An Overview of Targeted Alpha Therapy with (225)Actinium and (213)Bismuth. Curr. Radiopharm. 2018, 11, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Flux, G.; Murray, I.; Rushforth, D.; Gape, P.; Abreu, C.; Lee, M.; Ribeiro, A.; Gregory, R.; Chittenden, S.; Thurston, J.; et al. SOLLID—A single centre study to develop methods to investigate the effects of low radiation doses within nuclear medicine, to enable multicentre epidemiological investigations. Br. J. Radiol. 2021, 94, 20200072. [Google Scholar] [CrossRef] [PubMed]
- Howell, R.W.; Goddu, S.M.; Narra, V.R.; Fisher, D.R.; Schenter, R.E.; Rao, D.V. Radiotoxicity of gadolinium-148 and radium-223 in mouse testes: Relative biological effectiveness of alpha-particle emitters in vivo. Radiat. Res. 1997, 147, 342–348. [Google Scholar] [CrossRef] [PubMed]
- Feinendegen, L.E.; Bond, V.P.; Sondhaus, C.A. Relative biological effectiveness of ionizing radiations determined in tissue (RBE) fails in assessing comparative relative effectiveness in the tissue cells. Health Phys. 1996, 70, 852–858. [Google Scholar] [CrossRef]
- Murray, I.; Flux, G. Applying radiobiology to clinical molecular radiotherapy. Nucl. Med. Biol. 2021, 100–101, 1–3. [Google Scholar] [CrossRef]
- Uemura, H.; Uemura, H.; Matsubara, N.; Kinuya, S.; Hosono, M.; Yajima, Y.; Doi, T. Safety and efficacy of radium-223 dichloride in Japanese patients with castration-resistant prostate cancer and bone metastases. Int. J. Clin. Oncol. 2017, 22, 954–963. [Google Scholar] [CrossRef]
- Taprogge, J.; Murray, I.; Gear, J.; Chittenden, S.J.; Parker, C.C.; Flux, G.D. Compartmental Model for (223)Ra-Dichloride in Patients With Metastatic Bone Disease From Castration-Resistant Prostate Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2019, 105, 884–892. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, K.; Kaneta, T.; Takano, S.; Sugiura, M.; Kawano, T.; Hino, A.; Yamamoto, T.; Shizukuishi, K.; Kaneko, M.; Zurth, C.; et al. Pharmacokinetics of single dose radium-223 dichloride (BAY 88-8223) in Japanese patients with castration-resistant prostate cancer and bone metastases. Ann. Nucl. Med. 2016, 30, 453–460. [Google Scholar] [CrossRef] [Green Version]


| Radiobiological Parameter | Value | Reference |
|---|---|---|
| 10 Gy | [19] | |
| 1.4 h−1 | [19] | |
| experimental | 5 | [5] |
| 1 | ||
| d | 2 Gy/fr |
| Study | Reference | Total #Pts | Phase Study | A (kBq/kg) | nc | A (MBq/Cycle) | #Pts | f % (#Pts) with EBRT | 2y-OS (%) | TOX (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | [8] | 64 | 2 | 50 | 4 | 3.5 | 33 | 100% (33) | 30% (10) | 0% (0) |
| (placebo) | 0 | 0 | 31 | 100% (31) | 13% (4) | 0% (0) | ||||
| B | [7] | 122 | 2 | 25 | 3 | 1.75 | 41 | 29% (12) | 37% (15) | 0% (0) |
| 50 | 3 | 3.5 | 39 | 44% (17) | 44% (17) | 18% (7) | ||||
| 80 | 3 | 5.6 | 42 | 36% (15) | 48% (20) | 21% (9) | ||||
| C | [6] | 921 | 3 | 50 | 6 | 3.5 | 614 | 16% (98) | 30% (184) | 5% (31) |
| (placebo) | 0 | 0 | 307 | 16% (49) | 18% (55) | 1% (3) | ||||
| D | [10] | 49 | 2 | 55 | 6 | 4.125 | 49 | 29% (14) | 49% (24) | NA |
| Study | Reference | Total #Pts | A (kBq/kg) | #Pts | f % (#Pts) with EBRT | EQD2RN (Gy) | EQD2EBRT (Gy) | EQD2TOT (Gy) |
|---|---|---|---|---|---|---|---|---|
| A | [8] | 64 | 50 | 33 | 100% (33) | 103.2 | 12.0 | 115.2 |
| (placebo) | 31 | 100% (31) | 0.0 | 12.0 | 12.0 | |||
| B | [7] | 122 | 25 | 41 | 29% (12) | 34.2 | 3.5 | 37.7 |
| 50 | 39 | 44% (17) | 77.4 | 5.3 | 82.7 | |||
| 80 | 42 | 36% (15) | 140.7 | 4.3 | 145.0 | |||
| C | [6] | 921 | 50 | 614 | 16% (98) | 154.8 | 1.9 | 156.7 |
| (placebo) | 307 | 16% (49) | 0.0 | 1.9 | 1.9 | |||
| D | [10] | 49 | 55 | 49 | 29% (14) | 174.0 | 3.5 | 177.5 |
| Study | Reference | Total #Pts | A (kBq/kg) | #Pts | f % (#Pts) with EBRT | EQD2RN (Gy) | EQD2EBRT (Gy) | EQD2TOT (Gy) |
|---|---|---|---|---|---|---|---|---|
| A | [8] | 64 | 50 | 33 | 100% (33) | 103.2 | 23.3 | 126.5 |
| (placebo) | 31 | 100% (31) | 0.0 | 23.3 | 23.3 | |||
| B | [7] | 122 | 25 | 41 | 29% (12) | 34.2 | 6.8 | 41.0 |
| 50 | 39 | 44% (17) | 77.4 | 10.3 | 87.7 | |||
| 80 | 42 | 36% (15) | 140.7 | 8.4 | 149.1 | |||
| C | [6] | 921 | 50 | 614 | 16% (98) | 154.8 | 3.7 | 158.5 |
| (placebo) | 307 | 16% (49) | 0.0 | 3.7 | 3.7 | |||
| D | [10] | 49 | 55 | 49 | 29% (14) | 174.0 | 6.8 | 180.8 |
| Study | Reference | Total #Pts | A (kBq/kg) | #Pts | f % (#Pts) with EBRT | EQD2RN (Gy) | EQD2EBRT (Gy) | EQD2TOT (Gy) |
|---|---|---|---|---|---|---|---|---|
| A | [8] | 64 | 50 | 33 | 100% (33) | 103.2 | 32.5 | 135.7 |
| (placebo) | 31 | 100% (31) | 0.0 | 32.5 | 32.5 | |||
| B | [7] | 122 | 25 | 41 | 29% (12) | 34.2 | 9.4 | 43.6 |
| 50 | 39 | 44% (17) | 77.4 | 14.3 | 91.7 | |||
| 80 | 42 | 36% (15) | 140.7 | 11.7 | 152.4 | |||
| C | [6] | 921 | 50 | 614 | 16% (98) | 154.8 | 5.2 | 160.0 |
| (placebo) | 307 | 16% (49) | 0.0 | 5.2 | 5.2 | |||
| D | [10] | 49 | 55 | 49 | 29% (14) | 174.0 | 9.4 | 183.4 |
| 2y-OS Model | ||||
| β | SE | z Statistic | p-Value | |
| Intercept | −1.364 | 0.262 | −5.209 | <0.001 |
| EQD2TOT | 0.006 | 0.002 | 2.737 | 0.006 |
| TOX Model | ||||
| β | SE | z Statistic | p-Value | |
| Intercept | −5.035 | 1.100 | −4.578 | <0.001 |
| EQD2TOT | 0.018 | 0.009 | 1.962 | 0.050 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarnelli, A.; Belli, M.L.; Azzali, I.; Loi, E.; Severi, S.; Strigari, L. Alpha-Emitter Radiopharmaceuticals and External Beam Radiotherapy: A Radiobiological Model for the Combined Treatment. Cancers 2022, 14, 1077. https://doi.org/10.3390/cancers14041077
Sarnelli A, Belli ML, Azzali I, Loi E, Severi S, Strigari L. Alpha-Emitter Radiopharmaceuticals and External Beam Radiotherapy: A Radiobiological Model for the Combined Treatment. Cancers. 2022; 14(4):1077. https://doi.org/10.3390/cancers14041077
Chicago/Turabian StyleSarnelli, Anna, Maria Luisa Belli, Irene Azzali, Emiliano Loi, Stefano Severi, and Lidia Strigari. 2022. "Alpha-Emitter Radiopharmaceuticals and External Beam Radiotherapy: A Radiobiological Model for the Combined Treatment" Cancers 14, no. 4: 1077. https://doi.org/10.3390/cancers14041077
APA StyleSarnelli, A., Belli, M. L., Azzali, I., Loi, E., Severi, S., & Strigari, L. (2022). Alpha-Emitter Radiopharmaceuticals and External Beam Radiotherapy: A Radiobiological Model for the Combined Treatment. Cancers, 14(4), 1077. https://doi.org/10.3390/cancers14041077







