Multitask Learning with Convolutional Neural Networks and Vision Transformers Can Improve Outcome Prediction for Head and Neck Cancer Patients
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Cohorts
2.2. Image Preprocessing
2.3. Analysis Design
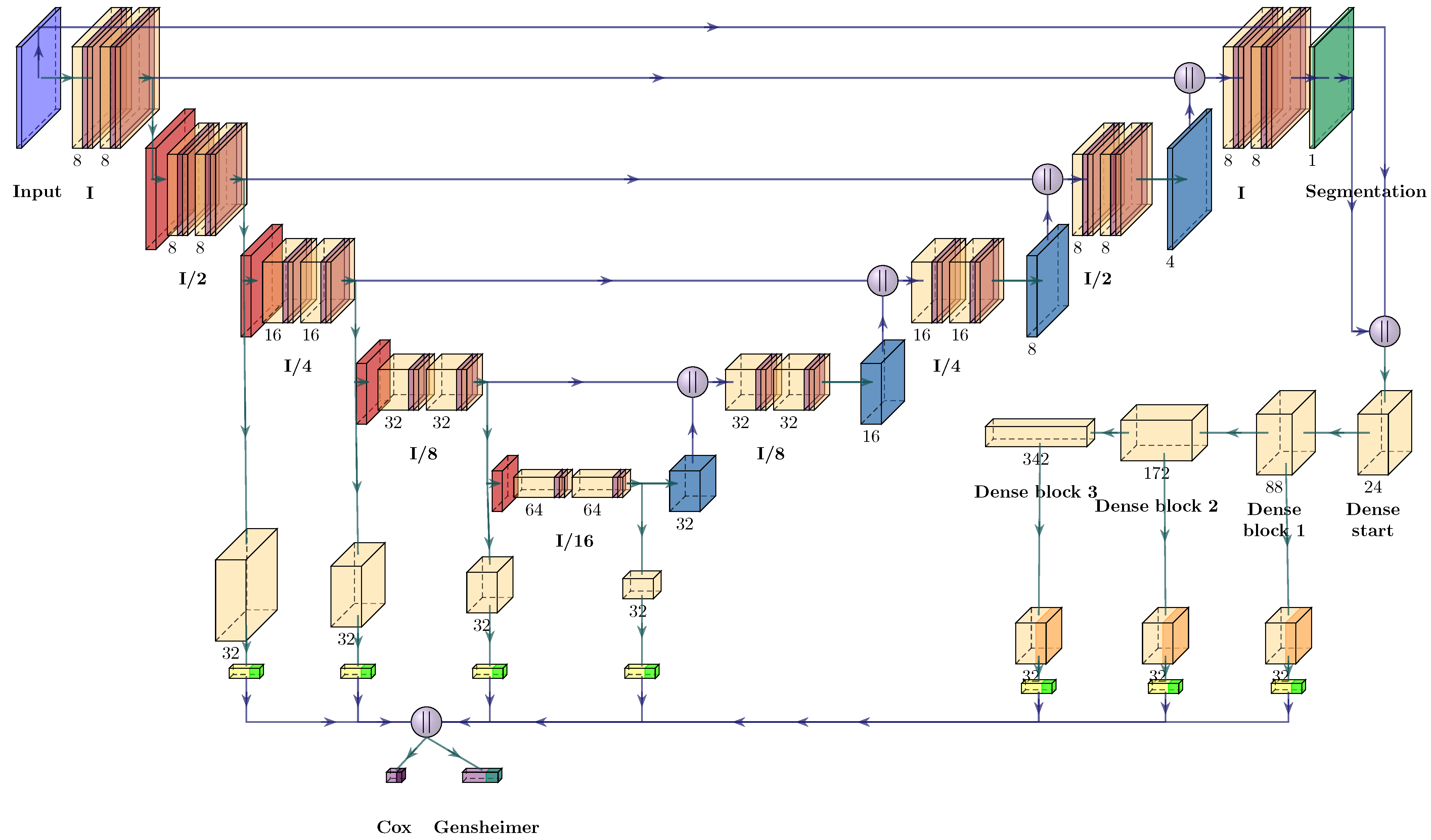
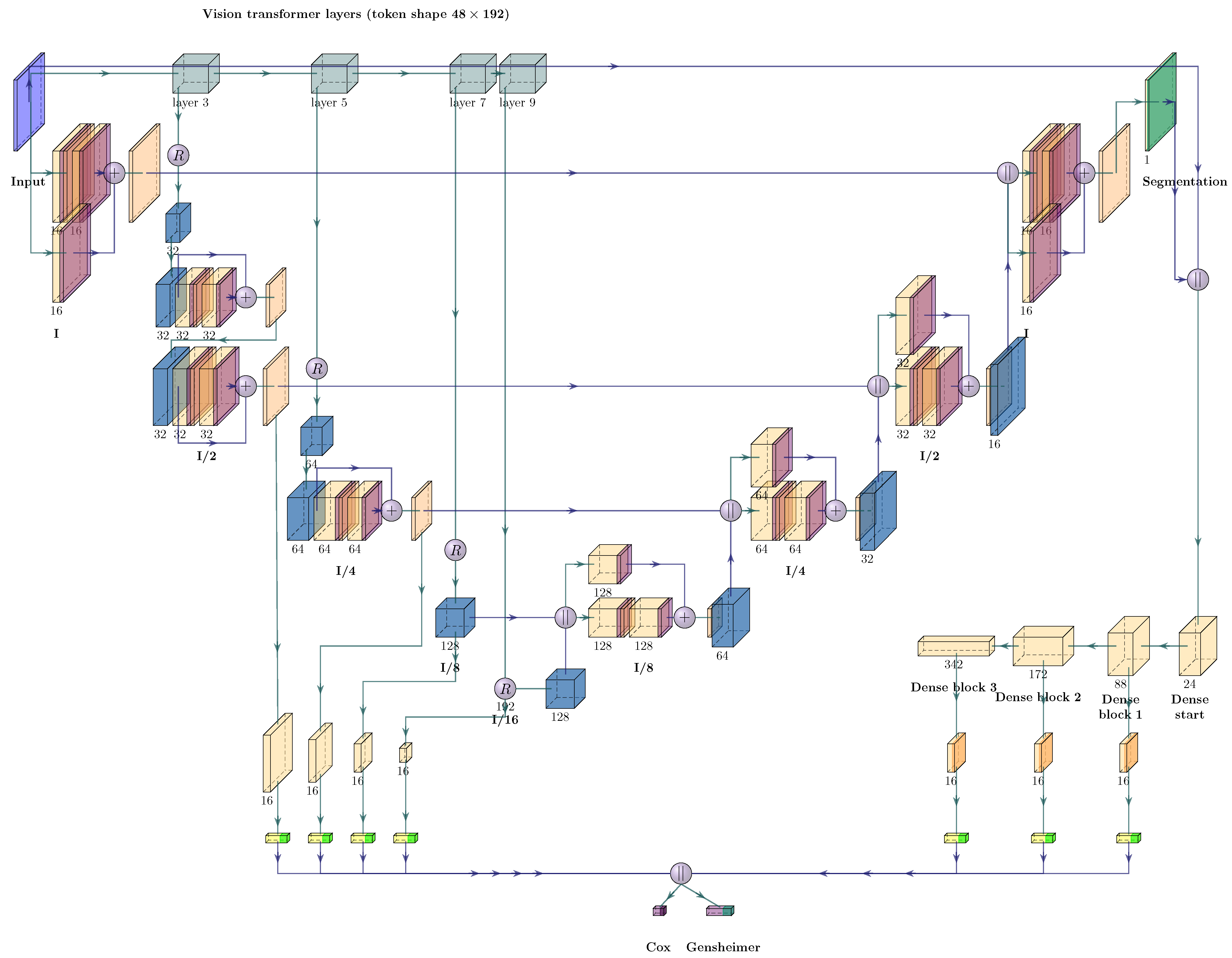
2.4. Neural Network Architectures
2.5. Neural Network Training
2.6. Performance Evaluation
3. Results
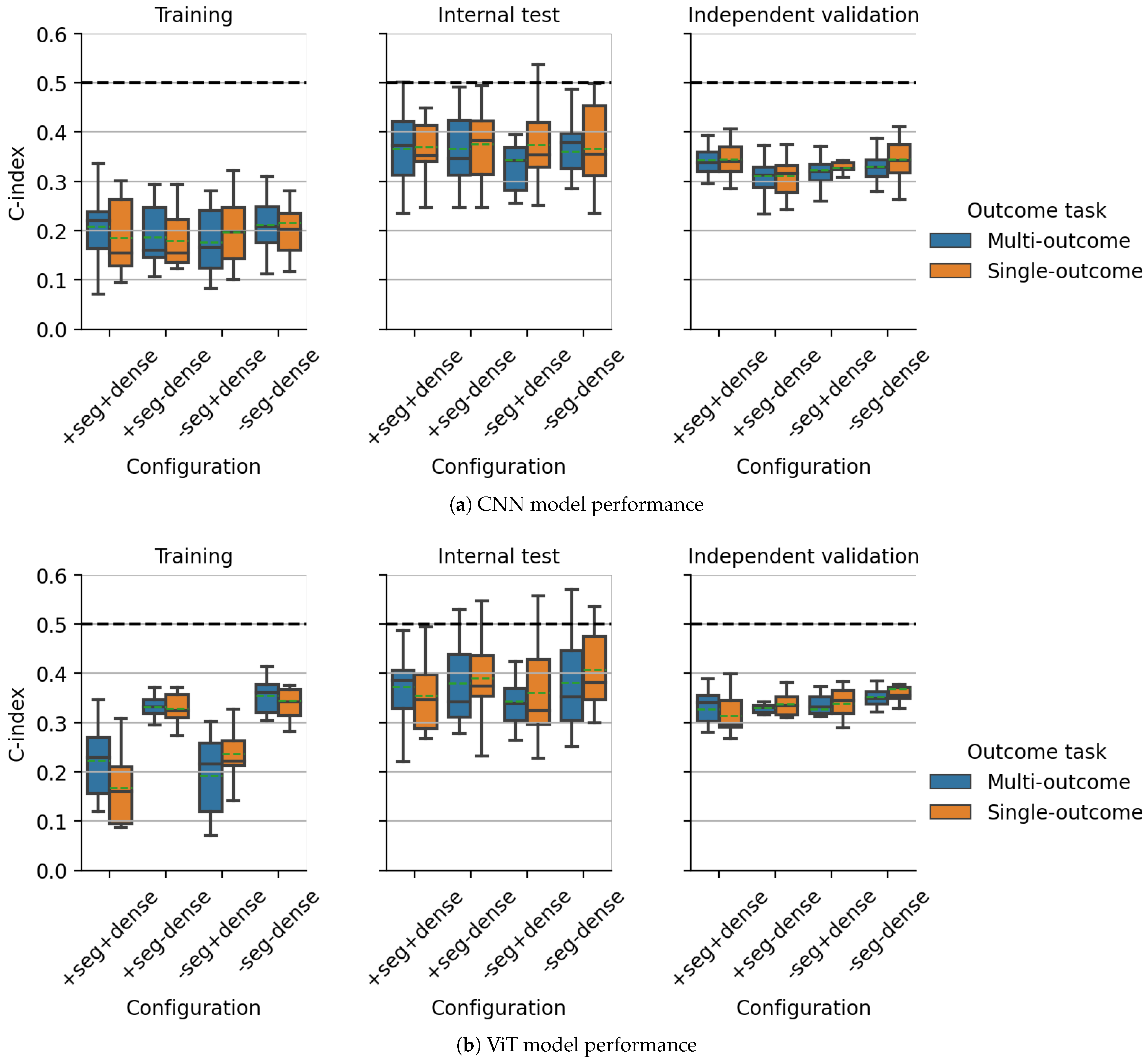
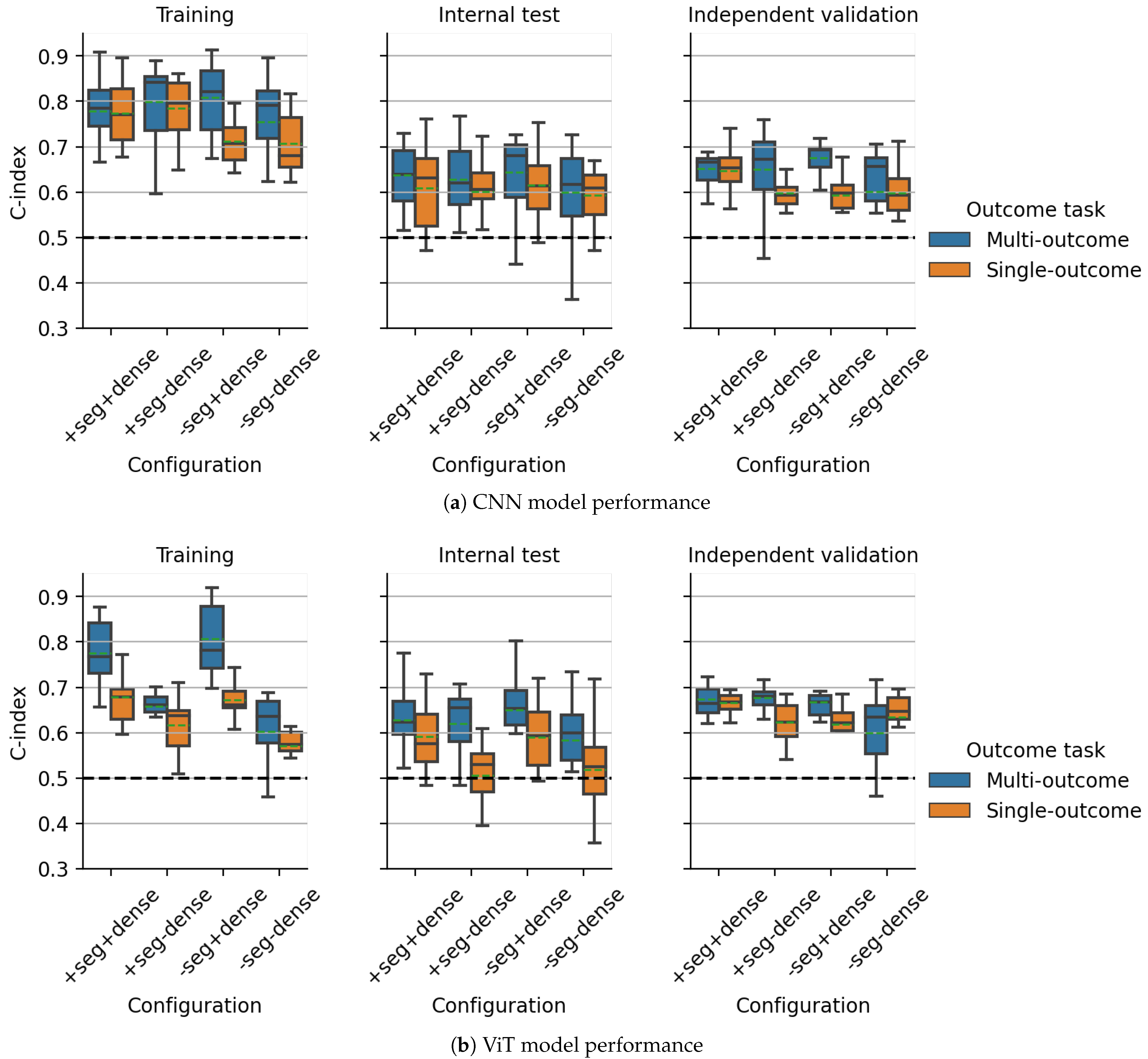
3.1. Multicentric DKTK CT Dataset
3.2. Multicentric HECKTOR2021 PET/CT Dataset
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, D.E.; Burtness, B.; Leemans, C.R.; Lui, V.W.Y.; Bauman, J.E.; Grandis, J.R. Head and neck squamous cell carcinoma. Nat. Rev. Dis. Primers 2020, 6, 92. [Google Scholar] [CrossRef] [PubMed]
- Leemans, C.R.; Snijders, P.J.F.; Brakenhoff, R.H. The molecular landscape of head and neck cancer. Nat. Rev. Cancer 2018, 18, 269–282. [Google Scholar] [CrossRef]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA A Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Baumann, M.; Krause, M.; Overgaard, J.; Debus, J.; Bentzen, S.M.; Daartz, J.; Richter, C.; Zips, D.; Bortfeld, T. Radiation oncology in the era of precision medicine. Nat. Rev. Cancer 2016, 16, 234–249. [Google Scholar] [CrossRef] [PubMed]
- Aerts, H.J.; Velazquez, E.R.; Leijenaar, R.T.; Parmar, C.; Grossmann, P.; Cavalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; Rietveld, D.; et al. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat. Commun. 2014, 5, 4006. [Google Scholar] [CrossRef] [PubMed]
- Vallières, M.; Freeman, C.R.; Skamene, S.R.; Naqa, I.E. A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities. Phys. Med. Biol. 2015, 60, 5471–5496. [Google Scholar] [CrossRef] [PubMed]
- Lambin, P.; Leijenaar, R.T.; Deist, T.M.; Peerlings, J.; De Jong, E.E.; Van Timmeren, J.; Sanduleanu, S.; Larue, R.T.; Even, A.J.; Jochems, A.; et al. Radiomics: The bridge between medical imaging and personalized medicine. Nat. Rev. Clin. Oncol. 2017, 14, 749–762. [Google Scholar] [CrossRef]
- Vallières, M.; Kay-Rivest, E.; Perrin, L.J.; Liem, X.; Furstoss, C.; Aerts, H.J.W.L.; Khaouam, N.; Nguyen-Tan, P.F.; Wang, C.S.; Sultanem, K.; et al. Radiomics strategies for risk assessment of tumour failure in head-and-neck cancer. Sci. Rep. 2017, 7, 10117. [Google Scholar] [CrossRef]
- Leger, S.; Zwanenburg, A.; Pilz, K.; Lohaus, F.; Linge, A.; Zöphel, K.; Kotzerke, J.; Schreiber, A.; Tinhofer, I.; Budach, V.; et al. A comparative study of machine learning methods for time-to-event survival data for radiomics risk modelling. Sci. Rep. 2017, 7, 13206. [Google Scholar] [CrossRef]
- Deist, T.M.; Dankers, F.J.; Valdes, G.; Wijsman, R.; Hsu, I.C.; Oberije, C.; Lustberg, T.; van Soest, J.; Hoebers, F.; Jochems, A.; et al. Machine learning algorithms for outcome prediction in (chemo)radiotherapy: An empirical comparison of classifiers. Med. Phys. 2018, 45, 3449–3459. [Google Scholar] [CrossRef]
- van Timmeren, J.E.; Cester, D.; Tanadini-Lang, S.; Alkadhi, H.; Baessler, B. Radiomics in medical imaging—“How-to” guide and critical reflection. Insights Imaging 2020, 11, 91. [Google Scholar] [CrossRef] [PubMed]
- Starke, S.; Leger, S.; Zwanenburg, A.; Leger, K.; Lohaus, F.; Linge, A.; Schreiber, A.; Kalinauskaite, G.; Tinhofer, I.; Guberina, N.; et al. 2D and 3D convolutional neural networks for outcome modelling of locally advanced head and neck squamous cell carcinoma. Sci. Rep. 2020, 10, 15625. [Google Scholar] [CrossRef] [PubMed]
- Rabasco Meneghetti, A.; Zwanenburg, A.; Leger, S.; Leger, K.; Troost, E.G.; Linge, A.; Lohaus, F.; Schreiber, A.; Kalinauskaite, G.; Tinhofer, I.; et al. Definition and validation of a radiomics signature for loco-regional tumour control in patients with locally advanced head and neck squamous cell carcinoma. Clin. Transl. Radiat. Oncol. 2021, 26, 62–70. [Google Scholar] [CrossRef]
- Meng, M.; Bi, L.; Feng, D.; Kim, J. Radiomics-Enhanced Deep Multi-task Learning for Outcome Prediction in Head and Neck Cancer. In Head and Neck Tumor Segmentation and Outcome Prediction; Andrearczyk, V., Oreiller, V., Hatt, M., Depeursinge, A., Eds.; Springer: Cham, Switzerland, 2023; pp. 135–143. [Google Scholar]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Krichen, M. Convolutional Neural Networks: A Survey. Computers 2023, 12, 151. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Andrearczyk, V.; Fontaine, P.; Oreiller, V.; Castelli, J.; Jreige, M.; Prior, J.O.; Depeursinge, A. Multi-task Deep Segmentation and Radiomics for Automatic Prognosis in Head and Neck Cancer. In Predictive Intelligence in Medicine; Rekik, I., Adeli, E., Park, S.H., Schnabel, J., Eds.; Springer: Cham, Switzerland, 2021; pp. 147–156. [Google Scholar] [CrossRef]
- Meng, M.; Gu, B.; Bi, L.; Song, S.; Feng, D.D.; Kim, J. DeepMTS: Deep Multi-Task Learning for Survival Prediction in Patients With Advanced Nasopharyngeal Carcinoma Using Pretreatment PET/CT. IEEE J. Biomed. Health Inform. 2022, 26, 4497–4507. [Google Scholar] [CrossRef]
- Baek, S.S.Y.; He, Y.; Allen, B.G.; Buatti, J.M.; Smith, B.J.; Tong, L.; Sun, Z.; Wu, J.; Diehn, M.; Loo, B.W.; et al. Deep segmentation networks predict survival of non-small cell lung cancer. Sci. Rep. 2019, 9, 17286. [Google Scholar] [CrossRef]
- Caruana, R. Multitask Learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Ruder, S. An Overview of Multi-Task Learning in Deep Neural Networks. arXiv 2017, arXiv:1706.05098. [Google Scholar] [CrossRef]
- Crawshaw, M. Multi-Task Learning with Deep Neural Networks: A Survey. arXiv 2020, arXiv:2009.09796. [Google Scholar] [CrossRef]
- Yu, C.N.; Greiner, R.; Lin, H.C.; Baracos, V. Learning Patient-Specific Cancer Survival Distributions as a Sequence of Dependent Regressors. In Proceedings of the 24th International Conference on Neural Information Processing Systems, NIPS’11, Red Hook, NY, USA, 11–15 July 2011; pp. 1845–1853. [Google Scholar]
- Cao, L.; Li, L.; Zheng, J.; Fan, X.; Yin, F.; Shen, H.; Zhang, J. Multi-Task Neural Networks for Joint Hippocampus Segmentation and Clinical Score Regression. Multimed. Tools Appl. 2018, 77, 29669–29686. [Google Scholar] [CrossRef]
- Fotso, S. Deep Neural Networks for Survival Analysis Based on a Multi-Task Framework. arXiv 2018, arXiv:1801.05512. [Google Scholar] [CrossRef]
- Weninger, L.; Liu, Q.; Merhof, D. Multi-Task Learning for Brain Tumor Segmentation. In Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 5th International Workshop, BrainLes 2019, Shenzhen, China, 17 October 2019; Revised Selected Papers, Part I; Springer: Berlin/Heidelberg, Germany, 2019; pp. 327–337. [Google Scholar] [CrossRef]
- Liu, M.; Li, F.; Yan, H.; Wang, K.; Ma, Y.; Shen, L.; Xu, M. A multi-model deep convolutional neural network for automatic hippocampus segmentation and classification in Alzheimer’s disease. NeuroImage 2020, 208, 116459. [Google Scholar] [CrossRef]
- Amyar, A.; Modzelewski, R.; Li, H.; Ruan, S. Multi-task deep learning based CT imaging analysis for COVID-19 pneumonia: Classification and segmentation. Comput. Biol. Med. 2020, 126, 104037. [Google Scholar] [CrossRef]
- Fu, S.; Lai, H.; Li, Q.; Liu, Y.; Zhang, J.; Huang, J.; Chen, X.; Duan, C.; Li, X.; Wang, T.; et al. Multi-task deep learning network to predict future macrovascular invasion in hepatocellular carcinoma. eClinicalMedicine 2021, 42, 101201. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, D.; Liu, Z.; Zhou, J.; Tian, J. Joint Multi-Task Learning for Survival Prediction of Gastric Cancer Patients using CT Images. In Proceedings of the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Virtual, 13–16 April 2021; pp. 895–898. [Google Scholar] [CrossRef]
- Jin, C.; Yu, H.; Ke, J.; Ding, P.; Yi, Y.; Jiang, X.; Duan, X.; Tang, J.; Chang, D.T.; Wu, X.; et al. Predicting treatment response from longitudinal images using multi-task deep learning. Nat. Commun. 2021, 12, 1851. [Google Scholar] [CrossRef]
- Park, S.; Kim, G.; Oh, Y.; Seo, J.B.; Lee, S.M.; Kim, J.H.; Moon, S.; Lim, J.K.; Ye, J.C. Multi-task vision transformer using low-level chest X-ray feature corpus for COVID-19 diagnosis and severity quantification. Med. Image Anal. 2022, 75, 102299. [Google Scholar] [CrossRef]
- Cox, D.R. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Yao, J.; Huang, J. Deep convolutional neural network for survival analysis with pathological images. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2017; pp. 544–547. [Google Scholar] [CrossRef]
- Mobadersany, P.; Yousefi, S.; Amgad, M.; Gutman, D.A.; Barnholtz-Sloan, J.S.; Velázquez Vega, J.E.; Brat, D.J.; Cooper, L.A.D. Predicting cancer outcomes from histology and genomics using convolutional networks. Proc. Natl. Acad. Sci. USA 2018, 115, E2970–E2979. [Google Scholar] [CrossRef] [PubMed]
- Ching, T.; Zhu, X.; Garmire, L.X. Cox-nnet: An artificial neural network method for prognosis prediction of high-throughput omics data. PLoS Comput. Biol. 2018, 14, e1006076. [Google Scholar] [CrossRef] [PubMed]
- Haarburger, C.; Weitz, P.; Rippel, O.; Merhof, D. Image-Based Survival Prediction for Lung Cancer Patients Using CNNS. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 1197–1201. [Google Scholar] [CrossRef]
- Gensheimer, M.F.; Narasimhan, B. A scalable discrete-time survival model for neural networks. PeerJ 2019, 7, e6257. [Google Scholar] [CrossRef] [PubMed]
- Andrearczyk, V.; Oreiller, V.; Boughdad, S.; Rest, C.C.L.; Elhalawani, H.; Jreige, M.; Prior, J.O.; Vallières, M.; Visvikis, D.; Hatt, M.; et al. Overview of the HECKTOR Challenge at MICCAI 2021: Automatic Head and Neck Tumor Segmentation and Outcome Prediction in PET/CT Images. In Head and Neck Tumor Segmentation and Outcome Prediction; Andrearczyk, V., Oreiller, V., Hatt, M., Depeursinge, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 1–37. [Google Scholar] [CrossRef]
- Andrearczyk, V.; Oreiller, V.; Vallières, M.; Castelli, J.; Elhalawani, H.; Jreige, M.; Boughdad, S.; Prior, J.O.; Depeursinge, A. Automatic Segmentation of Head and Neck Tumors and Nodal Metastases in PET-CT scans. In Proceedings of the Third Conference on Medical Imaging with Deep Learning, Montreal, QC, Canada, 6–8 July 2020; Arbel, T., Ben Ayed, I., de Bruijne, M., Descoteaux, M., Lombaert, H., Pal, C., Eds.; PMLR 2020; ML Research Press: Maastricht, The Netherlands, 2020; Volume 121, pp. 33–43. [Google Scholar]
- Oreiller, V.; Andrearczyk, V.; Jreige, M.; Boughdad, S.; Elhalawani, H.; Castelli, J.; Vallières, M.; Zhu, S.; Xie, J.; Peng, Y.; et al. Head and neck tumor segmentation in PET/CT: The HECKTOR challenge. Med. Image Anal. 2022, 77, 102336. [Google Scholar] [CrossRef]
- Zwanenburg, A.; Leger, S.; Agolli, L.; Pilz, K.; Troost, E.G.; Richter, C.; Löck, S. Assessing robustness of radiomic features by image perturbation. Sci. Rep. 2019, 9, 614. [Google Scholar] [CrossRef]
- Zwanenburg, A.; Leger, S.; Starke, S. Medical Image Radiomics Processor (MIRP). 2022. Available online: https://github.com/oncoray/mirp (accessed on 4 October 2023).
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv 2016, arXiv:1608.06993. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar] [CrossRef]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. UNETR: Transformers for 3D Medical Image Segmentation. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 4–8 January 2022; pp. 1748–1758. [Google Scholar] [CrossRef]
- Harrell, F.E.; Lee, K.L.; Mark, D.B. Tutorial in biostatistics multivariable prognostic models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat. Med. 1996, 15, 361–387. [Google Scholar] [CrossRef]
- Steck, H.; Krishnapuram, B.; Dehing-oberije, C.; Lambin, P.; Raykar, V.C. On Ranking in Survival Analysis: Bounds on the Concordance Index. Adv. Neural Inf. Process. Syst. 2008, 20, 1209–1216. [Google Scholar]
- Mayr, A.; Schmid, M. Boosting the concordance index for survival data–a unified framework to derive and evaluate biomarker combinations. PLoS ONE 2014, 9, e84483. [Google Scholar] [CrossRef] [PubMed]
- Haibe-Kains, B.; Desmedt, C.; Sotiriou, C.; Bontempi, G. A comparative study of survival models for breast cancer prognostication based on microarray data: Does a single gene beat them all? Bioinformatics 2008, 24, 2200–2208. [Google Scholar] [CrossRef] [PubMed]
- Schröder, M.S.; Culhane, A.C.; Quackenbush, J.; Haibe-Kains, B. Survcomp: An R/Bioconductor package for performance assessment and comparison of survival models. Bioinformatics 2011, 27, 3206–3208. [Google Scholar] [CrossRef]
- Mantel, N. Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemother. Rep. 1966, 50, 163–170. [Google Scholar]
- Hosny, A.; Parmar, C.; Coroller, T.P.; Grossmann, P.; Zeleznik, R.; Kumar, A.; Bussink, J.; Gillies, R.J.; Mak, R.H.; Aerts, H.J.W.L. Deep learning for lung cancer prognostication: A retrospective multi-cohort radiomics study. PLoS Med. 2018, 15, e1002711. [Google Scholar] [CrossRef] [PubMed]
- Saeed, N.; Sobirov, I.; Majzoub, R.A.; Yaqub, M. TMSS: An End-to-End Transformer-based Multimodal Network for Segmentation and Survival Prediction. arXiv 2022, arXiv:2209.05036. [Google Scholar] [CrossRef]
- Klyuzhin, I.S.; Xu, Y.; Ortiz, A.; Ferres, J.L.; Hamarneh, G.; Rahmim, A. Testing the Ability of Convolutional Neural Networks to Learn Radiomic Features. Comput. Methods Programs Biomed. 2022, 219, 106750. [Google Scholar] [CrossRef]
- Royston, P. The Lognormal Distribution as a Model for Survival Time in Cancer, With an Emphasis on Prognostic Factors. Stat. Neerl. 2001, 55, 89–104. [Google Scholar] [CrossRef]
- Chapman, J.W.; O’Callaghan, C.J.; Hu, N.; Ding, K.; Yothers, G.A.; Catalano, P.J.; Shi, Q.; Gray, R.G.; O’Connell, M.J.; Sargent, D.J. Innovative estimation of survival using log-normal survival modelling on ACCENT database. Br. J. Cancer 2013, 108, 784–790. [Google Scholar] [CrossRef]
- Suresh, K.; Severn, C.; Ghosh, D. Survival prediction models: An introduction to discrete-time modeling. BMC Med. Res. Methodol. 2022, 22, 207. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Liu, Q. Profiling Pareto Front With Multi-Objective Stein Variational Gradient Descent. In Proceedings of the Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021, Virtual, 6–14 December 2021; Ranzato, M., Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 14721–14733. [Google Scholar]
- Sener, O.; Koltun, V. Multi-Task Learning as Multi-Objective Optimization. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, BC, Canada, 3–5 December 2018; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Ruchte, M.; Grabocka, J. Scalable Pareto Front Approximation for Deep Multi-Objective Learning. In Proceedings of the IEEE International Conference on Data Mining, ICDM 2021, Auckland, New Zealand, 7–10 December 2021; Bailey, J., Miettinen, P., Koh, Y.S., Tao, D., Wu, X., Eds.; IEEE: Washington, DC, USA, 2021; pp. 1306–1311. [Google Scholar] [CrossRef]
- Haider, H.; Hoehn, B.; Davis, S.; Greiner, R. Effective Ways to Build and Evaluate Individual Survival Distributions. J. Mach. Learn. Res. 2020, 21, 1–63. [Google Scholar]
- Chen, L.; Bentley, P.; Mori, K.; Misawa, K.; Fujiwara, M.; Rueckert, D. Self-supervised learning for medical image analysis using image context restoration. Med. Image Anal. 2019, 58, 101539. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the 37th International Conference on Machine Learning, ICML’20, Virtual, 13–18 July 2020. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 14–19 June 2020; pp. 9726–9735. [Google Scholar] [CrossRef]
- Caron, M.; Touvron, H.; Misra, I.; Jegou, H.; Mairal, J.; Bojanowski, P.; Joulin, A. Emerging Properties in Self-Supervised Vision Transformers. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Virtual, 11–17 October 2021; pp. 9630–9640. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 15979–15988. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, D.; Li, W.; Roth, H.R.; Landman, B.; Xu, D.; Nath, V.; Hatamizadeh, A. Self-Supervised Pre-Training of Swin Transformers for 3D Medical Image Analysis. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 20698–20708. [Google Scholar] [CrossRef]
- Oquab, M.; Darcet, T.; Moutakanni, T.; Vo, H.; Szafraniec, M.; Khalidov, V.; Fernandez, P.; Haziza, D.; Massa, F.; El-Nouby, A.; et al. DINOv2: Learning Robust Visual Features without Supervision. arXiv 2023, arXiv:2304.07193. [Google Scholar] [CrossRef]

| Configuration | Head | CNN | ViT | |||||
|---|---|---|---|---|---|---|---|---|
| Seg | Dense | Training | IT | IV | Training | IT | IV | |
| Multi-Outcome (CPH + GH) | ||||||||
| ✓ | ✓ | CPH | 0.15 (0.11–0.18) | * (0.29–0.40) | * (0.24–0.43) | 0.15 (0.12–0.19) | * (0.30–0.42) | * (0.19–0.38) |
| GH (24 m) | 0.86 (0.83–0.89) | * (0.60–0.71) | 0.67 (0.57–0.76) | 0.87 (0.84–0.90) | * (0.59–0.71) | 0.72 * (0.62–0.81) | ||
| ✓ | ✗ | CPH | 0.13 (0.10–0.16) | * (0.30–0.42) | 0.26 * (0.18–0.34) | 0.32 (0.26–0.38) | * (0.32–0.44) | * (0.22–0.40) |
| GH (24 m) | 0.89 (0.86–0.92) | * (0.58–0.70) | 0.74 * (0.65–0.82) | 0.68 (0.62–0.74) | * (0.54–0.67) | * (0.61–0.79) | ||
| ✗ | ✓ | CPH | 0.11 (0.08–0.13) | * (0.27–0.39) | * (0.20–0.38) | 0.12 (0.09–0.15) | * (0.27–0.38) | * (0.22–0.39) |
| GH (24 m) | 0.90 (0.88–0.92) | * (0.61–0.72) | * (0.63–0.80) | 0.90 (0.87–0.92) | * (0.60–0.72) | * (0.62–0.79) | ||
| ✗ | ✗ | CPH | 0.15 (0.12–0.19) | * (0.30–0.41) | * (0.22–0.39) | 0.32 (0.26–0.38) | * (0.33–0.45) | * (0.23–0.41) |
| GH (24 m) | 0.88 (0.85–0.90) | * (0.56–0.68) | * (0.60–0.78) | 0.68 (0.61–0.74) | 0.60 (0.54–0.66) | * (0.59–0.77) | ||
| Single-Outcome (CPH) | ||||||||
| ✓ | ✓ | CPH | 0.12 (0.09–0.14) | * (0.28–0.40) | * (0.23–0.41) | 0.11 (0.09–0.14) | * (0.27–0.38) | 0.26 * (0.18–0.35) |
| ✓ | ✗ | CPH | 0.13 (0.10–0.16) | * (0.28–0.40) | * (0.19–0.37) | 0.31 (0.25–0.36) | 0.42 (0.36–0.48) | * (0.23–0.41) |
| ✗ | ✓ | CPH | 0.14 (0.11–0.18) | * (0.31–0.42) | * (0.23–0.40) | 0.16 (0.12–0.19) | * (0.29–0.42) | 0.33 (0.24–0.42) |
| ✗ | ✗ | CPH | 0.15 (0.11–0.18) | * (0.30–0.42) | * (0.22–0.39) | 0.33 (0.27–0.39) | * (0.38–0.51) | * (0.25–0.44) |
| Single-Outcome (GH) | ||||||||
| ✓ | ✓ | GH (24 m) | 0.87 (0.84–0.90) | * (0.57–0.69) | * (0.59–0.77) | 0.77 (0.72–0.82) | * (0.53–0.65) | * (0.60–0.79) |
| ✓ | ✗ | GH (24 m) | 0.84 (0.81–0.88) | * (0.56–0.68) | * (0.52–0.72) | 0.68 (0.62–0.74) | 0.52 (0.46–0.59) | * (0.57–0.76) |
| ✗ | ✓ | GH (24 m) | 0.77 (0.73–0.82) | * (0.56–0.68) | 0.62 (0.53–0.72) | 0.73 (0.68–0.79) | * (0.50–0.63) | 0.65 (0.56–0.75) |
| ✗ | ✗ | GH (24 m) | 0.80 (0.76–0.84) | 0.59 (0.53–0.65) | 0.64 (0.54–0.74) | 0.61 (0.54–0.67) | 0.54 (0.48–0.60) | * (0.59–0.78) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starke, S.; Zwanenburg, A.; Leger, K.; Lohaus, F.; Linge, A.; Kalinauskaite, G.; Tinhofer, I.; Guberina, N.; Guberina, M.; Balermpas, P.; et al. Multitask Learning with Convolutional Neural Networks and Vision Transformers Can Improve Outcome Prediction for Head and Neck Cancer Patients. Cancers 2023, 15, 4897. https://doi.org/10.3390/cancers15194897
Starke S, Zwanenburg A, Leger K, Lohaus F, Linge A, Kalinauskaite G, Tinhofer I, Guberina N, Guberina M, Balermpas P, et al. Multitask Learning with Convolutional Neural Networks and Vision Transformers Can Improve Outcome Prediction for Head and Neck Cancer Patients. Cancers. 2023; 15(19):4897. https://doi.org/10.3390/cancers15194897
Chicago/Turabian StyleStarke, Sebastian, Alex Zwanenburg, Karoline Leger, Fabian Lohaus, Annett Linge, Goda Kalinauskaite, Inge Tinhofer, Nika Guberina, Maja Guberina, Panagiotis Balermpas, and et al. 2023. "Multitask Learning with Convolutional Neural Networks and Vision Transformers Can Improve Outcome Prediction for Head and Neck Cancer Patients" Cancers 15, no. 19: 4897. https://doi.org/10.3390/cancers15194897
APA StyleStarke, S., Zwanenburg, A., Leger, K., Lohaus, F., Linge, A., Kalinauskaite, G., Tinhofer, I., Guberina, N., Guberina, M., Balermpas, P., Grün, J. v. d., Ganswindt, U., Belka, C., Peeken, J. C., Combs, S. E., Boeke, S., Zips, D., Richter, C., Troost, E. G. C., ... Löck, S. (2023). Multitask Learning with Convolutional Neural Networks and Vision Transformers Can Improve Outcome Prediction for Head and Neck Cancer Patients. Cancers, 15(19), 4897. https://doi.org/10.3390/cancers15194897






