Multiphysics Modeling of Low-Intensity Pulsed Ultrasound Induced Chemotherapeutic Drug Release from the Surface of Gold Nanoparticles
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. DOX-Loaded GNP Synthesis
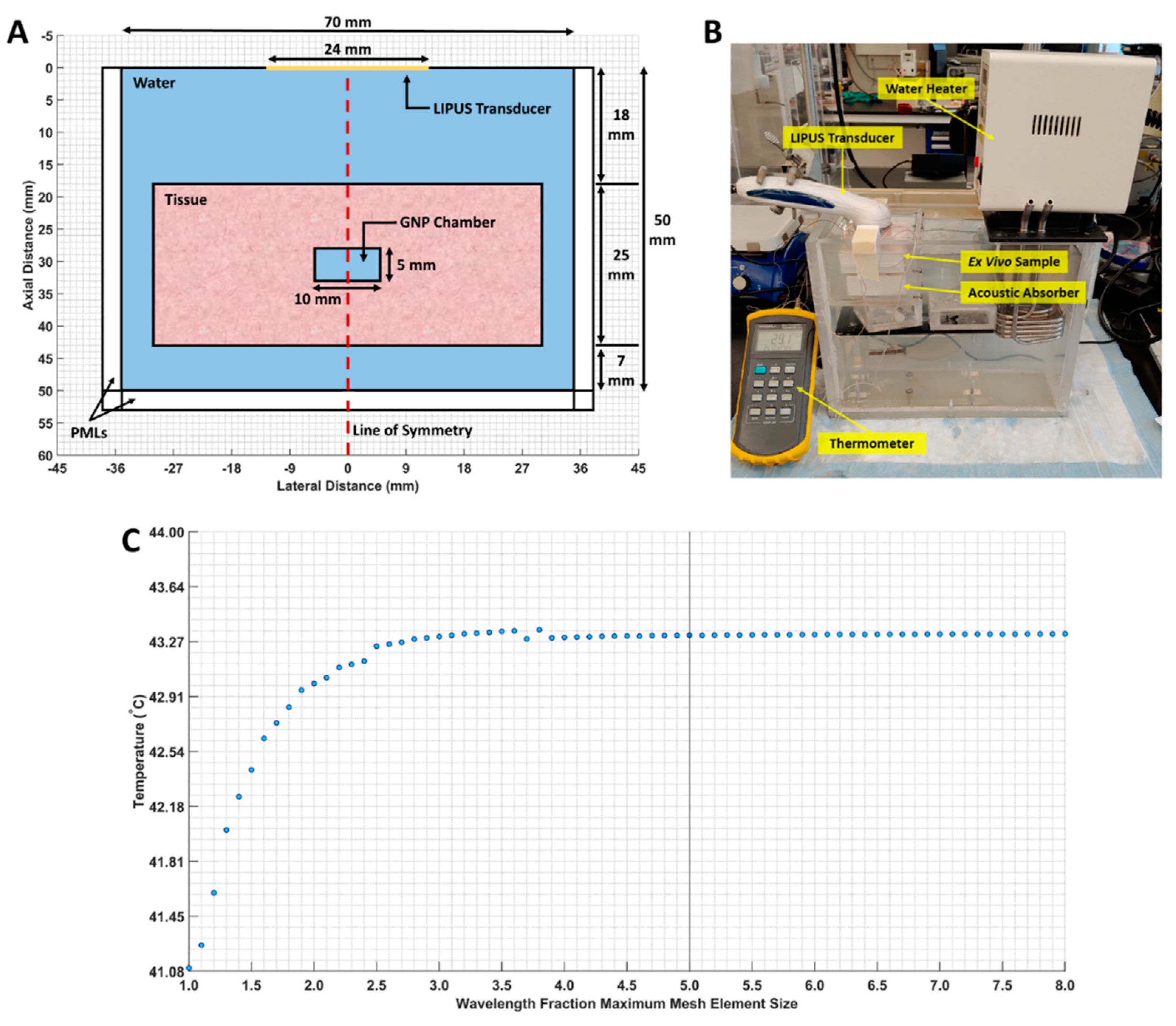
2.2. Ex Vivo LIPUS-Induced DOX Release
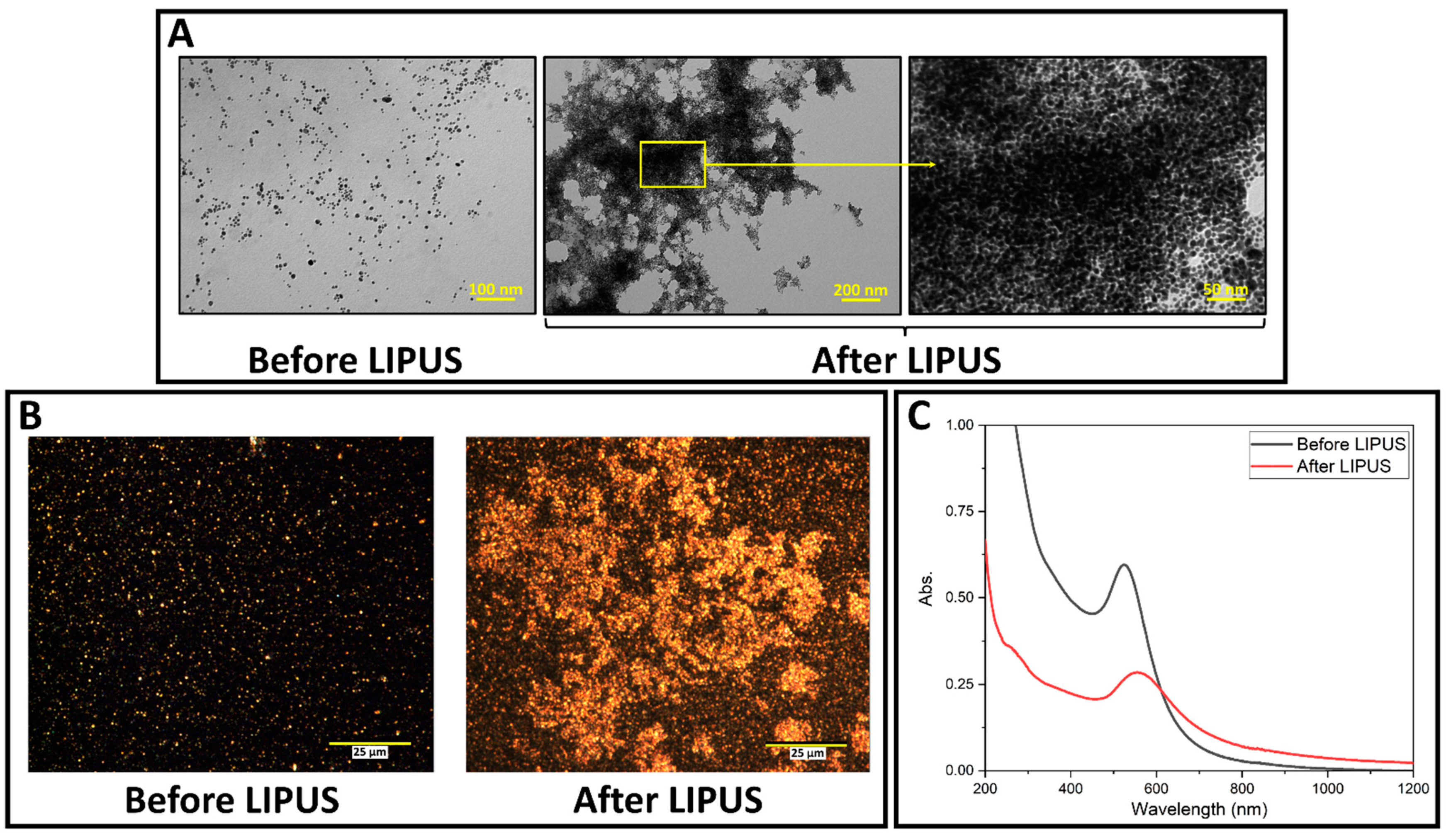
2.3. GNP Characterization and Zeta Potential Measurements
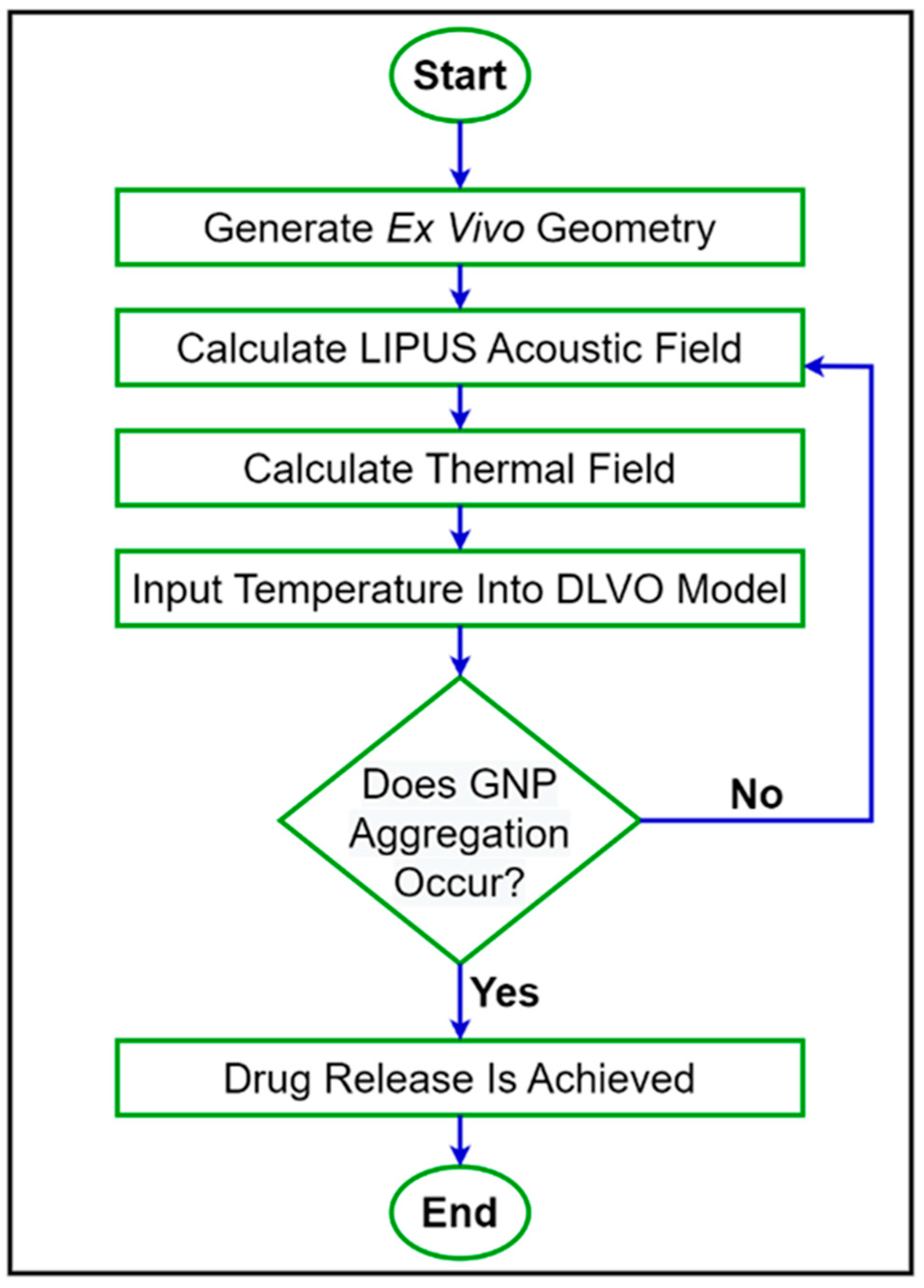
2.4. Developing a Numerical DLVO Model
2.4.1. Acoustic and Heat Transfer Models
2.4.2. DLVO Model
3. Results
3.1. LIPUS-Induced DOX Release in Ex Vivo Tisue Experiments
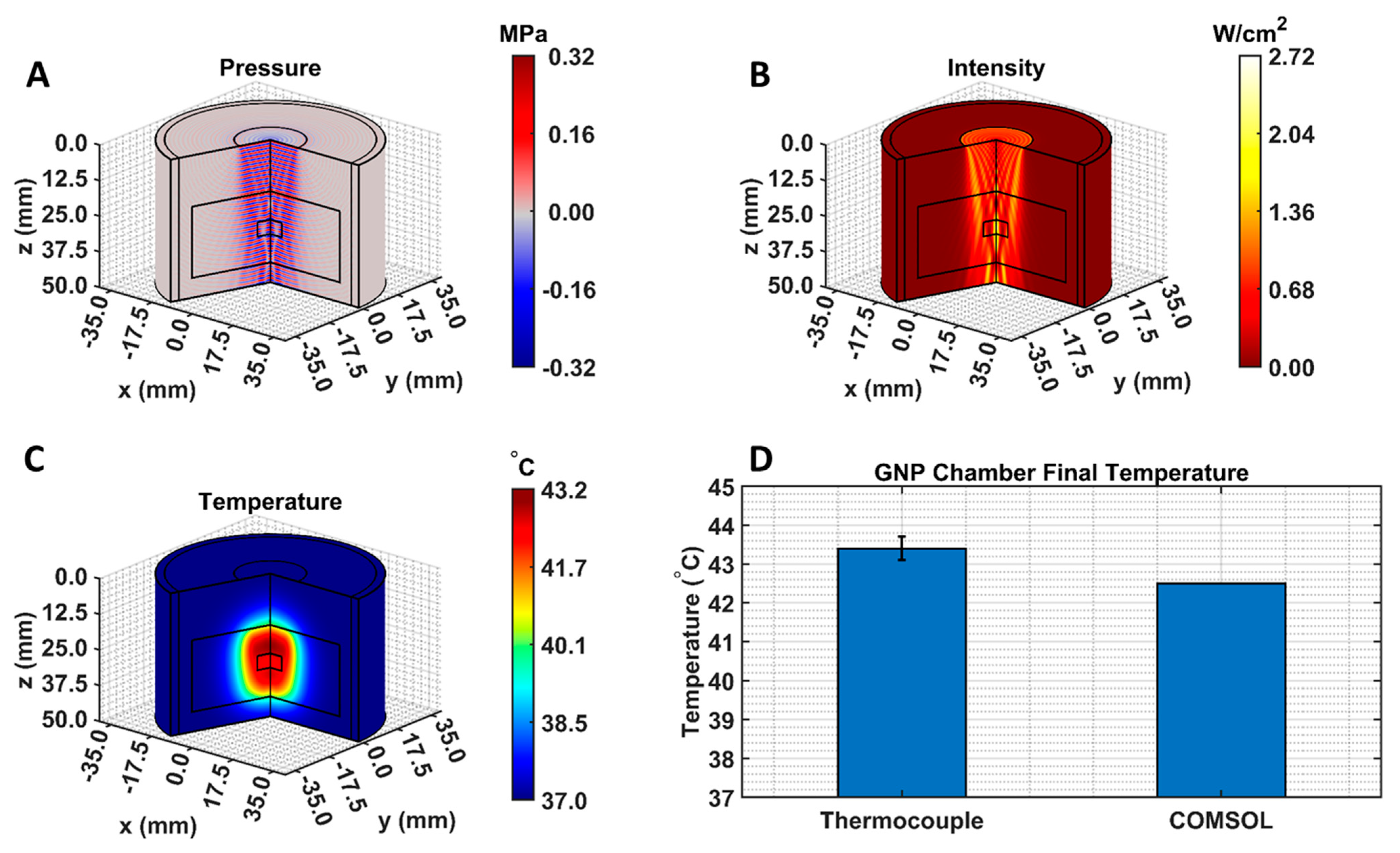
3.2. LIPUS Heating Simulation Model
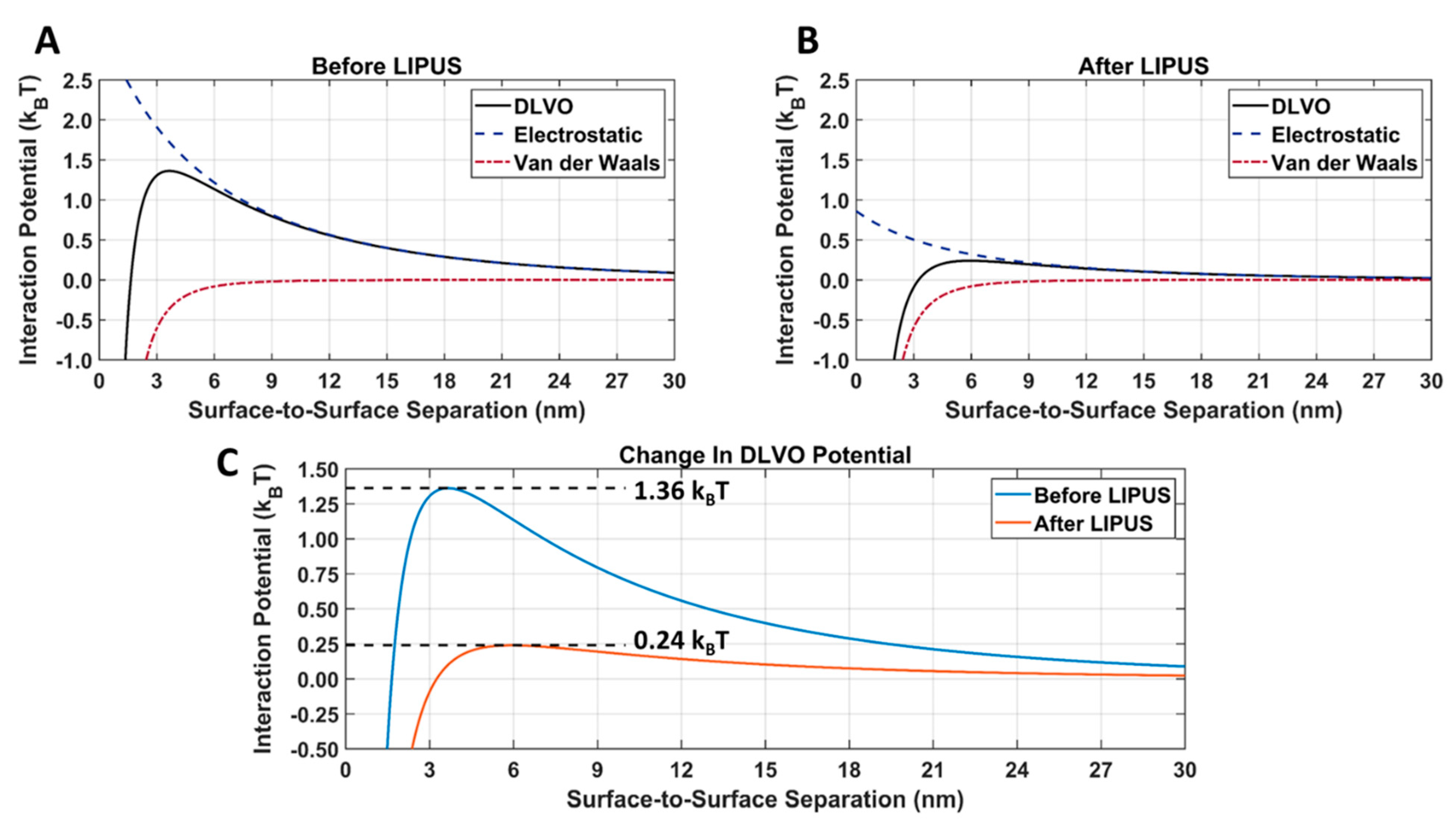
3.3. DLVO Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dadwal, A.; Baldi, A.; Kumar Narang, R. Nanoparticles as Carriers for Drug Delivery in Cancer. Artif. Cells Nanomed. Biotechnol. 2018, 46, 295–305. [Google Scholar] [CrossRef]
- May, J.; Li, S.-D. Hyperthermia-Induced Drug Targeting. Expert Opin. Drug Deliv. 2013, 10, 511–527. [Google Scholar] [CrossRef]
- Hornsby, T. Shaswary, E. Tavakkoli, J. Development of a Nonlinear Frequency Compounding Method With Applications in Tissue Thermometry. J. Acoust. Soc. Am. 2021, 150, 3192–3203. [Google Scholar] [CrossRef]
- Moradi Kashkooli, F.; Soltani, M.; Souri, M. Controlled Anti-Cancer Drug Release through Advanced Nano-Drug Delivery Systems: Static and Dynamic Targeting Strategies. J. Control. Release 2020, 327, 316–349. [Google Scholar] [CrossRef] [PubMed]
- Jakhmola, A.; Hornsby, T.; Rod, K.; Tavakkoli, J. A Novel Gold Nanoparticles Drug Delivery System: Design and Ex Vivo Tissue Testing. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–3. [Google Scholar]
- Hornsby, T.; Jakhmola, A.; Kolios, M.C.; Tavakkoli, J.J. Significance of Non-Thermal Effects in LIPUS Induced Drug Release from Gold Nanoparticle Drug Carriers. In Proceedings of the 2021 IEEE UFFC Latin America Ultrasonics Symposium (LAUS), Gainesville, FL, USA, 4–5 October 2021; pp. 1–4. [Google Scholar]
- Hornsby, T.; Kashkooli, F.M.; Jakhmola, A.; Kolios, M.C.; Tavakkoli, J. Measuring Drug Release Induced by Thermal and Non-Thermal Effects of Ultrasound in a Nanodrug Delivery System. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022; pp. 1–4. [Google Scholar]
- Jakhmola, A.; Tavakkoli, J.; Rod, K. Gold Nano-Delivery System for Pain and Cancer Therapy 2021. US20220040118A1, 25 October 2021. [Google Scholar]
- Zereshkian, G.H.; Tavakkoli, J.; Rod, K. Hand-Held Battery-Operated Therapeutic Ultrasonic Device 2019. US20190184202A1, 15 December 2017. [Google Scholar]
- Celentano, M.; Jakhmola, A.; Profeta, M.; Battista, E.; Guarnieri, D.; Gentile, F.; Netti, P.A.; Vecchione, R. Diffusion Limited Green Synthesis of Ultra-Small Gold Nanoparticles at Room Temperature. Coll. Surf. A Physicochem. Eng. Asp. 2018, 558, 548–557. [Google Scholar] [CrossRef]
- Arvizo, R.R.; Saha, S.; Wang, E.; Robertson, J.D.; Bhattacharya, R.; Mukherjee, P. Inhibition of Tumor Growth and Metastasis by a Self-Therapeutic Nanoparticle. Appl. Biol. Sci. 2013, 110, 6700–6705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhattacharya, R.; Patra, C.R.; Verma, R.; Kumar, S.; Greipp, P.R.; Mukherjee, P. Gold Nanoparticles Inhibit the Proliferation of Multiple Myeloma Cells. Adv. Mater. 2007, 19, 711–716. [Google Scholar] [CrossRef]
- Mukherjee, P.; Bhattacharya, R.; Wang, P.; Wang, L.; Basu, S.; Nagy, J.A.; Atala, A.; Mukhopadhyay, D.; Soker, S. Antiangiogenic Properties of Gold Nanoparticles. Clin. Cancer Res. 2005, 11, 3530–3534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Q.-L.; Chen, Z.-Y.; Wang, Y.-X.; Yang, F.; Lin, Y.; Liao, Y.-Y. Ultrasound-Mediated Local Drug and Gene Delivery Using Nanocarriers. BioMed Res. Int. 2014, 2014, e963891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tharkar, P.; Varanasi, R.; Wong, W.S.F.; Jin, C.T.; Chrzanowski, W. Nano-Enhanced Drug Delivery and Therapeutic Ultrasound for Cancer Treatment and Beyond. Front. Bioeng. Biotechnol. 2019, 7, 324. [Google Scholar] [CrossRef]
- Moradi Kashkooli, F.; Soltani, M.; Momeni, M.M.; Rahmim, A. Enhanced Drug Delivery to Solid Tumors via Drug-Loaded Nanocarriers: An Image-Based Computational Framework. Front. Oncol. 2021, 11, 655781. [Google Scholar] [CrossRef] [PubMed]
- Moradi Kashkooli, F.; Soltani, M.; Hamedi, M.-H. Drug Delivery to Solid Tumors with Heterogeneous Microvascular Networks: Novel Insights from Image-Based Numerical Modeling. Eur. J. Pharm. Sci. 2020, 151, 105399. [Google Scholar] [CrossRef] [PubMed]
- Moradi Kashkooli, F.; Soltani, M.; Souri, M.; Meaney, C.; Kohandel, M. Nexus between in Silico and in Vivo Models to Enhance Clinical Translation of Nanomedicine. Nano Today 2021, 36, 101057. [Google Scholar] [CrossRef]
- Cosgrove, T. Colloid Science: Principles, Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 978-1-4443-2019-0. [Google Scholar]
- Hunter, R.J. Foundations of Colloid Science, 2nd ed; Oxford University Press: Oxford, UK; New York, NY, USA, 2001; ISBN 978-0-19-850502-0. [Google Scholar]
- Doane, T.; Burda, C. Nanoparticle Mediated Non-Covalent Drug Delivery. Adv. Drug Deliv. Rev. 2013, 65, 607–621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toma, H.E.; Zamarion, V.M.; Toma, S.H.; Araki, K. The Coordination Chemistry at Gold Nanoparticles. J. Braz. Chem. Soc. 2010, 21, 1158–1176. [Google Scholar] [CrossRef]
- Buettner, K.M.; Rinciog, C.I.; Mylon, S.E. Aggregation Kinetics of Cerium Oxide Nanoparticles in Monovalent and Divalent Electrolytes. Coll. Surf. A Physicochem. Eng. Asp. 2010, 366, 74–79. [Google Scholar] [CrossRef]
- El Badawy, A.M.; Scheckel, K.G.; Suidan, M.; Tolaymat, T. The Impact of Stabilization Mechanism on the Aggregation Kinetics of Silver Nanoparticles. Sci. Total Environ. 2012, 429, 325–331. [Google Scholar] [CrossRef]
- Chen, K.L.; Elimelech, M. Aggregation and Deposition Kinetics of Fullerene (C60) Nanoparticles. Langmuir 2006, 22, 10994–11001. [Google Scholar] [CrossRef]
- Kim, T.; Lee, K.; Gong, M.; Joo, S.-W. Control of Gold Nanoparticle Aggregates by Manipulation of Interparticle Interaction. Langmuir 2005, 21, 9524–9528. [Google Scholar] [CrossRef]
- Kim, T.; Lee, C.-H.; Joo, S.-W.; Lee, K. Kinetics of Gold Nanoparticle Aggregation: Experiments and Modeling. J. Colloid Interface Sci. 2008, 318, 238–243. [Google Scholar] [CrossRef]
- Kim, C.; Guo, Y.; Velalopoulou, A.; Leisen, J.; Motamarry, A.; Ramajayam, K.; Aryal, M.; Haemmerich, D.; Arvanitis, C.D. Closed-Loop Trans-Skull Ultrasound Hyperthermia Leads to Improved Drug Delivery from Thermosensitive Drugs and Promotes Changes in Vascular Transport Dynamics in Brain Tumors. Theranostics 2021, 11, 7276. [Google Scholar] [CrossRef]
- Souri, M.; Soltani, M.; Moradi Kashkooli, F. Computational Modeling of Thermal Combination Therapies by Magneto-Ultrasonic Heating to Enhance Drug Delivery to Solid Tumors. Sci. Rep. 2021, 11, 19539. [Google Scholar] [CrossRef]
- Jakhmola, A.; Krishnan, S.; Onesto, V.; Gentile, F.; Profeta, M.; Manikas, A.; Battista, E.; Vecchione, R.; Netti, P.A. Sustainable Synthesis and Theoretical Studies of Polyhedral Gold Nanoparticles Displaying High SERS Activity, NIR Absorption, and Cellular Uptake. Mater. Today Chem. 2022, 26, 101016. [Google Scholar] [CrossRef]
- Jakhmola, A.; Vecchione, R.; Onesto, V.; Gentile, F.; Celentano, M.; Netti, P.A. Experimental and Theoretical Studies on Sustainable Synthesis of Gold Sol Displaying Dichroic Effect. Nanomater 2021, 11, 236. [Google Scholar] [CrossRef]
- Jakhmola, A.; Celentano, M.; Vecchione, R.; Manikas, A.; Battista, E.; Calcagno, V.; Netti, P.A. Self-Assembly of Gold Nanowire Networks into Gold Foams: Production, Ultrastructure and Applications. Inorg. Chem. Front. 2017, 4, 1033–1041. [Google Scholar] [CrossRef]
- Wessapan, T.; Rattanadecho, P. Acoustic Streaming Effect on Flow and Heat Transfer in Porous Tissue during Exposure to Focused Ultrasound. Case Stud. Therm. Eng. 2020, 21, 100670. [Google Scholar] [CrossRef]
- Cobbold, R.S. Foundations of Biomedical Ultrasound; Oxford University Press: Oxford, UK , 2006. [Google Scholar]
- Yang, D.; Converse, M.C.; Mahvi, D.M.; Webster, J.G. Expanding the Bioheat Equation to Include Tissue Internal Water Evaporation During Heating. IEEE Trans. Biomed. Eng. 2007, 54, 1382–1388. [Google Scholar] [CrossRef] [PubMed]
- Cortela, G.A.; Pereira, W.C.A.; Negreira, C.A. Ex Vivo Determined Experimental Correction Factor for the Ultrasonic Source Term in the Bioheat Equation. Ultrasonics 2018, 82, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Malinen, M.; Huttunen, T.; Kaipio, J.P. An Optimal Control Approach for Ultrasound Induced Heating. Int. J. Control 2003, 76, 1323–1336. [Google Scholar] [CrossRef]
- Kumar, D.; Dhar, P.; Paul, A. Thermal Response of Dielectric Nanoparticle-Infused Tissue Phantoms During Microwave-Assisted Hyperthermia. J. Therm. Sci. Eng. Appl. 2021, 13, 061029. [Google Scholar] [CrossRef]
- Paul, A.; Paul, A. Thermo-Mechanical Assessment of Nanoparticle Mixed Vascular Tissues under Pulsed Ultrasound and Laser Heating. Int. J. Therm. Sci. 2021, 163, 106815. [Google Scholar] [CrossRef]
- Duck, F.A. Physical Properties of Tissues: A Comprehensive Reference Book; Academic Press: Cambridge, MA, USA, 2013; ISBN 978-1-4832-8842-0. [Google Scholar]
- Sumnu, S.G.; Sahin, S. Advances in Deep-Fat Frying of Foods; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-1-4200-5559-7. [Google Scholar]
- Ohshima, H. Effective Surface Potential and Double-Layer Interaction of Colloidal Particles. J. Colloid Interface Sci. 1995, 174, 45–52. [Google Scholar] [CrossRef]
- Malmberg, C.G.; Maryott, A.A. Dielectric Constant of Water from 0 to 100 C. J. Res. Natl. Bur. Stan. 1956, 56, 1. [Google Scholar] [CrossRef]
- Lee, K.; Sathyagal, A.N.; McCormick, A.V. A Closer Look at an Aggregation Model of the Stöber Process. Coll. Surf. A Physicochem. Eng. Asp. 1998, 144, 115–125. [Google Scholar] [CrossRef]
- Hogg, R.; Healy, T.W.; Fuerstenau, D.W. Mutual Coagulation of Colloidal Dispersions. Trans. Faraday Soc. 1966, 62, 1638–1651. [Google Scholar] [CrossRef]
- Kashkooli, F.M.; Rezaeian, M.; Soltani, M. Drug Delivery through Nanoparticles in Solid Tumors: A Mechanistic Understanding. Nanomedicine 2022, 17, 695–716. [Google Scholar] [CrossRef] [PubMed]
- Moradi Kashkooli, F.; Soltani, M.; Momeni, M.M. Computational Modeling of Drug Delivery to Solid Tumors: A Pilot Study Based on a Real Image. J. Drug Deliv. Sci. Technol. 2021, 62, 102347. [Google Scholar] [CrossRef]
- Moradi Kashkooli, F.; Soltani, M.; Rezaeian, M.; Taatizadeh, E.; Hamedi, M.-H. Image-Based Spatio-Temporal Model of Drug Delivery in a Heterogeneous Vasculature of a Solid Tumor—Computational Approach. Microvasc. Res. 2019, 123, 111–124. [Google Scholar] [CrossRef]
- Hornsby, T.; Kashkooli, F.; Jakhmola, A.; Kolios, M.; Tavakkoli, J. Change In Temperature and Zetapotential of Doxorubicin-Loaded Gold Nanoparticle Under Low Intensity Pulsed Ultrasound Exposure. Mendeley Data 2022, V1. [Google Scholar] [CrossRef]

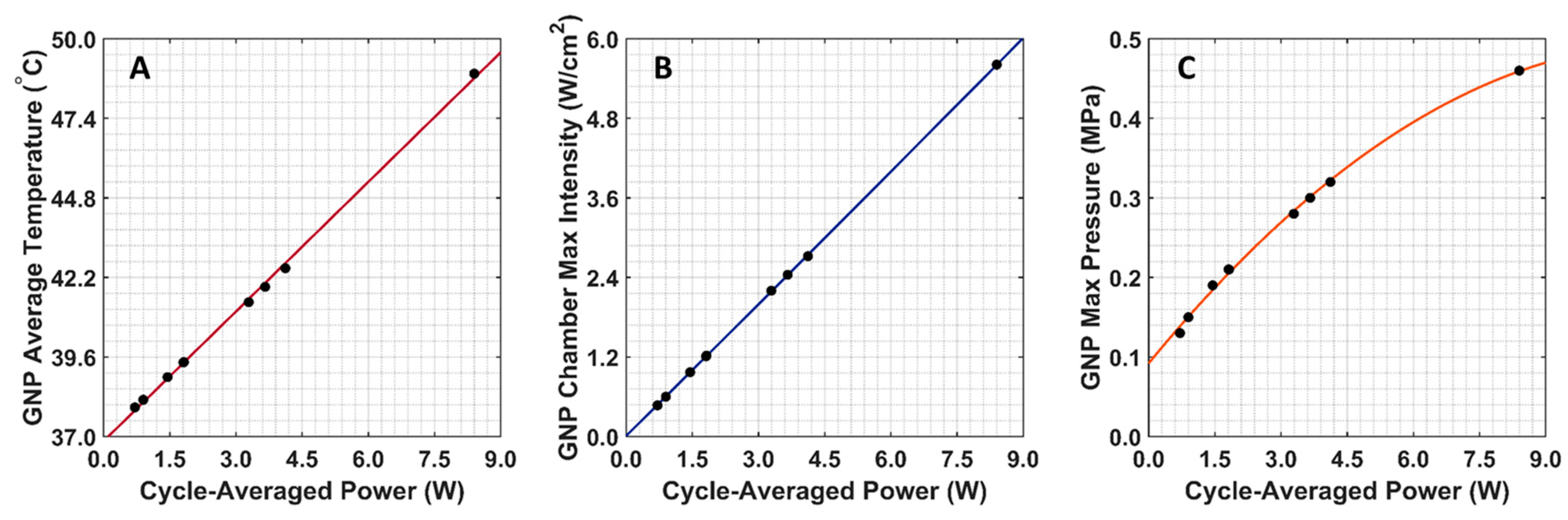


| Domain | Parameter | Value | Unit |
|---|---|---|---|
| LIPUS Transducer | Element Displacement | 24.944 | nm |
| Wavelength | 1.5206 | mm | |
| Frequency | 1.0 | MHz | |
| Power | 8.4 | W | |
| Duty Cycle | 50% | - | |
| Pulse Repetition Frequency | 100 | kHz | |
| Element Diameter | 24 | mm | |
| Water | Attenuation Coefficient | 0.0022 | dB/(cm∙MHz2) |
| Density | 994.23 | Kg/m3 | |
| Speed of Sound | 1520.6 | m/s | |
| Initial Temperature | 37.0 | °C | |
| Porcine Tissue | Attenuation Coefficient | 0.780 | dB/(cm∙MHz2) |
| Density | 1090 | Kg/m3 | |
| Speed of Sound | 1600 | m/s | |
| Initial Temperature | 37.0 | °C |
| Parameter (Unit) | Symbol | Before LIPUS | After LIPUS | Change Percentage |
|---|---|---|---|---|
| Measured GNP Temperature (°C) | 37.0 | 42.5 | 14.9 | |
| Measured GNP Zeta potential (mV) | −30.3 ± 1.0 | −15.8 ± 2.0 | 47.9 | |
| Measured Water Permittivity (10−9 [C2/(N∙m2)] | 1.26 | 1.23 | 2.2 | |
| Calculated DLVO Maximum Peak Amplitude (kBT) | 1.4 | 0.24 | 82.4 | |
| Parameter | Symbol | Constant Value | ||
| GNP Hamaker Constant (10−19 J) [20] | 2.5 | |||
| Measured GNP Diameter (nm) | 7.4 | |||
| Ionic Strength (mol/m3) [26] | 0.41 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hornsby, T.K.; Kashkooli, F.M.; Jakhmola, A.; Kolios, M.C.; Tavakkoli, J. Multiphysics Modeling of Low-Intensity Pulsed Ultrasound Induced Chemotherapeutic Drug Release from the Surface of Gold Nanoparticles. Cancers 2023, 15, 523. https://doi.org/10.3390/cancers15020523
Hornsby TK, Kashkooli FM, Jakhmola A, Kolios MC, Tavakkoli J. Multiphysics Modeling of Low-Intensity Pulsed Ultrasound Induced Chemotherapeutic Drug Release from the Surface of Gold Nanoparticles. Cancers. 2023; 15(2):523. https://doi.org/10.3390/cancers15020523
Chicago/Turabian StyleHornsby, Tyler K., Farshad Moradi Kashkooli, Anshuman Jakhmola, Michael C. Kolios, and Jahangir (Jahan) Tavakkoli. 2023. "Multiphysics Modeling of Low-Intensity Pulsed Ultrasound Induced Chemotherapeutic Drug Release from the Surface of Gold Nanoparticles" Cancers 15, no. 2: 523. https://doi.org/10.3390/cancers15020523
APA StyleHornsby, T. K., Kashkooli, F. M., Jakhmola, A., Kolios, M. C., & Tavakkoli, J. (2023). Multiphysics Modeling of Low-Intensity Pulsed Ultrasound Induced Chemotherapeutic Drug Release from the Surface of Gold Nanoparticles. Cancers, 15(2), 523. https://doi.org/10.3390/cancers15020523






