Topological Structures in the Space of Treatment-Naïve Patients with Chronic Lymphocytic Leukemia
Abstract
Simple Summary
Abstract
1. Introduction
2. Methods
2.1. Persistent Homology
2.2. Data
2.3. Statistics
3. Results
3.1. Clinical Characteristics
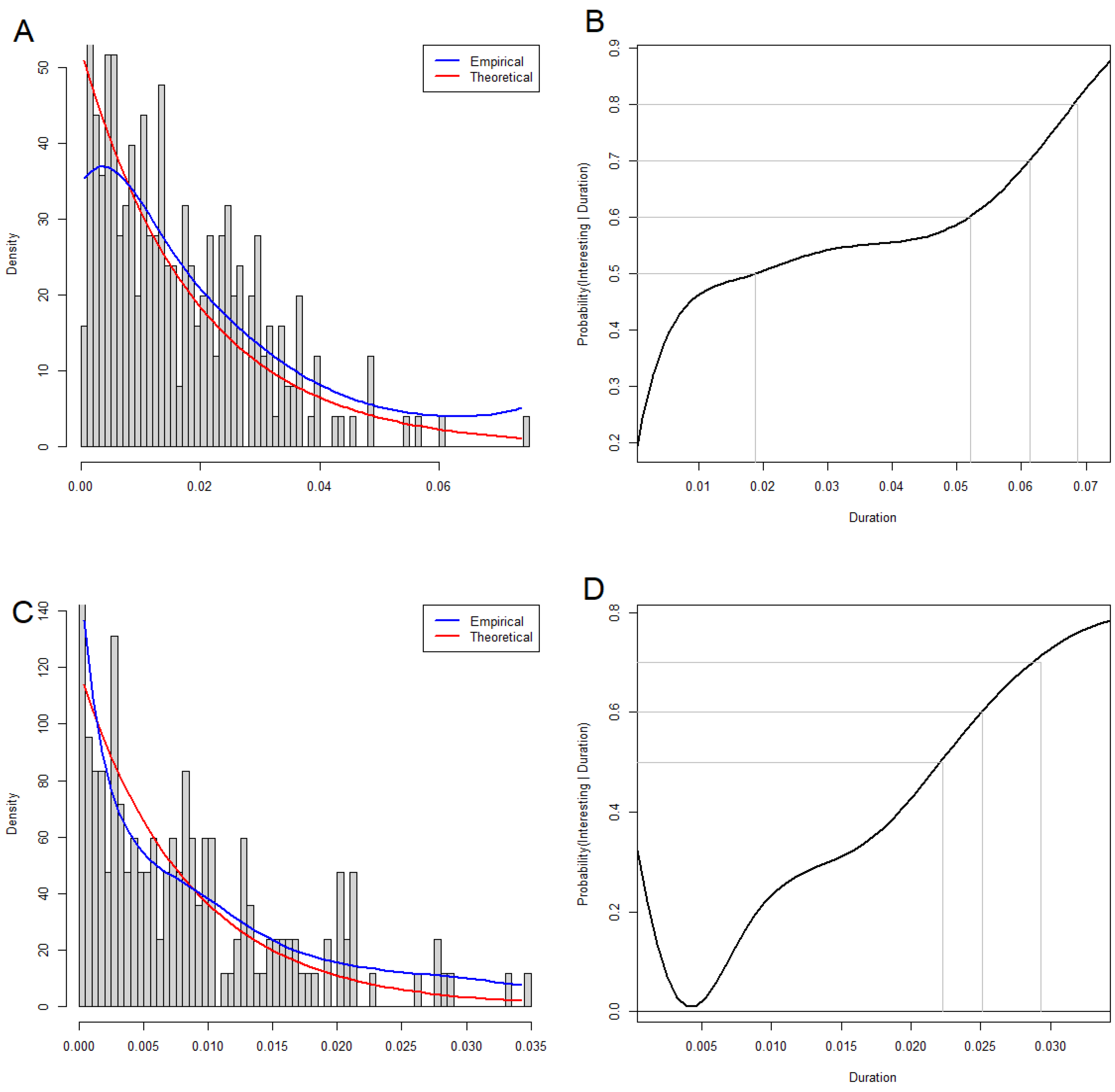
3.2. Time-to-Event Analyses
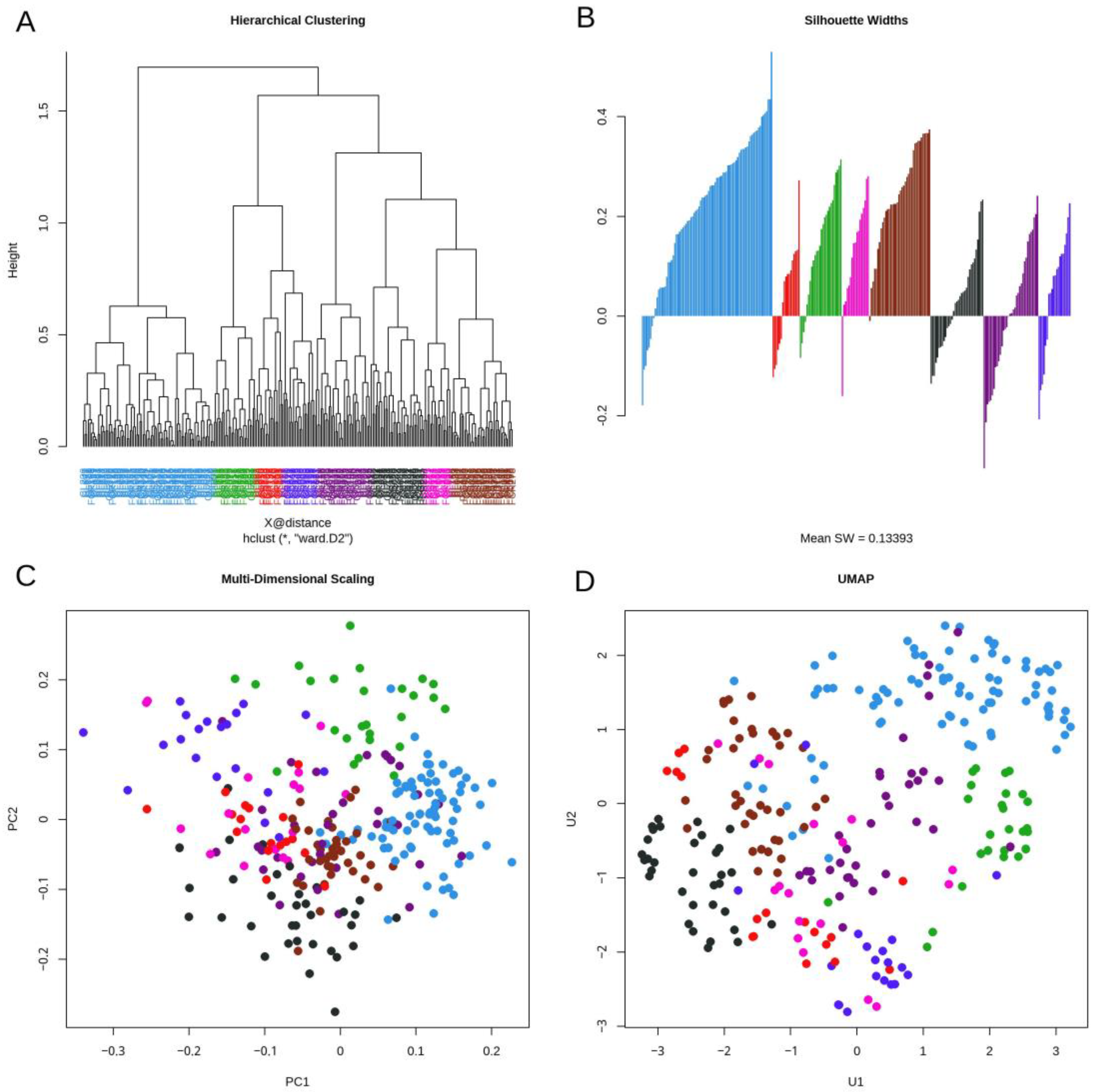
3.3. Daisy Distance
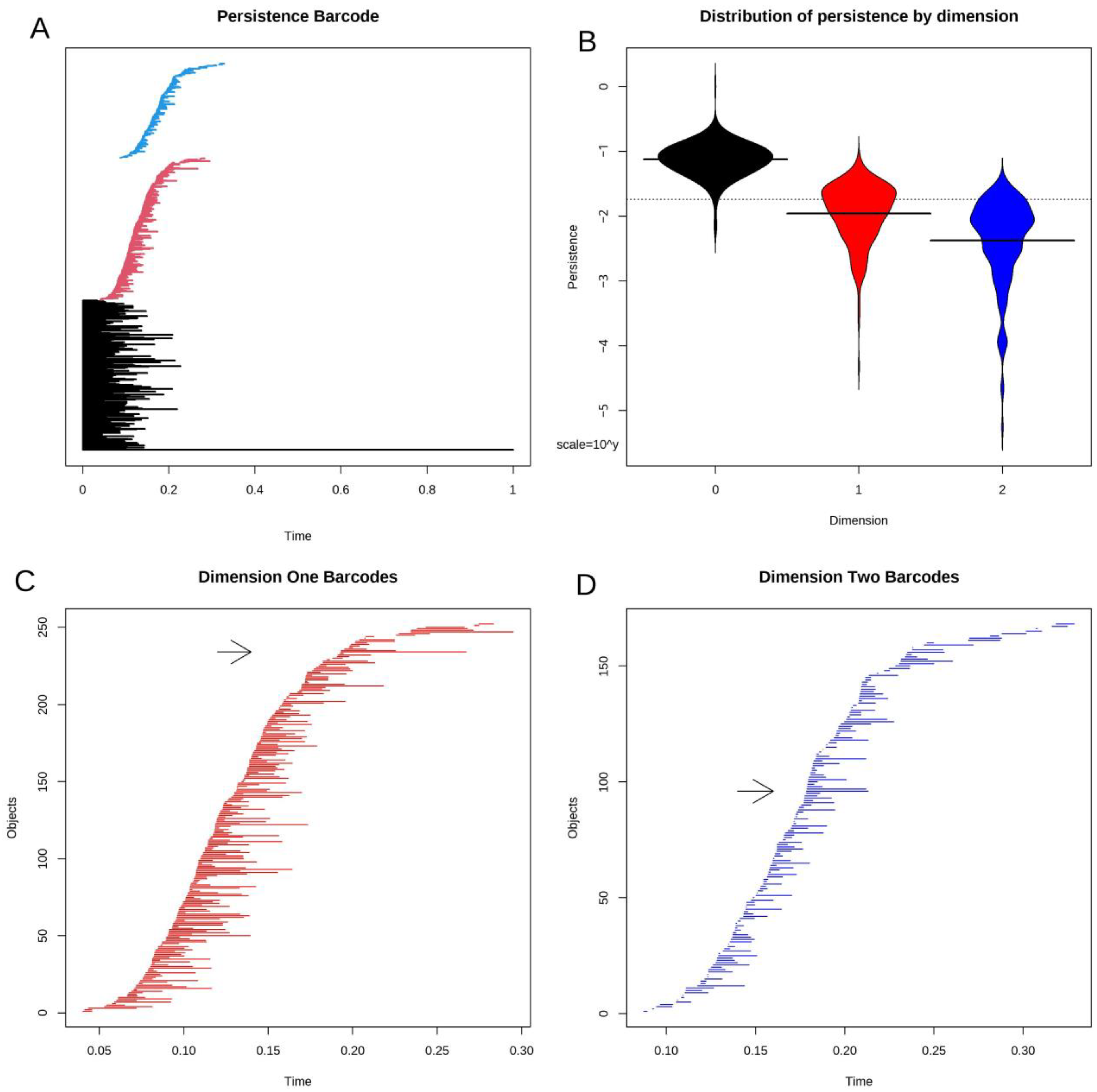
3.4. Topological Data Analysis
3.5. Statistical Significance of Loops and Voids
3.6. Interpreting Loops
3.7. Circos Plots
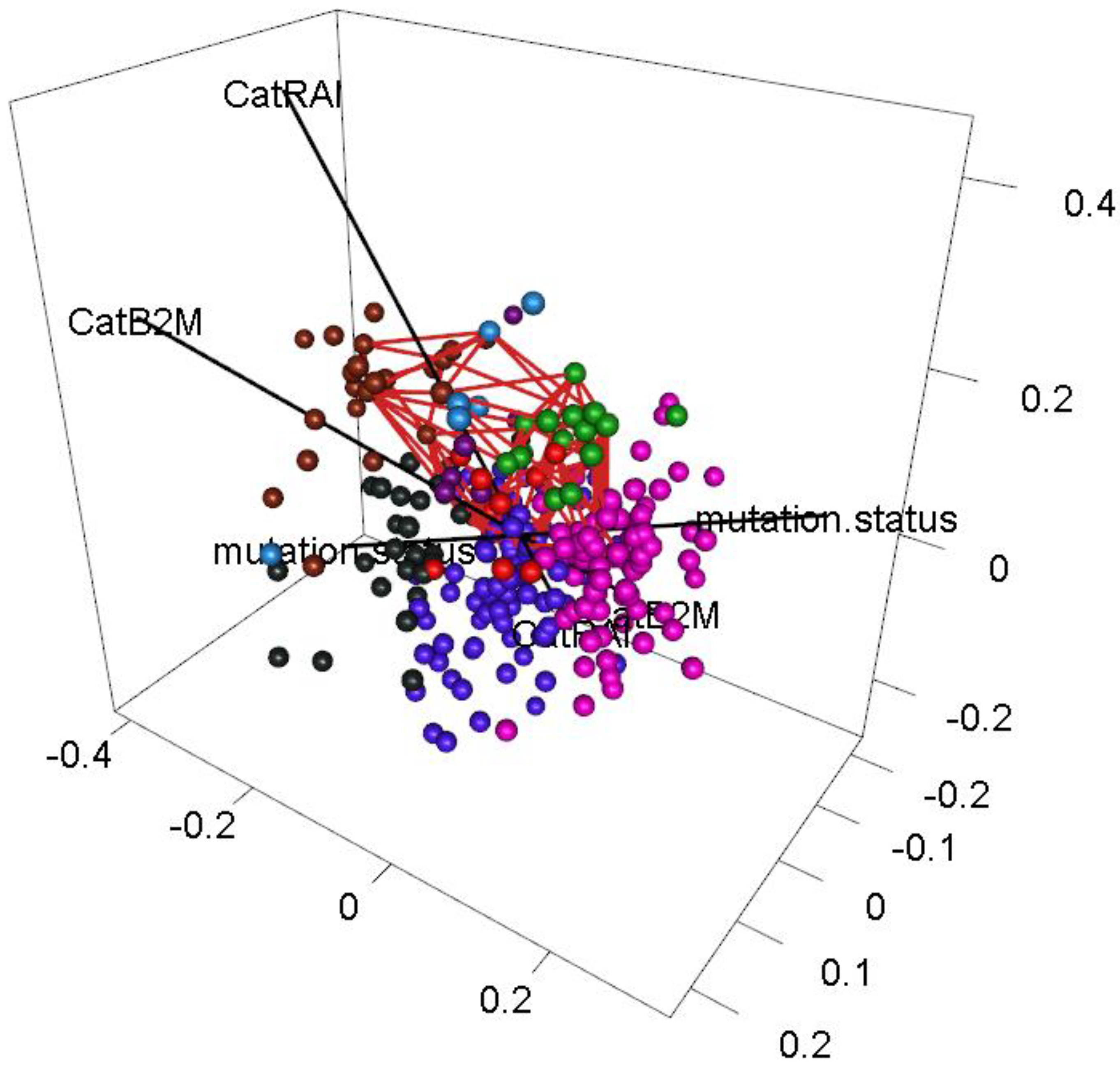
3.8. Voids
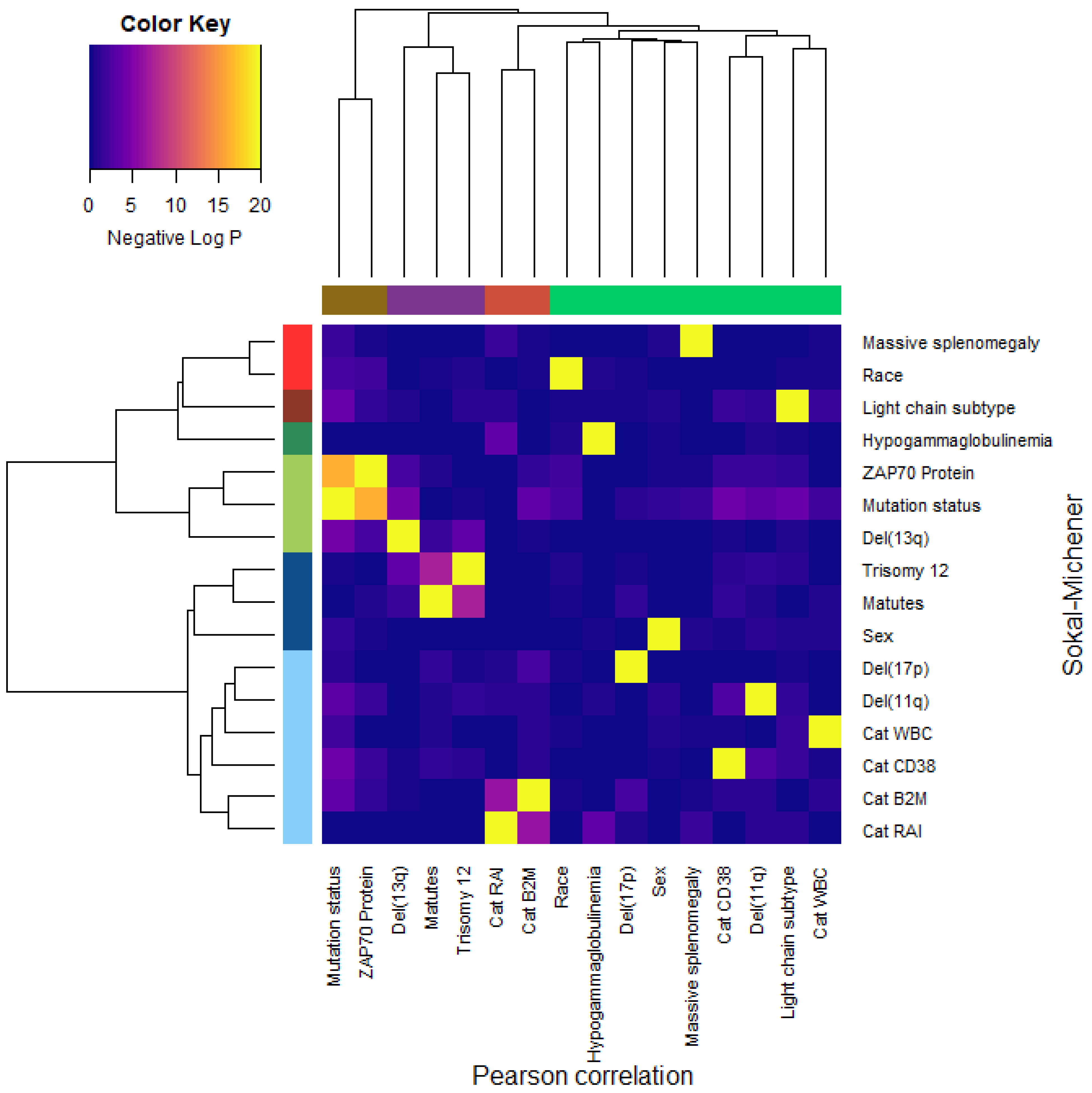
3.9. Dependence of Binary Features
- Dichotomous versions of serum beta-2 microglobulin (CatB2M) and Rai stage (CatRAI) are closely related (p = 3.257 × 10−7).
- Matutes score and trisomy 12 are closely related (p = 5.438 × 10−8).
- IGHV mutation status is closely related to ZAP70 protein levels (p = 4.456 × 10−17).We note that the del(13q) is somewhat related both to mutation status (p = 3.520 × 10−5) and to trisomy 12 (p = 1.868 × 10−4).
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Juhola, M.; Laurikkala, J. On distance computation in space of mixed-type variables in medical data mining. Stud. Health Technol. Inform. 2002, 90, 425–430. [Google Scholar] [PubMed]
- Hsu, C.-C.; Lin, S.-H. Visualized analysis of mixed numeric and categorical data via extended self-organizing map. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 72–86. [Google Scholar] [CrossRef]
- Hummel, M.; Edelmann, D.; Kopp-Schneider, A. Clustering of samples and variables with mixed-type data. PLoS ONE 2017, 12, e0188274. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Cao, J.; Ahn, C. Sample size calculation for before-after experiments with partially overlapping cohorts. Contemp. Clin. Trials 2018, 64, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Cabeli, V.; Verny, L.; Sella, N.; Uguzzoni, G.; Verny, M.; Isambert, H. Learning clinical networks from medical records based on information estimates in mixed-type data. PLoS Comput. Biol. 2020, 16, e1007866. [Google Scholar] [CrossRef] [PubMed]
- Coombes, C.E.; Abrams, Z.B.; Li, S.; Abruzzo, L.V.; Coombes, K.R. Unsupervised machine learning and prognostic factors of survival in chronic lymphocytic leukemia. J. Am. Med. Inform. Assoc. JAMIA 2020, 27, 1019–1027. [Google Scholar] [CrossRef] [PubMed]
- Faisal, S.; Tutz, G. Imputation methods for high-dimensional mixed-type datasets by nearest neighbors. Comput. Biol. Med. 2021, 135, 104577. [Google Scholar] [CrossRef] [PubMed]
- Coombes, C.E.; Liu, X.; Abrams, Z.B.; Coombes, K.R.; Brock, G. Simulation-derived best practices for clustering clinical data. J. Biomed. Inform. 2021, 118, 103788. [Google Scholar] [CrossRef] [PubMed]
- Borg, I.; Groenen, P. Modern multidimensional scaling: Theory and applications. J. Educ. Meas. 2003, 40, 277–280. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G.E. Visualizing high-dimensional data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Saul, N.; Großberger, L. UMAP: Uniform Manifold Approximation and Projection. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Letscher, D.; Zomorodian, A. Topological persistence and simplification. Discret. Comput. Geom. 2002, 28, 511–533. [Google Scholar] [CrossRef]
- Carlsson, G.; Zomorodian, A.; Collins, A.; Guibas, L.J. Persistence Barcodes for Shapes. Int. J. Shape Model. 2005, 11, 149–187. [Google Scholar] [CrossRef]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Carlsson, G. Topology and Data. Bull AMS 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Zomorodian, A.; Carlsson, G. Computing Persistent Homology. Discret. Comput. Geom. 2005, 33, 249–274. [Google Scholar] [CrossRef]
- Iuricich, F. Persistence Cycles for Visual Exploration of Persistent Homology. IEEE Trans. Vis. Comput. Graph. 2022, 28, 4966–4979. [Google Scholar] [CrossRef] [PubMed]
- Bigler, J.; Boedigheimer, M.; Schofield, J.P.R.; Skipp, P.J.; Corfield, J.; Rowe, A.; Sousa, A.R.; Timour, M.; Twehues, L.; Hu, X.; et al. A Severe Asthma Disease Signature from Gene Expression Profiling of Peripheral Blood from U-BIOPRED Cohorts. Am. J. Respir. Crit. Care Med. 2017, 195, 1311–1320. [Google Scholar] [CrossRef]
- Brandsma, J.; Goss, V.M.; Yang, X.; Bakke, P.S.; Caruso, M.; Chanez, P.; Dahlén, S.-E.; Fowler, S.J.; Horvath, I.; Krug, N.; et al. Lipid phenotyping of lung epithelial lining fluid in healthy human volunteers. Metabolomics Off. J. Metabolomic Soc. 2018, 14, 123. [Google Scholar] [CrossRef]
- Bruno, J.L.; Romano, D.; Mazaika, P.; Lightbody, A.A.; Hazlett, H.C.; Piven, J.; Reiss, A.L. Longitudinal identification of clinically distinct neurophenotypes in young children with fragile X syndrome. Proc. Natl. Acad. Sci. USA 2017, 114, 10767–10772. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, Y.; Liu, M. Identification of Subtypes of HCC Using Bioinformatics and the Hepatocyte Differentiation Model. Methods Mol. Biol. 2022, 2544, 253–258. [Google Scholar] [CrossRef]
- Hinks, T.S.C.; Brown, T.; Lau, L.C.K.; Rupani, H.; Barber, C.; Elliott, S.; Ward, J.A.; Ono, J.; Ohta, S.; Izuhara, K.; et al. Multidimensional endotyping in patients with severe asthma reveals inflammatory heterogeneity in matrix metalloproteinases and chitinase 3-like protein 1. J. Allergy Clin. Immunol. 2016, 138, 61–75. [Google Scholar] [CrossRef] [PubMed]
- Ba-Dhfari, T.O.F. Hypothesis Formulation in Medical Records Space. Ph.D. Thesis, University of Manchester, Manchester, UK, 2017. [Google Scholar]
- Herrero-Zazo, M.; Fitzgerald, T.; Taylor, V.; Street, H.; Chaudhry, A.N.; Bradley, J.R.; Birney, E.; Keevil, V.L. Using machine learning to model older adult inpatient trajectories from electronic health records data. iScience 2023, 26, 105876. [Google Scholar] [CrossRef] [PubMed]
- Waddington, C.H. The Strategy of Genes; Routledge: London, UK, 2014. [Google Scholar]
- Wright, S. The roles of mutation, inbreeding, crossbreeding, and selection in evolution. Proc. VI Int. Congr. Genet. 1932, 1, 356–366. [Google Scholar]
- Nijhout, H.F.; Best, J.; Reed, M. Escape from homeostasis. Math. Biosci. 2014, 257, 104–110. [Google Scholar] [CrossRef] [PubMed]
- American Cancer Society. Key Statistics for Chronic Lymphocytic Leukemia. (n.d.). Available online: https://www.cancer.org/cancer/chronic-lymphocytic-leukemia/about/key-statistics.html (accessed on 25 November 2023).
- Shustik, C.; Bence-Bruckler, I.; Delage, R.; Owen, C.J.; Toze, C.L.; Coutre, S. Advances in the treatment of relapsed/refractory chronic lymphocytic leukemia. Ann. Hematol. 2017, 96, 1185–1196. [Google Scholar] [CrossRef] [PubMed]
- Kay, N.E.; Hampel, P.J.; Van Dyke, D.L.; Parikh, S.A. CLL update 2022: A continuing evolution in care. Blood Rev. 2022, 54, 100930. [Google Scholar] [CrossRef] [PubMed]
- Duzkale, H.; Schweighofer, C.D.; Coombes, K.R.; Barron, L.L.; Ferrajoli, A.; O’Brien, S.; Wierda, W.G.; Pfeifer, J.; Majewski, T.; Czerniak, B.A. LDOC1 mRNA is differentially expressed in chronic lymphocytic leukemia and predicts overall survival in untreated patients. Blood 2011, 117, 4076–4084. [Google Scholar] [CrossRef] [PubMed]
- Abruzzo, L.V.; Herling, C.D.; Calin, G.A.; Oakes, C.; Barron, L.L.; Banks, H.E.; Katju, V.; Keating, M.J.; Coombes, K.R. Trisomy 12 chronic lymphocytic leukemia expresses a unique set of activated and targetable pathways. Haematologica 2018, 103, 2069–2078. [Google Scholar] [CrossRef] [PubMed]
- Zucker, M.R.; Abruzzo, L.V.; Herling, C.D.; Barron, L.L.; Keating, M.J.; Abrams, Z.B.; Heerema, N.; Coombes, K.R. Inferring clonal heterogeneity in cancer using SNP arrays and whole genome sequencing. Bioinformatics 2019, 35, 2924–2931. [Google Scholar] [CrossRef]
- Herling, C.D.; Coombes, K.R.; Benner, A.; Bloehdorn, J.; Barron, L.L.; Abrams, Z.B.; Majewski, T.; Bondaruk, J.E.; Bahlo, J.; Fischer, K.; et al. Time-to-progression after front-line fludarabine, cyclophosphamide, and rituximab chemoimmunotherapy for chronic lymphocytic leukaemia: A retrospective, multicohort study. Lancet Oncol. 2019, 20, 1576–1586. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Therneau, T.M.; Grambsch, P.M. Modeling Survival Data: Extending the Cox Model; Springer: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Kaufman, L. Finding Groups in Data; Wiley Online Library: Hoboken, NJ, USA, 1990. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Abrams, Z.B.; Coombes, C.E.; Li, S.; Coombes, K.R. Mercator: A Pipeline For Multi-Method, Unsupervised Visualization And Distance Generation. Bioinformatics 2021, 37, 2780–2781. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.-S.; Cha, S.-H.; Tappert, C.C. A survey of binary similarity and distance measures. J. Syst. Cybern. Inform. 2010, 8, 43–48. [Google Scholar]
- Efron, B.; Tibshirani, R. Empirical bayes methods and false discovery rates for microarrays. Genet. Epidemiol. 2002, 23, 70–86. [Google Scholar] [CrossRef]
- Amaya-Chanaga, C.I.; Rassenti, L.Z. Biomarkers in chronic lymphocytic leukemia: Clinical applications and prognostic markers, Best Practice & Research. Clin. Haematol. 2016, 29, 79–89. [Google Scholar] [CrossRef]
- Crespo, M.; Bosch, F.; Villamor, N.; Bellosillo, B.; Colomer, D.; Rozman, M.; Marcé, S.; López-Guillermo, A.; Campo, E.; Montserrat, E. ZAP-70 expression as a surrogate for immunoglobulin-variable-region mutations in chronic lymphocytic leukemia. N. Engl. J. Med. 2003, 348, 1764–1775. [Google Scholar] [CrossRef] [PubMed]
- Damle, R.N.; Wasil, T.; Fais, F.; Ghiotto, F.; Valetto, A.; Allen, S.L.; Buchbinder, A.; Budman, D.; Dittmar, K.; Kolitz, J.; et al. Ig V gene mutation status and CD38 expression as novel prognostic indicators in chronic lymphocytic leukemia. Blood 1999, 94, 1840–1847. [Google Scholar] [CrossRef]
- Capello, D.; Guarini, A.; Berra, E.; Mauro, F.R.; Rossi, D.; Ghia, E.; Cerri, M.; Logan, J.; Foà, R.; Gaidano, G. Evidence of biased immunoglobulin variable gene usage in highly stable B-cell chronic lymphocytic leukemia. Leukemia 2004, 18, 1941–1947. [Google Scholar] [CrossRef]
- Simonsson, B.; Wibell, L.; Nilsson, K. Beta 2-microglobulin in chronic lymphocytic leukaemia. Scand. J. Haematol. 1980, 24, 174–180. [Google Scholar] [CrossRef]
- Döhner, H.; Stilgenbauer, S.; Döhner, K.; Bentz, M.; Lichter, P. Chromosome aberrations in B-cell chronic lymphocytic leukemia: Reassessment based on molecular cytogenetic analysis. J. Mol. Med. 1999, 77, 266–281. [Google Scholar] [CrossRef] [PubMed]
- Matutes, E.; Polliack, A. Morphological and immunophenotypic features of chronic lymphocytic leukemia. Rev. Clin. Exp. Hematol. 2000, 4, 22–47. [Google Scholar] [CrossRef] [PubMed]
- Jenner, A.; Aogo, R.; Crowe, V.; Deng, X.; Smith, A.; Morel, P.; Davis, C.; Smith, A.; Craig, M. COVID-19 virtual patient cohort suggests immune mechanisms driving disease outcomes. PLoS Pathog. 2021, 17, e1009753. [Google Scholar] [CrossRef] [PubMed]


| Feature | Summary | N | OS HR a | OS Score | OS p Value | TTT HR b | TTT Score | TTT p Value |
|---|---|---|---|---|---|---|---|---|
| Age at Diagnosis | Mean = 56.38, SD = 10.973 | 266 | 1.05 | 27.27 | 0.0000002 | 1.00 | 0.26 | 0.6102950 |
| Sex | Female = 86, Male = 180 | 266 | 1.29 | 1.54 | 0.2142572 | 1.30 | 3.44 | 0.0635030 |
| Race | White = 244, Other = 22 | 266 | 2.04 | 6.90 | 0.0086211 | 1.03 | 0.01 | 0.9152445 |
| IGHV Mutation Status | Mutated = 116, Unmutated = 150 | 266 | 2.87 | 26.02 | 0.0000003 | 1.91 | 23.20 | 0.0000015 |
| Light Chain Subtype | kappa = 163, lambda = 93, NA’s = 10 | 256 | 0.87 | 0.47 | 0.4937125 | 1.02 | 0.02 | 0.8773925 |
| ZAP70 Protein | Negative = 118, Positive = 118, NA’s = 30 | 236 | 2.43 | 18.81 | 0.0000144 | 1.59 | 11.24 | 0.0008017 |
| Rai Stage | Stage 0 = 29, Stage 1 = 107, Stage 2 = 78, Stage 3 = 24, Stage 4 = 28 | 266 | 0.87 | 9.65 | 0.0467790 | 1.54 | 22.42 | 0.0001655 |
| Cat Rai c | High = 52, Low = 214 | 266 | 0.79 | 1.09 | 0.2964811 | 0.65 | 7.18 | 0.0073576 |
| B2M d | Mean = 3.35, SD = 1.389 | 266 | 1.32 | 26.40 | 0.0000003 | 1.23 | 23.52 | 0.0000012 |
| Log B2M | Mean = 1.13, SD = 0.392, NA’s = 1 | 265 | 3.20 | 23.43 | 0.0000013 | 2.35 | 26.05 | 0.0000003 |
| Cat B2M | High = 67, Low = 199 | 266 | 0.30 | 45.93 | 0.0000000 | 0.60 | 11.84 | 0.0005797 |
| Serum LDH e | Mean = 606.42, SD = 245.972, NA’s = 6 | 260 | 1.00 | 4.33 | 0.0374987 | 1.00 | 16.80 | 0.0000416 |
| Log LDH | Mean = 6.35, SD = 0.329, NA’s = 6 | 260 | 1.80 | 4.75 | 0.0292620 | 2.36 | 21.62 | 0.0000033 |
| WBC f | Mean = 84.57, SD = 65.563, NA’s = 1 | 265 | 1.00 | 3.76 | 0.0523956 | 1.00 | 8.39 | 0.0037712 |
| Log WBC | Mean = 4.14, SD = 0.812, NA’s = 1 | 265 | 1.19 | 2.06 | 0.1517028 | 1.26 | 6.89 | 0.0086757 |
| Cat WBC | High = 33, Low = 232, NA’s = 1 | 265 | 0.64 | 2.96 | 0.0854151 | 0.68 | 4.15 | 0.0416977 |
| Cat CD38 | High = 65, Low = 190, NA’s = 11 | 255 | 0.84 | 0.69 | 0.4056656 | 0.82 | 1.90 | 0.1686111 |
| Hypogammaglobulinemia | No = 142, Yes = 101, NA’s = 23 | 243 | 0.95 | 0.06 | 0.8065590 | 1.31 | 3.82 | 0.0507621 |
| Massive Splenomegaly | No = 246, Yes = 19, NA’s = 1 | 265 | 1.08 | 0.05 | 0.8246260 | 1.84 | 6.46 | 0.0110498 |
| Matutes Score | Atypical = 58, Typical = 197, NA’s = 11 | 255 | 0.96 | 0.03 | 0.8591107 | 0.90 | 0.49 | 0.4831143 |
| Hemoglobin | Mean = 12.93, SD = 1.719, NA’s = 1 | 265 | 0.96 | 0.53 | 0.4659581 | 0.93 | 3.51 | 0.0608374 |
| Platelets | Mean = 183.88, SD = 74.653, NA’s = 1 | 265 | 1.00 | 1.87 | 0.1716512 | 1.00 | 6.48 | 0.0109399 |
| Prolymphocytes | Mean = 4.61, SD = 4.587, NA’s = 4 | 262 | 1.02 | 0.95 | 0.3289335 | 1.04 | 9.47 | 0.0020933 |
| Del(13q) g | Abnormal = 118, Normal = 122, NA’s = 26 | 240 | 1.31 | 1.94 | 0.1634546 | 1.02 | 0.02 | 0.9024299 |
| Del(11q) | Abnormal = 35, Normal = 205, NA’s = 26 | 240 | 1.12 | 0.15 | 0.7026161 | 0.97 | 0.03 | 0.8592181 |
| Trisomy 12 | Abnormal = 39, Normal = 201, NA’s = 26 | 240 | 0.87 | 0.33 | 0.5670635 | 0.71 | 3.48 | 0.0619474 |
| Del(17p) | Abnormal = 12, Normal = 228, NA’s = 26 | 240 | 0.20 | 27.06 | 0.0000002 | 0.94 | 0.04 | 0.8343670 |
| Del(6q) | Abnormal = 14, Normal = 226, NA’s = 26 | 240 | 0.75 | 0.56 | 0.4530366 | 0.83 | 0.48 | 0.4903461 |
| Dohner | Del13q = 87, Normal = 69, Tri1Stage 2 = 38, Del11q = 34, Del17p = 12, NA’s = 26 | 240 | 1.42 | 29.96 | 0.0000050 | 1.05 | 3.55 | 0.4696192 |
| Purity | FALSE = 36, TRUE = 204, NA’s = 26 | 240 | 0.62 | 3.74 | 0.0530660 | 0.76 | 2.37 | 0.1236352 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGee, R.L., II; Reed, J.; Coombes, C.E.; Herling, C.D.; Keating, M.J.; Abruzzo, L.V.; Coombes, K.R. Topological Structures in the Space of Treatment-Naïve Patients with Chronic Lymphocytic Leukemia. Cancers 2024, 16, 2662. https://doi.org/10.3390/cancers16152662
McGee RL II, Reed J, Coombes CE, Herling CD, Keating MJ, Abruzzo LV, Coombes KR. Topological Structures in the Space of Treatment-Naïve Patients with Chronic Lymphocytic Leukemia. Cancers. 2024; 16(15):2662. https://doi.org/10.3390/cancers16152662
Chicago/Turabian StyleMcGee, Reginald L., II, Jake Reed, Caitlin E. Coombes, Carmen D. Herling, Michael J. Keating, Lynne V. Abruzzo, and Kevin R. Coombes. 2024. "Topological Structures in the Space of Treatment-Naïve Patients with Chronic Lymphocytic Leukemia" Cancers 16, no. 15: 2662. https://doi.org/10.3390/cancers16152662
APA StyleMcGee, R. L., II, Reed, J., Coombes, C. E., Herling, C. D., Keating, M. J., Abruzzo, L. V., & Coombes, K. R. (2024). Topological Structures in the Space of Treatment-Naïve Patients with Chronic Lymphocytic Leukemia. Cancers, 16(15), 2662. https://doi.org/10.3390/cancers16152662






