Radiomics-Based Classification of Tumor and Healthy Liver on Computed Tomography Images
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
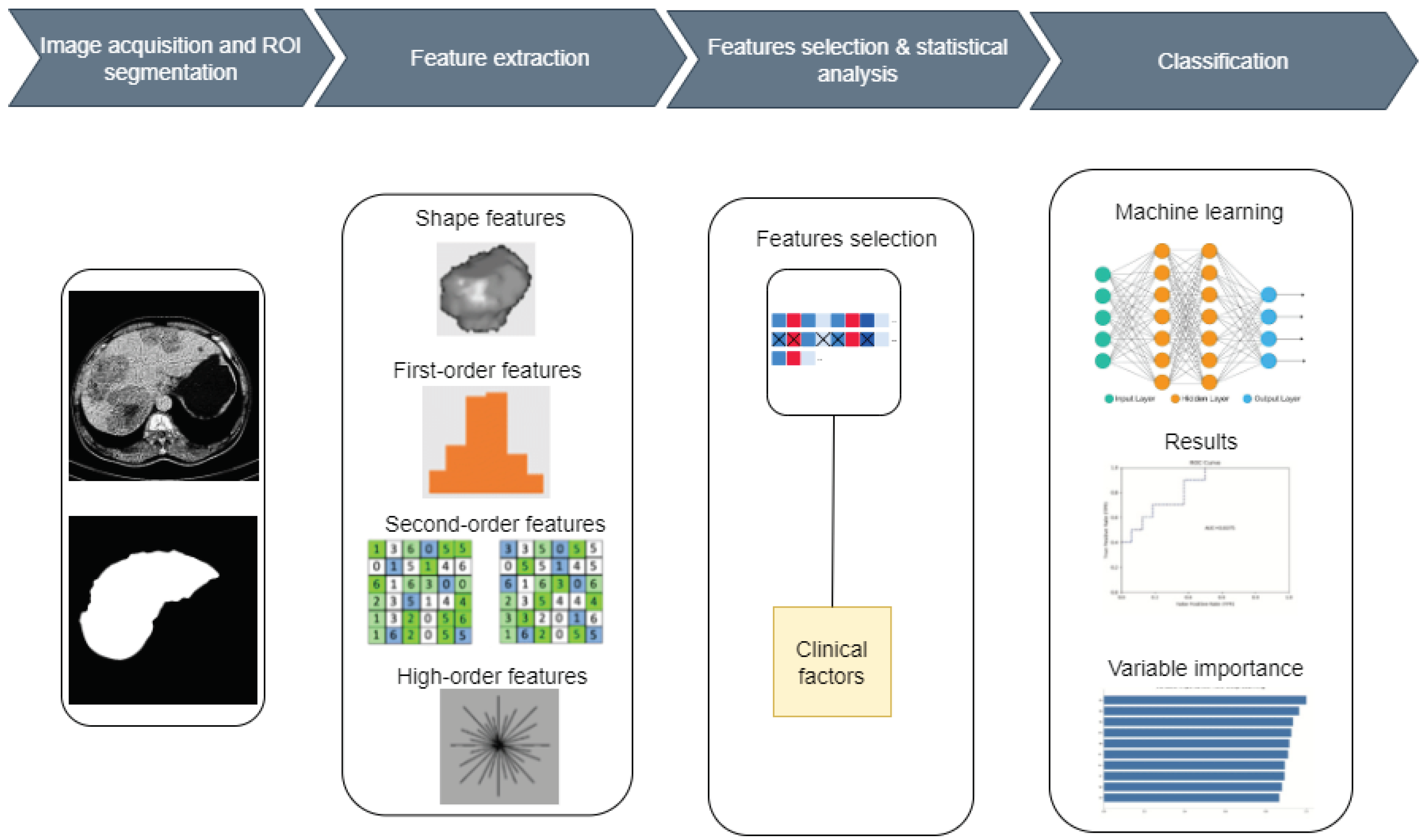
2.1. Proposed System
2.2. Dataset Description
2.3. ROI Segmentation
2.4. Intensity Normalization
2.5. Feature Extraction
- (i)
- The gray-level co-occurrence matrix (GLCM) that quantifies an image’s texture by computing the frequency of pairs of pixels with given values and a defined spatial connection [22].
- (ii)
- The gray-level run length matrix (GLRLM), a matrix that can extract texture features for texture analysis. The GLRLM technique is utilized to extract advanced statistical texture properties [23].
- (iii)
- The gray-level size zone matrix (GLSZM) measures the number of gray-level zones in an image. A gray-level zone is a group of connected voxels with the same gray-level intensity [24].
- (iv)
- The gray-level dependence matrix (GLDM), which measures the relationships between gray levels in an image. There is a gray-level dependency when a count of connected voxels within a distance of the center voxel depends on it [25].
2.6. Statistical Analysis and Feature Selection
2.7. Models and Evaluation
- SVM: “C” = 0.05050505;
- Naive Bayes: “” = 0, “” = 1.5, “” = ;
- XGBoost: “” = 100, “” = 3, “” = 0.01, “” = 0.2, “” = 0.5, “” = 3, “” = 1;
- RF: “” = 21;
- LR: “” = 1, “” = ;
- AdaBoost: “” = 150, “” = 5, “” = 1.
3. Results
3.1. Clinical Factors of Patients
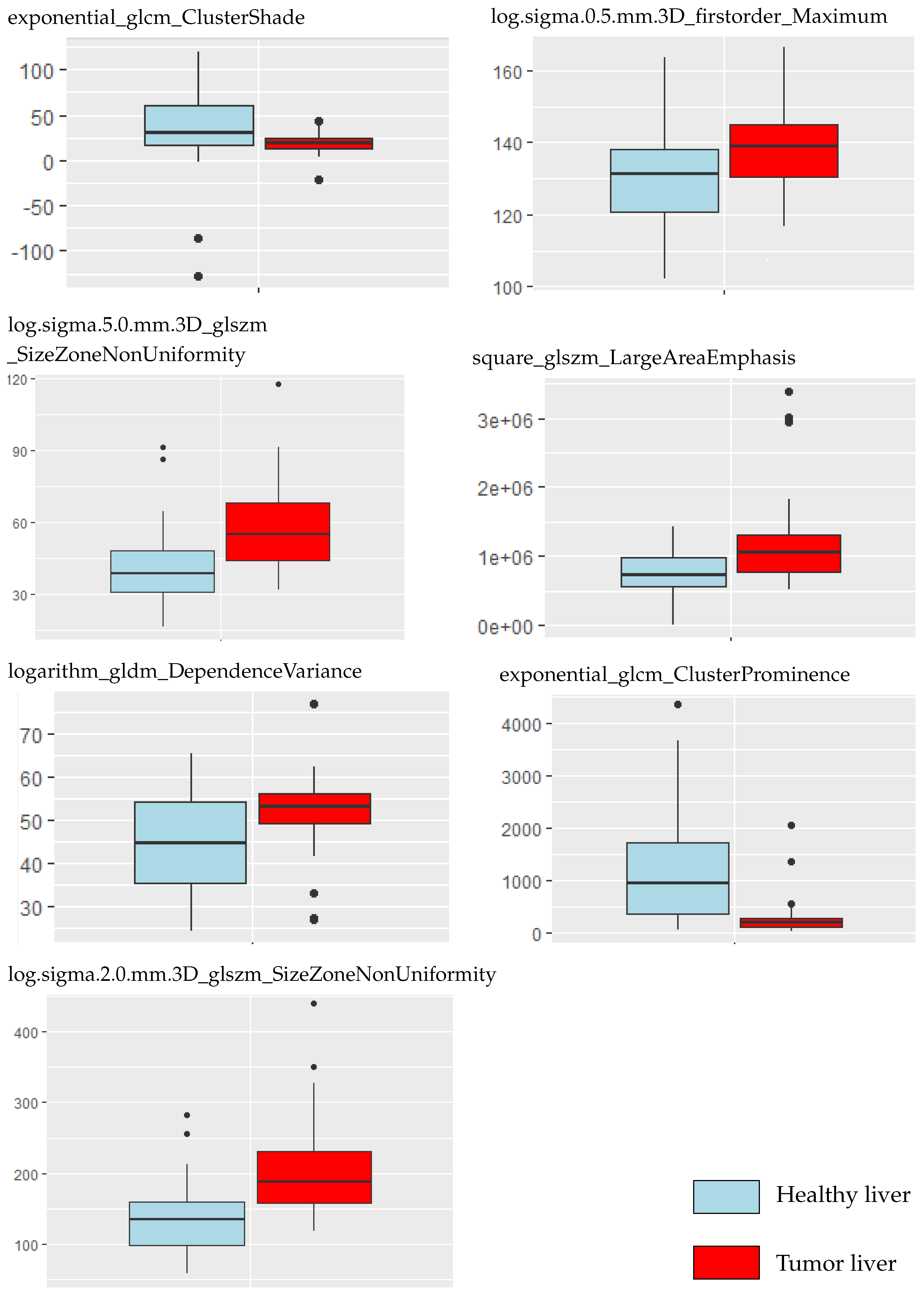
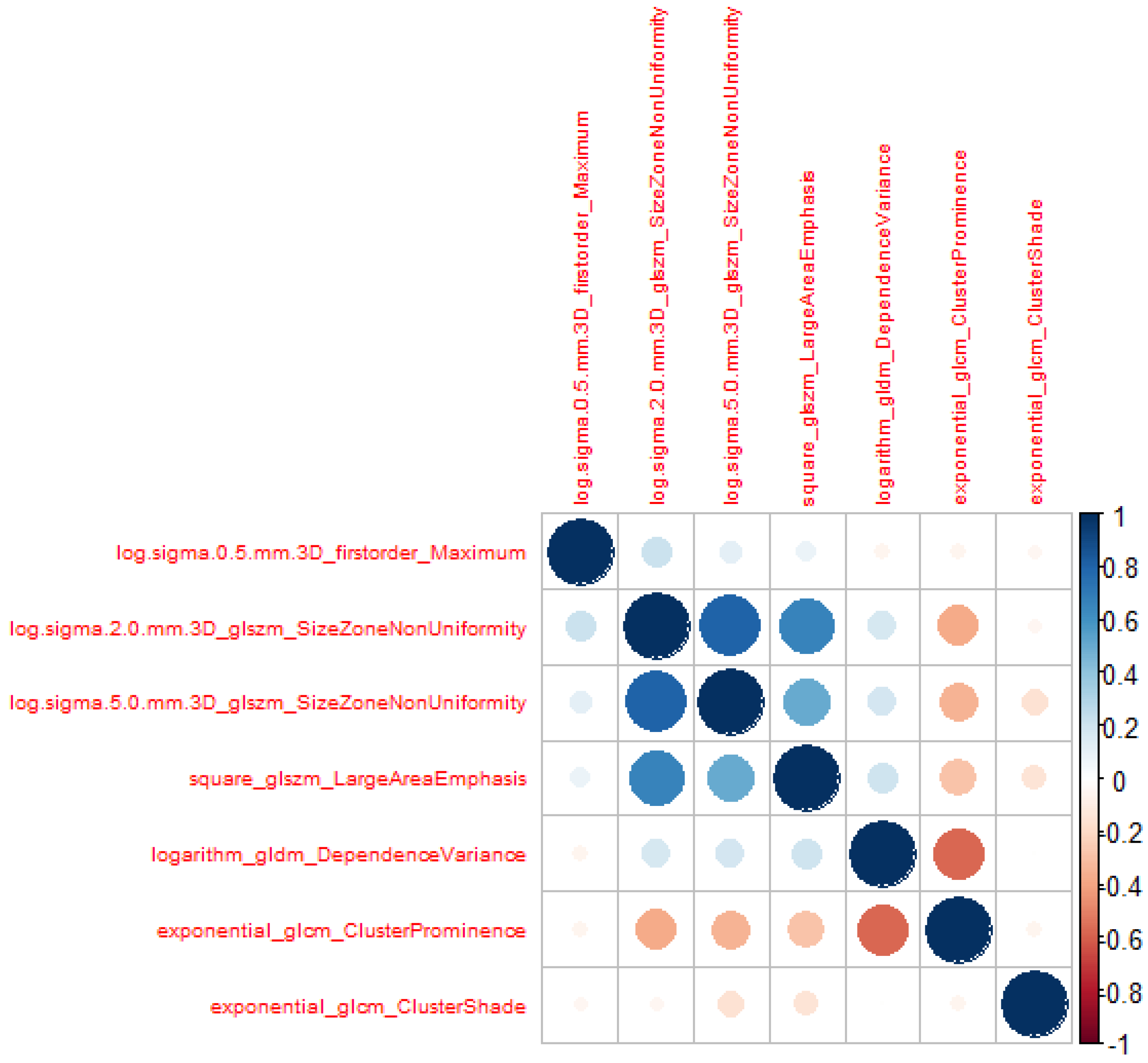
3.2. Radiomic Feature Selection
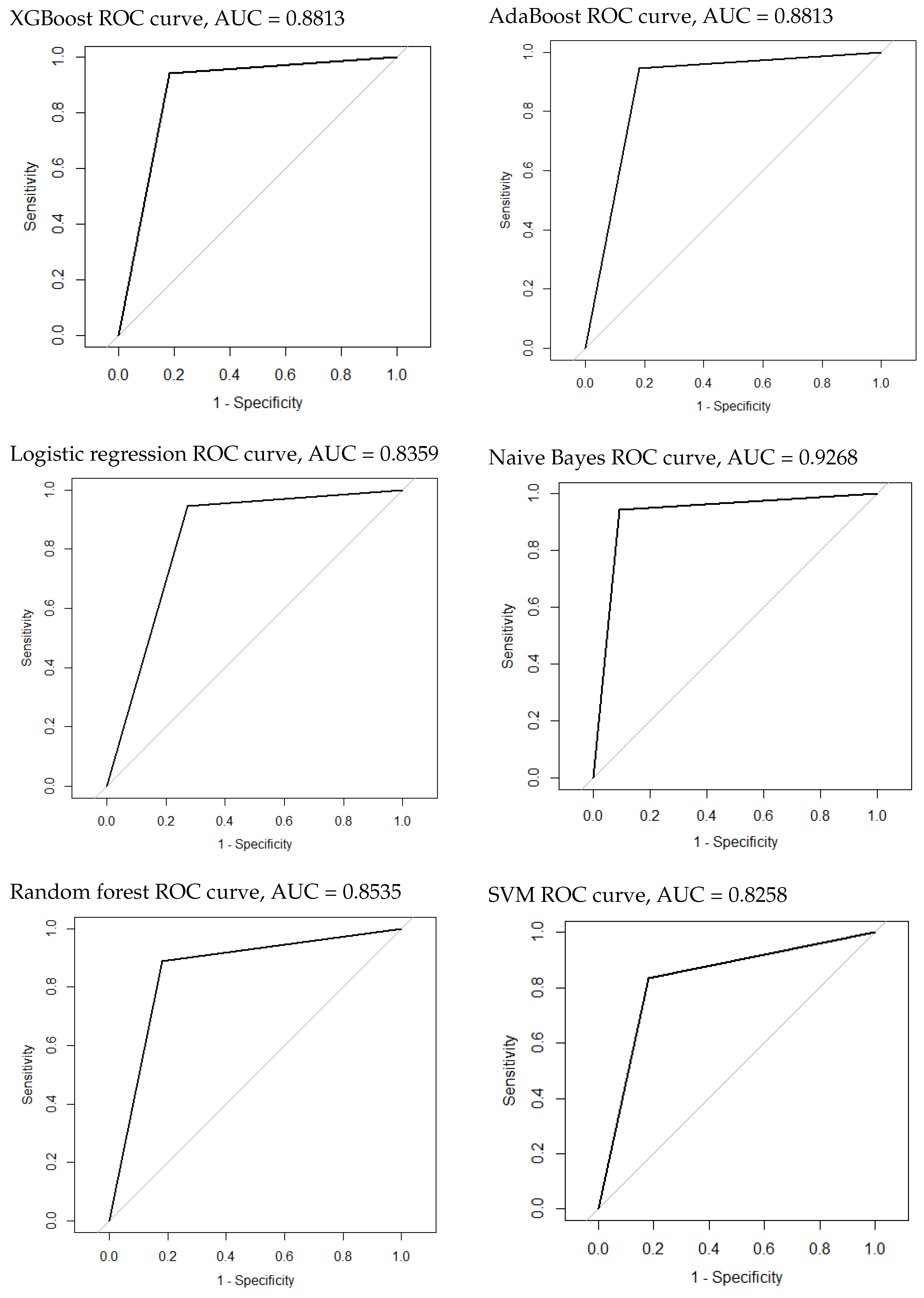
3.3. Construction and Evaluation of the Classification Model of Tumor Presence or Not
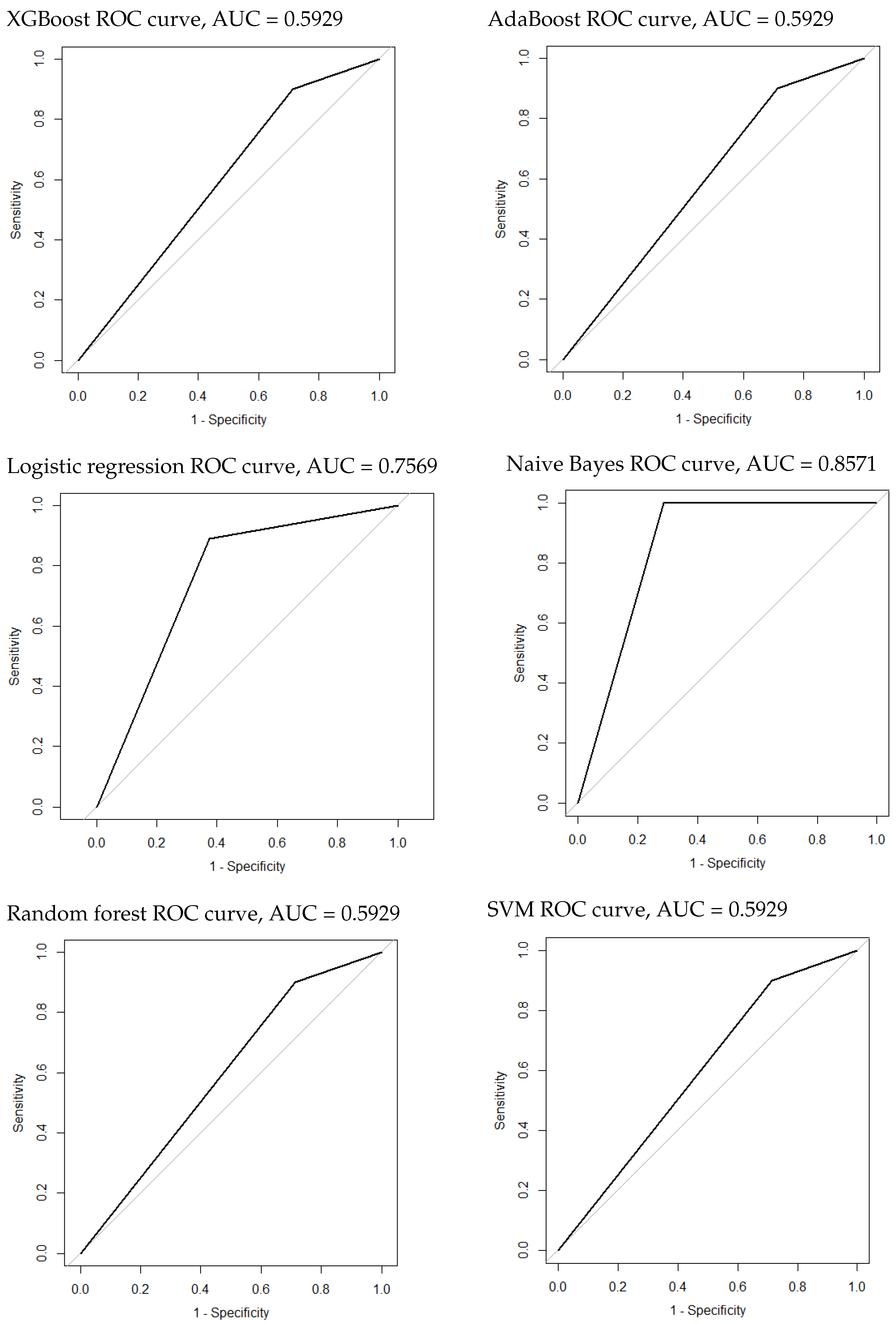
3.4. Construction and Evaluation of the Classification Model of HCC and Metastatic Tumors
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AdaBoost | adaptive boosting |
| AUROC | area under the receiver operating curve |
| CI | confidence interval |
| CNHU-HKM | Centre National Hospitalier Universitaire Hubert Koutoukou Maga |
| CT | computed tomography |
| FNH | focal nodular hyperplasia |
| GLCM | gray-level co-occurrence matrix |
| GLDM | gray-level dependence matrix |
| GLH | gray-level histogram |
| GLRLM | gray-level run length matrix |
| GLSZM | gray-level size zone matrix |
| H | high |
| HA | hepatocellular adenoma |
| HCC | hepatocellular carcinoma |
| HEM | hepatic hemangioma |
| HU | Hounsfield unit |
| L | low |
| LoG | Laplacian of Gaussian |
| LR | logistic regression |
| MCC | Matthews correlation coefficient |
| ML | machine learning |
| MRI | magnetic resonance imaging |
| NPV | negative prediction value |
| PNN | probabilistic neural network |
| PPV | positive prediction value |
| RCAD | radiomics-based computer-aided |
| RF | random forests |
| RIL-Contour | Radiology Informatics Laboratory Contour |
| ROI | region of interest |
| SVM | support vector machine |
| VIF | variance inflation factor |
| XGBoost | extreme gradient boosting |
References
- Sung, H.; Ferlay, J.; Siegel, R.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Hann, L.; Winston, C.; Brown, K.; Akhurst, T. Diagnostic imaging approaches and relationship to hepatobiliary cancer staging and therapy. Semin. Surg. Oncol. 2000, 19, 94–115. [Google Scholar] [CrossRef]
- Lambin, P.; Rios-Velazquez, E.; Leijenaar, R.; Carvalho, S.; Van Stiphout, R.; Granton, P.; Zegers, C.; Gillies, R.; Boellard, R.; Dekker, A.; et al. Radiomics: Extracting more information from medical images using advanced feature analysis. Eur. J. Cancer 2012, 48, 441–446. [Google Scholar] [CrossRef]
- Gillies, R.; Kinahan, P.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Balogh, J.; Victor, D.; Asham, E.; Burroughs, S.; Boktour, M.; Saharia, A.; Li, X.; Ghobrial, M.; Monsour, H. Hepatocellular carcinoma: A review. J. Hepatocell. Carcinoma 2016, 3, 41–53. [Google Scholar] [CrossRef] [PubMed]
- Grazioli, L.; Bondioni, M.P.; Haradome, H.; Motosugi, U.; Tinti, R.; Frittoli, B.; Gambarini, S.; Donato, F.; Colagrande, S. Hepatocellular adenoma and focal nodular hyperplasia: Value of gadoxetic acid-enhanced MR imaging in differential diagnosis. Radiology 2012, 262, 520–529. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, D.; Bruix, J.; Sherman, M.; Sirlin, C. LI-RADS (Liver Imaging Reporting and Data System): Summary, discussion, and consensus of the LI-RADS Management Working Group and future directions. Hepatology 2015, 61, 1056–1065. [Google Scholar] [CrossRef] [PubMed]
- Starmans, M.; Klein, S.; Van Der Voort, S.; Thomeer, M.; Miclea, R.; Niessen, W. Classification of malignant and benign liver tumors using a radiomics approach. In Medical Imaging 2018: Image Processing; SPIE: Bellingham, WA, USA, 2018; Volume 10574, p. 48. [Google Scholar]
- Candita, G.; Rossi, S.; Cwiklinska, K.; Fanni, S.C.; Cioni, D.; Lencioni, R.; Neri, E. Imaging Diagnosis of Hepatocellular Carcinoma: A State-of-the-Art Review. Diagnostics 2023, 13, 625. [Google Scholar] [CrossRef]
- Mougiakakou, S.; Valavanis, I.; Nikita, A.; Nikita, K. Differential diagnosis of CT focal liver lesions using texture features, feature selection and ensemble driven classifiers. Artif. Intell. Med. 2007, 41, 25–37. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Moni, R.; Rajeesh, J. An automatic computer-aided diagnosis system for liver tumours on computed tomography images. Comput. Electr. Eng. 2013, 39, 1516–1526. [Google Scholar] [CrossRef]
- Qiu, J.; Wu, Y.; Hui, B.; Chen, J.; Ji, L.; Wang, M. A Novel Texture Analysis Method Based on Reverse Biorthogonal Wavelet and Co-Occurrence Matrix Applied for Classification of Hepatocellular Carcinoma and Hepatic Hemangioma. J. Med. Imaging Health Inform. 2018, 8, 1835–1843. [Google Scholar] [CrossRef]
- Zhou, Y.; He, L.; Huang, Y.; Chen, S.; Wu, P.; Ye, W.; Liu, Z.; Liang, C. CT-based radiomics signature: A potential biomarker for preoperative prediction of early recurrence in hepatocellular carcinoma. Abdom. Radiol. 2017, 42, 1695–1704. [Google Scholar] [CrossRef]
- Nie, P.; Yang, G.; Guo, J.; Chen, J.; Li, X.; Ji, Q.; Wu, J.; Cui, J.; Xu, W. A CT-based radiomics nomogram for differentiation of focal nodular hyperplasia from hepatocellular carcinoma in the non-cirrhotic liver. Cancer Imaging 2020, 20, 20. [Google Scholar] [CrossRef]
- Nie, P.; Wang, N.; Pang, J.; Yang, G.; Duan, S.; Chen, J.; Xu, W. CT-Based Radiomics Nomogram: A Potential Tool for Differentiating Hepatocellular Adenoma From Hepatocellular Carcinoma in the Noncirrhotic Liver. Acad. Radiol. 2021, 28, 799–807. [Google Scholar] [CrossRef]
- Lysdahlgaard, S. Comparing Radiomics features of tumour and healthy liver tissue in a limited CT dataset: A machine learning study. Radiography 2022, 28, 718–724. [Google Scholar] [CrossRef]
- Thawani, R.; McLane, M.; Beig, N.; Ghose, S.; Prasanna, P.; Velcheti, V.; Madabhushi, A. Radiomics and radiogenomics in lung cancer: A review for the clinician. Lung Cancer 2018, 115, 34–41. [Google Scholar] [CrossRef]
- Wakabayashi, T.; Ouhmich, F.; Gonzalez-Cabrera, C.; Felli, E.; Saviano, A.; Agnus, V.; Savadjiev, P.; Baumert, T.; Pessaux, P.; Marescaux, J.; et al. Radiomics in hepatocellular carcinoma: A quantitative review. Hepatol. Int. 2019, 13, 546–559. [Google Scholar] [CrossRef] [PubMed]
- Philbrick, K.; Weston, A.; Akkus, Z.; Kline, T.; Korfiatis, P.; Sakinis, T.; Kostandy, P.; Boonrod, A.; Zeinoddini, A.; Takahashi, N.; et al. RIL-Contour: A Medical Imaging Dataset Annotation Tool for and with Deep Learning. J. Digit. Imaging 2019, 32, 571–581. [Google Scholar] [CrossRef] [PubMed]
- DenOtter, T.; Schubert, J. Hounsfield Unit; StatPearls: Treasure Island, FL, USA, 2024. [Google Scholar]
- Wu, J.; Liu, A.; Cui, J.; Chen, A.; Song, Q.; Xie, L. Radiomics-based classification of hepatocellular carcinoma and hepatic haemangioma on precontrast magnetic resonance images. BMC Med. Imaging 2019, 19, 23. [Google Scholar] [CrossRef] [PubMed]
- Thibault, G.; Angulo, J.; Meyer, F. Advanced statistical matrices for texture characterization: Application to cell classification. IEEE Trans. Bio-Med. Eng. 2014, 61, 630–637. [Google Scholar] [CrossRef]
- Kairuddin, W.; Mahmud, W. Texture Feature Analysis for Different Resolution Level of Kidney Ultrasound Images. IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 012136. [Google Scholar] [CrossRef]
- Thibault, G.; Fertil, B.; Navarro, C.; Pereira, S.; Ley, N.; Sequeira, J.; Mari, J. Texture Indexes and Gray Level Size Zone Matrix Application to Cell Nuclei Classification. In Proceedings of the Pattern Recognition and Information Processing (PRIP), Minsk, Belarus, 19–21 May 2009; pp. 140–145. [Google Scholar]
- Khalil, M.M. Radiomics Feature Selection in 18F-FDG PET Imaging: Investigation of the Most robust and Reproducible Candidates. Egypt. J. Nucl. Med. 2020, 21, 80–102. [Google Scholar]
- Student. The probable error of a mean. Biometrika 1908, 6, 1–25. [Google Scholar] [CrossRef]
- Lindstrom, J.; Dahl, F. Model Selection with Lasso in Multi-group Structural Equation Models. Struct. Equ. Model. Multidiscip. J. 2019, 27, 33–42. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Owens, C.; Peterson, C.; Tang, C.; Koay, E.; Yu, W.; Mackin, D.; Li, J.; Salehpour, M.; Fuentes, D.; Court, L.; et al. Lung tumor segmentation methods: Impact on the uncertainty of radiomics features for non-small cell lung cancer. PLoS ONE 2018, 13, e0205003. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Huang, D.; Wang, Y.; Zhong, H.; Pang, H. CT radiomics based on different machine learning models for classifying gross tumor volume and normal liver tissue in hepatocellular carcinoma. Cancer Imaging 2024, 24, 20. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Dong, Y.; Wu, G.; Zhang, Q.; Yang, D.; Yu, J.; Wang, W. Preoperative diagnosis and prediction of hepatocellular carcinoma: Radiomics analysis based on multi-modal ultrasound images. BMC Cancer 2018, 18, 1089. [Google Scholar] [CrossRef] [PubMed]
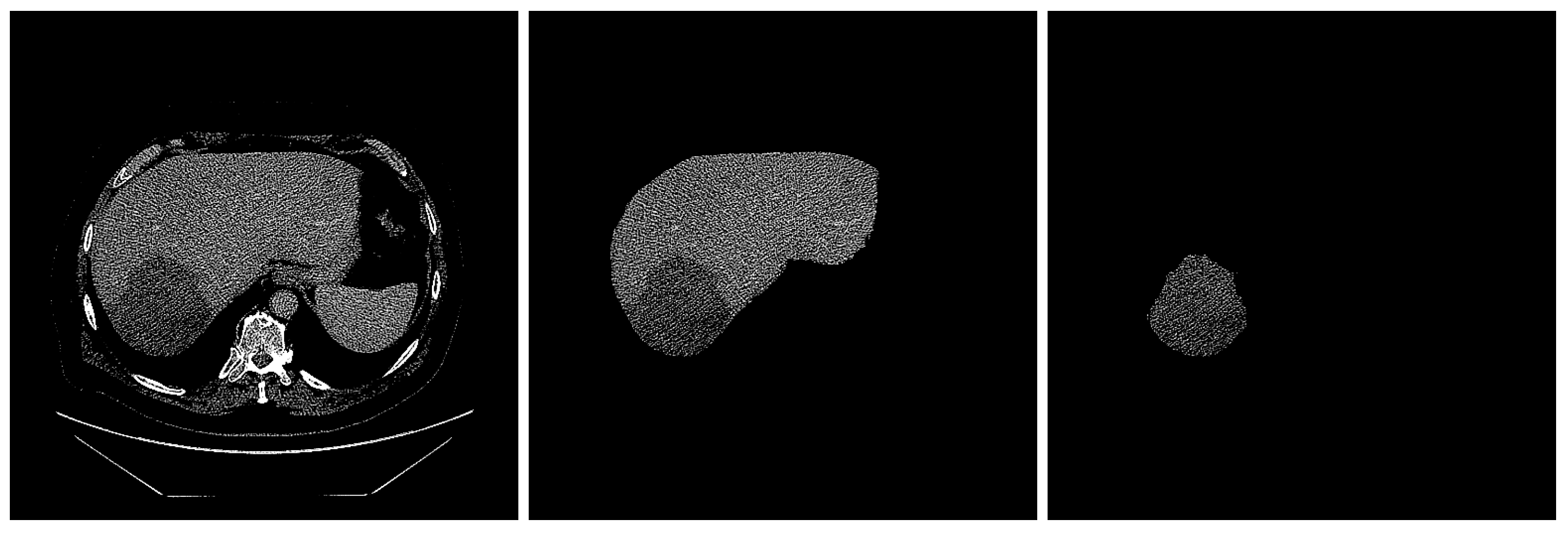
| Image Size | Slice Thickness | Pixel Spacing | Slice Number |
|---|---|---|---|
| mm | mm | 1200–1700 |
| Types | Features |
|---|---|
| Shape () | Elongation, Flatness, Least Axis Length, Major Axis Length, Maximum 2D Diameter Column, Maximum 2D Diameter Row, Maximum 2D Diameter Slice, Maximum 3D Diameter, Mesh Volume, Minor Axis Length, Sphericity, Surface Area, Surface Volume Ratio, Voxel Volume |
| First-order statistics () | 10 Percentile, 90th Percentile, Energy, Entropy, Interquartile Range, Kurtosis, Maximum, Mean Absolute Deviation, Mean, Median, Minimum, Range, Robust Mean Absolute Deviation, Root Mean Square, Skewness, Total Energy, Uniformity, Variance |
| Second-order statistics | |
| GLCM () | Auto-Correlation, Cluster Prominence, Cluster Shade, Cluster Tendency, Contrast, Correlation, Difference Average, Difference Entropy, Difference Variance, Id, Idm, Idmn, Idn, Imc1, Imc2, Inverse Variance, Joint Average, Joint Energy, Joint Entropy, MCC, Maximum Probability, Sum Average, Sum Entropy, Sum of Squares |
| GLRLM () | Gray-Level Non-Uniformity, Gray-Level Non-Uniformity Normalized, Gray-Level Variance, High Gray-Level Run Emphasis, Long-Run Emphasis, Long-Run High Gray-Level Emphasis, Long-Run Low Gray-Level Emphasis, Low Gray-Level Run Emphasis, Run Entropy, Run Length Non-Uniformity, Run Length Non-Uniformity Normalized, Run Percentage, Run Variance, Short-Run Emphasis, Short-Run High Gray-Level Emphasis, Short-Run Low Gray-Level Emphasis |
| GLSZM () | Gray-Level Non-Uniformity, Gray-Level Non-Uniformity Normalized, Gray-Level Variance, High Gray-Level Zone Emphasis, Large Area Emphasis, Large Area High Gray-Level Emphasis, Large Area Low Gray-Level Emphasis, Low Gray-Level Zone Emphasis, Size Zone Non-Uniformity, Size Zone Non-Uniformity Normalized, Small Area Emphasis, Small Area High Gray-Level Emphasis, Small Area Low Gray-Level Emphasis, Zone Entropy, Zone Percentage, Zone Variance |
| GLDM () | Dependence Entropy, Dependence Non-Uniformity, Dependence Non-Uniformity Normalized, Dependence Variance, Gray-Level Non-Uniformity, Gray-Level Variance, High Gray-Level Emphasis, Large Dependence Emphasis, Large Dependence High Gray-Level Emphasis, Large Dependence Low Gray-Level Emphasis, Low Gray-Level Emphasis, Small Dependence Emphasis, Small Dependence High Gray-Level Emphasis, Small Dependence Low Gray-Level Emphasis |
| High-order statistics () | First-Order and Second-Order Features Are Transformed by LoG, Exponential, Square, Square Root, Logarithm, Wavelet (Wavelet-LHL, Wavelet-LHH, Wavelet-HLL, Wavelet-LLH, Wavelet-HLH, Wavelet-HHH, Wavelet-HHL, Wavelet-LLL) |
| Clinical Characteristics | Tumor | Non-Tumor | p-Value |
|---|---|---|---|
| Sex | |||
| Male | |||
| Female | |||
| Age |
| Features | VIF |
|---|---|
| log.sigma.0.5.mm.3D_firstorder_Maximum | |
| log.sigma.2.0.mm.3D_glszm_SizeZoneNonUniformity | |
| log.sigma.5.0.mm.3D_glszm_SizeZoneNonUniformity | |
| square_glszm_LargeAreaEmphasis | |
| logarithm_gldm_DependenceVariance | |
| exponential_glcm_ClusterProminence | |
| exponential_glcm_ClusterShade |
| Algorithm | AUROC (95% CI) | Sensitivity | Specificity | NPV | PPV | MCC |
|---|---|---|---|---|---|---|
| SVM | 0.8258 (0.677–0.9745) | |||||
| NaiveBayes | 0.9268(0.8224–1) | |||||
| XGBoost | 0.8813 (0.75–1) | |||||
| RF | 0.8535 (0.7126–0.9945) | |||||
| Logistic | 0.8359 (0.6875–0.9842) | |||||
| AdaBoost | 0.8813 (0.75–1) |
| Feature | Importance |
|---|---|
| log.sigma.2.0.mm.3D_firstorder_Median | |
| wavelet.LLL_glcm_Autocorrelation | |
| log.sigma.2.0.mm.3D_firstorder_Kurtosis | |
| log.sigma.2.0.mm.3D_firstorder_InterquartileRange | |
| logarithm_glcm_ClusterShade | |
| wavelet.LHL_firstorder_Maximum | |
| wavelet.LLH_gldm_SmallDependenceHighGrayLevelEmphasis | |
| exponential_firstorder_MeanAbsoluteDeviation | |
| log.sigma.1.0.mm.3D_glcm_SumAverage | |
| original_glszm_HighGrayLevelZoneEmphasis | |
| log.sigma.1.0.mm.3D_glszm_HighGrayLevelZoneEmphasis | |
| wavelet.LLH_glrlm_LongRunHighGrayLevelEmphasis | |
| wavelet.LLL_firstorder_Kurtosis | |
| wavelet.HHH_glszm_LargeAreaLowGrayLevelEmphasis | |
| log.sigma.2.0.mm.3D_glszm_SizeZoneNonUniformity | |
| log.sigma.2.0.mm.3D_firstorder_MeanAbsoluteDeviation | |
| wavelet.LHL_glcm_ClusterShade | |
| original_firstorder_Mean | |
| log.sigma.0.5.mm.3D_glrlm_LongRunHighGrayLevelEmphasis | |
| log.sigma.5.0.mm.3D_glszm_SmallAreaHighGrayLevelEmphasis | |
| log.sigma.1.0.mm.3D_glszm_GrayLevelNonUniformity | |
| original_glrlm_RunLengthNonUniformity |
| Algorithm | AUROC (95% CI) | Sensitivity | Specificity | NPV | PPV | MCC |
|---|---|---|---|---|---|---|
| SVM | 0.5929 (0.3873–0.7985) | |||||
| NaiveBayes | 0.8571(0.6764–1) | 1 | 1 | |||
| XGBoost | 0.5929 (0.3873–0.7985) | |||||
| RF | 0.5929 (0.3873–0.7985) | |||||
| Logistic | 0.7569 (0.5472–0.9667) | |||||
| AdaBoost | 0.5929 (0.3873–0.7985) |
| Feature | Importance |
|---|---|
| exponential_glrlm_HighGrayLevelRunEmphasis | |
| original_shape_Maximum2DDiameterColumn | |
| original_shape_Maximum2DDiameterRow | |
| original_shape_Maximum3DDiameter | |
| exponential_glrlm_GrayLevelVariance | |
| square_firstorder_RobustMeanAbsoluteDeviation | |
| exponential_glcm_ClusterTendency | |
| exponential_glszm_HighGrayLevelZoneEmphasis | |
| exponential_firstorder_RootMeanSquared | |
| squareroot_glszm_HighGrayLevelZoneEmphasis | |
| wavelet.LHL_firstorder_Range | |
| wavelet.LLH_gldm_GrayLevelNonUniformity | |
| exponential_glszm_GrayLevelNonUniformity | |
| original_gldm_GrayLevelNonUniformity | |
| log.sigma.3.0.mm.3D_glszm_LargeAreaLowGrayLevelEmphasis | |
| square_glrlm_ShortRunHighGrayLevelEmphasis | |
| squareroot_firstorder_90Percentile | |
| logarithm_firstorder_90Percentile |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zossou, V.-B.S.; Gnangnon, F.H.R.; Biaou, O.; de Vathaire, F.; Allodji, R.S.; Ezin, E.C. Radiomics-Based Classification of Tumor and Healthy Liver on Computed Tomography Images. Cancers 2024, 16, 1158. https://doi.org/10.3390/cancers16061158
Zossou V-BS, Gnangnon FHR, Biaou O, de Vathaire F, Allodji RS, Ezin EC. Radiomics-Based Classification of Tumor and Healthy Liver on Computed Tomography Images. Cancers. 2024; 16(6):1158. https://doi.org/10.3390/cancers16061158
Chicago/Turabian StyleZossou, Vincent-Béni Sèna, Freddy Houéhanou Rodrigue Gnangnon, Olivier Biaou, Florent de Vathaire, Rodrigue S. Allodji, and Eugène C. Ezin. 2024. "Radiomics-Based Classification of Tumor and Healthy Liver on Computed Tomography Images" Cancers 16, no. 6: 1158. https://doi.org/10.3390/cancers16061158
APA StyleZossou, V.-B. S., Gnangnon, F. H. R., Biaou, O., de Vathaire, F., Allodji, R. S., & Ezin, E. C. (2024). Radiomics-Based Classification of Tumor and Healthy Liver on Computed Tomography Images. Cancers, 16(6), 1158. https://doi.org/10.3390/cancers16061158






