Rapid Experimental Protocol for PMSM via MBD: Modeling, Simulation, and Experiment
Abstract
1. Introduction
- (a)
- The constructed REP is based on a semi-automatic code generation design. It inherits the advantages of automatic code generation.
- (b)
- The framework becomes reusable upon completion of its construction. Users need only the model modification at the application layer to accomplish simulation and code generation. This facilitates rapid and efficient validation of algorithms.
- (c)
- The REP is independent of complex toolboxes, requiring only the use of fundamental modules for its construction, thus ensuring notable portability.
- (d)
- REP is built upon the principles of MBD, enabling effective handling of complex mathematical models.
2. Mathematical Model
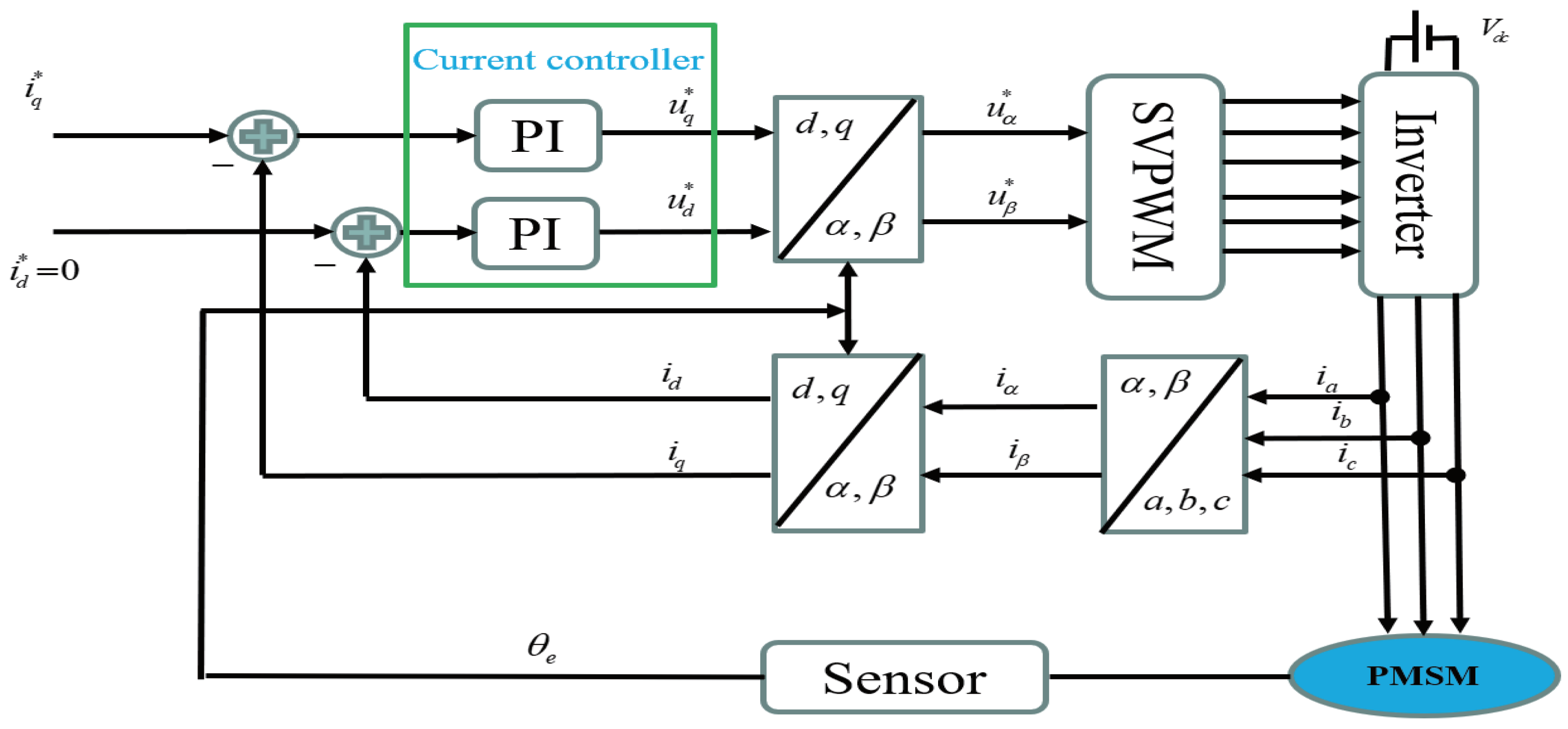
2.1. Sensor–Encoder Control
- (a)
- Saturation of the motor core is neglected;
- (b)
- Eddy current and hysteresis losses in the motor are not taken into account;
- (c)
- The current in the motor is a symmetrical three-phase sinusoidal waveform.
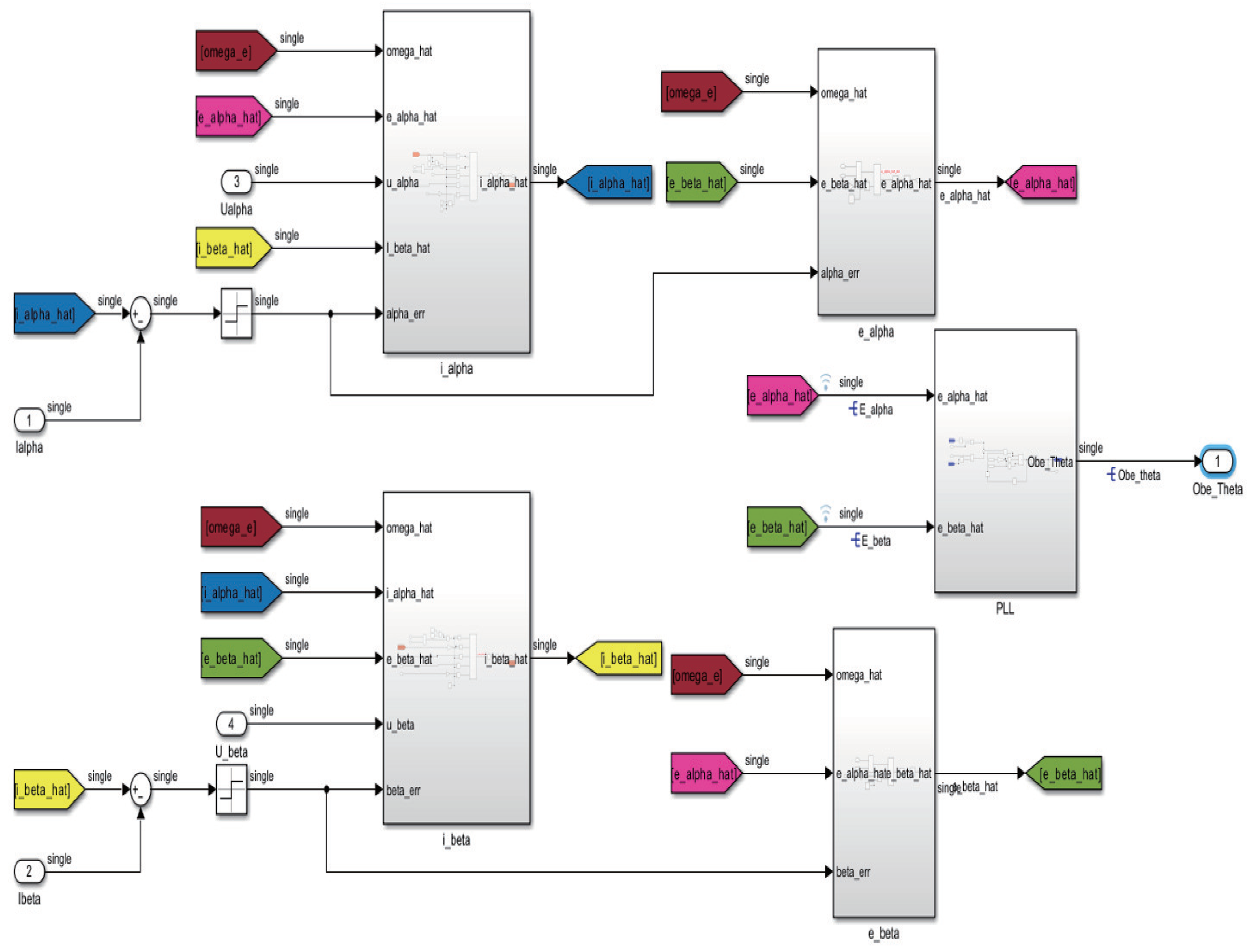
2.2. Sensorless Control
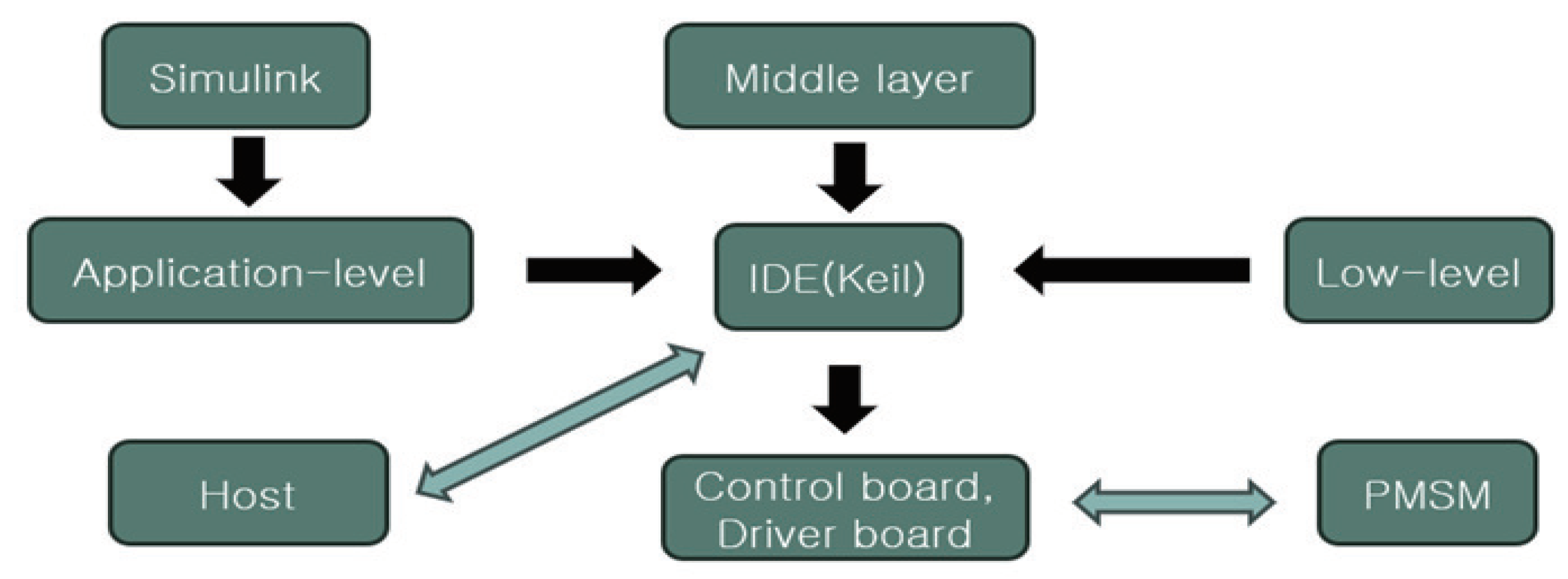
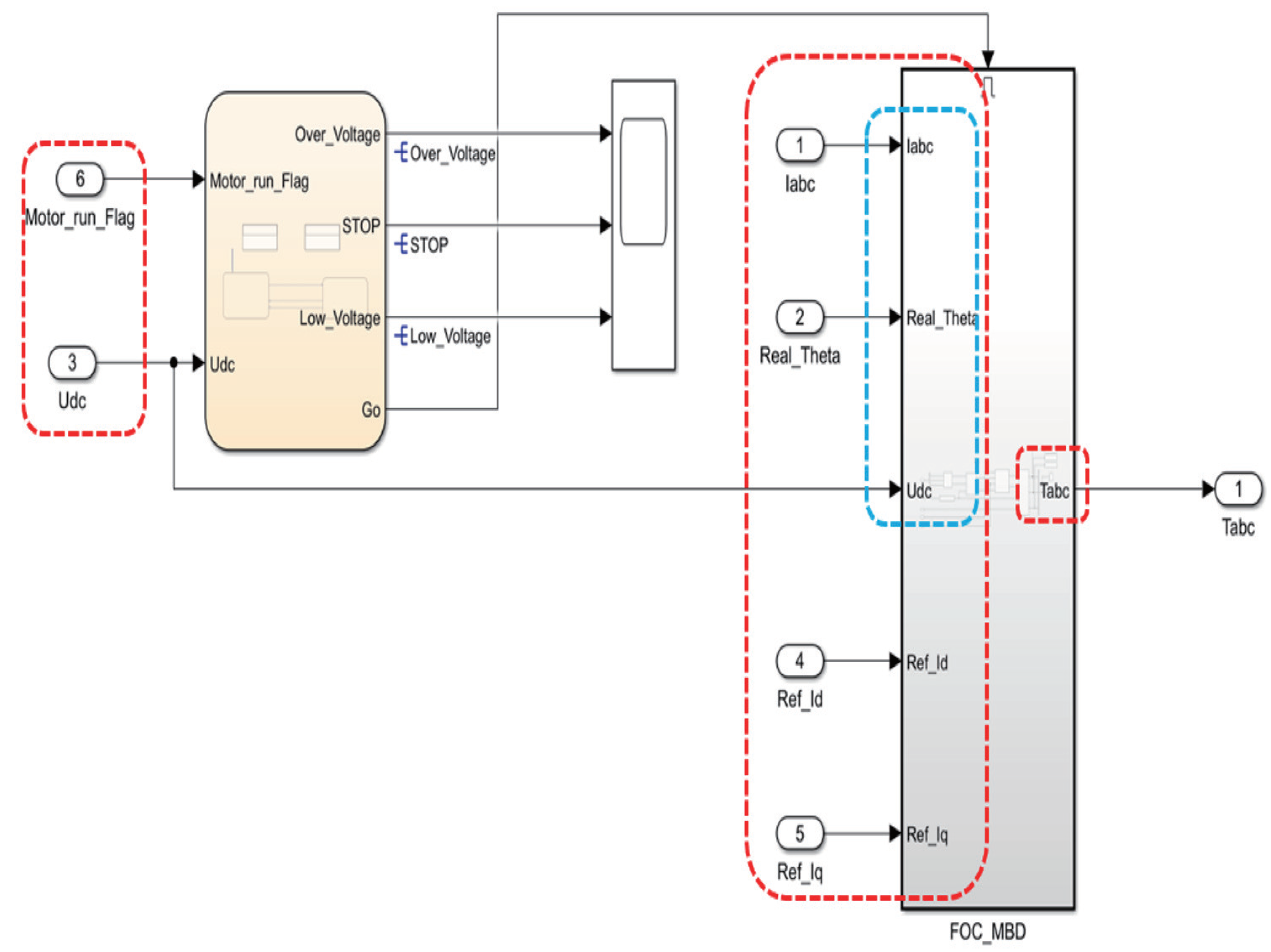
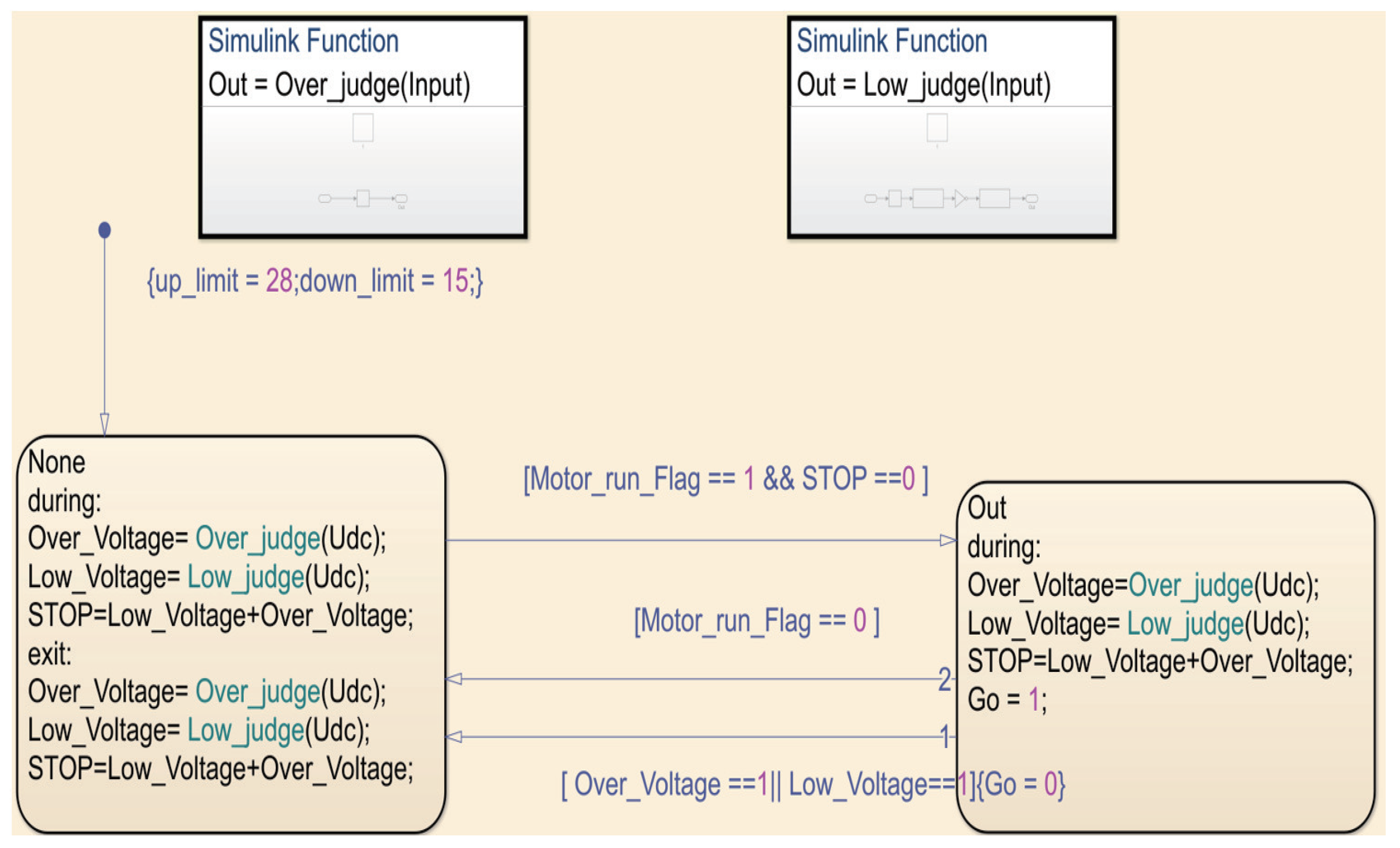
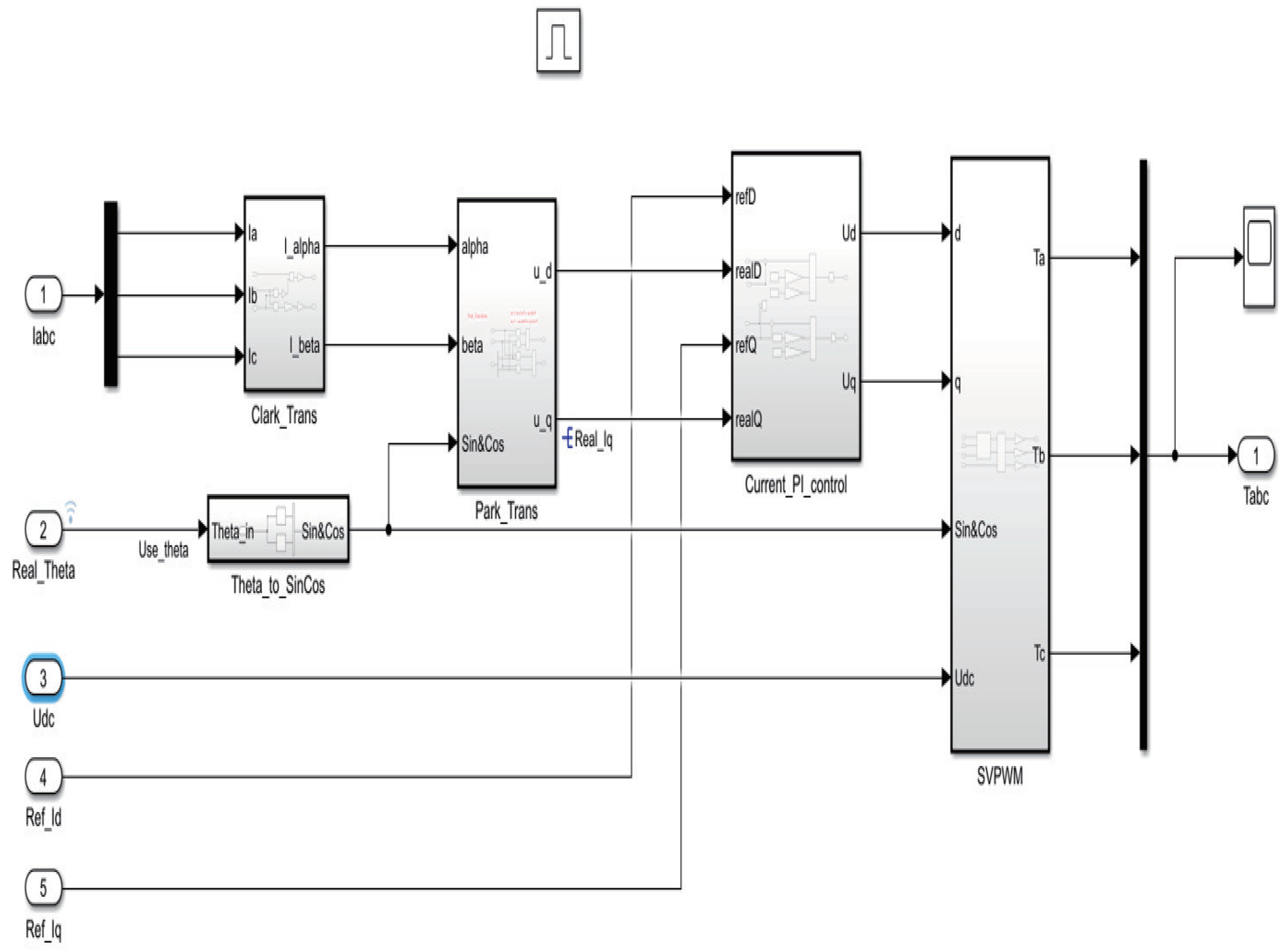
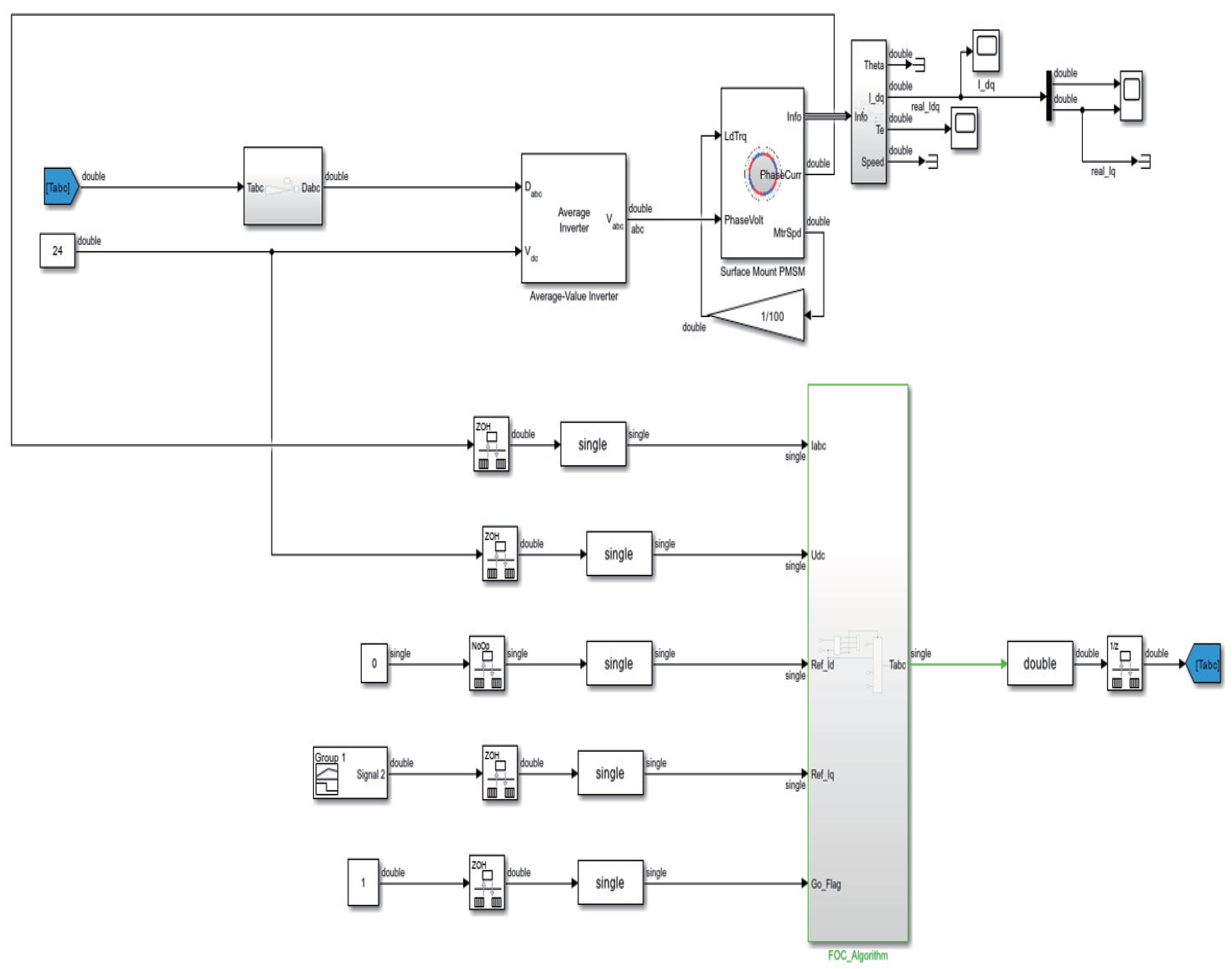
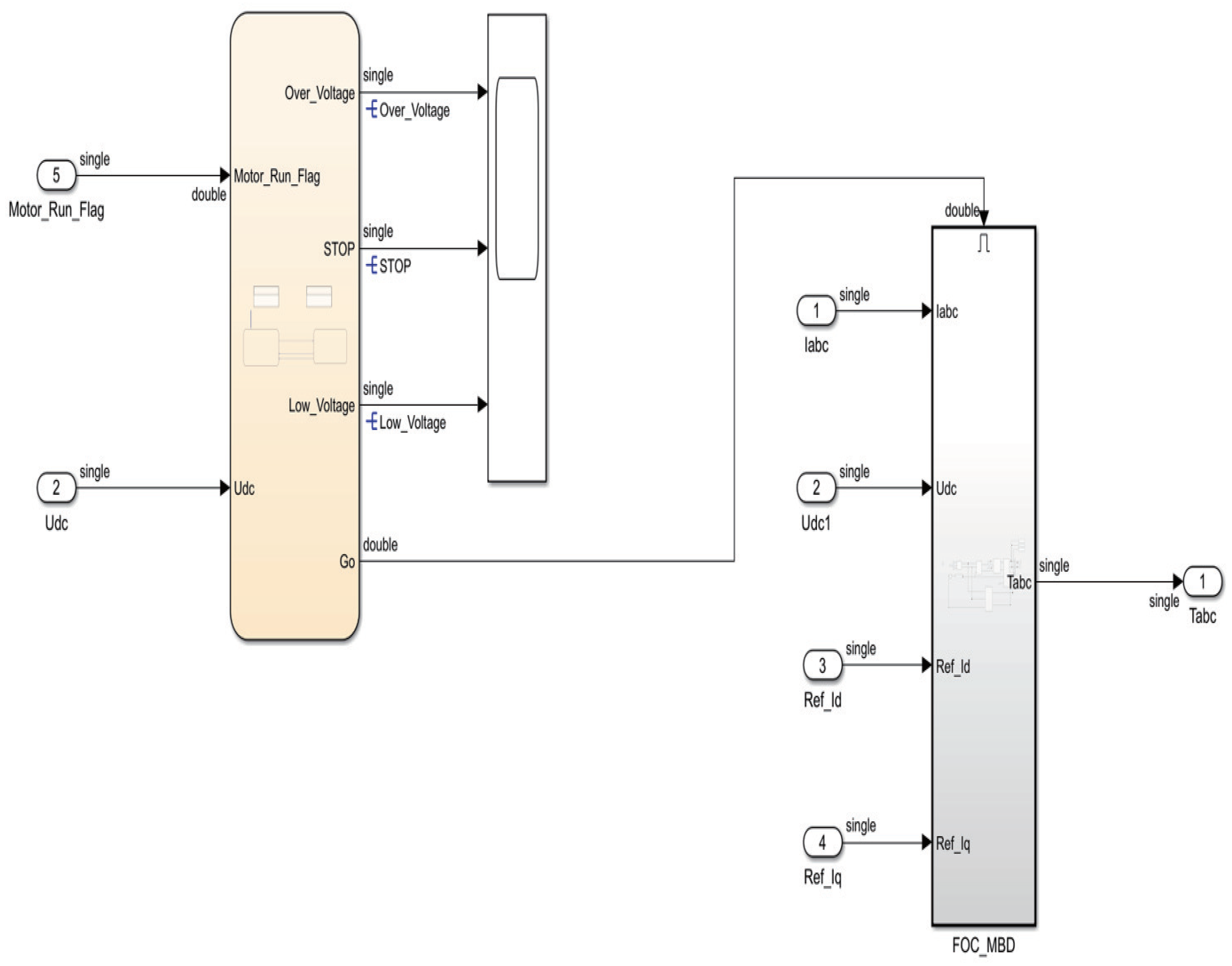
3. Flow Chart for Code Generation via Simulink
3.1. Sensor–Encoder Design
3.2. Design of Sensorless Control
4. Simulation Results
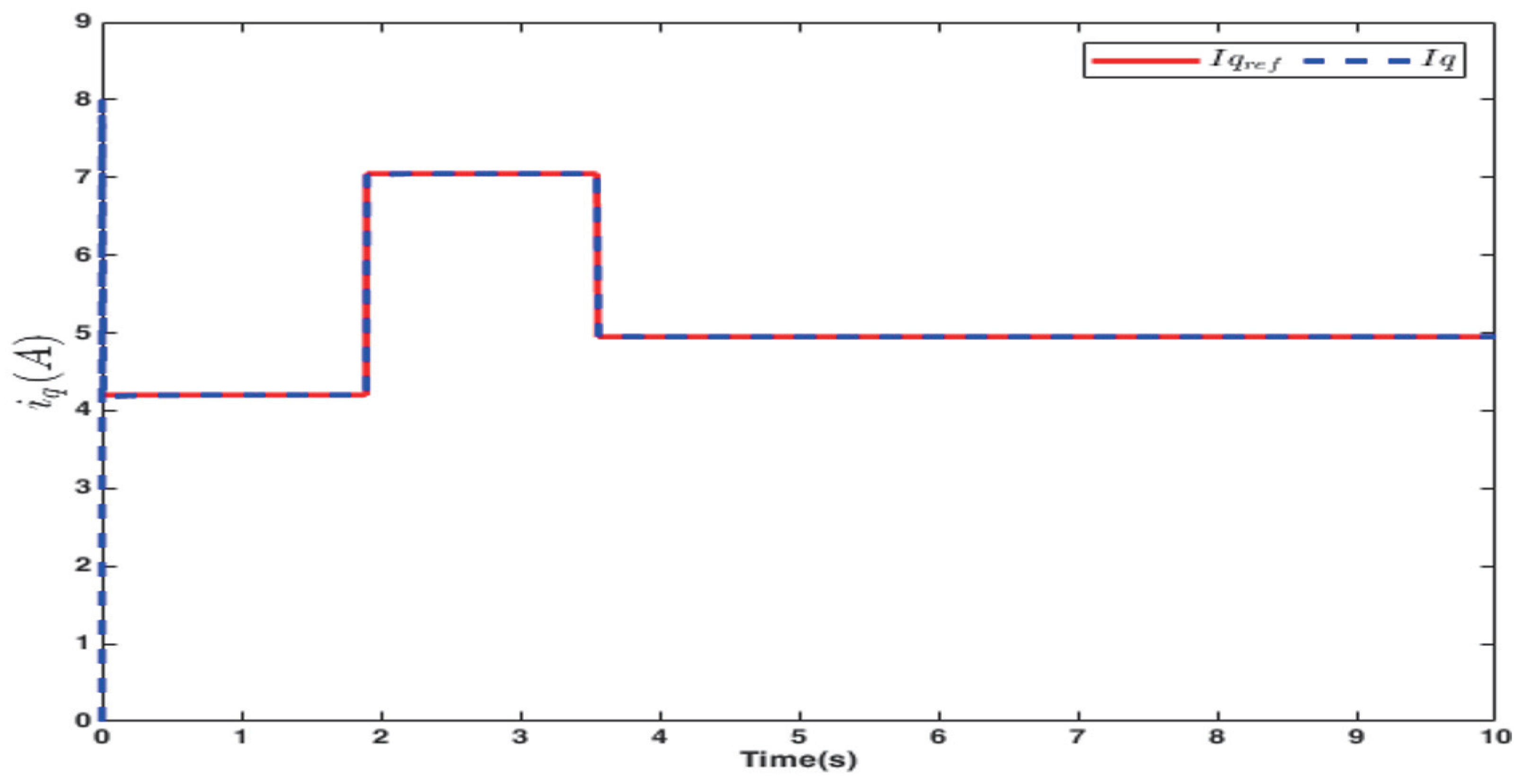
4.1. Sensor–Encoder Simulation Results
4.2. Simulation Results Using Sensorless Control
5. Results of Experiment
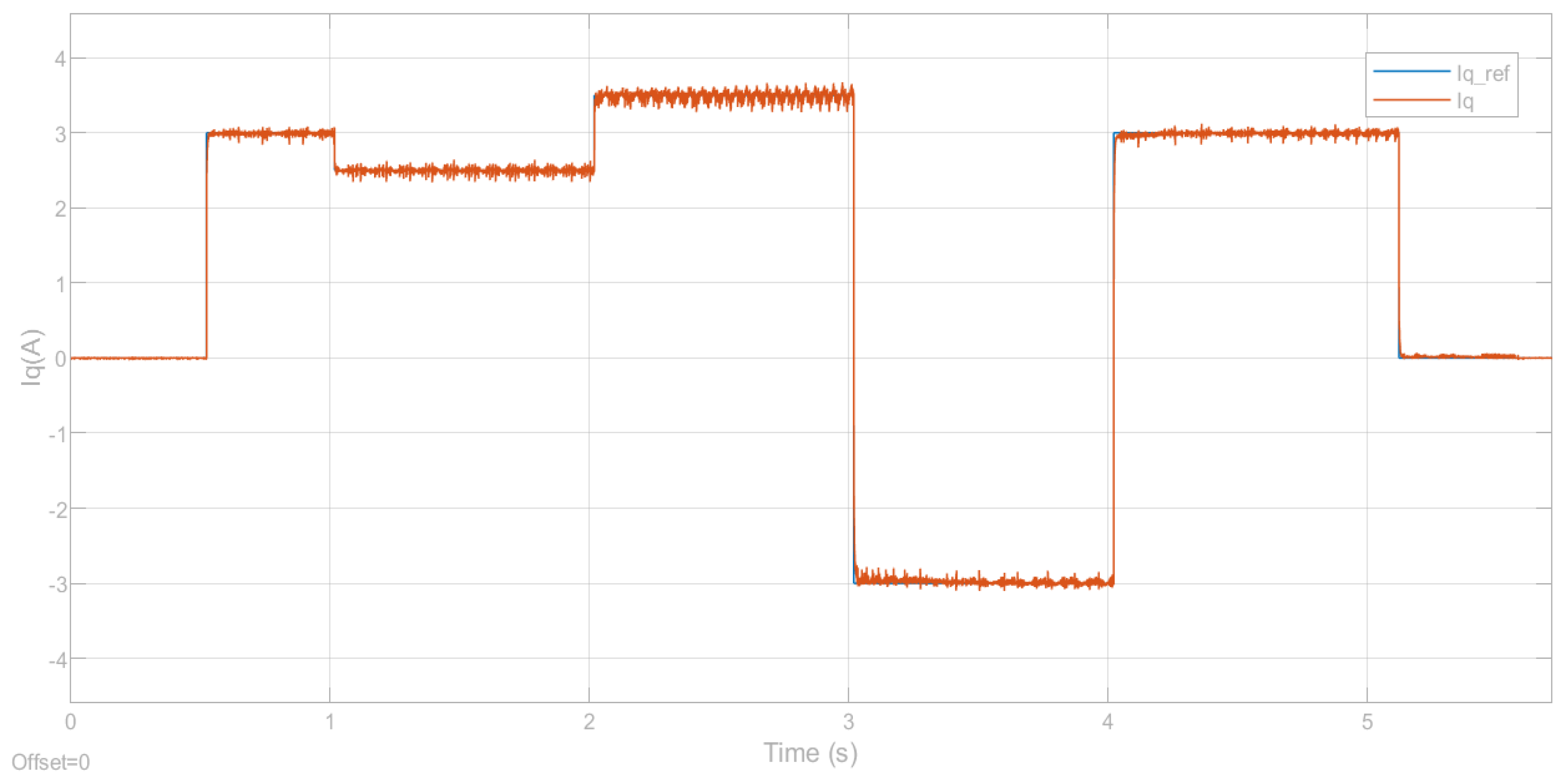
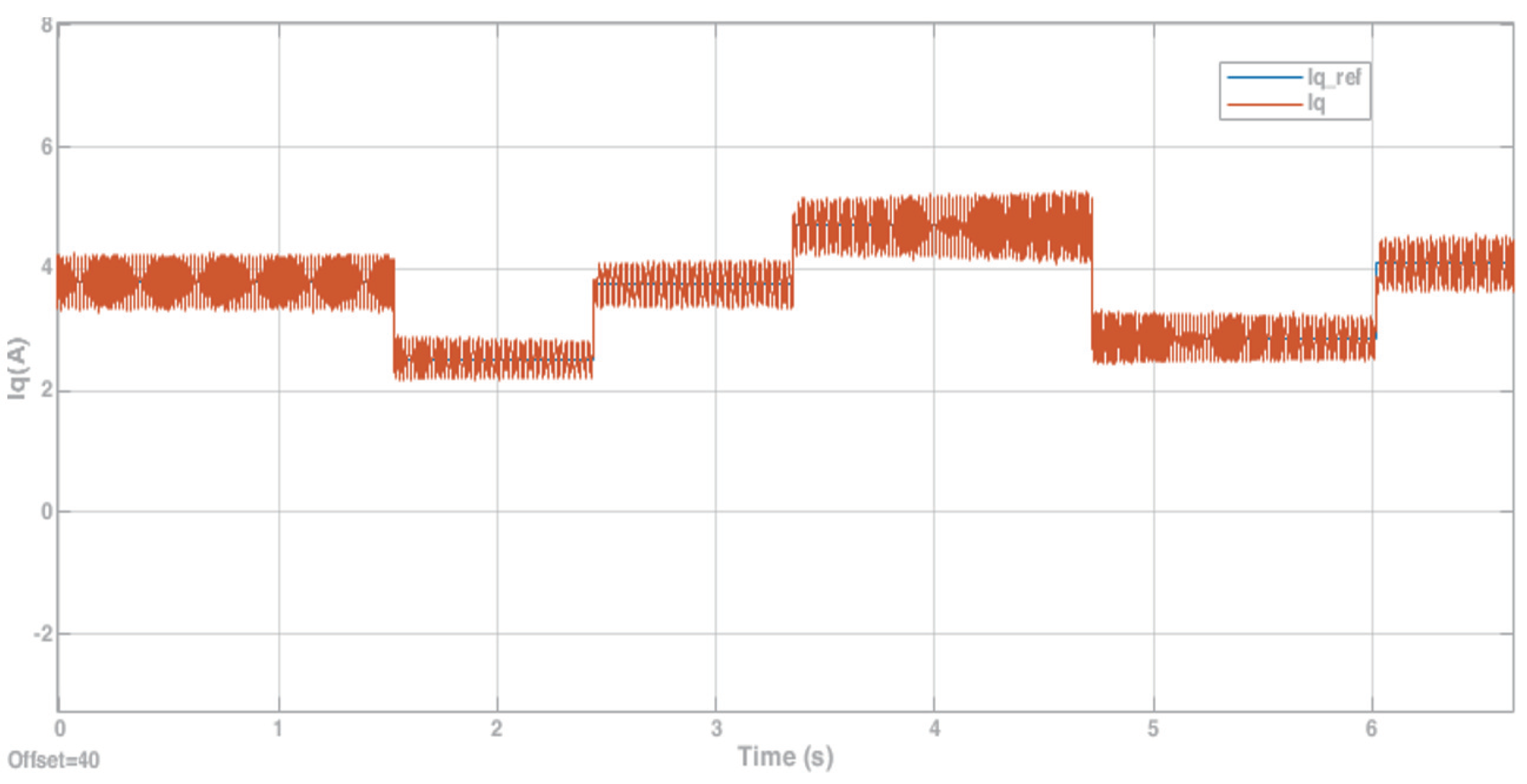
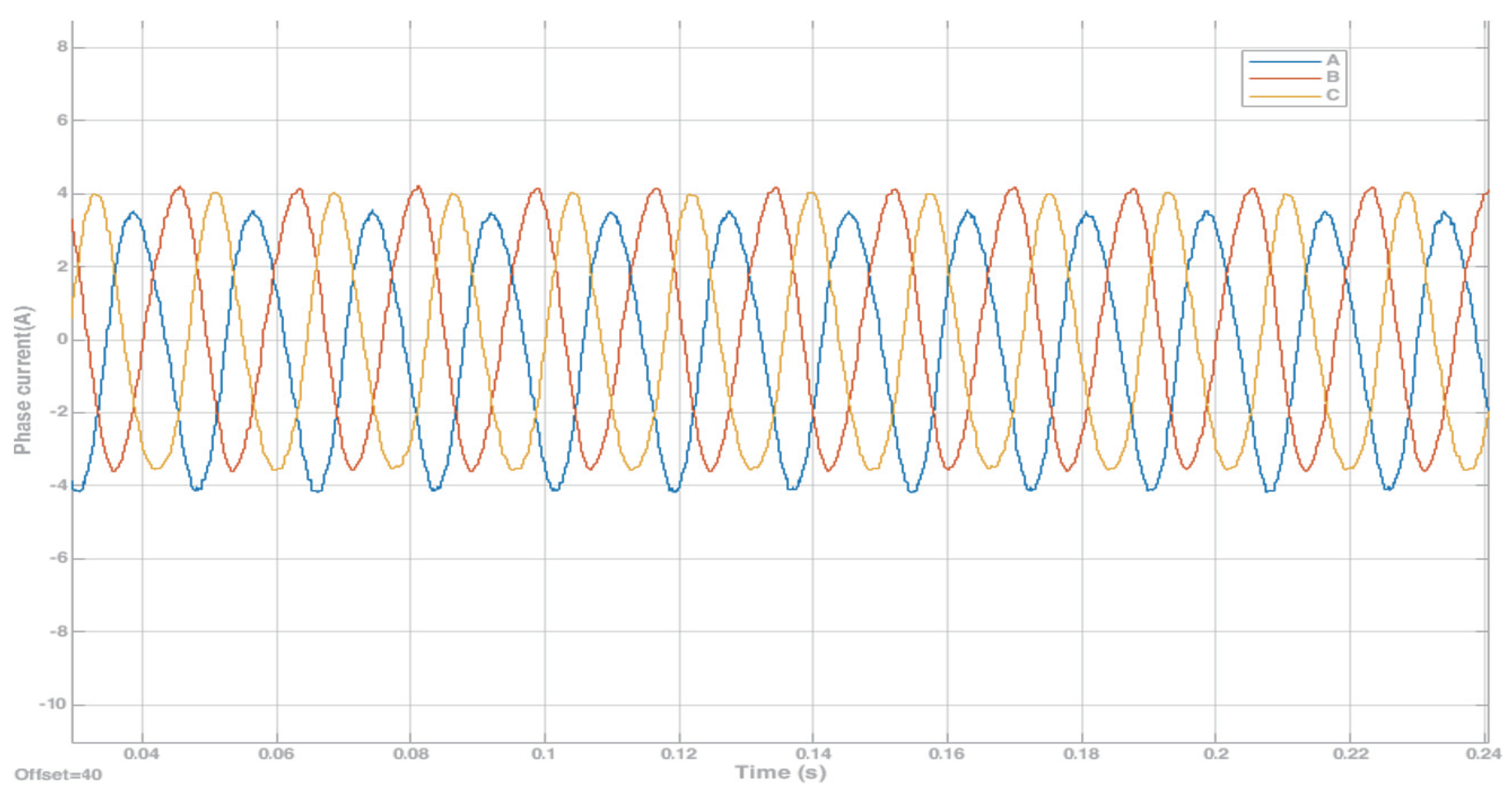
5.1. Results of Sensor–Encoder Experiment
5.2. Results of Sensorless Control Experiment
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krizan, J.; Ertl, L.; Bradac, M.; Jasansky, M.; Andreev, A. Automatic code generation from Matlab/Simulink for critical applications. In Proceedings of the 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE), Toronto, ON, Canada, 4–7 May 2014. [Google Scholar]
- Andrs, O.; Hadas, Z.; Kovar, J.; Vetiška, J.; Singule, V. Model-Based Design of Mobile Platform with Integrated Actuator–Design with Respect to Mechatronic Education. In Mechatronics 2013: Recent Technological and Scientific Advances; Springer: Cham, Switzerland, 2014; pp. 891–898. [Google Scholar]
- Su, Z.; Wang, D.; Yu, Z.; Yang, Y.; Jiang, Y.; Wang, R.; Chang, W.; Li, W.; Cui, A.; Sun, J. PHCG: Optimizing Simulink Code Generation for Embedded System With SIMD Instructions. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2023, 42, 1072–1084. [Google Scholar] [CrossRef]
- Hu, D.; Alsmadi, Y.M.; Xu, L. High-Fidelity Nonlinear IPM Modeling Based on Measured Stator Winding Flux Linkage. IEEE Trans. Ind. Appl. 2015, 51, 3012–3019. [Google Scholar] [CrossRef]
- Rademacher, F.; Sorgalla, J.; Sachweh, S.; Zündorf, A. A model-driven workflow for distributed microservice development. In Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing, Limassol, Cyprus, 8–12 April 2019. [Google Scholar]
- Bosso, A.; Tilli, A.; Conficoni, C. A Hybrid sensorless observer for the robust global asymptotic flux reconstruction of permanent magnet synchronous machines. IEEE Control Syst. Lett. 2022, 6, 3367–3372. [Google Scholar] [CrossRef]
- Chatri, C.; Labbadi, M.; Ouassaid, M.; Elyaalaoui, K.; Houm, Y.E. Design and implementation of finite-time control for speed tracking of permanent magnet synchronous mtors. IEEE Control Syst. Lett. 2023, 7, 721–726. [Google Scholar] [CrossRef]
- Chen, B.; Wang, K.; Le, Y. High-precision position error correction method for the PMSM based on low-order harmonic Suppression. IEEE Trans. Power Electron. 2021, 36, 4500–4512. [Google Scholar] [CrossRef]
- Chen, H.; Demerdash, N.A.O.; EL-Refaie, A.M.; Guo, Y.; Hua, W.; Lee, C.H.T. Investigation of a 3D-magnetic flux PMSM with high torque density for electric vehicles. IEEE Trans. Energy Convers. 2022, 37, 1442–1454. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Yu, J.; Yu, H. Time-varying disturbance oserver based improved sliding mode single-loop control of PMSM drives with a hybrid reaching law. IEEE Trans. Energy Convers. 2023, 38, 2539–2549. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved non-singular fast terminal sliding mode control with disturbance observer for PMSM drives. IEEE Trans. Transp. Electrif. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.S. Rapid control prototyping for PMSM drives using DSPs and PLECS. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongiu, Republic of Korea, 31 October 31–3 November 2021. [Google Scholar]
- Saralegui, R.; Sanchez, A.; de Castro, A. Efficient hardware-in-the-loop models using automatic code generation with MATLAB/Simulink. Electronics 2023, 12, 2786. [Google Scholar] [CrossRef]
- Srivastava, A.; Padgil, R.; Gupta, A.; Lohia, A.; Nair, N.P. Model-based sensored field oriented control implementation for permanent magnet synchronous motor. In Proceedings of the 2021 International Symposium of Asian Control Association on Intelligent Robotics and Industrial Automation (IRIA), Goa, India, 20–22 September 2021. [Google Scholar]
- Jin, X.; Zhang, T.; Zhang, H.; Zeng, P.; Wang, A. Research on servo system of permanent magnet synchronous motor based on model design. In Proceedings of the 2018 International Conference on Advanced Control, Automation and Artificial Intelligence (ACAAI 2018), Shenzhen, China, 21–22 January 2018. [Google Scholar]
- Belhamel, L.; Buscarino, A.; Cucuccio, A.; Fortuna, L.; Rascona, G. Model-based design streamlines for STM32 motor control embedded software system. In Proceedings of the 2020 7th International Conference on Control, Decision and Information Technologies (CoDIT), Prague, Czech Republic, 29 June–2 July 2020. [Google Scholar]
- Wild, L.; Incurvati, M.; Schiestl, M.; Staerz, R. Rapid prototyping framework for integrated modular motor drives: Modelling, simulation and automated code generation. In Proceedings of the PCIM Europe 2022; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2022; pp. 1–10. [Google Scholar]
- Zhao, G.; Zhang, S. Development of permanent magnet synchronous motor RCP based on hardware-in-the-loop simulation. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018. [Google Scholar]
- Jiang, W.; Han, W.; Wang, L.; Liu, Z.; Du, W. Linear golden section speed adaptive control of permanent magnet synchronous motor based on model Design. Processes 2022, 10, 1010. [Google Scholar] [CrossRef]
- Ma, Z.; Saeidi, S.; Kennel, R. FPGA implementation of model predictive control with constant switching frequency for PMSM drives. IEEE Trans. Ind. Inform. 2014, 10, 2055–2063. [Google Scholar] [CrossRef]
- Koga, T.; Abe, T.; Otomo, Y.; Yamamoto, M.; Rosu, M. Reduced order modeling of half-wave rectified brushless synchronous motor for model-based design. IEEJ J. Ind. Appl. 2023, 12, 826–834. [Google Scholar] [CrossRef]
- Liu, K.; Jiang, D.; Sun, W.; Liu, Z. A motor controller development framework based on switch model simulation and all code automatic generation. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Sun, X.; Yu, H.; Yu, J.; Liu, X. Design and implementation of a novel adaptive backstepping control scheme for a PMSM with unknown load torque. IET Electr. Power Appl. 2019, 13, 445–455. [Google Scholar] [CrossRef]
- Petrovic, V.; Ortega, R.; Stankovi, A. Interconnection and damping assignment approach to control of PM synchronous motors. IEEE Trans. Control Syst. Technol. 2001, 9, 811–820. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehensive analysis [three-phase inverters]. IEEE Trans. Ind. Electron. 2002, 49, 186–196. [Google Scholar] [CrossRef]
- Wang, G.; Li, Z.; Zhang, G.; Yu, Y.; Xu, D. Quadrature PLL-based high-order sliding-mode observer for IPMSM sensorless control with online MTPA control strategy. IEEE Trans. Energy Convers. 2013, 28, 214–224. [Google Scholar] [CrossRef]













| Parameters | Value | Unit |
|---|---|---|
| Resistance | 0.05 | |
| Inductance | ||
| Flux linkage | 0.0065 | |
| Inertia J | ||
| Damping coefficient | ||
| Pole pairs | 5 |
| Parameters | Value |
|---|---|
| 0.1470 | |
| 75 | |
| 0.1470 | |
| 75 |
| Parameters | Value |
|---|---|
| 0.1470 | |
| 75 | |
| 0.1470 | |
| 75 | |
| k | 1 |
| m | 0.17 |
| 5 | |
| 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Ahn, H.; Kang, H.; Chung, Y.; You, K. Rapid Experimental Protocol for PMSM via MBD: Modeling, Simulation, and Experiment. Computers 2024, 13, 73. https://doi.org/10.3390/computers13030073
Hu M, Ahn H, Kang H, Chung Y, You K. Rapid Experimental Protocol for PMSM via MBD: Modeling, Simulation, and Experiment. Computers. 2024; 13(3):73. https://doi.org/10.3390/computers13030073
Chicago/Turabian StyleHu, Mingyuan, Hyeongki Ahn, Hyein Kang, Yoonuh Chung, and Kwanho You. 2024. "Rapid Experimental Protocol for PMSM via MBD: Modeling, Simulation, and Experiment" Computers 13, no. 3: 73. https://doi.org/10.3390/computers13030073
APA StyleHu, M., Ahn, H., Kang, H., Chung, Y., & You, K. (2024). Rapid Experimental Protocol for PMSM via MBD: Modeling, Simulation, and Experiment. Computers, 13(3), 73. https://doi.org/10.3390/computers13030073








