A Review of Theoretical Studies on Indirect Reciprocity
Abstract
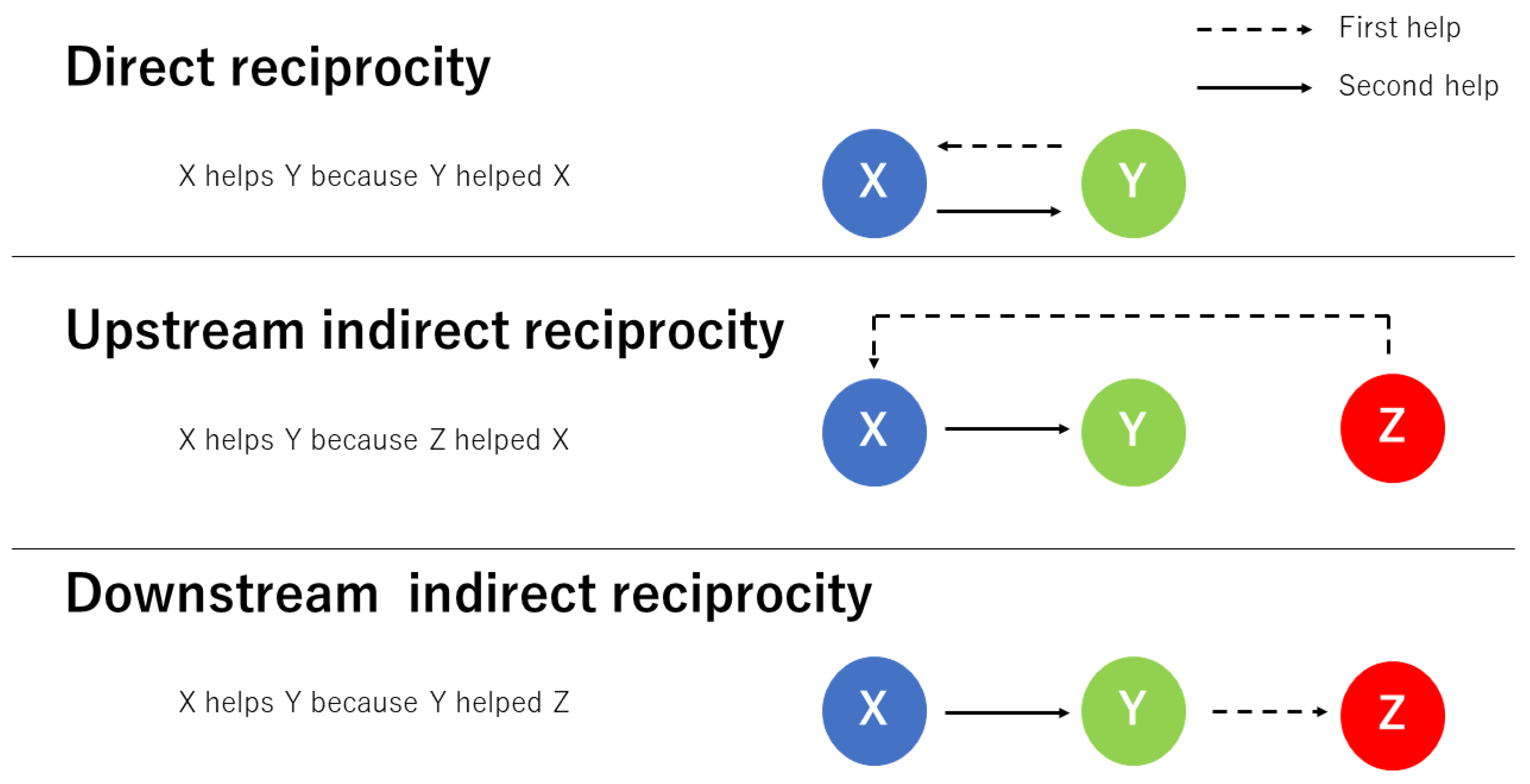
:1. Introduction
2. Development of Research Areas and Research Methods
3. Analytical Models of Indirect Reciprocity
4. Problems with Image Scoring Norm
5. Refinement of Assessment Function
6. Resolving the Punishment Dilemma
7. Remaining Issues in Study of Indirect Reciprocity Using Evolutionary Game Theory
8. Indirect Reciprocity in Various Disciplines
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hamilton, W.D. The evolution of altruistic behavior. Am. Nat. 1963, 97, 354–356. [Google Scholar] [CrossRef] [Green Version]
- Trivers, R. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Milinski, M. Tit for tat in sticklebacks and the evolution of cooperation. Nature 1987, 325, 433–435. [Google Scholar] [CrossRef] [PubMed]
- Riolo, R.L.; Cohen, M.D.; Axelrod, R. Evolution of cooperation without reciprocity. Nature 2001, 414, 441–443. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [Green Version]
- Traulsen, A.; Nowak, M.A. Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. USA 2006, 103, 10952–10955. [Google Scholar] [CrossRef] [Green Version]
- Dawes, R.M. Social Dilemmas. Ann. Rev. Psychol. 1980, 31, 169–193. [Google Scholar] [CrossRef]
- Yamagishi, T. The provision of a sanctioning system as a public good. J. Pers. Soc. Psychol. 1986, 51, 110–116. [Google Scholar] [CrossRef]
- Yamagishi, T.; Cook, K.S. Generalized exchange and social dilemmas. Soc. Psychol. Q. 1993, 56, 235–248. [Google Scholar] [CrossRef]
- Macy, M.W.; Flache, A. Learning dynamics in social dilemmas. Proc. Natl. Acad. Sci. USA 2002, 99, 7229–7236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balliet, D.P.; Parks, C.D.; Joireman, J. Social value orientation and cooperation in social dilemmas: A meta-analysis. Group Process. Interg. 2009, 12, 533–547. [Google Scholar] [CrossRef]
- Van Lange, P.A.M.; Joireman, J.; Parks, C.D.; Van Dijk, E. The psychology of social dilemmas: A review. Organ. Behav. Hum. Dec. 2013, 120, 125–141. [Google Scholar] [CrossRef]
- Eisenberg–Berg, N. Development of children’s prosocial moral judgment. Dev. Psychol. 1979, 15, 128–137. [Google Scholar] [CrossRef]
- Alexander, R.D. The search for an evolutionary philosophy of man. Proc. R. Soc. Vic. 1971, 84, 99–120. [Google Scholar]
- Alexander, R.D. The search for a general theory of behavior. Behav. Sci. 1975, 20, 77–100. [Google Scholar] [CrossRef]
- Alexander, R.D. The Biology of Moral Systems; Aldine De Gruyter: New York, NY, USA, 1987. [Google Scholar]
- Maynard Smith, J. The theory of games and the evolution of animal conflicts. J. Theor. Biol. 1974, 47, 209–221. [Google Scholar] [CrossRef] [Green Version]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Ohtsuki, H.; Nowakm, M.A. Direct reciprocity on graphs. J. Theor. Biol. 2007, 247, 462–470. [Google Scholar] [CrossRef] [Green Version]
- Delton, A.W.; Krasnow, M.M.; Cosmides, L.; Tooby, J. Evolution of direct reciprocity under uncertainty can explain human generosity in one-shot encounters. Proc. Natl. Acad. Sci. USA 2011, 108, 13335–13340. [Google Scholar] [CrossRef] [Green Version]
- Boyd, R.; Richerson, R.J. The evolution of indirect reciprocity. Soc. Netw. 1989, 11, 213–236. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 437, 1291–1298. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Rutte, C. Taborsky, Generalized reciprocity in rats. PLoS Biol. 2007, 5, e196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engelmann, D.; Fischbauer, U. Indirect reciprocity and strategic reputation building in an experimental helping game. Games Econ. Behav. 2009, 67, 399–407. [Google Scholar] [CrossRef] [Green Version]
- Horita, Y.; Takezawa, M.; Kinjo, T.; Nakawake, Y.; Masuda, N. Transient nature of cooperation by pay-it-forward reciprocity. Sci. Rep. 2016, 6, 19471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfeiffer, T.; Rutte, C.; Killingback, T.; Taborsky, M.; Bonhoeffer, S. Evolution of cooperation by generalized reciprocity. Pract. R. Soc. B 2005, 272, 1115–1120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bshary, R.; Grutter, A.S. Punishment and partner switching causes cooperative behavior in a cleaning mutualism. Biol. Lett. 2005, 1, 396–399. [Google Scholar] [CrossRef]
- Nowak, M.A.; Roch, S. Upstream reciprocity and the evolution of gratitude. Pract. R. Soc. B 2007, 274, 605–609. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity by image scoring. Nature 1998, 393, 573–577. [Google Scholar] [CrossRef]
- Milinski, M.; Semmann, D.; Krambeck, H.J. Reputation helps solve the ‘tragedy of the commons’. Nature 2002, 415, 424–426. [Google Scholar] [CrossRef]
- Sommerfeld, R.D.; Krambeck, H.J.; Semmann, D.; Milinski, M. Gossip as an alternative for direct observation in games of indirect reciprocity. Proc. Natl. Acad. Sci. USA 2007, 44, 17435–17440. [Google Scholar] [CrossRef] [Green Version]
- Melis, A.P.; Semmann, D. How is human cooperation different? Philos. Tans. R. Soc. B 2010, 365, 2663–2674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rand, D.G.; Nowak, M.A. Human cooperation. Trends Cogn. Sci. 2012, 117, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. The dynamics of indirect reciprocity. J. Theor. Biol. 1998, 194, 561–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Brandt, H.; Sigmund, K. The logic of reprobation: Action and assessment rules in indirect reciprocity. J. Theor. Biol. 2004, 231, 475–486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brandt, H.; Sigmund, K. Indirect reciprocity, image scoring, and moral hazard. Proc. Natl. Acad. Sci. USA 2005, 102, 2666–2670. [Google Scholar] [CrossRef] [Green Version]
- Brandt, H.; Sigmund, K. The good, the bad and the discriminator? Errors in direct and indirect reciprocity. J. Theor. Biol. 2006, 239, 183–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ohtsuki, H.; Iwasa, Y.; Nowak, M.A. Reputation effects in public and private interactions. PLoS Comput. Biol. 2015, 11, e1004527. [Google Scholar] [CrossRef] [Green Version]
- Okada, I.; Sasaki, T.; Nakai, Y. A solution of private assessment in indirect reciprocity using solitary observation. J. Theor. Biol. 2018, 455, 7–15. [Google Scholar] [CrossRef]
- Wedekind, C.; Milinski, M. Cooperation through image scoring in humans. Science 2000, 288, 850–852. [Google Scholar] [CrossRef]
- Leimar, O.; Hammerstein, P. Evolution of cooperation through indirect reciprocity. Proc. Natl. Acad. Sci. USA 2001, 268, 745–753. [Google Scholar] [CrossRef]
- Berger, U. Learning to cooperate via indirect reciprocity. Games Econ. Behav. 2011, 72, 30–37. [Google Scholar] [CrossRef] [Green Version]
- Panchanathan, K.; Boyd, R. Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature 2004, 432, 499–502. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D.; Szolnoki, A.; Perc, M.; Szabó, G. Evolutionary establishment of moral and double moral standards through spatial interactions. PLoS Comput. Biol. 2010, 6, e1000758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hilbe, C.; Traulsen, A. Emergence of responsible sanctions without second order free riders, antisocial punishment or spite. Sci. Rep. 2012, 2, 458. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Okada, I.; Nakai, Y. Indirect reciprocity can overcome free-rider problems on costly moral assessment. Biol. Lett. 2016, 12, 20160341. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, H.; Okada, I. How to keep punishment to maintain cooperation: Introducing social vaccine. Physica A 2016, 443, 526–536. [Google Scholar] [CrossRef] [Green Version]
- Ozono, H.; Kamijo, Y.; Shimizu, K. Punishing second-order free riders before first-order free riders: The effect of pool punishment priority on cooperation. Sci. Rep. 2017, 7, 14379. [Google Scholar] [CrossRef]
- Szolnoki, A.; Perc, M. Second-order free-riding on antisocial punishment restores the effectiveness of prosocial punishment. Phys. Rev. X 2017, 7, 041027. [Google Scholar] [CrossRef] [Green Version]
- Weber, T.O.; Weisel, O.; Gächter, S. Dispositional free riders do not free ride on punishment. Nat. Commun. 2018, 9, 2390. [Google Scholar] [CrossRef]
- Roberts, G. Partner choice drives the evolution of cooperation via indirect reciprocity. PLoS ONE 2015, 10, e0129442. [Google Scholar] [CrossRef]
- Sasaki, T.; Okada, I.; Nakai, Y. The evolution of conditional moral assessment in indirect reciprocity. Sci. Rep. 2017, 7, 41870. [Google Scholar] [CrossRef] [PubMed]
- Okada, I.; Yamamoto, H.; Uchida, S. Hybrid assessment scheme based on the stern-Judging rule for maintaining cooperation under indirect reciprocity. Games 2020, 11, 13. [Google Scholar] [CrossRef] [Green Version]
- Lotem, A.; Fishman, M.A.; Stone, L. Evolution of cooperation between individuals. Nature 1999, 400, 226–227. [Google Scholar] [CrossRef] [PubMed]
- Panchanathan, K.; Boyd, R. A tale of two defectors: The importance of standing for evolution of indirect reciprocity. J. Theor. Biol. 2003, 224, 115–126. [Google Scholar] [CrossRef]
- Tanabe, S.; Suzuki, H.; Masuda, N. Indirect Reciprocity With Trinary Reputations. J. Theor. Biol. 2013, 317, 338–347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berger, U.; Grune, A. On the stability of cooperation under indirect reciprocity with first-order information. Games Econ. Behav. 2016, 98, 19–33. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, S.; Akiyama, E. Evolution of indirect reciprocity in groups of various sizes and comparison with direct reciprocity. J. Theor. Biol. 2007, 245, 539–552. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y. How should we define goodness? reputation dynamics in indirect reciprocity. J. Theor. Biol. 2004, 231, 107–120. [Google Scholar] [CrossRef]
- Santos, F.P.; Santos, F.C.; Pacheco, J.M. Social norm complexity and past reputations in the evolution of cooperation. Nature 2018, 555, 242–245. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y. The leading eight: Social norms that can maintain cooperation by indirect reciprocity. J. Theor. Biol. 2006, 239, 435–444. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y. Global analyses of evolutionary dynamics and exhaustive search for social norms that maintain cooperation by reputation. J. Theor. Biol. 2007, 244, 518–531. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Kimura, H. Indirect reciprocity is sensitive to costs of information transfer. Sci. Rep. 2013, 3, 1435. [Google Scholar] [CrossRef] [Green Version]
- Okada, I.; Sasaki, T.; Nakai, Y. Tolerant indirect reciprocity can boost social welfare through solidarity with unconditional cooperators in private monitoring. Sci. Rep. 2017, 7, 9737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swakman, V.; Molleman, L.; Ule, A.; Egas, M. Reputation-based cooperation: Empirical evidence for behavioral strategies. Evol. Hum. Behav. 2016, 37, 230–235. [Google Scholar] [CrossRef]
- Okada, I.; Yamamoto, H.; Sato, Y.; Uchida, S.; Sasaki, T. Experimental evidence of selective inattention in reputation-based cooperation. Sci. Rep. 2018, 8, 14813. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H.; Ohtsuki, H.; Ohtsubo, Y. The price of being seen to be just: An intention signalling strategy for indirect reciprocity. Proc. R. Soc. B 2016, 283, 20160694. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chalub, F.; Santos, F.C.; Pacheco, J.M. The evolution of norms. J. Theor. Biol. 2006, 241, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Sugden, R. The Economics of Rights, Cooperation and Welfare; Basil Blackwell: Oxford, UK, 1986. [Google Scholar]
- Panchanathan, K. Two wrongs don’t make a right: The initial viability of different assessment rules in the evolution of indirect reciprocity. J. Theor. Biol. 2011, 277, 48–54. [Google Scholar] [CrossRef]
- Watanabe, T.; Takezawa, M.; Nakawake, Y.; Kunimatsu, A.; Yamasue, H.; Nakamura, M.; Miyashita, Y.; Masuda, N. Two distinct neural mechanisms underlying indirect reciprocity. Proc. Natl. Acad. Sci. USA 2014, 111, 3990–3995. [Google Scholar] [CrossRef] [Green Version]
- Uchida, S.; Sigmund, K. The competition of assessment rules for indirect reciprocity. J. Theor. Biol. 2010, 263, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Seinen, I.; Schram, A. Social status and group norms: Indirect reciprocity in a repeated helping experiment. Eur. Econ. Rev. 2006, 50, 581–602. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Santos, F.C.; Chalub, F.A.C.C. Stern-judging: A simple, successful norm which promotes cooperation under indirect reciprocity. PLoS Comput. Biol. 2006, 2, 1634–1638. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.P.; Pacheco, J.M.; Santos, F.C. Evolution of cooperation under indirect reciprocity and arbitrary exploration rates. Sci. Rep. 2016, 6, 37517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inaba, M.; Takahashi, N. Linkage Based on the Kandori Norm Successfully Sustains Cooperation in Social Dilemmas. Games 2019, 10, 10. [Google Scholar] [CrossRef] [Green Version]
- Kandori, M. Social norms and community enforcement. Rev. Econ. Stud. 1992, 59, 63–80. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, N.; Mashima, R. The importance of subjectivity in perceptual errors on the emergence of indirect reciprocity. J. Theor. Biol. 2006, 243, 418–436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uchida, S. Effect of private information on indirect reciprocity. Phy. Rev. E 2010, 82, 036111. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. Moral assessment in indirect reciprocity. J. Theor. Biol. 2012, 299, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Vaquero, L.A.; Cuesta, J.A. Evolutionary stability and resistance to cheating in an indirect reciprocity model based on reputation. Phys. Rev. E 2013, 87, 052810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uchida, S.; Sasaki, T. Effect of assessment error and private information on stern-judging in indirect reciprocity. Chaos Solitons Fract. 2013, 56, 175–180. [Google Scholar] [CrossRef] [Green Version]
- Olejarz, J.; Ghang, W.; Nowak, M.A. Indirect reciprocity with optional interactions and private information. Games 2015, 6, 438–457. [Google Scholar] [CrossRef] [Green Version]
- Hilbe, C.; Schmid, L.; Tkadlec, J.; Chatterjee, K.; Nowak, M.A. Indirect reciprocity with private, noisy, and incomplete information. Proc. Natl. Acad. Sci. USA 2018, 115, 12241–12246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, D.; Fudenberg, D.; Wolitzky, A. Indirect reciprocity with simple records. Proc. Natl. Acad. Sci. USA 2020. [Google Scholar] [CrossRef] [PubMed]
- Okada, I. Computational social science on adaptive norms in social dilemmas: Integrating theory, experiments, and simulations. Socio-Informatics 2019, 8, 19–33. [Google Scholar]
- Okada, I. Two ways to overcome the three social dilemmas of indirect reciprocity. in review.
- McNamara, J.M.; Doodson, P. Reputation can enhance or suppress cooperation through positive feedback. Nat. Commun. 2015, 6, 6134. [Google Scholar] [CrossRef] [Green Version]
- Whitaker, R.M.; Colombo, G.B.; Allen, S.M.; Dunbar, R.I. A dominant social comparison heuristic unites alternative mechanisms for the evolution of indirect reciprocity. Sci. Rep. 2016, 6, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, H.; Okada, I.; Uchida, S.; Sasaki, T. A norm knockout method on indirect reciprocity to reveal indispensable norms. Sci. Rep. 2017, 7, 44146. [Google Scholar] [CrossRef] [Green Version]
- Uchida, S.; Yamamoto, H.; Okada, I.; Sasaki, T. A theoretical approach to norm ecosystems: Two adaptive architectures of indirect reciprocity show different paths to the evolution of cooperation. Front. Phys. 2018, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Gaudeul, A.; Keser, C.; Muller, S. The Evolution of Morals under Indirect Reciprocity; Center for European, Governance and Economic Development Research: Wilhelmsplatz, Germany, 2019; p. 370. [Google Scholar]
- Boyd, R.; Richerson, P. Punishment allows the evolution of cooperation (or anything else) in sizable groups. Ethol. Sociobiol. 1992, 13, 171–195. [Google Scholar] [CrossRef]
- Rockenbach, B.; Milinski, M. The efficient interaction of indirect reciprocity and costly punishment. Nature 2006, 444, 718–723. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y.; Nowak, M.A. Indirect reciprocity provides only a narrow margin of efficiency for costly punishment. Nature 2009, 457, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E.; Gächter, S. Cooperation and punishment in public goods experiments. Am. Econ. Rev. 2000, 90, 980–994. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, T.; Brännström, Å.; Dieckmann, U.; Sigmund, K. The take-it-or-leave-it option allows small penalties to overcome social dilemmas. Proc. Natl. Acad. Sci. USA 2012, 109, 1165–1169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasaki, T.; Okada, I.; Uchida, S.; Chen, X. Commitment to cooperation and peer punishment: Its evolution. Games 2015, 6, 574–587. [Google Scholar] [CrossRef] [Green Version]
- Diekmann, A.; Przepiorka, W. Punitive preferences, monetary incentives and tacit coordination in the punishment of defectors promote cooperation in humans. Sci. Rep. 2015, 5, 10321. [Google Scholar] [CrossRef] [Green Version]
- Grimalda, G.; Pondorfer, A.; Tracer, D.P. Social image concerns promote cooperation more than altruistic punishment. Nat. Commun. 2016, 7, 12288. [Google Scholar] [CrossRef] [Green Version]
- Sigmund, K.; De Silva, H.; Traulsen, A.; Hauert, C. Social learning promotes institutions for governing the commons. Nature 2010, 466, 861–863. [Google Scholar] [CrossRef] [Green Version]
- Szolnoki, A.; Szabó, G.; Perc, M. Phase diagrams for the spatial public goods game with pool punishment. Phys. Rev. E 2011, 83, 036101. [Google Scholar] [CrossRef] [Green Version]
- Perc, M. Sustainable institutionalized punishment requires elimination of second-order free-riders. Sci. Rep. 2012, 2, 344. [Google Scholar] [CrossRef] [Green Version]
- Traulsen, A.; Röhl, T.; Milinski, M. An economic experiment reveals that humans prefer pool punishment to maintain the commons. Proc. Natl. Acad. Sci. USA 2012, 279, 3716–3721. [Google Scholar] [CrossRef] [Green Version]
- Schoenmakers, S.; Hilbe, C.; Blasius, B.; Traulsen, A. Sanctions as honest signals?the evolution of pool punishment by public sanctioning institutions. J. Theor. Biol. 2014, 356, 36–46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hilbe, C.; Traulsen, A.; Röhl, T.; Milinski, M. Democratic decisions establish stable authorities that overcome the paradox of second-order punishment. Proc. Natl. Acad. Sci. USA 2014, 111, 752–756. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasaki, T.; Uchida, S.; Chen, X. Voluntary rewards mediate the evolution of pool punishment for maintaining public goods in large populations. Sci. Rep. 2015, 5, 8917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balliet, D.; Mulder, L.B.; Van Lange, P.A.M. Reward, punishment, and cooperation: A meta-analysis. Psychol. Bull. 2011, 137, 594–615. [Google Scholar] [CrossRef] [PubMed]
- Andreoni, J.; Harbaugh, W.; Versterlund, L. The carrot or the stick; Rewards, punishments, and cooperation. Am. Econ. Rev. 2003, 93, 893–902. [Google Scholar] [CrossRef] [Green Version]
- Kendal, J.; Feldman, M.W.; Aoki, K. Cultural coevolution of norm adoption and enforcement when punishers are rewarded or non-punishers are punished. Theor. Popul. Biol. 2006, 70, 10–25. [Google Scholar] [CrossRef] [PubMed]
- Sefton, M.; Shupp, R.; Walker, J.M. The effect of rewards and sanctions in provision of public goods. Econ. Inq. 2007, 45, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Sutter, M.; Haigner, S.; Kocher, M.G. Choosing the carrot or the stick? Endogenous institutional choice in social dilemma situations. Rev. Econ. Stud. 2010, 77, 1540–1566. [Google Scholar] [CrossRef] [Green Version]
- Hilbe, C.; Sigmund, K. Incentives and opportunism: From the carrot to the stick. Pract. R. Soc. B 2010, 277, 2427–2433. [Google Scholar] [CrossRef] [Green Version]
- Okada, I.; Yamamoto, H.; Toriumi, F.; Sasaki, T. The effect of incentives and meta-incentives on the evolution of cooperation. PLoS Comput. Biol. 2015, 11, e1004232. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, B.; Thoni, C.; Gächter, S. Antisocial Punishment Across Societies. Science 2008, 319, 1362–1367. [Google Scholar] [CrossRef] [PubMed]
- Rand, D.G.; Nowak, M.A. The evolution of anti-social punishment in optional public goods games. Nat. Commun. 2011, 2, 434. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, M.; Peña, J. Antisocial rewarding in structured populations. Sci. Rep. 2017, 7, 6212. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Jusup, M.; Wang, Z.; Li, H.; Shi, L.; Podobnik, B.; Stanley, H.E.; Havlin, S.; Boccaletti, S. Punishment diminishes the benefits of network reciprocity in social dilemma experiments. Proc. Natl. Acad. Sci. USA 2018, 115, 30–35. [Google Scholar] [CrossRef] [Green Version]
- Fehr, E.; Gächter, S. Altruistic punishment in humans. Nature 2002, 415, 137–140. [Google Scholar] [CrossRef]
- Gürerk, Ö.; Irlenbusch, B.; Rockenbach, B. The competitive advantage of sanctioning institutions. Science 2006, 312, 108–111. [Google Scholar] [CrossRef] [Green Version]
- Dreber, A.; Rand, D.G.; Fudenberg, D.; Nowak, M.A. Winners don’t punish. Nature 2008, 452, 348–351. [Google Scholar] [CrossRef]
- Egas, M.; Riedl, A. The economics of altruistic punishment and the maintenance of cooperation. Proc. R. Soc. B 2008, 275, 871–878. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.J.; Zhang, B.Y.; Zhou, Z.X.; He, Q.Q.; Zheng, X.D.; Cressman, R.; Tao, Y. Costly punishment does not always increase cooperation. Proc. Natl. Acad. Sci. USA 2009, 106, 17448–17451. [Google Scholar] [CrossRef] [Green Version]
- Milinski, M.; Rockenback, B. On the interaction of the stick and the carrot in social dilemmas. J. Theor. Biol. 2012, 299, 139–143. [Google Scholar] [CrossRef]
- Jordan, J.J.; Hoffman, M.; Bloom, P.; Rand, D.G. Third-party punishment as a costly signal of trustworthiness. Nature 2016, 530, 473–476. [Google Scholar] [CrossRef] [PubMed]
- Henrich, J.; Boyd, R. Why people punish defectors? Weak conformist transmission can stabilize costly enforcement of norms in cooperative dilemmas. J. Theor. Biol. 2001, 208, 79–89. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Uchida, S. The evolution of cooperation by social exclusion. Proc. R. Soc. B 2013, 280, 20122498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giardini, F.; Vilone, D. Evolution of gossip-based indirect reciprocity on a bipartite network. Sci. Rep. 2016, 6, 37931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, H.N.; Perc, M.; Szolnoki, A.; Helbing, D. Stability of cooperation under image scoring in group interactions. Sci. Rep. 2015, 5, 12145. [Google Scholar]
- Ghang, W.; Nowak, M.A. Indirect reciprocity with optional interactions. J. Theor. Biol. 2015, 365, 1–11. [Google Scholar] [CrossRef]
- Sasaki, T.; Yamamoto, H.; Okada, I.; Uchida, S. The evolution of reputation-based cooperation in regular networks. Games 2017, 8, 8. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Liu, S.; Bai, Y. Reputation-based co-evolutionary model promotes cooperation in prisoner’s dilemma game. Phys. Lett. A 2020, 384, 126233. [Google Scholar] [CrossRef]
- Sethi, R.; Somanathan, E. The evolution of social norms in common property resource use. Am. Econ. Rev. 1996, 86, 766–788. [Google Scholar]
- Masuda, N.; Ohtsuki, H. Tag-based indirect reciprocity by incomplete social information. Proc. R. Soc. B 2007, 274, 689–695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suzuki, S.; Akiyama, E. Three-person game facilitates indirect reciprocity under image scoring. J. Theor. Biol. 2007, 249, 93–100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fishman, M.A. Indirect reciprocity among imperfect. individuals. J. Theor. Biol. 2003, 225, 285–292. [Google Scholar] [CrossRef]
- Pollock, G.B.; Dugatkin, L.A. Reciprocity and the evolution of reputation. J. Theor. Biol. 1992, 159, 25–37. [Google Scholar] [CrossRef]
- Dufwenberg, M.; Gneezy, U.; Güth, W.; van Damme, E. Direct vs. indirect reciprocation: An experiment. Homo Oeconomicus 2001, 18, 19–30. [Google Scholar]
- Roberts, G. Evoluation of direct and indirect reciprocity. Pract. R. Soc. B 2008, 275, 173–179. [Google Scholar] [CrossRef] [Green Version]
- Milinski, M.; Semmann, D.; Bakker, T.C.M.; Krambeck, H.J. Cooperation through indirect reciprocity: Image scoring or standing strategy? Pract. R. Soc. B 2001, 268, 2495–2501. [Google Scholar] [CrossRef]
- Nava, E.; Croci, E.; Turati, C. ‘I see you sharing, thus I share with you’: Indirect reciprocity in toddlers but not infants. Palgrave Commun. 2019, 5, 66. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Ma, J.; Luan, Z.; Dubas, J.S.; Xi, J. Adolescent indirect reciprocity: Evidence from incentivized economic paradigms. J. Adolesc. 2019, 74, 221–228. [Google Scholar] [CrossRef]
- Khadjavi, M. Indirect reciprocity and charitable giving? Evidence from a field experiment. Manag. Sci. 2016, 63, 3708–3717. [Google Scholar] [CrossRef]
- Mujcic, R.; Leibbrandt, A. Indirect reciprocity and prosocial behaviour: Evidence from a natural field experiment. Econ. J. 2017, 128, 1683–1699. [Google Scholar] [CrossRef]
- Yoeli, E.; Hoffman, M.; Rand, D.G.; Nowak, M.A. Powering up with indirect reciprocity in a large-scale field experiment. Proc. Natl. Acad. Sci. USA 2013, 110, 10424–10429. [Google Scholar] [CrossRef] [Green Version]
- van Apeldoorn, J.; Schram, A. Indirect reciprocity; a field experiment. PLoS ONE 2016, 11, e0152076. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, G. Competitive altruism: From reciprocity to the handicap principle. Proc. R. Soc. Lond. B 1998, 265, 427–431. [Google Scholar] [CrossRef] [Green Version]
- Gintis, H.; Smith, E.A.; Bowles, S. Costly signaling and cooperation. J. Theor. Biol. 2001, 213, 103–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uchida, S.; Yamamoto, H.; Okada, I.; Sasaki, T. Evolution of cooperation with peer punishment under prospect theory. Games 2019, 10, 11. [Google Scholar] [CrossRef] [Green Version]
- Sylwester, K.; Roberts, G. Reputation-based partner choice is an effective alternative to indirect reciprocity in solving social dilemmas. Evol. Hum. Behav. 2013, 34, 201–206. [Google Scholar] [CrossRef]
- Masuda, N. In-group favouritism and intergroup cooperation under indirect reciprocity based on group reputation. J. Theor. Biol. 2012, 311, 8–18. [Google Scholar] [CrossRef] [Green Version]
- Nakai, Y.; Muto, M. Evolutionary simulation of peace with altruistic strategy for selected friends. J. Socio-Inf. Stud. 2005, 9, 59–71. [Google Scholar]
- Nakai, Y.; Muto, M. Emergence and collapse of peace with friend selection strategies. J. Artif. Soc. Simul. 2008, 11, 6. [Google Scholar]
- Bedewi, W.; Whitaker, R.M.; Colombo, G.B.; Allen, S.M.; Dunham, Y. The implications of shared identity on indirect reciprocity. J. Inform. Telecommun. 2020, 1741858. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.L.; Li, M.C.; Wang, Z. Cooperation enhanced by indirect reciprocity in spatial prisoner’s dilemma games for social P2P systems. Physica A 2016, 462, 1252–1260. [Google Scholar] [CrossRef]
- Toriumi, F.; Yamamoto, H.; Okada, I. A belief in rewards accelerates cooperation on consumer-generated media. J. Comput. Soc. Sci. 2020, 3, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Szolnoki, A.; Perc, M. If players are sparse social dilemmas are too: Importance of percolation for evolution of cooperation. Sci. Rep. 2012, 2, 369. [Google Scholar] [CrossRef]
- Jia, M.; Xiang, Y.; Zhang, Z. Indirect reciprocity and corporate philanthropic giving: How visiting officials influence investment in privately owned chinese firms. J. Manag. Stud. 2019, 56, 372–407. [Google Scholar] [CrossRef]
- Nordin, A. Indirect reciprocity and reputation management in religious morality relating to concepts of supernatural agents. J. Cogn. Sci. Relig. 2015, 3, 125–153. [Google Scholar] [CrossRef]
| 1. | “Norm” has often been used in theoretical studies of indirect reciprocity. In psychology and sociology, it means shared societal rules. In the studies of the evolution of cooperation, it means assessment rules for determining reputation and action rules for selecting cooperative behaviors. |
| 2. | |
| 3. | Of the leading eight norms, two (simple-standing and stern-judging) use up to second-order information and the other six use up to third-order information. Of the first two, only the stern-judging norm breaks cooperative regimes in a private assessment scheme. |
| 4. | This is because the definition of the conjunctive probability of v players whose images of a specified player are the same needs the conjunctive probability of players. Therefore, the definition of the conjunctive probability of two players whose images of a specified player are the same requires an infinite system of simultaneous equations when the number of game observers is infinite. |
| 5. | In this paper, we use the terms ’first-order’ and ’second-order’ in two different contexts: ’Free riders’ and ’information used for rules assessment’. First-order free riders are players who do not cooperate while second-order free riders are players who do not punish first-order free riders. First-order information refers to donor action while second-order information refers to recipient reputation. |




© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okada, I. A Review of Theoretical Studies on Indirect Reciprocity. Games 2020, 11, 27. https://doi.org/10.3390/g11030027
Okada I. A Review of Theoretical Studies on Indirect Reciprocity. Games. 2020; 11(3):27. https://doi.org/10.3390/g11030027
Chicago/Turabian StyleOkada, Isamu. 2020. "A Review of Theoretical Studies on Indirect Reciprocity" Games 11, no. 3: 27. https://doi.org/10.3390/g11030027
APA StyleOkada, I. (2020). A Review of Theoretical Studies on Indirect Reciprocity. Games, 11(3), 27. https://doi.org/10.3390/g11030027




