Picosecond Lifetime Hot Electrons in TiO2 Nanoparticles for High Catalytic Activity
Abstract
:1. Introduction
2. Results
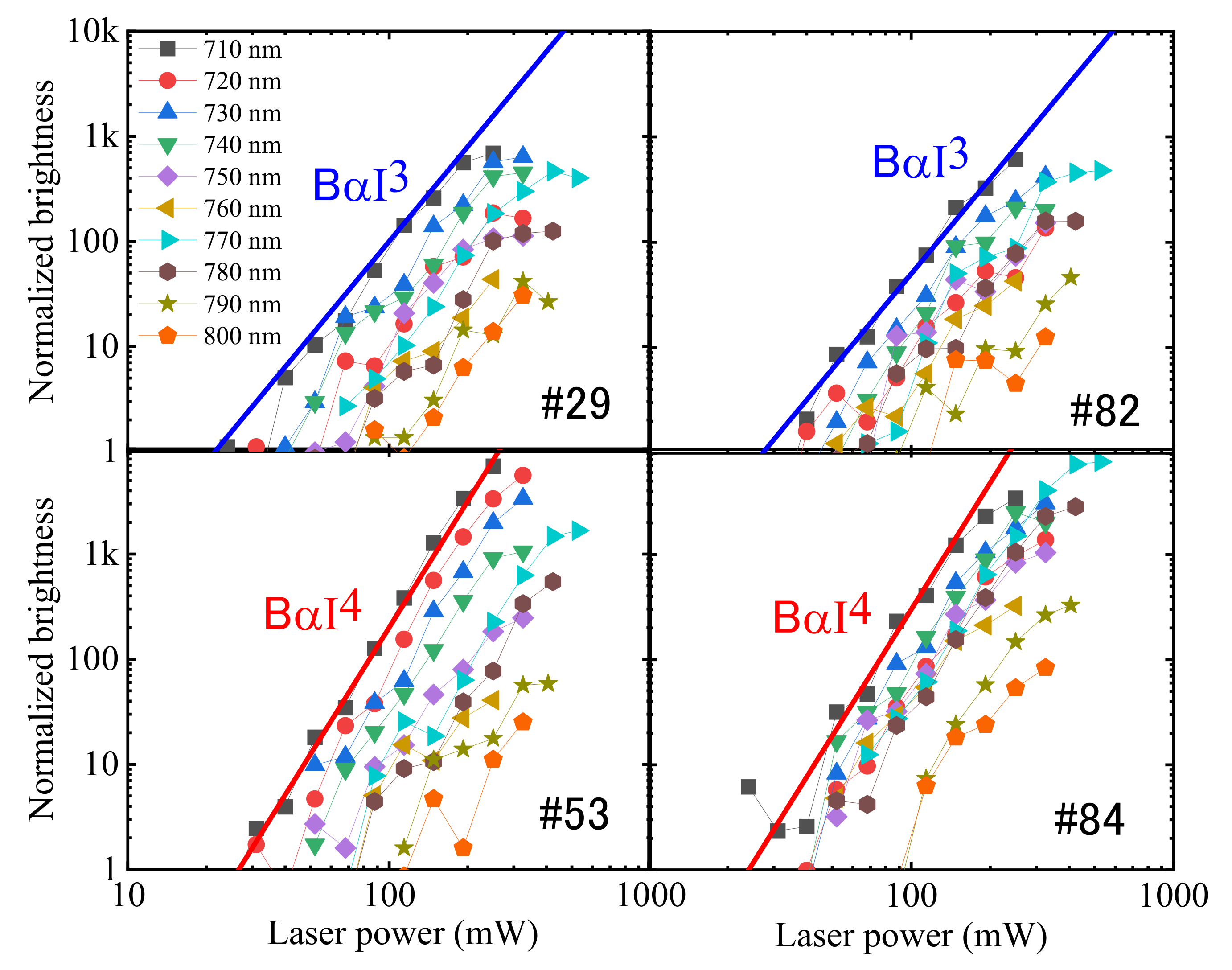
2.1. Three and Four-Photon Slopes
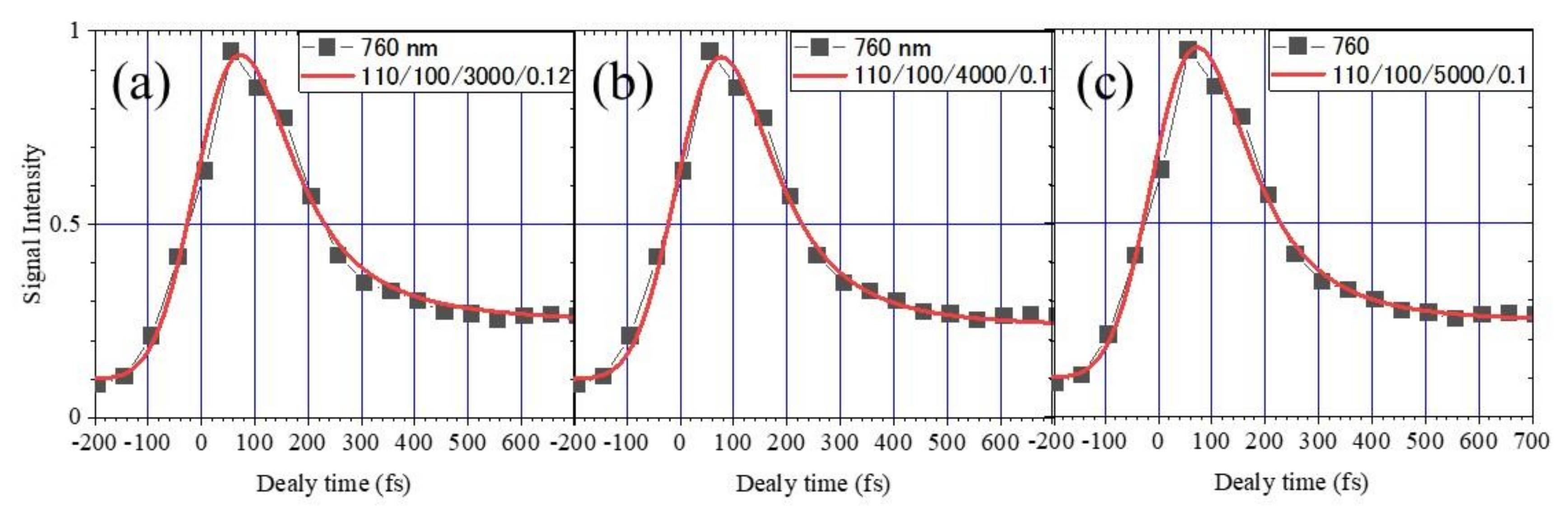
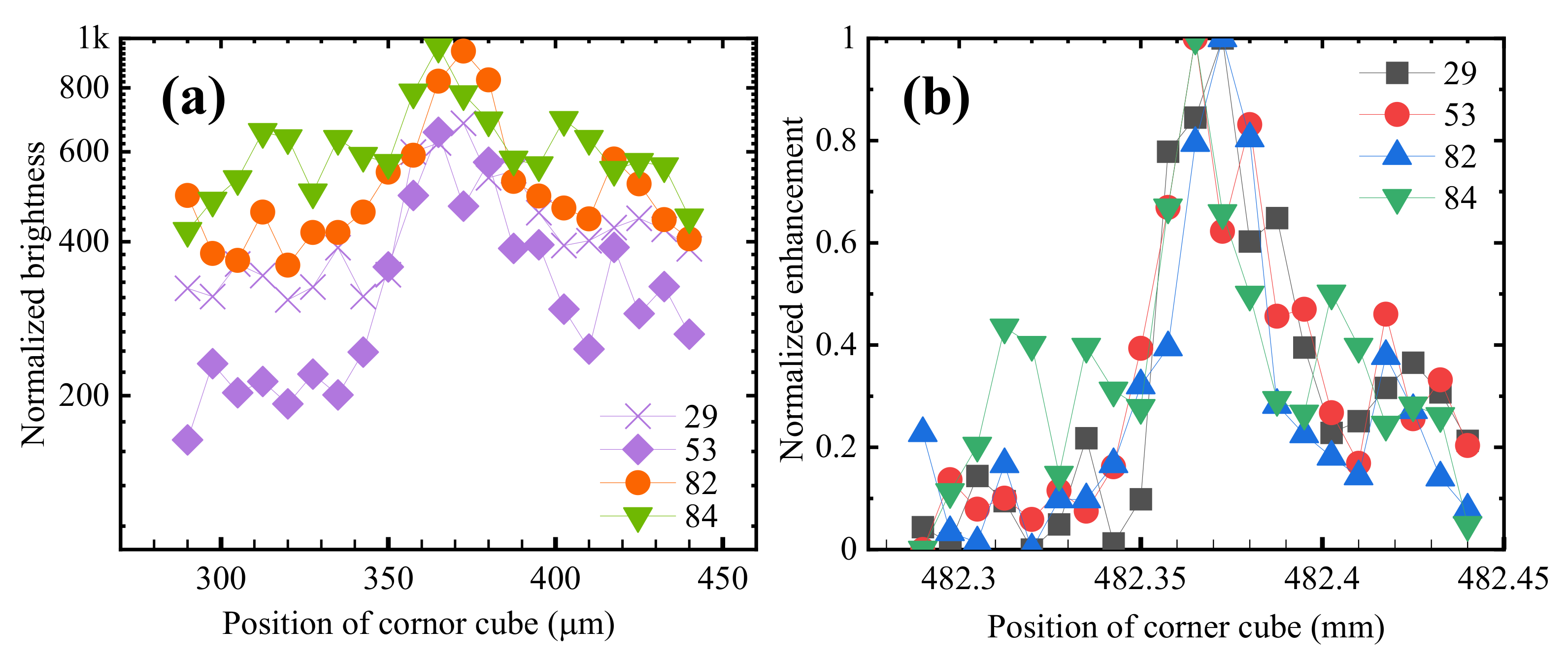
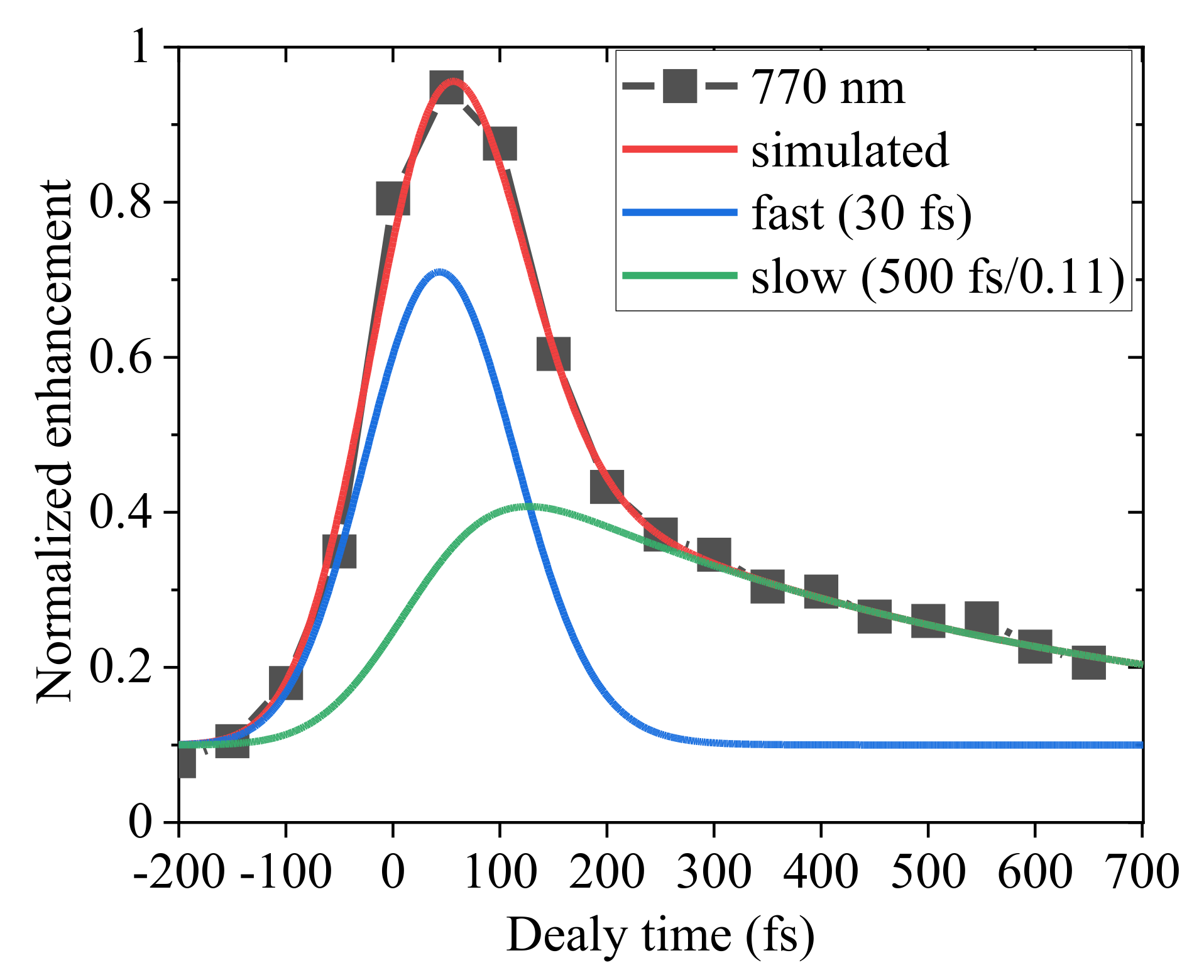
2.2. Measurement of the Electron Lifetime
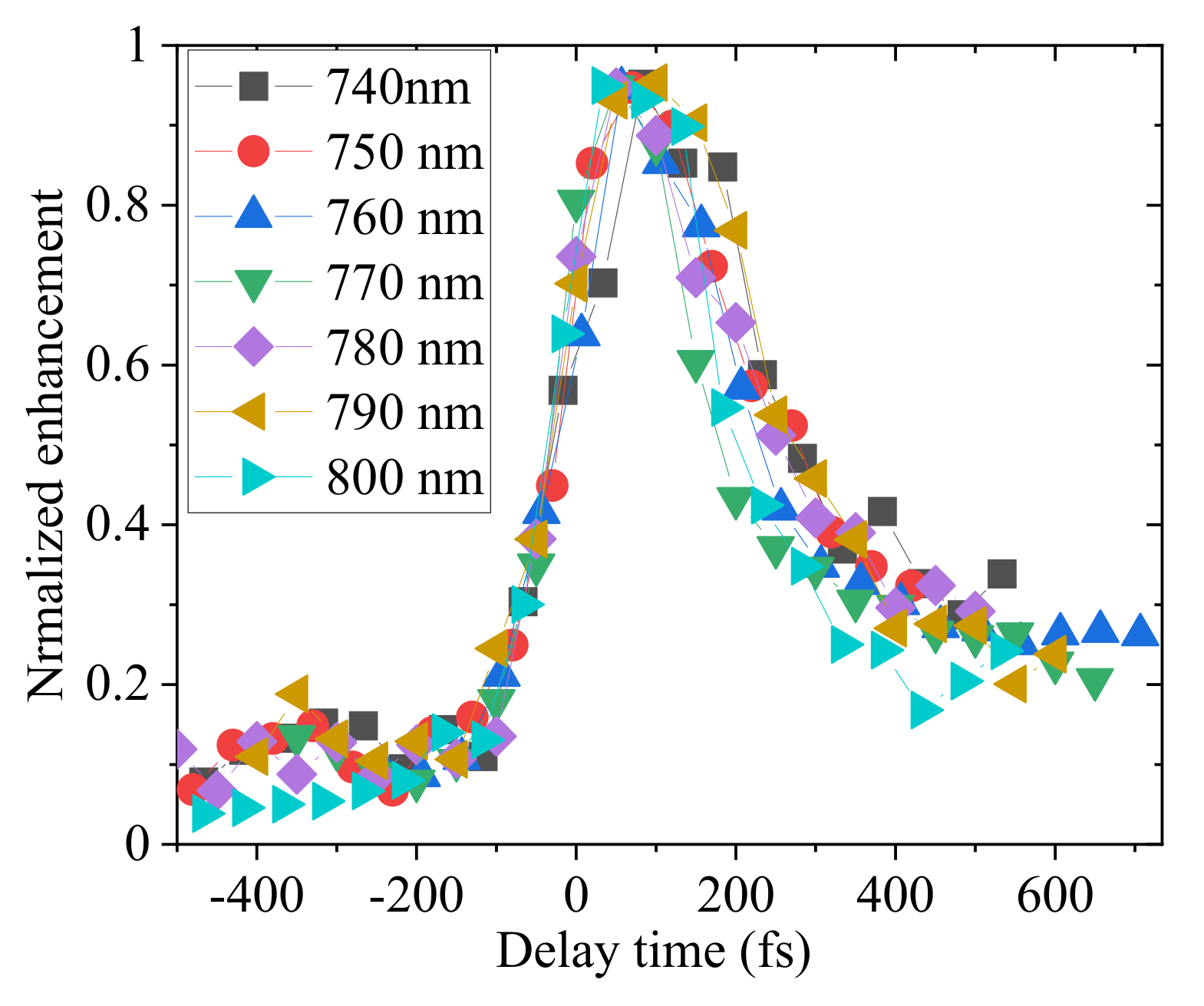
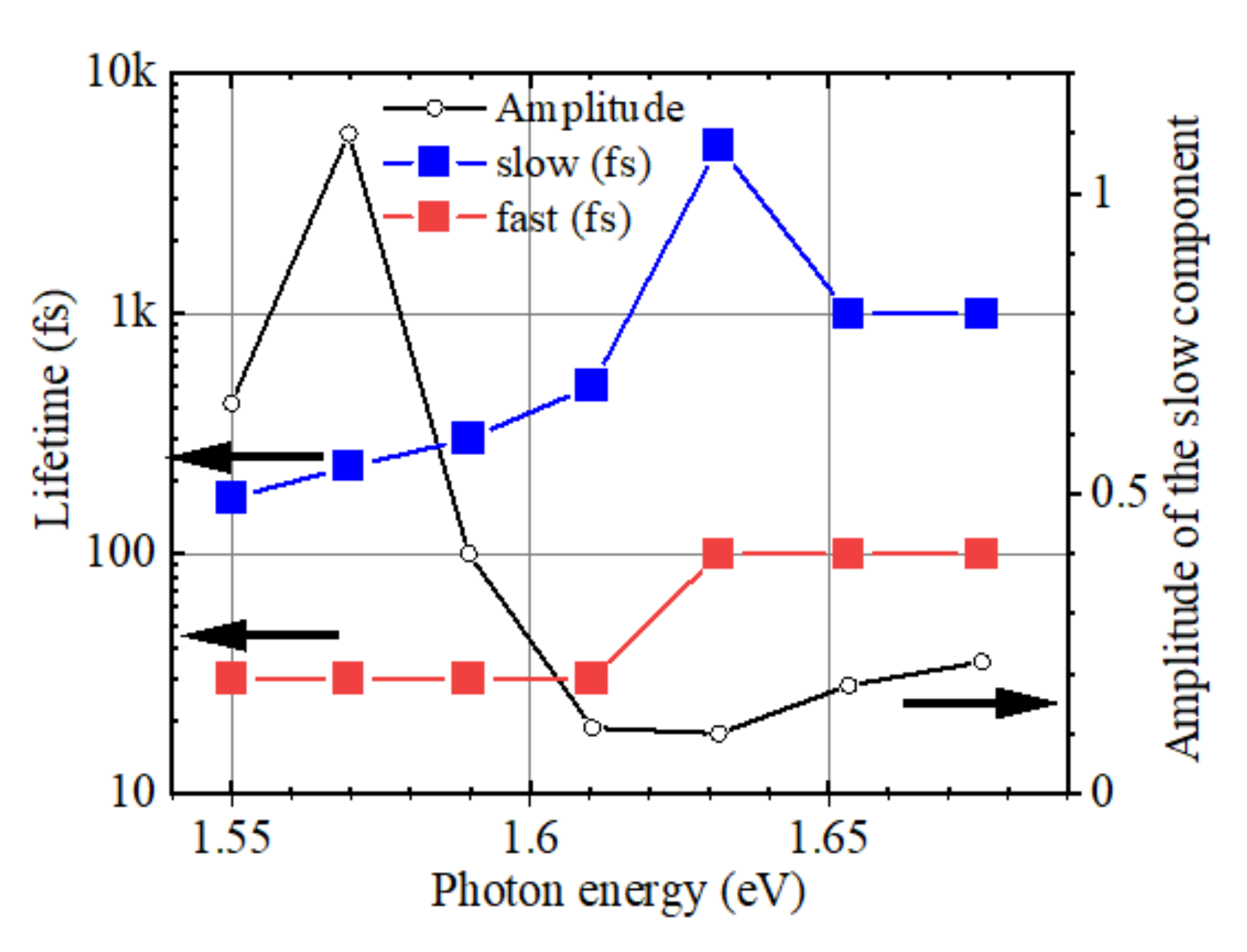
2.3. Detailed Analysis of the Delay Dependence of the Enhancement in Pump-Probe
3. Discussions
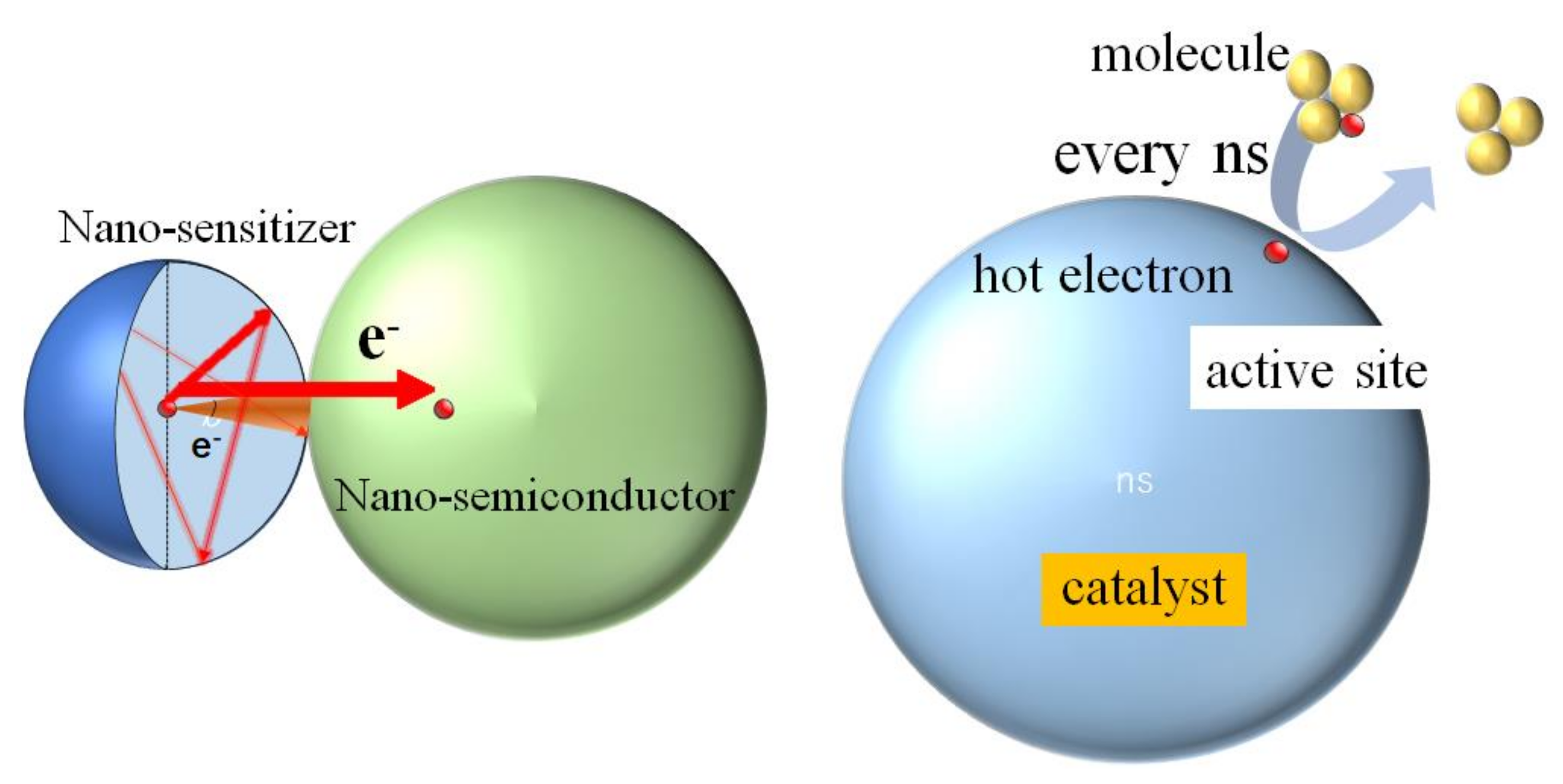
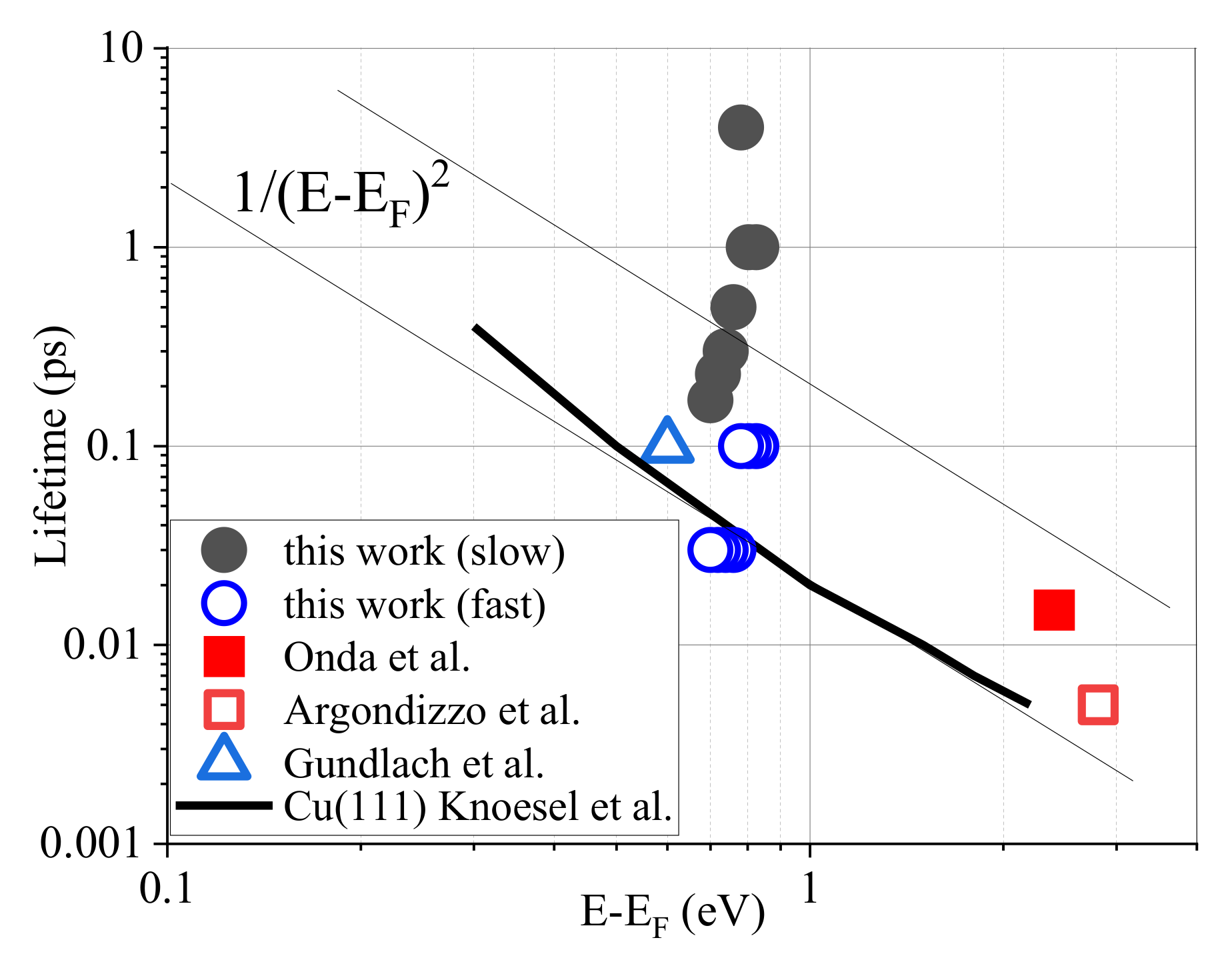
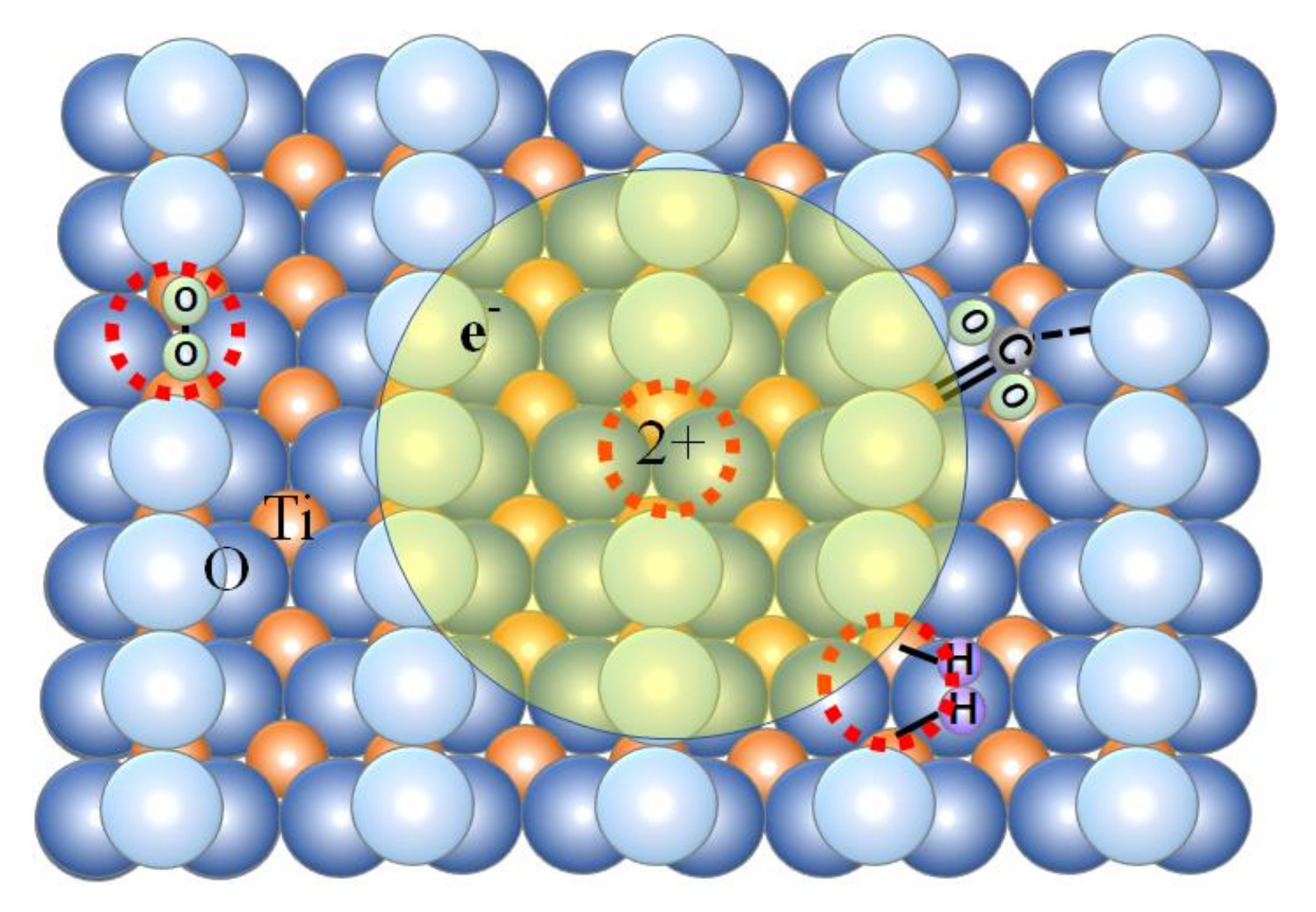
3.1. Picosecond Lifetime Hot Electrons and High Catalytic Activities
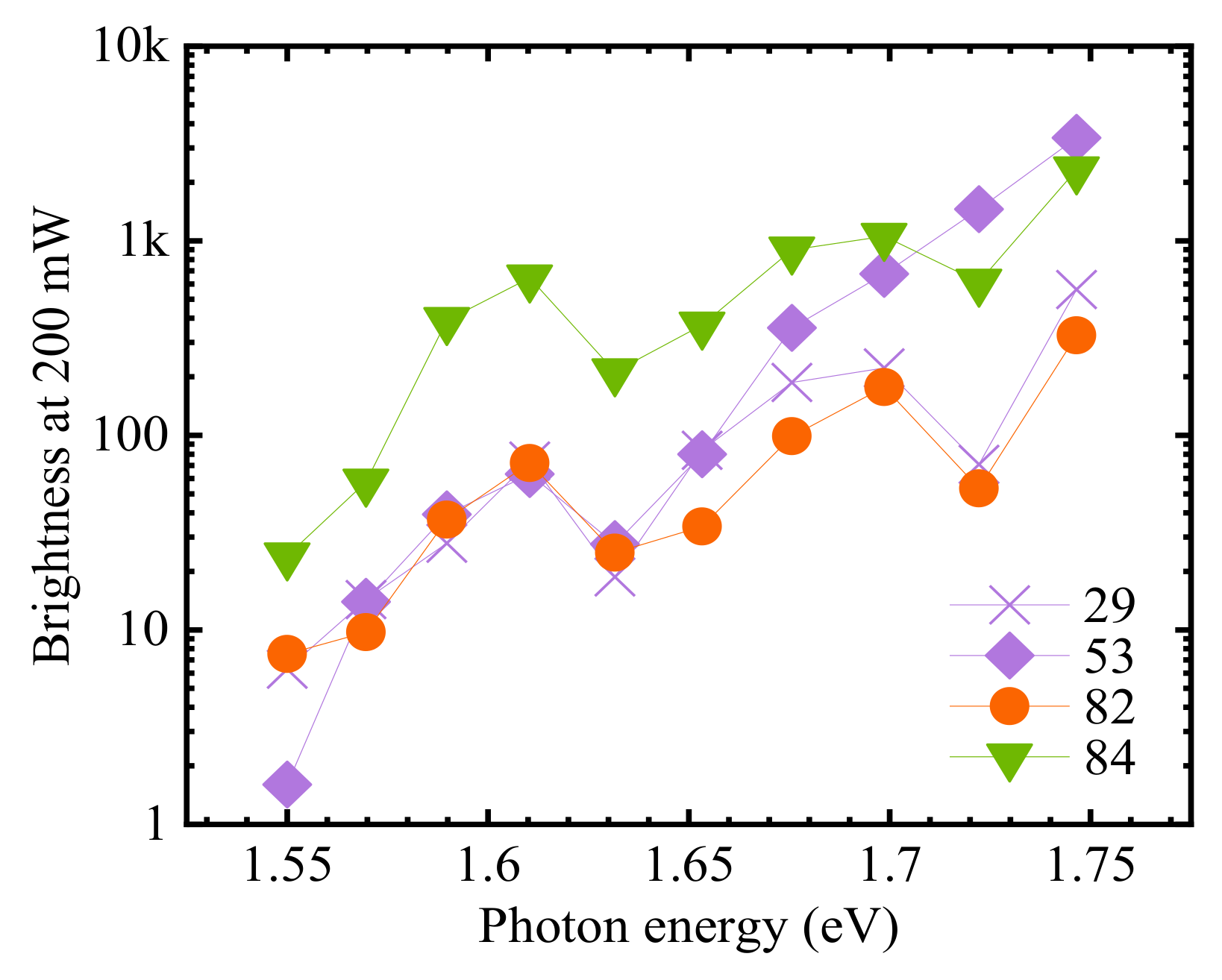
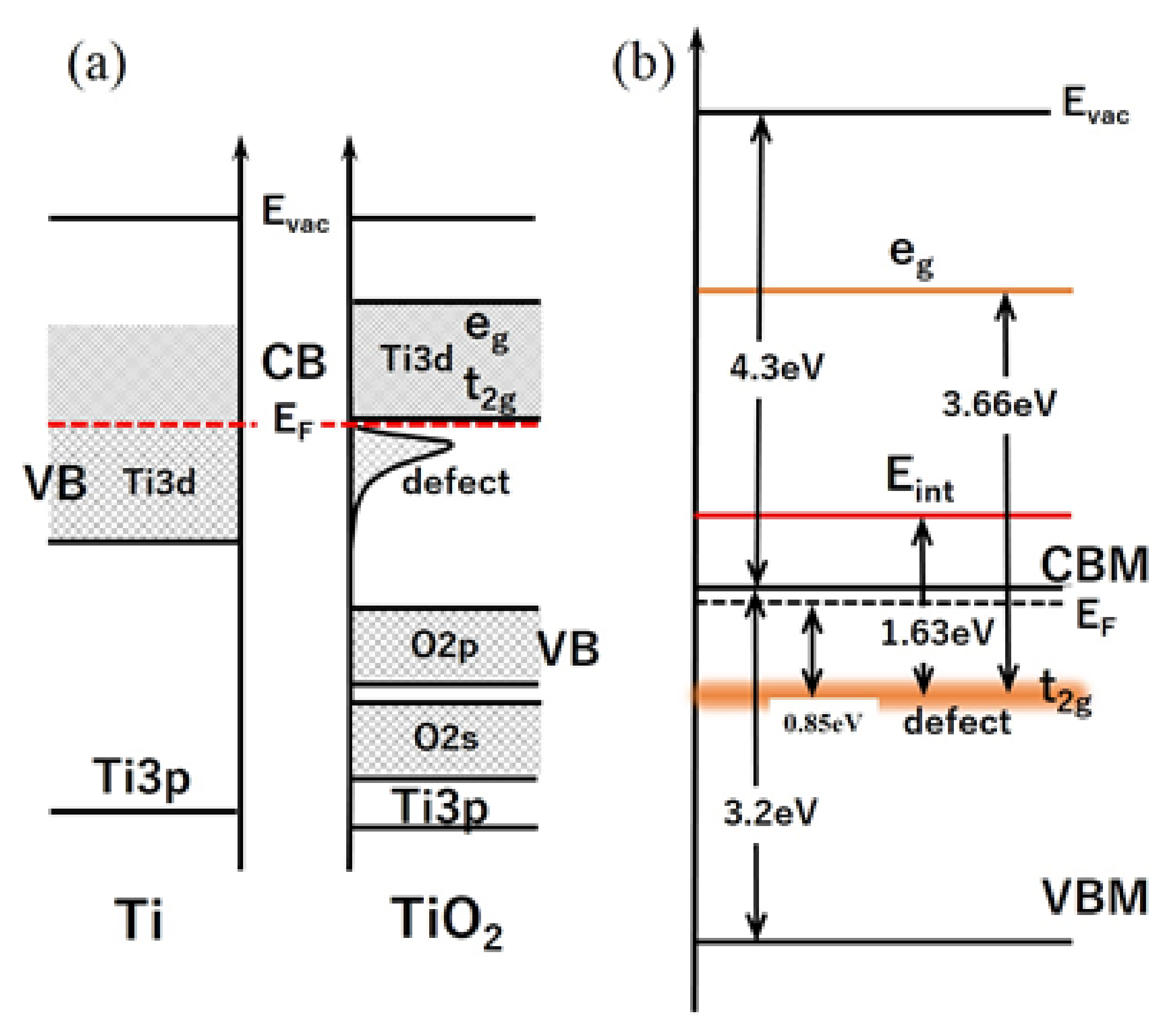
3.2. Electronic Structure
3.3. Fast and Slow Decay Components
4. Materials and Methods
5. Summary
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (1)
- Equations
- (2)
- Determination of the Laser pulse width
- (3)
- The lifetime of the fast component

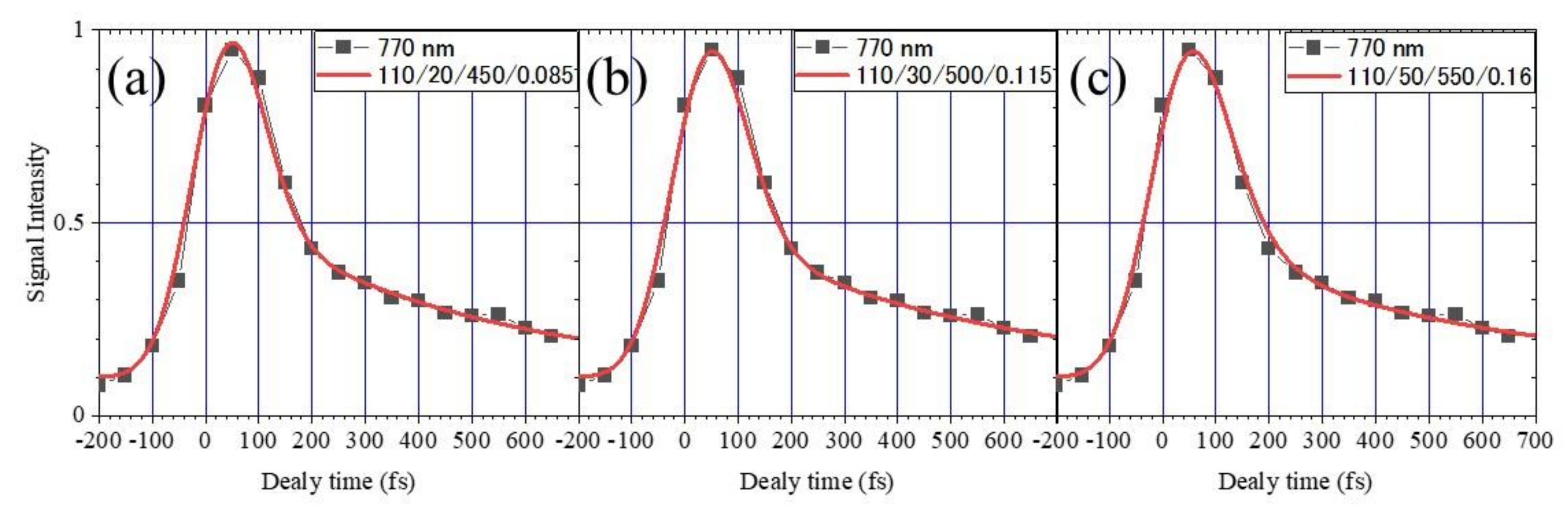
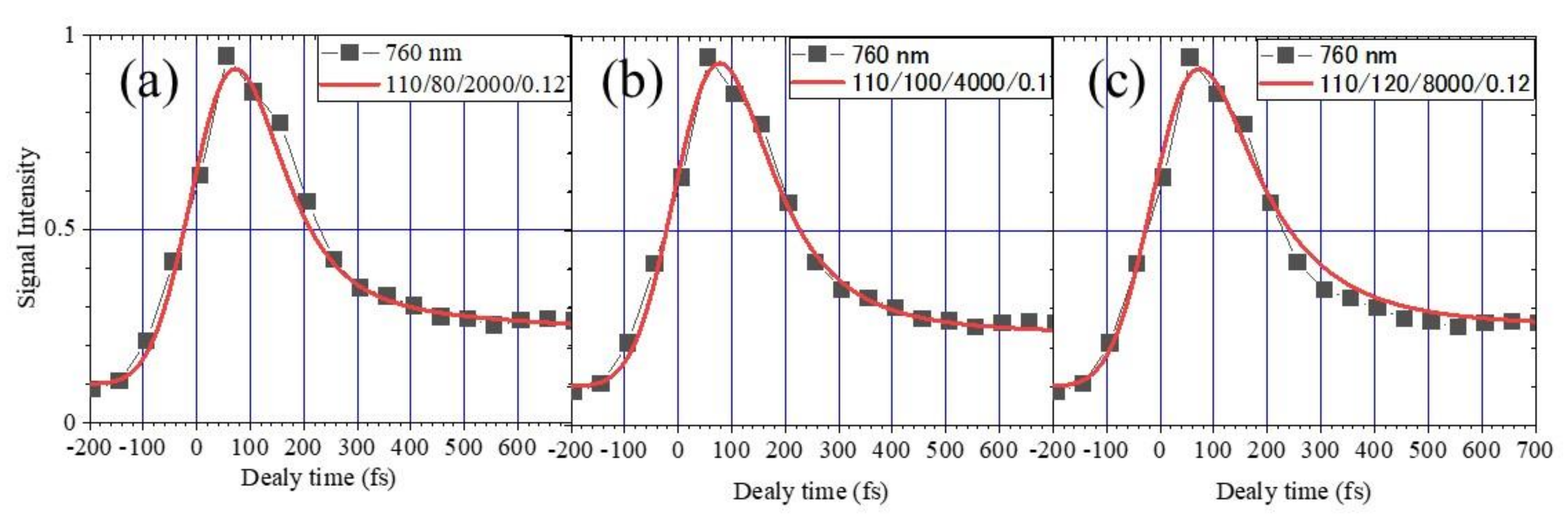
- (4)
- The lifetime of the slow component
References
- Linic, S.; Christopher, P.; Ingram, D.B. Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat. Mater. 2011, 10, 911–921. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Libisch, F.; Large, N.; Neumann, O.; Brown, L.V.; Cheng, J.; Lassiter, J.B.; Carter, E.A.; Nordlander, P.; Halas, N.J. Hot electrons do the impossible: Plasmon-induced dissociation of H2 on Au. Nano Lett. 2013, 13, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Kale, M.J.; Avanesian, T.; Christopher, P. Direct photocatalysis by plasmonic nanostructures. ACS Catal. 2014, 4, 116–128. [Google Scholar] [CrossRef]
- Wu, K.; Chen, J.; McBride, J.R.; Lian, T. Efficient hot-electron transfer by a plasmon-induced interfacial charge-transfer transition. Science 2015, 349, 632–635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; He, S.; Guo, W.; Hu, Y.; Huang, J.; Mulcahy, J.R.; Wei, W.D. Surface-plasmon-driven hot electron photochemistry. Chem. Rev. 2018, 118, 2927–2954. [Google Scholar] [CrossRef]
- Kodiyath, R.; Manikandan, M.; Lequan, L.; Ramesh, G.V.; Koyasu, S.; Miyauchi, M.; Sakuma, Y.; Tanabe, T.; Gunji, T.; Duy Thang, D.; et al. Visible-light photodecomposition of acetaldehyde by TiO2-coated gold nanocages: Plasmon-mediated hot electron transport via defect states. Chem. Commun. 2014, 50, 15553–15556. [Google Scholar] [CrossRef]
- Kazuma, E.; Jung, J.; Ueba, H.; Trenary, M.; Kim, Y. A direct pathway to molecular photodissociation on metal surfaces using visible light. J. Am. Chem. Soc. 2017, 139, 3115–3121. [Google Scholar] [CrossRef]
- Richardson, O.W. Electron emission from metals as a function of temperature. Phys. Rev. 1924, 23, 153–155. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, H.; Renzas, J.R.; Zhang, Y.; Somorjai, G.A. Probing hot electron flow generated on Pt nanoparticles with Au/TiO2 schottky diodes during catalytic CO oxidation. Nano Lett. 2008, 8, 2388–2392. [Google Scholar] [CrossRef] [Green Version]
- Akbari, A.; Berini, P. Schottky contact surface-plasmon detector integrated with an asymmetric metal stripe waveguide. Appl. Phys. Lett. 2009, 95, 021104. [Google Scholar] [CrossRef]
- Giugni, A.; Torre, B.; Toma, A.; Francardi, M.; Malerba, M.; Alabastri, A.; Proietti Zaccaria, R.; Stockman, M.I.; Di Fabrizio, E. Hot-electron nanoscopy using adiabatic compression of surface plasmons. Nat. Nanotechnol. 2013, 8, 845–852. [Google Scholar]
- Leenheer, A.J.; Narang, P.; Lewis, N.S.; Atwater, H.A. Solar energy conversion via hot electron internal photoemission in metallic nanostructures: Efficiency estimates. J. Appl. Phys. 2014, 115, 134301. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Yang, C.; Li, H.; Ji, B.; Lin, J.; Tomie, T. Thermionic emission in gold nanoparticles under femtosecond laser irradiation observed with photoemission electron microscopy. AIP Adv. 2019, 9, 025112. [Google Scholar] [CrossRef]
- Weik, F.; De Meijere, A.; Hasselbrink, E. Wavelength dependence of the photochemistry of O2 on Pd(111) and the role of hot electron cascades. J. Chem. Phys. 1993, 99, 682. [Google Scholar] [CrossRef]
- Clavero, C. Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices. Nat. Photonics 2014, 8, 95–103. [Google Scholar] [CrossRef]
- Chalabi, H.; Brongersma, M.L. Harvest season for hot electrons. Nat. Nanotechnol. 2013, 8, 229–230. [Google Scholar]
- Furube, A.; Hashimoto, S. Insight into plasmonic hot-electron transfer and plasmon molecular drive: New dimensions in energy conversion and nanofabrication. NPG Asia Mater. 2017, 9, e454. [Google Scholar] [CrossRef]
- Haruta, M.; Kobayashi, T.; Sano, H.; Yamada, N. Novel gold catalysts for the oxidation of carbon monoxide at a temperature far below 0°C. Chem. Lett. 1987, 16, 405–408. [Google Scholar] [CrossRef]
- Lopez, N.; Janssens, T.V.W.; Clausen, B.S.; Xu, Y.; Mavrikakis, M.; Bligaard, T.; Nørskov, J.K. On the origin of the catalytic activity of gold nanoparticles for low-temperature CO oxidation. J. Catal. 2004, 223, 232–235. [Google Scholar] [CrossRef]
- Li, B.; Li, H.; Yang, C.; Ji, B.; Lin, J.; Tomie, T. Excited states in the conduction band and long-lifetime hot electrons in TiO2 nanoparticles observed with photoemission electron microscopy. AIP Adv. 2019, 9, 085321. [Google Scholar] [CrossRef]
- Thompson, T.L.; Yates, J.T., Jr. Surface science studies of the photoactivation of TiO2—New photochemical processes. Chem. Rev. 2006, 106, 4428–4453. [Google Scholar] [CrossRef] [PubMed]
- Henderson, M.A. A surface science perspective on TiO2 photocatalysis. Surf. Sci. Rep. 2011, 66, 185–297. [Google Scholar] [CrossRef]
- Onda, K.; Li, B.; Zhao, J.; Jordan, K.D.; Yang, J.; Petek, H. Wet electrons at the H2O/TiO2(110) surface. Science 2005, 308, 1154–1158. [Google Scholar] [CrossRef]
- Argondizzo, A.; Cui, X.; Wang, C.; Sun, H.; Shang, H.; Zhao, J.; Petek, H. Ultrafast multiphoton pump-probe photoemission excitation pathways in rutile TiO2(110). Phys. Rev. B 2015, 91, 155429. [Google Scholar] [CrossRef] [Green Version]
- Du, L.; Furube, A.; Hara, K.; Katoh, R.; Tachiya, M. Ultrafast plasmon induced electron injection mechanism in gold–TiO2 nanoparticle system. J. Photochem. Photobiol. C Photochem. Rev. 2013, 15, 21–30. [Google Scholar] [CrossRef]
- Ignatiev, I.V.; Kozin, I.E.; Nair, S.; Ren, H.; Sugou, S.; Masumoto, Y. Carrier relaxation dynamics in InP quantum dots studied by artificial control of nonradiative losses. Phys. Rev. B 2000, 61, 15633. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, D.O.; Dunnill, C.W.; Buckeridge, J.; Shevlin, S.A.; Logsdail, A.J.; Woodley, S.M.; Cartlow, C.R.A.; Powell, M.J.; Palgrave, R.G.; Parkin, I.P.; et al. Band alignment of rutile and anatase TiO2. Nat. Mater. 2013, 12, 798–801. [Google Scholar] [CrossRef]
- Toyoda, T.; Yindeesuk, W.; Okuno, T.; Akimoto, M.; Kamiyama, K.; Hayase, S.; Shen, Q. Electronic structures of two types of TiO2 electrodes: Inverse opal and nanoparticulate cases. RSC Adv. 2015, 5, 49623. [Google Scholar] [CrossRef]
- Fujisawa, J.; Eda, T.; Hanaya, M. Comparative study of conduction-band and valence-band edges of TiO2, SrTiO3, and BaTiO3 by ionization potential measurements. Chem. Phys. Lett. 2017, 685, 23–26. [Google Scholar] [CrossRef]
- Ghosh, A.M.; Wakim, F.G.; Addiss, R.R., Jr. Photoelectronic processes in rutile. Phys. Rev. 1969, 184, 979. [Google Scholar] [CrossRef]
- Yoshihara, T.; Katoh, R.; Furube, A.; Tamaki, Y. Identification of reactive species in photoexcited nanocrystalline TiO2 films by wide-wavelength-range (400–2500 nm) transient absorption spectroscopy. J. Phys. Chem. B 2004, 108, 3817–3823. [Google Scholar] [CrossRef]
- Cronemeyer, D.C. Electrical and optical properties of rutile single crystals. Phys. Rev. 1952, 87, 876. [Google Scholar] [CrossRef]
- Breckenridge, R.G.; Hosler, W.R. Electrical properties of titanium dioxide semiconductors. Phys. Rev. 1953, 91, 793. [Google Scholar] [CrossRef]
- Knoesel, E.; Hotzel, A.; Hertel, T.; Wolf, M.; Ertl, G. Dynamics of photoexcited electrons in metals studied with time-resolved two-photon photoemission. Surf. Sci. 1996, 368, 76–81. [Google Scholar] [CrossRef]
- Link, S.; El-Sayed, M.A. Spectral properties and relaxation dynamics of surface plasmon electronic oscillations in gold and silver nanodots and nanorods. J. Phys. Chem. B 1999, 103, 8410–8426. [Google Scholar] [CrossRef]
- Zhukov, V.P.; Andreyev, O.; Hoffmann, D.; Bauer, M.; Aeschlimann, M.; Chulkov, E.V.; Echenique, P.M. Lifetimes of excited electrons in Ta: Experimental time-resolved photoemission data and first-principles GW+T theory. Phys. Rev. B 2004, 70, 233106. [Google Scholar] [CrossRef] [Green Version]
- Bauer, M.; Aeschlimann, M. Dynamics of excited electrons in metals, thin films and nanostructures. J. Electron. Spectros. Relat. Phenom. 2002, 124, 225–243. [Google Scholar] [CrossRef]
- Gundlach, L.; Ernstorfer, R.; Willig, F. Escape dynamics of photoexcited electrons at catechol: TiO2(110). Phys. Rev. B 2006, 74, 035324. [Google Scholar] [CrossRef] [Green Version]
- Tisdale, W.A.; Muntwiler, M.; Norris, D.J.; Aydil, E.S.; Zhu, X.Y. Electron dynamics at the ZnO (101j0) surface. J. Phys. Chem. C 2008, 112, 14682–14692. [Google Scholar] [CrossRef]
- Deinert, J.C.; Wegkamp, D.; Meyer, M.; Richter, C.; Wolf, M.; Stähler, J. Ultrafast exciton formation at the ZnO(1010) surface. Phys. Rev. Lett. 2014, 113, 057602. [Google Scholar] [CrossRef] [Green Version]
- Vos, K. Reflectance and electroreflectance of TiO2 single crystals. II. Assignment to electronic energy levels. J. Phys. C Solid State Phys. 1977, 10, 3917. [Google Scholar] [CrossRef]
- Fisher, D.W. X-ray band spectra and molecular-orbital structure of rutile TiO2. Phys. Rev. B 1972, 5, 4219. [Google Scholar] [CrossRef]
- Henrich, V.E.; Dresselhaus, G.; Zeiger, H.J. Observation of two-dimensional phases associated with defect states on the surface of TiO2. Phys. Rev. Lett. 1976, 36, 1335. [Google Scholar] [CrossRef]
- Pan, J.M.; Maschhoff, B.L.; Diebold, U.; Madey, T.E. Interaction of water, oxygen, and hydrogen with TiO2(110) surfaces having different defect densities. J. Vac. Sci. Tech. A 1992, 10, 2470. [Google Scholar] [CrossRef]
- Brinkley, D.; Engel, T. Active site density and reactivity for the photocatalytic dehydrogenation of 2-propanol on TiO2 (110). Surf. Sci. 1998, 415, L1001–L1006. [Google Scholar] [CrossRef]
- Schaub, R.; Thostrup, P.; Lopez, N.; Lægsgaard, E.; Stensgaard, I.; Nørskov, J.K.; Besenbacher, F. Oxygen vacancies as active sites for water dissociation on rutile TiO2(110). Phys. Rev. Lett. 2001, 87, 266104. [Google Scholar] [CrossRef] [Green Version]
- Wahlström, E.; Lopez, N.; Schaub, R.; Thostrup, P.; Rønnau, A.; Africh, C.; Lægsgaard, E.; Nørskov, J.K.; Besenbacher, F. Bonding of gold nanoclusters to oxygen vacancies on rutile TiO2(110). Phys. Rev. Lett. 2003, 90, 026101. [Google Scholar] [CrossRef] [Green Version]
- Hasiguti, R.R.; Minami, K.; Yonemitsu, H. Electrical resistivity and defect energy levels in reduced titanium dioxide at low temperatures. J. Phys. Soc. Jpn. 1961, 16, 2223–2226. [Google Scholar] [CrossRef]
- Chen, J.; Lin, L.; Jing, F. Theoretical study of F-type color center in rutile TiO2. J. Phys. Chem. Solids 2001, 62, 1257–1262. [Google Scholar] [CrossRef]
- Henderson, M.A.; Epling, W.S.; Peden, C.H.F.; Perkins, C.L. Insights into photoexcited electron scavenging processes on TiO2 obtained from studies of the reaction of O2 with OH groups adsorbed at electronic defects on TiO2(110). J. Phys. Chem. B 2003, 107, 534–545. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Li, H.; Yang, C.; Ji, B.; Lin, J.; Tomie, T. Picosecond Lifetime Hot Electrons in TiO2 Nanoparticles for High Catalytic Activity. Catalysts 2020, 10, 916. https://doi.org/10.3390/catal10080916
Li B, Li H, Yang C, Ji B, Lin J, Tomie T. Picosecond Lifetime Hot Electrons in TiO2 Nanoparticles for High Catalytic Activity. Catalysts. 2020; 10(8):916. https://doi.org/10.3390/catal10080916
Chicago/Turabian StyleLi, Bochao, Hao Li, Chang Yang, Boyu Ji, Jingquan Lin, and Toshihisa Tomie. 2020. "Picosecond Lifetime Hot Electrons in TiO2 Nanoparticles for High Catalytic Activity" Catalysts 10, no. 8: 916. https://doi.org/10.3390/catal10080916
APA StyleLi, B., Li, H., Yang, C., Ji, B., Lin, J., & Tomie, T. (2020). Picosecond Lifetime Hot Electrons in TiO2 Nanoparticles for High Catalytic Activity. Catalysts, 10(8), 916. https://doi.org/10.3390/catal10080916




