Acidic Stabilization of the Dual-Aromatic Heterocyclic Anions
Abstract
:1. Introduction
2. Results and Discussion
2.1. Presence of Dual Aromaticity in the Heterocyclic Anions Studied
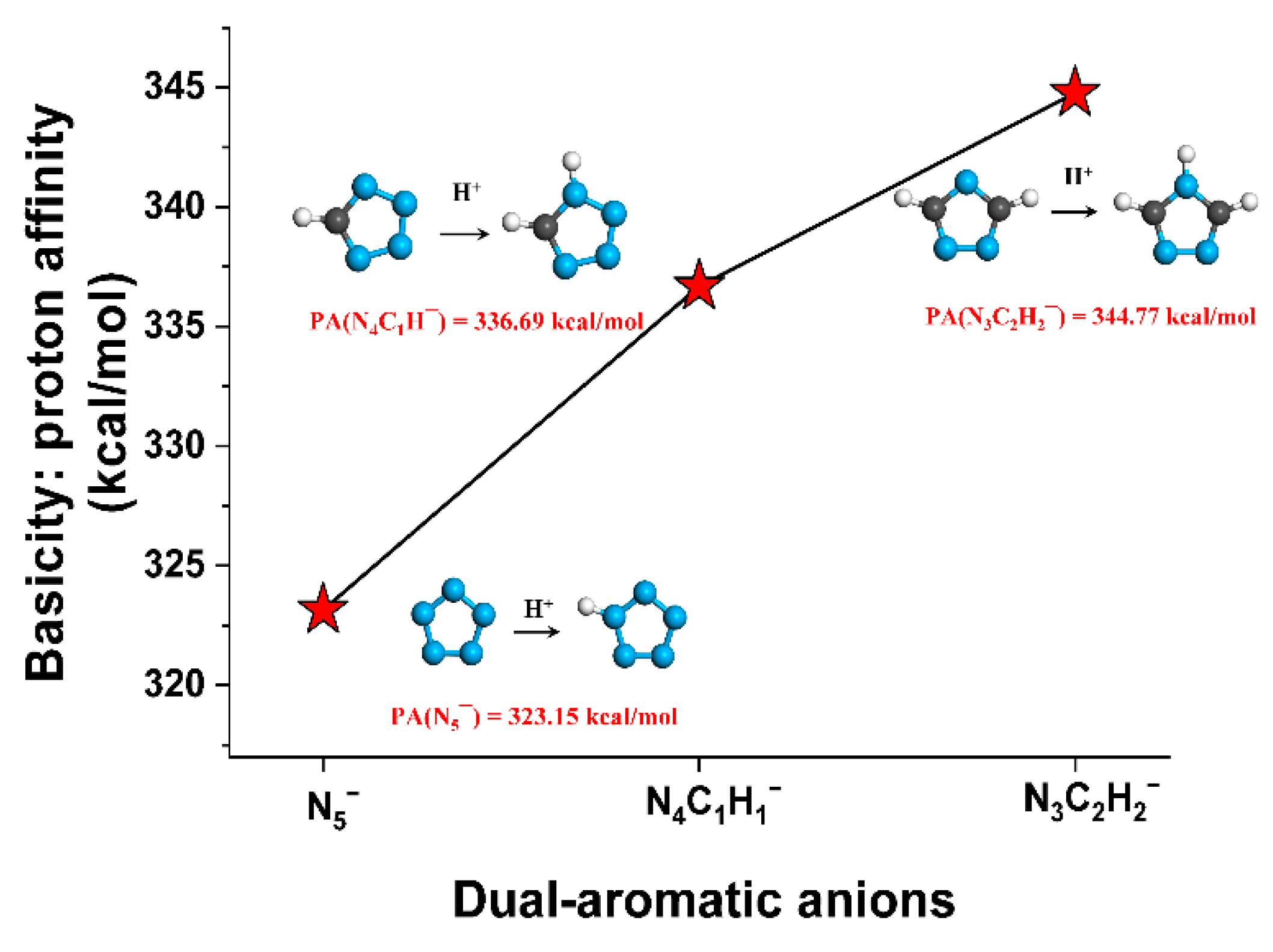
2.2. Basicity of Heterocyclic Anions and Acidity of Solvents Studied
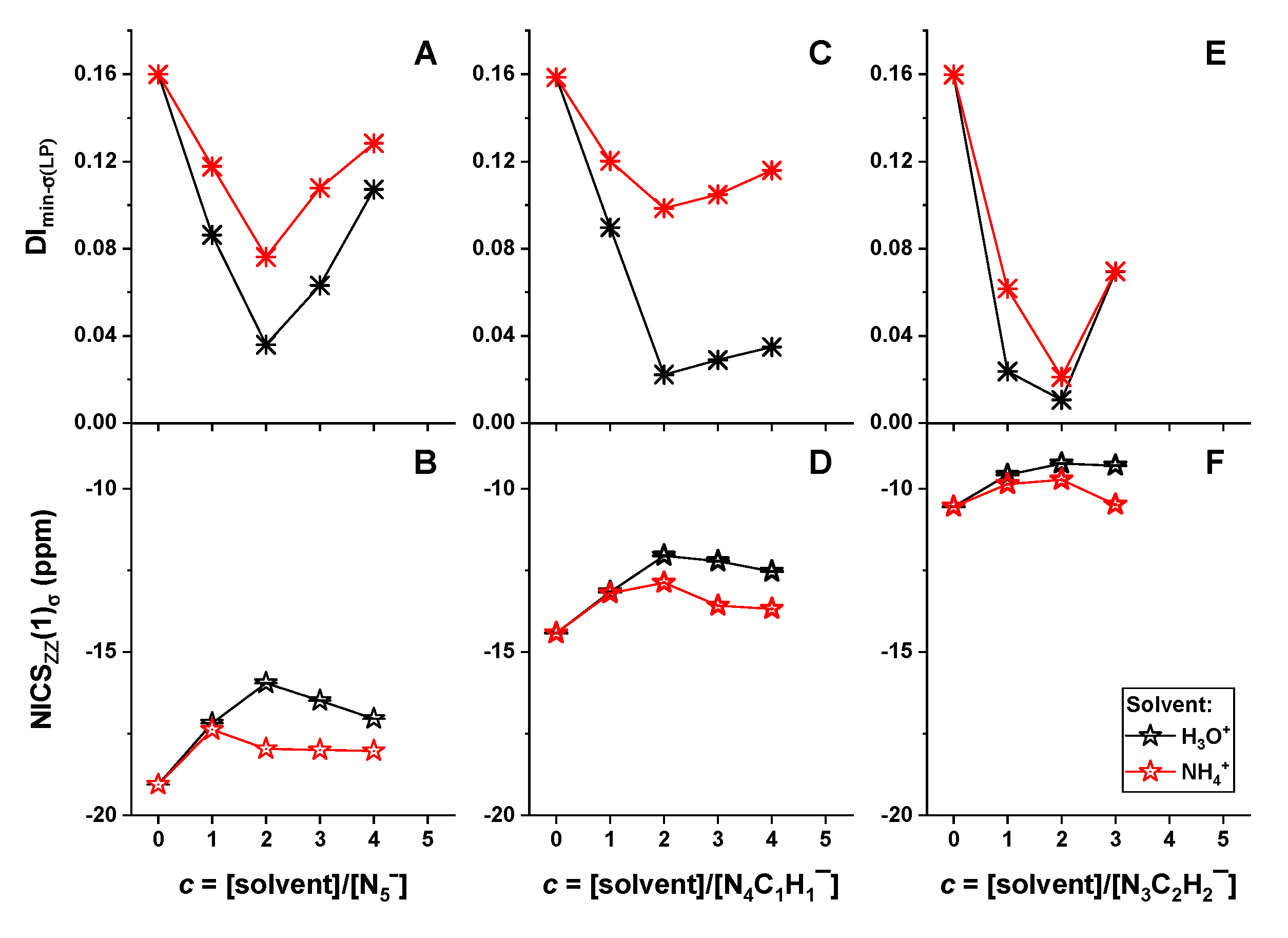
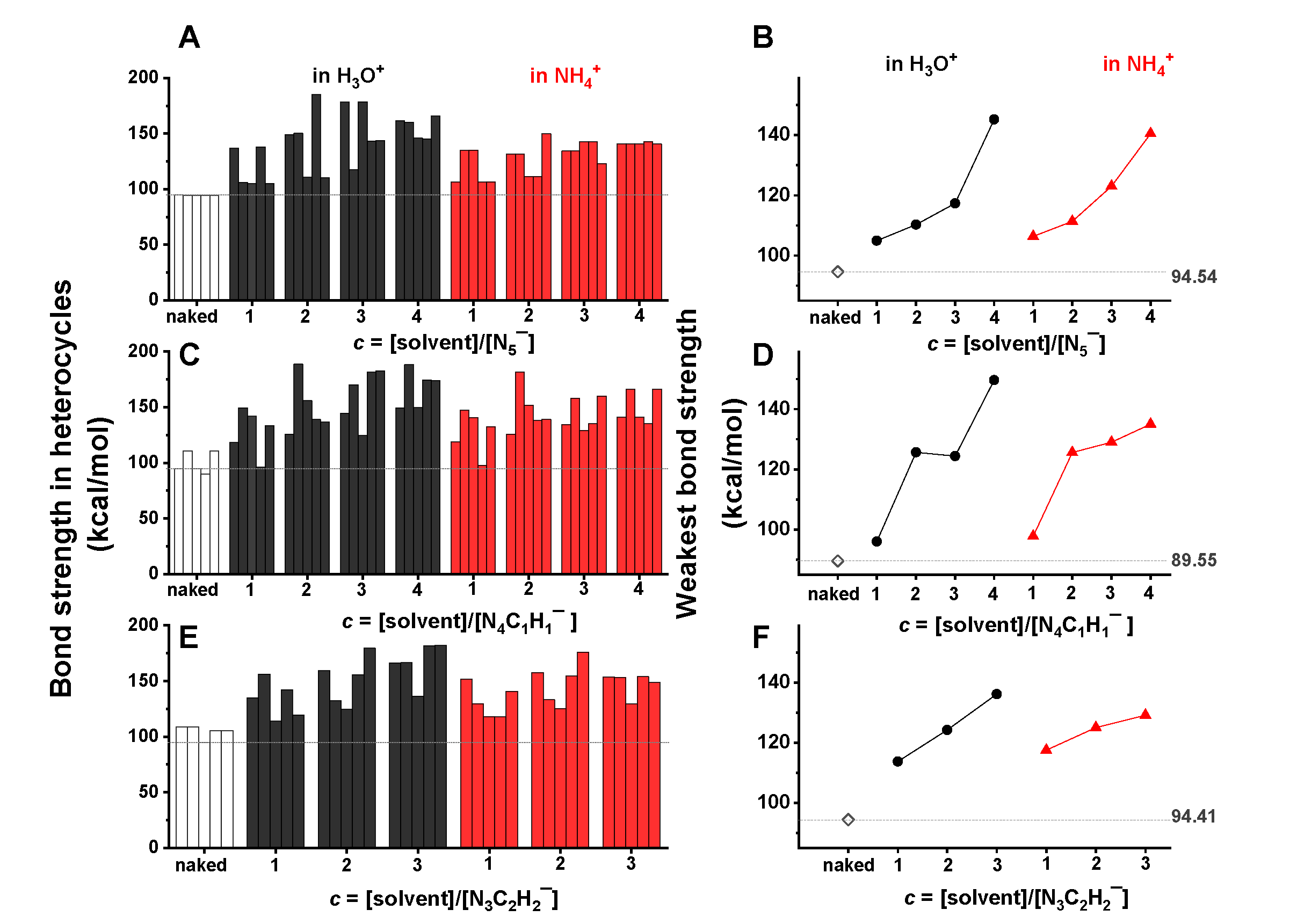
2.3. Different Reactivity of Heterocyclic Anions Depending on Solvent Types and Concentrations
2.4. Mechanism of Anomalous Reactivity of Heterocyclic Anions
2.5. Acidic Stablization of the Dual-Aromatics Studied
3. Methodology
4. Conclusions
- (1)
- Through the analysis of electron density, atomistic structure, interatomic interactions, molecular orbital, magnetic shielding, and energetics, we confirmed the basicity of N5¯, N4C1H1¯, and N3C2H2¯, and the presence of dual aromaticity in the three heterocyclic anions;
- (2)
- The three heterocyclic anions were found to violate the acid–base neutralization rule when confronting more than three H3O+/NH4+ ions. The mechanism of the anomalous reactivity of heterocyclic anions was found to be a competition between their basicity and dual aromaticity;
- (3)
- Due to the stretching effect of hydrogen bonding on the nitrogen lone-pair electrons, the H3O+/NH4+ ions showed a significant stabilization effect on the studied heterocyclic structures, in particular at a high concentration of H3O+/NH4+. In contrast, benzene and THF presented little influence on the structural stability of heterocyclic anions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Note
- Klapötke, T.M. Chemistry of High-Energy Materials, 5th ed.; De Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Politzer, P.; Murray, J.S. (Eds.) Energetic Materials Part 1. Decomposition, Crystal, and Molecular Properties; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Shukla, M.K.; Boddu, V.M.; Steevens, J.A.; Damavarapu, R.; Leszczynski, J. Energetic Materials: From Cradle to Grave; Springer International Publishing: Cham, Switzerland, 2017; Volume 25. [Google Scholar]
- Zhang, C.; Xue, X.; Cao, Y.; Zhou, J.; Zhang, A.; Li, H.; Zhou, Y.; Xu, R.; Gao, T. Toward low-sensitive and high-energetic co-crystal II: Structural, electronic and energetic features of CL-20 polymorphs and the observed CL-20-based energetic–energetic co-crystals. CrystEngComm 2014, 16, 5905–5916. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, H.; Imler, G.H.; Parrish, D.A.; Cheng, G.; Shreeve, J.N.M. Derivatives of 3,6-Bis(3-aminofurazan-4-ylamino)- 1,2,4,5-tetrazine: Excellent energetic properties with lower sensitivities. ACS Appl. Mater. Interfaces 2020, 12, 31522–31531. [Google Scholar] [CrossRef]
- Tang, Y.; Huang, W.; Imler, G.H.; Parrish, D.A.; Shreeve, J.N.M. Enforced planar FOX-7-like molecules: A strategy for thermally stable and insensitive π-conjugated energetic materials. J. Am. Chem. Soc. 2020, 142, 7153–7160. [Google Scholar] [CrossRef]
- Zhong, K.; Xiong, Y.; Liu, J.; Zhang, C. Enhanced shockwave-absorption ability of the molecular disorder rooting for the reactivity elevation of energetic materials. Energ. Mater. Front. 2020, 1, 103–116. [Google Scholar] [CrossRef]
- Sabin, J.R. Advances in Quantum Chemistry; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Jiao, F.; Xiong, Y.; Li, H.; Zhang, C. Alleviating the energy & safety contradiction to construct new low sensitivity and highly energetic materials through crystal engineering. CrystEngComm 2018, 20, 1757–1768. [Google Scholar]
- Lee, K.-Y.; Chapman, L.B.; Cobura, M.D. 3-Nitro-1,2,4-triazol-5-one, a less sensitive explosive. J. Energ. Mater. 1987, 5, 27–33. [Google Scholar] [CrossRef]
- Trzciński, W.A.; Szymańczyk, L. Detonation properties of low-sensitivity NTO-based explosives. J. Energ. Mater. 2005, 23, 151–168. [Google Scholar] [CrossRef]
- Klapötke, T.M.; Sabaté, C.M. Bistetrazoles: Nitrogen-rich, high-performing, insensitive energetic compounds. Chem. Mater. 2008, 20, 3629–3637. [Google Scholar] [CrossRef]
- Bölter, M.F.; Klapötke, T.M.; Kustermann, T.; Lenz, T.; Stierstorfer, J. Improving the energetic properties of dinitropyrazoles by utilization of current concepts. Eur. J. Inorg. Chem. 2018, 2018, 4125–4132. [Google Scholar] [CrossRef]
- Dippold, A.A.; Izsák, D.; Klapötke, T.M. A Study of 5-(1,2,4-Triazol-C-yl)tetrazol-1-ols: Combining the benefits of different heterocycles for the design of energetic materials. Chem. Eur. J. 2013, 19, 12042–12051. [Google Scholar] [CrossRef] [PubMed]
- Dippold, A.A.; Klapötke, T.M. Synthesis and characterization of 5-(1,2,4-Triazol-3-yl)tetrazoles with various energetic functionalities. Chem. Asian J. 2013, 8, 1463–1471. [Google Scholar] [CrossRef]
- Steinhauser, G.; Klapötke, T.M. “Green” pyrotechnics: A chemists’ challenge. Angew. Chem. Int. Ed. 2008, 47, 3330–3347. [Google Scholar] [CrossRef] [PubMed]
- Huynh, M.H.V.; Hiskey, M.A.; Meyer, T.J.; Wetzler, M. Green primaries: Environmentally friendly energetic complexes. Proc. Natl. Acad. Sci. USA 2006, 103, 5409–5412. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Tang, J.; Xiong, H.; Yang, H.; Cheng, G. Combining triazole and furazan frameworks via methylene bridges for new insensitive energetic materials. Energ. Mater. Front. 2020, 1, 34–39. [Google Scholar] [CrossRef]
- Liao, S.; Zhou, Z.; Wang, K.; Jin, Y.; Luo, J.; Liu, T. Synthesis of 5/6/5-fused tricyclic-cation-based cyclo-N5−salt with high density and heat of formation. Energ. Mater. Front. 2020, 3, 172–177. [Google Scholar] [CrossRef]
- Chen, S.; Jin, Y.; Xia, H.; Wang, K.; Liu, Y.; Zhang, Q. Synthesis of fused tetrazolo[1,5-b]pyridazine-based energetic compounds. Energ. Mater. Front. 2020, 1, 16–25. [Google Scholar] [CrossRef]
- Glukhovtsev, M.N.; Dransfeld, A.; Schleyer, P.v.R. Why pentaphosphole, P5H, is planar in contrast to phosphole, (CH)4PH. J. Phys. Chem. 1996, 100, 13447–13454. [Google Scholar] [CrossRef]
- Clayden, J.; Greeves, N.; Warren, S. Organic Chemistry, 2nd ed.; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Vegard, L. Crystal structure of solid nitrogen. Nature 1929, 124, 337. [Google Scholar] [CrossRef]
- Patai, S. The Chemistry of the Hydrazo, Azo and Azoxy Groups; Wiley: New York, NY, USA, 1977; Volume 2. [Google Scholar]
- Gray, P. Chemistry and Physics of Energetic Materials; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Nguyen, M.T. Polynitrogen compounds: 1. Structure and stability of N4 and N5 systems. Coord. Chem. Rev. 2003, 244, 93–113. [Google Scholar] [CrossRef]
- Velian, A.; Cummins, C.C. Synthesis and characterization of P2N3−: An aromatic ion composed of phosphorus and nitrogen. Science 2015, 348, 1001–1004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, C.; Zhang, L.; Sun, C.; Zhang, C.; Yang, C.; Chen, J.; Hu, B. Response to comment on “Synthesis and characterization of the pentazolate anion cyclo-N5− in (N5)6(H3O)3(NH4)4Cl”. Science 2018, 359, eaas8953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, R.-Y.; Xu, H. Comment on “Synthesis and characterization of the pentazolate anion cyclo-N5− in (N5)6(H3O)3(NH4)4Cl”. Science 2018, 359, eaao3672. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, M.T.; McGinn, M.A.; Hegarty, A.F.; Elguéro, J. Can the pentazole anion (N5ˉ) be isolated and/or trapped in metal complexes? Polyhedron 1985, 4, 1721–1726. [Google Scholar] [CrossRef]
- Glukhovtsev, M.N.; Jiao, H.; Schleyer, P.v.R. Besides N2, What is the most stable molecule composed only of nitrogen atoms? Inorg. Chem. 1996, 35, 7124–7133. [Google Scholar] [CrossRef]
- Najafpour, J.; Foroutan-Nejad, C.; Shafiee, G.H.; Peykani, M.K. How does electron delocalization affect the electronic energy? A survey of neutral poly-nitrogen clusters. Comput. Theor. Chem. 2011, 974, 86–91. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, C.; Yu, Y.; Wang, X.; Sun, C.Q.; Chen, J. Mechanism and functionality of pnictogen dual aromaticity in pentazolate crystals. ChemPhysChem 2019, 20, 2525–2530. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, C.; Yu, Y.; Jiang, S.-L.; Sun, C.Q.; Chen, J. Stabilization of the dual-aromatic cyclo-N5− anion by acidic entrapment. J. Phys. Chem. Lett. 2019, 10, 2378–2385. [Google Scholar] [CrossRef]
- Zong, H.-H.; Yao, C.; Sun, C.Q.; Zhang, J.-G.; Zhang, L. Structure and stability of aromatic nitrogen heterocycles used in the field of energetic materials. Molecules 2020, 25, 3232. [Google Scholar] [CrossRef]
- Li, Z.-H.; Moran, D.; Fan, K.-N.; Schleyer, P.v.R. σ-Aromaticity and σ-antiaromaticity in saturated inorganic rings. J. Phys. Chem. A 2005, 109, 3711–3716. [Google Scholar] [CrossRef] [PubMed]
- Note: Current values of aromaticity indices of pentazole anion have slight difference from our previous publication on Stabilization of the Dual-Aromatic cyclo-N5– Anion by Acidic Entrapment. J. Phys. Chem. Lett. 2019, 10, 2378, because of the use of a different optimization method. The NICSzz(1)_sigma value for benzene is corrected to be −0.113.
- Satchell, J.F.; Smith, B.J. Calculation of aqueous dissociation constants of 1,2,4-triazole and tetrazole: A comparison of solvation models. Phys. Chem. Chem. Phys. 2002, 4, 4314–4318. [Google Scholar] [CrossRef]
- Lindstrom, P.; Mallard, W. NIST Chemistry WebBook; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2003. [Google Scholar]
- EP Serjeant, B.D. Ionization Constants of Organic Acids in Solution; Pergamon Press: Oxford, UK; New York, NY, USA, 1979. [Google Scholar]
- Zhang, Z.; Li, D.; Jiang, W.; Wang, Z. The electron density delocalization of hydrogen bond systems. Adv. Phys. X 2018, 3, 1428915. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Sun, C.; Hu, B.; Yu, C.; Lu, M. Synthesis and characterization of the pentazolate anion cyclo-N5− in (N5)6(H3O)3(NH4)4Cl. Science 2017, 355, 374–376. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian: Wallingford, CT, USA, 2013. [Google Scholar]
- Zhang, L.; Jiang, S.-L.; Yu, Y.; Long, Y.; Zhao, H.-Y.; Peng, L.-J.; Chen, J. Phase transition in octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX) under static compression: An application of the first-principles method specialized for CHNO solid explosives. J. Phys. Chem. B 2016, 120, 11510–11522. [Google Scholar] [CrossRef] [PubMed]
- Mo, Z.; Zhang, A.; Cao, X.; Liu, Q.; Xu, X.; An, H.; Pei, W.; Zhu, S. JASMIN: A parallel software infrastructure for scientific computing. Front. Comput. Sci. China 2010, 4, 480–488. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solà, M. The delocalization index as an electronic aromaticity criterion: Application to a series of planar polycyclic aromatic hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef]
- Schleyer, P.v.R. Introduction: Aromaticity. Chem. Rev. 2001, 101, 1115–1118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Almeida, M.O.; Faria, S.H.D. Computational study of the alkylation reaction of the nitrogen mustard mechlorethamine using NBO model and the QTAIM theory. Open J. Phys. Chem. 2013, 3, 127–137. [Google Scholar] [CrossRef] [Green Version]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near-Hartree–Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Bader R F, W. Atoms in Molecules: A Quantum Theory, International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Bader, R.F. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Matijssen, C.; Kinsella, G.K.; Watson, G.W.; Rozas, I. Computational study of the proton affinity and basicity of structurally diverse α1-adrenoceptor ligands. J. Phys. Org. Chem. 2012, 25, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Camaioni, D.M.; Schwerdtfeger, C.A. Comment on “Accurate experimental values for the free energies of hydration of H+, OH−, and H3O+”. J. Phys. Chem. A 2005, 109, 10795–10797. [Google Scholar] [CrossRef] [PubMed]


| Indices | N5¯ | N4C1H1¯ | N3C2H2¯ | Benzene | |
|---|---|---|---|---|---|
| Total | NICSzz(1)total | −45.16 | −40.24 | −35.78 | −29.07 |
| NICSzz(rextreme)total | −51.81 | −43.44 | −37.53 | - | |
| π | DI min-π | 0.16 | 0.16 | 0.16 | 0.11 |
| NICSzz(1)π | −26.09 | −25.81 | −25.23 | −28.96 | |
| σ | DI min-σ(LP) | 0.16 | 0.16 | 0.16 | - |
| NICSzz(1)σ | −19.06 | −14.42 | −10.55 | −0.11 | |
| NICSzz(rextreme)σ | −19.87 | −14.42 | −10.55 | - | |
| Type | Compounds | PA (kcal/mol) | −Log of Dissociation Constant | |
|---|---|---|---|---|
| This Work | Exp. | Exp. | ||
| Heterocyclic anions | N5¯ | 323.2 | - | - |
| N4C1H1¯ | 336.7 | - | pKb = 9.1 | |
| N3C2H2¯ | 344.8 | - | pKb = 4.0 | |
| Solvents | H3O+ | 176.3 | 165.0 [39] | pKa = −1.74 [40] |
| NH4+ | 211.9 | 204.0 [39] | pKa = 9.3 [40] | |
| Benzene | 409.7 | - | pKa = 43 [40] | |
| THF | 411.1 | - | - | |
| H2O | 396.1 | 390.3 [39] | pKa = 15.74 [40] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Huang, Y.; Sun, C.Q.; Zhang, L. Acidic Stabilization of the Dual-Aromatic Heterocyclic Anions. Catalysts 2021, 11, 766. https://doi.org/10.3390/catal11070766
Li C, Huang Y, Sun CQ, Zhang L. Acidic Stabilization of the Dual-Aromatic Heterocyclic Anions. Catalysts. 2021; 11(7):766. https://doi.org/10.3390/catal11070766
Chicago/Turabian StyleLi, Chongyang, Yongli Huang, Chang Q Sun, and Lei Zhang. 2021. "Acidic Stabilization of the Dual-Aromatic Heterocyclic Anions" Catalysts 11, no. 7: 766. https://doi.org/10.3390/catal11070766
APA StyleLi, C., Huang, Y., Sun, C. Q., & Zhang, L. (2021). Acidic Stabilization of the Dual-Aromatic Heterocyclic Anions. Catalysts, 11(7), 766. https://doi.org/10.3390/catal11070766






