Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor
Abstract
1. Introduction
2. The Reactor Model
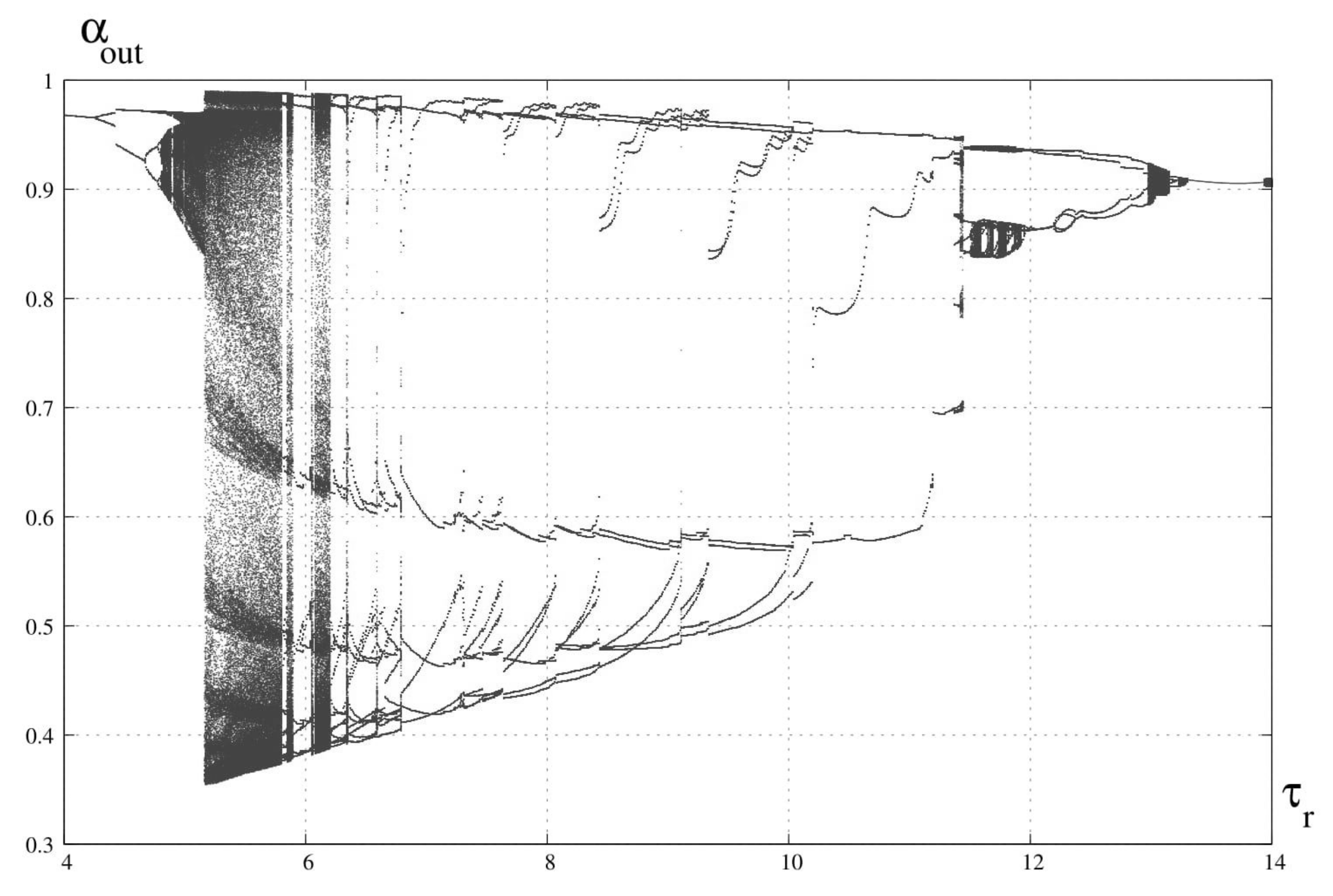
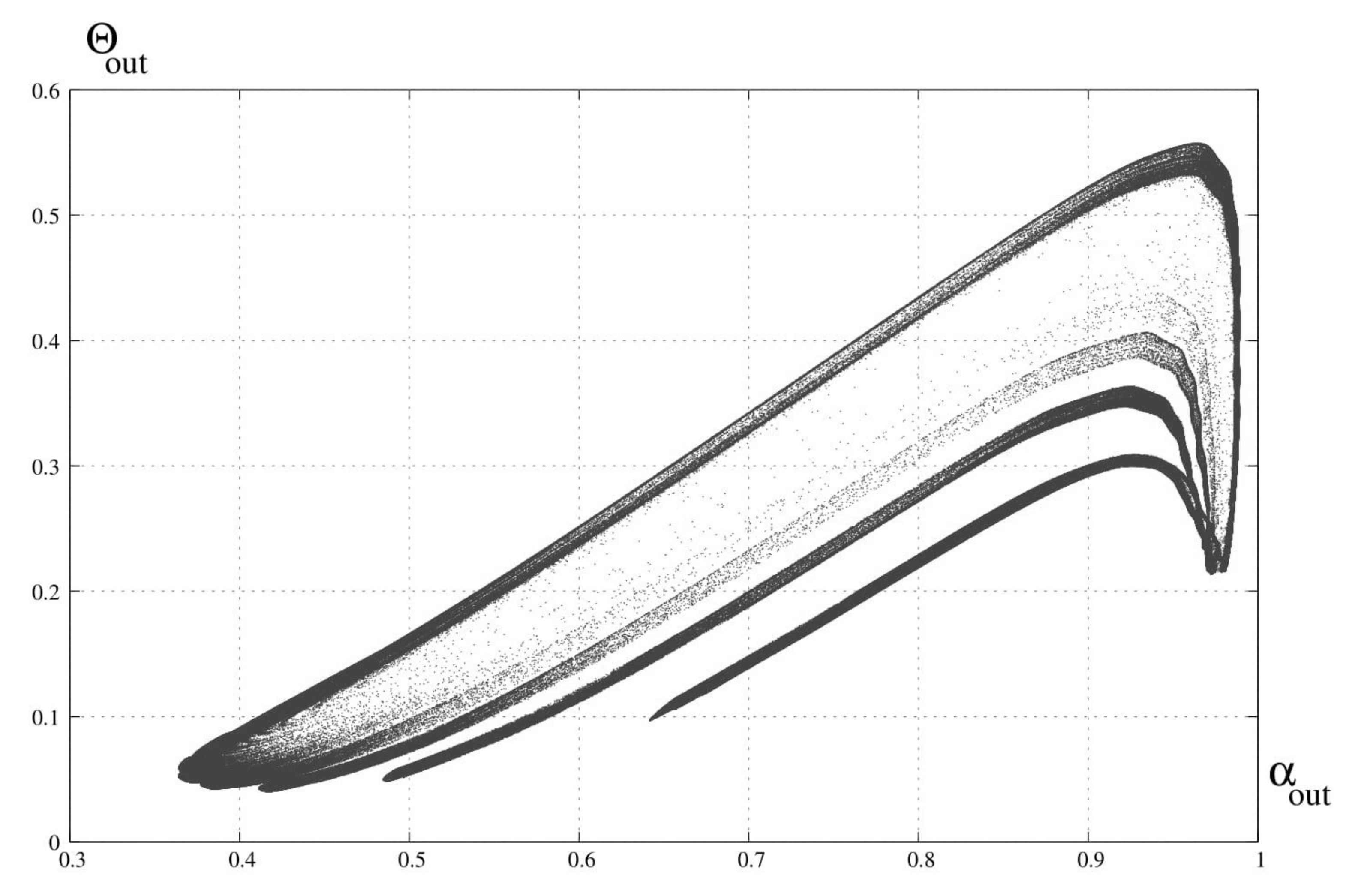
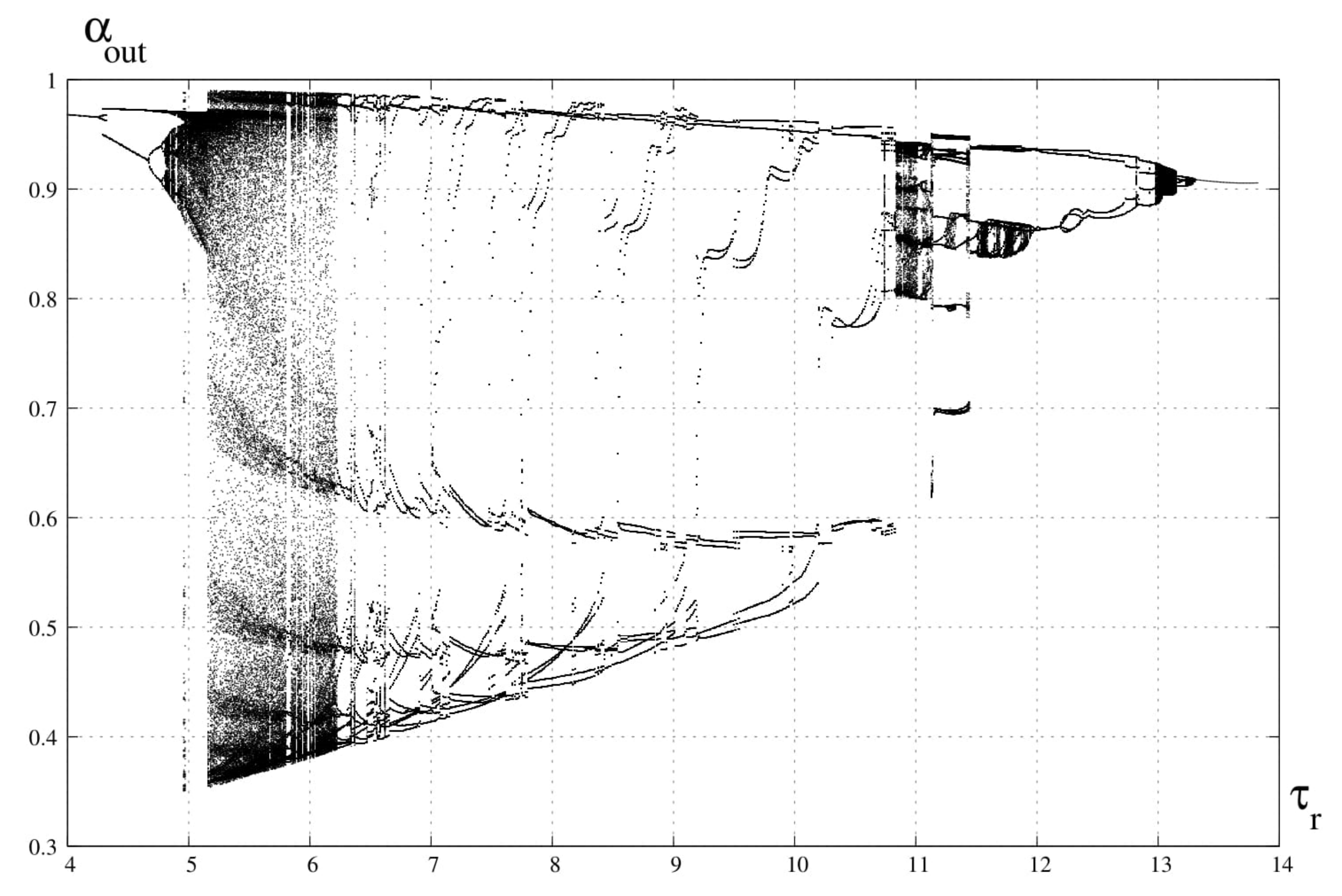
3. Bifurcation Analysis
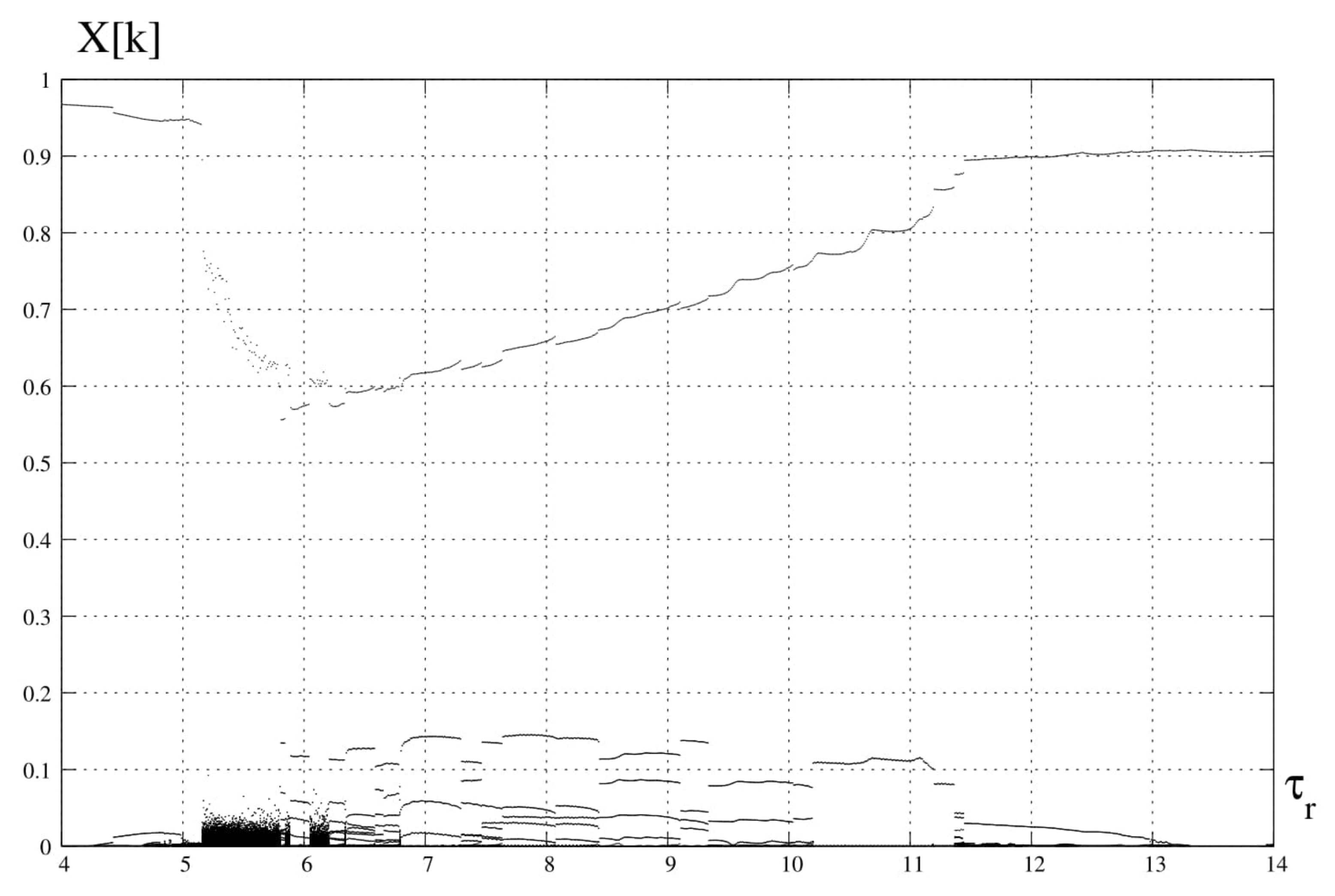
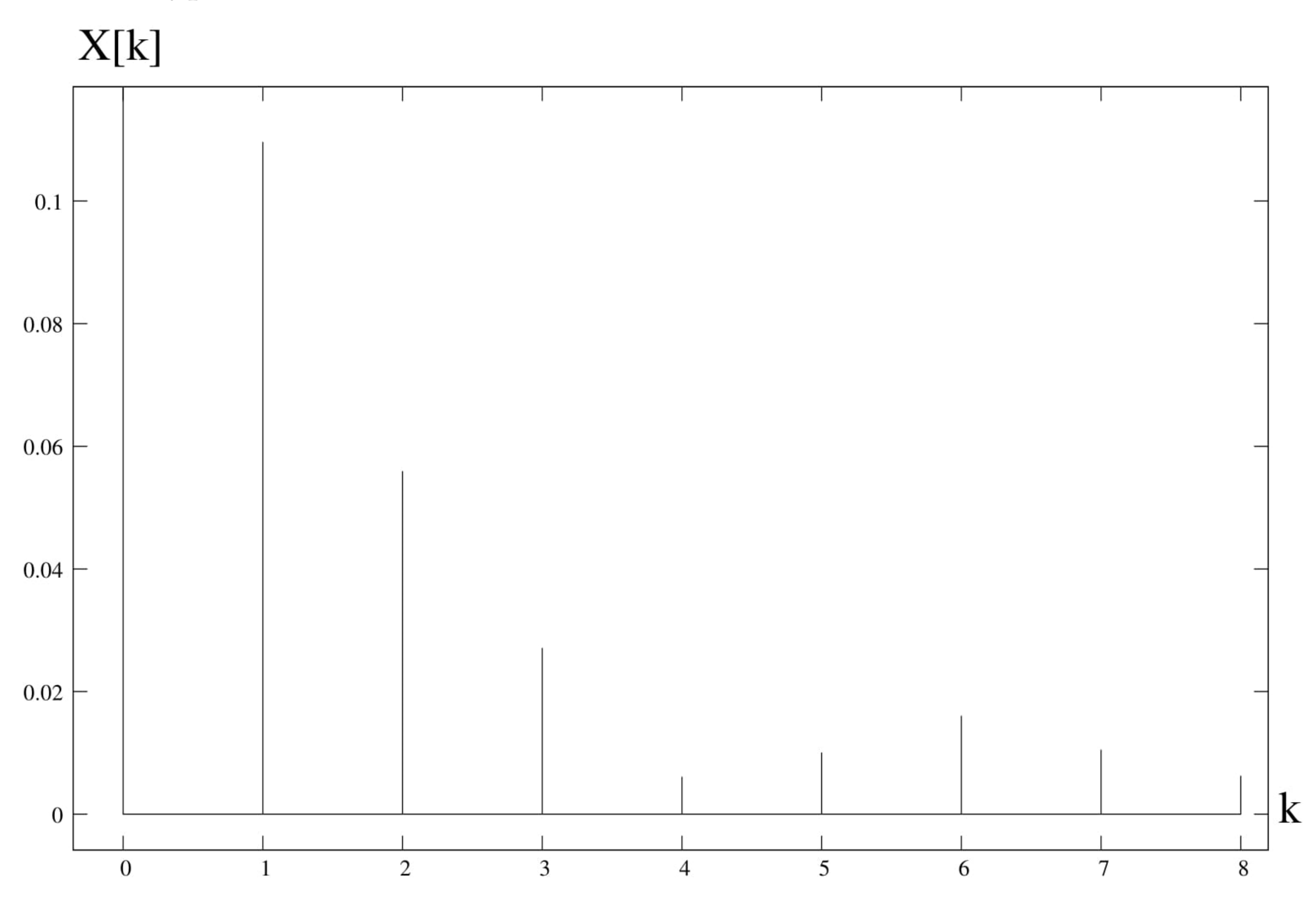
4. Spectral Analysis
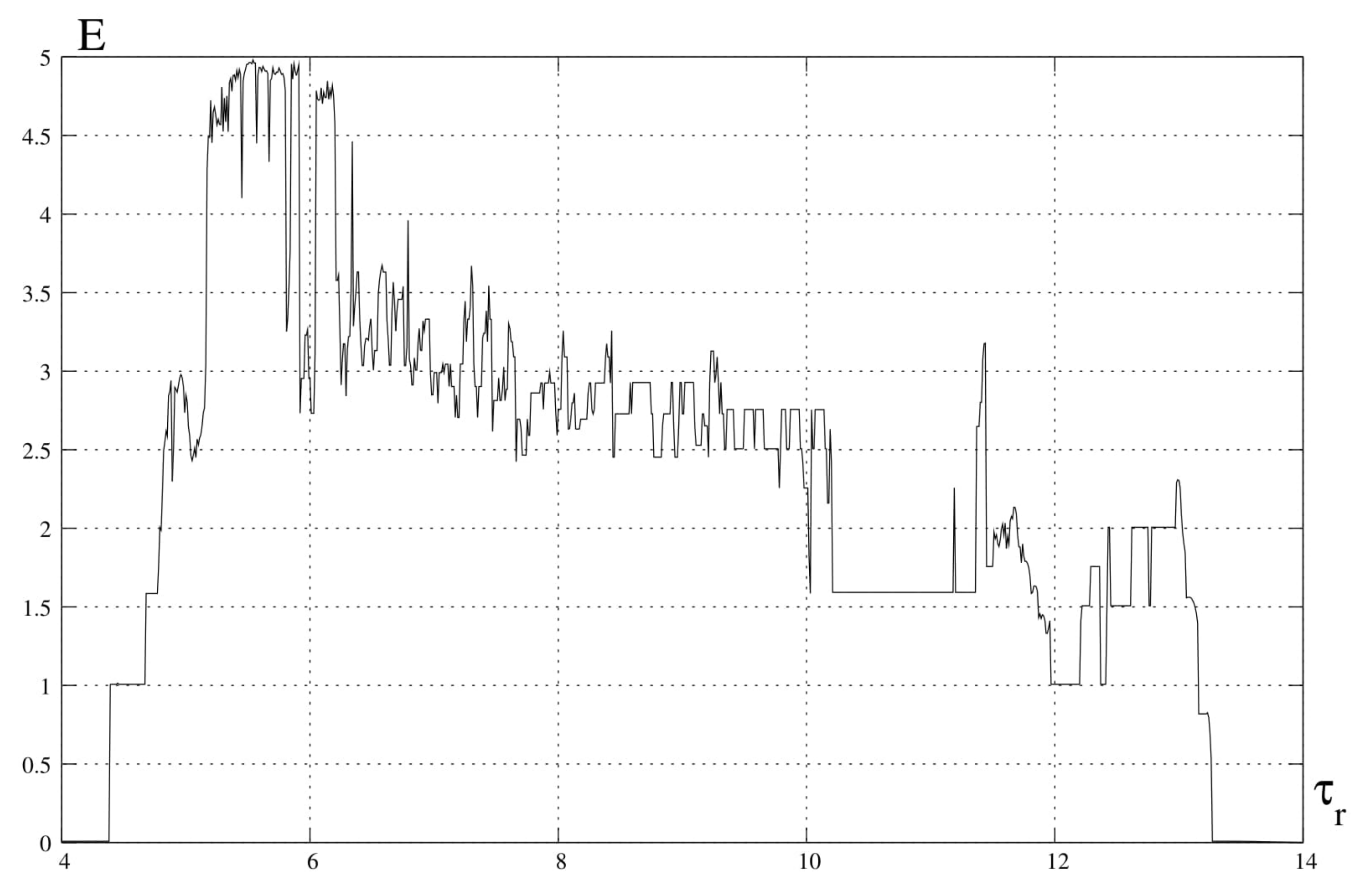
5. Entropy Analysis
6. Discussion
7. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| heat capacity, kJ/(kg K) | |
| concentration of component A, kmol/m | |
| Damköhler number | |
| E | activation energy, kJ/kmol |
| volumetric flow rate, m/s | |
| heat of reaction, kJ/kmol | |
| k | reaction rate constant, (m/kmol)/s |
| L | length, m |
| Lewis number, | |
| m | order of reaction |
| Peclet number | |
| rate of reaction, , kmol/(m s) | |
| R | gas constant, kJ/(kmol K) |
| t | time, s |
| T | temperature, K |
| V | volume, m |
| z | position, m |
| Greek letters | |
| degree of conversion | |
| dimensionless number related to adiabatic temperature increase | |
| dimensionless number related to activation energy | |
| dimensionless heat exchange coefficient | |
| dimensionless temperature | |
| dimensionless position, | |
| density, | |
| dimensionless time, | |
| Subscripts | |
| 0 | refers to feed |
| H | refers to heat |
| M | refers to mass |
| output of system | |
| r | refers to reverse flow; switching times |
| R | refers to reactor |
| s | refers to solid phase |
References
- Aubé, F.; Sapoundjiev, H. Mathematical model and numerical simulations of catalytic flow reversal reactors for industrial applications. Comput. Chem. Eng. 2000, 24, 2623–2632. [Google Scholar] [CrossRef]
- Berezowski, M. Fractal solutions of recirculation tubular chemical reactors. Chaos Solitons Fractals 2003, 16, 1–12. [Google Scholar] [CrossRef][Green Version]
- Berezowski, M. Spatio-temporal chaos in tubular chemical reactors with the recycle of mass. Chaos Solitons Fractals 2000, 11, 1197–1204. [Google Scholar] [CrossRef]
- Berezowski, M.; Kulik, B. Periodicity of chaotic solutions of the model of thermally coupled cascades of chemical tank reactors with flow reversal. Chaos Solitons Fractals 2009, 40, 331–336. [Google Scholar] [CrossRef]
- Elnashaie, S.; Abashar, M. On the chaotic behaviour of forced fluidized bed catalytic reactors. Chaos Solitons Fractals 1995, 5, 797–831. [Google Scholar] [CrossRef]
- Femat, R.; Méndez-Acosta, H.; Steyer, J.; González-Alvarez, V. Temperature oscillations in a biological reactor with recycle. Chaos Solitons Fractals 2004, 19, 875–889. [Google Scholar] [CrossRef]
- Khinast, J.; Luss, D. Mapping regions with different bifurcation diagrams of a reverse-flow reactor. AIChE J. 1997, 43, 2034–2047. [Google Scholar] [CrossRef]
- Khinast, J.; Gurumoothy, A.; Luss, D. Complex Dynamic Features of a Cooled Reverse-Flow Reactor. AIChE J. 1998, 44, 1128–1140. [Google Scholar] [CrossRef]
- Matros, Y.S.; Bunimovich, G.A. Reverse-Flow Operation in Fixed Bed Catalytic Reactors. Catal. Rev. 1996, 38, 1–68. [Google Scholar] [CrossRef]
- Merta, H. Characteristic time series and operation region of the system of two tank reactors (CSTR) with variable division of recirculation stream. Chaos Solitons Fractals 2006, 27, 279–285. [Google Scholar] [CrossRef]
- Merta, H.; Pelka, R. Chaotic dynamics of a cascade of plug flow tubular reactors (PFTRs) with division of recirculating stream. Chaos Solitons Fractals 2005, 23, 1211–1219. [Google Scholar] [CrossRef]
- Řeháček, J.; Kubíček, M.; Marek, M. Periodic, quasiperiodic and chaotic spatiotemporal patterns in a tubular catalytic reactor with periodic flow reversal. Comput. Chem. Eng. 1998, 22, 283–297. [Google Scholar] [CrossRef]
- Russo, L.; Altimari, P.; Mancusi, E.; Maffettone, P.L.; Crescitelli, S. Complex dynamics and spatio-temporal patterns in a network of three distributed chemical reactors with periodical feed switching. Chaos Solitons Fractals 2006, 28, 682–706. [Google Scholar] [CrossRef]
- Russo, L.; Mancusi, E.; Maffettone, P.L.; Crescitelli, S. Symmetry properties and bifurcation analysis of a class of periodically forced chemical reactors. Chem. Eng. Sci. 2002, 57, 5065–5082. [Google Scholar] [CrossRef]
- Salinger, A.G.; Eigenberger, G. The direct calculation of periodic states of the reverse flow reactior—I. Methodology and propane combustion results. Chem. Eng. Sci. 1996, 51, 4903–4913. [Google Scholar] [CrossRef]
- Salinger, A.G.; Eigenberger, G. The direct calculation of periodic states of the reverse flow reactor—II. Multiplicity and instability. Chem. Eng. Sci. 1996, 51, 4915–4922. [Google Scholar] [CrossRef]
- Żukowski, W.; Berezowski, M. Generation of chaotic oscillations in a system with flow reversal. Chem. Eng. Sci. 2000, 55, 339–343. [Google Scholar] [CrossRef]
- Wibowo, R.B.E.; Suzuki, T.; Takahashi, R. A Mathematical Study on the System of Partial Differential Equations Describing Reverse-Flow Reactor. Math. Model. Anal. 2016, 21, 550–568. [Google Scholar] [CrossRef][Green Version]
- Ray, W.; Marek, M.; Elnashaie, S. The effect of heat and mass dispersion on tubular reactor performance. Chem. Eng. Sci. 1972, 27, 1527–1536. [Google Scholar] [CrossRef]
- Di Sarli, V.; Marra, F.S.; Di Benedetto, A. Spontaneous Oscillations in Lean Premixed Combustors: CFD Simulation. Combust. Sci. Technol. 2007, 179, 2335–2359. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A.; Marra, F.S. Influence of system parameters on the dynamic behaviour of an LPM combustor: Bifurcation analysis through CFD simulations. Combust. Theory Model. 2008, 12, 1109–1124. [Google Scholar] [CrossRef]
- Garcia-Agreda, A.; Di Sarli, V.; Di Benedetto, A. Bifurcation analysis of the effect of hydrogen addition on the dynamic behavior of lean premixed pre-vaporized ethanol combustion. Int. J. Hydrogen Energy 2012, 37, 6922–6932. [Google Scholar] [CrossRef]
- Berezowski, M. Crisis phenomenon in a chemical reactor with recycle. Chem. Eng. Sci. 2013, 101, 451–453. [Google Scholar] [CrossRef]
- Bizon, K.; Continillo, G.; Berezowski, M.; Smuła-Ostaszewska, J. Optimal model reduction by empirical spectral methods via sampling of chaotic orbits. Phys. D Nonlinear Phenom. 2012, 241, 1441–1449. [Google Scholar] [CrossRef]
- Batty, M. Spatial Entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezowski, M.; Kozioł, N.; Lawnik, M. Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor. Catalysts 2022, 12, 37. https://doi.org/10.3390/catal12010037
Berezowski M, Kozioł N, Lawnik M. Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor. Catalysts. 2022; 12(1):37. https://doi.org/10.3390/catal12010037
Chicago/Turabian StyleBerezowski, Marek, Natalia Kozioł, and Marcin Lawnik. 2022. "Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor" Catalysts 12, no. 1: 37. https://doi.org/10.3390/catal12010037
APA StyleBerezowski, M., Kozioł, N., & Lawnik, M. (2022). Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor. Catalysts, 12(1), 37. https://doi.org/10.3390/catal12010037







