Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor
Abstract
:1. Introduction
2. The Reactor Model
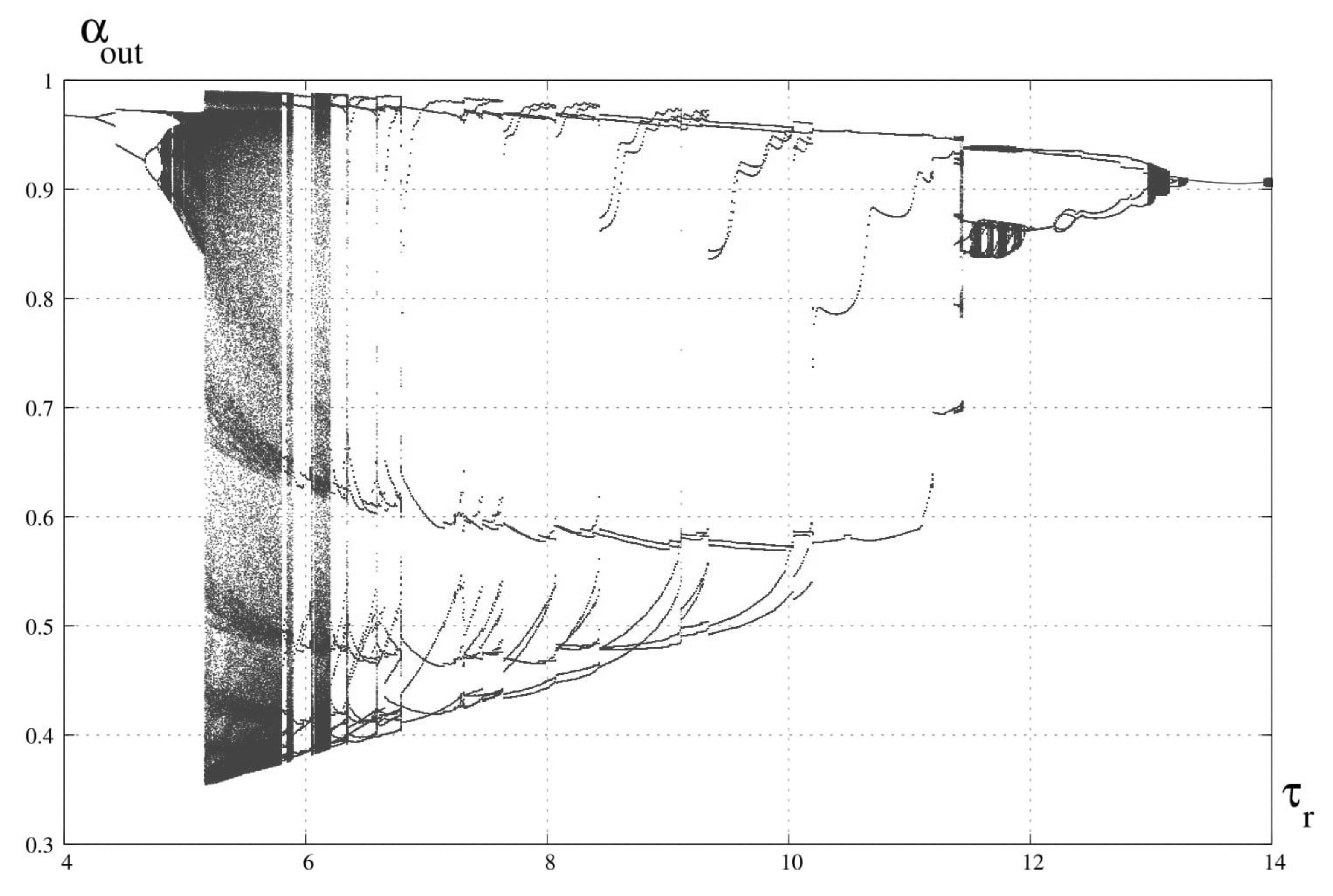
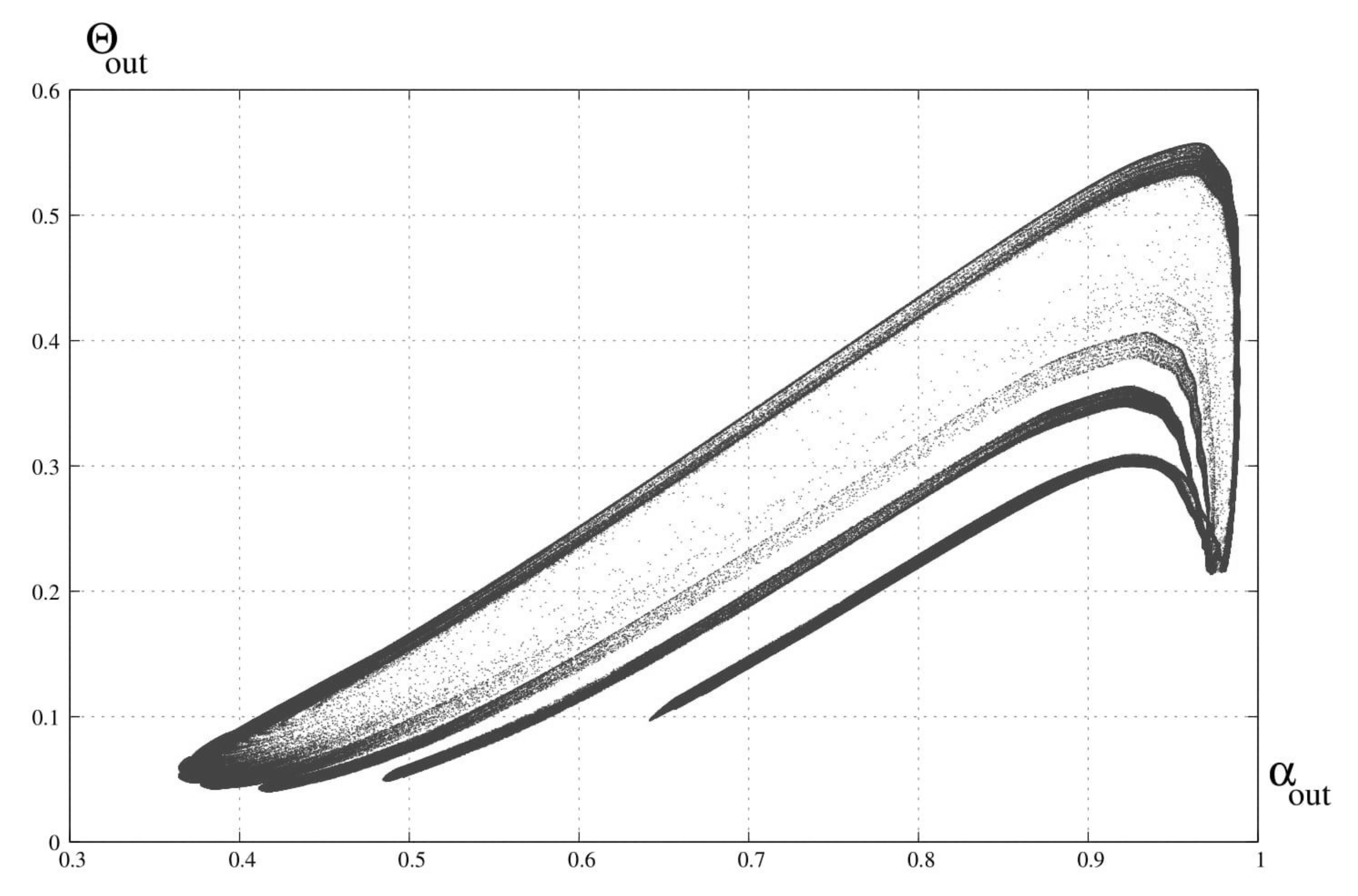
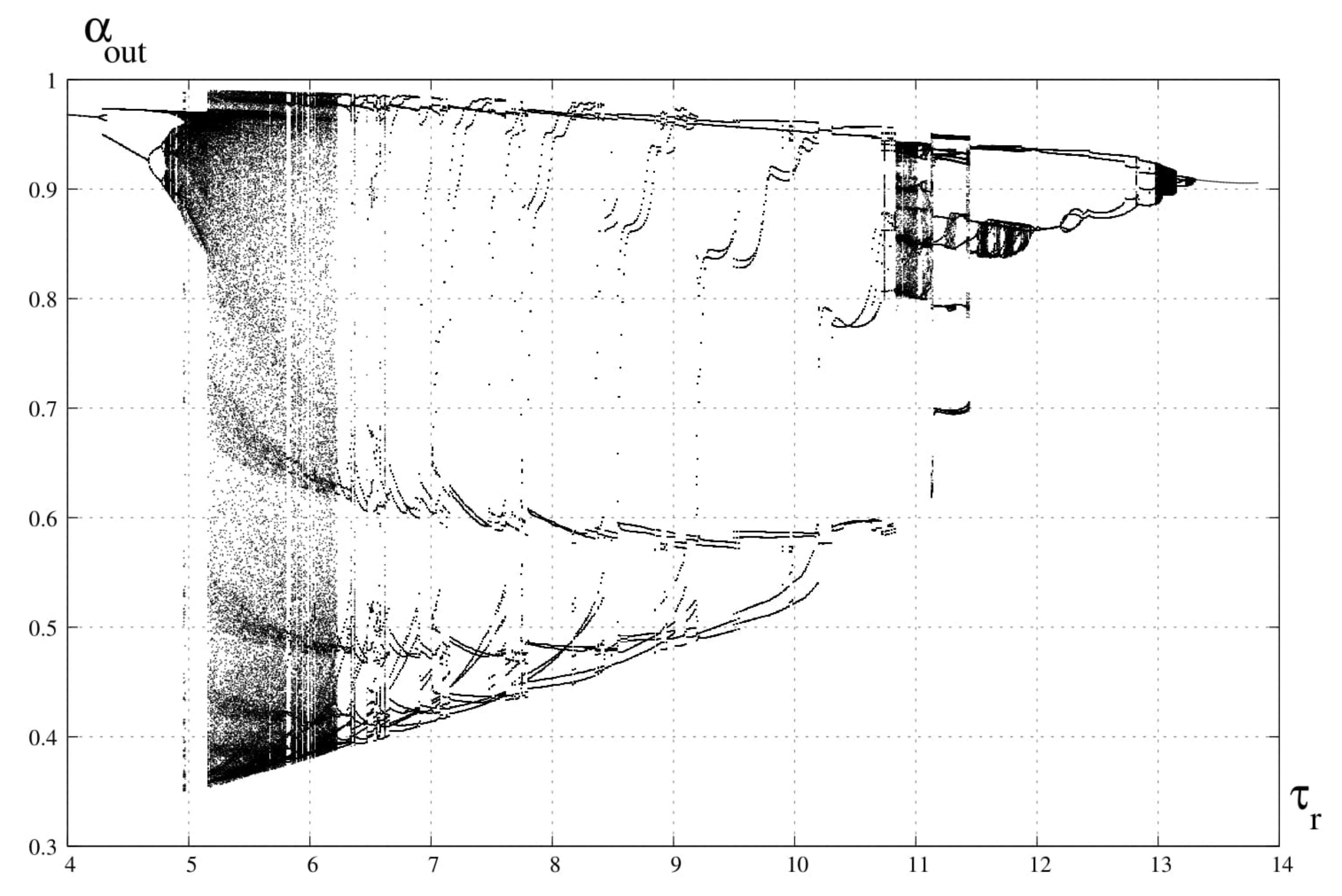
3. Bifurcation Analysis
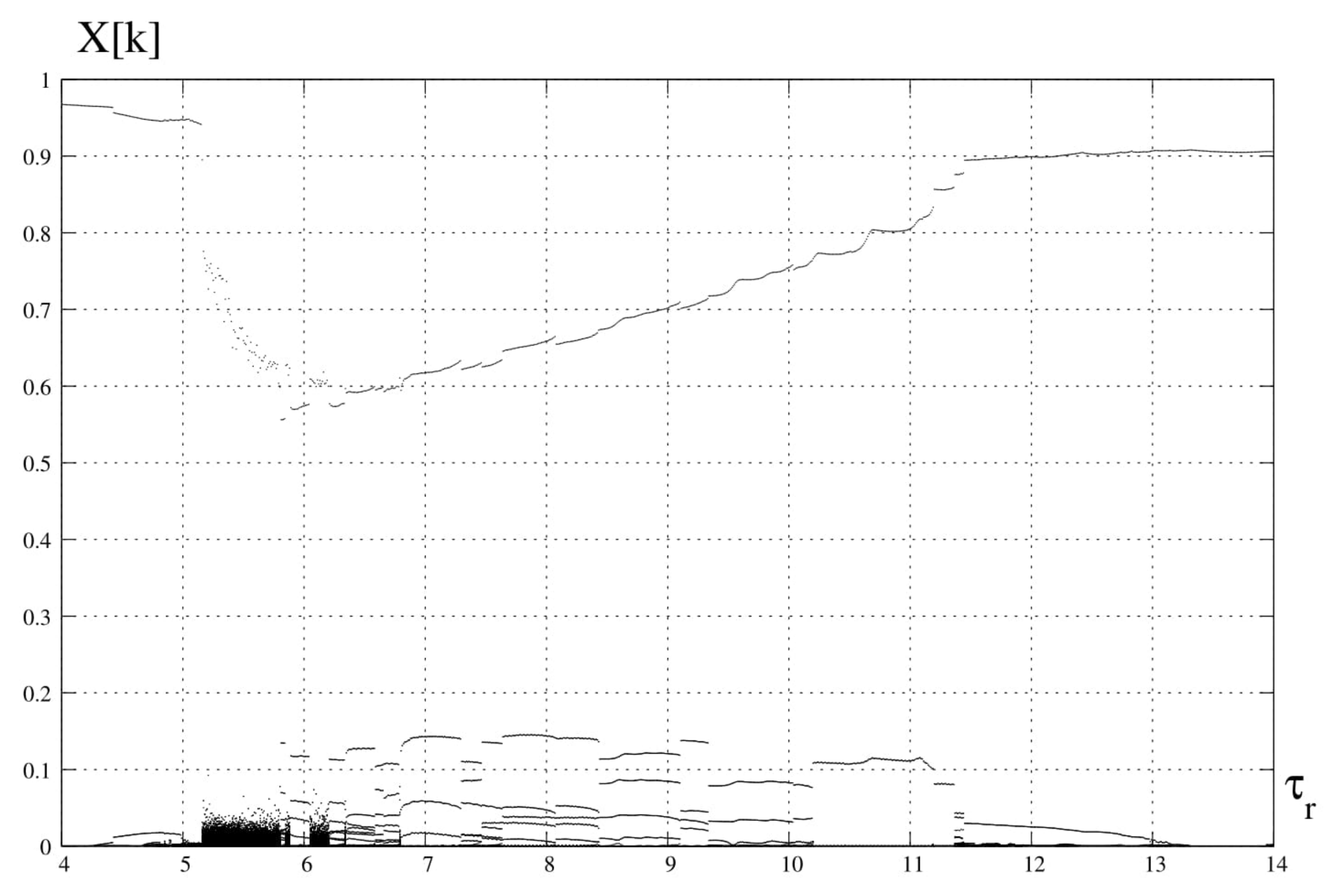
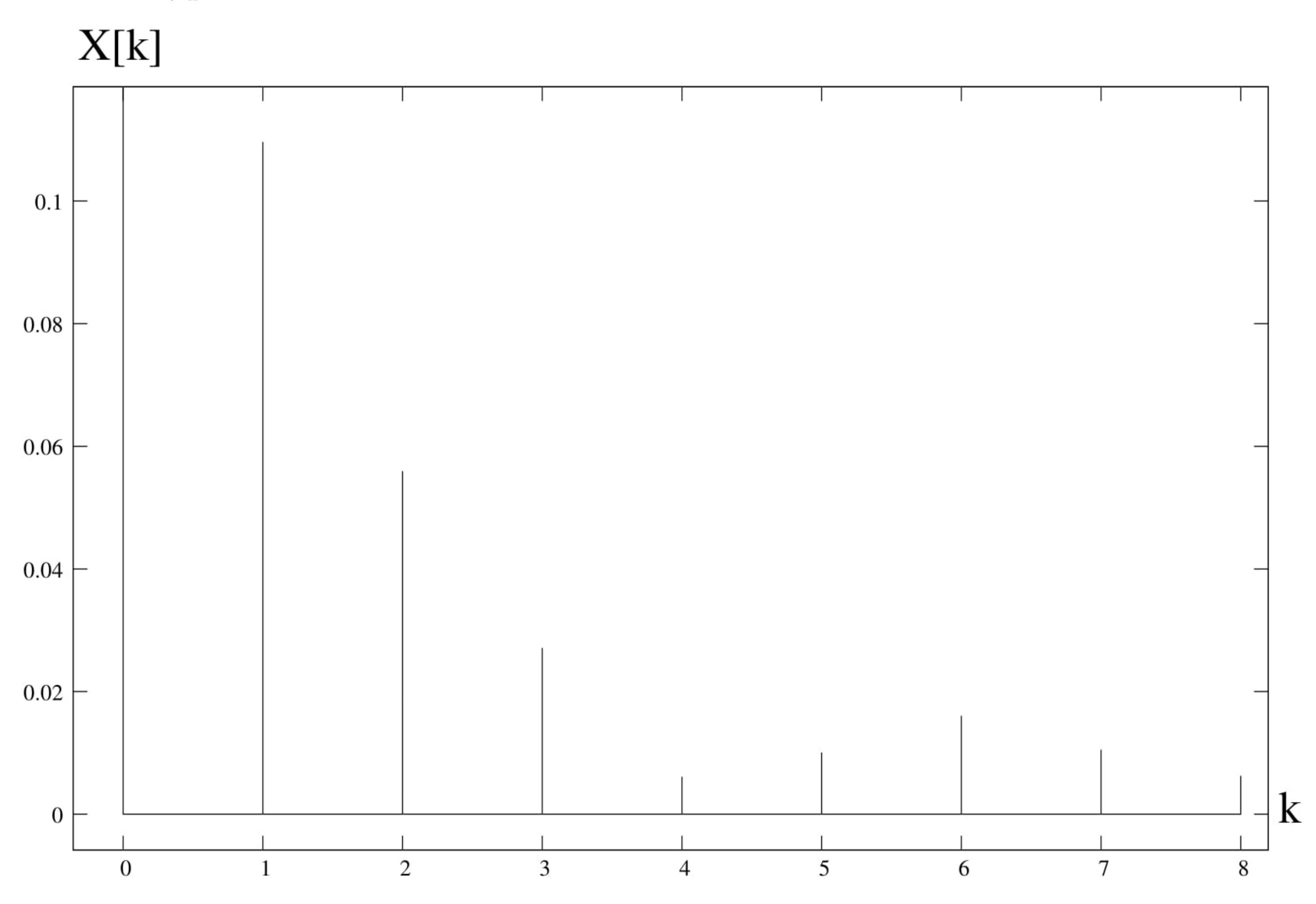
4. Spectral Analysis
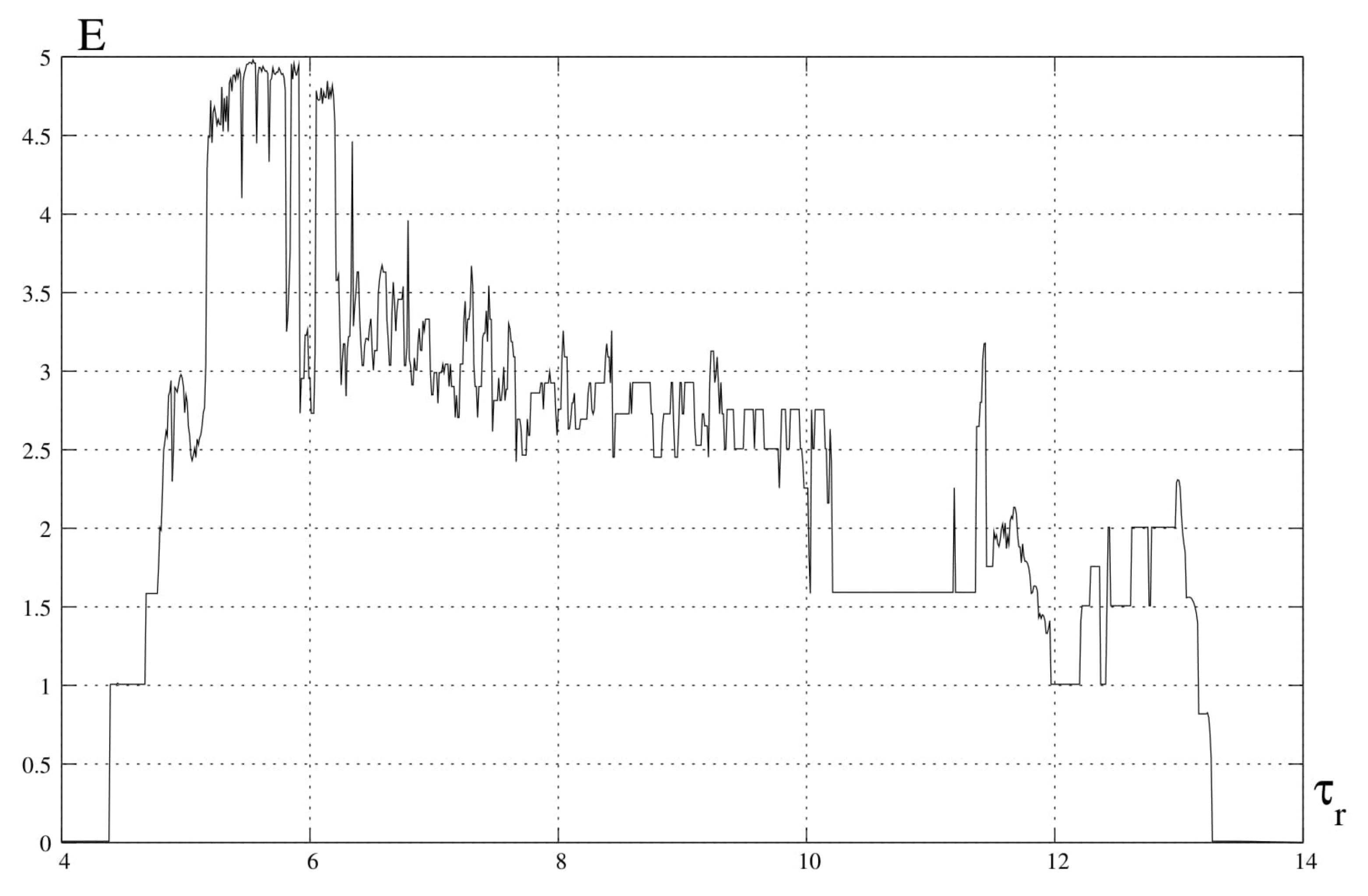
5. Entropy Analysis
6. Discussion
7. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| heat capacity, kJ/(kg K) | |
| concentration of component A, kmol/m | |
| Damköhler number | |
| E | activation energy, kJ/kmol |
| volumetric flow rate, m/s | |
| heat of reaction, kJ/kmol | |
| k | reaction rate constant, (m/kmol)/s |
| L | length, m |
| Lewis number, | |
| m | order of reaction |
| Peclet number | |
| rate of reaction, , kmol/(m s) | |
| R | gas constant, kJ/(kmol K) |
| t | time, s |
| T | temperature, K |
| V | volume, m |
| z | position, m |
| Greek letters | |
| degree of conversion | |
| dimensionless number related to adiabatic temperature increase | |
| dimensionless number related to activation energy | |
| dimensionless heat exchange coefficient | |
| dimensionless temperature | |
| dimensionless position, | |
| density, | |
| dimensionless time, | |
| Subscripts | |
| 0 | refers to feed |
| H | refers to heat |
| M | refers to mass |
| output of system | |
| r | refers to reverse flow; switching times |
| R | refers to reactor |
| s | refers to solid phase |
References
- Aubé, F.; Sapoundjiev, H. Mathematical model and numerical simulations of catalytic flow reversal reactors for industrial applications. Comput. Chem. Eng. 2000, 24, 2623–2632. [Google Scholar] [CrossRef]
- Berezowski, M. Fractal solutions of recirculation tubular chemical reactors. Chaos Solitons Fractals 2003, 16, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Berezowski, M. Spatio-temporal chaos in tubular chemical reactors with the recycle of mass. Chaos Solitons Fractals 2000, 11, 1197–1204. [Google Scholar] [CrossRef]
- Berezowski, M.; Kulik, B. Periodicity of chaotic solutions of the model of thermally coupled cascades of chemical tank reactors with flow reversal. Chaos Solitons Fractals 2009, 40, 331–336. [Google Scholar] [CrossRef] [Green Version]
- Elnashaie, S.; Abashar, M. On the chaotic behaviour of forced fluidized bed catalytic reactors. Chaos Solitons Fractals 1995, 5, 797–831. [Google Scholar] [CrossRef]
- Femat, R.; Méndez-Acosta, H.; Steyer, J.; González-Alvarez, V. Temperature oscillations in a biological reactor with recycle. Chaos Solitons Fractals 2004, 19, 875–889. [Google Scholar] [CrossRef]
- Khinast, J.; Luss, D. Mapping regions with different bifurcation diagrams of a reverse-flow reactor. AIChE J. 1997, 43, 2034–2047. [Google Scholar] [CrossRef]
- Khinast, J.; Gurumoothy, A.; Luss, D. Complex Dynamic Features of a Cooled Reverse-Flow Reactor. AIChE J. 1998, 44, 1128–1140. [Google Scholar] [CrossRef]
- Matros, Y.S.; Bunimovich, G.A. Reverse-Flow Operation in Fixed Bed Catalytic Reactors. Catal. Rev. 1996, 38, 1–68. [Google Scholar] [CrossRef]
- Merta, H. Characteristic time series and operation region of the system of two tank reactors (CSTR) with variable division of recirculation stream. Chaos Solitons Fractals 2006, 27, 279–285. [Google Scholar] [CrossRef]
- Merta, H.; Pelka, R. Chaotic dynamics of a cascade of plug flow tubular reactors (PFTRs) with division of recirculating stream. Chaos Solitons Fractals 2005, 23, 1211–1219. [Google Scholar] [CrossRef]
- Řeháček, J.; Kubíček, M.; Marek, M. Periodic, quasiperiodic and chaotic spatiotemporal patterns in a tubular catalytic reactor with periodic flow reversal. Comput. Chem. Eng. 1998, 22, 283–297. [Google Scholar] [CrossRef]
- Russo, L.; Altimari, P.; Mancusi, E.; Maffettone, P.L.; Crescitelli, S. Complex dynamics and spatio-temporal patterns in a network of three distributed chemical reactors with periodical feed switching. Chaos Solitons Fractals 2006, 28, 682–706. [Google Scholar] [CrossRef]
- Russo, L.; Mancusi, E.; Maffettone, P.L.; Crescitelli, S. Symmetry properties and bifurcation analysis of a class of periodically forced chemical reactors. Chem. Eng. Sci. 2002, 57, 5065–5082. [Google Scholar] [CrossRef]
- Salinger, A.G.; Eigenberger, G. The direct calculation of periodic states of the reverse flow reactior—I. Methodology and propane combustion results. Chem. Eng. Sci. 1996, 51, 4903–4913. [Google Scholar] [CrossRef]
- Salinger, A.G.; Eigenberger, G. The direct calculation of periodic states of the reverse flow reactor—II. Multiplicity and instability. Chem. Eng. Sci. 1996, 51, 4915–4922. [Google Scholar] [CrossRef]
- Żukowski, W.; Berezowski, M. Generation of chaotic oscillations in a system with flow reversal. Chem. Eng. Sci. 2000, 55, 339–343. [Google Scholar] [CrossRef]
- Wibowo, R.B.E.; Suzuki, T.; Takahashi, R. A Mathematical Study on the System of Partial Differential Equations Describing Reverse-Flow Reactor. Math. Model. Anal. 2016, 21, 550–568. [Google Scholar] [CrossRef] [Green Version]
- Ray, W.; Marek, M.; Elnashaie, S. The effect of heat and mass dispersion on tubular reactor performance. Chem. Eng. Sci. 1972, 27, 1527–1536. [Google Scholar] [CrossRef]
- Di Sarli, V.; Marra, F.S.; Di Benedetto, A. Spontaneous Oscillations in Lean Premixed Combustors: CFD Simulation. Combust. Sci. Technol. 2007, 179, 2335–2359. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A.; Marra, F.S. Influence of system parameters on the dynamic behaviour of an LPM combustor: Bifurcation analysis through CFD simulations. Combust. Theory Model. 2008, 12, 1109–1124. [Google Scholar] [CrossRef]
- Garcia-Agreda, A.; Di Sarli, V.; Di Benedetto, A. Bifurcation analysis of the effect of hydrogen addition on the dynamic behavior of lean premixed pre-vaporized ethanol combustion. Int. J. Hydrogen Energy 2012, 37, 6922–6932. [Google Scholar] [CrossRef]
- Berezowski, M. Crisis phenomenon in a chemical reactor with recycle. Chem. Eng. Sci. 2013, 101, 451–453. [Google Scholar] [CrossRef]
- Bizon, K.; Continillo, G.; Berezowski, M.; Smuła-Ostaszewska, J. Optimal model reduction by empirical spectral methods via sampling of chaotic orbits. Phys. D Nonlinear Phenom. 2012, 241, 1441–1449. [Google Scholar] [CrossRef]
- Batty, M. Spatial Entropy. Geogr. Anal. 1974, 6, 1–31. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezowski, M.; Kozioł, N.; Lawnik, M. Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor. Catalysts 2022, 12, 37. https://doi.org/10.3390/catal12010037
Berezowski M, Kozioł N, Lawnik M. Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor. Catalysts. 2022; 12(1):37. https://doi.org/10.3390/catal12010037
Chicago/Turabian StyleBerezowski, Marek, Natalia Kozioł, and Marcin Lawnik. 2022. "Spectral, Entropy and Bifurcation Analysis of the Dynamics of a Catalyst Chemical Reverse-Flow Tubular Reactor" Catalysts 12, no. 1: 37. https://doi.org/10.3390/catal12010037






