Effect of Water and Formic Acid on ·OH + CH4 Reaction: An Ab Initio/DFT Study
Abstract
:1. Introduction
2. Theoretical Methodology
2.1. Computational Method
2.2. Chemical Kinetics Calculations
3. Results and Discussion
3.1. Reaction Pathways for OH + CH4
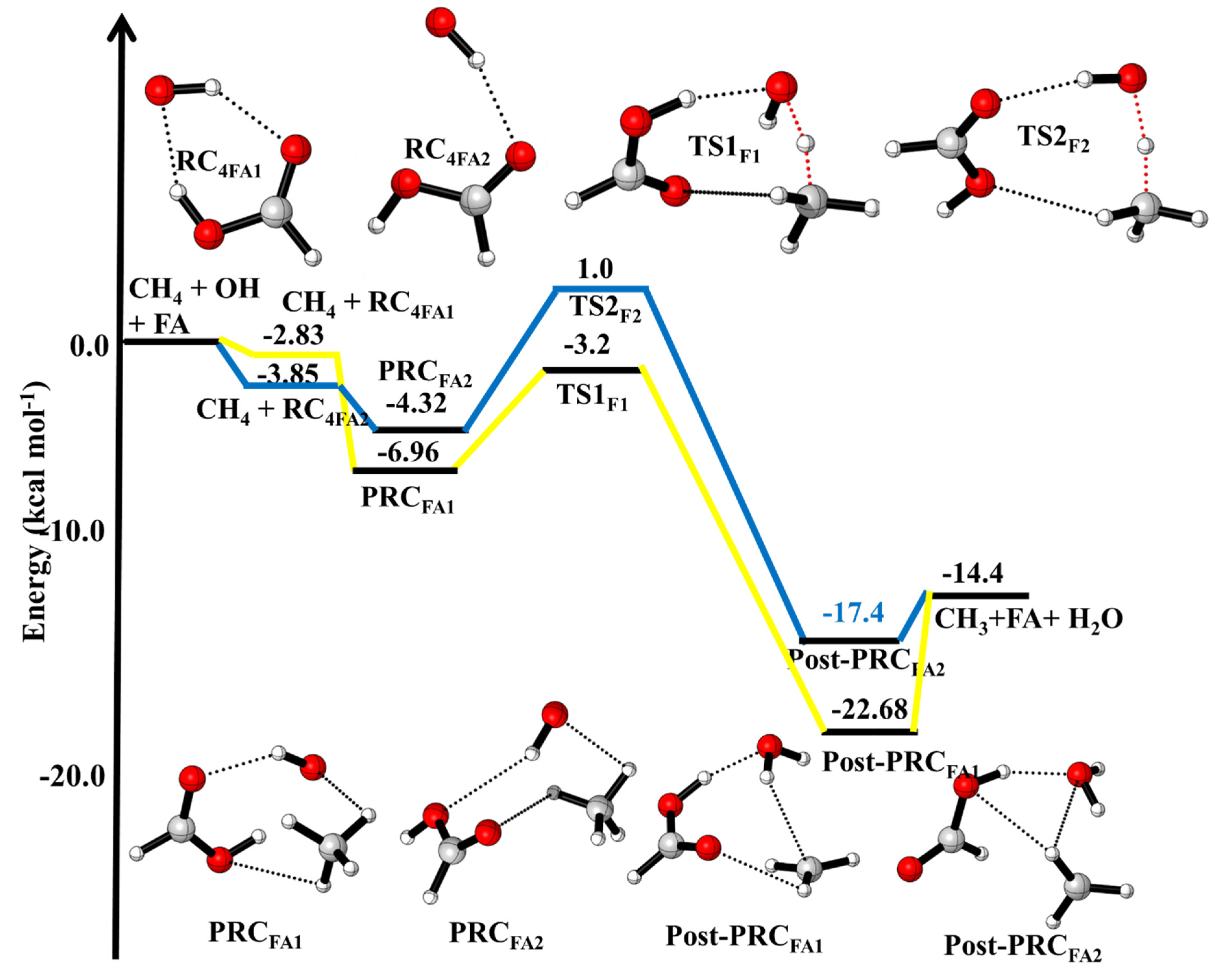
3.1.1. Reaction Pathways for ·OH + CH4 (+HCOOH)
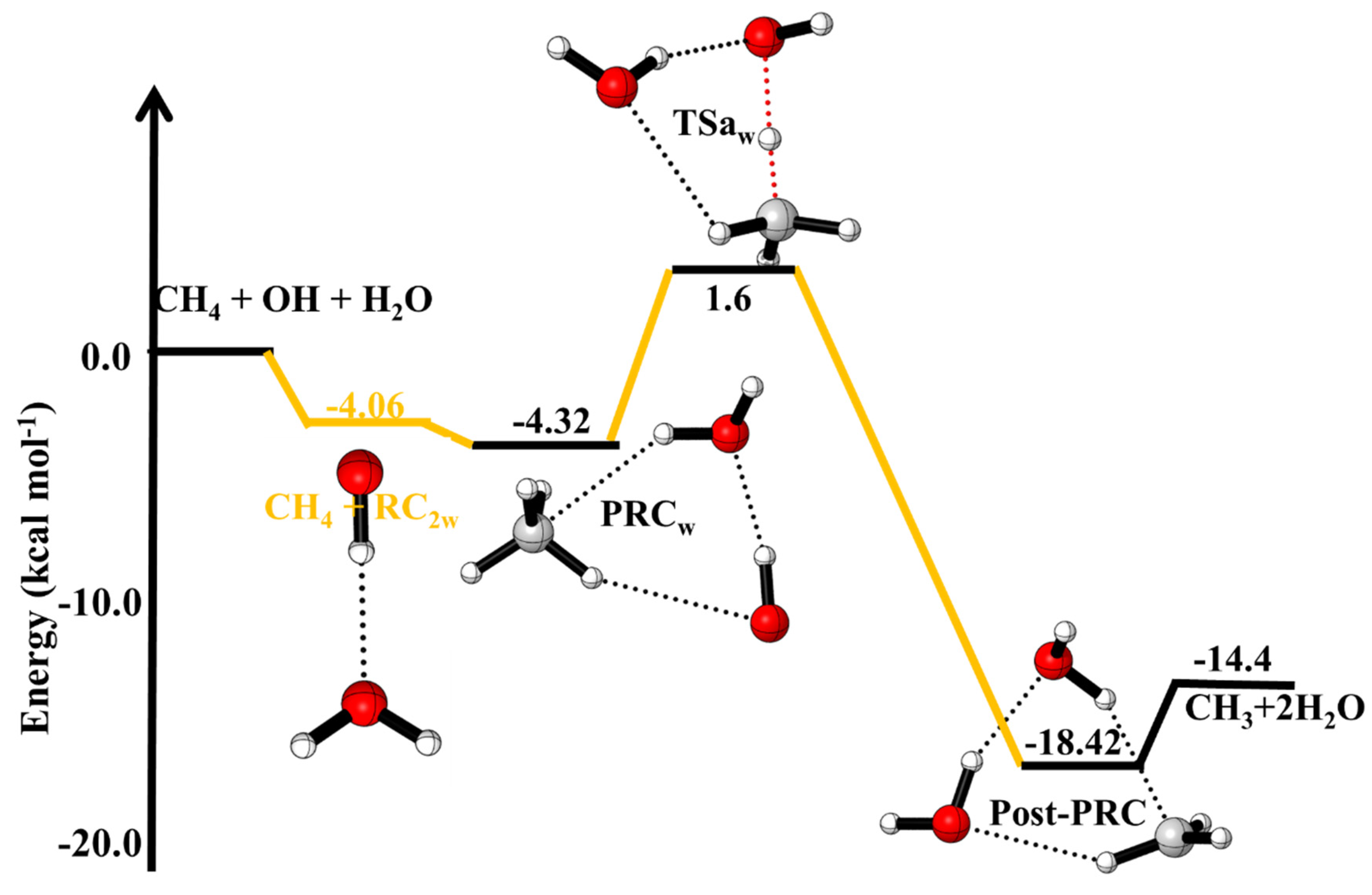
3.1.2. Reaction Pathways for ·OH + CH4 (+H2O)
3.2. Enthalpies of Reactions (∆Hrxn (0 K))
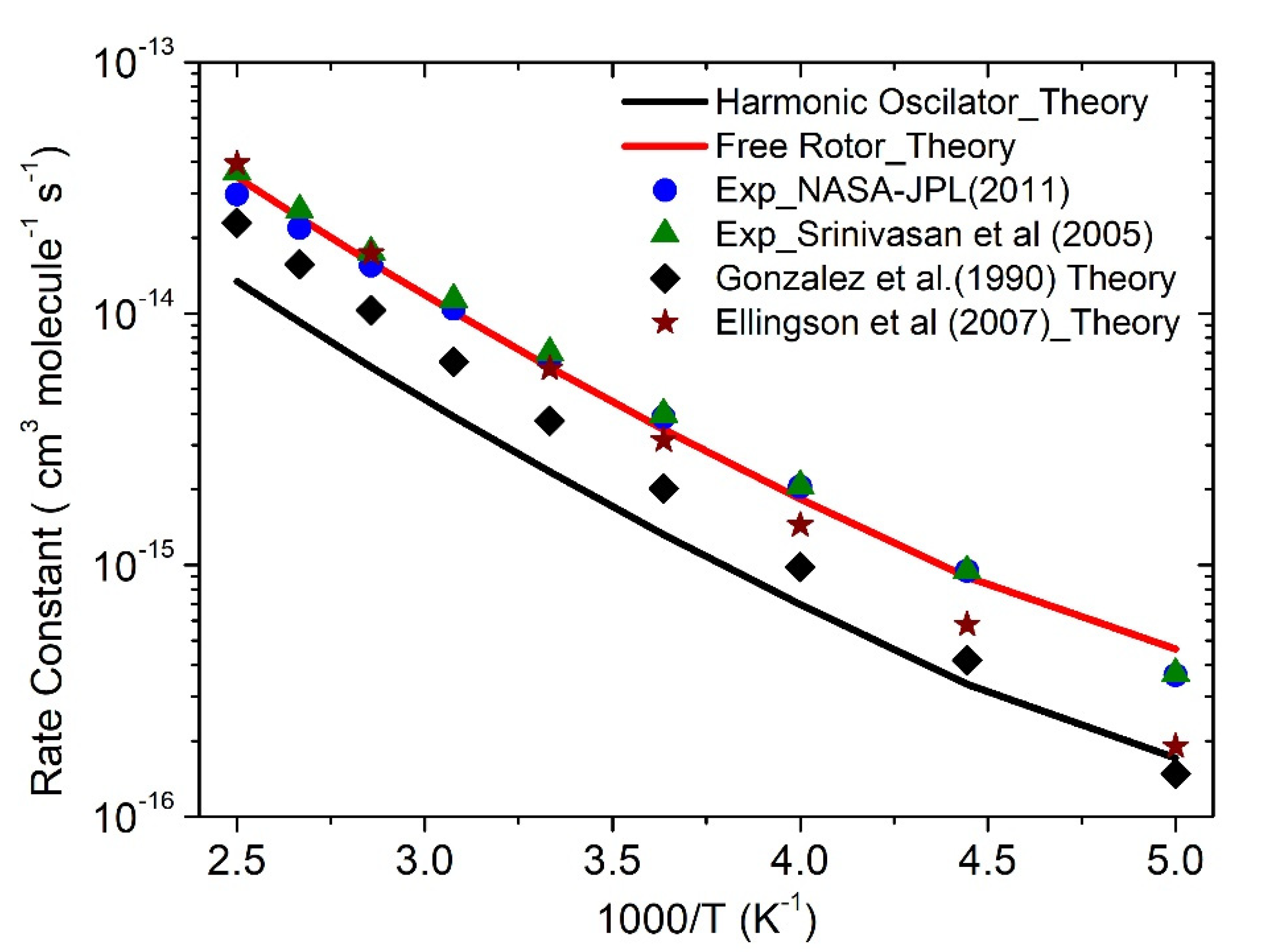
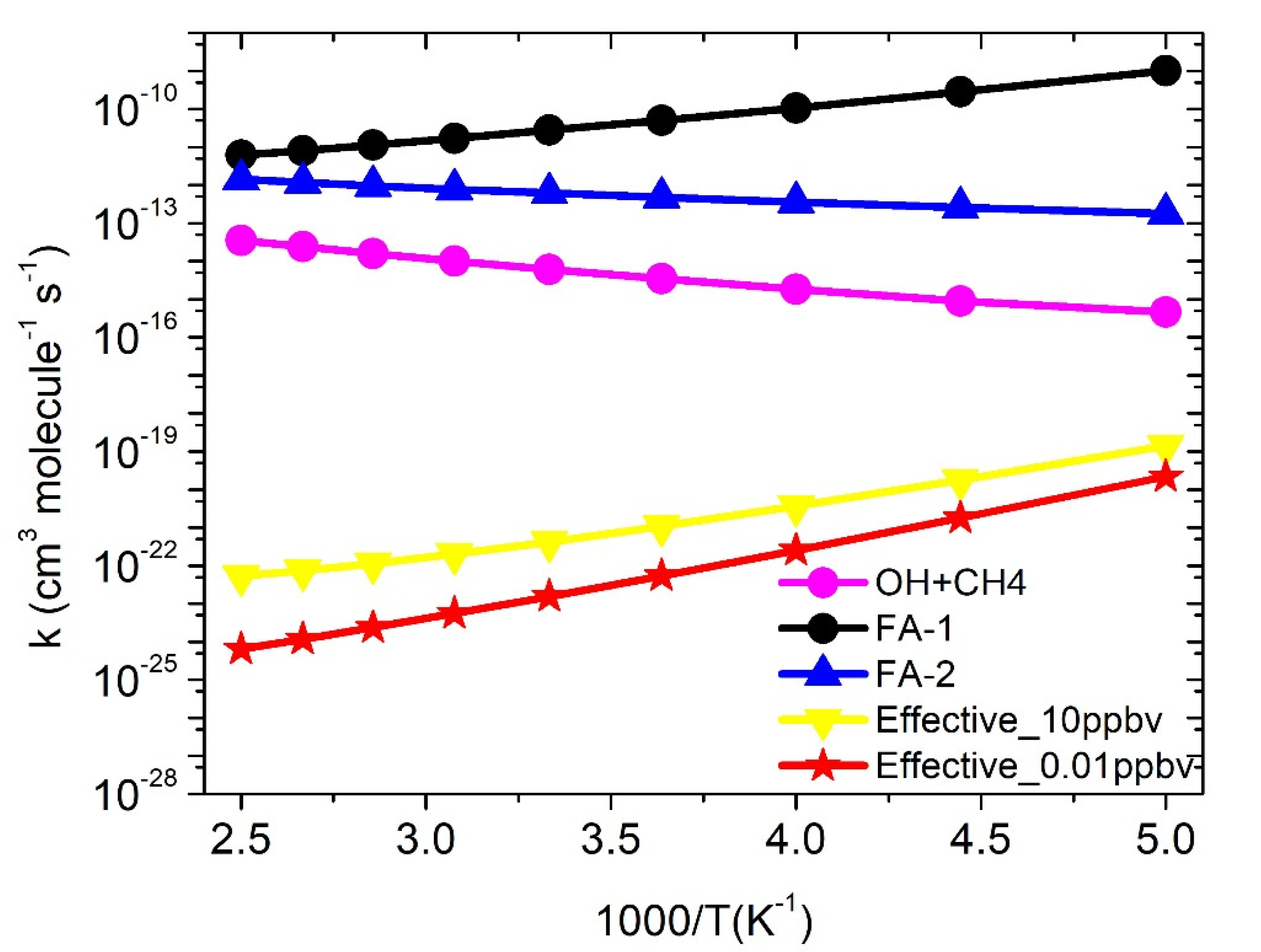
3.3. Rate Constants
·OH + CH4 Reaction
3.4. Formic Acid Assisted ·OH + CH4 Reaction
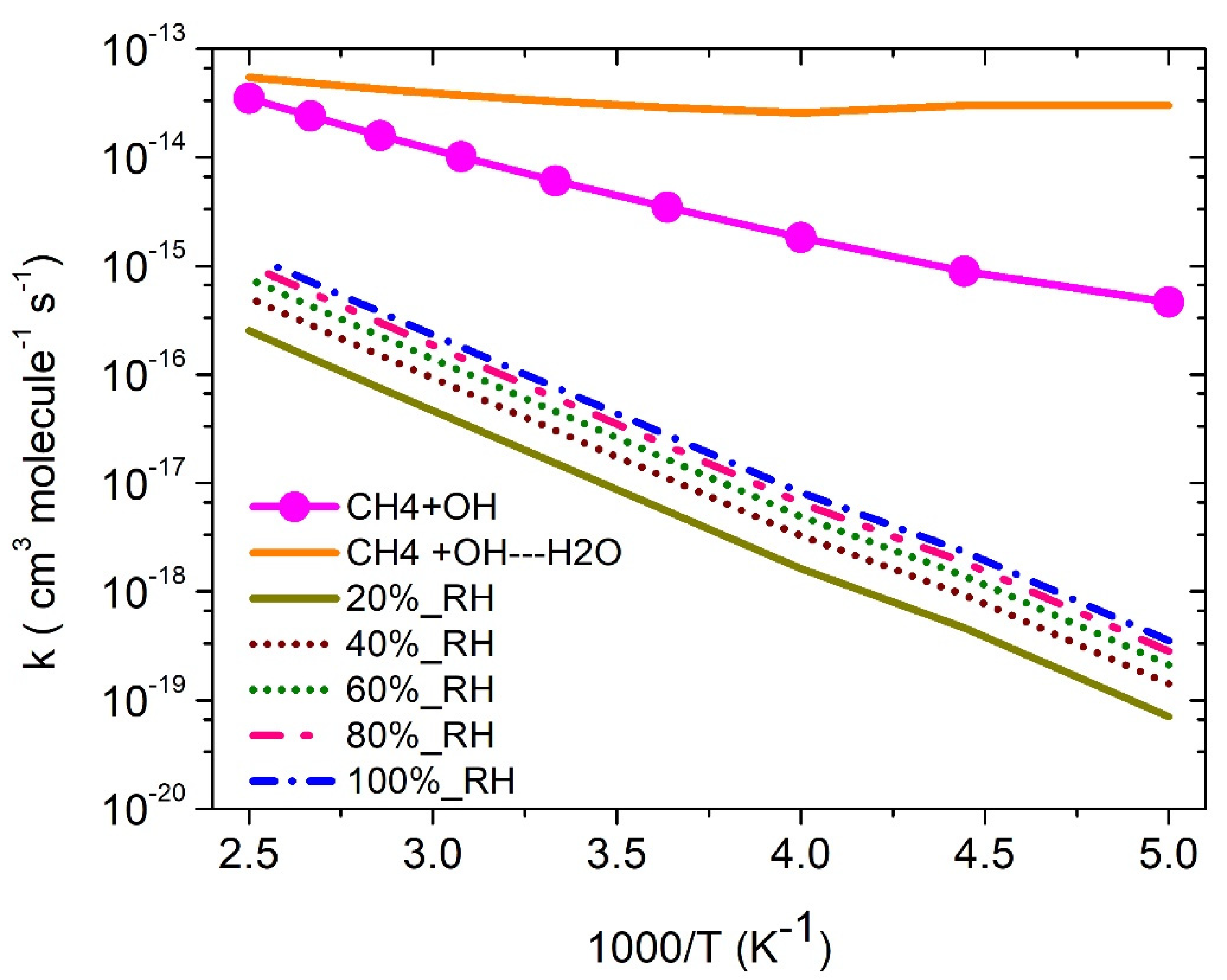
3.5. Water-Assisted ·OH + CH4 Reaction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crabtree, R.H. Aspects of Methane Chemistry. Chem. Rev. 1995, 95, 987–1007. [Google Scholar] [CrossRef]
- Vaghjiani, G.L.; Ravishankara, A.R. New measurement of the rate coefficient for the reaction of OH with methane. Nature 1991, 350, 406–409. [Google Scholar] [CrossRef]
- Jackson, R.B.; Saunois, M.; Bousquet, P.; Canadell, J.G.; Poulter, B.; Stavert, A.R.; Bergamaschi, P.; Niwa, Y.; Segers, A.; Tsuruta, A. Increasing anthropogenic methane emissions arise equally from agricultural and fossil fuel sources. Environ. Res. Lett. 2020, 15, 071002. [Google Scholar] [CrossRef]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Srinivasan, N.K.; Su, M.C.; Sutherland, J.W.; Michael, J.V. Reflected Shock Tube Studies of High-Temperature Rate Constants for OH + CH4 → CH3 + H2O and CH3 + NO2 → CH3O + NO. J. Phys. Chem. A 2005, 109, 1857–1863. [Google Scholar] [CrossRef]
- Li, J.; Guo, H. Thermal Rate Coefficients and Kinetic Isotope Effects for the Reaction OH + CH4 → H2O + CH3 on an ab Initio-Based Potential Energy Surface. J. Phys. Chem. A 2018, 122, 2645–2652. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, C.; McDouall, J.J.W.; Schlegel, H.B. Ab initio study of the reactions between methane and hydroxyl, hydrogen atom, and triplet oxygen atom. J. Phys. Chem. 1990, 94, 7467–7471. [Google Scholar] [CrossRef]
- Li, J.; Guo, H. Communication: An accurate full 15 dimensional permutationally invariant potential energy surface for the OH + CH4 → H2O + CH3 reaction. J. Chem. Phys. 2015, 143, 221103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ellingson, B.A.; Pu, J.; Lin, H.; Zhao, Y.; Truhlar, D.G. Multicoefficient Gaussian-3 Calculation of the Rate Constant for the OH + CH4 Reaction and Its 12C/13C Kinetic Isotope Effect with Emphasis on the Effects of Coordinate System and Torsional Treatment. J. Phys. Chem. A 2007, 111, 11706–11717. [Google Scholar] [CrossRef] [PubMed]
- Franco, B.; Blumenstock, T.; Cho, C.; Clarisse, L.; Clerbaux, C.; Coheur, P.F.; De Mazière, M.; De Smedt, I.; Dorn, H.P.; Emmerichs, T.; et al. Ubiquitous atmospheric production of organic acids mediated by cloud droplets. Nature 2021, 593, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Millet, D.B.; Baasandorj, M.; Farmer, D.K.; Thornton, J.A.; Baumann, K.; Brophy, P.; Chaliyakunnel, S.; de Gouw, J.A.; Graus, M.; Hu, L.; et al. A large and ubiquitous source of atmospheric formic acid. Atmos. Chem. Phys. 2015, 15, 6283–6304. [Google Scholar] [CrossRef] [Green Version]
- Keene, W.C.; Galloway, J.N. The biogeochemical cycling of formic and acetic acids through the troposphere: An overview of current understanding. Tellus 1988, 40B, 322–334. [Google Scholar] [CrossRef]
- Kumar, A.; Mallick, S.; Mishra, B.K.; Kumar, P. Effect of ammonia and formic acid on the CH3O˙ + O2 reaction: A quantum chemical investigation. Phys. Chem. Chem. Phys. 2020, 22, 2405–2413. [Google Scholar] [CrossRef]
- Mallick, S.; Sarkar, S.; Bandyopadhyay, B.; Kumar, P. Effect of Ammonia and Formic Acid on the OH• + HCl Reaction in the Troposphere: Competition between Single and Double Hydrogen Atom Transfer Pathways. J. Phys. Chem. A 2017, 122, 350–363. [Google Scholar] [CrossRef]
- Louie, M.K.; Francisco, J.S.; Verdicchio, M.; Klippenstein, S.J.; Sinha, A. Hydrolysis of Ketene Catalyzed by Formic Acid: Modification of Reaction Mechanism, Energetics, and Kinetics with Organic Acid Catalysis. J. Phys. Chem. A 2015, 119, 4347–4357. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Wen, M.; Tang, Z.; Long, B.; Yu, X.; Zhao, C.; Wang, W. Effects of water, ammonia and formic acid on HO2 + Cl reactions under atmospheric conditions: Competition between a stepwise route and one elementary step. RSC Adv. 2019, 9, 21544–21556. [Google Scholar] [CrossRef] [Green Version]
- Hazra, M.K.; Francisco, J.S.; Sinha, A. Gas Phase Hydrolysis of Formaldehyde To Form Methanediol: Impact of Formic Acid Catalysis. J. Phys. Chem. A 2013, 117, 11704–11710. [Google Scholar] [CrossRef]
- Monge-Palacios, M.; Rissanen, M.P.; Wang, Z.; Sarathy, S.M. Theoretical kinetic study of the formic acid catalyzed Criegee intermediate isomerization: Multistructural anharmonicity and atmospheric implications. Phys. Chem. Chem. Phys. 2018, 20, 10806–10814. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Du, B.; Qin, Z. Catalytic Effect of Water, Formic Acid, or Sulfuric Acid on the Reaction of Formaldehyde with OH Radicals. J. Phys. Chem. A 2014, 118, 4797–4807. [Google Scholar] [CrossRef]
- Jara-Toro, R.A.; Hernández, F.J.; Taccone, R.A.; Lane, S.I.; Pino, G.A. Water catalysis of the reaction between methanol and OH at 294 K and the atmospheric implications. Angew. Chem. Int. Ed. 2017, 56, 2166–2170. [Google Scholar] [CrossRef]
- Wu, J.; Gao, L.G.; Varga, Z.; Xu, X.; Ren, W.; Truhlar, D.G. Water catalysis of the Reaction of Methanol with OH Radical in the Atmosphere is Negligible. Angew. Chem. Int. Ed. 2020, 59, 10826–10830. [Google Scholar] [CrossRef]
- Vöhringer-Martinez, E.; Hansmann, B.; Hernandez, H.; Francisco, J.S.; Troe, J.; Abel, B. Water Catalysis of a Radical-Molecule Gas-Phase Reaction. Science 2007, 315, 497–501. [Google Scholar] [CrossRef]
- Thomsen, D.L.; Kurtén, T.; Jørgensen, S.; Wallington, T.J.; Baggesen, S.B.; Aalling, C.; Kjaergaard, H.G. On the possible catalysis by single water molecules of gas-phase hydrogen abstraction reactions by OH radicals. Phys. Chem. Chem. Phys. 2012, 14, 12992–12999. [Google Scholar] [CrossRef]
- Inaba, S. Catalytic Role of H2O Molecules in Oxidation of CH3OH in Water. Catalysts 2018, 8, 157. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.A.; Balaganesh, M.; Lin, K.C. Catalytic effect of a single water molecule on the OH + CH2NH reaction. Phys. Chem. Chem. Phys. 2018, 20, 4297–4307. [Google Scholar] [CrossRef]
- Ali, M.A.; Balaganesh, M.; Jang, S. Can a single water molecule catalyze the OH+CH2CH2 and OH+CH2O reactions? Atmos. Environ. 2019, 207, 82–92. [Google Scholar] [CrossRef]
- Ali, M.A.; Balaganesh, M.; Al-Odail, F.A.; Lin, K.C. Effect of ammonia and water molecule on OH + CH3OH reaction under tropospheric condition. Sci. Rep. 2021, 11, 12185. [Google Scholar] [CrossRef]
- Ali, M.A. Computational studies on the gas phase reaction of methylenimine (CH2NH) with water molecules. Sci. Rep. 2020, 10, 10995. [Google Scholar] [CrossRef]
- Buszek, R.J.; Torrent-Sucarrat, M.; Anglada, J.M.; Francisco, J.S. Effects of a Single Water Molecule on the OH + H2O2 Reaction. J. Phys. Chem. A 2012, 116, 5821–5829. [Google Scholar] [CrossRef]
- Iuga, C.; Alvarez-Idaboy, J.R.; Vivier-Bunge, A. On the possible catalytic role of a single water molecule in the acetone + OH gas phase reaction: A theoretical pseudo-second-order kinetics study. Theor. Chem. Accounts 2011, 129, 209–217. [Google Scholar] [CrossRef]
- Iuga, C.; Alvarez-Idaboy, J.R.; Reyes, L.; Vivier-Bunge, A. Can a Single Water Molecule Really Catalyze the Acetaldehyde + OH Reaction in Tropospheric Conditions? J. Phys. Chem. Lett. 2010, 1, 3112–3115. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, W.; Li, C.; Du, Y.; Lü, J. Catalytic effect of a single water molecule on the atmospheric reaction of HO2 + OH: Fact or fiction? A mechanistic and kinetic study. RSC Adv. 2013, 3, 7381–7391. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Zhang, S.; Lynch, B.J.; Corchado, J.C.; Chuang, Y.-Y.; Fast, P.L.; Hu, W.P.; Liu, Y.P.; Lynch, G.C.; Nguyen, K.A.; et al. POLYRATE, Version 2008; University of Minnesota: Minneapolis, MN, USA, 2009. [Google Scholar]
- Zheng, J.; Zhang, S.; Corchado, J.C.; Chuang, Y.Y.; Coitino, E.L.; Ellingson, B.A.; Truhlar, D.G. GAUSSRATE, Version 2009-A; University of Minnesota: Minneapolis, MN, USA, 2010. [Google Scholar]
- Barker, J.R.; Ortiz, N.F.; Preses, J.M.; Lohr, L.L.; Maranzana, A.; Stimac, P.J.; Lam, N.T.; Dhilip Kumar, T.J. MultiWell-2016 Software; University of Michigan: Ann Arbor, MI, USA, 2016. [Google Scholar]
- Ruscic, B.; Pinzon, R.E.; Morton, M.L.; von Laszevski, G.; Bittner, S.J.; Nijsure, S.G.; Amin, K.A.; Minkoff, M.; Wagner, A.F. Introduction to Active Thermochemical Tables: Several “Key” Enthalpies of Formation Revisited. J. Phys. Chem. A 2004, 108, 9979–9997. [Google Scholar] [CrossRef]
- Ruscic, B.; Pinzon, R.E.; Von Laszewski, G.; Kodeboyina, D.; Burcat, A.; Leahy, D.; Montoy, D.; Wagner, A.F. Active Thermochemical Tables: Thermochemistry for the 21st century. J. Phys. Conf. Ser. 2005, 16, 561–570. [Google Scholar] [CrossRef]
- Ruscic, B.; Bross, D.H. Active Thermochemical Tables (ATcT) Enthalpies of Formation Values Based on ver. 1.112d of the Thermochemical Network. 2018. Available online: https://atct.anl.gov/ (accessed on 26 December 2021).
- Sander, S.P.; Abbatt, J.P.D.; Barker, J.R.; Burkholder, J.B.; Friedl, R.R.; Golden, D.M.; Huie, R.E.; Kolb, C.E.; Kurylo, M.J.; Moortgat, G.K.; et al. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies: Evaluation Number 17; JPL Publication 10-6; Jet Propulsion Laboratory: Pasadena, CA, USA, 2011. [Google Scholar]
- Kulongoski, J.T.; McMahon, P.B. Methane emissions from groundwater pumping in the USA. npj Clim. Atmos. Sci. 2019, 2, 11. [Google Scholar] [CrossRef] [Green Version]
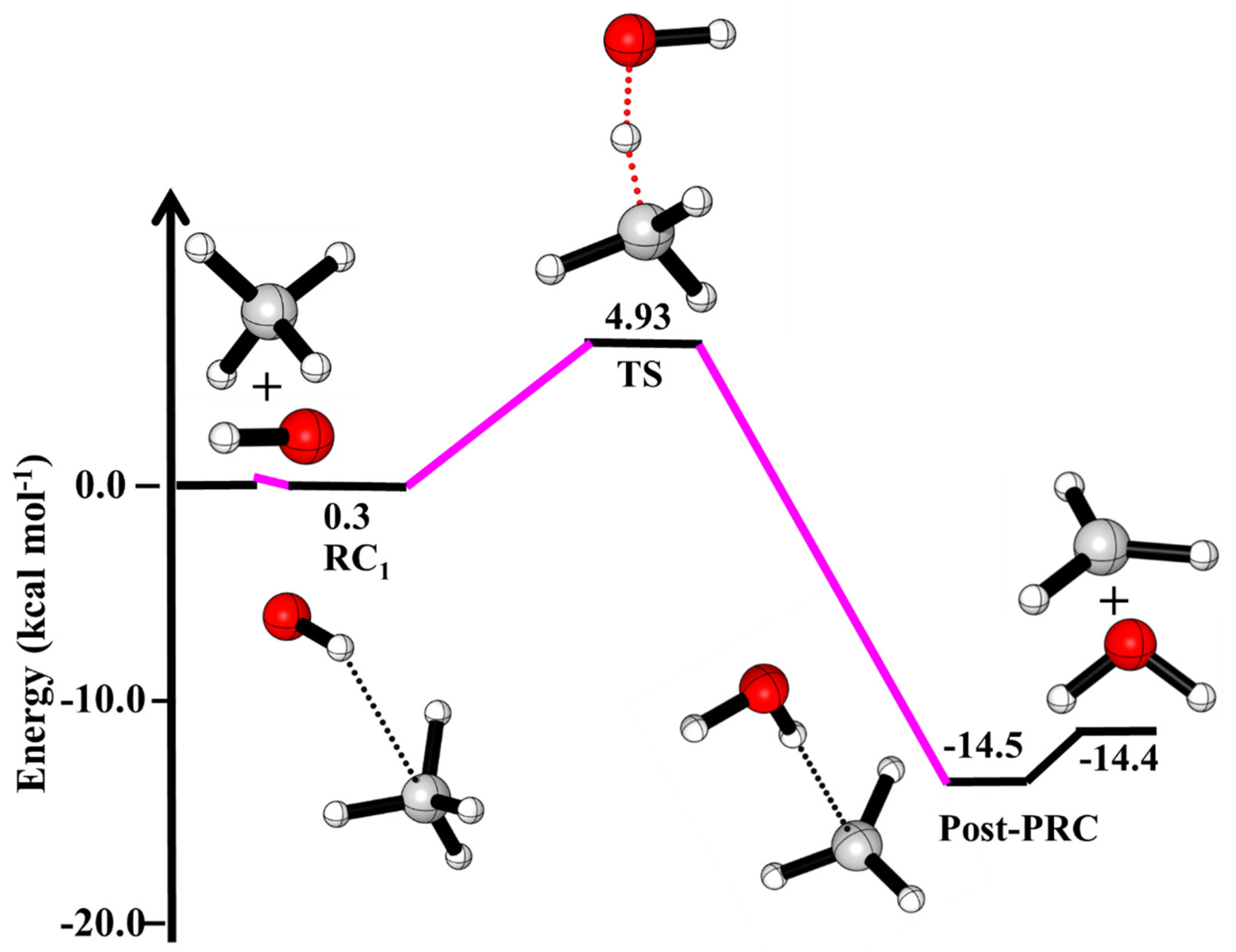

| ·OH + CH4→ | This Work | Literature a,b,c |
|---|---|---|
| ·OH···CH4 (RC1) | 0.30 | |
| HO···HCH3 (TS) | 4.93 | |
| ·CH3 + H2O | −14.4 | −14.3 a, −13.9 b, −13.4 c |
| ·OH + CH4 + HCOOH → | This Work | |
| ·OH···CH4···HCOOH (PRCFA1) | −6.96 | |
| ·OH···CH4···HCOOH(PRCFA) | −4.32 | |
| ·OH···HCH3···HCOOH (TSFA1) | −3.2 | |
| ·OH···HCOOH···HCH3 (TSFA2) | +1.0 | |
| H2O···HCOOH···CH3 (Post-PRCFA1) H2O···HCOOH···CH3 (Post-PRCFA2) CH3 + H2O + FA | −17.4 −22.7 −14.4 | |
| ·OH + CH4 +H2O→ | This Work | |
| ·OH···CH4···H2O (PRCw) | −4.32 | |
| ·OH···HCH3···H2O (TSw) | +1.6 | |
| H2O···H2O···CH3(Post-PRCw) | −18.42 | |
| ·CH3 + 2H2O | −14.4 |
| Temp (K) | k-HO | k-FR | Exp [2,39] | Exp [5] | Theory [9] |
|---|---|---|---|---|---|
| 200 | 1.7 × 10−16 | 4.6 × 10−16 | 3.6 × 10−16 | 3.7 × 10−16 | 1.5 × 10−16 |
| 225 | 3.4 × 10−16 | 8.9 × 10−16 | 9.5 × 10−16 | 9.5 × 10−16 | 4.2 × 10−16 |
| 250 | 7.0 × 10−16 | 1.8 × 10−15 | 2.0 × 10−15 | 2.1 × 10−15 | 9.8 × 10−16 |
| 275 | 1.3 × 10−15 | 3.5 × 10−15 | 3.9 × 10−15 | 4.0 × 10−15 | 2.0 × 10−15 |
| 300 | 2.3 × 10−15 | 6.1 × 10−15 | 6.6 × 10−15 | 6.9 × 10−15 | 3.8 × 10−15 |
| 325 | 3.9 × 10−15 | 1.0 × 10−14 | 1.0 × 10−14 | 1.1 × 10−14 | 6.4 × 10−15 |
| 350 | 6.1 × 10−15 | 1.6 × 10−14 | 1.5 × 10−14 | 1.8 × 10−14 | 1.0 × 10−14 |
| 375 | 9.2 × 10−15 | 2.4 × 10−14 | 2.2 × 10−14 | 2.6 × 10−14 | 1.6 × 10−14 |
| 400 | 1.3 × 10−14 | 3.5 × 10−14 | 2.9 × 10−14 | 3.6 × 10−14 | 2.3 × 10−14 |
| k = ATn exp(−B/T) | A = 1.2 × 10−28 N = 5.9 B = 134 | A = 3 × 10−29 N = 5.9 B = 134 | A = 3 × 10−14 N = 0.67 B = 1575 | A = 1.6 × 10−18 N = 2.1 B = 1231 | A = 3.7 × 10−13 N = 2.3 B = 1377 |
| Temp (K) | kCH4+OH | keff FA | keffW |
|---|---|---|---|
| 200 | 4.6 × 10−16 | 1.4 × 10−19 | 3.5 × 10−19 |
| 225 | 8.9 × 10−16 | 1.8 × 10−20 | 4.9 × 10−18 |
| 250 | 1.8 × 10−15 | 3.7 × 10−21 | 8.2 × 10−18 |
| 275 | 3.5 × 10−15 | 1.1 × 10−21 | 2.8 × 10−17 |
| 300 | 6.1 × 10−15 | 4.2 × 10−22 | 7.6 × 10−17 |
| 325 | 1.0 × 10−14 | 2.0 × 10−22 | 1.8 × 10−16 |
| 350 | 1.6 × 10−14 | 1.1 × 10−22 | 3.8 × 10−16 |
| 375 | 2.4 × 10−14 | 7.4 × 10−23 | 7.1 × 10−16 |
| 400 | 3.5 × 10−14 | 5.4 × 10−23 | 1.3 × 10−15 |
| k = ATn exp(−B/T) | A = 3.0 × 10−29 N = 5.9 B = 134 | A = 1.0 × 10−54 N = 9.7 B = −5872 | A = 7.4 × 10−18 N = 2.0 B = 2717 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.A.; Muthiah, B. Effect of Water and Formic Acid on ·OH + CH4 Reaction: An Ab Initio/DFT Study. Catalysts 2022, 12, 133. https://doi.org/10.3390/catal12020133
Ali MA, Muthiah B. Effect of Water and Formic Acid on ·OH + CH4 Reaction: An Ab Initio/DFT Study. Catalysts. 2022; 12(2):133. https://doi.org/10.3390/catal12020133
Chicago/Turabian StyleAli, Mohamad Akbar, and Balaganesh Muthiah. 2022. "Effect of Water and Formic Acid on ·OH + CH4 Reaction: An Ab Initio/DFT Study" Catalysts 12, no. 2: 133. https://doi.org/10.3390/catal12020133
APA StyleAli, M. A., & Muthiah, B. (2022). Effect of Water and Formic Acid on ·OH + CH4 Reaction: An Ab Initio/DFT Study. Catalysts, 12(2), 133. https://doi.org/10.3390/catal12020133






