Hydrocarbon Oxidation Depth: H2O2/Cu2Cl4·2DMG/CH3CN System
Abstract
:1. Introduction
2. Results and Discussion
2.1. Hydrocarbon Oxidation Depth
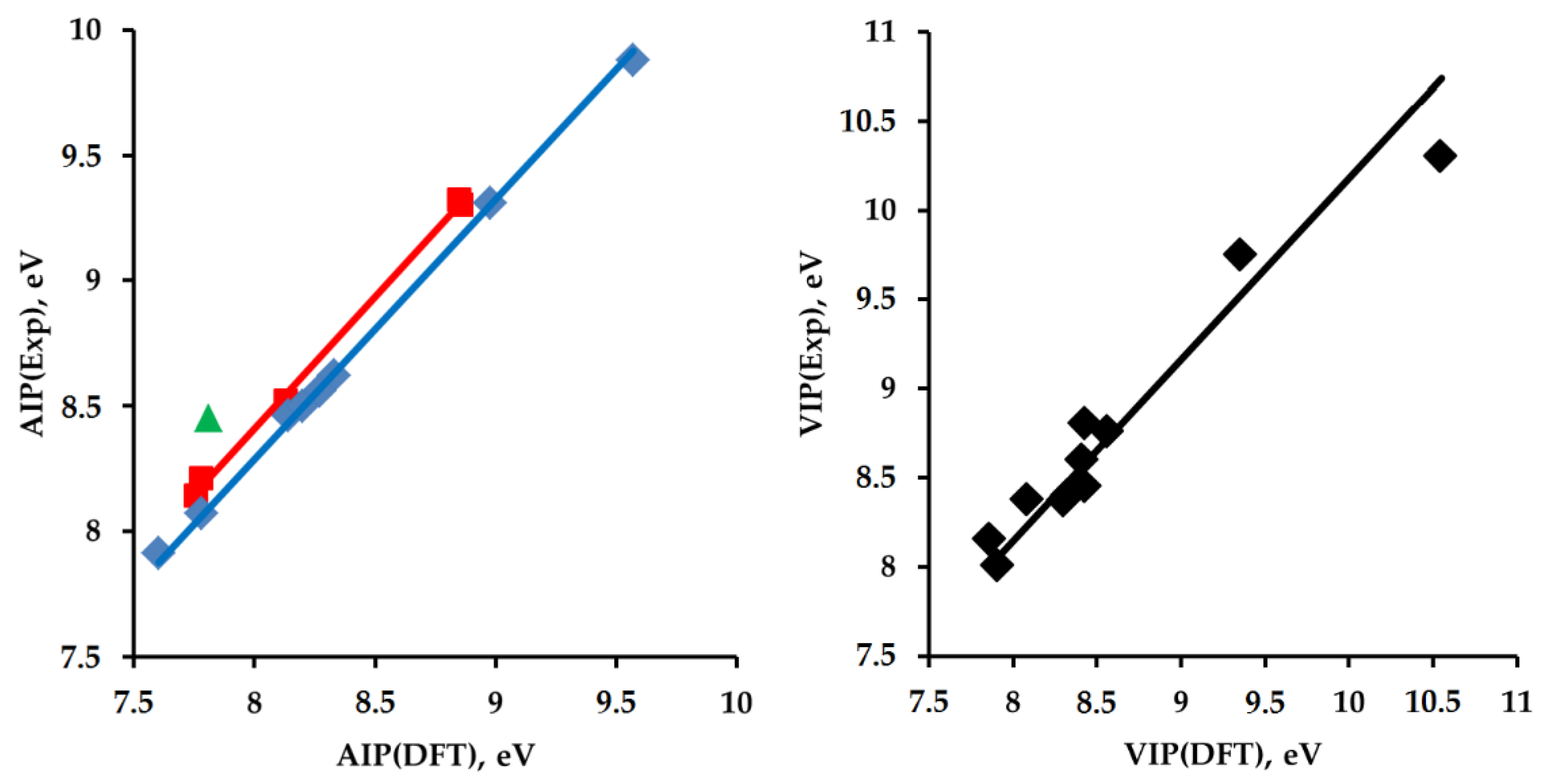
2.2. Adiabatic Ionization Potentials of the Hydrocarbons
2.3. Comparison of Two Hydrocarbon Characteristics: Oxidation Depth D(O) and Adiabatic Ionization Potential
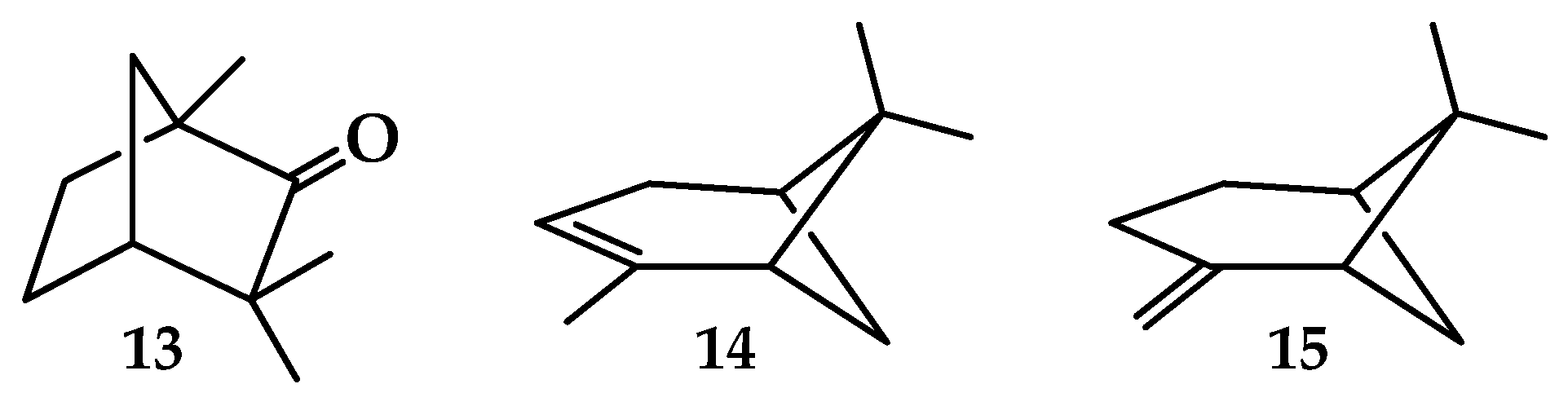
2.4. Molecule X with Adiabatic Ionization Potentials Equal 8.55 ± 0.03 eV
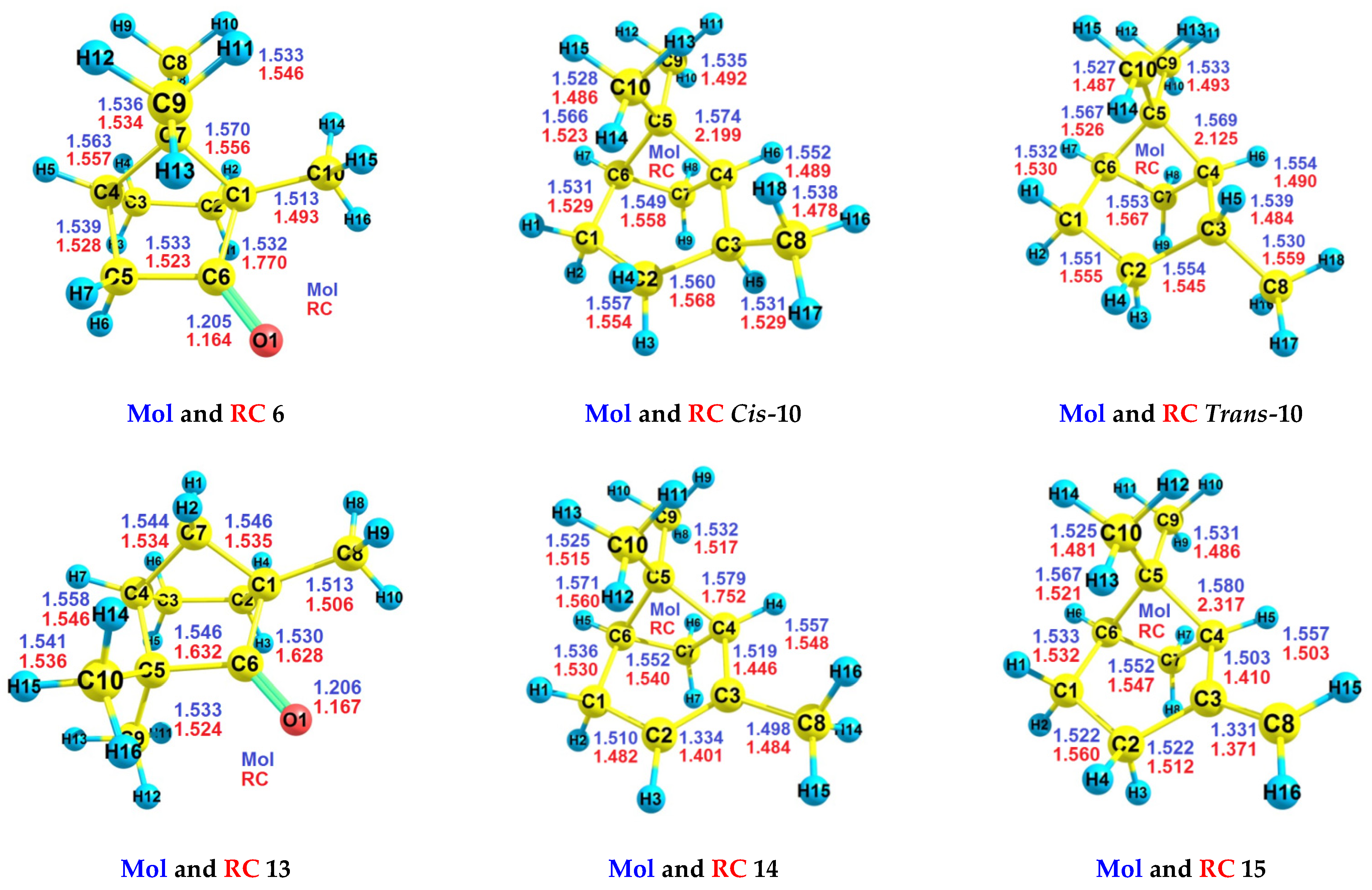
2.5. Additional Methodological Comments
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Costa, I.F.; Kirillova, M.V.; André, V.; Fernandes, T.A.; Kirillov, A.M. Time-Dependent Self-Assembly of Copper(II) Coordination Polymers and Tetranuclear Rings: Catalysts for Oxidative Functionalization of Saturated Hydrocarbons. Inorg. Chem. 2021, 60, 14491–14503. [Google Scholar] [CrossRef] [PubMed]
- Marais, L.; Vosloo, H.C.M.; Swarts, A.J. Homogeneous oxidative transformations mediated by copper catalyst systems. Coord. Chem. Rev. 2021, 440, 213958. [Google Scholar] [CrossRef]
- Lawal, N.S.; Ibrahim, H.; Bala, M.D. Facile Peroxidation of Cyclohexane Catalysed by In Situ Generated Triazole-Functionalised Schiff Base Copper Complexes. Catal. Lett. 2021, 1–12. [Google Scholar] [CrossRef]
- Xu, B.; Xu, Q.; Wang, Q.; Liu, Z.; Zhao, R.; Li, D.; Ma, P.; Wang, J.; Niu, J. A Copper-Containing Polyoxometalate-Based Metal—Organic Framework as an Efficient Catalyst for Selective Catalytic Oxidation of Alkylbenzenes. Inorg. Chem. 2021, 60, 4792–4799. [Google Scholar] [CrossRef]
- Jurgeleit, R.; Grimm-Lebsanft, B.; Flöser, B.M.; Teubner, M.; Buchenau, S.; Senft, L.; Hoffmann, J.; Naumova, M.; Ivanović-Burmazović, I.; Rübhausen, M.; et al. Catalytic Oxygenation of Hydrocarbons by Mono-μ-oxo Dicopper(II) Species Resulting from O–O Cleavage of Tetranuclear CuI/CuII Peroxo Complexes. Angew. Chem. Int. Ed. 2021, 60, 14154–14162. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, J.; Ma, J.; Pang, S.; Zhang, T. A review on advanced oxidation processes homogeneously initiated by copper(II). Chem. Eng. J. 2022, 427, 131721. [Google Scholar] [CrossRef]
- Komiya, N.; Murahashi, S.I. Transition Metal-Catalyzed C–H Oxidation of Saturated Hydrocarbons with Molecular Oxygen. Chem. Rec. 2021, 21, 1928–1940. [Google Scholar] [CrossRef]
- Nagababu, P.; Paul, P.S.; Reddy, T.B.; Krupadam, R.J. Efficient and region-selective conversion of octanes to epoxides under ambient conditions: Performance of tri-copper catalyst, [Cu3I(L)]+1 (L=7-N-Etppz). Ind. J. Chem. Sec. B (IJC-B) 2021, 60, 742–745. Available online: http://nopr.niscair.res.in/handle/123456789/57584 (accessed on 15 March 2022).
- Wu, T.; MacMillan, S.N.; Rajabimoghadam, K.; Siegler, M.A.; Lancaster, K.M.; Garcia-Bosch, I. Structure, spectroscopy and reactivity of a mononuclear copper hydroxide complex in three molecular oxidation states. J. Am. Chem. Soc. 2020, 142, 12265–12276. [Google Scholar] [CrossRef]
- Chan, S.I.; Yu, S.S.F.; Liu, C.C.; Mou, C.Y. Selective oxidation of light alkanes under mild conditions. Curr. Opin. Green Sustain. Chem. 2020, 22, 39–46. [Google Scholar] [CrossRef]
- Liu, H.; Shen, Q. Well-defined organometallic Copper(III) complexes: Preparation, characterization and reactivity. Coord. Chem. Rev. 2021, 442, 213923. [Google Scholar] [CrossRef]
- Zhong, X.; Bouchey, C.J.; Kabir, E.; Tolman, W.B. Using a monocopper-superoxo complex to prepare multicopper-peroxo species relevant to proposed enzyme intermediates. J. Inorg. Biochem. 2021, 222, 111498. [Google Scholar] [CrossRef] [PubMed]
- Shul’pin, G.B.; Shul’pina, L.S. Oxidation of Organic Compounds with Peroxides Catalyzed by Polynuclear Metal Compounds. Catalysts 2021, 11, 186. [Google Scholar] [CrossRef]
- DiMucci, I.M.; Lukens, J.T.; Chatterjee, S.; Carsch, K.M.; Titus, C.J.; Lee, S.J.; Nordlund, D.; Betley, T.A.; MacMillan, S.N.; Lancaster, K.M. The Myth of d8 Copper(III). J. Am. Chem. Soc. 2019, 141, 18508–18520. [Google Scholar] [CrossRef]
- Sutradhar, M.; Alegria, E.C.B.A.; Guedes da Silva, M.F.C.; Liu, C.M.; Pombeiro, A.J.L. Peroxidative Oxidation of Alkanes and Alcohols under Mild Conditions by Di- and Tetranuclear Copper(II) Complexes of Bis(2-Hydroxybenzylidene)Isophthalohydrazide. Molecules 2018, 23, 2699. [Google Scholar] [CrossRef] [Green Version]
- Jana, R.D.; Das, A.; Paine, T.K. Enhancing Chemo- and Stereoselectivity in C–H Bond Oxygenation with H2O2 by Nonheme High-Spin Iron Catalysts: The Role of Lewis Acid and Multimetal Centers. Inorg. Chem. 2021, 60, 5969–5979. [Google Scholar] [CrossRef]
- Wu, C.; Liu, B.; Geng, X.; Zhang, Z.; Liu, S.; Hu, Q. Selective Catalytic Oxidation of Aromatic Substrates Employing Mononuclear Copper(II) Catalyst with H2O2. Polyhedron 2019, 158, 334–341. [Google Scholar] [CrossRef]
- Nesterov, D.S.; Nesterova, O.V.; Pombeiro, A.J.L. Homo- and heterometallic polynuclear transition metal catalysts for alkane C–H bonds oxidative functionalization: Recent advances. Coord. Chem. Rev. 2018, 355, 199–222. [Google Scholar] [CrossRef]
- Ghosh, M.; Pattanayak, S.; Dhar, B.B.; Singh, K.K.; Panda, C.; Gupta, S.S. Selective C–H Bond Oxidation Catalyzed by the Fe-bTAML Complex: Mechanistic Implications. Inorg. Chem. 2017, 56, 10852–10860. [Google Scholar] [CrossRef]
- Sarkheil, M.; Lashanizadegan, M. Copper(II) Schiff Base Complex Immobilized on Superparamagnetic Fe3O4@SiO2 as a Magnetically Separable Nanocatalyst for Oxidation of Alkenes and Alcohols. Appl. Organometal. Chem. 2017, 31, e3726. [Google Scholar] [CrossRef]
- Hüppe, H.M.; Keisers, K.; Fink, F.; Mürtz, S.D.; Hoffmann, A.; Iffland, L.; Apfel, U.P.; Herres-Pawlis, S. Catalytically Active Iron(IV)oxo Species Based on a Bis(pyridinyl)phenanthrolinylmethane. Isr. J. Chem. 2020, 60, 987–998. [Google Scholar] [CrossRef] [Green Version]
- Hazra, S.; Rocha, B.G.M.; Guedes da Silva, M.F.C.; Karmakar, A.; Pombeiro, A.J.L. Syntheses, Structures, and Catalytic Hydrocarbon Oxidation Properties of N-Heterocycle-Sulfonated Schiff Base Copper(II) Complexes. Inorganics 2019, 7, 17. [Google Scholar] [CrossRef] [Green Version]
- Nesterova, O.V.; Kasyanova, K.V.; Makhankova, V.G.; Kokozay, V.N.; Vassilyeva, O.Y.; Skelton, B.W.; Nesterov, D.S.; Pombeiro, A.J.L. Stereospecific sp3 C–H Oxidation with m-CPBA: A CoIII Schiff Base Complex as Pre-catalyst vs. its CoIIICdII Heterometallic Derivative. Appl. Catal. Gen. 2018, 560, 171–184. [Google Scholar] [CrossRef]
- Seo, K.; Kim, H.; Lee, J.; Kim, M.G.; Seo, S.Y.; Kim, C. Cooperative behavior of perfluoro carboxylic acid on cyclohexane oxidation catalyzed by μ-nitrido diiron phthalocyanine complex. J. Ind. Eng. Chem. 2017, 53, 371–374. [Google Scholar] [CrossRef]
- Hitomi, Y.; Arakawa, K.; Kodera, M. Electronic Tuning of Iron–Oxo-Mediated C–H Activation: Effect of Electron-Donating Ligand on Selectivity. Chem. Eur. J. 2013, 19, 14697–14701. [Google Scholar] [CrossRef] [PubMed]
- Trusau, K.I.; Kirillova, M.V.; André, V.; Usevich, A.I.; Kirillov, A.M. Mild oxidative functionalization of cycloalkanes catalyzed by novel dicopper(II) cores. Mol. Catal. 2021, 503, 111401. [Google Scholar] [CrossRef]
- Mishra, S.; Bal, R.; Dey, R.K. Heterogeneous recyclable copper oxide supported on activated red mud as an efficient and stable catalyst for the one pot hydroxylation of benzene to phenol. Mol. Catal. 2021, 499, 111310. [Google Scholar] [CrossRef]
- Bai, J.; Huang, J.; Jiang, Q.; Li, Y.; Wang, H.; Yu, H.; Zhang, Q.; Cao, Y.; Peng, F. Radical Propagation Facilitating Aerobic Oxidation of Substituted Aromatics Promoted by Tert-Butyl Hydroperoxide. ChemistrySelect 2021, 6, 6895–6903. [Google Scholar] [CrossRef]
- Li, D.; Ma, X.; Wang, Q.; Ma, P.; Niu, J.; Wang, J. Copper-Containing Polyoxometalate-Based Metal–Organic Frameworks as Highly Efficient Heterogeneous Catalysts toward Selective Oxidation of Alkylbenzenes. Inorg. Chem. 2019, 58, 15832–15840. [Google Scholar] [CrossRef]
- Armakola, E.; Colodrero, R.M.P.; Bazaga-García, M.; Salcedo, I.R.; Choquesillo-Lazarte, D.; Cabeza, A.; Kirillova, M.V.; Kirillov, A.M.; Demadis, K.D. Three-Component Copper-Phosphonate-Auxiliary Ligand Systems: Proton Conductors and Efficient Catalysts in Mild Oxidative Functionalization of Cycloalkanes. Inorg. Chem. 2018, 57, 10656–10666. [Google Scholar] [CrossRef]
- Sasmal, H.S.; Bag, S.; Chandra, B.; Majumder, P.; Kuiry, H.; Karak, S.; Gupta, S.S.; Banerjee, R. Heterogeneous C–H Functionalization in Water via Porous Covalent Organic Framework Nanofilms: A Case of Catalytic Sphere Transmutation. J. Am. Chem. Soc. 2021, 143, 8426–8436. [Google Scholar] [CrossRef] [PubMed]
- Shul’pina, L.S.; Vinogradov, M.M.; Kozlov, Y.N.; Nelyubina, Y.V.; Ikonnikov, N.S.; Shul’pin, G.B. Copper complexes with 1,10-phenanthrolines as efficient catalysts for oxidation of alkanes by hydrogen peroxide. Inorg. Chim. Acta 2020, 512, 119889. [Google Scholar] [CrossRef]
- Kirillova, M.V.; Fernandes, T.A.; André, V.; Kirillov, A.M. Mild C–H Functionalization of Alkanes Catalyzed by Bioinspired Copper(II) Cores. Org. Biomol. Chem. 2019, 17, 7706–7714. [Google Scholar] [CrossRef] [PubMed]
- Nesterova, O.V.; Kopylovich, M.N.; Nesterov, D.S. A Comparative Study of the Catalytic Behaviour of Alkoxy-1,3,5-Triazapentadiene Copper(II) Complexes in Cyclohexane Oxidation. Inorganics 2019, 7, 82. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Su, X.J.; Jurss, J.W. Selective Alkane C–H Bond Oxidation Catalyzed by a Non-Heme Iron Complex Featuring a Robust Tetradentate Ligand. Organometallics 2018, 37, 4535–4539. [Google Scholar] [CrossRef]
- Doiuchi, D.; Nakamura, T.; Hayashi, H.; Uchida, T. Non-Heme-Type Ruthenium Catalyzed Chemo- and Site-Selective C–H Oxidation. Chem. Asian J. 2020, 15, 762–765. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Li, Y.; Gu, J.; Fernandes, T.A.; Kirillova, M.V.; Kirillov, A.M. New Copper(II) Coordination Compounds Assembled from Multifunctional Pyridine-Carboxylate Blocks: Synthesis, Structures, and Catalytic Activity in Cycloalkane Oxidation. Molecules 2019, 24, 6. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Xu, D.; Sun, Q.; Sun, W. Efficient Aliphatic C–H Bonds Oxidation Catalyzed by Manganese Complex with Hydrogen Peroxide. Chem. Asian J. 2018, 13, 2458–2464. [Google Scholar] [CrossRef]
- Tse, C.W.; Liu, Y.; Chow, T.W.S.; Ma, C.; Yip, W.P.; Chang, X.Y.; Low, K.H.; Huang, J.S.; Che, C.M. cis-Oxoruthenium complexes supported by chiral tetradentate amine (N4) ligands for hydrocarbon oxidations. Chem. Sci. 2018, 9, 2803–2816. [Google Scholar] [CrossRef] [Green Version]
- Busa, A.V.; Lalancette, R.; Nordlander, E.; Onani, M. New copper(II) salicylaldimine derivatives for mild oxidation of cyclohexane. J. Chem. Sci. 2018, 130, 59. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Tan, C.H.; Wang, H.; Ye, X. Molybdenum/Tungsten-Based Heteropoly Salts in Oxidations. Chem. Asian J. 2021, 16, 2753–2772. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.M.; Wang, X.; Ning, L.; Guo, A.B.; Deng, J.H.; She, Y.B. Efficient oxidation of cycloalkanes with simultaneously increased conversion and selectivity using O2 catalyzed by metalloporphyrins and boosted by Zn(AcO)2: A practical strategy to inhibit the formation of aliphatic diacids. Appl. Catal. Gen. 2021, 609, 117904. [Google Scholar] [CrossRef]
- Sonobe, K.; Tanabe, M.; Yamamoto, K. Enhanced Catalytic Performance of Subnano Copper Oxide Particles. ACS Nano 2020, 14, 1804–1810. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Pan, Y.; Wan, G.; Liu, H.; Wang, L.; Zhou, H.; Yu, S.H.; Jiang, H.L. Turning on visible-light photocatalytic C–H oxidation over metalorganic frameworks by introducing metal-to-cluster charge transfer. J. Am. Chem. Soc. 2019, 141, 19110–19117. [Google Scholar] [CrossRef] [PubMed]
- Cousin, T.; Chatel, G.; Kardos, N.; Andrioletti, B.; Draye, M. Recent trends in the development of sustainable catalytic systems for the oxidative cleavage of cycloalkenes by hydrogen peroxide. Catal. Sci. Technol. 2019, 9, 5256–5278. [Google Scholar] [CrossRef]
- Shchapin, I.Y.; Ramazanov, D.N.; Nekhaev, A.I.; Borisov, R.S.; Buravlev, E.A.; Maximov, A.L. One-Stage Catalytic Oxidation of Adamantane to Tri-, Tetra-, and Penta-Ols. Catalysts 2021, 11, 1017. [Google Scholar] [CrossRef]
- Maurya, A.; Haldar, C. Liquid-phase oxidation of olefins with rare hydronium ion salt of dinuclear dioxido-vanadium(V) complexes and comparative catalytic studies with analogous copper complexes. Appl. Organomet. Chem. 2021, 35, e6203. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Du, R.; Yuan, H.; Wang, Y.; Yao, J.; Li, H. Selective One-step Aerobic Oxidation of Cyclohexane to ε-Caprolactone Mediated by N-hydroxyphthalimide (NHPI). ChemCatChem 2019, 11, 2260–2264. [Google Scholar] [CrossRef]
- Petrosyan, A.; Hauptmann, R.; Pospech, J. Heteroarene N-Oxides as Oxygen Source in Organic Reactions. Eur. J. Org. Chem. 2018, 2018, 5237–5252. [Google Scholar] [CrossRef]
- Dantignana, V.; Milan, M.; Cussó, O.; Company, A.; Bietti, M.; Costas, M. Chemoselective Aliphatic C–H Bond Oxidation Enabled by Polarity Reversal. ACS Cent. Sci. 2017, 3, 1350–1358. [Google Scholar] [CrossRef] [Green Version]
- Buvaylo, E.A.; Kokozay, V.N.; Vassilyeva, O.Y.; Skelton, B.W.; Nesterova, O.V.; Pombeiro, A.J.L. Copper(II) complex of the 2-pyridinecarbaldehyde aminoguanidine Schiff base: Crystal structure and catalytic behaviour in mild oxidation of alkanes. Inorg. Chem. Commun. 2017, 78, 85–90. [Google Scholar] [CrossRef]
- Garcia-Bosch, I. Copper-Catalyzed Oxidation of Alkanes under Mild Conditions. Synlett 2017, 28, 1237–1243. [Google Scholar] [CrossRef]
- Mello, R.; Fiorentino, M.; Fusco, C.; Curci, R. Oxidations by methyl(trifluoromethyl)dioxirane. 2. Oxyfunctionalization of saturated hydrocarbons. J. Am. Chem. Soc. 1989, 111, 6749–6757. [Google Scholar] [CrossRef]
- Mello, R.; Cassidei, L.; Fiorentino, M.; Fusco, C.; Curci, R. Oxidations by methyl(trifluoromethyl)dioxirane. 3. Selective polyoxyfunctionalization of adamantane. Tetrahedron Lett. 1990, 31, 3067–3070. [Google Scholar] [CrossRef]
- Shen, H.M.; Zhang, L.; Deng, J.H.; Sun, J.; She, Y.B. Enhanced catalytic performance of porphyrin cobalt(II) in the solvent-free oxidation of cycloalkanes (C5~C8) with molecular oxygen promoted by porphyrin zinc(II). Catal. Commun. 2019, 132, 105809. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Y.; Deng, J.; Zhang, L.; She, Y. Catalyst-free and solvent-free oxidation of cycloalkanes (C5–C8) with molecular oxygen: Determination of autoxidation temperature and product distribution. Chin. J. Chem. Eng. 2018, 26, 1064–1070. [Google Scholar] [CrossRef]
- Mukherjee, M.; Dey, A. A Heterogeneous Bio-Inspired Peroxide Shunt for Catalytic Oxidation of Organic Molecules. Chem. Commun. 2020, 56, 11593–11596. [Google Scholar] [CrossRef]
- Ghosh, I.; Banerjee, S.; Paul, S.; Corona, T.; Paine, T.K. Highly Selective and Catalytic Oxygenations of C–H and C=C Bonds by a Mononuclear Nonheme High-Spin Iron(III)–Alkylperoxo Species. Angew. Chem. 2019, 131, 12664–12669. [Google Scholar] [CrossRef]
- Tiago, G.A.O.; Ribeiro, A.P.C.; Guedes da Silva, M.F.C.; Mahmudov, K.T.; Branco, L.C.; Pombeiro, A.J.L. Copper(II) Complexes of Arylhydrazone of 1H-Indene-1,3(2H)-dione as Catalysts for the Oxidation of Cyclohexane in Ionic Liquids. Catalysts 2018, 8, 636. [Google Scholar] [CrossRef] [Green Version]
- Serrano-Plana, J.; Acuña-Parés, F.; Dantignana, V.; Oloo, W.N.; Castillo, E.; Draksharapu, A.; Costas, M. Acid-Triggered O–O Bond Heterolysis of a Nonheme FeIII (OOH) Species for the Stereospecific Hydroxylation of Strong C–H Bonds. Chem. Eur. J. 2018, 24, 5331–5340. [Google Scholar] [CrossRef] [Green Version]
- Narulkar, D.D.; Srivastava, A.K.; Butcher, R.J.; Ansy, K.M.; Dhuri, S.N. Synthesis and Characterization of N3Py2 Ligand-Based Cobalt(II), Nickel(II) and Copper(II) Catalysts for Efficient Conversion of Hydrocarbons to Alcohols. Inorg. Chim. Acta 2017, 467, 405–414. [Google Scholar] [CrossRef]
- Lee, H.; Seong, J.; Lee, K.M.; Kim, H.H.; Choi, J.; Kim, J.H.; Lee, C. Chloride-enhanced oxidation of organic contaminants by Cu(II)-catalyzed Fenton-like reaction at neutral pH. J. Hazard. Mater. 2018, 344, 1174–1180. [Google Scholar] [CrossRef] [PubMed]
- Pham, A.N.; Xing, G.; Miller, C.J.; Waite, T.D. Fenton-like copper redox chemistry revisited: Hydrogen peroxide and superoxide mediation of copper-catalyzed oxidant production. J. Catal. 2013, 301, 54–64. [Google Scholar] [CrossRef]
- Perez-Benito, J.F. Reaction pathways in the decomposition of hydrogen peroxide catalyzed by copper(II). J. Inorg. Biochem. 2004, 98, 430–438. [Google Scholar] [CrossRef] [PubMed]
- Bieri, G.; Burger, F.; Heilbronner, E.; Maier, J.P. Valence ionization energies of hydrocarbons. Helv. Chim. Acta 1977, 60, 2213–2233. [Google Scholar] [CrossRef]
- Mikaya, A.I.; Zaikin, V.G. Ionization and appearance potentials in organic chemistry. Russ. Chem. Bull. 1980, 29, 907–912. [Google Scholar] [CrossRef]
- Fedorova, M.S.; Denisov, Y.V.; Potapov, V.K. Mass-spectrometric study of the photoionization processes of tricyclo[5.2.1.02,6]decane and its alkyl derivatives. Russ. J. Phys. Chem. 1973, 47, 1498. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C2825823&Units=SI&Mask=20 (accessed on 15 March 2022).
- Fedorova, M.S.; Potapov, V.K.; Denisov, Y.V.; Sorokin, V.V.; Evlasheva, T.I. A mass-spectrometric study of the photoionization of certain cyclic hydrocarbons. Russ. J. Phys. Chem. 1974, 48, 1078. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C6004382&Units=SI&Mask=20#Ion-Energetics (accessed on 15 March 2022).
- Worrell, C.; Verhoeven, J.W.; Speckamp, W.N. Through-bond interaction in 1-aza-adamantane derivatives. Tetrahedron 1974, 30, 3525–3531. [Google Scholar] [CrossRef]
- Raymonda, J.W. Rydberg states in cyclic alkanes. J. Chem. Phys. 1972, 56, 3912–3920. [Google Scholar] [CrossRef]
- Pollmann, J.; Franke, R.; Hormes, J. Ultraviolet photoelectron spectra of fenchone, camphor and bromocamphor. Spectrochim. Acta Part A 1997, 53, 491–493. [Google Scholar] [CrossRef]
- Rennie, E.E.; Powis, I.; Hergenhahn, U.; Kugeler, O.; Garcia, G.; Lischke, T.; Marburger, S. Valence and C 1s core level photoelectron spectra of camphor. J. Electron Spectrosc. Relat. Phenom. 2002, 125, 197–203. [Google Scholar] [CrossRef]
- Vilesov, F.I. The photoionization of vapors of compounds whose molecules contain carbonyl groups. Dokl. Phys. Chem. 1960, 132, 521–528. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C76222&Units=SI&Mask=20 (accessed on 15 March 2022).
- Maier, J.P.; Turner, D.W. Steric inhibition of resonance studied by molecular photoelectron spectroscopy. Part 2.—Phenylethylenes. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1973, 69, 196–206. [Google Scholar] [CrossRef]
- Diedhiou, M.; West, B.J.; Bouwman, J.; Mayer, P.M. Ion Dissociation Dynamics of 1,2,3,4-Tetrahydronaphthalene: Tetralin as a Test Case For Hydrogenated Polycyclic Aromatic Hydrocarbons. J. Phys. Chem. A 2019, 123, 10885–10892. [Google Scholar] [CrossRef] [PubMed]
- Meot-Ner, M. Ion thermochemistry of low-volatility compounds in the gas phase. 3. Polycyclic aromatics: Ionization energies, proton and hydrogen affinities. Extrapolations to graphite. J. Phys. Chem. 1980, 84, 2716–2723. [Google Scholar] [CrossRef]
- Mayer, P.M.; Blanchet, V.; Joblin, C. Threshold photoelectron study of naphthalene, anthracene, pyrene, 1,2-dihydronaphthalene, and 9,10-dihydroanthracene. J. Chem. Phys. 2011, 134, 244312. [Google Scholar] [CrossRef]
- Schmidt, W. Photoelectron spectra of polynuclear aromatics. V. Correlations with ultraviolet absorption spectra in the catacondensed series. J. Chem. Phys. 1977, 66, 828–845. [Google Scholar] [CrossRef]
- Gotkis, I.; Lifshitz, C. Time-dependent mass spectra and breakdown graphs. 16–The methylnaphthalenes. Org. Mass Spectrom. 1993, 28, 372–377. [Google Scholar] [CrossRef]
- Tzeng, S.Y.; Shivatare, V.S.; Tzeng, W.B. Cation Vibrations of 1-Methylnaphthalene and 2-Methylnaphthalene through Mass-Analyzed Threshold Ionization Spectroscopy. J. Phys. Chem. A 2019, 123, 5969–5979. [Google Scholar] [CrossRef]
- Heilbronner, E.; Hoshi, T.; von Rosenberg, J.L.; Hafner, K. Alkyl-induced, natural hypsochromic shifts of the 2A←2X and 2B←2X transitions of azulene and naphthalene radical cations. Nouv. J. Chim. 1976, 1, 105–112. Available online: https://webbook.nist.gov/cgi/cbook.cgi?ID=C91576&Units=SI&Mask=20#ref-11 (accessed on 15 March 2022).
- Frost, D.C.; Westwood, N.P.; Werstiuk, N.H. Ultraviolet photoelectron spectra of 2-norbornanone, 2,5-norbornanedione, their alkyl derivatives and thio-analogues. An investigation of transannular interactions by photoelectron spectroscopy. Can. J. Chem. 1980, 58, 1659–1665. [Google Scholar] [CrossRef]
- Kastner, A.; Ring, T.; Kruger, B.C.; Park, G.B.; Schafer, T.; Senftleben, A.; Baumert, T. Intermediate state dependence of the photoelectron circular dichroism of fenchone observed via femtosecond resonance-enhanced multi-photon ionization. J. Chem. Phys. 2017, 147, 013926. [Google Scholar] [CrossRef]
- Singh, D.; De Oliveira, N.; Garcia, G.; Vredenborg, A.; Powis, I. An Experimental and Theoretical Investigation of the 3sp(d) Rydberg States of Fenchone by Polarized laser Resonance-Enhanced-Multiphoton-ionization and Fourier Transform VUV Absorption Spectroscopy. ChemPhysChem 2020, 21, 2468–2483. [Google Scholar] [CrossRef]
- Al-Joboury, M.I.; Turner, D.W. 851. Molecular photoelectron spectroscopy. Part II. A summary of ionization potentials. J. Chem. Soc. 1964, 4434–4441. [Google Scholar] [CrossRef]
- Ganjitabar, H.; Hadidi, R.; Garcia, G.A.; Nahon, L.; Powis, I. Vibrationally-resolved photoelectron spectroscopy and photoelectron circular dichroism of bicyclic monoterpene enantiomers. J. Mol. Spectrosc. 2018, 353, 11–19. [Google Scholar] [CrossRef]
- Kubala, D.; Drage, E.A.; Al-Faydhi, A.M.E.; Kočišek, J.; Papp, P.; Matejčík, V.; Mach, P.; Urban, J.; Limão-Vieira, P.; Hoffman, S.V.; et al. Electron impact ionisation and UV absorption study of α-and β-pinene. Int. J. Mass Spectrom. 2009, 280, 169–173. [Google Scholar] [CrossRef]
- Novak, I.; Kovač, B. Photoelectron spectroscopy of natural products: Terpenes. Spectrochim. Acta A 2005, 61, 277–280. [Google Scholar] [CrossRef]
- Cao, M.; Chen, J.; Fang, W.; Li, Y.; Ge, S.; Shan, X.; Liu, F.; Zhao, Y.; Wang, Z.; Sheng, L. Dissociative photoionization of β-Pinene: An experimental and theoretical study. Eur. J. Mass Spectrom. 2014, 20, 419–428. [Google Scholar] [CrossRef]
- Szabó, A.; Kovács, A. Structure and molecular vibrations of dimethylglyoxime. J. Mol. Struct. 2003, 651, 615–619. [Google Scholar] [CrossRef]
- Kinoshita, S.; Wakita, H.; Masuda, I. Estimation of isomer ratio of 2,3-alkanedione dioxime using high-resolution 13C NMR in the solid state. Bull. Chem. Soc. Jpn. 1986, 59, 653–654. [Google Scholar] [CrossRef] [Green Version]
- Merritt, L.L.; Lanterman, E. The crystal structure of dimethylglyoxime. Acta Crystallogr. 1952, 5, 811–817. [Google Scholar] [CrossRef]
- Bikas, R.; Valadbeigi, Y.; Otręba, M.; Lis, T. Mechanistic studies on the in-situ generation of furoxan ring during the formation of Cu(II) coordination compound from dioxime ligand: Theoretical and experimental study. Inorg. Chim. Acta 2020, 510, 119756. [Google Scholar] [CrossRef]
- Das, O.; Paria, S.; Paine, T.K. Copper(II)-mediated oxidation of 1,2-dioxime to furoxan. Tetrahedron Lett. 2008, 49, 5924–5927. [Google Scholar] [CrossRef]
- Yu, Z.X.; Caramella, P.; Houk, K.N. Dimerizations of nitrile oxides to furoxans are stepwise via dinitrosoalkene diradicals: A density functional theory study. J. Am. Chem. Soc. 2003, 125, 15420–15425. [Google Scholar] [CrossRef]
- Sheremetev, A.B.; Makhova, N.N.; Friedrichsen, W. Monocyclic furazans and furoxans. Adv. Heterocycl. Chem. 2001, 78, 66–188. [Google Scholar] [CrossRef]
- Pasinszki, T.; Westwood, N.P. Gas-Phase Spectroscopy of the Unstable Acetonitrile N-Oxide Molecule, CH3CNO. J. Phys. Chem. A 2001, 105, 1244–1253. [Google Scholar] [CrossRef]
- Vass, G.; Dzsotján, D.; Lajgut, G.G.; Pasinszki, T. Photoelectron spectroscopic investigation of the electronic structure of furoxans. Eur. Chem. Bull. 2012, 1, 22–26. [Google Scholar] [CrossRef]
- Reutt, J.E.; Wang, L.S.; Lee, Y.T.; Shirley, D.A. Molecular beam photoelectron spectroscopy and femtosecond intramolecular dynamics of H2O+ and D2O+. J. Chem. Phys. 1986, 85, 6928–6939. [Google Scholar] [CrossRef]
- Ashmore, F.S.; Burgess, A.R. Study of some medium size alcohols and hydroperoxides by photoelectron spectroscopy. J. Chem. Soc. Faraday Trans. 2 1977, 73, 1247–1261. [Google Scholar] [CrossRef]
- Gochel-Dupuis, M.; Delwiche, J.; Hubin-Franskin, M.-J.; Collin, J.E. High-resolution HeI photoelectron spectrum of acetonitrile. Chem. Phys. Lett. 1992, 193, 41–48. [Google Scholar] [CrossRef]
- Dognon, J.P.; Pouchan, C.; Dargelos, A.; Flament, J.P. Ab initio CI study and vibronic analysis of the photoelectron spectra of formaldoxime. Chem. Phys. Lett. 1984, 109, 492–499. [Google Scholar] [CrossRef]
- Dargelos, A.; Sandorfy, C. The photoelectron and far-ultraviolet absorption spectra of simple oximes. J. Chem. Phys. 1977, 67, 3011–3013. [Google Scholar] [CrossRef]
- Golubitskii, A.E.; Kulikov, N.S.; Zyakun, A.M.; Valovoi, V.A.; Alekseev, A.M.; Volkov, V.N. Photoionization mass spectra of alicyclic compounds with various substituents, and their ionization energies and appearance energies. Russ. Chem. Bull. 1979, 28, 2418–2420. [Google Scholar] [CrossRef]
- Maier, J.P.; Muller, J.-F.; Kubota, T. Ionisation Energies and the Electronic Structures of the N-oxides of diazabenzenes. Helv. Chim. Acta. 1975, 58, 1634–1640. [Google Scholar] [CrossRef]
- Egdell, R.; Green, J.C.; Rao, C.N.R. Photoelectron spectra of substituted benzenes. Chem. Phys. Lett. 1975, 33, 600–607. [Google Scholar] [CrossRef]
- Svedung, D.H. The crystal structure of copper dimethylglyoxime dichloride. Acta Chem. Scand. 1969, 23, 2865–2878. [Google Scholar] [CrossRef]
- Stein, S.E. NIST/EPA/NIH Mass Spectral Database (NIST 11, 17) and NIST Mass Spectral Search Program, Version 2.0g; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011. Available online: https://chemdata.nist.gov/mass-spc/ms-search/docs/Ver20Man_11.pdf (accessed on 15 March 2022).
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. ORCA—An Ab Initio, DFT and Semiempirical SCF-MO Package—Version 3.0.1; Max-Plank-Institute for Chemical Energy Conversion: Ruhr, Germany, 2013; Available online: https://orcaforum.kofo.mpg.de/ (accessed on 15 March 2022).
- Chemcraft—Graphical Software for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com (accessed on 15 March 2022).
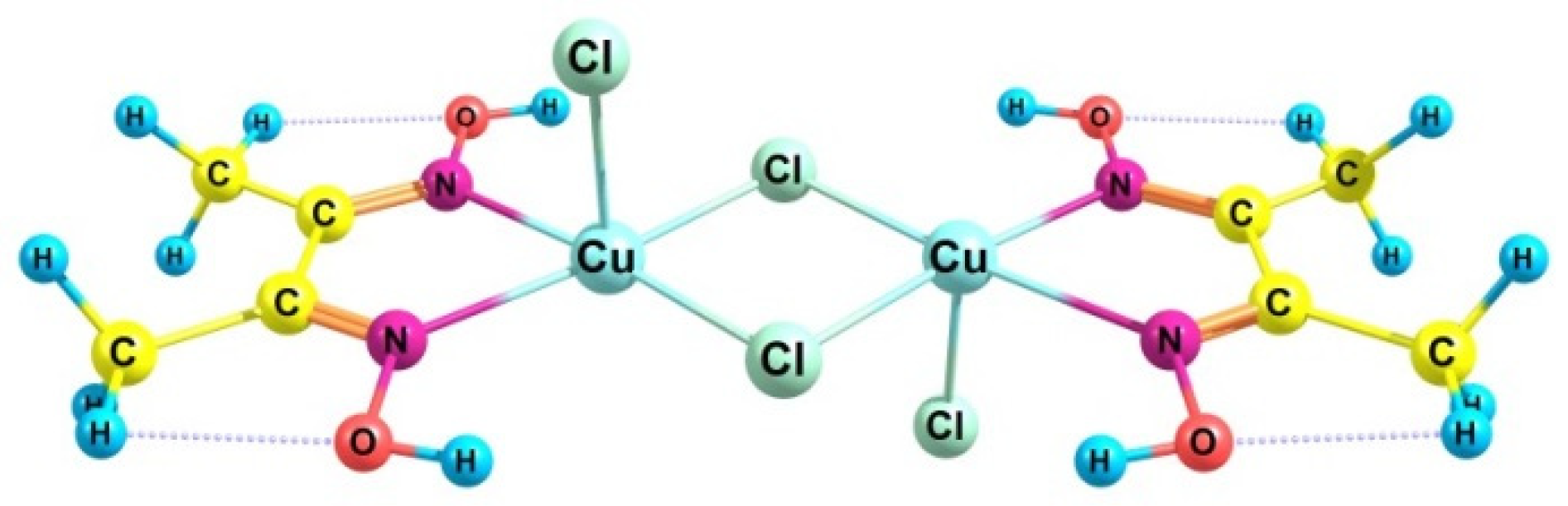
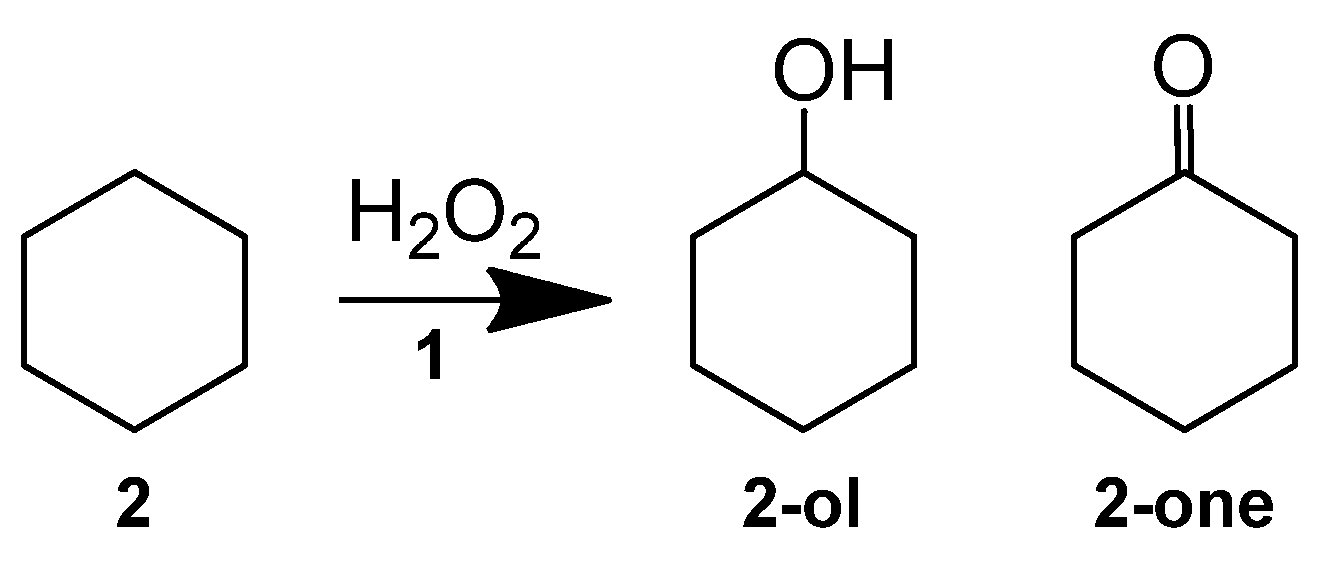
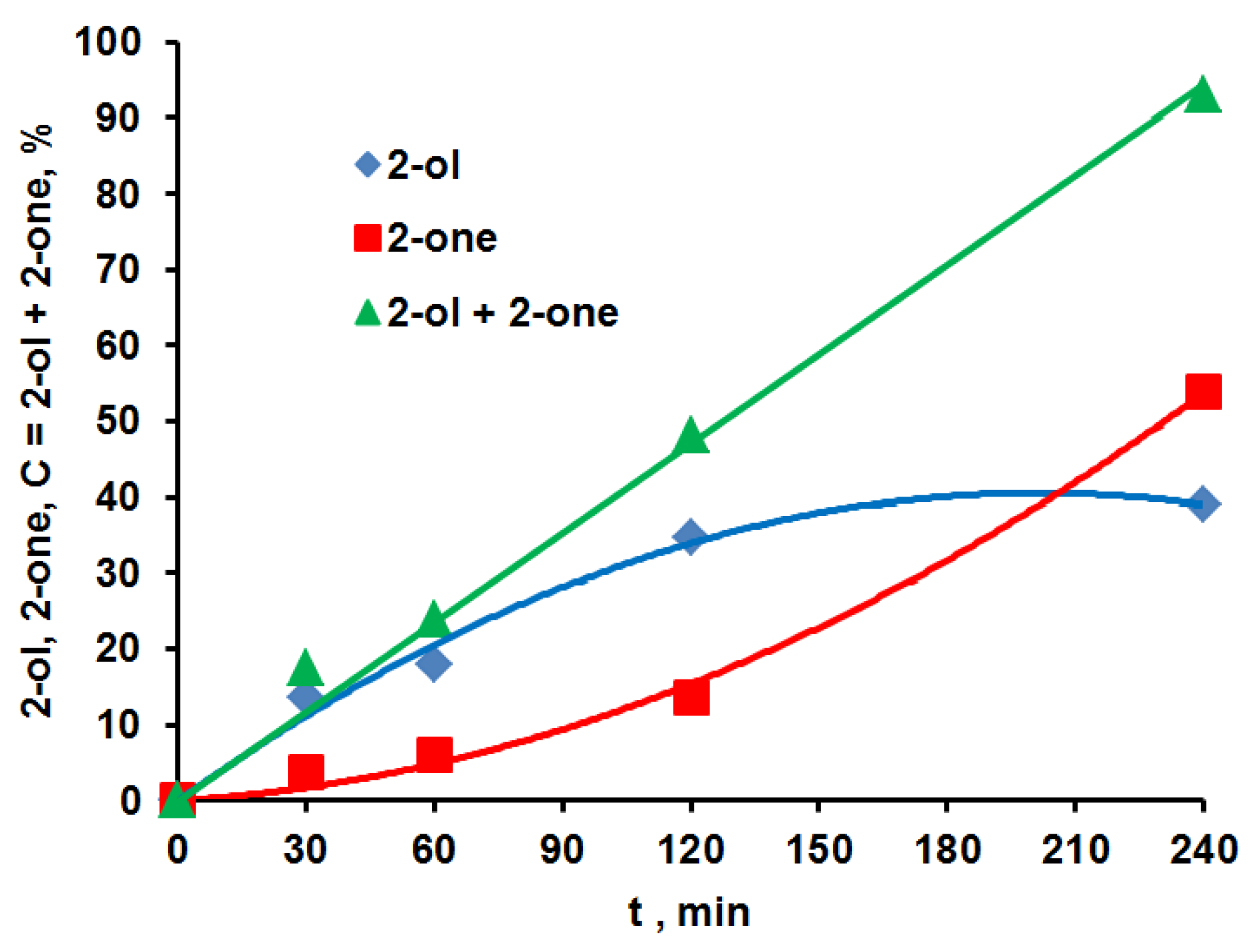
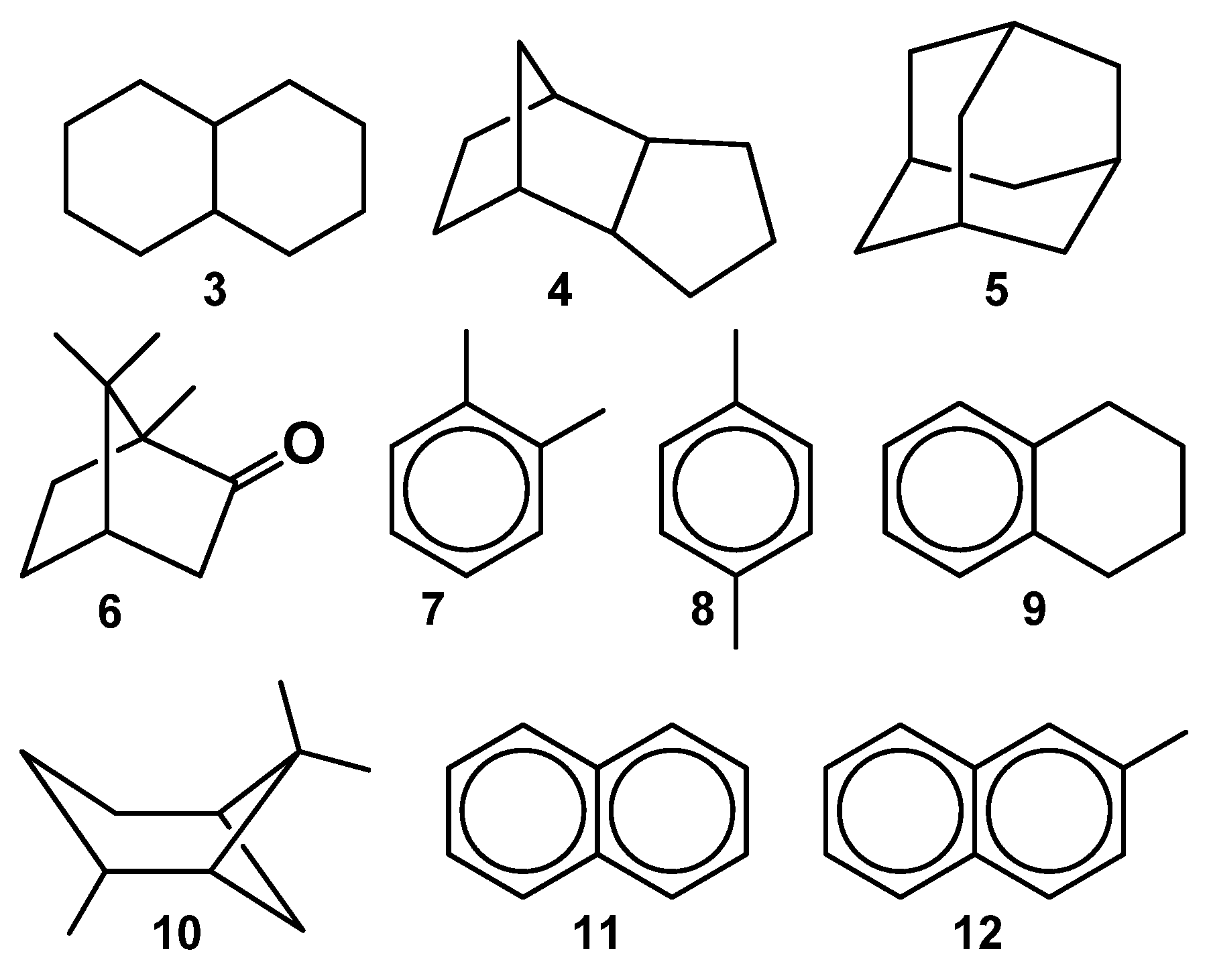

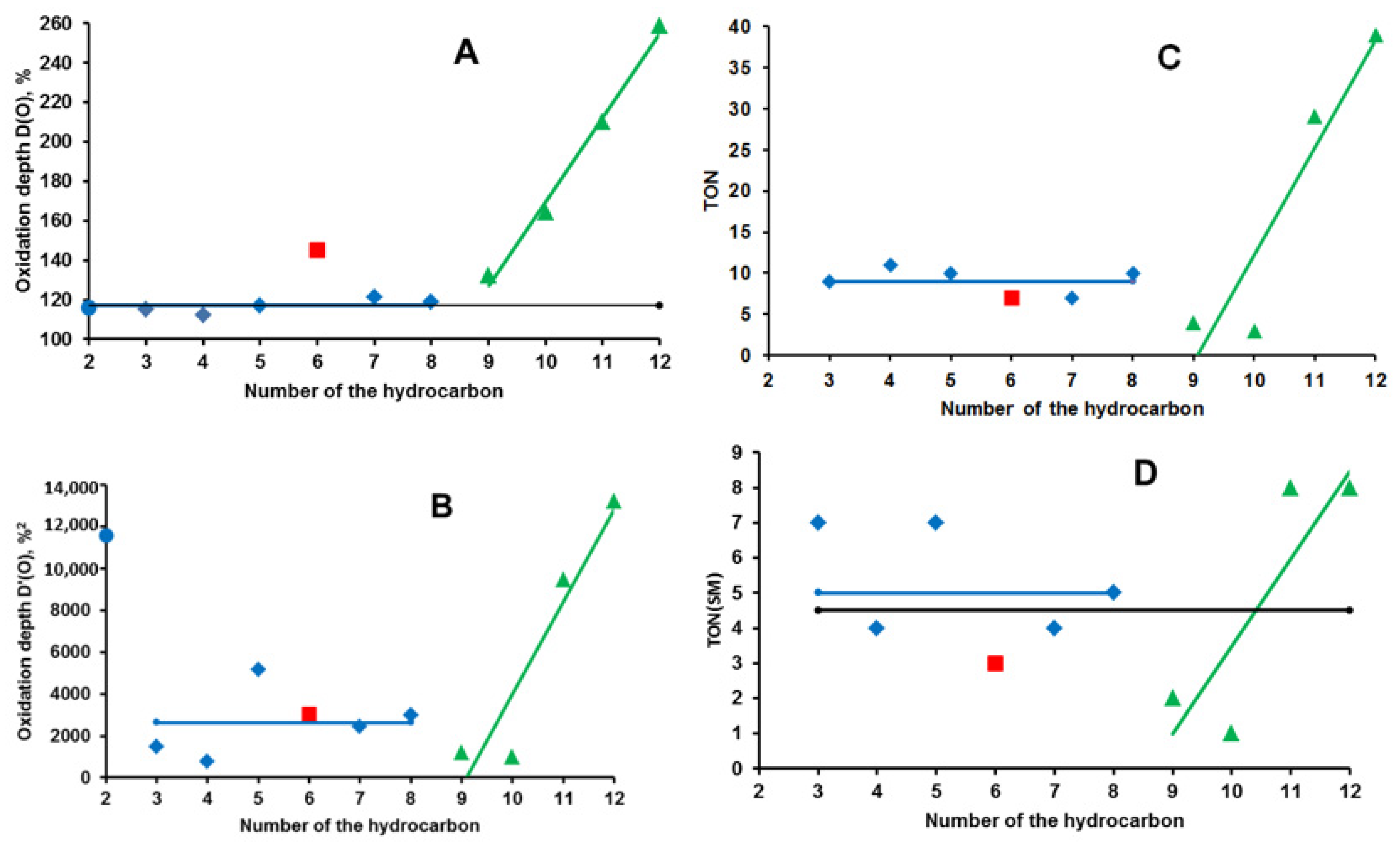




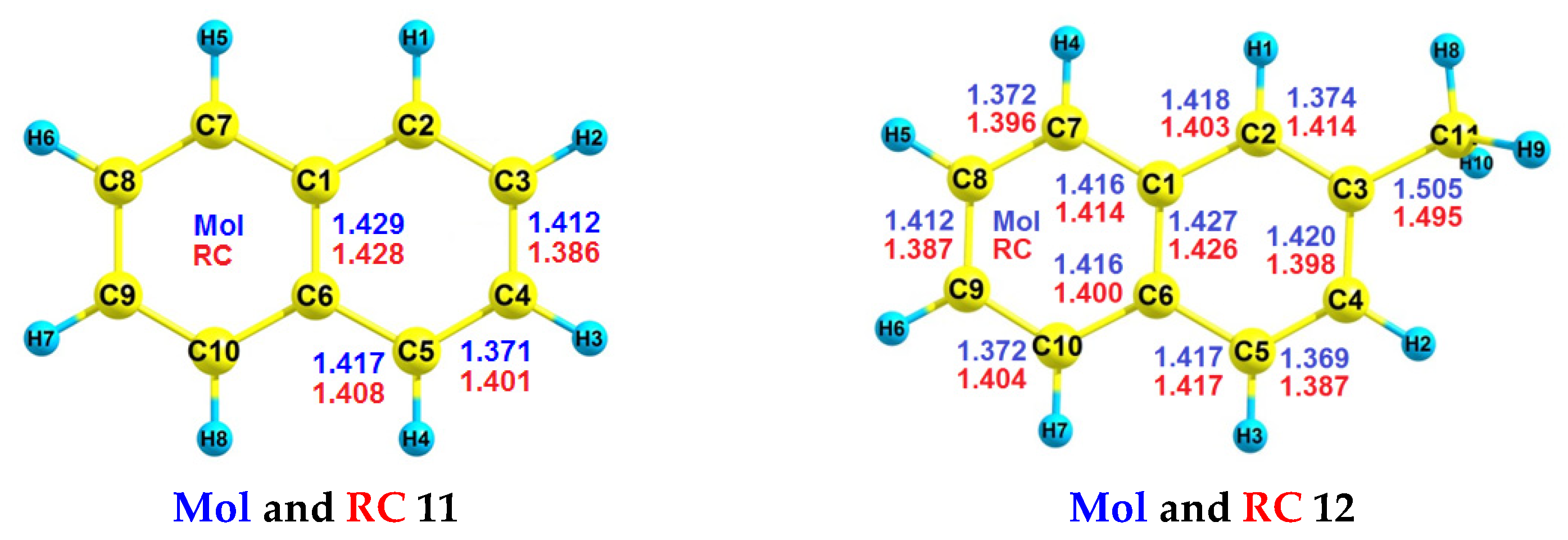

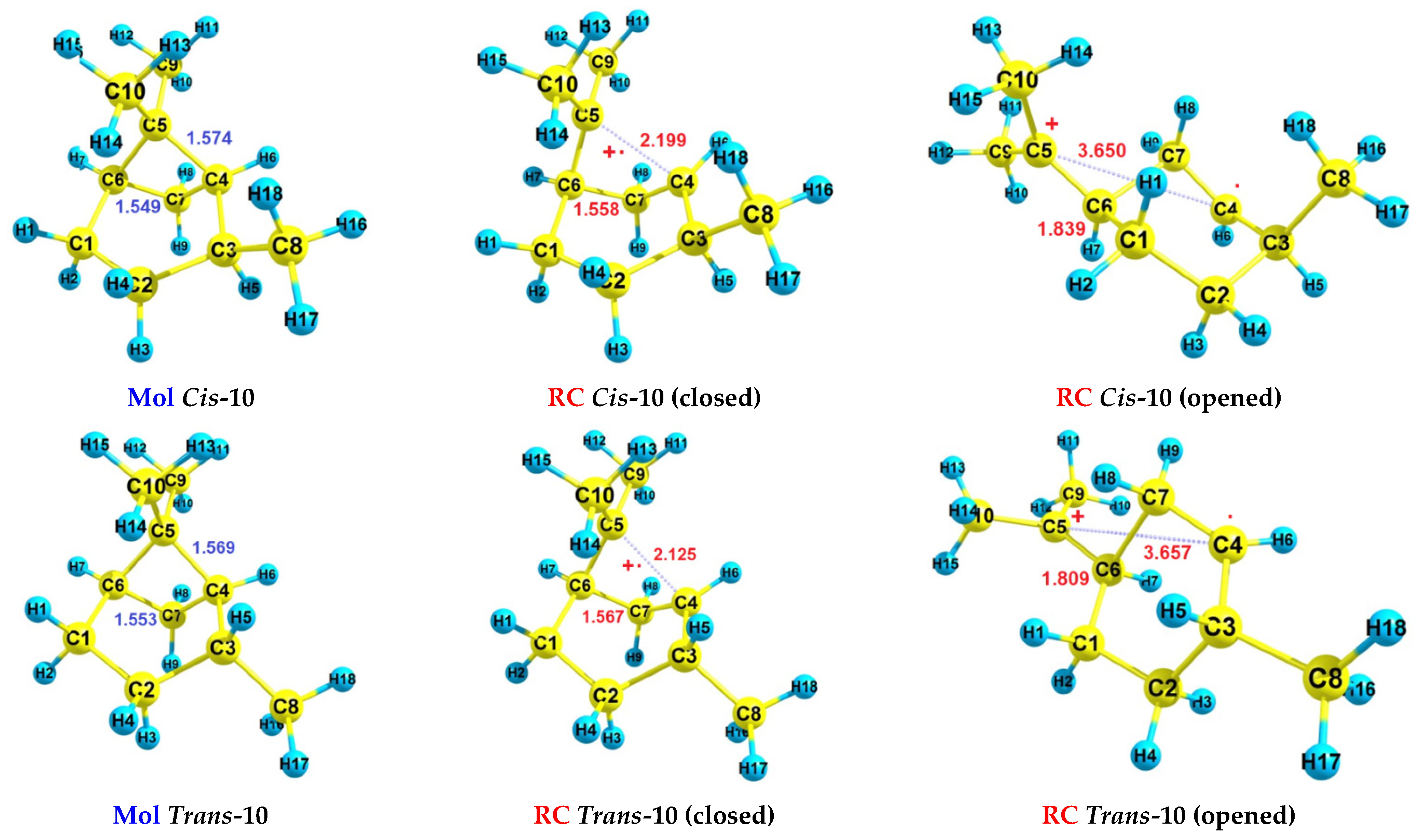
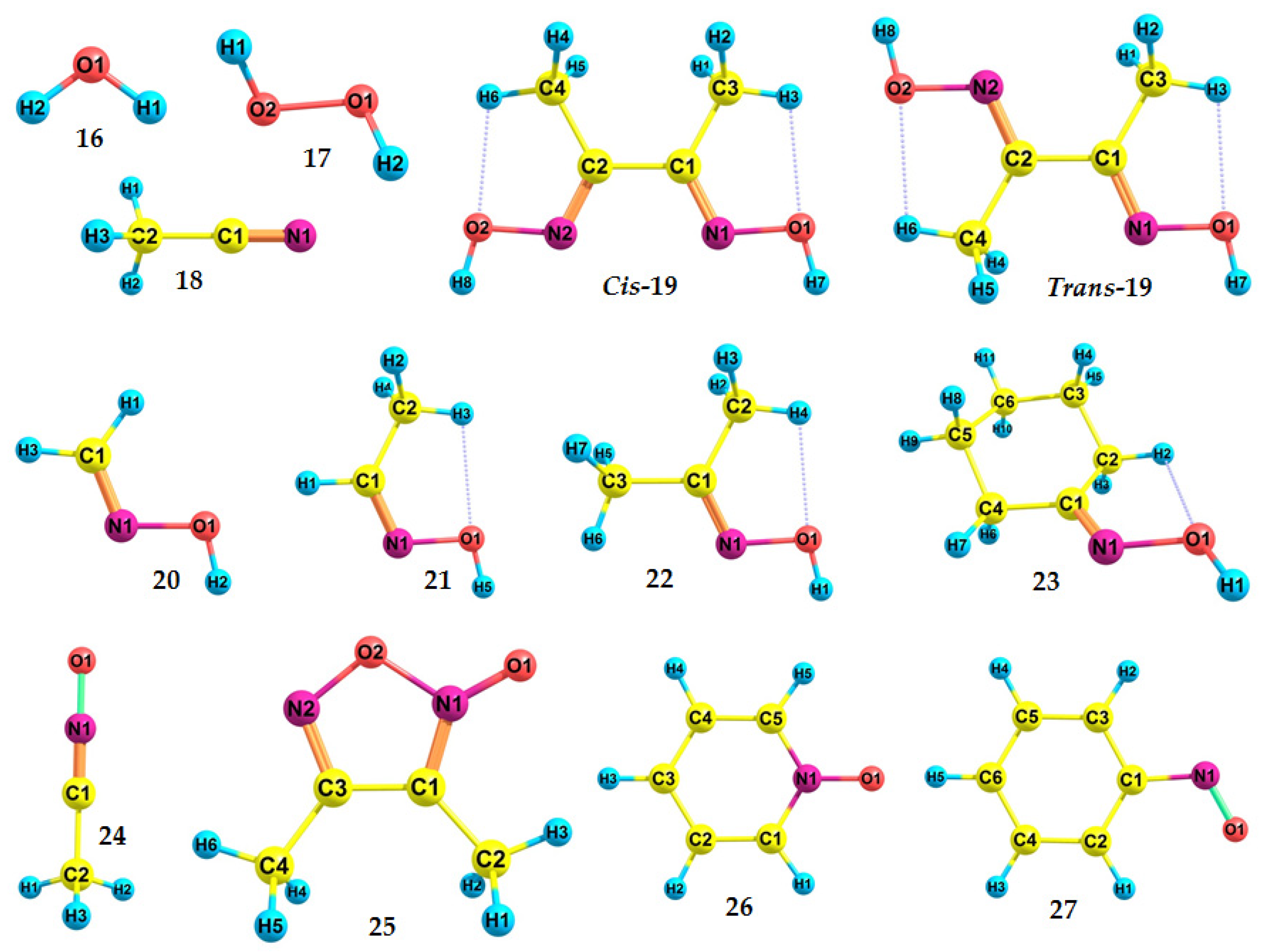

| RH | MR | C, % | Product(i) (Corrected %) N(i) | SOP, % | TON |
|---|---|---|---|---|---|
| 3 | 52.4 | 13 | 3a (46) 1; 3b (39) 2; 3c (6) 2; 3d (5) 3; 3e (4) 4 | 167 | 11 |
| 4 | 53 | 7 | 4a (51) 1; 4b (37) 2; 4c (12) 3 | 161 | 9 |
| 5 | 16.0 | 44 | tert-5a (37) 1; sec-5a (26) 1; 5b (21) 2; 5c (13) 2; 5d (0.5) 3; 5e (0.5) 4; 5f (1) 3; 5g (1) 3 | 139 | 10 |
| 6 | 14.1 | 21 | 6a (16) 1; 6b (37) 2; 6c (8) 3; 6d (11) 2; 6e (21) 3; 6f (7) 3 | 220 | 7 |
| 7 | 20.5 | 20 | 7a (19) 1; 7b (22) 1; 7c (8) 1; 7d (36) 2; 7e (10) 2; 7f (2) 4; 7g (3) 6 | 167 | 7 |
| 8 | 20.5 | 25 | 8a (36) 1; 8b (5) 1; 8c (36) 2; 8d (5) 3; 8e (4) 3; 8f (12) 4 | 188 | 10 |
| 9 | 16.4 | 9 | 9a (5) 1; 9b (4) 1; α-9c (64) 2; β-9c (7) 2; 9d (3) 2; 9e (5) 3; 9f (12) 6 | 244 | 4 |
| 10 | 15.7 | 6 | 10a (4) 1; 10b (32) 2; 10c 2, 10d 3, 10e 4, (64) 3 * | 260 | 3 |
| 11 | 17.0 | 45 | 11a (29) 1; 11b (32) 4; 11c,d (18) 5; 11e (21) 6 | 373 | 29 |
| 12 | 15.3 | 51 | 12a (1) 1; 12b (5) 2; 12c (21) 4; 12d (8) 4; 12e (5) 5; 12f (2) 5; 12g (19) 6; 12h (29) 6; 12i (10) 5 | 500 | 39 |
| Cat *, (Ratio) ** | Based on Substrate % *** | Σ, % | ||||
|---|---|---|---|---|---|---|
| 5a | 5b | 5c | 5g | |||
| tert | sec | ditert | tritert | |||
| H4, (I) | 47.3 | 4.4 | 3.0 | 25.2 | - | 79.9 |
| H4, (II) | 3.01 | 0.17 | 3.57 | 18.9 | 27.2 | 52.85 |
| D4, (II) | 1.48 | 0.10 | 3.16 | 12.1 | 32.4 | 49.24 |
| Corrected on ΣnO = 100% | D(O), % | |||||
| 1O | 2O | 3O | ||||
| H4, (I) | 59.2 | 5.5 | 3.8 | 31.5 | - | 131.5 |
| H4, (II) | 5.7 | 0.3 | 6.7 | 35.8 | 51.5 | 238.8 |
| D4, (II) | 3.0 | 0.2 | 6.4 | 24.6 | 65.8 | 256.2 |
| RH | AIP, eV | VIP, eV | ||||
|---|---|---|---|---|---|---|
| Exp. | DFT | AC·DFT | Exp. | DFT | VC·DFT | |
| 2 | 9.88 ± 0.02 [65] | 9.57 | 9.92 | 10.3 ± 0.1 [65] | 10.55 | 10.74 |
| Cis-3 | 9.32 ± 0.05 [66] 9.427 ± 0.003 [66] | 8.84 | 9.16 | - | 9.64 | 9.81 |
| Trans-3 | 9.32 ± 0.05 [66] 9.383 ± 0.003 [66] | 8.86 | 9.18 | - | 9.42 | 9.59 |
| Exo-4 | 9.35 ± 0.05 [67] 9.3 [68] | 8.85 | 9.17 | - | 9.71 | 9.88 |
| Endo-4 | 9.3 [68] | 8.86 | 9.18 | - | 9.54 | 9.71 |
| 5 | 9.25 [68] 9.32 ± 0.02 *2 [69] 9.31 ± 0.01 [70] | 8.98 | 9.31 | 9.75 ± 0.02 [69] | 9.35 | 9.52 |
| 6 | 8.62 ± 0.05 *2 [71] | 8.33 | 8.63 | 8.70 ± 0.05 [72] 8.76 ± 0.03 [73] 8.94 ± 0.05 [71] | 8.56 | 8.71 |
| 7 | 8.56 ± 0.01 [71] | 8.27 | 8.57 | 8.45 ± 0.02 [74] | 8.43 | 8.58 |
| 8 | 8.52 ± 0.01 [71] | 8.13 | 8.42 | 8.37 ± 0.02 [74] | 8.31 | 8.46 |
| 9 | 8.46 ± 0.01 [75] 8.48 ± 0.05 [76] | 8.14 | 8.43 | 8.40 ± 0.02 [74] | 8.32 | 8.47 |
| Cis-10 | - | 8.19 | 8.49 | - | 9.13 | 9.29 |
| Trans-10 | - | 8.21 | 8.51 | - | 9.12 | 9.28 |
| 11 | 8.14 ± 0.01 [77] | 7.76 | 8.04 | 8.15 ± 0.02 [78] | 7.86 | 8.00 |
| 12 | 7.91 ± 0.02 [79] 7.9752 ± 0.0006 [80] | 7.60 | 7.88 | 8.01 ± 0.03 [81] | 7.91 | 8.05 |
| 13 | 8.50 ± 0.05 *2 [71] 8.50 ± 0.02 *3 [82] 8.49 ± 0.06 [83] 8.495 ± 0.01 [84] | 8.20 | 8.50 | 8.80 ± 0.02 [82] 8.86 ± 0.05 [71] | 8.43 | 8.58 |
| 14 | 8.07 [85] 8.21 [86] | 7.78 | 8.06 | 8.30 ± 0.02 [87] 8.38 [86] 8.38 [88] | 8.08 | 8.22 |
| 15 | 8.45 ± 0.03 [89] | 7.81 | 8.09 | 8.60 ± 0.03 [87] | 8.41 | 8.56 |
| RH | Mol | RC(v) | RC(a) |
|---|---|---|---|
| 2 | −235.796416446930 | −235.408821451747 | −235.444603623664 |
| Cis-3 | −391.789367615470 | −391.435245998176 | −391.464651533436 |
| Trans-3 | −391.794723133146 | −391.448608828165 | −391.469260219338 |
| Exo-4 | −390.566031933795 | −390.209283033454 | −390.240966496249 |
| Endo-4 | −390.560161543720 | −390.209697591623 | −390.234485149963 |
| 5 | −390.571017840896 | −390.227479460936 | −390.241205996154 |
| 6 | −465.795123302806 | −465.480695959193 | −465.489025147050 |
| 7 | −310.790774450045 | −310.480825898414 | −310.486706493782 |
| 8 | −310.791222286329 | −310.486082427306 | −310.492657788520 |
| 9 | −388.186775526325 | −387.881181849912 | −387.887710689243 |
| Cis-10 | −391.740816783849 | −391.405373341772 | −391.439831739236 |
| Trans-10 | −391.744786580034 | −391.409802263156 | −391.443377526896 |
| 11 | −385.786100633399 | −385.497367408886 | −385.500788851354 |
| 12 | −425.089647255078 | −424.806993355110 | −424.810540387290 |
| 13 | −465.797429387663 | −465.487666485169 | −465.496018891036 |
| 14 | −390.527843271624 | −390.230811813852 | −390.241999967480 |
| 15 | −390.523793840712 | −390.214663060525 | −390.236902273183 |
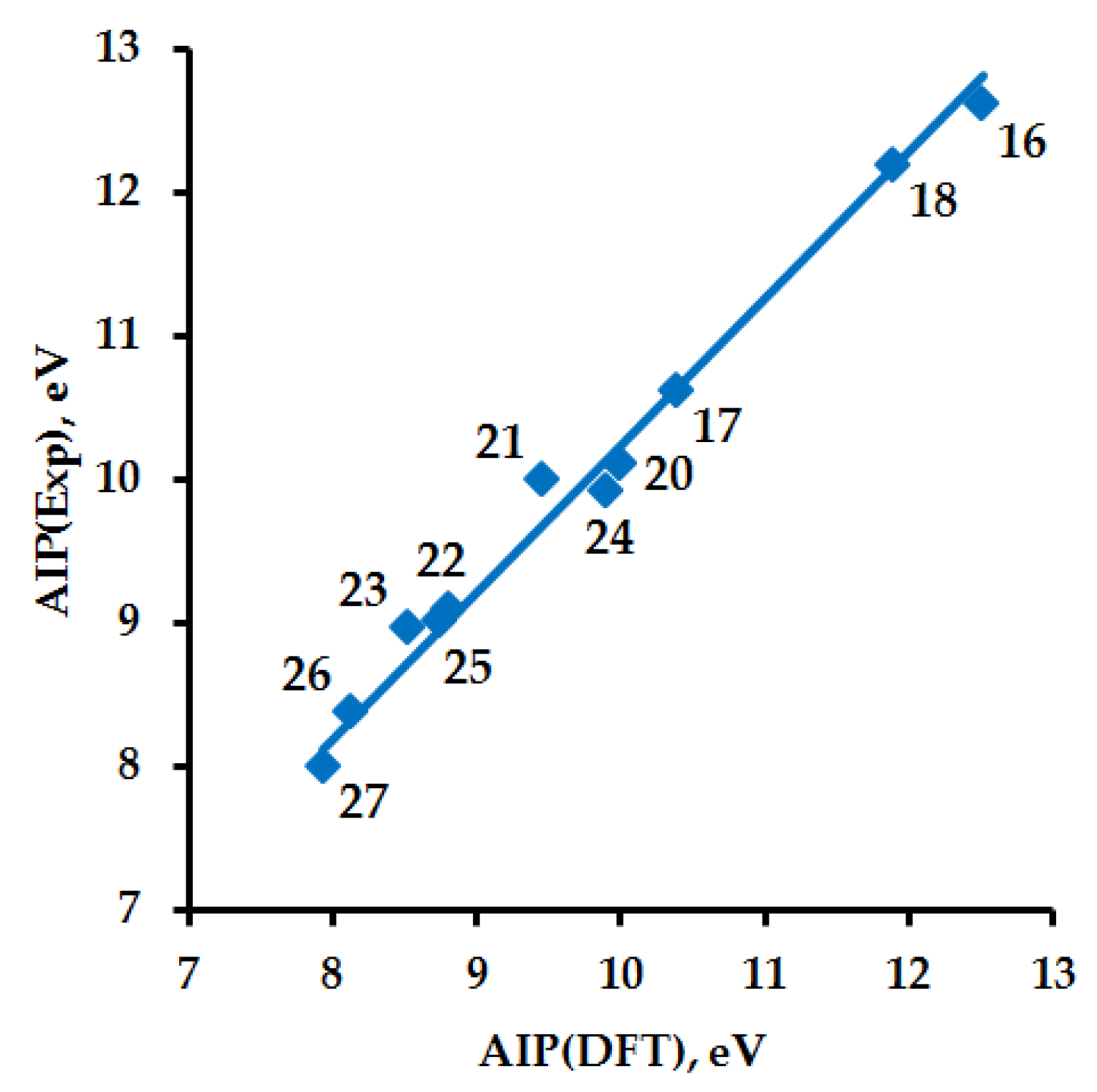
| No. | Exp. | DFT | AC·DFT | Mol | RC(a) |
|---|---|---|---|---|---|
| 16 | 12.6223 ± 0.0003 [99] | 12.51 | 12.81 | −76.429588867406 | −75.969951537539 |
| 17 | 10.62 [100] | 10.38 | 10.63 | −151.553995970550 | −151.172707685586 |
| 18 | 12.201 ± 0.002 [101] | 11.89 | 12.18 | −132.730425658549 | −132.293392421907 |
| Cis-19 | - | 8.07 | 8.27 | −417.022028262935 | −416.725628407721 |
| Trans-19 | - | 8.33 | 8.53 | −417.034738983103 | −416.728471544019 |
| 20 | 10.11 *2 [102] | 10.00 | 10.24 | −169.802678736992 | −169.435077031170 |
| 21 | 10.0 *3 [103] | 9.45 | 9.68 | −209.110507501338 | −208.763348867177 |
| 22 | 9.1 *3 [103] | 8.81 | 9.02 | −248.417877328829 | −248.094069626012 |
| 23 | 8.97 ± 0.03 [104] | 8.52 | 8.73 | −365.112887996007 | −364.799893373906 |
| 24 | 9.92 [97] (VIP) | 9.64 | 9.87 | −207.879576709614 | −207.525434053952 |
| 25 | 9.01 [98] (VIP) | 8.75 | 8.96 | −415.802311396769 | −415.480874509974 |
| 26 | 8.38 ± 0.02 [105] (VIP) | 8.13 | 8.33 | −323.394811420757 | −323.096133440060 |
| 27 | 8.0 [106] | 7.93 | 8.12 | −361.475462562199 | −361.183887006740 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shchapin, I.Y.; Nekhaev, A.I.; Ramazanov, D.N.; Al-Yusufi, M.; Samoilov, V.O.; Maximov, A.L. Hydrocarbon Oxidation Depth: H2O2/Cu2Cl4·2DMG/CH3CN System. Catalysts 2022, 12, 409. https://doi.org/10.3390/catal12040409
Shchapin IY, Nekhaev AI, Ramazanov DN, Al-Yusufi M, Samoilov VO, Maximov AL. Hydrocarbon Oxidation Depth: H2O2/Cu2Cl4·2DMG/CH3CN System. Catalysts. 2022; 12(4):409. https://doi.org/10.3390/catal12040409
Chicago/Turabian StyleShchapin, Igor Yu., Andrey I. Nekhaev, Dzhamalutdin N. Ramazanov, Mohammed Al-Yusufi, Vadim O. Samoilov, and Anton L. Maximov. 2022. "Hydrocarbon Oxidation Depth: H2O2/Cu2Cl4·2DMG/CH3CN System" Catalysts 12, no. 4: 409. https://doi.org/10.3390/catal12040409






