Computational Studies of Molybdenum-Containing Metal–Sulfur and Metal–Hydride Clusters
Abstract
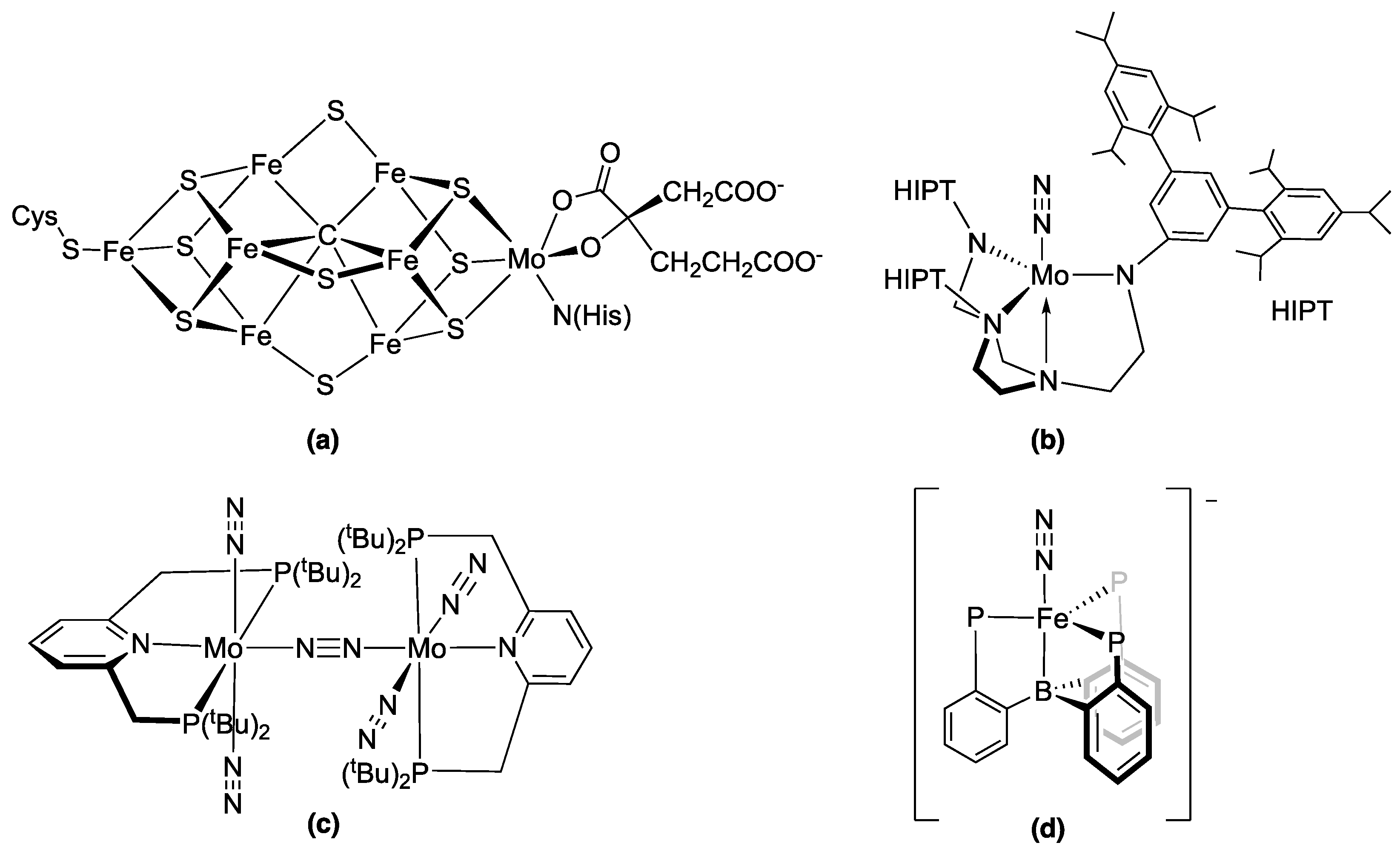
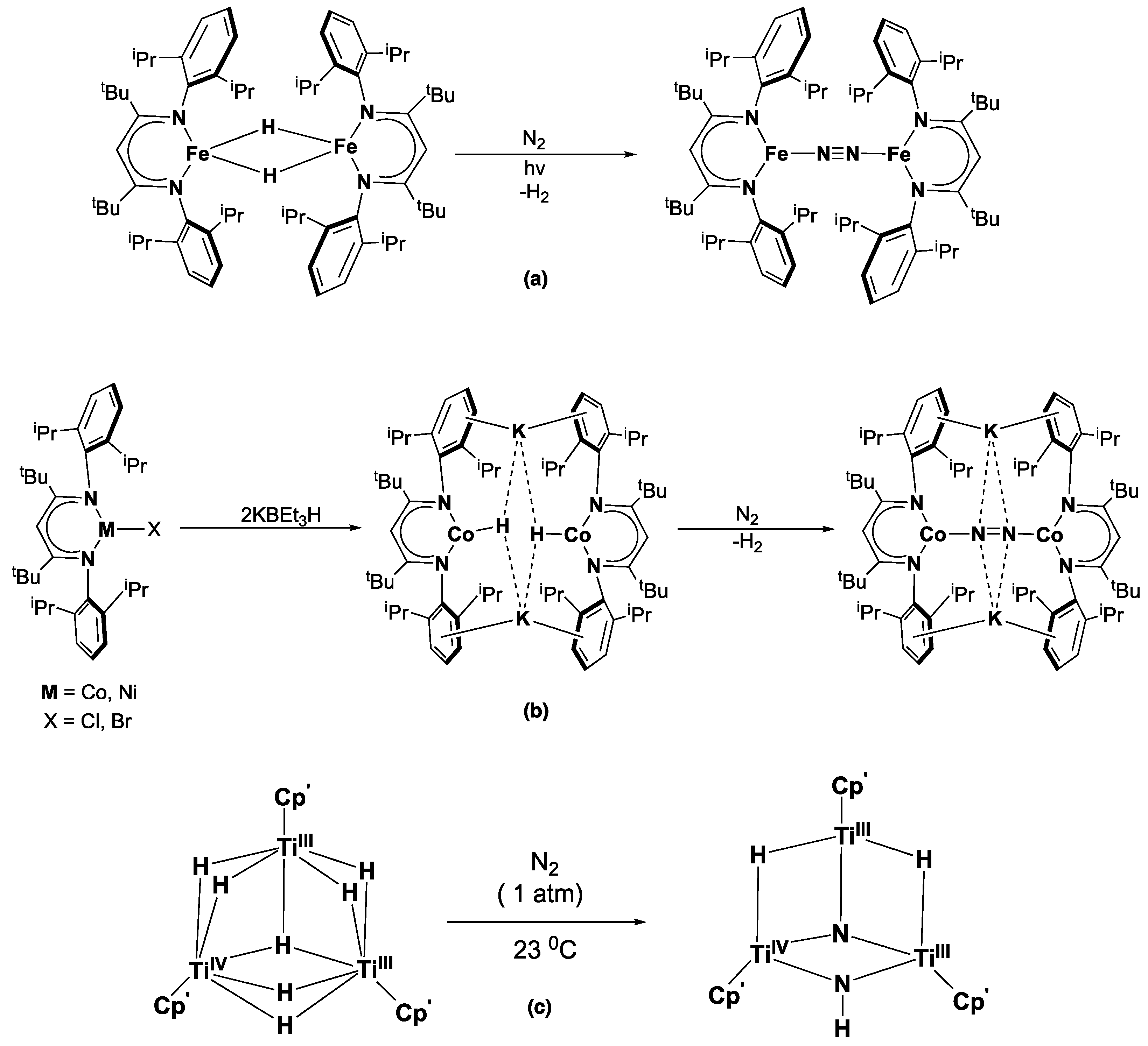
:1. Introduction
2. Results and Discussion
2.1. The Electronic Ground State of the Clusters
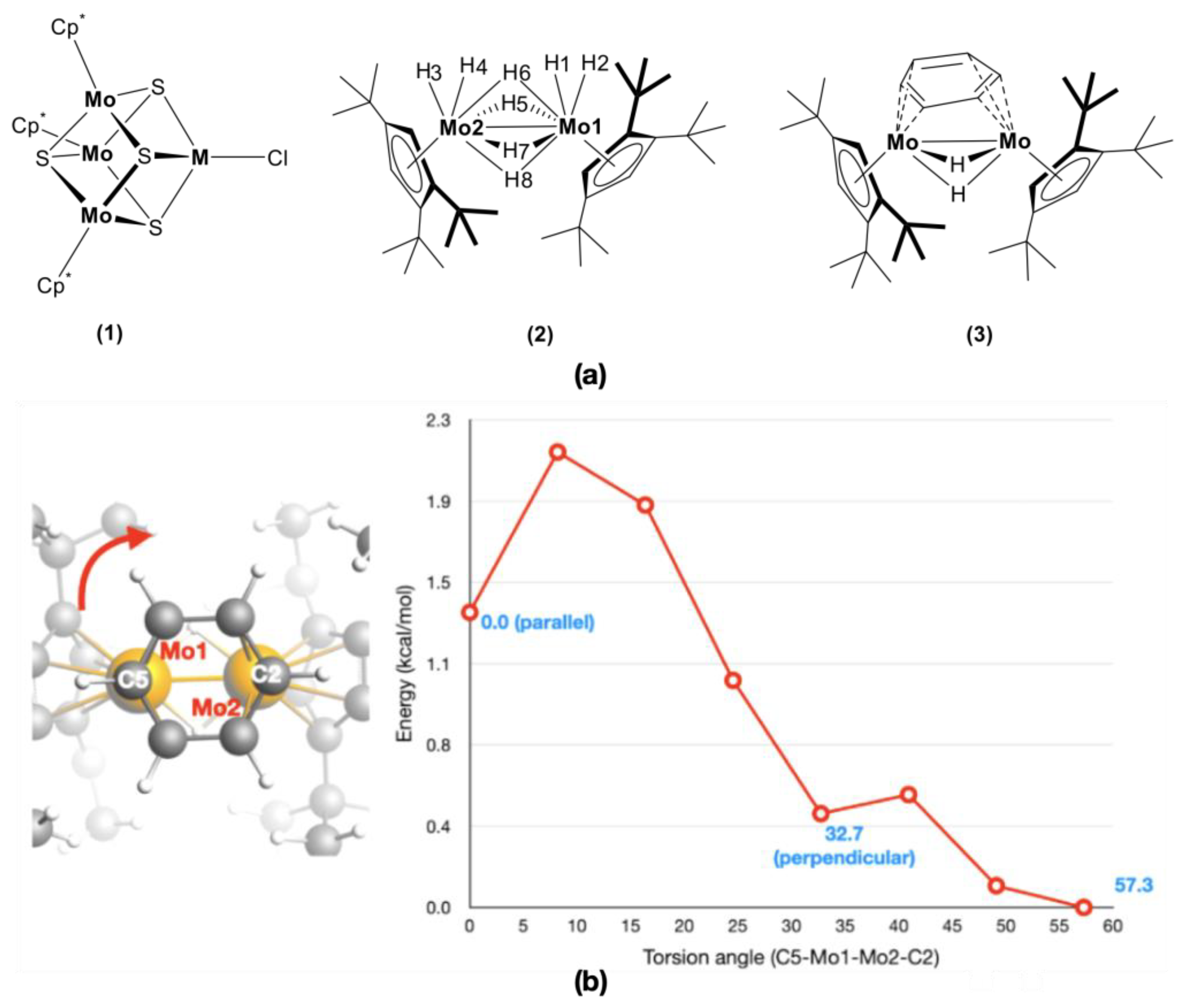
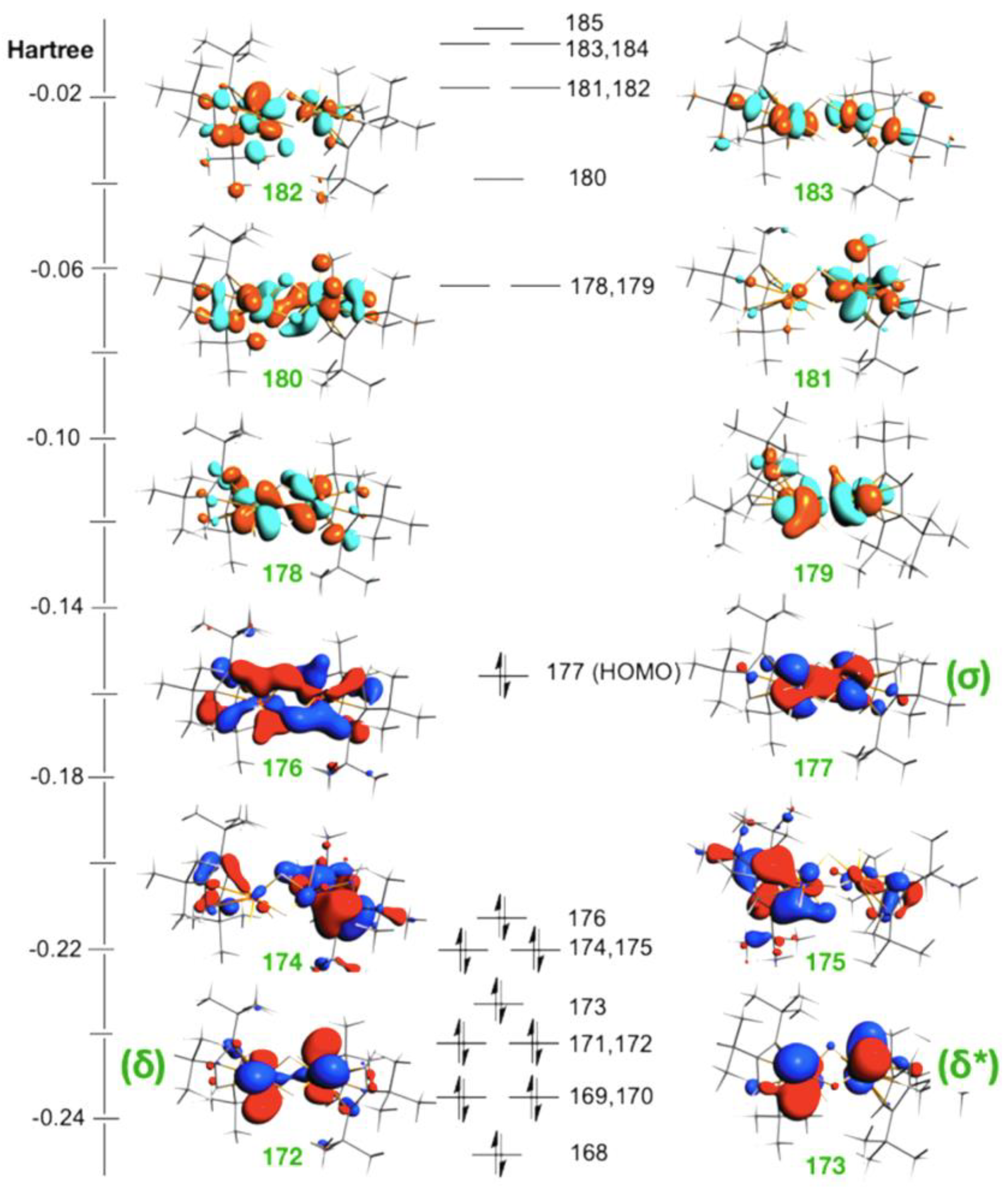
2.2. Characterization of Metal–Metal Bonding
2.3. Fluxional Behavior of Ligands
2.4. Intermolecular Interactions
2.5. Determination of Oxidation States
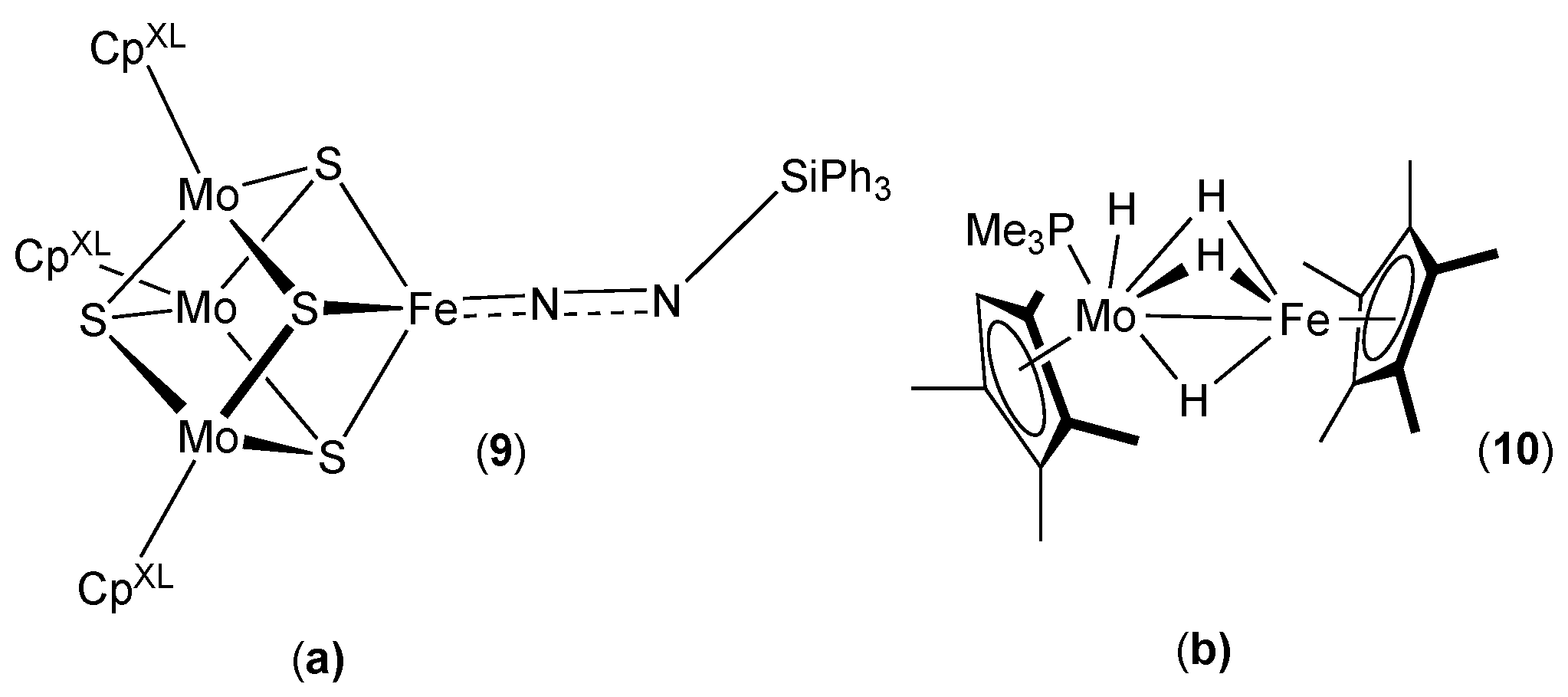
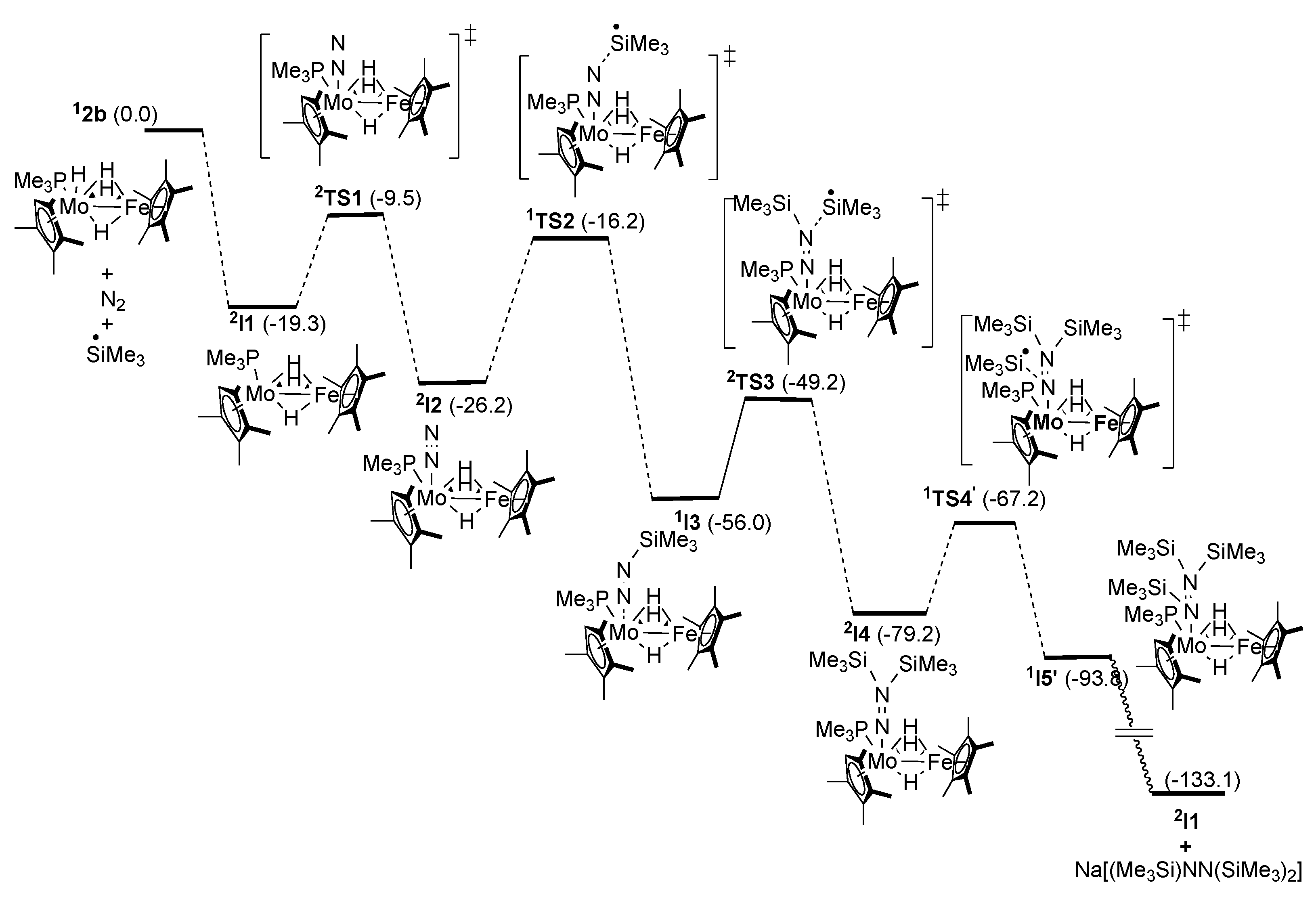
2.6. Reaction Mechanisms
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanifuji, K.; Ohta, S.; Ohki, Y.; Seino, H. Activation of unsaturated small molecules by bio-relevant multinuclear metal-sulfur clusters. Coord. Chem. Rev. 2023, 475, 214838. [Google Scholar] [CrossRef]
- Tanifuji, K.; Ohki, Y. Metal-sulfur compounds in N2 reduction nitrogenase-related chemistry. Chem. Rev. 2020, 120, 5194–5251. [Google Scholar] [CrossRef]
- Ohta, S.; Ohki, Y. Impact of ligands and media on the structure and properties of biological and biomimetic iron-sulfur clusters. Coord. Chem. Rev. 2017, 338, 207–225. [Google Scholar] [CrossRef]
- Araake, R.; Sakadani, K.; Tada, M.; Sakai, Y.; Ohki, Y. [Fe4] and [Fe6] hydride clusters supported by phosphines: Synthesis, characterization, and application in N2 reduction. J. Am. Chem. Soc. 2017, 139, 5596–5606. [Google Scholar] [CrossRef]
- Yandulov, D.V.; Schrock, R.R. Catalytic reduction of dinitrogen to ammonia at a single molybdenum center. Science 2023, 301, 76. [Google Scholar] [CrossRef] [PubMed]
- Arashiba, K.; Miyake, Y.; Nishibayashi, Y. A molybdenum complex bearing PNP-type pincer ligands leads to the catalytic reduction of dinitrogen into ammonia. Nat. Chem. 2011, 3, 120–125. [Google Scholar] [CrossRef]
- Ung, G.; Peters, J.C. Low-temperature N2 binding to two-coordinate L2Fe0 enables reductive trapping of L2FeN2− and NH3 generation. Angew. Chem. Int. Ed. 2015, 54, 532–535. [Google Scholar] [CrossRef] [PubMed]
- Creutz, S.E.; Peters, J.C. Catalytic Reduction of N2 to NH3 by an Fe-N2 complex featuring a C-atom anchor. J. Am. Chem. Soc. 2014, 136, 1105–1115. [Google Scholar] [CrossRef]
- Anderson, J.S.; Rittle, J.; Peters, J.C. Catalytic conversion of nitrogen to ammonia by an iron model complex. Nature 2013, 501, 84–87. [Google Scholar] [CrossRef]
- Mori, H.; Seino, H.; Hidai, M.; Mizobe, Y. Isolation of a cubane-type metal sulfido clusters with a nolecular nitrogen ligand. Angew. Chem. Int. Ed. 2007, 46, 5431–5434. [Google Scholar] [CrossRef]
- McSkimming, A.; Suess, D.L.M. Dinitrogen binding and activation at a molybdenum-iron-sulfur cluster. Nat. Chem. 2021, 13, 666–670. [Google Scholar] [CrossRef] [PubMed]
- Ohki, Y.; Munakata, K.; Matsuoka, Y.; Hara, R.; Kachi, M.; Uchida, K.; Tada, M.; Cramer, R.E.; Sameera, W.M.C.; Takayama, T.; et al. Nitrogen reduction by the Fe sites of synthetic [Mo3S4Fe] cubes. Nature 2022, 607, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Ohki, Y.; Shimizu, Y.; Araake, R.; Tada, M.; Sameera, W.M.C.; Ito, J.I.; Nishiyama, H. Co6H8(PiPr3)6: A cobalt octahedron with face-capping hydrides. Angew. Chem. Int. Ed. 2016, 55, 15821–15825. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.M.; Sadique, A.R.; Cundari, T.R.; Rodgers, K.R.; Lukat-Rodgers, G.; Lachicotte, R.J.; Flaschenriem, C.J.; Vela, J.; Holland, P.L. Studies of low-coordinate iron dinitrogen complexes. J. Am. Chem. Soc. 2006, 128, 756–769. [Google Scholar] [CrossRef]
- Yu, Y.; Sadique, A.R.; Smith, J.M.; Dugan, T.R.; Cowley, R.E.; Brennessel, W.W.; Flaschenriem, C.J.; Bill, E.; Cundari, T.R.; Holland, P.L. The reactivity patterns of low-coordinate iron–hydride complexes. J. Am. Chem. Soc. 2008, 130, 6624–6638. [Google Scholar] [CrossRef]
- Ding, K.; Brennessel, W.W.; Holland, P.L. Three-coordinate and four-coordinate cobalt hydride complexes that react with dinitrogen. J. Am. Chem. Soc. 2009, 131, 10804–10805. [Google Scholar] [CrossRef] [PubMed]
- Shima, T.; Hu, S.; Luo, G.; Kang, X.; Luo, Y.; Hou, Z. Dinitrogen cleavage and hydrogenation by a trinuclear titanium polyhydride complex. Science 2013, 340, 1549–1552. [Google Scholar] [CrossRef]
- Ohki, Y.; Uchida, K.; Hara, R.; Kachi, M.; Fujisawa, M.; Tada, M.; Sakai, Y.; Sameera, W.M.C. Cubane-type [Mo3S4M] clusters with first-row groups 4-10 transition-metal halides supported by C5Me5 ligands on molybdenum. Chem. Eur. J. 2018, 24, 17138–17147. [Google Scholar] [CrossRef]
- Cao, Z.; Zhou, Z.; Wan, H.; Zhang, Q. Enzymatic and catalytic reduction of dinitrogen to ammonia: Density functional theory characterization of alternative molybdenum active sites. Int. J. Quantum Chem. 2005, 103, 344–353. [Google Scholar] [CrossRef]
- Magistrato, A.; Robertazzi, A.; Carloni, P. Nitrogen Fixation by a Molybdenum Catalyst Mimicking the Function of the Nitrogenase Enzyme: A Critical Evaluation of DFT and Solvent Effects. J. Chem. Theory Comput. 2007, 3, 1708–1720. [Google Scholar] [CrossRef]
- Studt, F.; Tuczek, F. Energetics and mechanism of a room-temperature catalytic process for ammonia synthesis (Schrock cycle): Comparison with biological nitrogen fixation. Angew. Chem. Int. Ed. 2005, 44, 5639–5642. [Google Scholar] [CrossRef] [PubMed]
- Reiher, M.; Le Guennic, B.; Kirchner, B. Theoretical study of catalytic dinitrogen reduction under mild conditions. Inorg. Chem. 2005, 44, 9640–9642. [Google Scholar] [CrossRef] [PubMed]
- Le Guennic, B.; Kirchner, B.; Reiher, M. Nitrogen fixation under mild ambient conditions: Part I—The initial dissociation/association step at molybdenum triamidoamine complexes. Chem. Eur. J. 2005, 11, 7448–7460. [Google Scholar] [CrossRef] [PubMed]
- Schenk, S.; Le Guennic, B.; Kirchner, B.; Reiher, M. First-principles investigation of the Schrock mechanism of dinitrogen reduction employing the full HIPTN3N Ligand. Inorg. Chem. 2008, 47, 3634–3650. [Google Scholar] [CrossRef] [PubMed]
- Schenk, S.; Kirchner, B.; Reiher, M.A. Stable Six-coordinate intermediate in ammonia–dinitrogen exchange at Schrock’s molybdenum catalyst. Chem. Eur. J. 2009, 15, 5073–5082. [Google Scholar] [CrossRef]
- Schenk, S.; Reiher, M. Ligands for dinitrogen fixation at Schrock-type catalysts. Inorg. Chem. 2009, 48, 1638–1648. [Google Scholar] [CrossRef]
- Bergeler, M.; Simm, G.N.; Proppe, J.; Reiher, M. Heuristics-guided exploration of reaction mechanisms. J. Chem. Theory Comput. 2015, 11, 5712–5722. [Google Scholar] [CrossRef]
- Tian, Y.-H.; Pierpont, A.W.; Batista, E.R. How does Nishibayashi’s molybdenum complex catalyze dinitrogen reduction to ammonia? Inorg. Chem. 2014, 53, 4177–4183. [Google Scholar] [CrossRef]
- Tanaka, H.; Arashiba, K.; Kuriyama, S.; Sasada, A.; Nakajima, K.; Yoshizawa, K.; Nishibayashi, Y. Unique behaviour of dinitrogen-bridged dimolybdenum complexes bearing pincer ligand towards catalytic formation of ammonia. Nat. Commun. 2014, 5, 3737. [Google Scholar] [CrossRef]
- Tanaka, H.; Yoshizawa, K. Computational Approach to Nitrogen Fixation on Molybdenum–Dinitrogen Complexes. Top. Organomet. Chem. 2017, 60, 171–196. [Google Scholar]
- Klopsch, I.; Yu, E.; Klimova, Y.; Schneider, S. Functionalization of N2 by mid to late transition metals via N-N bond cleavage. Top. Organomet. Chem. 2017, 60, 71–112. [Google Scholar]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonian. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. I. The effect of the exchange only gradient correction. J. Chem. Phys. 1992, 96, 2155–2160. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H.A. Consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F.J. All-electron scalar relativistic basis sets for third-row transition metal atoms. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Mayer, I. Charge, bond order and valence in the AB initio SCF theory. Chem. Phys. Lett. 1983, 97, 270–274. [Google Scholar] [CrossRef]
- Bader, R.F.W.A. quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Ohki, Y.; Ishihara, K.; Yaoi, M.; Tada, M.; Sameera, W.M.C.; Cramer, R.E.A. Dinuclear Mo2H8 complex supported by bulky C5H2tBu3 ligands. Chem. Commun. 2020, 56, 8035–8038. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Lenthe, C.V.; Ehlers, A.; Baerends, E.J. Geometry optimization in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef]
- Klamt, A.; Schuurmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Tanifuji, K.; Sakai, Y.; Matsuoka, Y.; Tada, M.; Sameera, W.M.C.; Ohki, Y. CO binding onto the vertex heterometals of [Mo3S4M] (M=Fe, Co, Ni) cubes. Bull. Chem. Soc. Jpn. 2022, 95, 1190–1195. [Google Scholar] [CrossRef]
- Ziegler, T.; Rauk, A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 1977, 46, 1–10. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A. Donor-acceptor properties of ligands from the natural orbitals for chemical valence. Organometallics 2007, 26, 6576–6580. [Google Scholar] [CrossRef]
- Vincenzo, B.; Maurizio, C. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Rolfes, J.D.; Neese, F.; Pantazis, D.A. All-electron scalar relativistic basis sets for the elements Rb-Xe. J. Comput. Chem. 2020, 41, 1842–1849. [Google Scholar] [CrossRef] [PubMed]
- Bjornsson, R.; Neese, F.; DeBeer, S. Revisiting the Mossbauer isomer shifts of the FeMoco cluster of nitrigenase and the cofactor charge. Inorg. Chem. 2017, 56, 1470–1477. [Google Scholar] [CrossRef] [PubMed]
- Takeda, Y.; Sameera, W.M.C.; Minakata, S. Palladium-catalyzed regioselective and stereospecific ring-opening cross-coupling of aziridines: Experimental and computational studies. Acc. Chem. Res. 2020, 53, 1686–1702. [Google Scholar] [CrossRef]
- Sameera, W.M.C.; Takeda, Y.; Ohki, Y. Transition metal catalyzed cross-coupling and nitrogen reduction reactions: Lessons from computational studies. Adv. Organomet. Chem. 2022, 78, 35–78. [Google Scholar]
- Ishihara, K.; Araki, Y.; Tada, M.; Takayama, T.; Sakai, Y.; Sameera, W.M.C.; Ohki, Y. Synthesis of dinuclear Mo-Fe hydride complexes and catalytic silylation of N2. Chem. Eur. J. 2020, 26, 9537–9546. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Fuentealba, P.; Preuss, H.; Stoll, H.; Szentpály, L.V. A proper accounts of core-polarization with pseudopotentials: Single valence-electron alkali compounds. Chem. Phys. Lett. 1982, 89, 418–422. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr.; Hay, P.J. Gaussian Basis Sets for Molecular Calculations. In Modern Theoretical Chemistry; Springer: Berlin/Heidelberg, Germany, 1977; Volume 3, pp. 1–27. [Google Scholar]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]

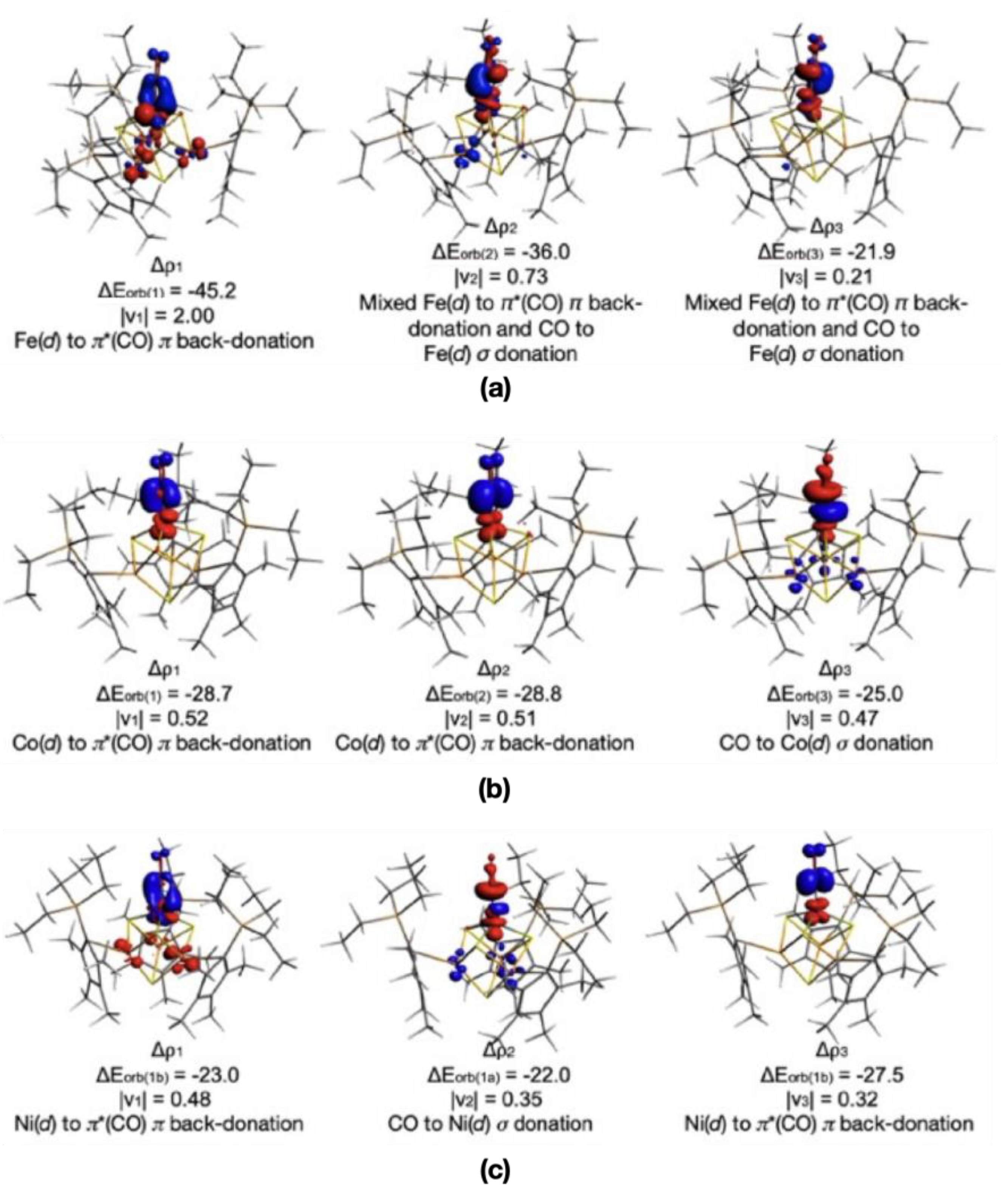
| (4, M = Fe) | (5, M = Co) | (6, M = Ni) | |
|---|---|---|---|
| ∆Eint | −101.1 | −81.5 | −77.3 |
| ∆EPauli | 196.9 | 170.5 | 149.6 |
| ∆Eelstat | −130.2 | −122.0 | −115.3 |
| ∆Eorb | −125.8 | −93.5 | −79.8 |
| ∆Edisp | −9.26 | −10.5 | −7.1 |
| ∆Esol | −32.8 | −26.0 | −24.7 |
| Transition Metal Cluster | Isomer-Shift (mm s−1) | ||
|---|---|---|---|
| X-Ray | Optimized | Experimental | |
| 7 | 0.46, 0.46 | 0.35, 0.35 | 0.48 |
| 8 | 0.39 | 0.26 | 0.40 |
| 9 | 0.26 | 0.14 | 0.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakshan, N.M.; Aluthge, D.C.; Sameera, W.M.C. Computational Studies of Molybdenum-Containing Metal–Sulfur and Metal–Hydride Clusters. Catalysts 2024, 14, 816. https://doi.org/10.3390/catal14110816
Lakshan NM, Aluthge DC, Sameera WMC. Computational Studies of Molybdenum-Containing Metal–Sulfur and Metal–Hydride Clusters. Catalysts. 2024; 14(11):816. https://doi.org/10.3390/catal14110816
Chicago/Turabian StyleLakshan, Nishshanka M., Dinesh C. Aluthge, and W. M. C. Sameera. 2024. "Computational Studies of Molybdenum-Containing Metal–Sulfur and Metal–Hydride Clusters" Catalysts 14, no. 11: 816. https://doi.org/10.3390/catal14110816
APA StyleLakshan, N. M., Aluthge, D. C., & Sameera, W. M. C. (2024). Computational Studies of Molybdenum-Containing Metal–Sulfur and Metal–Hydride Clusters. Catalysts, 14(11), 816. https://doi.org/10.3390/catal14110816






