Prediction of In-Situ Gasification Chemical Looping Combustion Effects of Operating Conditions
Abstract
:1. Introduction
2. Results and Discussion
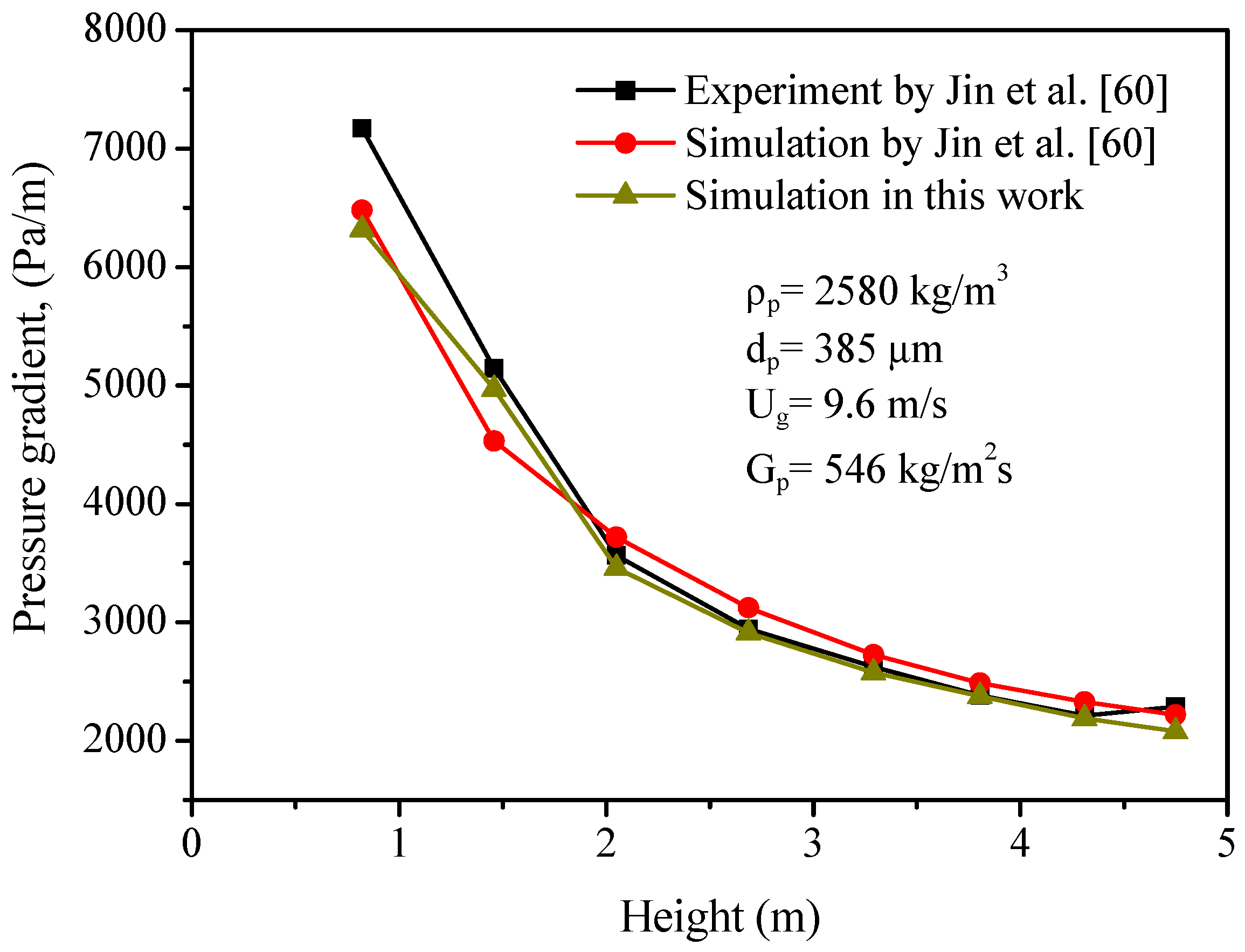
2.1. Further Validation of the Hydrodynamics and Reaction Models
2.2. Distributions of Solids Holdup and Gas–solid Components
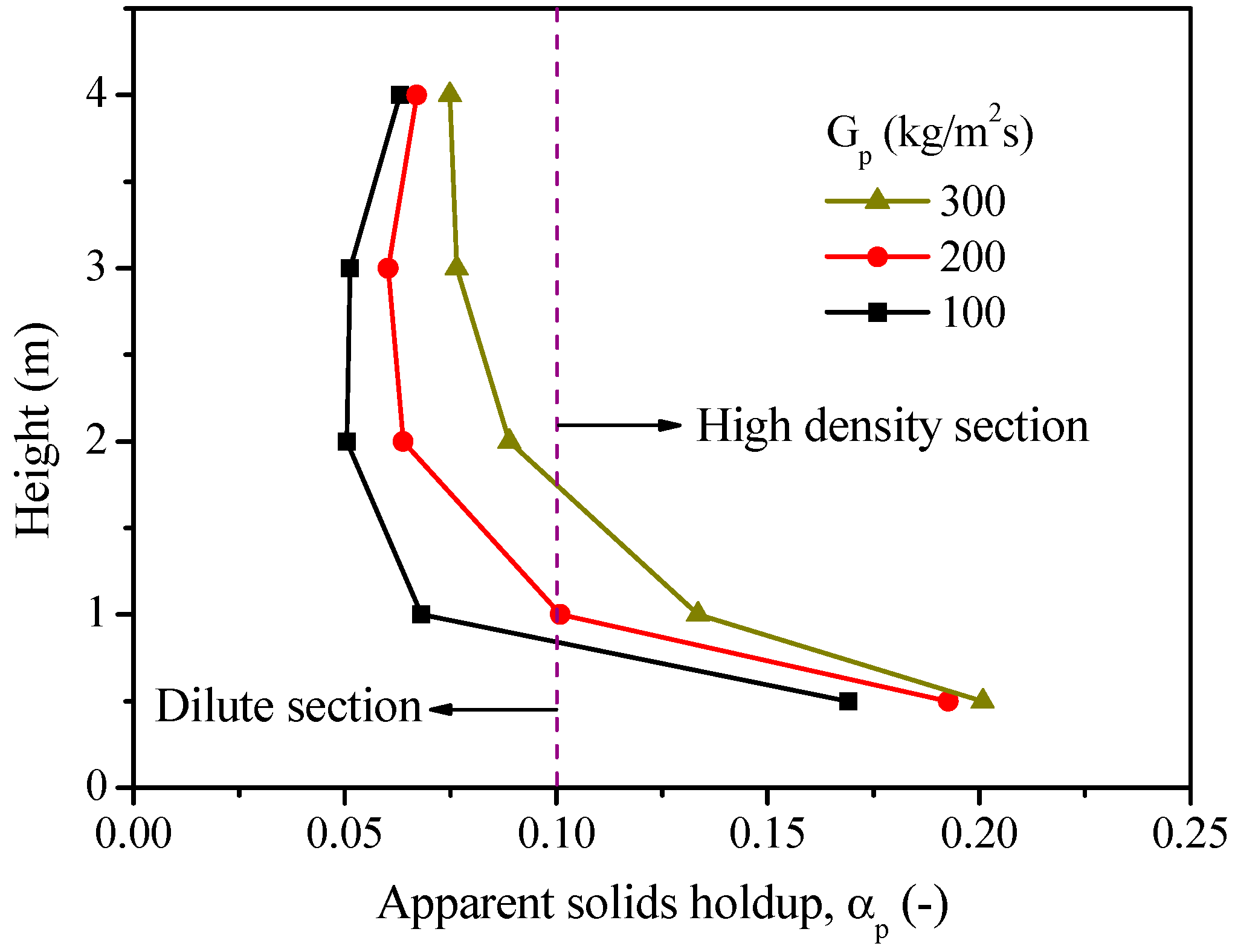
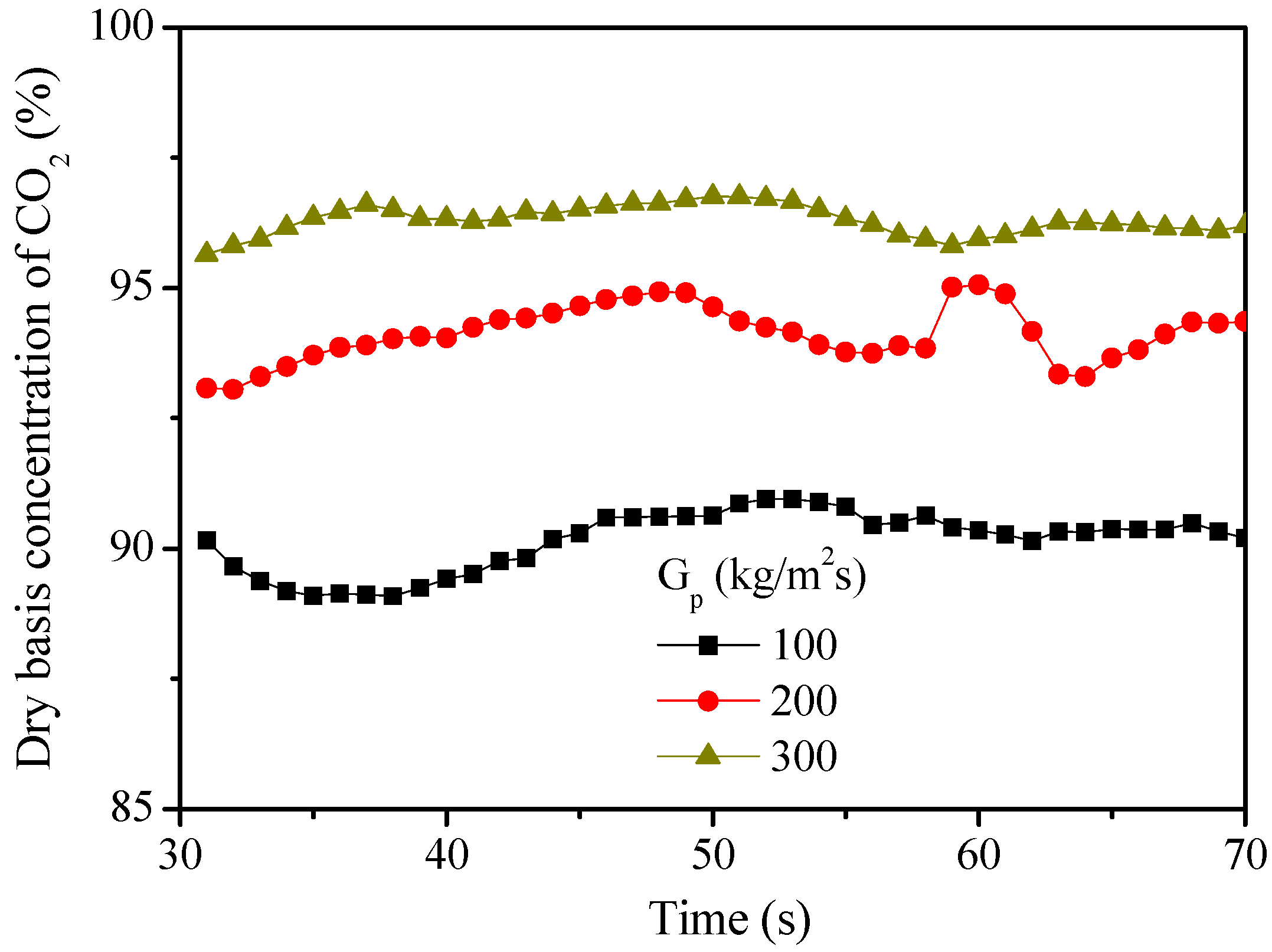
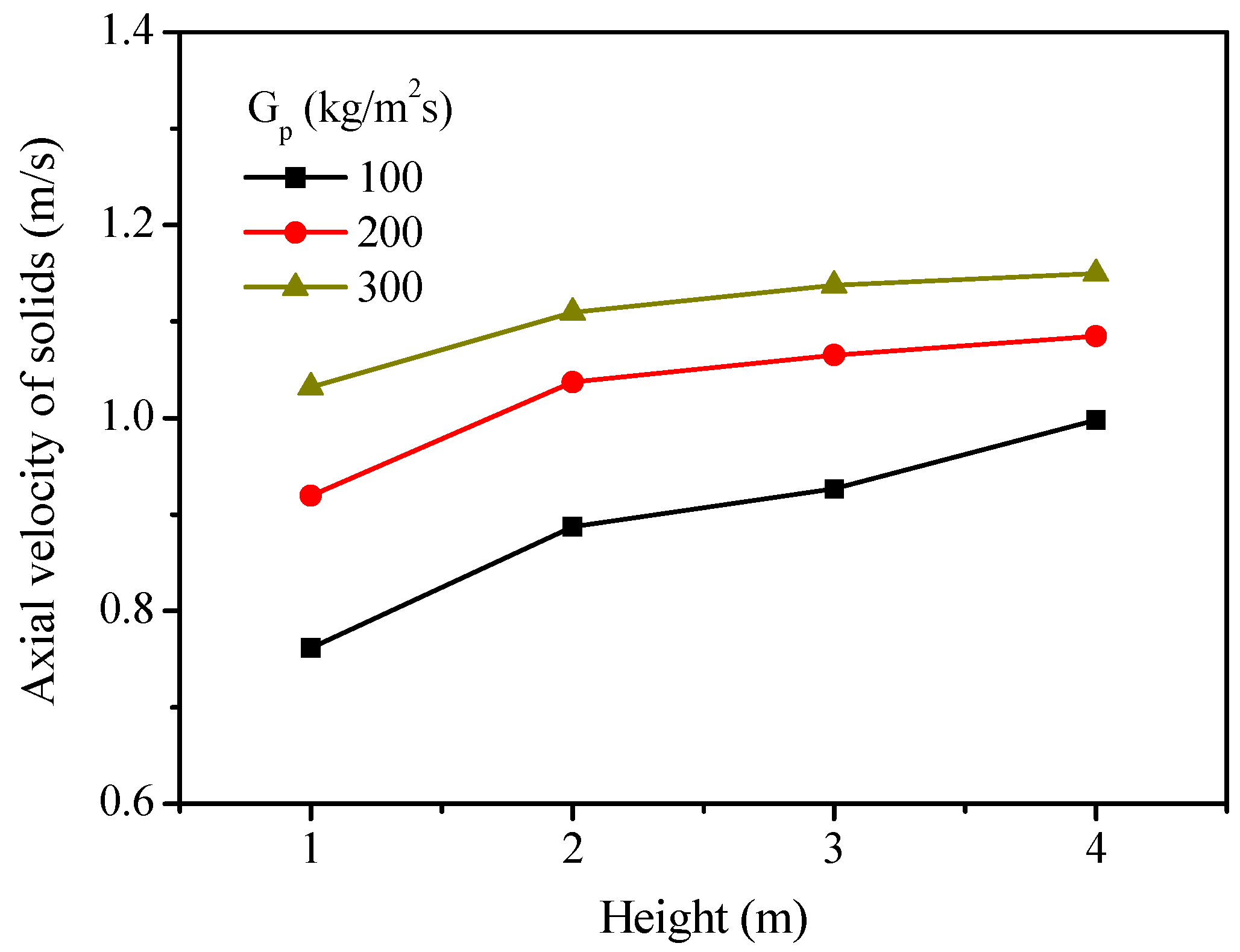
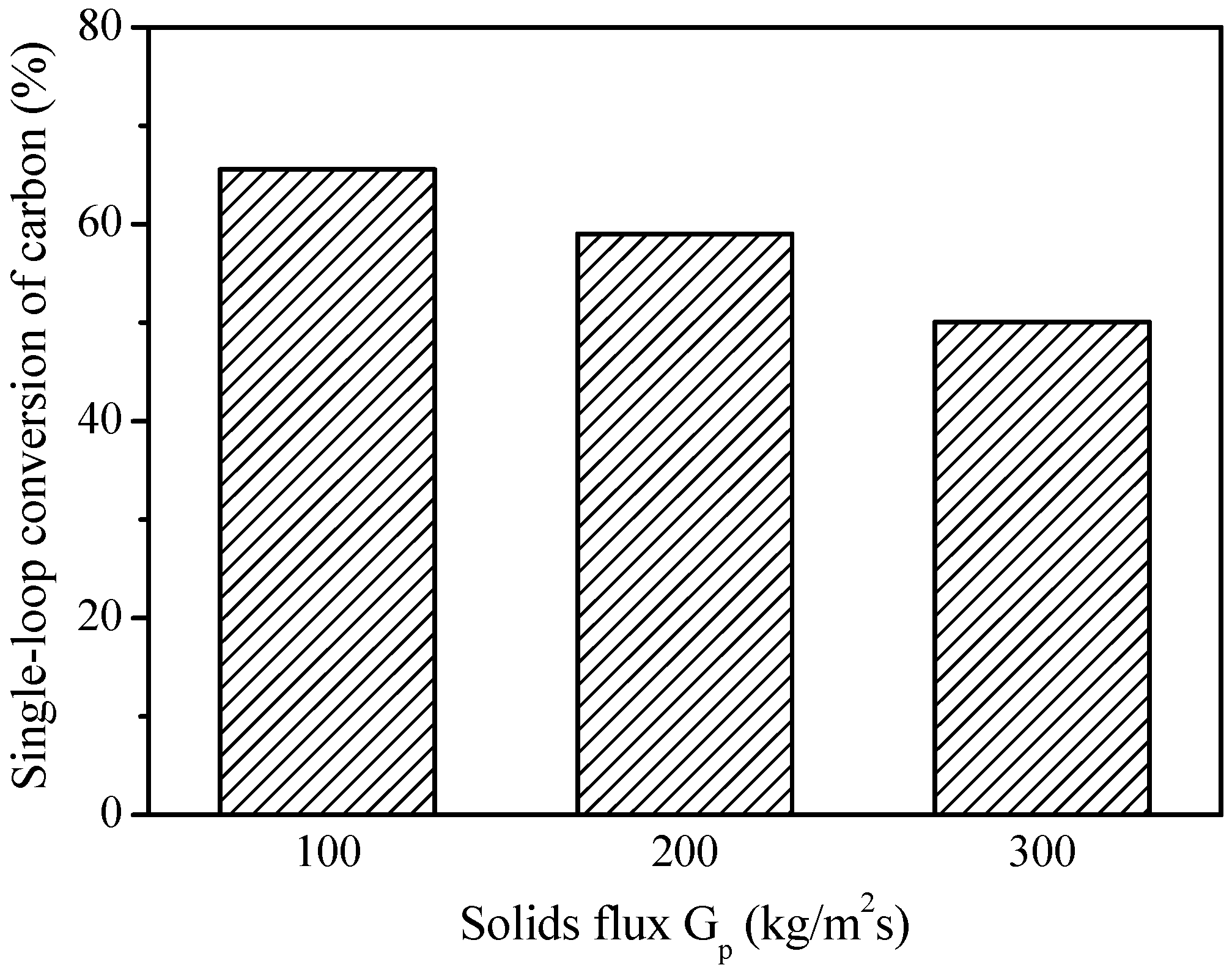
2.3. Effect of Solids Flux
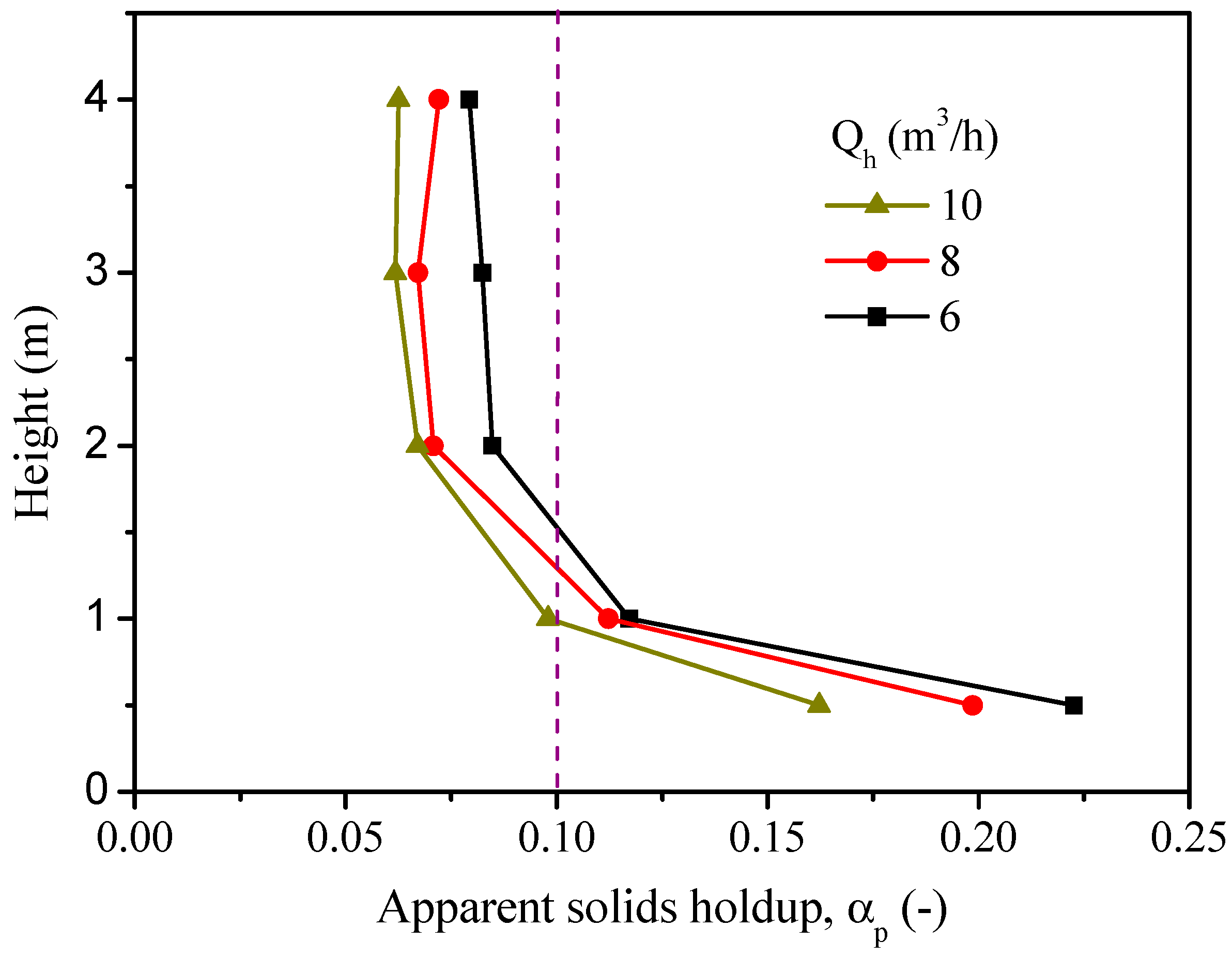
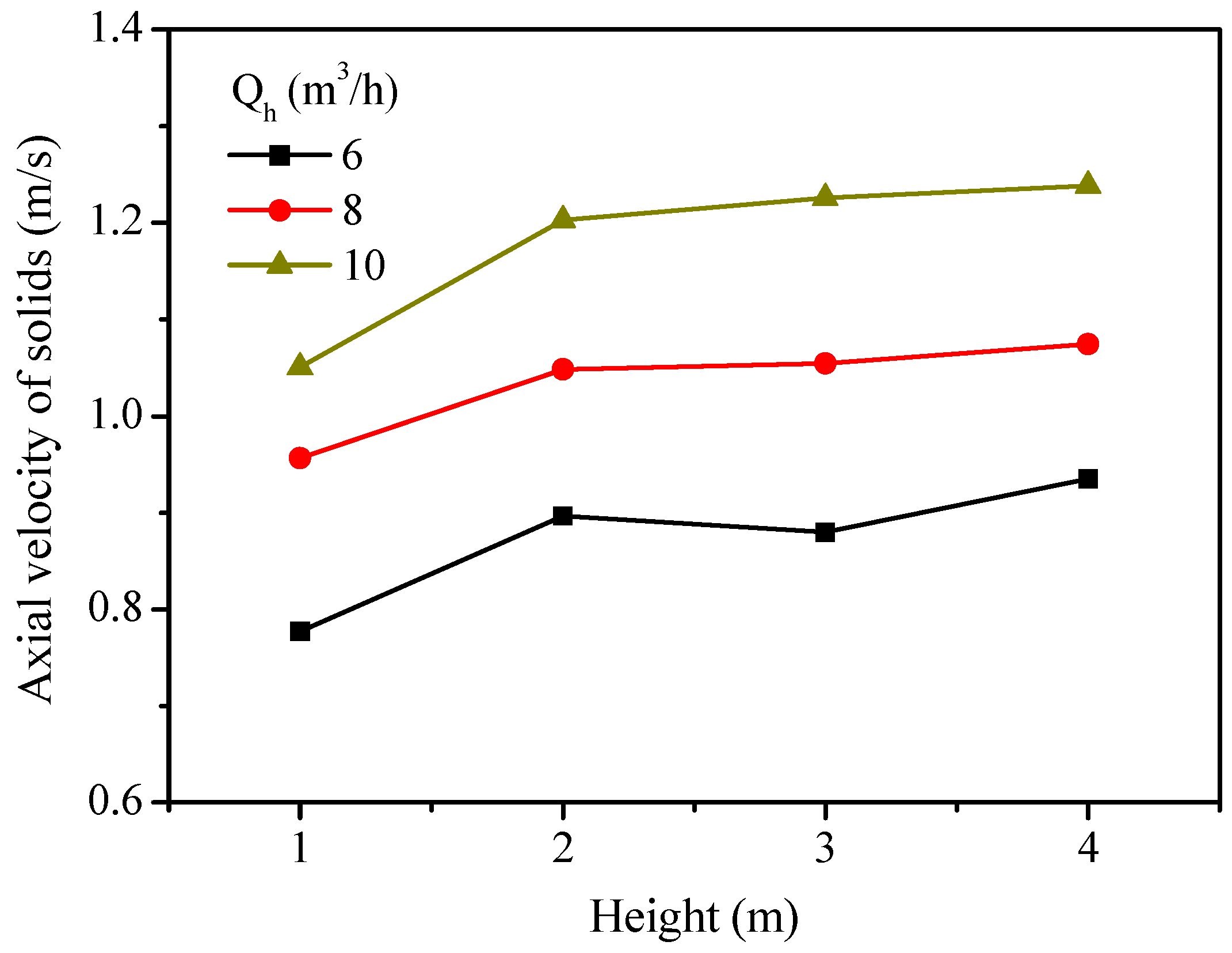
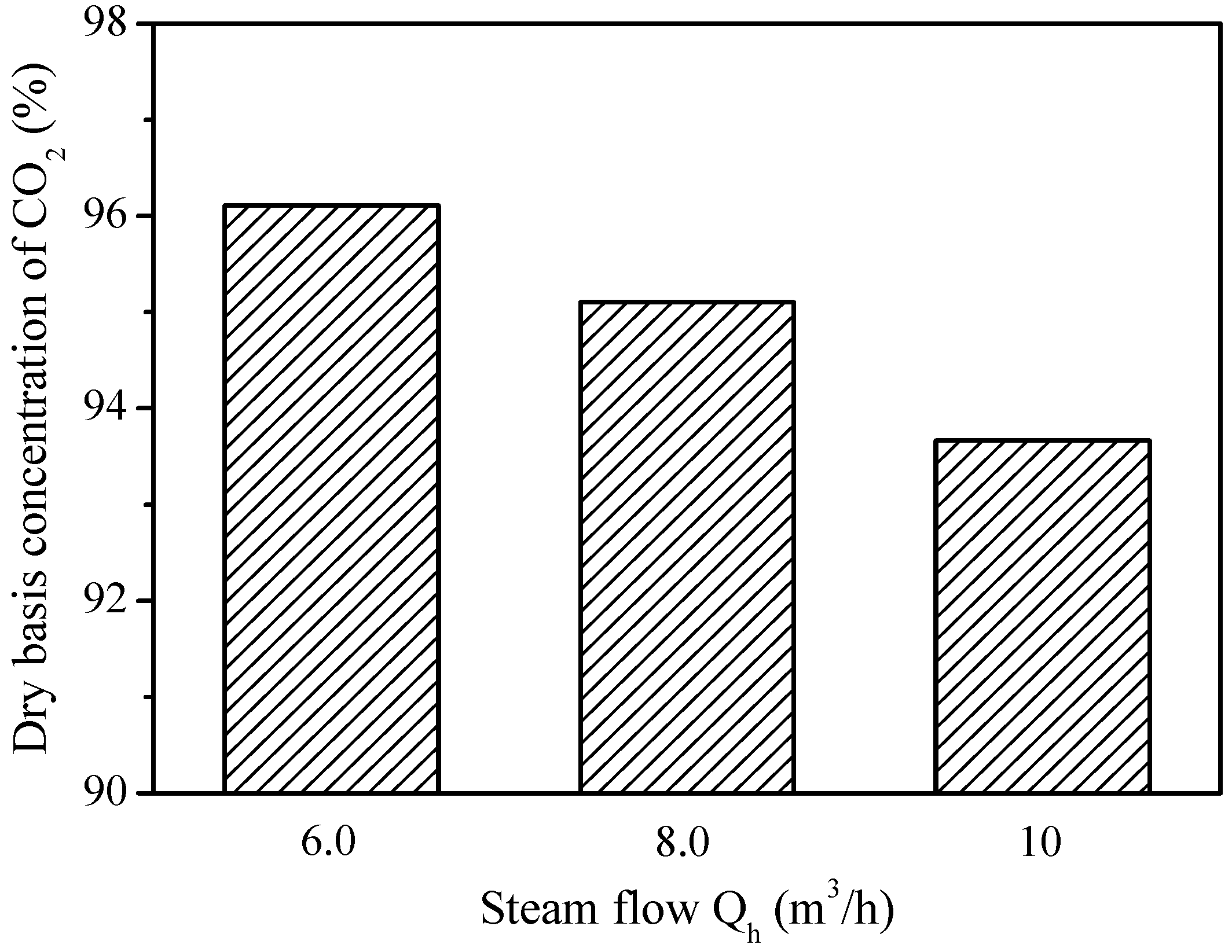
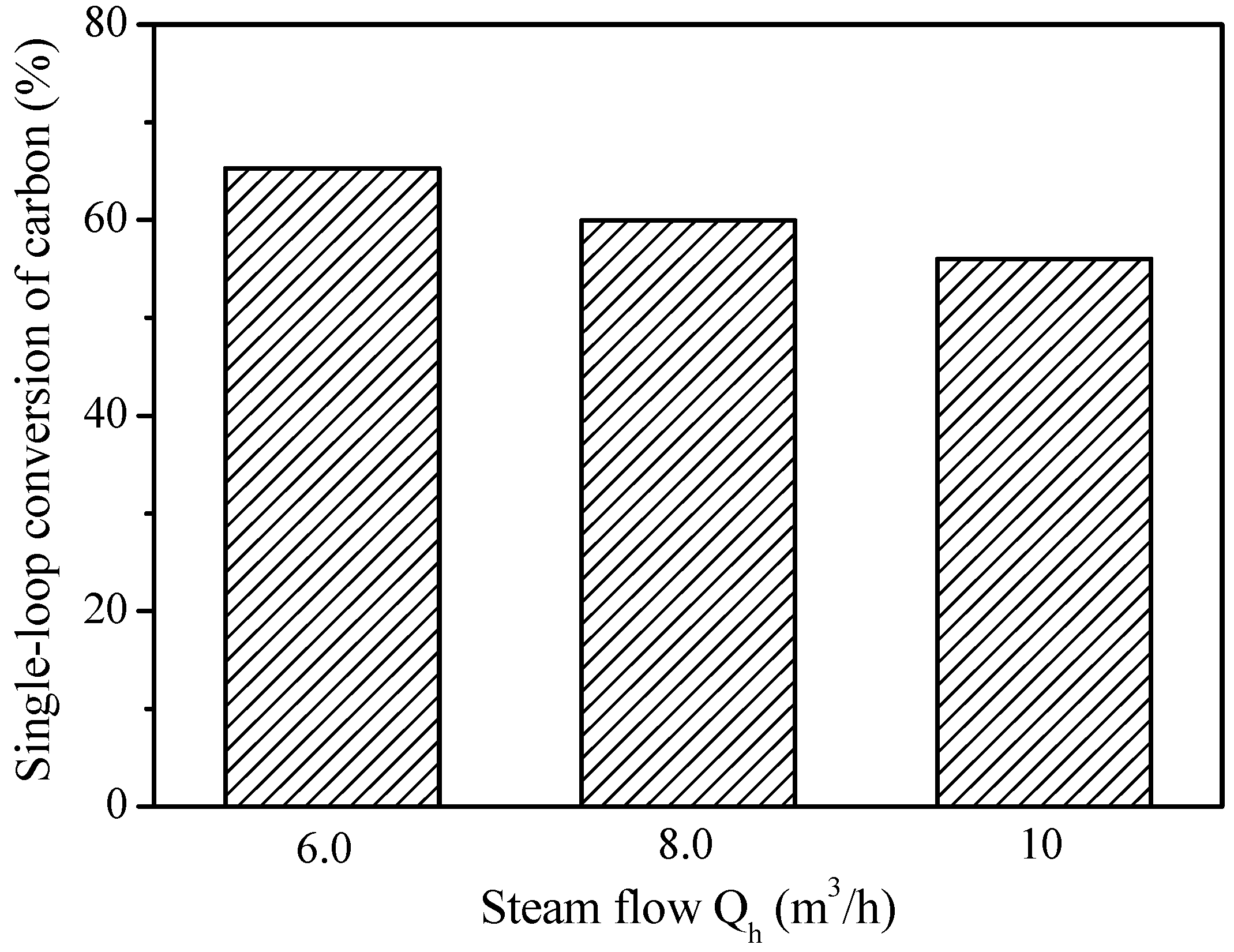
2.4. Effect of Steam Flow
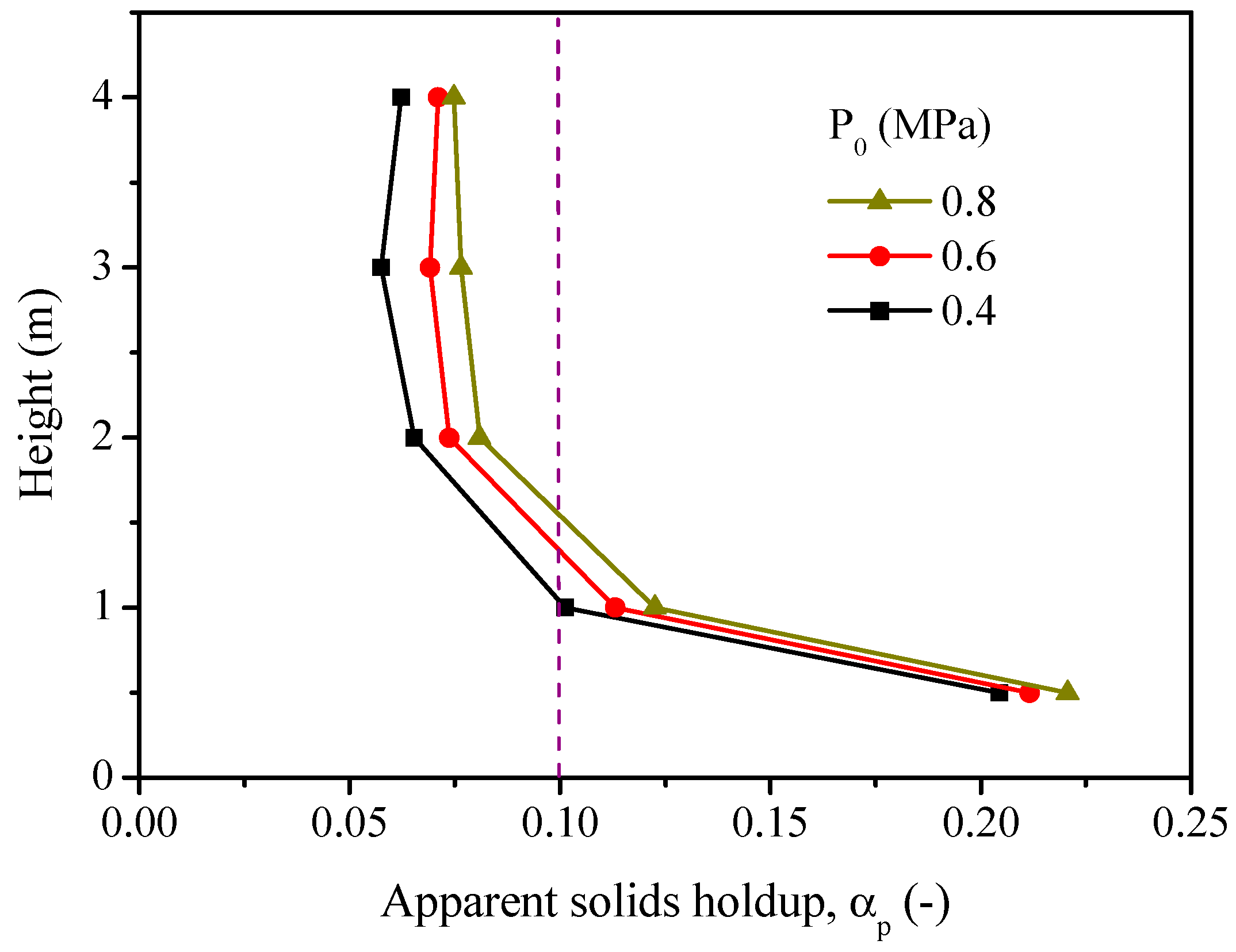
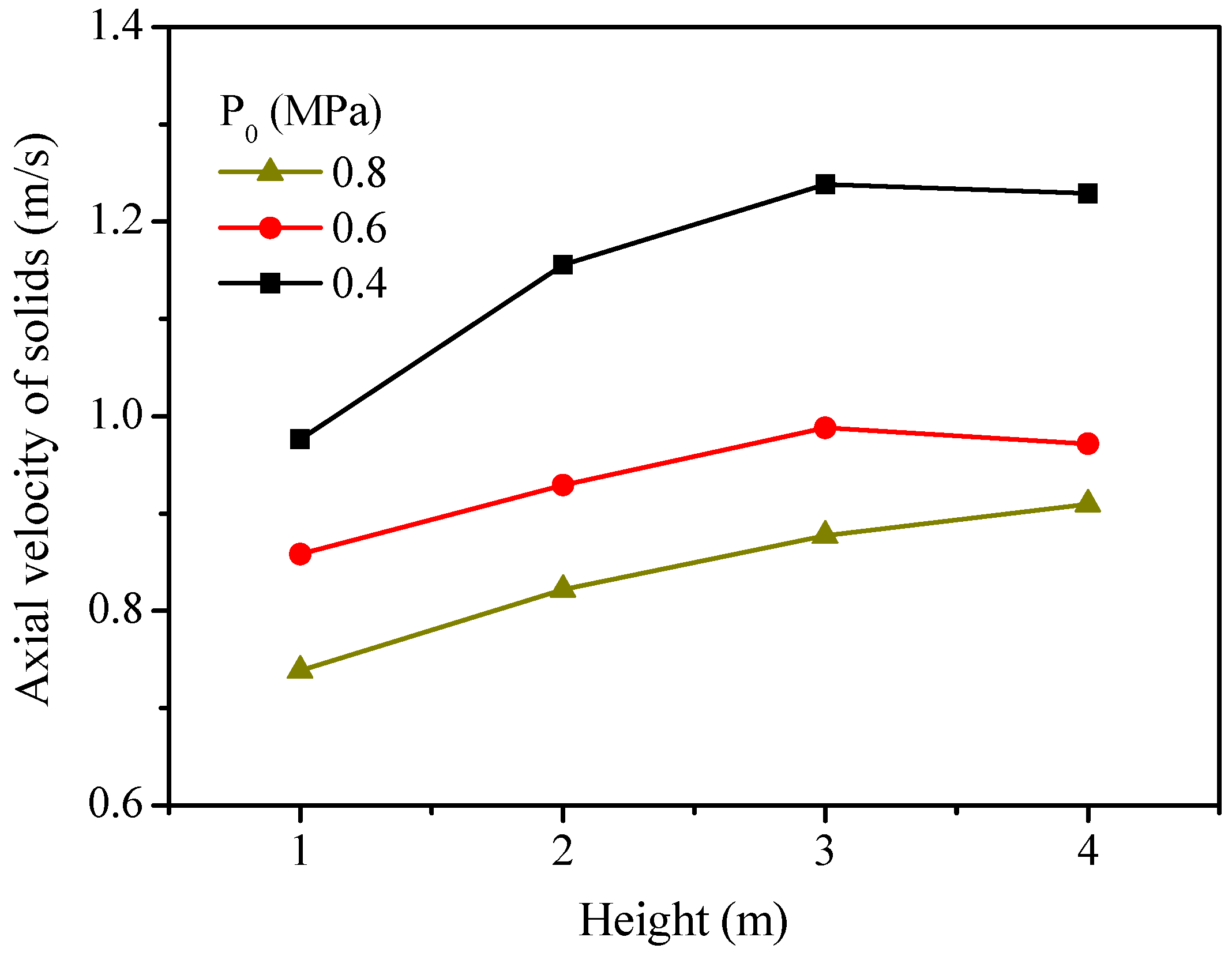
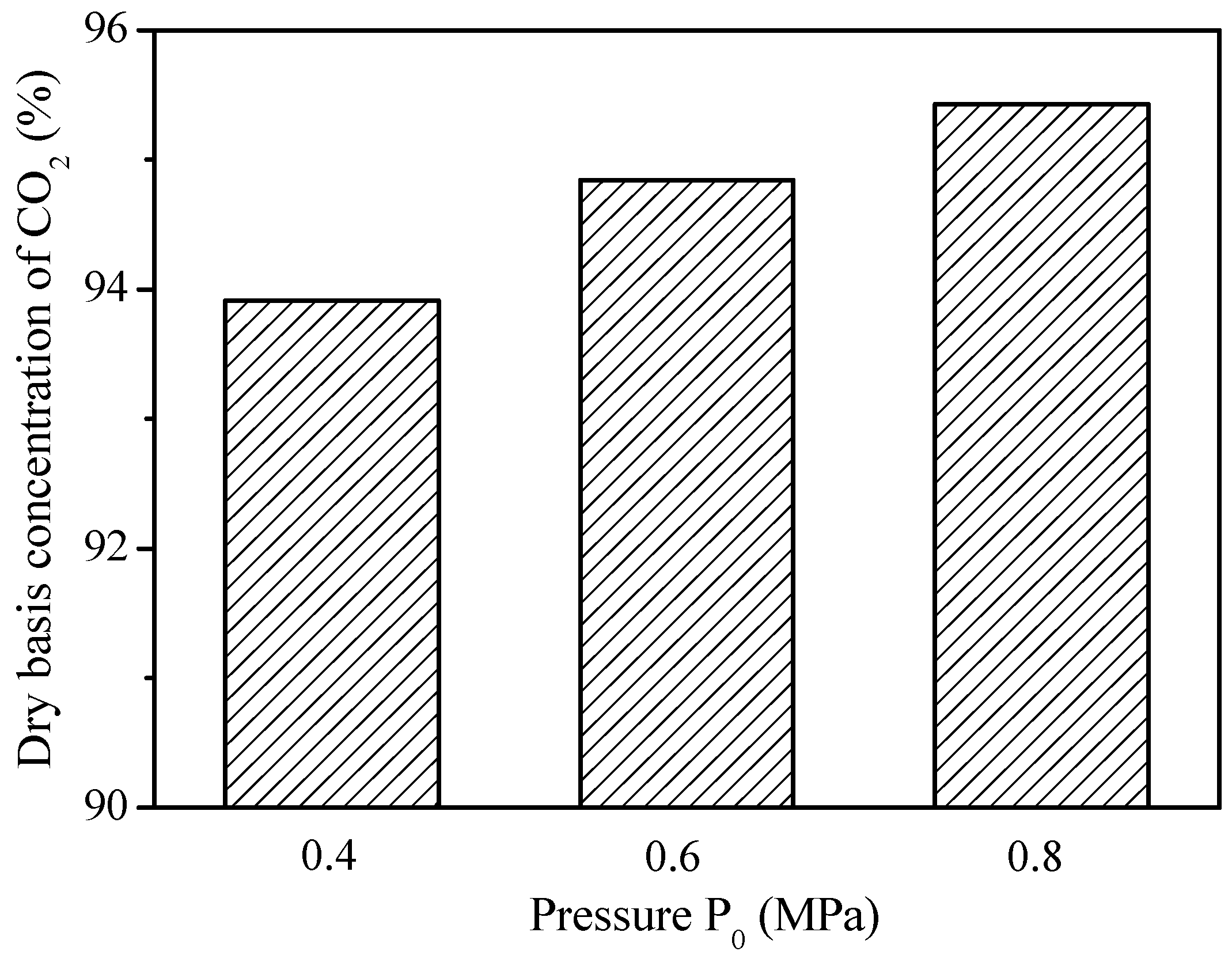
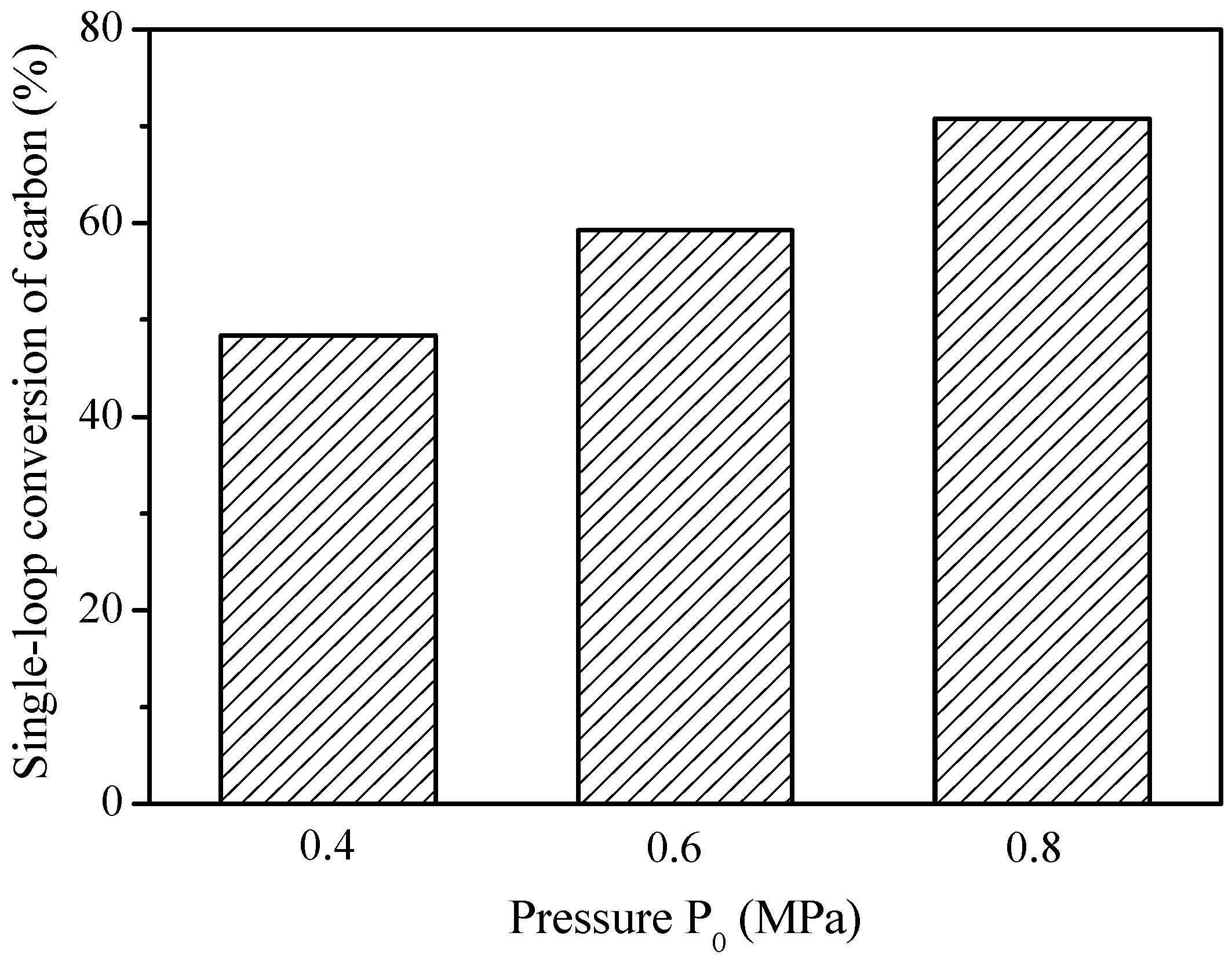
2.5. Effect of Operating Pressure
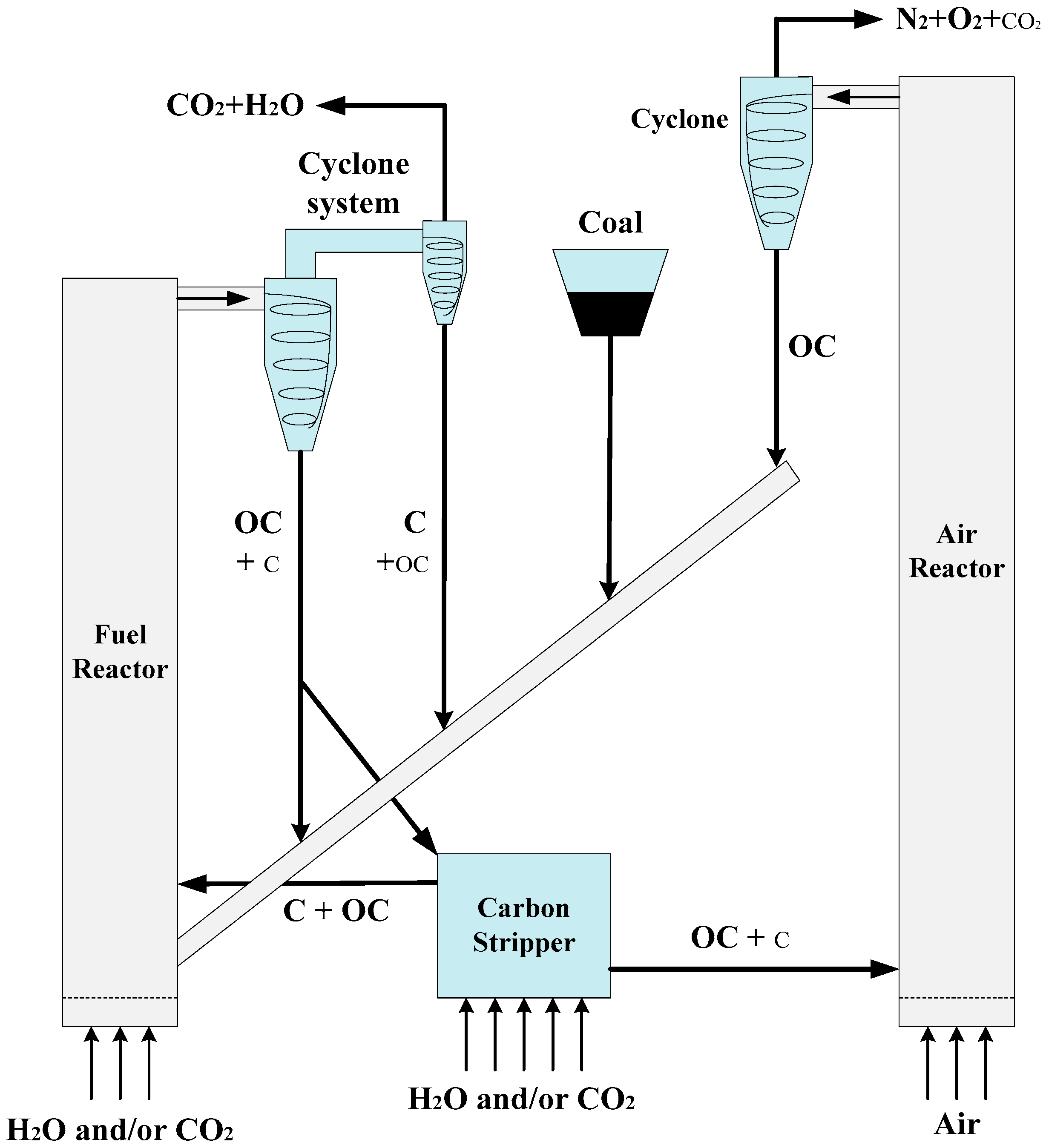
3. Materials and Methods
3.1. Governing Equations
3.2. Chemical Reactions
3.3. Data Evaluation
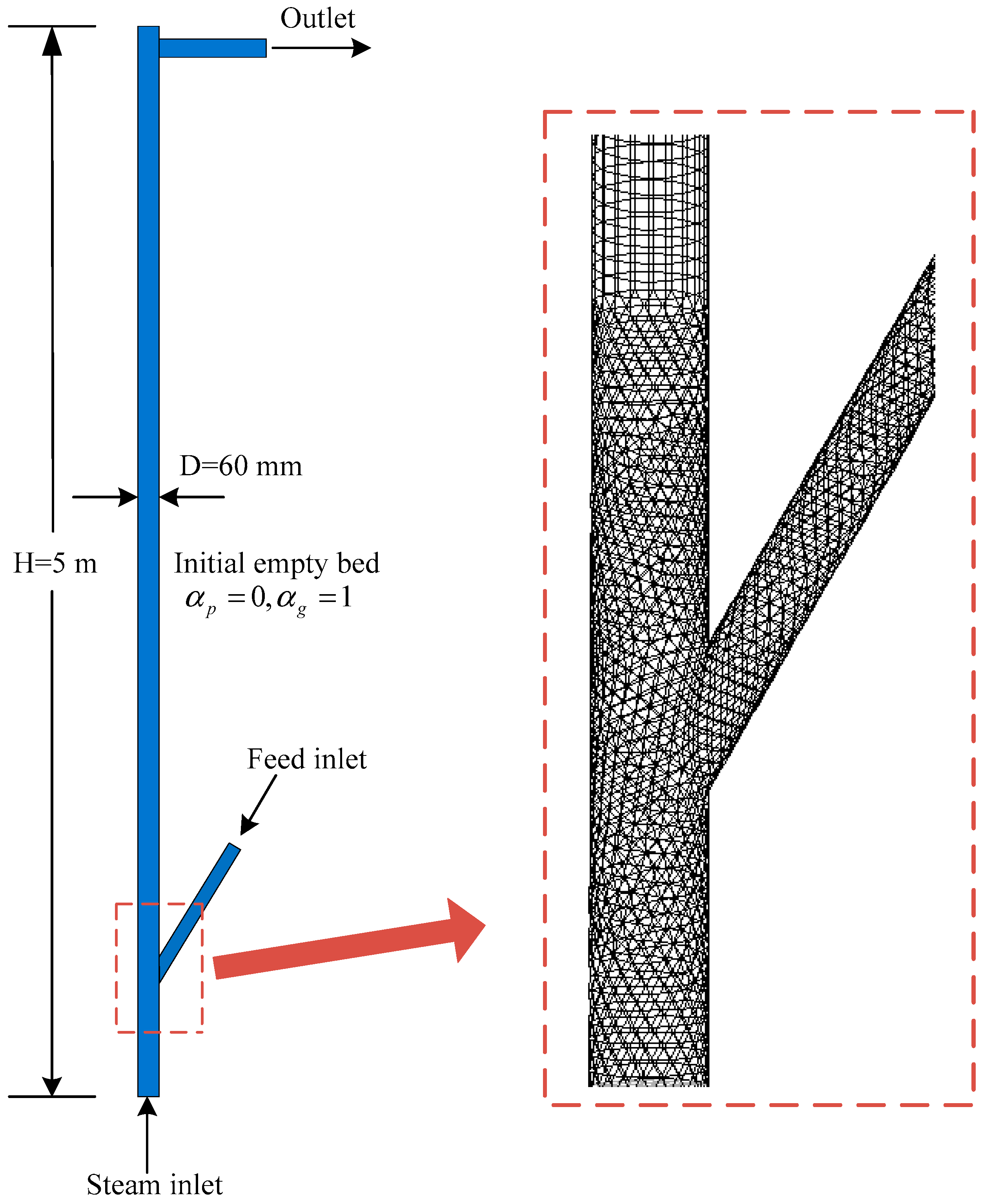
3.4. Numerical Considerations
4. Conclusions
- (1)
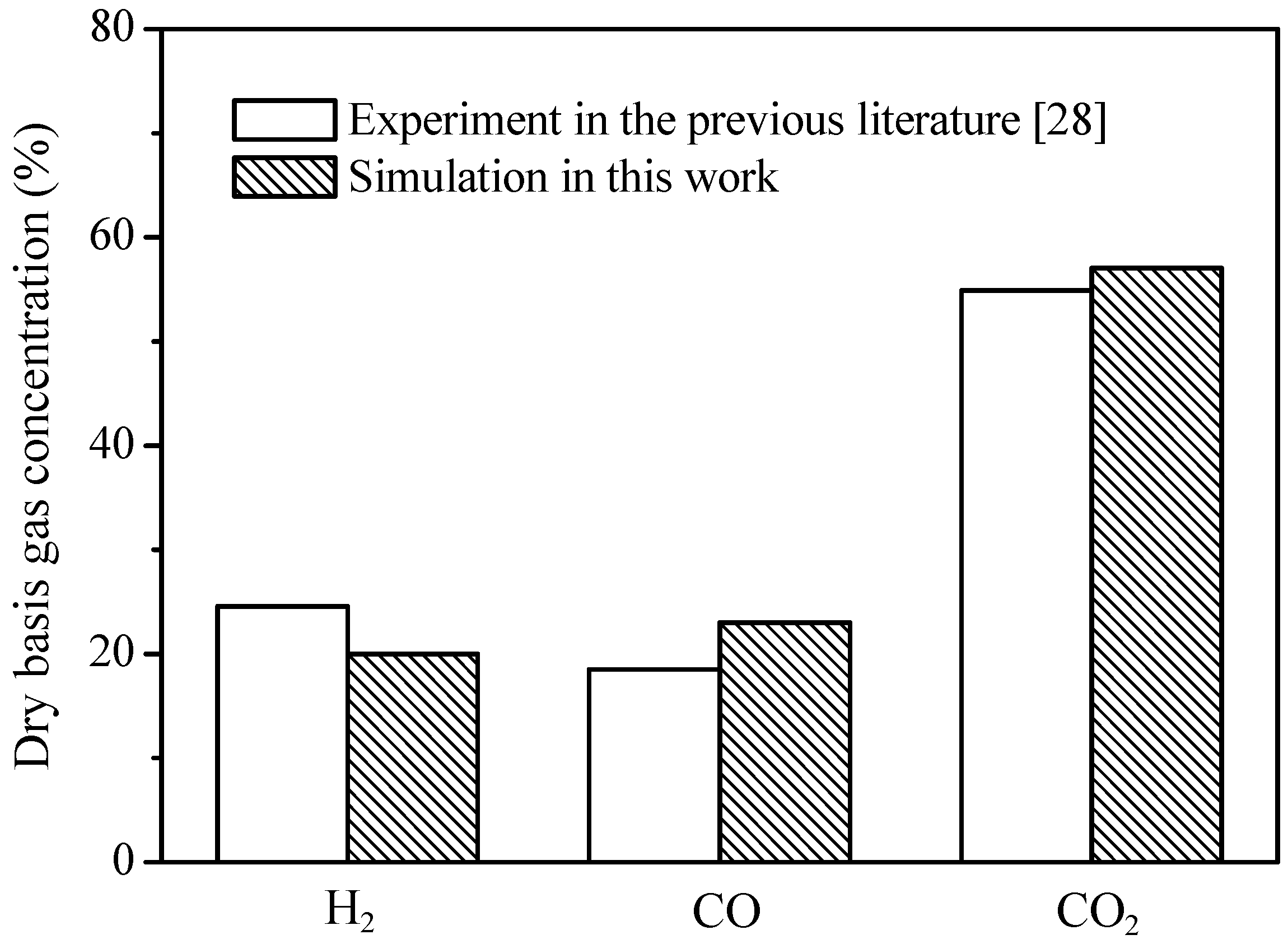
- The single-loop conversion of carbon and CO2 dry-basis concentration at the fuel reactor outlet under the reference condition are comparable to those from the previous experimental system, demonstrating the CFB riser with high solids flux is a potential candidate for the fuel reactor of iG-CLC.
- (2)
- An increase in the solids flux results in an increase in the CO2 concentration at the outlet, which is believed to be mainly due to the increased solids holdup and better gas–solid contacts that promote gas–solid reactions. However, a higher solids flux has a slightly negative effect on the single-loop carbon conversion. This is mainly due to the decrease in the solids residence time.
- (3)
- A decrease in the steam flow gives rise to an increase in CO2 concentration at the fuel reactor outlet because of the higher solids holdup and the lower gas velocity, which further enhances the gas–solid contacts and the residence time of gas for reactions. In addition, a decrease in the steam flow promotes the single-loop conversion of carbon mainly as a result of the increased solids residence time. However, in order to ensure the circulation and fluidization of the particles, there exists a minimum requirement for the steam flow under the conditions of the given operating temperature, pressure and particle flows.
- (4)
- An increase in the operating pressure leads to an increase in the CO2 concentration at the outlet of the fuel reactor due to the higher concentrations of gasification intermediates, higher solids holdup and the lower gas velocity, which promote the reduction reactions (8)–(10) with the oxygen carrier. The elevated steam partial pressure and longer gas residence time facilitate the char gasification. Moreover, the elevated pressure leads to a decrease in solids velocity, thus longer solids residence time and higher carbon conversion. Therefore, it should be beneficial for a practical CFB fuel reactor of iG-CLC system to be designed and operated under a certain pressurized conditions.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Af | sectional area of the feed inlet [m2] |
| As | sectional area of the fuel reactor [m2] |
| fi | dry basis concentration of gas component |
| acceleration due to gravity [m/s2] | |
| Gp | solids flux [kg/(m2·s)] |
| H | specific enthalpy [J/kg] |
| Ji | diffusion flux of species i [kg/(m2·s)] |
| p | pressure [Pa] |
| P0 | operating pressure [MPa] |
| QC,out | mass flux of unreacted char at the outlet [kg/h] |
| QCoal,in | mass flux of coal at the solids inlet [kg/h] |
| Qh | steam flow under the operating temperature and pressure [m3/h] |
| mass source term [kg/(m3·s)] | |
| Si | net rate of production of species i [kg/(m3·s)] |
| Up,f | particle velocity at the feed inlet [m/s] |
| v | velocity [m/s] |
| xi | molar fraction of species i in the gas phase |
| XC | single-loop conversion of carbon [%] |
| Y | mass fraction |
| volume fraction | |
| drag [kg/(m3·s)] | |
| thermal conductivity [W/(m2·K)] | |
| density [kg/m3] | |
| stress-strain tensor [Pa] |
References
- Lyngfelt, A.; Leckner, B.; Mattisson, T. A fluidized-bed combustion process with inherent CO2 separation; application of chemical-looping combustion. Chem. Eng. Sci. 2001, 56, 3101–3113. [Google Scholar] [CrossRef]
- Abad, A.; Mattisson, T.; Lyngfelt, A.; Johansson, M. The use of iron oxide as oxygen carrier in a chemical-looping reactor. Fuel 2007, 86, 1021–1035. [Google Scholar] [CrossRef]
- Mattisson, T.; García-Labiano, F.; Kronberger, B.; Lyngfelt, A.; Adánez, J.; Hofbauer, H. Chemical-Looping Combustion using syngas as fuel. Int. J. Greenh. Gas Control 2007, 1, 158–169. [Google Scholar] [CrossRef]
- Ishida, M.; Jin, H.; Okamoto, T. A fundamental study of a new kind of medium material for chemical-looping combustion. Energy Fuels 1996, 10, 958–963. [Google Scholar] [CrossRef]
- Jin, H.; Okamoto, T.; Ishida, M. Development of a novel chemical-looping combustion: Synthesis of a solid looping material of NiO/NiAl2O4. Ind. Eng. Chem. Res. 1999, 38, 126–132. [Google Scholar] [CrossRef]
- Cho, P.; Mattisson, T.; Lyngfelt, A. Comparison of iron-, nickel-, copper-and manganese-based oxygen carriers for chemical-looping combustion. Fuel 2004, 83, 1215–1225. [Google Scholar] [CrossRef]
- Garcia-Labiano, F.; Adanez, J.; de Diego, L.F.; Gayán, P.; Abad, A. Effect of pressure on the behavior of copper-, iron-, and nickel-based oxygen carriers for chemical-looping combustion. Energy Fuels 2006, 20, 26–33. [Google Scholar] [CrossRef]
- De Diego, L.F.; García-Labiano, F.; Gayán, P.; Celaya, J.; Palacios, J.M.; Adánez, J. Operation of a 10 kWth chemical-looping combustor during 200 h with a CuO-Al2O3 oxygen carrier. Fuel 2007, 86, 1036–1045. [Google Scholar] [CrossRef] [Green Version]
- Adánez, J.; Dueso, C.; de Diego, L.F.; García-Labiano, F.; Gayán, P.; Abad, A. Methane combustion in a 500 Wth chemical-looping combustion system using an impregnated Ni-based oxygen carrier. Energy Fuels 2008, 23, 130–142. [Google Scholar] [CrossRef]
- Kolbitsch, P.; Bolhàr-Nordenkampf, J.; Pröll, T.; Hofbauer, H. Operating experience with chemical looping combustion in a 120kW dual circulating fluidized bed (DCFB) unit. Int. J. Greenh. Gas Control 2010, 4, 180–185. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, H.; Tian, X.; Wei, Y.; Zhang, Y.; Zheng, C. Continuous Operation of Interconnected Fluidized Bed Reactor for Chemical Looping Combustion of CH4 Using Hematite as Oxygen Carrier. Energy Fuels 2015, 29, 3257–3267. [Google Scholar] [CrossRef]
- Berguerand, N.; Lyngfelt, A. Design and operation of a 10 kWth chemical-looping combustor for solid fuels-testing with South African coal. Fuel 2008, 87, 2713–2726. [Google Scholar] [CrossRef]
- Leion, H.; Mattisson, T.; Lyngfelt, A. Solid fuels in chemical-looping combustion. Int. J. Greenh. Gas Control 2008, 2, 180–193. [Google Scholar] [CrossRef]
- Shen, L.H.; Wu, J.H.; Xiao, J. Experiments on chemical looping combustion of coal with a NiO based oxygen carrier. Combust. Flame 2009, 156, 721–728. [Google Scholar] [CrossRef]
- Fan, L.S.; Li, F. Chemical looping technology and its fossil energy conversion applications. Ind. Eng. Chem. Res. 2010, 49, 10200–10211. [Google Scholar] [CrossRef]
- Abad, A.; Gayán, P.; de Diego, L.F.; García-Labiano, F.; Adánez, J. Fuel reactor modelling in chemical-looping combustion of coal: 1. Model formulation. Chem. Eng. Sci. 2013, 87, 277–293. [Google Scholar] [CrossRef] [Green Version]
- García-Labiano, F.; de Diego, L.F.; Gayán, P.; Abad, A.; Adánez, J. Fuel reactor modelling in chemical-looping combustion of coal: 2-simulation and optimization. Chem. Eng. Sci. 2013, 87, 173–182. [Google Scholar] [CrossRef] [Green Version]
- Forero, C.R.; Gayán, P.; de Diego, L.F.; Abad, A.; García-Labiano, F.; Adánez, J. Syngas combustion in a 500 Wth chemical-looping combustion system using an impregnated Cu-based oxygen carrier. Fuel Process. Technol. 2009, 90, 1471–1479. [Google Scholar] [CrossRef] [Green Version]
- Jin, H.; Ishida, M. A new type of coal gas fueled chemical-looping combustion. Fuel 2004, 83, 2411–2417. [Google Scholar] [CrossRef]
- Spallina, V.; Gallucci, F.; Romano, M.C.; Chiesa, P.; Lozza, G.; van Sint Annaland, M. Investigation of heat management for CLC of syngas in packed bed reactors. Chem. Eng. J. 2013, 225, 174–191. [Google Scholar] [CrossRef]
- Hamers, H.P.; Romano, M.C.; Spallina, V.; Chiesa, P.; Gallucci, F.; van Sint Annaland, M. Energy analysis of two stage packed-bed chemical looping combustion configurations for integrated gasification combined cycles. Energy 2015, 85, 489–502. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Jin, B.; Zhang, Y.; Zhang, Y.; Liu, X. Three Dimensional Modeling of a Coal-Fired Chemical Looping Combustion Process in the Circulating Fluidized Bed Fuel Reactor. Energy Fuels 2013, 27, 2173–2184. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Liu, X.; Zhang, Y.; Liu, H. Experimental investigation on flow behaviors in a novel in situ gasification chemical looping combustion apparatus. Ind. Eng. Chem. Res. 2013, 52, 14208–14218. [Google Scholar] [CrossRef]
- Abad, A.; Adánez, J.; Cuadrat, A.; García-Labiano, F.; Gayán, P.; Luis, F. Kinetics of redox reactions of ilmenite for chemical-looping combustion. Chem. Eng. Sci. 2011, 66, 689–702. [Google Scholar] [CrossRef] [Green Version]
- Adánez, J.; Cuadrat, A.; Abad, A.; Gayán, P.; de Diego, L.; García-Labiano, F. Ilmenite activation during consecutive redox cycles in chemical-looping combustion. Energy Fuels 2010, 24, 1402–1413. [Google Scholar] [CrossRef]
- Xiao, R.; Song, Q.; Song, M.; Lu, Z.; Zhang, S.; Shen, L. Pressurized chemical-looping combustion of coal with an iron ore-based oxygen carrier. Combust. Flame 2010, 157, 1140–1153. [Google Scholar] [CrossRef]
- Cuadrat, A.; Abad, A.; Adánez, J.; de Diego, L.; García-Labiano, F.; Gayán, P. Behavior of ilmenite as oxygen carrier in chemical-looping combustion. Fuel Process. Technol. 2012, 94, 101–112. [Google Scholar] [CrossRef] [Green Version]
- Cuadrat, A.; Abad, A.; García-Labiano, F.; Gayán, P.; de Diego, L.; Adánez, J. Effect of operating conditions in Chemical-Looping Combustion of coal in a 500 Wth unit. Int. J. Greenh. Gas Control 2012, 6, 153–163. [Google Scholar] [CrossRef] [Green Version]
- Bayham, S.; McGiveron, O.; Tong, A.; Chung, E.; Kathe, M.; Wang, D.; Zeng, L.; Fan, L.S. Parametric and dynamic studies of an iron-based 25-kWth coal direct chemical looping unit using sub-bituminous coal. Appl. Energy 2015, 145, 354–363. [Google Scholar] [CrossRef]
- Linderholm, C.; Schmitz, M. Chemical-looping combustion of solid fuels in a 100 kW dual circulating fluidized bed system using iron ore as oxygen carrier. J. Environ. Chem. Eng. 2016, 4, 1029–1039. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, H.; Tian, X.; Wei, Y.; Rajendran, S.; Zhang, Y.; Bhattacharya, S.; Zheng, C. Chemical looping combustion of coal in a 5 kWth interconnected fluidized bed reactor using hematite as oxygen carrier. Appl. Energy 2015, 157, 304–313. [Google Scholar] [CrossRef]
- Pérez-Vega, R.; Abad, A.; García-Labiano, F.; Gayán, P.; Luis, F.; Adánez, J. Coal combustion in a 50 kWth Chemical Looping Combustion unit: Seeking operating conditions to maximize CO2 capture and combustion efficiency. Int. J. Greenh. Gas Control 2016, 50, 80–92. [Google Scholar] [CrossRef]
- Ströhle, J.; Orth, M.; Epple, B. Design and operation of a 1 MWth chemical looping plant. Appl. Energy 2014, 113, 1490–1495. [Google Scholar] [CrossRef]
- Thon, A.; Kramp, M.; Hartge, E.-U.; Heinrich, S.; Werther, J. Operational experience with a system of coupled fluidized beds for chemical looping combustion of solid fuels using ilmenite as oxygen carrier. Appl. Energy 2014, 118, 309–317. [Google Scholar] [CrossRef]
- Xiao, R.; Chen, L.; Saha, C.; Zhang, S.; Bhattacharya, S. Pressurized chemical-looping combustion of coal using an iron ore as oxygen carrier in a pilot-scale unit. Int. J. Greenh. Gas Control 2012, 10, 363–373. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Zhu, X.; Liu, H. Experimental Evaluation of a Novel 20 kWth in Situ Gasification Chemical Looping Combustion Unit with an Iron Ore as the Oxygen Carrier. Ind. Eng. Chem. Res. 2016, 55, 11775–11784. [Google Scholar] [CrossRef]
- Gayán, P.; Abad, A.; de Diego, L.F.; García-Labiano, F.; Adánez, J. Assessment of technological solutions for improving chemical looping combustion of solid fuels with CO2 capture. Chem. Eng. J. 2013, 233, 56–69. [Google Scholar] [CrossRef]
- Abad, A.; Mendiara, T.; Gayán, P.; García-Labiano, F.; de Diego, L.F.; Bueno, J.A.; Pérez-Vega, R.; Adánez, J. Comparative Evaluation of the Performance of Coal Combustion in 0.5 and 50 kWth Chemical Looping Combustion units with ilmenite, redmud or iron ore as oxygen carrier. Energy Procedia 2017, 114, 285–301. [Google Scholar] [CrossRef]
- Adánez, J.; Abad, A.; Mendiara, T.; Gayán, P.; de Diego, L.F.; García-Labiano, F. Chemical looping combustion of solid fuels. Prog. Energy Combust. 2018, 65, 6–66. [Google Scholar] [CrossRef]
- Cheng, M.; Sun, H.; Li, Z.; Cai, N. Annular carbon stripper for chemical-looping combustion of coal. Ind. Eng. Chem. Res. 2017, 56, 1580–1593. [Google Scholar] [CrossRef]
- Wang, P.; Means, N.; Howard, B.H.; Shekhawat, D.; Berry, D. The reactivity of CuO oxygen carrier and coal in Chemical-Looping with Oxygen Uncoupled (CLOU) and In-situ Gasification Chemical-Looping Combustion (iG-CLC). Fuel 2018, 217, 642–649. [Google Scholar] [CrossRef]
- Chen, X.; Shi, D.; Gao, X.; Luo, Z. A fundamental CFD study of the gas–solid flow field in fluidized bed polymerization reactors. Powder Technol. 2011, 205, 276–288. [Google Scholar] [CrossRef]
- Maghrebi, R.; Yaghobi, N.; Seyednejadian, S.; Tabatabaei, M.H. CFD modeling of catalyst pellet for oxidative coupling of methane: Heat transfer and reaction. Particuology 2013, 11, 506–513. [Google Scholar] [CrossRef]
- Shah, M.T.; Utikar, R.P.; Pareek, V.K. CFD study: Effect of pulsating flow on gas–solid hydrodynamics in FCC riser. Particuology 2017, 31, 25–34. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Wang, Y.; Hu, C. Three-dimensional multi-phase simulation of the mixing and segregation of binary particle mixtures in a two-jet spout fluidized bed. Particuology 2015, 22, 185–193. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Zhong, W. Three-dimensional simulation of fluidized bed coal gasification. Chem. Eng. Process. 2009, 48, 695–705. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, C.S.; Duan, L.B.; Qu, C.R.; Chen, X.P. Two-dimensional computational fluid dynamics simulation of coal combustion in a circulating fluidized bed combustor. Chem. Eng. J. 2011, 166, 306–314. [Google Scholar] [CrossRef]
- Deng, Z.; Xiao, R.; Jin, B.; Song, Q.; Huang, H. Multiphase CFD Modeling for a Chemical Looping Combustion Process (Fuel Reactor). Chem. Eng. Technol. 2008, 31, 1754–1766. [Google Scholar] [CrossRef]
- Jung, J.; Gamwo, I. Multiphase CFD-based models for chemical looping combustion process: Fuel reactor modeling. Powder Technol. 2008, 183, 401–409. [Google Scholar] [CrossRef]
- Mahalatkar, K.; Kuhlman, J.; Huckaby, E.; O’Brien, T. Computational fluid dynamic simulations of chemical looping fuel reactors utilizing gaseous fuels. Chem. Eng. Sci. 2011, 66, 469–479. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Zhang, Y.; Zhong, W.; Yin, S. Multiphase Computational Fluid Dynamics (CFD) Modeling of Chemical Looping Combustion Using a CuO/Al2O3 Oxygen Carrier: Effect of Operating Conditions on Coal Gas Combustion. Energy Fuels 2011, 25, 3815–3824. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Zhong, W.; Zhang, Y.; Song, M. Three-dimensional simulation of a coal gas fueled chemical looping combustion process. Int. J. Greenh. Gas Control 2011, 5, 1498–1506. [Google Scholar] [CrossRef]
- Wang, S.; Lu, H.; Zhao, F.; Liu, G. CFD studies of dual circulating fluidized bed reactors for chemical looping combustion processes. Chem. Eng. J. 2014, 236, 121–130. [Google Scholar] [CrossRef]
- Mahalatkar, K.; Kuhlman, J.; Huckaby, E.; O’Brien, T. CFD simulation of a chemical-looping fuel reactor utilizing solid fuel. Chem. Eng. Sci. 2011, 66, 3617–3627. [Google Scholar] [CrossRef]
- Su, M.; Zhao, H.; Ma, J. Computational fluid dynamics simulation for chemical looping combustion of coal in a dual circulation fluidized bed. Energy Convers. Manag. 2015, 105, 1–12. [Google Scholar] [CrossRef]
- Shao, Y.; Zhang, Y.; Wang, X.; Wang, X.; Jin, B.; Liu, H. Three-dimensional full loop modeling and optimization of an in situ gasification chemical looping combustion system. Energy Fuels 2017, 31, 13859–13870. [Google Scholar] [CrossRef]
- Alobaid, F.; Ohlemüller, P.; Ströhle, J.; Epple, B. Extended Euler–Euler model for the simulation of a 1 MWth chemical–looping pilot plant. Energy 2015, 93, 2395–2405. [Google Scholar] [CrossRef]
- May, J.; Alobaid, F.; Ohlemüller, P.; Stroh, A.; Ströhle, J.; Epple, B. Reactive two–fluid model for chemical–looping combustion–Simulation of fuel and air reactors. Int. J. Greenh. Gas Control 2018, 76, 175–192. [Google Scholar] [CrossRef]
- Pärssinen, J.; Zhu, J. Particle velocity and flow development in a long and high-flux circulating fluidized bed riser. Chem. Eng. Sci. 2001, 56, 5295–5303. [Google Scholar] [CrossRef]
- Jin, B.; Wang, X.; Zhong, W.; Tao, H.; Ren, B.; Xiao, R. Modeling on high-flux circulating fluidized bed with Geldart group B particles by kinetic theory of granular flow. Energy Fuels 2010, 24, 3159–3172. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Zhong, W.; Zhang, M.; Huang, Y.; Duan, F. Flow behaviors in a high-flux circulating fluidized bed. Int. J. Chem. React. Eng. 2008, 6, A79. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Liu, H.; Wang, W.; Liu, X.; Zhang, Y. Optimization of in Situ Gasification Chemical Looping Combustion through Experimental Investigations with a Cold Experimental System. Ind. Eng. Chem. Res. 2015, 54, 5749–5758. [Google Scholar] [CrossRef]
- Contractor, R.M.; Patience, G.S.; Garnett, D.I.; Horowitz, H.S.; Sisler, G.M.; Bergna, H.E. A new process for n-butane oxidation to maleic anhydride using a circulating fluidized bed reactor. In Circulating Fluidized Bed Technology IV; Avidan, A., Ed.; AIChE: New York, NY, USA, 1994. [Google Scholar]
- Mei, J.S.; Shadle, L.J.; Yue, P.; Monazam, E.R. Hydrodynamics of a transport reactor operating in dense suspension upflow conditions for coal combustion applications. In Proceedings of the 18th International Conference on Fluidized Bed Combustion, Toronto, ON, Canada, 22–25 May 2005. [Google Scholar]
- Morton, F.; Pinkston, T.; Salazar, N.; Stalls, D. Orlando gasification project: Demonstration of a nominal 285 MW coal-based transport gasifier. In Proceedings of the 23rd Annual International Pittsburgh Coal Conference, Pittsburgh, PA, USA, 25–28 September 2006. [Google Scholar]
- Li, Z.; Wu, C.; Wei, F.; Jin, Y. Experimental study of high-density gas—Solids flow in a new coupled circulating fluidized bed. Powder Technol. 2004, 139, 214–220. [Google Scholar] [CrossRef]
- Malcus, S.; Cruz, E.; Rowe, C.; Pugsley, T. Radial solid mass flux profiles in a high-suspension density circulating fluidized bed. Powder Technol. 2002, 125, 5–9. [Google Scholar] [CrossRef]
- Liu, G.; Niksa, S. Coal conversion submodels for design applications at elevated pressures. Part II. Char gasification. Prog. Energy Combust. Sci. 2004, 30, 679–717. [Google Scholar] [CrossRef]
- Yin, S.; Jin, B.; Zhong, W.; Lu, Y.; Zhang, Y.; Shao, Y.; Liu, H. Solids holdup of high flux circulating fluidized bed at elevated pressure. Chem. Eng. Technol. 2012, 35, 904–910. [Google Scholar] [CrossRef]
- Cuadrat, A.; Abad, A.; Gayán, P.; de Diego, L.F.; García-Labiano, F.; Adánez, J. Theoretical approach on the CLC performance with solid fuels: Optimizing the solids inventory. Fuel 2012, 97, 536–551. [Google Scholar] [CrossRef] [Green Version]
- Benyahia, S.; Syamlal, M.; O’Brien, T.J. Study of the ability of multiphase continuum models to predict core-annulus flow. AIChE J. 2007, 53, 2549–2568. [Google Scholar] [CrossRef]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of circulating fluidized beds: Kinetic theory approach. In Proceedings of the 7th Engineering Foundation Conference on Fluidization, Brisbane, Australia, 3–8 May 1992. [Google Scholar]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Donskoi, E.; McElwain, D.; Wibberley, L. Estimation and modeling of parameters for direct reduction in iron ore/coal composites: Part II. Kinetic parameters. Metall. Mater. Trans. B 2003, 34, 255–266. [Google Scholar] [CrossRef]
- Smoot, L.; Smith, P. Coal Combustion and Gasification; Plenum Press: New York, NY, USA, 1985. [Google Scholar]
- Carrero-Mantilla, J.; Llano-Restrepo, M. Chemical equilibria of multiple-reaction systems from reaction ensemble Monte Carlo simulation and a predictive equation of state: Combined hydrogenation of ethylene and propylene. Fluid Phase Equilibr. 2006, 242, 189–203. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Reactor diameter (mm) | 60 |
| Reactor height (m) | 5 |
| Coal feeding rate (kg/h) | 10 |
| Thermal Power (kWth) | ~60 |
| Reactor temperature (K) | 1273 |
| Case | Solids Flux, Gp (kg/m2·s) | Steam Flow, Qh (m3/h) | Operating Pressure, P0 (MPa) |
|---|---|---|---|
| 1–3 | 100–200–300 | 7.5 | 0.55 |
| 4–6 | 220 | 6–8–10 | 0.6 |
| 7–9 | 200 | 7 | 0.4–0.6–0.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jin, B.; Liu, H.; Zhang, B.; Zhang, Y. Prediction of In-Situ Gasification Chemical Looping Combustion Effects of Operating Conditions. Catalysts 2018, 8, 526. https://doi.org/10.3390/catal8110526
Wang X, Jin B, Liu H, Zhang B, Zhang Y. Prediction of In-Situ Gasification Chemical Looping Combustion Effects of Operating Conditions. Catalysts. 2018; 8(11):526. https://doi.org/10.3390/catal8110526
Chicago/Turabian StyleWang, Xiaojia, Baosheng Jin, Hao Liu, Bo Zhang, and Yong Zhang. 2018. "Prediction of In-Situ Gasification Chemical Looping Combustion Effects of Operating Conditions" Catalysts 8, no. 11: 526. https://doi.org/10.3390/catal8110526
APA StyleWang, X., Jin, B., Liu, H., Zhang, B., & Zhang, Y. (2018). Prediction of In-Situ Gasification Chemical Looping Combustion Effects of Operating Conditions. Catalysts, 8(11), 526. https://doi.org/10.3390/catal8110526






