Abstract
A molecular-statistical theory of the high frequency dielectric susceptibility of the nematic nanocomposites has been developed and approximate analytical expressions for the susceptibility have been obtained in terms of the effective polarizability of a nanoparticle in the nematic host, volume fraction of the nanoparticles and the susceptibility of the pure nematic phase. A simple expression for the split of the plasmon resonance of the nanoparticles in the nematic host has been obtained and it has been shown that in the resonance frequency range the high frequency dielectric anisotropy of the nanocomposite may be significantly larger than that of the pure nematic host. As a result, all dielectric and optical properties of the nanocomposite related to the anisotropy are significantly enhanced which may be important for emerging applications. The components of the dielectric susceptibility have been calculated numerically for particular nematic nanocomposites with gold and silver nanoparicles as functions of the nanoparticle volume fraction and frequency. The splitting of the plasmon resonance has been observed together with the significant dependence on the nanoparticle volume fraction and the parameters of the nematic host phase.
1. Introduction
Nematic liquid crystals (LCs) have a long history and numerous contemporary applications. During the past decade there has been significant interest in LC nanocomposite, in which metal, dielectric or semiconductor nanoparticles (NPs), which are close to the size of typical mesogenic molecules, modify and improve the LC properties. It has been shown that doping of a nematic LC with small NP volume concentration can affect many important nematic phase properties, e.g., decrease in threshold and switching voltages as well as switching times of LC displays (see, for example, Refs. [1,2,3,4,5]). Suspensions of NPs in various nematic LCshave been investigated by many authors and, in particular, doping of nematics with ferroelectric NPs is known to enhance dielectric and optical anisotropy, increase the electro-optic response [6,7] and improve the photorefractive properties [8]. Suspensions of para- and ferromagnetic particles in nematics are promising candidates for magnetically tunable structures, and doping of ferroelectric LCs with metal and silica nanoparticles enables one to improve the spontaneous polarization and dielectric permittivity and to decrease switching times [9,10,11,12,13]. Finally, distributing semiconductor quantum dots in smectic LC-polymers enables one to achieve the positional ordering of nanosize particles [14,15]. At the same time, the LC medium may also affect the properties of NPs including, in particular, their polarizability. For instance, the localized plasmon resonance of gold NPs can be tuned by changing the refractive index and, in particular, the birefringence of the surrounding LC medium [16,17,18,19].
The effect of NPs on various properties of nematic LCs is mainly determined by the anisotropic interactions between NPs and mesogenic molecules. Many NPs are approximately spherical or weakly anisometric. In this case, the corresponding anisotropic interaction potential is determined by anisotropic charge distribution and the anisotropy of the polarizability of a NP or a mesogenic molecule. For nonpolar particles, the anisotropic interaction is dominated by the dispersion interaction which is determined by the dielectric properties of the interacting particles. In particular, the leading contribution is the so-called dipole-dipole dispersion interaction potential which is given by the following general expression (see, for example, [20]):
where is the polarizabiity tensor of a NP, is the polarizability tensor of a mesogenic molecule, h is the Plank constant and is the dipole-dipole propagator tensor where is the intermolecular vector.
One can readily see that the anisotropic interaction (which depends on the direction of the intermolecular vector ) is determined by the anisotropy of the polarizability of both NPs and mesogenic molecules. One notes also that typical NPs have the size of several mesogenic molecues, and in this case the effective polarizability of such a NP is renormalized by the dielectric properties of the surrounding LC medium as the NP is interacting simultaneously with many mesogenic molecules. Thus it is very important to obtain at least qualitative expressions for the effective polarizability of a NP embedded in the LC dielectric medium which is the aim of the present paper.
2. Results
2.1. High Frequency Dielectric Susceptibility of the Nematic Nanocomposite
As shown in [21], the general expression for the tensor dielectric constant of the nematic phase doped with NPs can be expressed in the form of the generalized Clausius-Mossotti equation in which the average polarizability of a single molecule is replaced by the effective renormalized polarizability that depends both on intermolecular interactions and correlations and on interactions and correlations between NPs and neighboring mesogenic molecules:
where
and where is the weighted sum of the microscopic polarizabiities of the mesogenic molecule and the NP which depends on the fluctuating orientation and position of both mesogenic molecules and the NPs:
and is the microscopic number density of molecules of type :
Here the operator when and when , where D is the molecular diameter and the operator is equal to the dipole-dipole propagator if the correlation radius of the nematic is smaller then the wavelength of light:
The renormalized polarizability can be expanded in powers of the polarizability fluctuation where is the average polarizability:
where .
Taking into account Equation (4), the renormalized weighted polarizability can be written in the form:
where is the average polarizability of the component and
Here where m denotes the mesogenic molecules of the host nematic phase and n denotes the NPs. The functions are the pair correlation functions between the particles of the components and , and is the kernel of the operator . The higher order terms in Equations (6) and (7) depend on higher order correlation functions.
Usually the volume fraction of NPs in the nematic nanocomposite is very small, and then the correlations between NPs can be neglected in the first approximation. As a result, Equation (2) can be written in the following form taking into account also Equation (7):
where is the volume fraction of the NPs and the effective nondimentional polarizability of a mesogenic molecule is expressed as
Here is the volume of the mesogenic molecule while is determined by the correlations between neighboring mesogenic molecules and is given by the general Equation (8).
Similarly, the effective nondimentional polarizability of an NP reads:
where is the volume of the mesogenic molecule and is determined by the correlations between the NP and the neighboring mesogenic molecules.
At small volume fraction of NPs, the effective polarizability of the mesogenic molecule is independent on the NPs in the first approximation and hence it can be expressed in terms of the dielectric tensor of the nematic host phase:
2.2. Effective Polarizability of a Nanoparticle in the Nematic Liquid Crystal Medium
We will use a simple model of a spherical metal nanoparticle with a plasmon response which is described in the first approximation by the Drude model:
where is the metal plasmon frequency and is the mean free time of electrons. In the simplest case can be expressed as where is the concentration of the conductivity electrons and is their effective mass. One notes that in the optical range in noble metals .
Effective dielectric properties of a relatively small NP in the nematic medium is determined by the interaction with the first layer of mesogenic molecules. This layer can be considered isotropic in the first approximation because of the competing tendencies to align along the macroscopic director and parallel (or perpendicular) to the strongly curved surface of an NP. In particular, gold and silver NPs are usually dressed by organic molecules with chains penetrating into the surrounding LC medium. Such chains can induce a significant orientational disorder around the NP which at least partially justifies the model of a NP in an isotropic dielectric medium with the dielectric susceptibility equal to the average susceptibility of the nematic LC.
Here and is the longitudinal and the transverse susceptibility of a nematic phase, respectively.
Such an approximation is sufficient to estimate the effective polarizability of a spherical NP renormalized by the interaction with the surrounding medium. In the framework of the quasi static approach, the effective polarizability of an NP can be expressed as [22]:
where a is the radius of the NP. The effective polarizability is characterized by the Mi plasmonic resonance [23] at the frequency which corresponds to the solution of the equation yielding .
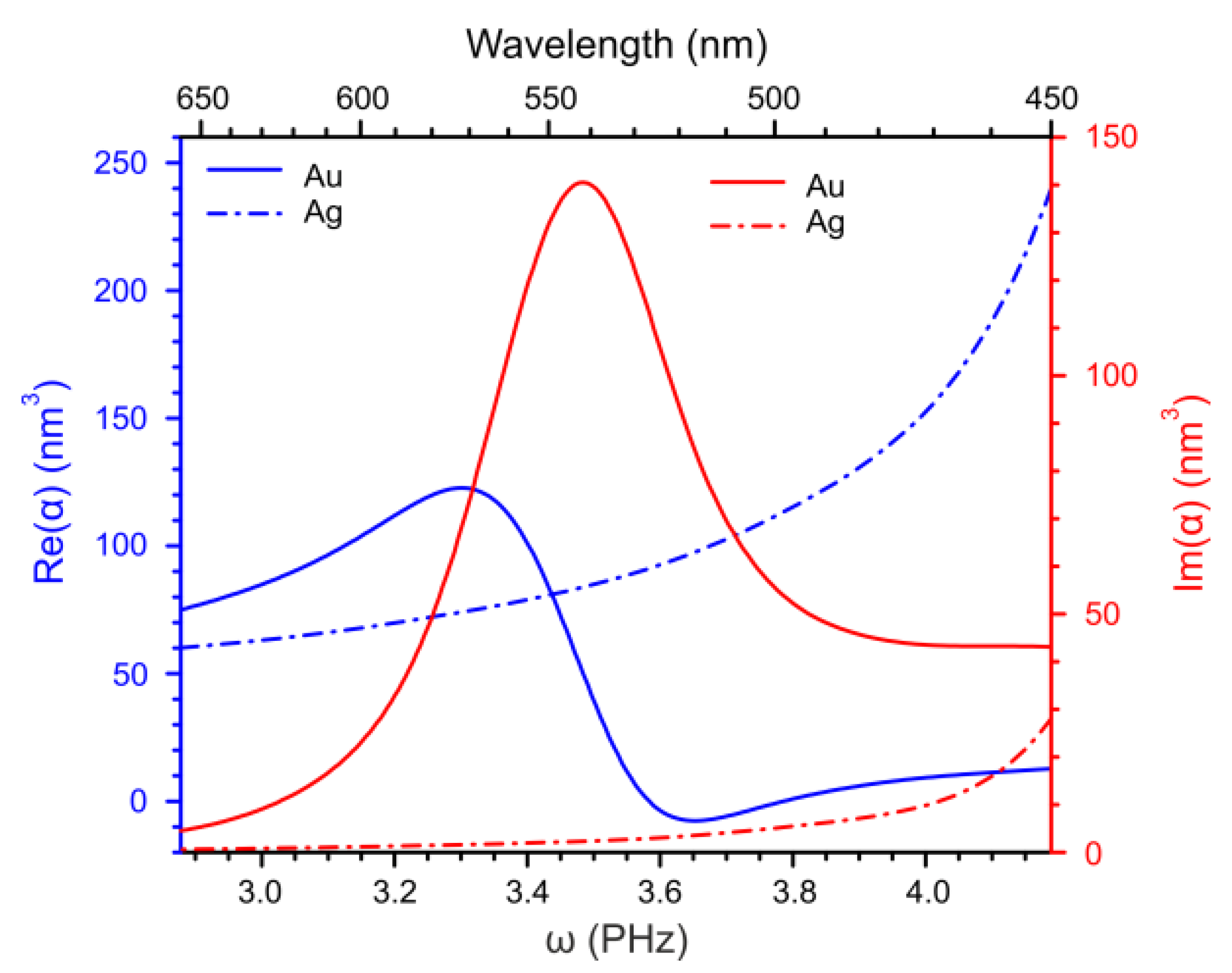
The real and imaginary parts of the effective polarizability of the AuNPs and silver NPs (AgNPs) in the nematic host 4-cyano-4’-pentylbiphenyl () are presented in Figure 1 as functions of cyclic frequency. The polarizability has been calculated numerically using the data on the frequency dependent susceptibility of gold and silver [24] and of the nematic [25]. The dielectric properties of all nematic LC materials used in the numerical calculations are presented in Figure A1 in the Appendix. In these calculations we have set the temperature range which corresponds to room temperatures (20–25 °C). In this range the LC materials considered in this paper exhibit the nematic phase. The selected frequency range corresponds to the one where the dispersion of both longitudinal and transverse susceptibility of has been carefully measured [25]. It should be noted that the plasmonic resonance frequency of the AuNP in the nematic host is within the selected frequency range while the resonance frequency of the AgNP is outside the range at higher frequency.
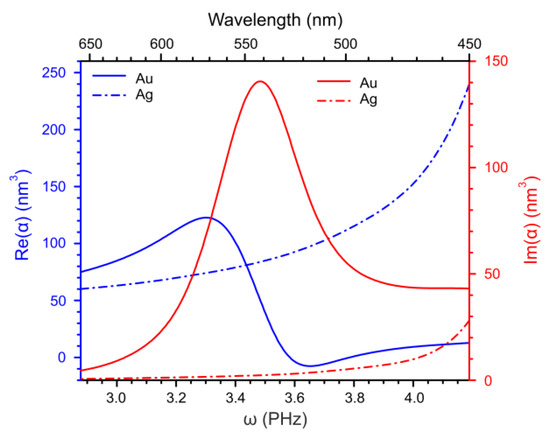
Figure 1.
Frequency dependence of the effective polarizability of AuNP and AgNP of the radius 2.5 nm in the nematic host .
Substituting Equation (16) into Equation (13) one obtains the final expression for the dielectric tensor of the nanocomposite:
The longitudinal and transverse components of the dielectric tensor can now be expressed as:
Equations (19) and (20) can be expanded in powers of small NP volume fraction keeping the linear terms:
where
The first term in the right hand side of Equation (13), as well as the terms proportional to in Equations (19) and (20), describe the so-called dilution effect, that is a decrease of the dielectric constant of the nematic host due to decrease of the volume fraction of mesogenic molecules in the presence of NPs. In contrast, the second term in (13), as well as terms proportional to in Equations (19) and (20), describe the increase of the dielectric constants of the nanocomposite determined by the direct contribution from the renormalized polarizability of NPs. These two effects compete with each other and this is reflected in the opposite signs of the two terms, proportional to , in Equations (21) and (22). Numerical calculations presented below indicate that for real nematic hosts doped with gold or silver NPs, the positive contribution from highly polarizable NPs strongly dominates which is very important for applications of such nanocomposites.
Equations (19)–(22) can be used both in the nematic and in the smectic A phase because both phases are uniaxial. Indeed, the point symmetry of the smectic A phase is the same as that of the uniaxial nematic phase, and the smectic positional order does not practically effect the optical properties of the smectic A phase because the period of the smectic structure is much smaller then the wavelength of light.
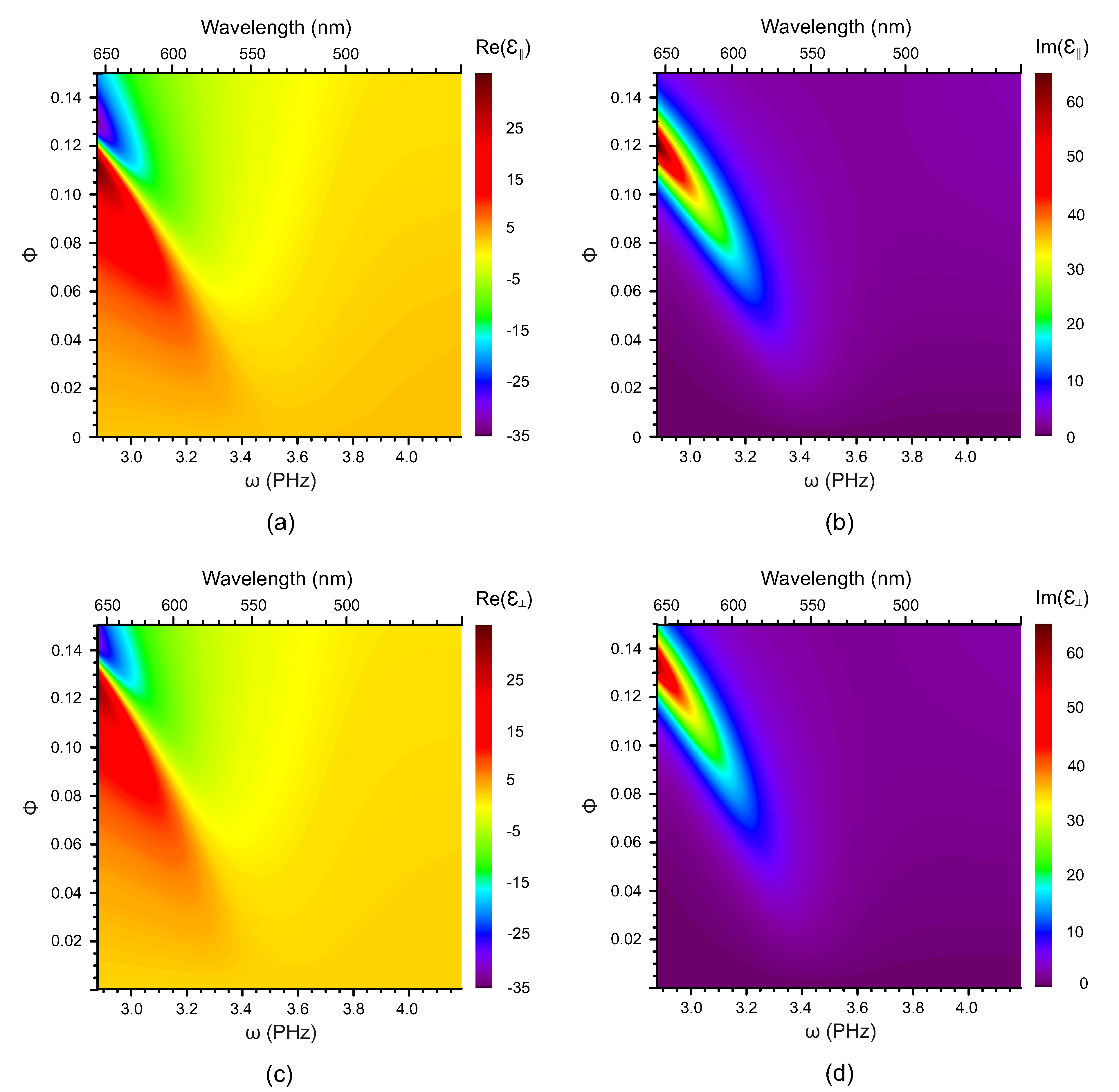
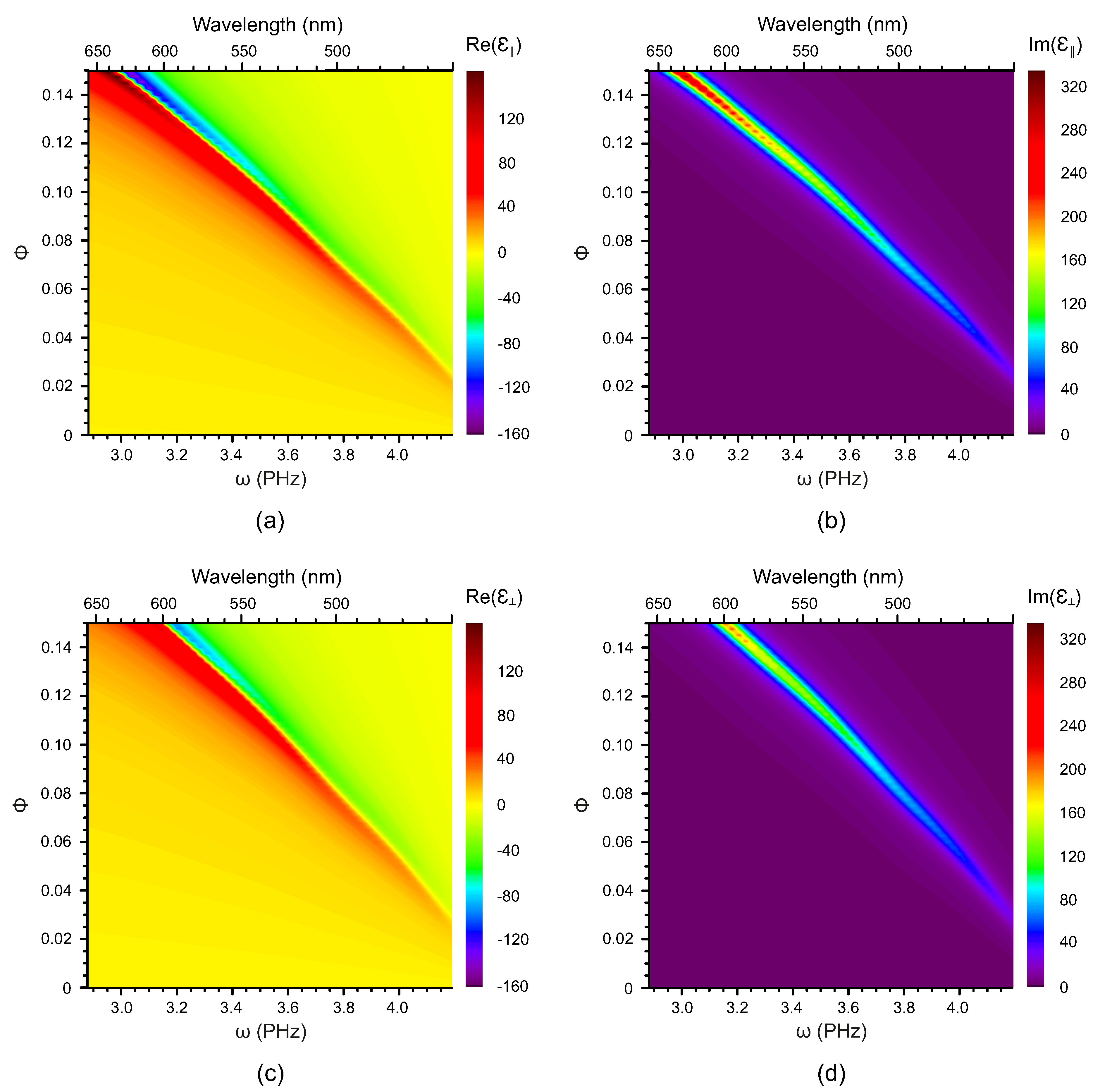
The real and imaginary parts of the longitudinal and the transverse components of the dielectric susceptibility are presented in Figure 2 and Figure 3 as functions of both frequency and the volume fraction of the NPs for nanocomposites based on the nematic host and AuNPs and AgNPs, respectively. In the nanocomposite with gold NPs, the plasmon resonance is clearly visible and its frequency range is rather broad. In contrast, in the same nematic host doped with silver NPs, the plasmon resonance is less pronounced and its frequency range is much smaller.
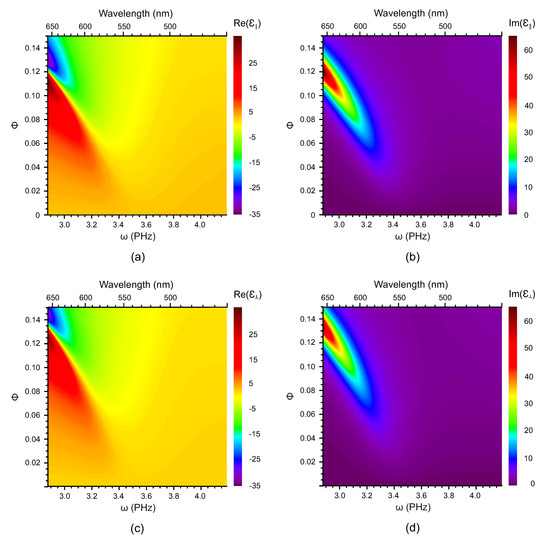
Figure 2.
The dependence of (a), (b), (c) and (d) of the nematic nanocomposite (host plus AuNPs) on the volume fraction of AuNPs and cyclic frequency .
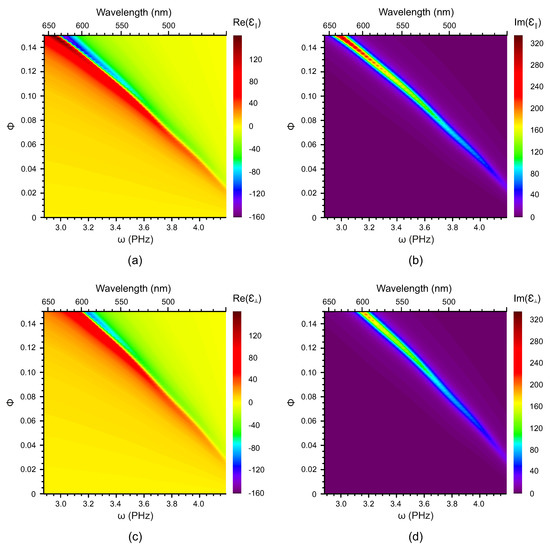
Figure 3.
The dependence of (a), (b), (c) and (d) of the nematic nanocomposite (host plus AgNPs) on the volume fraction of AgNPs and cyclic frequency .
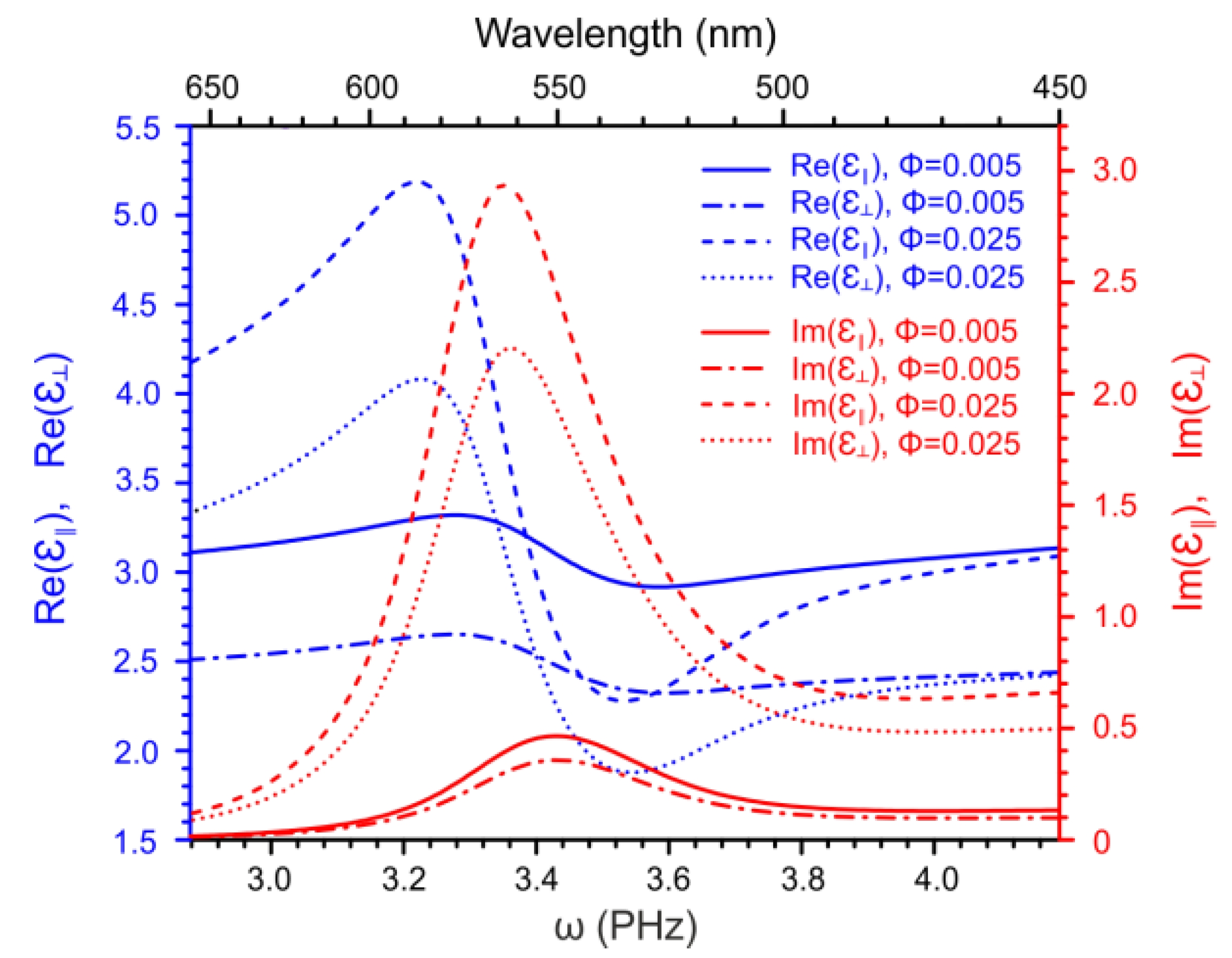
Frequency dependence of the components of the dielectric susceptibility of the same nematic nanocomposites with AuNPs and AgNPs is presented separately in Figure 4 and Figure 5 for two different values of the NP volume fraction . One can readily see that in the nanocomposite with AgNPs, the plasmonic resonance is not observed because the resonance frequency of the effective polarizability of silver NPs (see Figure 1) is outside the selected frequency range. At the same time, both real and imaginary components of the dielectric susceptibility of the nanocomposite increase steeply with the increasing frequency and thus one may assume that the resonance may be observed at higher frequencies. Unfortunately, as far as know, the dispersion of the susceptibility of the nematic host has not been measured outside the selected frequency range. In the nanocomposite with gold NPs, the splitting of the plasmon resonance is found which manifests itself in the difference between the resonance frequencies of the longitudinal and transverse components of the dielectric susceptibility. One can also see the shift of the resonance caused by the change of the NP volume fraction.
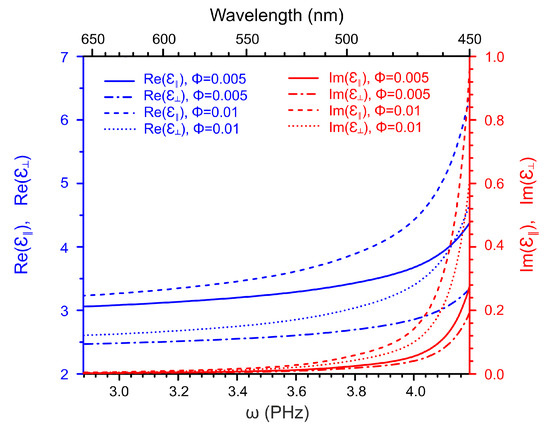
Figure 4.
Frequency dependence of , , and of the nematic nanocomposite (host plus AgNPs) for the two values of the NP volume fraction and .
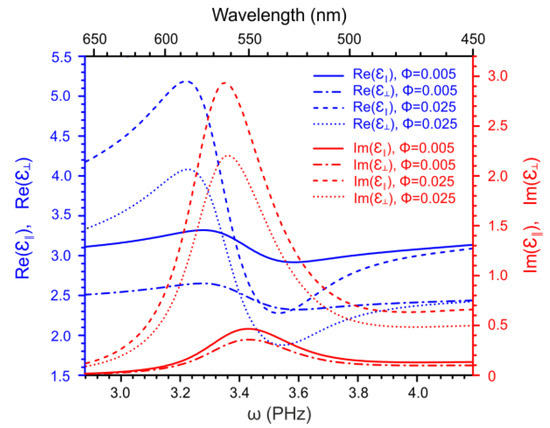
Figure 5.
Frequency dependence of , , and of the nematic nanocomposite (host plus AuNPs) for the two values of the NP volume fraction and .
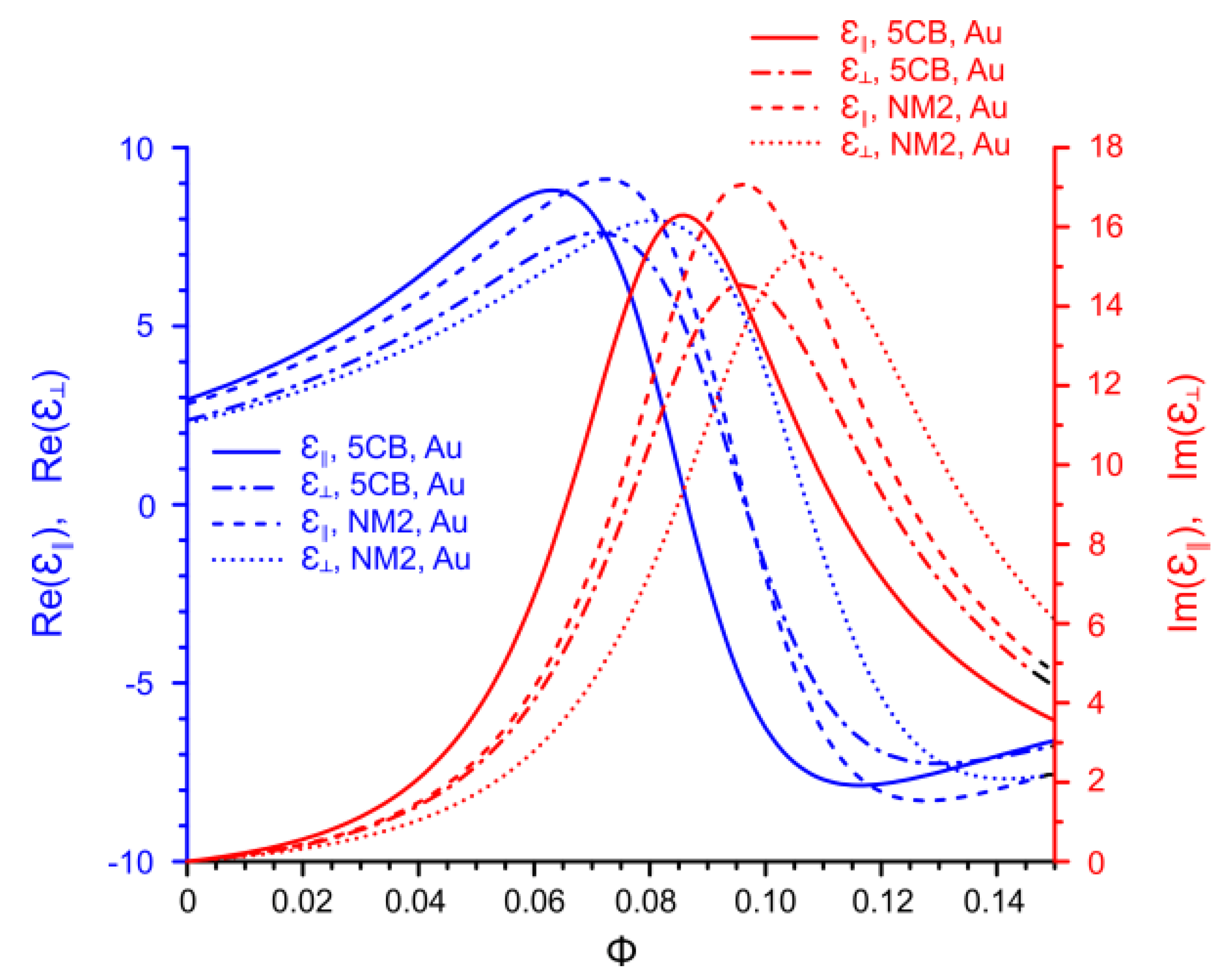
Finally, we present the dependence of the real and imaginary components of the dielectric susceptibility on the volume fraction of AuNPs for two different nematic hosts and , where is a mixture of various cyanobiphenyls [26]. The chemical composition of the nematic mixture is presented in the Appendix A. It follows from Figure 6 that within a certain frequency range, the plasmonic resonance in the nanocomposite with gold NPs can be observed at a fixed frequency by changing the volume fraction of NPs. Moreover, the splitting of the resonance is also observed as a function of the NP concentration. It should be noted that both the plasmonic resonance and its splitting are observed in both nematic hosts in a qualitatively similar way although the values of the resonant frequencies strongly depend on the parameters of the nematic host. Taking into consideration that is a single component cyanobiphenyl compound while is a mixture of cyanobiphenyl compounds of different lengths, one concludes that a moderate change of the molecular structure does not effect the resonance properties of nematic nanocomposites.
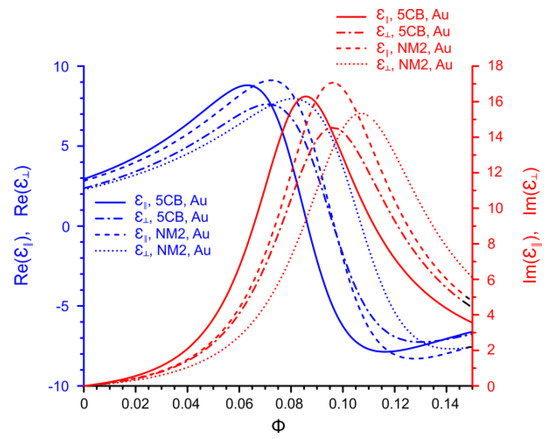
Figure 6.
The dependence of , , and on the volume fraction of AuNPs for the two different nematic hosts and a fixed wavelength of light 589 nm.
2.3. Shifting of the Plasmon Resonance Frequency in the Nematic Matrix
Let us consider now the shift and splitting of the plasmon resonance of the NPs caused by the nematic LC medium. The resonances of the NPs in the nematic medium are determined by the poles of the Equations (18) and (19) which are considered as functions of . Assuming that the LC medium is transparent, one may also assume that the frequency dependence of the dielectric susceptibility of the nanocomposite is determined by that of which is a weakly complex number for according to Equation (16).
Substituting Equation (15) for into Equations (18) and (19) and taking into consideration that the volume fraction of NPs is small , one obtains the following expressions for the resonance plasmon frequencies for the two orientations of the electric field of the light wave (parallel and perpendicular to the local director, respectively):
Thus, in the framework of the present model, the split of the plasmon resonance increases linearly as a function of the NP volume fraction:
It is important to find out at what volume fraction of nanoparticles the splitting of the plasmon resonance peak becomes strong. Qualitatively, strong splitting occurs when splitting at least exceeds the full width at half maximum of the plasmon resonance frequency in the nanocomposite. Such a width is determined by the light absorption in the NPs which is controlled by the imaginary part of the NP polarizability (Equation (17)) which should satisfy the inequality . This inequality, in turn, imposes the following lower bound on the mean free time of conductivity electrons in the metal according to Equation (15):
When this condition is satisfied, the split between resonance plasmon frequencies, which correspond to different polarizations of the light wave, is sufficiently large and the anisotropy of the effective polarizability of the nanocomposite in the resonance frequency domain is significantly larger then the anisotropy of the pure LC matrix . As a result, all effects related to the local dielectric anisotropy and its helical distribution in the cholesteric phase become particularly pronounced. The split of the plasmon resonance in the nematic nanocomposites and its dependence on the NP volume fraction cam be clearly seen in Figure 4, Figure 5 and Figure 6.
3. Discussion
A rather general expression for the dielectric susceptibility of the nematic nanocomposite has been obtained using the molecular-statistical theory of the dielectric properties of mixtures of LCs developed by one of the authors and M. V. Gorkunov [21,27]. In this theory, the local electric field in the anisotropic LC medium is taken into account and the susceptibility of the composite is expressed in terms of the effective polarizability of the NPs, renormalized by the interaction with the first layer of mesogenic molecules and the susceptibility of the pure nematic host. Simple analytical expression for the frequency dependent effective polarizability of a NP has been obtained using the model of a spherical metal NP embedded into the the dielectric medium.
The final expressions (Equations (18) and (19)) for the components of the high frequency dielectric susceptibility of the nematic composite appear to be nonlinear functions of the NP volume fraction although numerical calculations indicate that the deviation from the linear variation is relatively small. In any case, such a deviation is beyond the validity of the present theory. At the same time, the rate of change of the susceptibility of the nanocomposite with the increasing NP concentration strongly depends on the ratio of the NP polarizability and the average susceptibility of the pure nematic host. The contribution from the NPs to the total dielectric susceptibility of the nematic composite is particularly large when the frequency is in the plasmon resonance range.
Both real and imaginary parts of the longitudinal and the transverse components of the dielectric susceptibility of the nematic nanocomposites with gold and silver NPs have been calculated numerically as functions of frequency and the NP volume fraction using the experimental data for frequency dependence of the dielectric constants for the two nematic hosts and for gold and silver nano particles. The splitting of the plasmon resonance has been observed as well as the dependence on the NP volume fraction. The components of the dielectric susceptibility have also been calculated for nanocomposites based on the two different nematic hosts and and it has been shown that the resonance frequencies strongly depend on the parameters of the nematic host phase even in the case when the host has similar molecular structure.
In conclusion, it has been shown that explicit analytical expressions for the dielectric susceptibility of nematic nanocomposites obtained in this paper can be used to describe the split and the shift of the plasmon resonance as functions of both frequency and the NP volume fraction. It has been shown that the split of the plasmon resonance (i.e., the difference between the resonance frequencies corresponding to the parallel and perpendicular orientation of the electric field with respect to the local director) is proportional to the volume fraction of nanoparticles in the first approximation. In the resonance frequency range, the anisotropy of the dielectric susceptibility of the nanocomposite may become significantly larger then that of the pure nematic phase and as a result all effects related to the anisotropy are strongly enhanced which may be important for optical applications of nanocomposites. This has been confirmed by numerical calculations for the two nematic hosts composed of cyanobipnenyl molecules. These calculations indicate that a moderate change of the molecular structure does not qualitatively effect the resonance properties of nematic nanocomposites and hence they may be observed in a large variety of nematic hosts. It has also been shown that the resonance optical properties of nematic nanocomposites with gold NPs are more pronounced that those with silver NPs.
It should be noted also that in the high optical frequency range, the expression for the dielectric tensor of the nanocomposite is also valid in the smectic A phase because this phase is also uniaxial and the smectic order does not contribute to the optical properties because the smectic periodicity is much smaller then the wavelength of light. The present theory can also be applied to cholesteric nanocomposites where the susceptibility tensor rotates in space together with local director according to the equation , where and where and are given by Equations (19) and (20). Here the director describes the helix with the pitch q. Finally, it should be noted that a similar formalism can be used to obtain analytical expressions for the dielectric anisotropy of the nematic and cholesteric nanocomposites with anisotropic NPs. This will be done in our next publication.
Author Contributions
Conceptualization, M.A.O.; methodology, M.A.O. and A.A.E.; formal analysis, A.A.E. and A.S.M.; writing—original draft preparation, M.A.O., A.S.M. and A.A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation grant number 20-13-00341.
Acknowledgments
M.A.O. is grateful to M. V. Gorkunov for many valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
Appendix A. Dispersion of the Dielectric Susceptibility in the Pure Nematic Host 5CB and in the Nematic Mixture
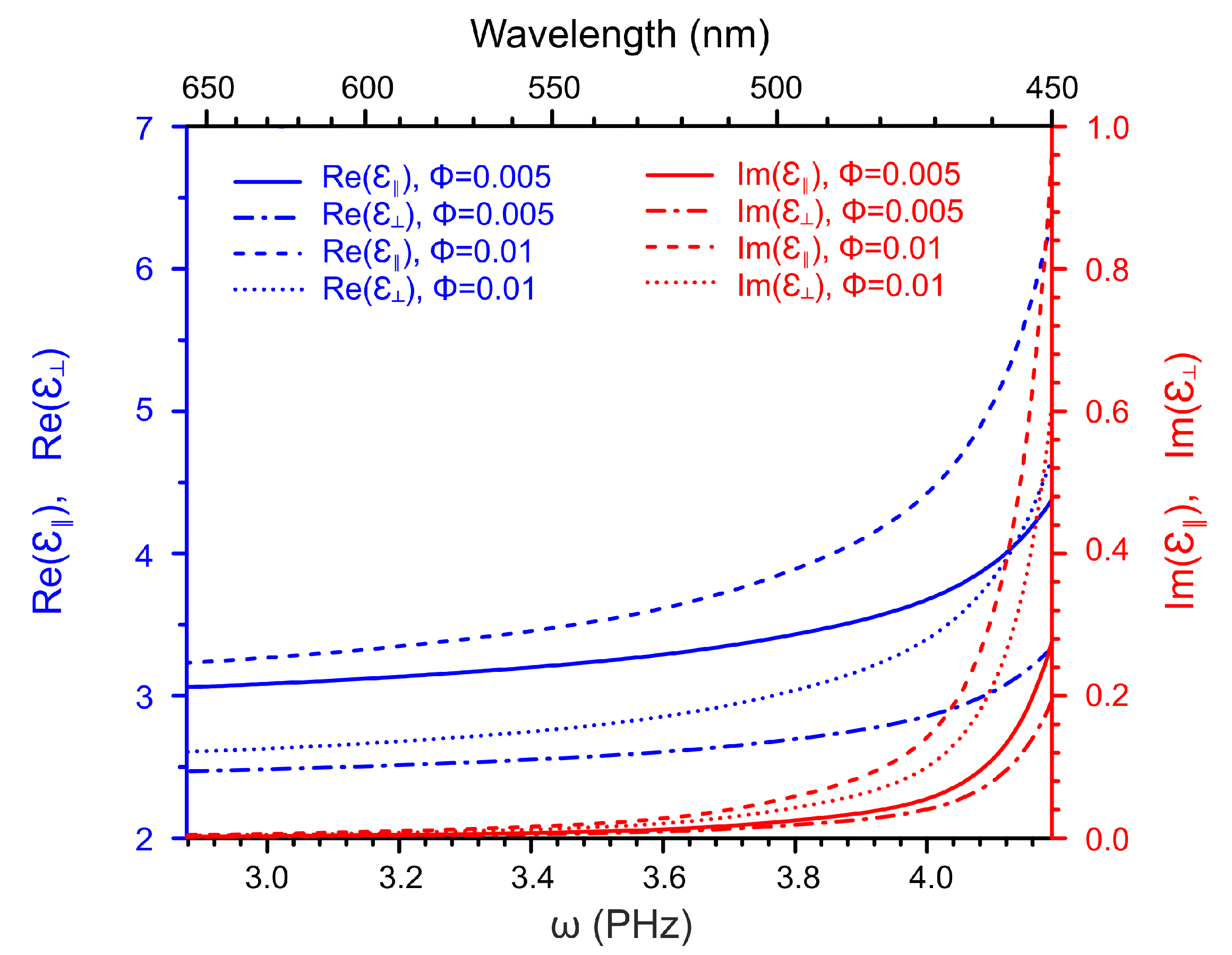
The dielectric properties of the nematic hosts and used in the numerical calculation are presented in Figure A1 The temperature range has been set to be in the room temperature interval (20–25 °C). In this temperature range, both LC materials exhibit the nematic phase.
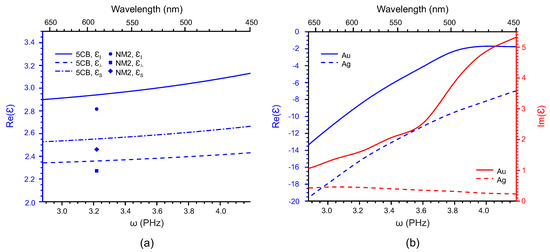
Figure A1.
Frequency dependence of the components of the dielectric susceptibility of the nematic hosts [25] and [26] (a) and gold and silver (b) [24].
Figure A1.
Frequency dependence of the components of the dielectric susceptibility of the nematic hosts [25] and [26] (a) and gold and silver (b) [24].
Liquid crystal mixture composition: 4-pentyl-4’-cyanobiphenyl 32 wt.%, 4-pentyloxy-4’-cyanobiphenyl 13 wt.%, 4-propyloxy-4’-cyanobiphenyl, 25 wt.%, 4’-cyano-4-biphenyl ester of trans-4-butylcyclohexanecarboxylic acid 20 wt.%, 4-ethoxyphenylester of trans-4-butylcyclohexanecarboxylic acid 10 wt.%.
References
- Qi, H.; Kinkead, B.; Hegmann, T. Effects of functionalized metal and semiconductor nanoparticles in nematic liquid crystal phases. Proc. SPIE 2008, 6911, 691106. [Google Scholar]
- Qi, H.; Hegmann, T. Formation of periodic stripe patterns in nematic liquid crystals doped with functionalized gold nanoparticles. J. Mater. Chem. 2006, 16, 4197–4205. [Google Scholar] [CrossRef]
- Shiraishi, Y.; Toshima, N.; Maeds, H.; Yoshikawa, K.; Xu, J.; Kobayashi, S. Frequency modulation response of a liquid-crystal electro-optic device doped with nanoparticles. Appl. Phys. Lett. 2002, 81, 2845–2847. [Google Scholar] [CrossRef]
- Kobayashi, S.; Toshima, N. Nanoparticles and lcds: It’s a surprising world. Inf. Disp. 2007, 23, 26. [Google Scholar]
- Yoshida, H.; Kawamoto, K.; Kubo, H.; Tsuda, A.; Fujii, T.A.; Kuwabata, S.; Ozaki, M. Nanoparticle-dispersed liquid crystals fabricated by sputter doping. Adv. Mater. 2010, 22, 622–626. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.; Singh, S.P.; Biradar, A.M.; Choudhary, A.; Sreeniva, K. Enhanced electro-optical properties in gold nanoparticles doped ferroelectric liquid crystals. Appl. Phys. Lett. 2007, 91, 023120. [Google Scholar] [CrossRef]
- Kumar, A.; Prakash, J.; Mehta, A.M.; Biradar, D.S.; Haase, W. Enhanced photoluminescence in gold nanoparticles doped ferroelectric liquid crystals. Appl. Phys. Lett. 2009, 95, 023117. [Google Scholar] [CrossRef]
- Buchnev, O.; Dyadyusha, A.; Kaczmarek, M.; Reshetnyak, V.; Reznikov, Y. Enhanced two-beam coupling in colloids of ferroelectric nanoparticles in liquid crystals. J. Opt. Soc. Am. B 2007, 24, 1512–1516. [Google Scholar] [CrossRef]
- Reznikov, Y.; Buchnev, O.; Tereshchenko, O.; Reshetnyak, V.; Glushchenko, A.; West, J. Ferroelectric nematic suspension. Appl. Phys. Lett. 2003, 82, 1917–1919. [Google Scholar] [CrossRef]
- Li, F.; Buchnev, C.; Cheon, O.; Glushchenko, A.; Reshetnyak, V.; Reznikov, Y.; Sluckin, T.; West, J. Orientational coupling amplification in ferroelectric nematic colloids. Phys. Rev. Lett. 2006, 97, 147801. [Google Scholar] [CrossRef]
- Lopatina, L.; Selinger, J. Theory of ferroelectric nanoparticles in nematic liquid crystals. Phys. Rev. Lett. 2009, 102, 197802. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, H.; Tanaka, Y.; Kawamoto, H.T.T.; Kubo, K.; Fujii, A.; Kuwabata, S.; Kikuchi, H.; Ozaki, M. Nanoparticle-stabilized cholesteric blue phases. Appl. Phys. Express 2009, 2, 121501. [Google Scholar] [CrossRef]
- Wiersma, S. The physics and applications of random lasers. Nat. Phys. 2008, 4, 359–367. [Google Scholar] [CrossRef]
- Shandryuk, G.A.; Matukhina, E.V.; Vasil’ev, R.B.; Rebrov, A.; Bondarenko, G.N.; Merekalov, A.S.; Gas’kov, A.; Talroze, R. Effect of h-bonded liquid crystal polymers on cdse quantum dot alignment within nanocomposite. Macromolecules 2008, 41, 2178–2185. [Google Scholar] [CrossRef]
- Tal’roze, R.V.; Shandryuk, G.A.; Merekalov, A.S.; Shatalova, A.M.; Otmakhova, O.A. Alignment of nanoparticles in polymer matrices. Polym. Sci. Ser. A 2009, 51, 1194–1203. [Google Scholar] [CrossRef]
- Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pratibha, R.; Park, K.; Smalykh, I.; Park, W. Tunable optical metamaterial based on liquid crystal-gold nanosphere composite. Opt. Express 2009, 17, 19459–19469. [Google Scholar] [CrossRef] [PubMed]
- Kossyrev, A.; Yin, P.A.; Cloutier, S.G.; Cardimona, D.A.; Huang, D.; Alsing, P.M.; Xu, J.M. Electric field tuning of plasmonic response of nanodot array in liquid crystal matrix. Nano Lett. 2005, 5, 1978–1981. [Google Scholar] [CrossRef]
- Chu, C.Y.; Chao, K.C.A.; Chen, Y.F.; Wu, Y.C.; Chen, C.C. Electrically controlled surface plasmon resonance frequency of gold nanorods. Appl. Phys. Lett. 2006, 89, 103107. [Google Scholar] [CrossRef]
- Israelachvili, J. Intermolecular and Surface Forces; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Osipov, M.A.; Gorkunov, M.V. Effect of nanoparticle chain formation on dielectric anisotropy of nematic composites. Phys. Rev. E 2015, 92, 032501. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Electrodynamics of Continuous Media; Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377. (In German) [Google Scholar] [CrossRef]
- PJohnson, B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Li, J.; Wen, C.H.; Gauza, S.; Lu, R.; Wu, S.T. Refractive indices of liquid crystals for display applications. J. Disp. Technol. 2005, 1, 51–61. [Google Scholar] [CrossRef]
- Bezborodov, V.S.; Mikhalyonok, S.G.; Kuz’menok, N.M.; Arol, A.S.; Shandryuk, G.A.; Merekalov, A.S.; Otmakhova, O.A.; Bondarenko, G.N.; Talroze, R.V. Anisotropic derivatives of (-)-L-lactic acid and their nanocomposites. Liq. Cryst. 2018, 45, 1223–1233. [Google Scholar]
- Osipov, M.A.; Gorkounov, M.V. Nematic Liquid Crystals Doped With Nanoparticles: Phase Behavior and Dielectric Properties Liquid Crystals with Nano and Microparticles; Lagerwall, J.P.F., Scalia, G., Eds.; World Scientific Publishing Company: Singapore, 2016; p. 41. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).