Removal Characteristics of Sapphire Lapping using Composite Plates with Consciously Patterned Resinoid-Bonded Semifixed Diamond Grits
Abstract
:1. Introduction
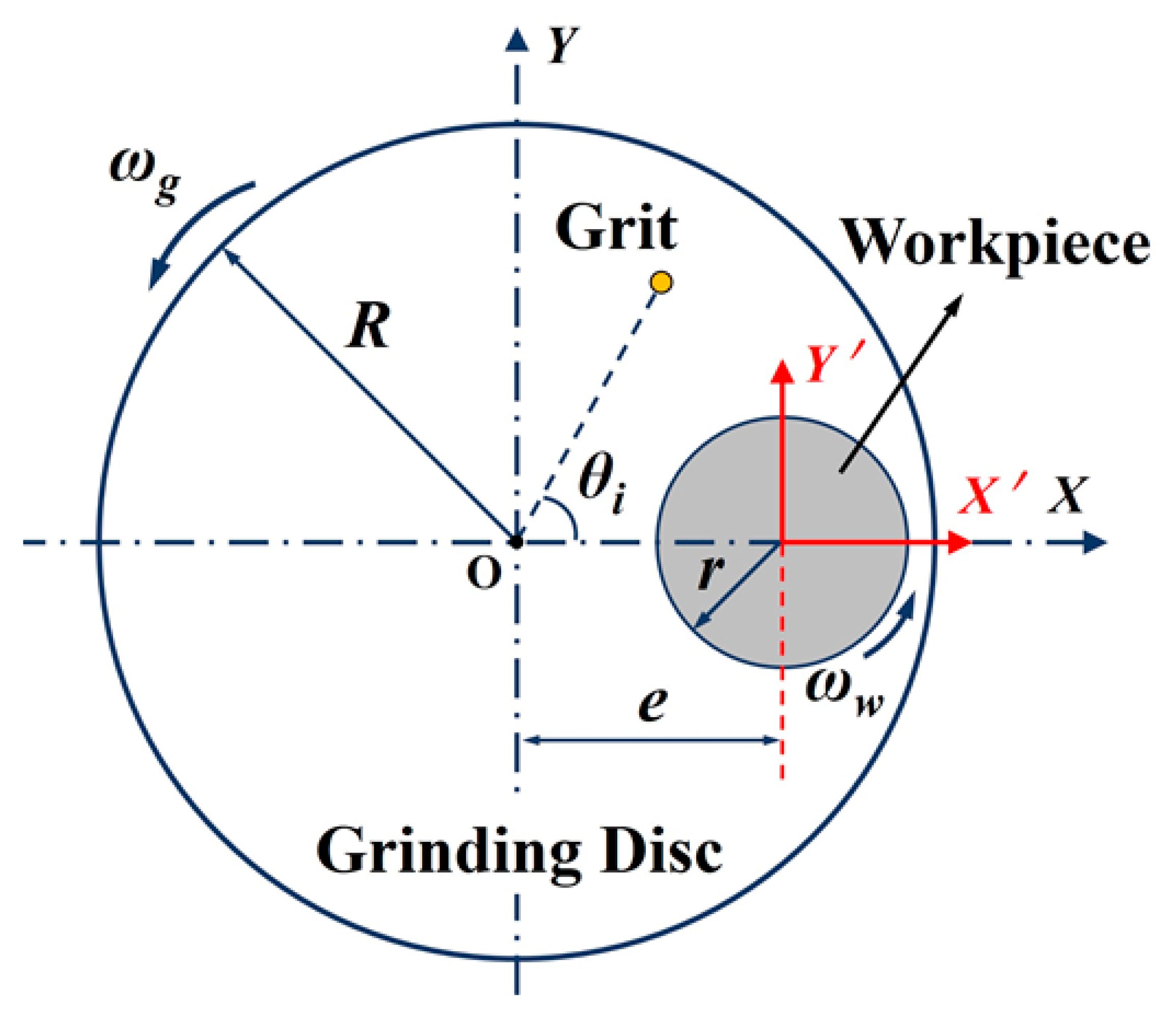
2. Trajectory Analysis and Pattern Design
2.1. Trajectory Modelling
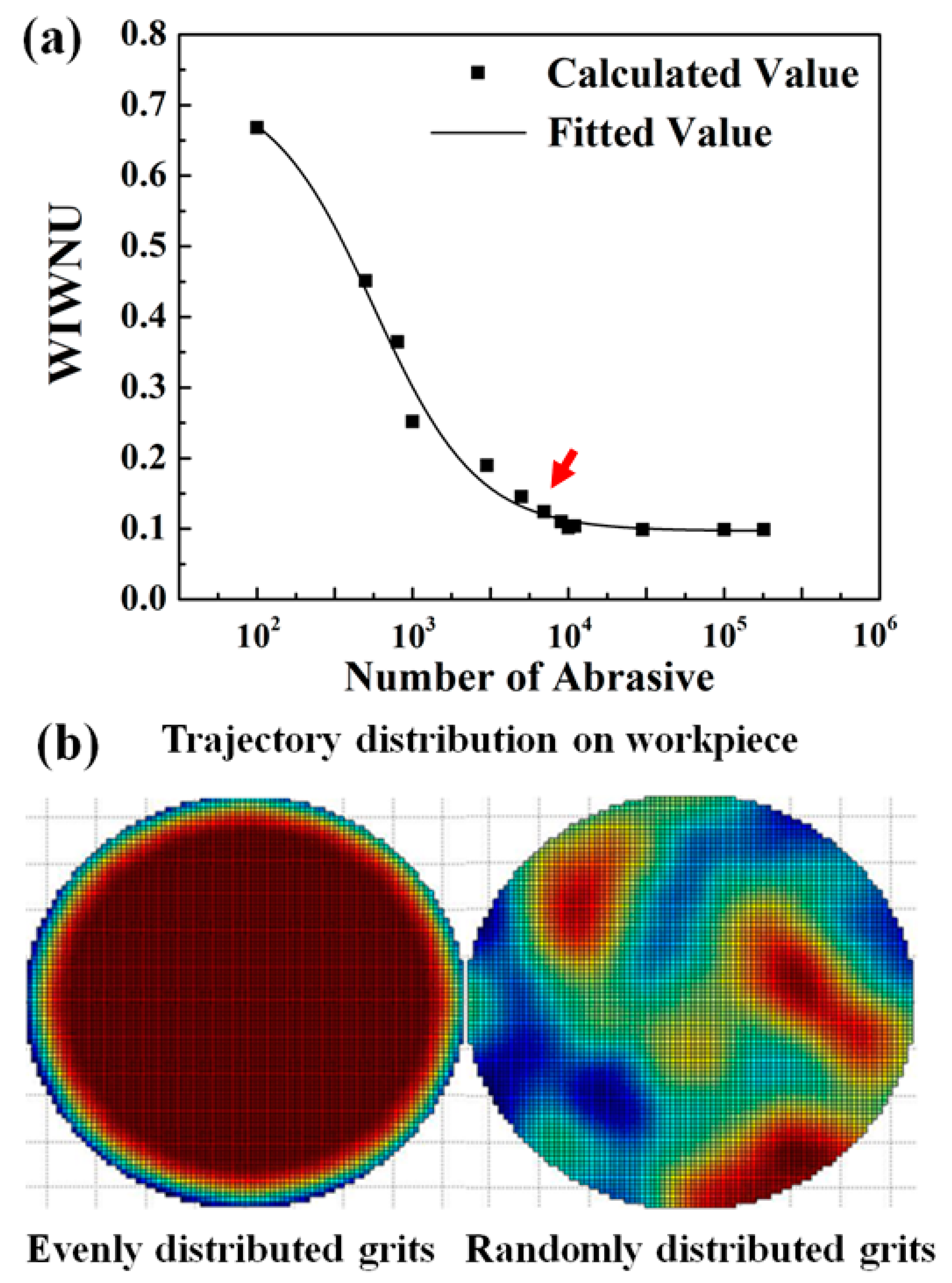
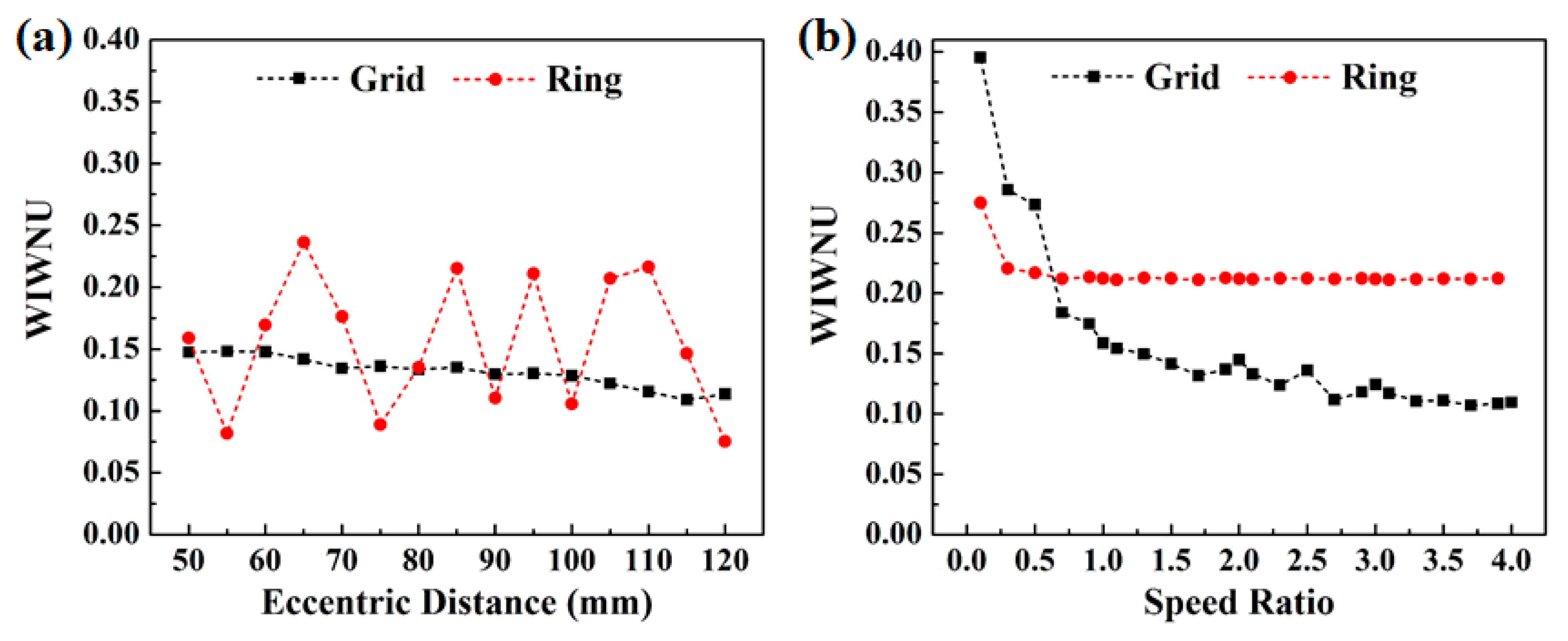
2.2. Trajectory Uniformity Estimation
3. Experimental validation
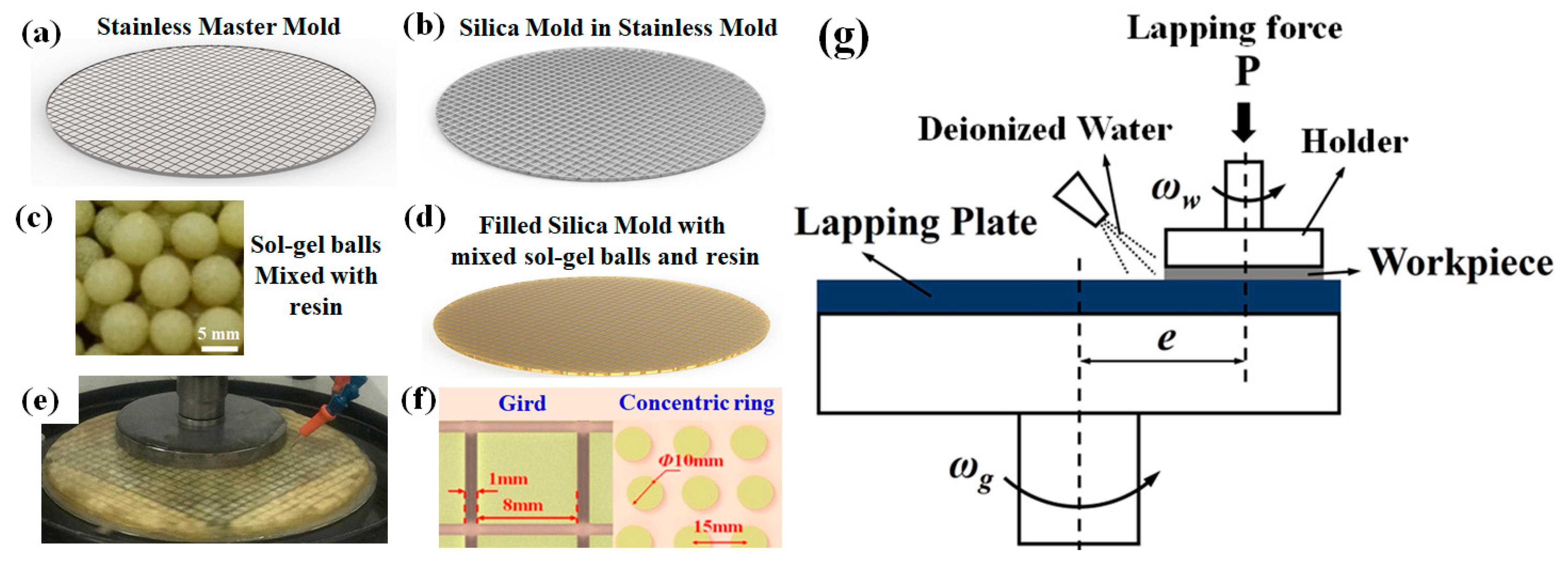
3.1. Materials and Method
3.2. Surface Roughness and Thickness Variation
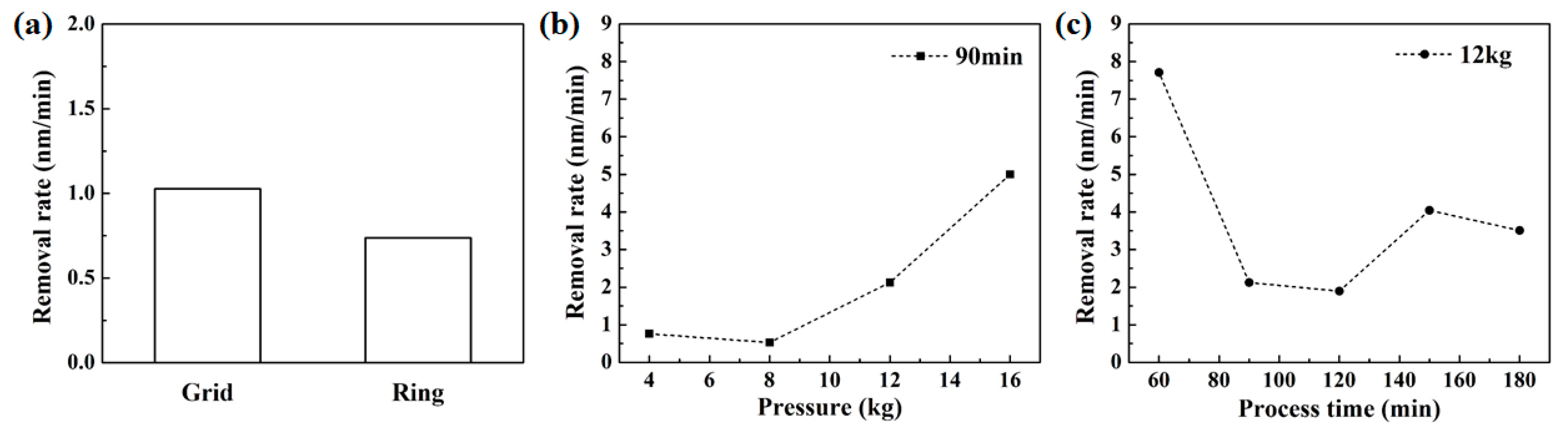
3.3. Material Removal Characteristics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gagliardi, J.J.; Kim, D.; Sokol, J.J.; Zazzera, L.A.; Romero, V.D.; Atkinson, M.R.; Nabulsi, F.; Zhang, H. A case for 2-body material removal in prime LED sapphire substrate lapping and polishing. J. Manuf. Process. 2013, 15, 348–354. [Google Scholar] [CrossRef]
- Kim, D.; Kim, H.; Lee, S.; Lee, T.; Jeong, H. Characterization of diamond wire-cutting performance for lifetime estimation and process optimization. J. Mech. Sci. Technol. 2016, 30, 847–852. [Google Scholar] [CrossRef]
- Kim, D.; Kim, H.; Lee, S.; Jeong, H. Effect of initial deflection of diamond wire on thickness variation of sapphire wafer in multi-wire saw. Int. J. Precis. Eng. Manuf.-Green Technol. 2015, 2, 117–121. [Google Scholar] [CrossRef]
- Aida, H.; Doi, T.; Takeda, H.; Katakura, H.; Kim, S.-W.; Koyama, K.; Yamazaki, T.; Uneda, M. Ultraprecision CMP for sapphire, GaN, and SiC for advanced optoelectronics materials. Curr. Appl. Phys. 2012, 12, S41–S46. [Google Scholar] [CrossRef]
- Li, J.; Nutt, S.R.; Kirby, K.W. Surface Modification of Sapphire by Magnesium-Ion Implantation. J. Am. Ceram. Soc. 1999, 82, 3260–3262. [Google Scholar] [CrossRef]
- Lee, T.; Jeong, H.; Kim, H.; Lee, S.; Kim, D. Effect of platen shape on evolution of total thickness variation in single-sided lapping of sapphire wafer. Int. J. Precis. Eng. Manuf.-Green Technol. 2016, 3, 225–229. [Google Scholar] [CrossRef]
- Smith, M.B.; Schmid, F.; Khattak, C.P.; Schmid, K.A.; Golini, D.; Lambropoulos, J.C.; Atwood, M.A.; Zhou, Y.; Funkenbusch, P.D. Sapphire fabrication for precision optics. In Advanced Materials for Optical and Precision Structures; International Society for Optics and Photonics: Denver, CO, USA, 1996; pp. 99–112. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, Z.; Hong, T.; Deng, Q.; Wen, D.; Lv, B. A semi-fixed abrasive machining technique. J. Micromech. Microeng. 2009, 19, 054006. [Google Scholar] [CrossRef]
- Nakamura, H.; Yan, J.W.; Syoji, K.; Wakamatsu, Y. Development of a polishing disc containing granulated fine abrasives. In Key Engineering Materials; Trans Tech Publ.: Zürich, Switzerland, 2003; pp. 257–262. [Google Scholar] [CrossRef]
- Lv, B.H.; Yuan, J.L.; Wang, Z.W. Simulation of compacting process for semi-fixed abrasive wheel. In Key Engineering Materials; Trans Tech Publ.: Zürich, Switzerland, 2009; pp. 87–92. [Google Scholar] [CrossRef]
- Luo, Q.; Lu, J.; Xu, X. A comparative study on the material removal mechanisms of 6H-SiC polished by semi-fixed and fixed diamond abrasive tools. Wear 2016, 350, 99–106. [Google Scholar] [CrossRef]
- Luo, Q.; Lu, J.; Xu, X. Study on the processing characteristics of SiC and sapphire substrates polished by semi-fixed and fixed abrasive tools. Tribol. Int. 2016, 104, 191–203. [Google Scholar] [CrossRef]
- Yiqing, Y.; Zhongwei, H.; Wenshan, W.; Huan, Z.; Jing, L.; Xipeng, X. The double-side lapping of SiC wafers with semifixed abrasives and resin–combined plates. Int. J. Adv. Manuf. Technol. 2019, 1–10. [Google Scholar] [CrossRef]
- Yuan, J.; Yao, W.; Zhao, P.; Lyu, B.; Chen, Z.; Zhong, M. Kinematics and trajectory of both-sides cylindrical lapping process in planetary motion type. Int. J. Mach. Tools Manuf. 2015, 92, 60–71. [Google Scholar] [CrossRef]
- Wang, L.; Hu, Z.; Fang, C.; Yu, Y.; Xu, X. Study on the double-sided grinding of sapphire substrates with the trajectory method. Precis. Eng. 2018, 51, 308–318. [Google Scholar] [CrossRef]
- Fang, C.; Zhao, Z.; Lu, L.; Lin, Y. Influence of fixed abrasive configuration on the polishing process of silicon wafers. Int. J. Adv. Manuf. Technol. 2017, 88, 575–584. [Google Scholar] [CrossRef]
- Su, J.X.; Guo, D.M.; Kang, R.K.; Jin, Z.J.; Li, X.; Tian, Y. Modeling and analyzing on nonuniformity of material removal in chemical mechanical polishing of silicon wafer. In Materials Science Forum; Trans Tech Publications: Zürich, Switzerland, 2004; pp. 26–31. [Google Scholar] [CrossRef]
- Lu, J.; Li, Y.; Xu, X. The effects of abrasive yielding on the polishing of SiC wafers using a semi-fixed flexible pad. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229 (Suppl. 1), 170–177. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, J.; Xu, X. Study on planarization machining of sapphire wafer with soft-hard mixed abrasive through mechanical chemical polishing. Appl. Surf. Sci. 2016, 389, 713–720. [Google Scholar] [CrossRef]
- Mu, D.; Feng, K.; Lin, Q.; Huang, H. Low-temperature wetting of sapphire using Sn–Ti active solder alloys. Ceram. Int. 2019, 45, 22175–22182. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Yu, Y.; Hu, Z.; Fang, C.; Lu, J.; Xu, X. Removal Characteristics of Sapphire Lapping using Composite Plates with Consciously Patterned Resinoid-Bonded Semifixed Diamond Grits. Crystals 2020, 10, 293. https://doi.org/10.3390/cryst10040293
Wang W, Yu Y, Hu Z, Fang C, Lu J, Xu X. Removal Characteristics of Sapphire Lapping using Composite Plates with Consciously Patterned Resinoid-Bonded Semifixed Diamond Grits. Crystals. 2020; 10(4):293. https://doi.org/10.3390/cryst10040293
Chicago/Turabian StyleWang, Wenshan, Yiqing Yu, Zhongwei Hu, Congfu Fang, Jing Lu, and Xipeng Xu. 2020. "Removal Characteristics of Sapphire Lapping using Composite Plates with Consciously Patterned Resinoid-Bonded Semifixed Diamond Grits" Crystals 10, no. 4: 293. https://doi.org/10.3390/cryst10040293
APA StyleWang, W., Yu, Y., Hu, Z., Fang, C., Lu, J., & Xu, X. (2020). Removal Characteristics of Sapphire Lapping using Composite Plates with Consciously Patterned Resinoid-Bonded Semifixed Diamond Grits. Crystals, 10(4), 293. https://doi.org/10.3390/cryst10040293



