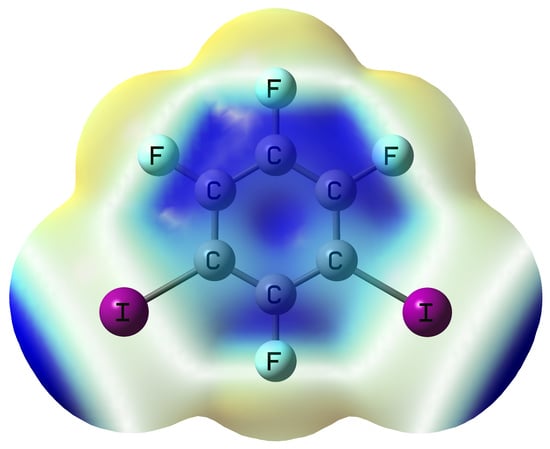
Unexpected Sandwiched-Layer Structure of the Cocrystal Formed by Hexamethylbenzene with 1,3-Diiodotetrafluorobenzene: A Combined Theoretical and Crystallographic Study

Abstract

The cocrystal formed by hexamethylbenzene (HMB) with 1,3-diiodotetrafluorobenzene (1,3-DITFB) was first synthesized and found to have an unexpected sandwiched-layer structure with alternating HMB layers and 1,3-DITFB layers. To better understand the formation of this special structure, all the noncovalent interactions between these molecules in the gas phase and the cocrystal structure have been investigated in detail by using the dispersion-corrected density functional theory calculations. In the cocrystal structure, the theoretically predicted π···π stacking interactions between HMB and the 1,3-DITFB molecules in the gas phase can be clearly seen, whereas there are no π···π stacking interactions between HMB molecules or between 1,3-DITFB molecules. The attractive interactions between HMB molecules in the corrugated HMB layers originate mainly in the dispersion forces. The 1,3-DITFB molecules form a 2D sheet structure via relatively weak C–I···F halogen bonds. The theoretically predicted much stronger C–I···π halogen bonds between HMB and 1,3-DITFB molecules in the gas phase are not found in the cocrystal structure. We concluded that it is the special geometry of 1,3-DITFB that leads to the formation of the sandwiched-layer structure of the cocrystal.

1. Introduction

Noncovalent interactions play key roles in crystal growth and design. In 1989, Desiraju defined the term “crystal engineering” as “the understanding of intermolecular interactions in the context of crystal packing and the utilization of such understanding in the design of new solids with desired physical and chemical properties” [1]. There are many kinds of noncovalent interactions, such as the hydrogen bond, π···π stacking interaction, dispersive interaction, σ-hole interaction, π-hole interaction, etc. [2,3,4,5,6]. In the preceding paper of this Special Issue, Alkorta, Elguero, and Frontera presented an excellent review of the noncovalent interactions formed by the electron-deficient elements of groups 1, 2, and 10–18 in the periodic table [7]. Here, we want to stress that the term noncovalent interaction is more general than the term noncovalent bond, and some of the noncovalent interactions such as the dispersive interactions are not noncovalent bonds [4]. What is a noncovalent bond? According to Bader’s theory of atoms in molecules, in a noncovalent bond there usually is a bond path connecting the two interacting atoms and a (3, –1) bond critical point between the two interacting atoms [8]. Evidently, crystal packing is the result of the synergistic contributions of different types of strong or weak noncovalent interactions. Hence, in the field of crystal engineering, it is always significant and important to study the cooperativity and competition of these noncovalent interactions.

The π···π stacking interaction is one of the most common noncovalent interactions in crystal engineering [9]. The benzene dimer is always considered as a model for the study of the π···π stacking interaction [10]. Comparing with the π···π stacking interaction in the benzene dimer, the π···π stacking interaction in the complex between hexamethylbenzene (HMB) and hexafluorobenzene (HFB) is much stronger due to the strong attractive quadrupole–quadrupole electrostatic interaction between the two monomers. The quadrupole–quadrupole interaction is repulsive in the face-to-face structure of the benzene dimer with an interaction energy of +13.68 kcal/mol, whereas the quadrupole–quadrupole interaction is attractive in the face-to-face structure of the complex between HMB and HFB with an interaction energy of −8.53 kcal/mol [11]. The crystal structure of the complex between HMB and HFB has been reported in 1972, in which the partner molecules are stacked alternately to form infinite columns [12]. Naturally, HMB can also form π-stacked complexes with other electron-deficient perfluoro aromatic compounds. Perfluoroiodobenzenes are such compounds that we are very interested in because they are always employed as the halogen atom donors for the halogen bonds [13]. Figure 1 shows the molecular electrostatic potentials on the 0.001 a.u. electron density isodensity surfaces of HMB and 1,3-diiodotetrafluorobenzene (1,3-DITFB) along with some selected surface minima and surface maxima. The computational details of the molecular electrostatic potentials are given in the following section. As shown in Figure 1, the most negative electrostatic potentials of −22.47 kcal/mol on the surface of HMB are located 1.76 Å above or below the center of mass of HMB; the most positive electrostatic potentials of +30.76 kcal/mol on the surface of 1,3-DITFB are located on the extensions of the C–I bonds. For the 1,3-DITFB, besides the two electropositive σ-holes on the extensions of the C-I bonds, there are also electropositive regions (π-holes) that are perpendicular to the molecular plane. As a result, 1,3-DITFB can form the C–I···π halogen bond with HMB on the one hand, and on the other hand it can also form the strong π···π stacking interaction with HMB [13,14,15]. Certainly, the π···π stacking interactions can also be formed between two HMB molecules or between two 1,3-DITFB molecules. What is the order of strengths of all these noncovalent interactions? Will one of them, some of them, or all of them contribute to the formation of the cocrystal between HMB and 1,3-DITFB? Will there be other noncovalent interactions that we could not predict in the cocrystal structure? In this study, we solve these issues by employing a combined theoretical and crystallographic method.

This paper is organized as follows: First, we present and discuss the calculated results for the abovementioned noncovalent interactions in the gas phase; then, after describing the structure of the cocrystal between HMB and 1,3-DITFB, we calculate and analyze the noncovalent interactions in the crystal structure in detail. Finally, we give explanations for the formation of the special cocrystal structure.

2. Materials and Methods

2.1. Quantum Chemical Calculation

The geometries of the monomers and complexes in the gas phase were fully optimized at the PBE0-D3(BJ)/def2-TZVPP level of theory [16,17,18,19]. According to the corresponding frequency calculations, all the structures of these monomers and complexes are true minima on their respective potential energy surfaces. The interaction energies were calculated at the same theory level. For the complexes in the crystal structure, their geometries were directly extracted from the crystal structure, and only single-point interaction energies were calculated at the PBE0-D3(BJ)/def2-TZVPP theory level. All the interaction energies were calculated with the supermolecule method and corrected for the basis set superposition error using the conventional counterpoise method [20]. The molecular electrostatic potentials on the 0.001 a.u. electron density isodensity surfaces of HMB and 1,3-DITFB were also calculated at the PBE0-D3(BJ)/def2-TZVPP level of theory. The “ultrafine” integration grids were used for the PBE0-D3(BJ)/def2-TZVPP calculations to eliminate possible integration grid errors. All the calculations were performed with the GAUSSIAN 09 program package [21].

For the calculations of strong noncovalent interactions, many computational methods can give comparable results with experiments. The main challenges for the electronic structure calculations lie in the accurate descriptions of weak noncovalent interactions. In previous studies, we employed the PBE0-D3(BJ)/def2-TZVPP method to calculate the interaction energies of the different configurations of the complex between benzene and hexahalobenzene, the complex between benzene and naphthalene, and the complex between fullerene C₆₀ and benzene [22,23,24]. It was found that the results from the PBE0-D3(BJ)/def2-TZVPP calculations are in excellent agreement with the results from the “gold standard” coupled-cluster calculations. Considering that the noncovalent interactions studied in this work are very similar to those in previously studied complexes, the results from the PBE0-D3(BJ)/def2-TZVPP calculations should be reliable throughout this paper.

2.2. Crystal Preparation

The chemical reagents HMB and 1,3-DITFB were purchased from J&K Scientific Ltd. in China and used as received. The solvent for the crystallization in this study was trichloromethane and also used without further purification. The HMB (0.0162 g, 0.10 mmol) and 1,3-DITFB (0.0402 g, 0.10 mmol) were dissolved in 10 mL trichloromethane, and the mixture was refluxed gently with stirring for half an hour. Then, the solution was filtered, and the filtrate was naturally volatilized at room temperature. After about three days, colorless block crystals that are suitable for the X-ray diffraction analyses were obtained.

2.3. Measurement

Single-crystal X-ray diffraction data were collected on a Rigaku AFC10 diffractometer (Rigaku Corporation, Tokyo, Japan) equipped with a Rigaku SuperNova X-ray generator (graphite-monochromatic Mo-Kα radiation, λ = 0.71073 Å). The structure of the cocrystal was solved and refined by a combination of direct methods and difference Fourier syntheses, employing the SHELX-2014 and Olex2.0 programs [25,26]. The hydrogen atoms of the methyl groups in HMB were placed in calculated positions and refined with the riding model approximation. Anisotropic thermal parameters were assigned to the nonhydrogen atoms. Crystallographic data have been deposited at the Cambridge Crystallographic Data Centre (deposition number CCDC 1996547). Copies of the data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html.

3. Results and Discussion

3.1. Noncovalent Interactions in the Gas Phase

The study of the noncovalent interactions in the gas phase is significant and can provide useful information for the crystal growth and design, although in some cases the noncovalent interactions in the gas phase maybe be very different with the noncovalent interactions in the crystalline state. Figure 2 illustrates the PBE0-D3(BJ)/def2-TZVPP optimized structures and the corresponding interaction energies for the stacked complex between HMB and 1,3-DITFB, a stacked HMB dimer, a halogen-bonded complex between HMB and 1,3-DITFB, and a stacked 1,3-DITFB dimer. In fact, we also fully optimized the planar structures of the HMB dimer and the 1,3-DITFB dimer, but both of them were transformed into the stacked ones in Figure 2. This indicates that the planar structures of the HMB dimer and the 1,3-DITFB dimer are not stable in the gas phase.

It can be clearly seen from Figure 2 that the π···π stacking interaction between HMB and 1,3-DITFB is the strongest one among all the noncovalent interactions. The π···π stacking interaction energies for the complexes C₆H₆···C₆X₆ (X = F, Cl, Br, and I) are in the range of −9.70 to −5.50 kcal/mol [22]. Thus, the π···π stacking interaction between HMB and 1,3-DITFB is much stronger than the π···π stacking interactions in the complexes C₆H₆···C₆X₆ (X = F, Cl, Br, and I). This is understandable because the van der Waals surface area of HMB is larger than that of benzene, and the minimum value of the electrostatic potential of HMB is much more negative than that of benzene. The quadrupole–quadrupole electrostatic interactions in the HMB dimer and 1,3-DITFB dimer are repulsive, and this will weaken the π···π stacking interactions in the two dimers. The π···π stacking interaction energies for the HMB dimer and 1,3-DITFB dimer are −10.32 and −7.01 kcal/mol, respectively. As a contrast, the π···π stacking interaction energy for the complex between benzene and HFB is about −6.00 kcal/mol, and the π···π stacking interaction energy for the parallel-displaced configuration of the benzene dimer is about −2.70 kcal/mol [22,27]. The π-stacked HMB dimer and 1,3- DITFB dimer can also exist in the crystal structures. The CCDC database (version 5.41) was used in a search for the structures containing HMB or 1,3-DITFB [28]. It was found that there are 8 structures containing the π-stacked HMB dimer and 27 structures containing the π-stacked 1,3-DITFB dimer.

Another focus in Figure 2 is the halogen-bonded complex between HMB and 1,3-DITFB with the interaction energy of −7.40 kcal/mol. The binding energy of the conventional C–I···N halogen bond is below 7.00 kcal/mol [29]. Here, the strength of the C–I···π halogen bond is obviously close to or even stronger than the strength of the conventional strong C–I···N halogen bond. As shown in Figure 2c, the C–I bond does not point to the centroid of HMB but points to the site which is close to the carbon atom. Tsuzuki and coworkers calculated the C–I···π interaction energies for three orientations of the complex between benzene and pentafluoroiodobenzene, and they found that the difference of the interaction energies is not very marked [30]. Bosch and coworkers performed a statistical analysis of the C–I···π halogen bonds in the crystal structures by using the Cambridge Structural Database, and their results showed that the number of the structures in which the C–I bond points to the centroid of the benzene ring is very small [31]. In other words, the C–I···π halogen bond predicted in the gas phase may also exist in the crystal structure of the complex between HMB and 1,3-DITFB.

3.2. Noncovalent Interactions in the Crystal Structure

HMB and 1,3-DITFB form a 1:1 cocrystal. The cocrystal has an unexpected sandwiched-layer structure with alternating HMB layers and 1,3-DITFB layers (Figure 3). The HMB layer is corrugated, and the 1,3-DITFB layer is a 2D sheet. Crystal data for the cocrystal (M = 564.12 g/mol) are as follows: orthorhombic, space group Cmcm (no. 63), a = 16.3241(6) Å, b = 8.7254(5) Å, c = 13.6411(8) Å, β = 90°, V = 1942.96(18) ų, Z = 4, T = 290 K, μ(CuKα) = 3.270 mm⁻¹, D_calc = 1.928 g/cm³, 11066 reflections measured (7.786° ≤ 2Θ ≤ 56.726°), 1219 unique (R_int = 0.0324, R_sigma = 0.0151), which were used in all calculations. The final R₁ was 0.0883 (I > 2σ(I)) and wR₂ was 0.2298 (all data).

As expected from the gas-phase calculation, the π···π stacking interactions between HMB and 1,3-DITFB are found in the crystal structure. The interaction energy for the stacked two-body complex in the crystal structure is −11.16 kcal/mol, which is almost the same as the corresponding value of −11.27 kcal/mol) in the gas phase. In the crystal structure, the HMB and 1,3-DITFB molecules are stacked alternately in infinite columns. It is interesting to study the cooperativity of these π···π stacking interactions. Figure 4 shows the total interaction energies for the stacked two-body, three-body, and four-body complexes. Here, we use the three-body [Δ³E(123)] and four-body [Δ⁴E(1234)] interaction terms to assess the cooperativity of these π···π stacking interactions, such as the study of the benzene trimer and the benzene tetramer [32]. The three-body and four-body interaction terms can be defined as follows:

$$\begin{gathered} {\mathsf{\Delta }}^{3}E\left(123\right)=E\left(123\right)-{\displaystyle \sum }_{i}E\left(i\right)-{\displaystyle \sum }_{ij}{\mathsf{\Delta }}^{2}E\left(ij\right) \\ {\mathsf{\Delta }}^{4}E\left(1234\right)=E\left(1234\right)-{\displaystyle \sum }_{i}E\left(i\right)-{\displaystyle \sum }_{ij}{\mathsf{\Delta }}^{2}E\left(ij\right)-{\displaystyle \sum }_{ijk}{\mathsf{\Delta }}^{3}E\left(ijk\right) \end{gathered}$$

The three-body interaction terms for the two three-body complexes are −0.32 and −0.56 kcal/mol, respectively. The four-body interaction term for the four-body complex is −0.90 kcal/mol. The three-body and four-body interaction terms are all negative and obviously have stabilizing contributions to the total interactions. Considering that the total interaction energy is very large, it is still reasonable to estimate the total interaction energy of a large complex simply from the sum of the two-body interaction energies.

Figure 5 and Figure 6 show the noncovalent interactions in the HMB layer and 1,3-DITFB layer. Let us add here that these noncovalent interactions do not exist in the gas phase. The HMB molecules form the corrugated layers via dispersion forces. In the corrugated HMB layer, two methyl groups of HMB along the crystallographic a axis are disordered, and the other four methyl groups form four H···H contacts with other HMB molecules. The disorder of the two methyl groups of the one HMB molecule indicates that the H···H contacts make negligible contribution to the stability of the cocrystal from another perspective. The 1,3-DITFB molecules form the 2D sheets via the weak C–I···F halogen bonds. One 1,3-DITFB molecule can form four C–I···F halogen bonds with four neighboring 1,3-DITFB molecules. It is the special structure of 1,3-DITFB that leads to the formation of the 2D sheet and furthers the formation of the sandwiched-layer structure of the cocrystal. A similar structure can be found in the cocrystal formed between HMB and 1,2,4,5-tetracyanobenzene [33]. This cocrystal also has a layer structure. However, the 1,2,4,5-tetracyanobenzene layer is not a 2D sheet but a corrugated layer.

Figure 5 and Figure 6 also list the interaction energies for two neighboring monomers and the total interaction energies for the 1,3-DITFB tetramer and HMB tetramer. In the 1,3-DITFB tetramer, the interaction energy of one C–I···F halogen bond is −1.65 kcal/mol, and the interaction energy for the dimer without a C–I···F halogen bond is only −0.51 kcal/mol. The four-body interaction term for the 1,3-DITFB tetramer is about 0.05 kcal/mol, which means that the cooperativity of the noncovalent interactions in the 1,3-DITFB tetramer is negligible. The case for the HMB tetramer is quite similar. The interaction energy of two neighboring HMB molecules is a little smaller than that of two C–I···F halogen-bonded 1,3-DITFB molecules. The four-body interaction term of the HMB tetramer is also about 0.05 kcal/mol and can also be neglected.

Figure 7 lists the interaction energies for two neighboring monomers and the total interaction energies for the four-body complex formed by two HMB molecules and two 1,3-DITFB molecules. Different from the complexes in Figure 4, Figure 5 and Figure 6, the complex in Figure 7 is formed via mixed noncovalent interactions, which include a π···π stacking interaction, a C–I···F halogen bond, and a dispersion-dominated interaction. The four-body interaction term of this complex is about 0.09 kcal/mol, which is a little larger than that of the 1,3-DITFB tetramer and HMB tetramer. However, the absolute value of the total interaction energy of this complex is over three times larger than that of the 1,3-DITFB tetramer or HMB tetramer. Again, it is reasonable to estimate the total interaction energy of a large complex simply from the sum of the two-body interaction energies.

4. Conclusions

In this study, the cocrystal formed by HMB with 1,3-DITFB was successfully synthesized, and the noncovalent interactions in the crystal structure were calculated at the PBE0-D3(BJ)/def2-TZVPP level of theory. Unexpectedly, the cocrystal has a sandwiched-layer structure with alternating HMB layers and 1,3-DITFB layers. In the corrugated HMB layer, the HMB molecules attract each other mainly via the dispersion forces. In the 1,3-DITFB layer, the 1,3-DITFB molecules form a 2D sheet via the C–I···F halogen bonds, and one 1,3-DITFB molecule can form four C–I···F halogen bonds with four neighboring 1,3-DITFB molecules. The alternating HMB layers and 1,3-DITFB layers are stacked together by strong π···π stacking interactions between HMB and 1,3-DITFB molecules. No C–I···π halogen bonds and π···π stacking interactions between the HMB molecules or between the 1,3-DITFB molecules were found in the crystal structure. It was also found that the cooperativity of the noncovalent interactions in each layer is not very obvious. However, the cooperativity of the π···π stacking interactions in the sequence of alternating HMB and 1,3-DITFB molecules is considerable.

The formation of the unexpected sandwiched-layer structure of the molecular cocrystal is attributed to the special geometry of 1,3-DITFB. Other perfluoroiodobenzenes such as the 1,2-diiodotetrafluorobenzene, 1,4-diiodotetrafluorobenzene, and 1,3,5-trifluoro-2,4,6-triiodobenzene do not have such geometries and cannot form 2D sheets via the weak C–I···F halogen bonds. Hence, we predict that the cocrystals formed by HMB with these molecules will not have such a sandwiched-layer structure. The controlled experiments are in progress in our laboratory. The preliminary results show that these predicted cocrystals are a little more difficult to be synthesized than the cocrystal reported in this study.