Modelling Propagating Bloch Waves in Magnetoelectroelastic Phononic Structures with Kagomé Lattice Using the Improved Plane Wave Expansion
Abstract
:1. Introduction
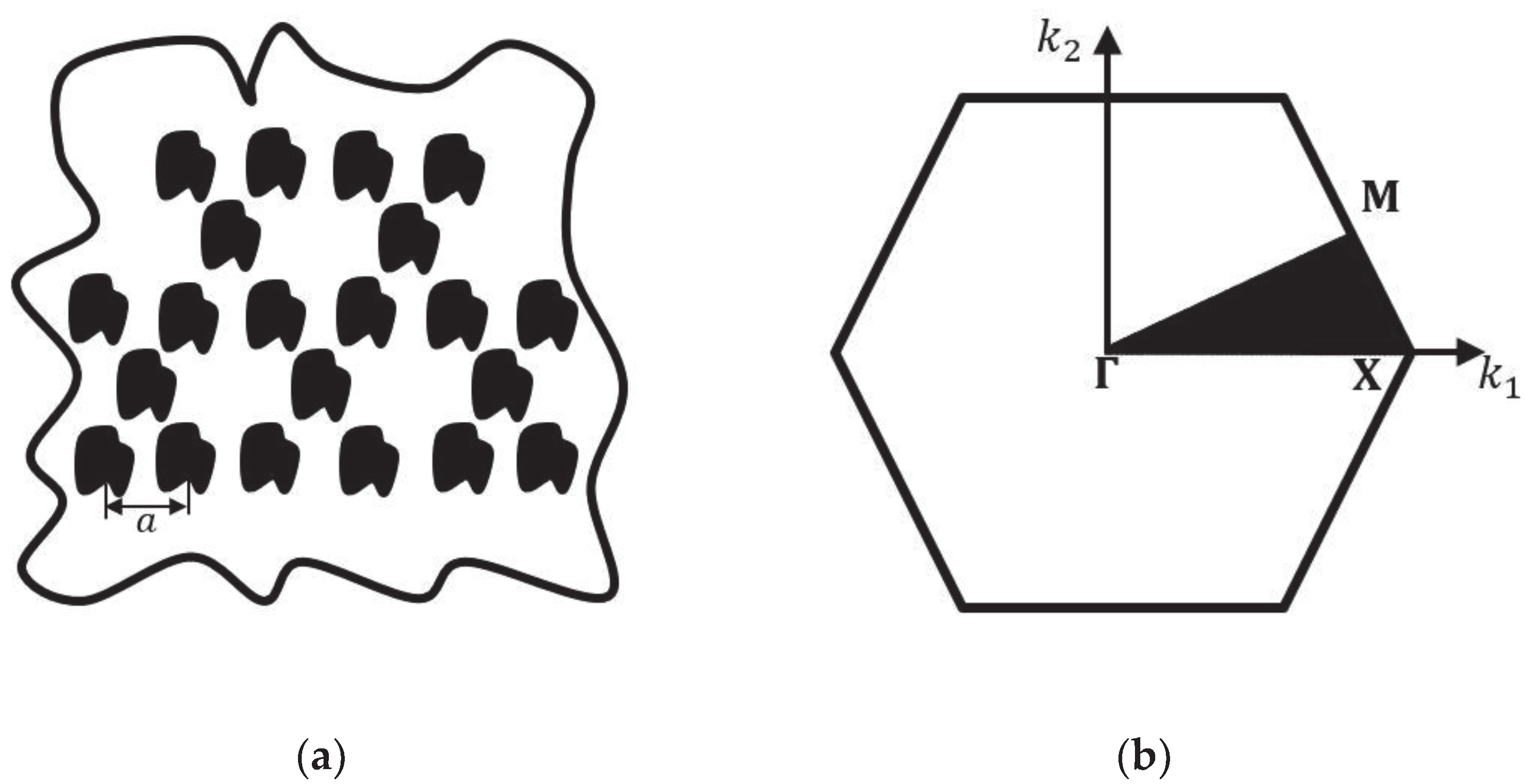
2. Magnetoelectroelastic Phononic Crystal Modelling
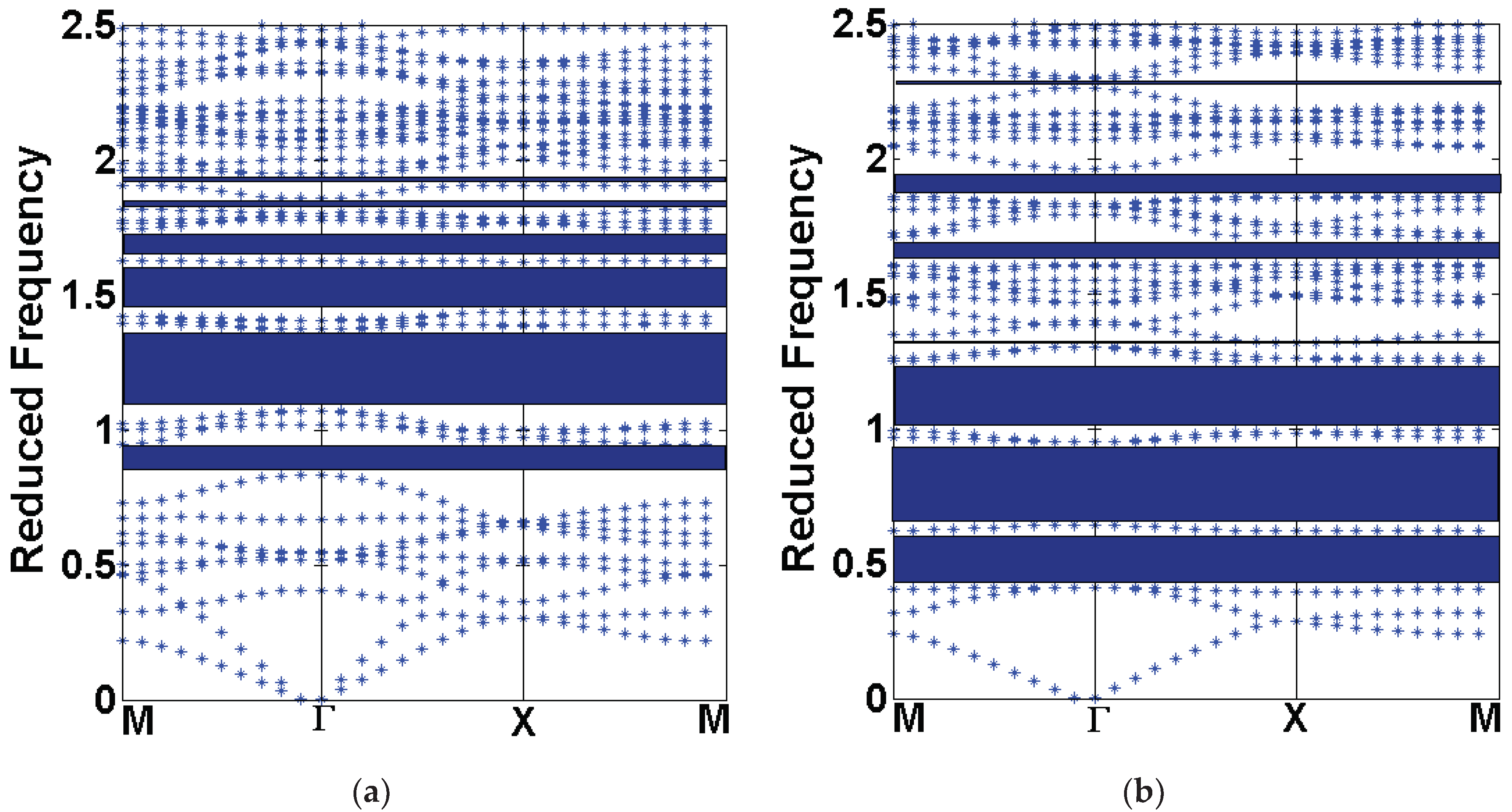
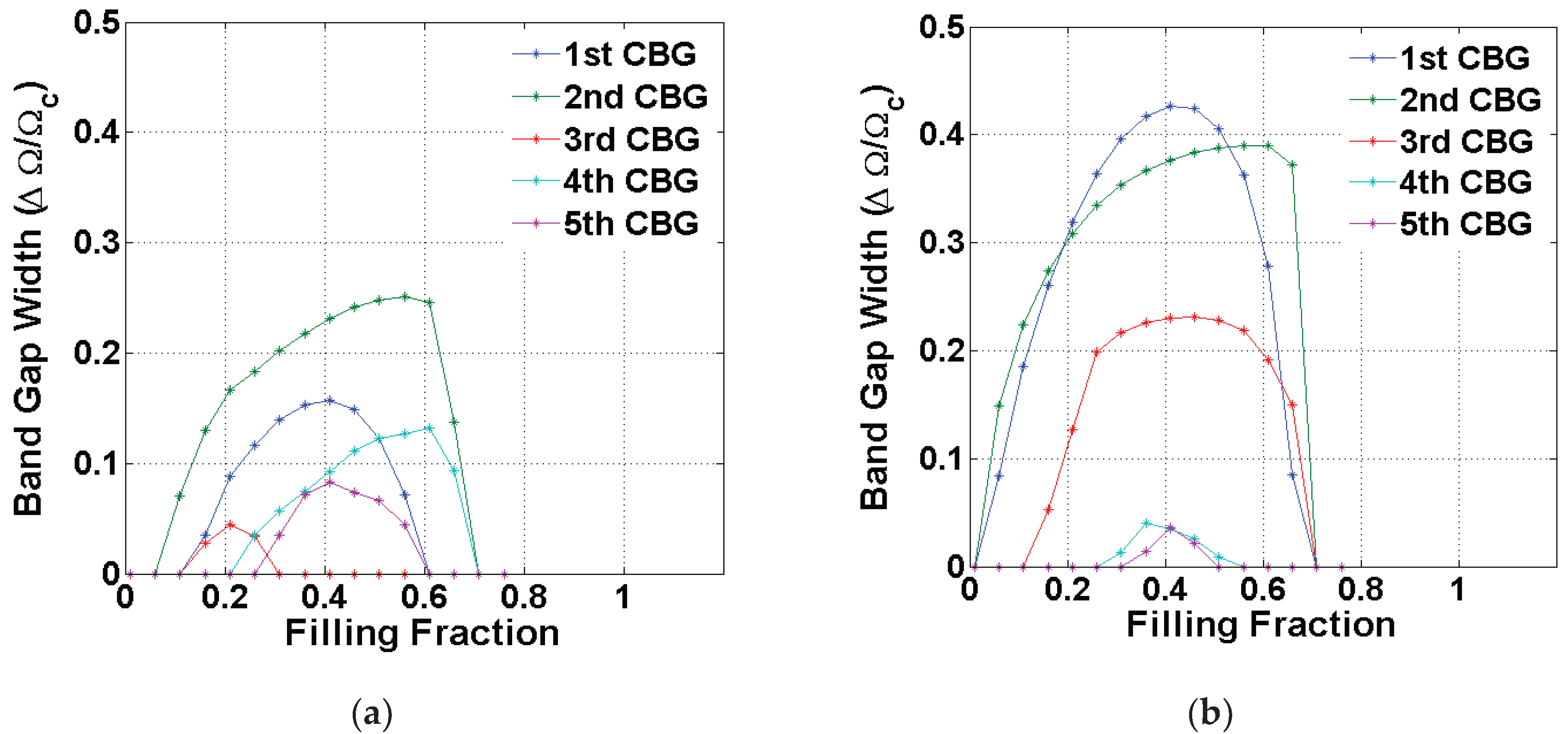
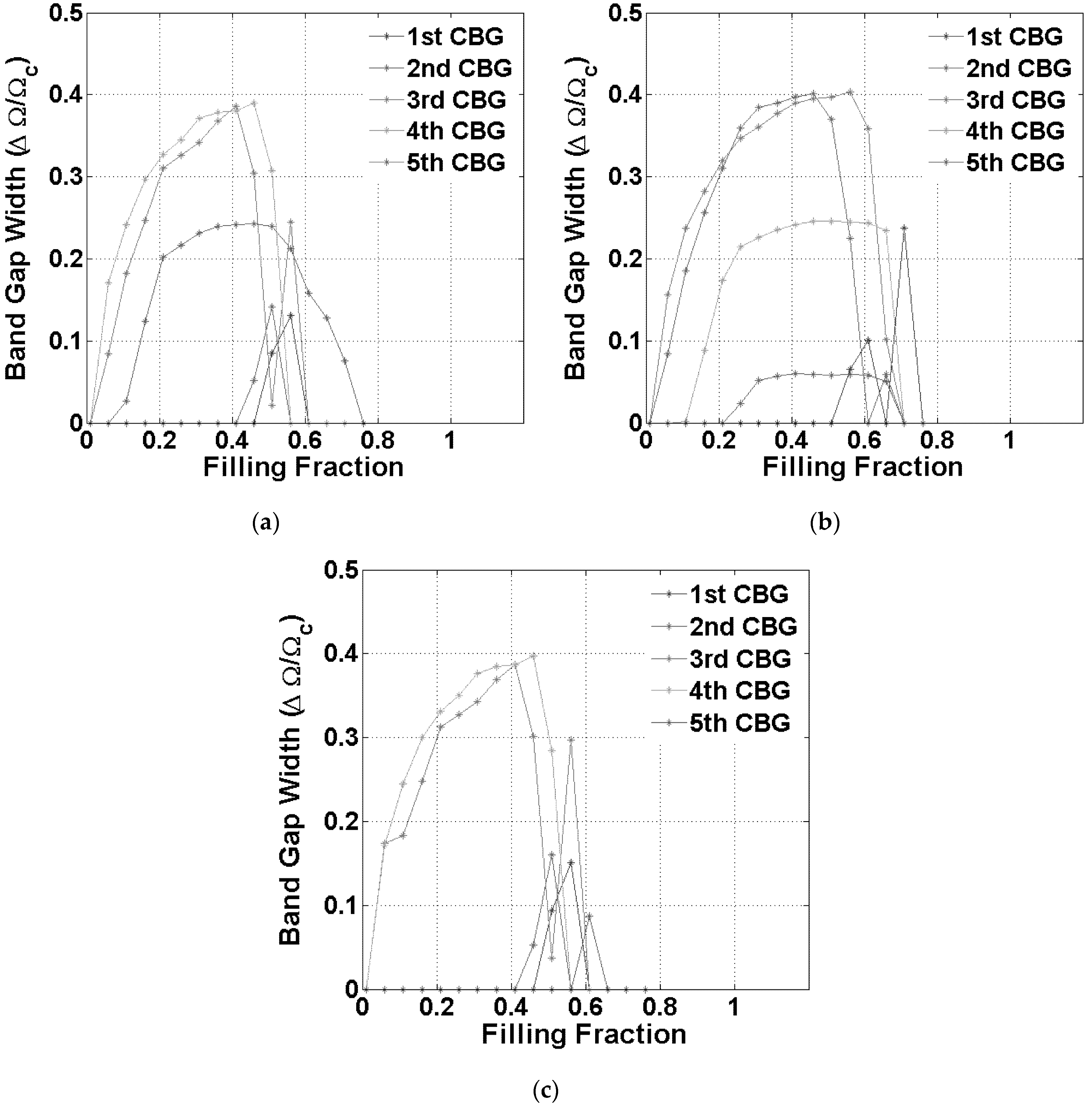
3. Simulated Examples
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sigalas, M.M.; Economou, E.N. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Martínez, G.; Dobrzynski, L.; Djafari-Rouhani, B. Theory of acoustic band structure of periodic elastic composites. Phys. Rev. B Condens. Matter 1994, 49, 2313–2322. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Shen, C.; Li, J.; Reit, E.; Bachman, H.; Socolar, J.E.S.; Cummer, S.A.; Huang, T.J. Dispersion tuning and route reconfiguration of acoustic waves in valley topological phononic crystals. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, D. Electro-mechanical coupling wave propagating in a locally resonant piezoelectric/elastic phononic crystal nanobeam with surface effects. Appl. Math. Mech. 2020, 41, 425–438. [Google Scholar] [CrossRef]
- Chen, Z.-G.; Zhao, J.; Mei, J.; Wu, Y. Acoustic frequency filter based on anisotropic topological phononic crystals. Sci. Rep. 2017, 7, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Gkantzounis, G.; Florescu, M. Freeform phononic waveguides. Crystals 2017, 7, 353. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, S.; Eskandari-Ghadi, M.; Rahimian, M. Simulation-based conceptual design of an acoustic metamaterial with full band gap using an air-based 1-3 piezoelectric composite for ultrasonic noise control. C. R. Mec. 2017, 345, 137–152. [Google Scholar] [CrossRef]
- Miranda, E.J.P., Jr.; Dos Santos, J.M.C. Complete band gaps in nano-piezoelectric phononic crystals. Mat. Res. 2017, 20 (Suppl. 1), 15–38. [Google Scholar] [CrossRef] [Green Version]
- Vasseur, J.O.; Matar, O.B.; Robillard, J.F.; Hladky-Hennion, A.-C.; Deymier, P.A. Band structures tunability of bulk 2D phononic crystals made of magneto-elastic materials. AIP Adv. 2011, 1, 041904–041915. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-Z.; Li, F.-M.; Huang, W.-H.; Jiang, X.; Wang, Y.-S.; Kishimoto, K. Wave band gaps in two-dimensional piezoelectric/piezomagnetic phononic crystals. Int. J. Solids Struct. 2008, 45, 4203–4210. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K.; Wang, Y.-S.; Huang, W.-H. Band gap behaviours of periodic magnetoelectroelastic composite structures with Kagome lattices. Waves Random Complex Media 2009, 19, 509–520. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K.; Wang, Y.-S.; Huang, W.-H. Elastic wave band gaps in magnetoelectroelastic phononic crystals. Wave Motion. 2009, 46, 47–56. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M. Band gap properties of magnetoelectroelastic grid structures with initial stress. Chin. Phys. Lett. 2012, 29, 034301–034311. [Google Scholar] [CrossRef]
- Guo, X.; Wei, P.; Lan, M.; Li, L. Dispersion relations of elastic waves in one-dimensional piezoelectric/piezomagnetic phononic crystal with functionally graded interlayers. Ultrasonics 2016, 70, 158–171. [Google Scholar] [CrossRef]
- Miranda, E.J.P., Jr.; Dos Santos, J.M.C. Evanescent Bloch waves and complex band structure in magnetoelectroelastic phononic crystals. Mech. Syst. Signal Pr. 2018, 112, 280–304. [Google Scholar] [CrossRef]
- Hutchinson, R.G.; Fleck, N.A. The structural performance of the periodic truss. J. Mech. Phys. Solids 2006, 54, 756–782. [Google Scholar] [CrossRef]
- Souslov, A.; Liu, A.J.; Lubensky, T.C. Elasticity and response in nearly isostatic periodic lattices. Phys. Rev. Lett. 2009, 103, 205503–205506. [Google Scholar] [CrossRef] [Green Version]
- Sun, K.; Souslov, A.; Mao, X.; Lubensky, T.C. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc. Natl. Acad. Sci. USA 2012, 109, 12369–12374. [Google Scholar] [CrossRef] [Green Version]
- Riva, E.; Quadrelli, D.E.; Cazzulani, G.; Braghin, F. Tunable in-plane topologically protected edge waves in continuum Kagome lattices. J. Appl. Phys. 2018, 124, 164903–164912. [Google Scholar] [CrossRef]
- Ghimire, N.J.; Mazin, I.I. Topology and correlations on the kagome lattice. Nat. Mater. 2020, 19, 137–138. [Google Scholar] [CrossRef]
- Cao, Y.; Hou, Z.; Liu, Y. Convergence problem of plane-wave expansion method for phononic crystals. Phys. Lett. A 2004, 327, 247–253. [Google Scholar] [CrossRef]
- Dyogtyev, A.V.; Sukhoivanov, I.A.; De La Rue, R.M. Photonic band-gaps maps for different two dimensionally periodic photonic crystal structures. J. Appl. Phys. 2010, 107, 013108–0131114. [Google Scholar] [CrossRef]

| Geometry/Property | Value |
|---|---|
| Lattice parameter | 0.022 m |
| Filling fraction | 0.5 |
| Mass density (,) | 5730 kg/m3, 1150 kg/m3 |
| Elastic constant | 166 × 109 N/m2, 7.8 × 109 N/m2 |
| Elastic constant | 77 × 109 N/m2, 4.7 × 109 N/m2 |
| Elastic constant | 43 × 109 N/m2, 1.6 × 109 N/m2 |
| Elastic constant | 44.5 × 109 N/m2, 1.55 × 109 N/m2 |
| Piezoelectric coefficient | 11.6 C/m2, 0 C/m2 |
| Dielectric coefficient | 11.2 × 10−9 C2/Nm2, 0.0398 × 10−9 C2/Nm2 |
| Piezomagnetic coefficient | 550 N/Am, 0 N/Am |
| Magnetic permeability coefficient () | 5 × 10−6 Ns2/C2, 5 × 10−6 Ns2/C2 |
| Electromagnetic coefficient () | 0.005 × 10−9 Ns/VC, 0 Ns/VC |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miranda, E.J.P.d., Jr.; Rodrigues, S.F.; Aranas, C., Jr.; Silva, H.V.C.d.; Silva, E.S.; Reis, G.S.; Paiva, A.E.M.; Dos Santos, J.M.C. Modelling Propagating Bloch Waves in Magnetoelectroelastic Phononic Structures with Kagomé Lattice Using the Improved Plane Wave Expansion. Crystals 2020, 10, 586. https://doi.org/10.3390/cryst10070586
Miranda EJPd Jr., Rodrigues SF, Aranas C Jr., Silva HVCd, Silva ES, Reis GS, Paiva AEM, Dos Santos JMC. Modelling Propagating Bloch Waves in Magnetoelectroelastic Phononic Structures with Kagomé Lattice Using the Improved Plane Wave Expansion. Crystals. 2020; 10(7):586. https://doi.org/10.3390/cryst10070586
Chicago/Turabian StyleMiranda, Edson Jansen Pedrosa de, Jr., Samuel Filgueiras Rodrigues, Clodualdo Aranas, Jr., Hélio Vitor Cantanhêde da Silva, Eden Santos Silva, Gedeon Silva Reis, Antônio Ernandes Macedo Paiva, and José Maria Campos Dos Santos. 2020. "Modelling Propagating Bloch Waves in Magnetoelectroelastic Phononic Structures with Kagomé Lattice Using the Improved Plane Wave Expansion" Crystals 10, no. 7: 586. https://doi.org/10.3390/cryst10070586







