Elucidation of the Mechanism of Phase Transition in a Zinc Formate Framework Templated by a Diammonium Cation—Structural, Phonon and Dielectric Studies
Abstract
:1. Introduction
2. Experimental
2.1. Synthesis
2.2. Single-Crystal X-ray Data Collection
2.3. Differential Scanning Calorimetry (DSC)
2.4. Dielectric Properties
2.5. Raman and IR Studies
3. Results and Discussion
3.1. Structural Studies
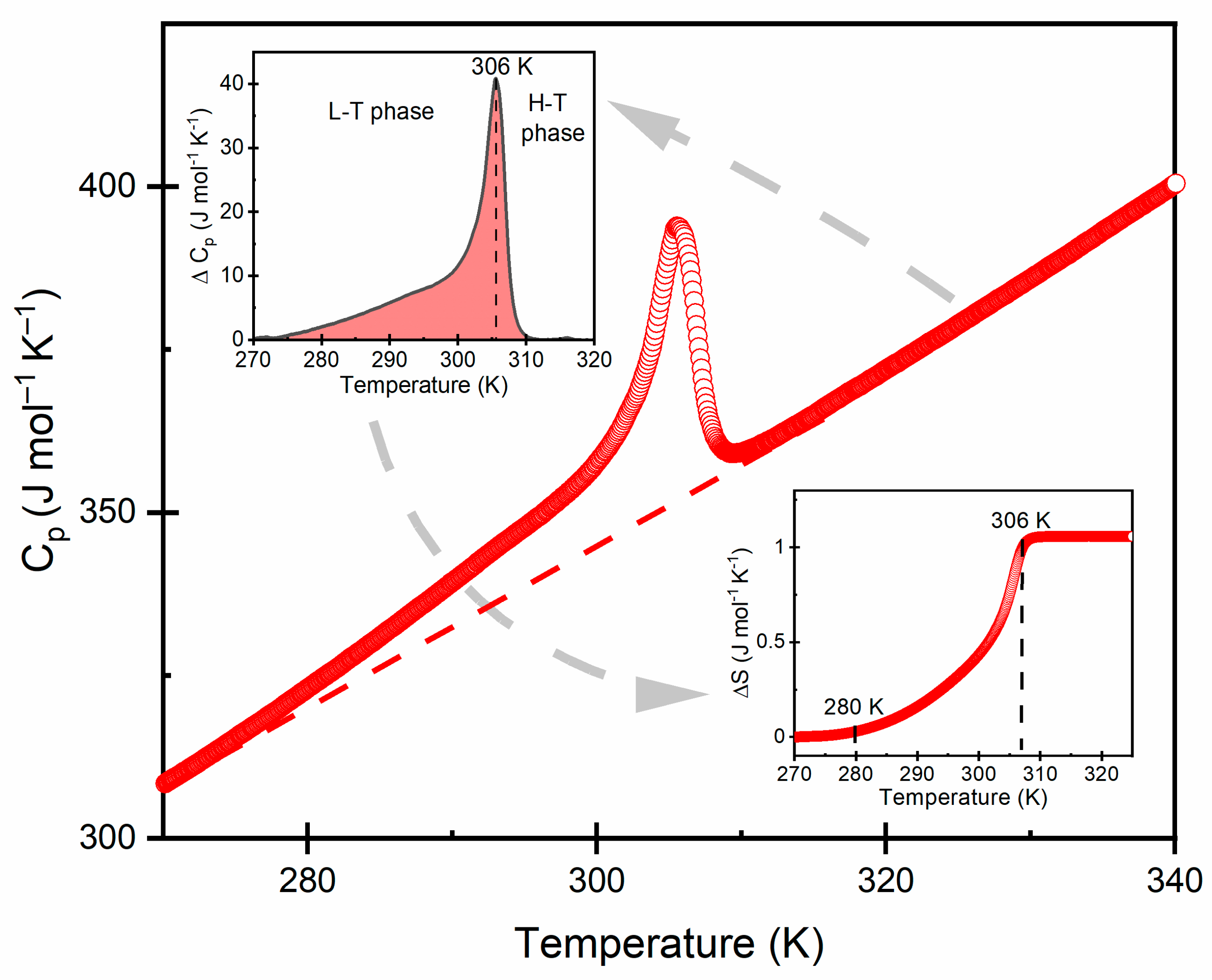
3.2. Thermal Properties
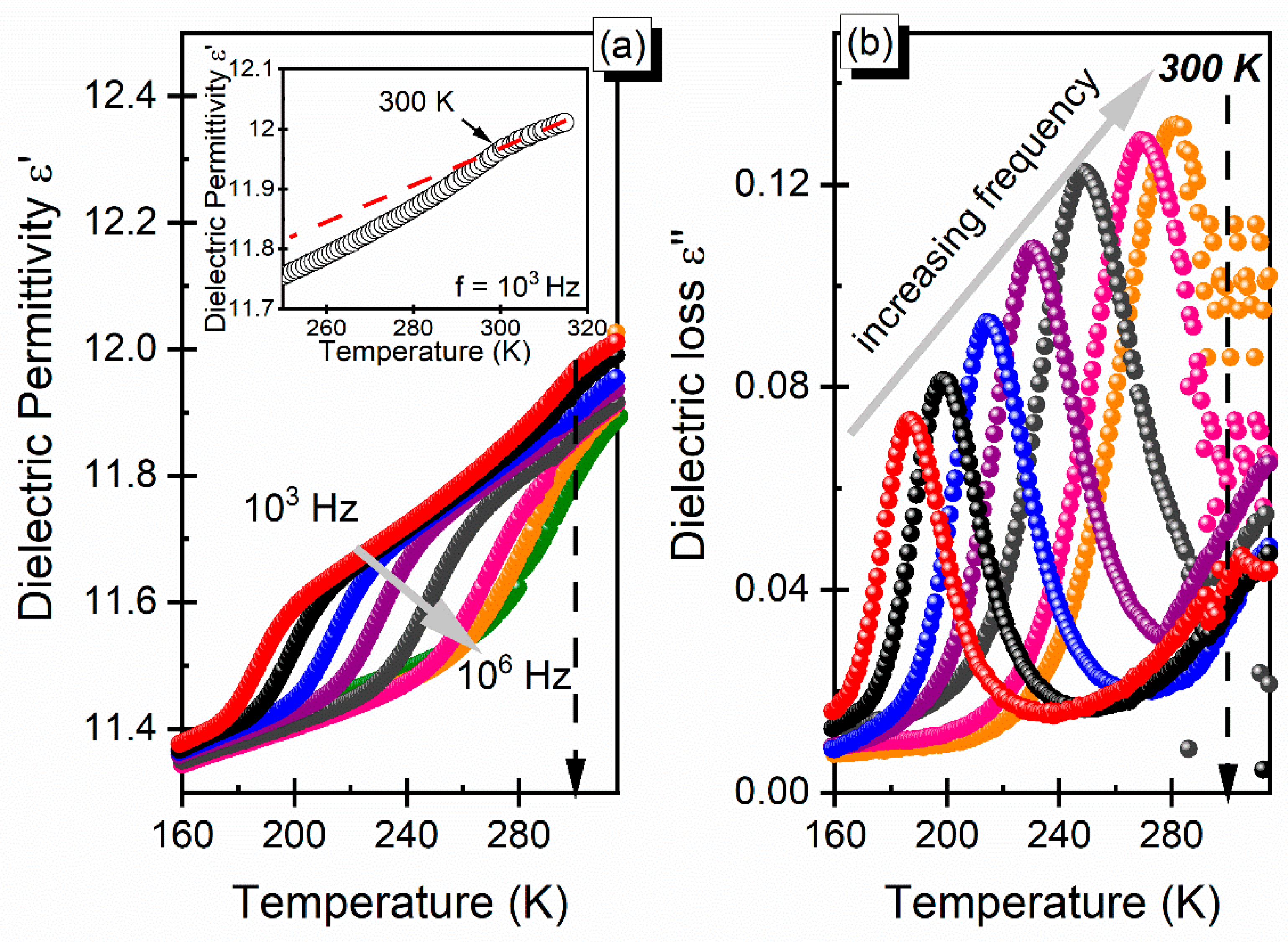
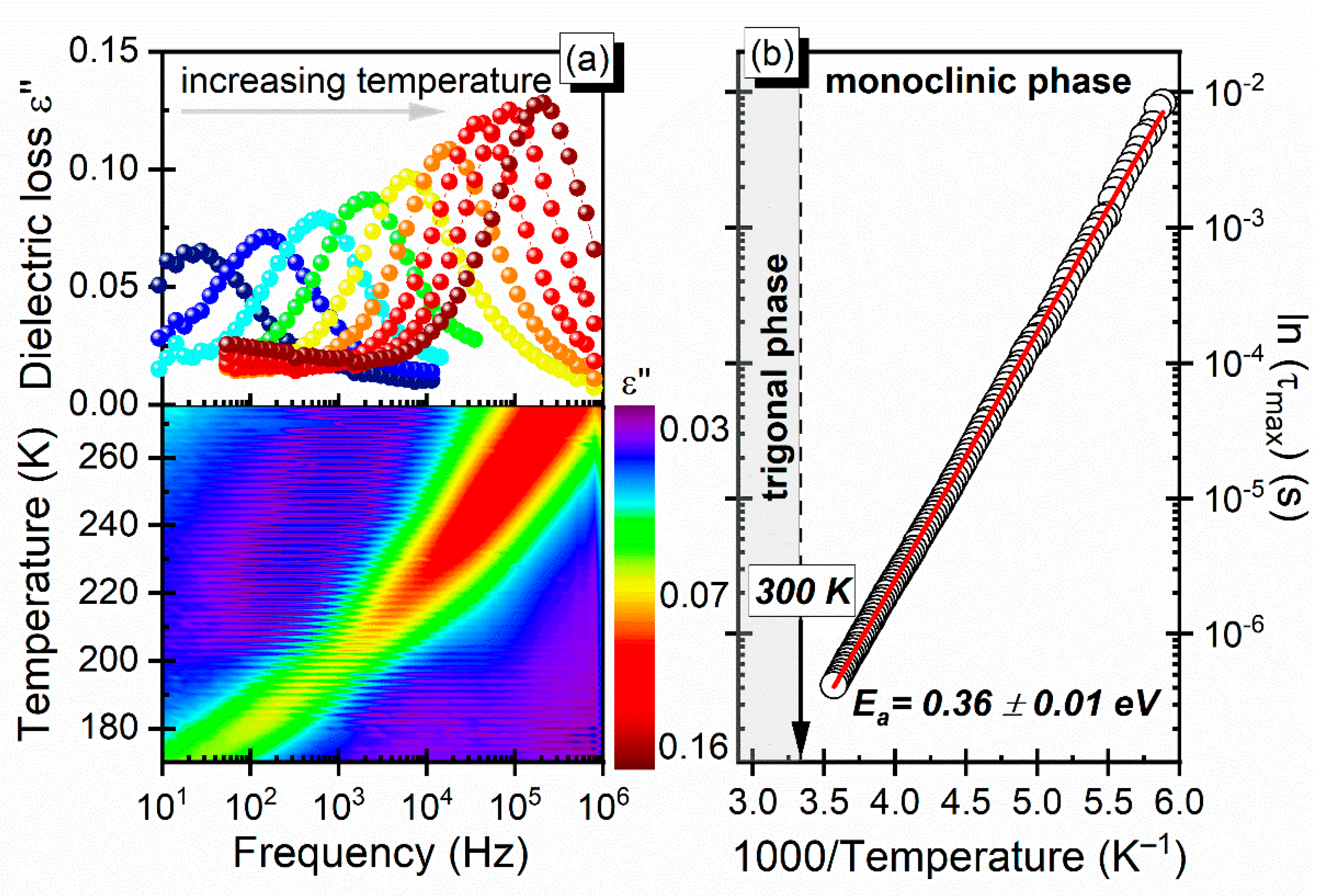
3.3. Dielectric Properties
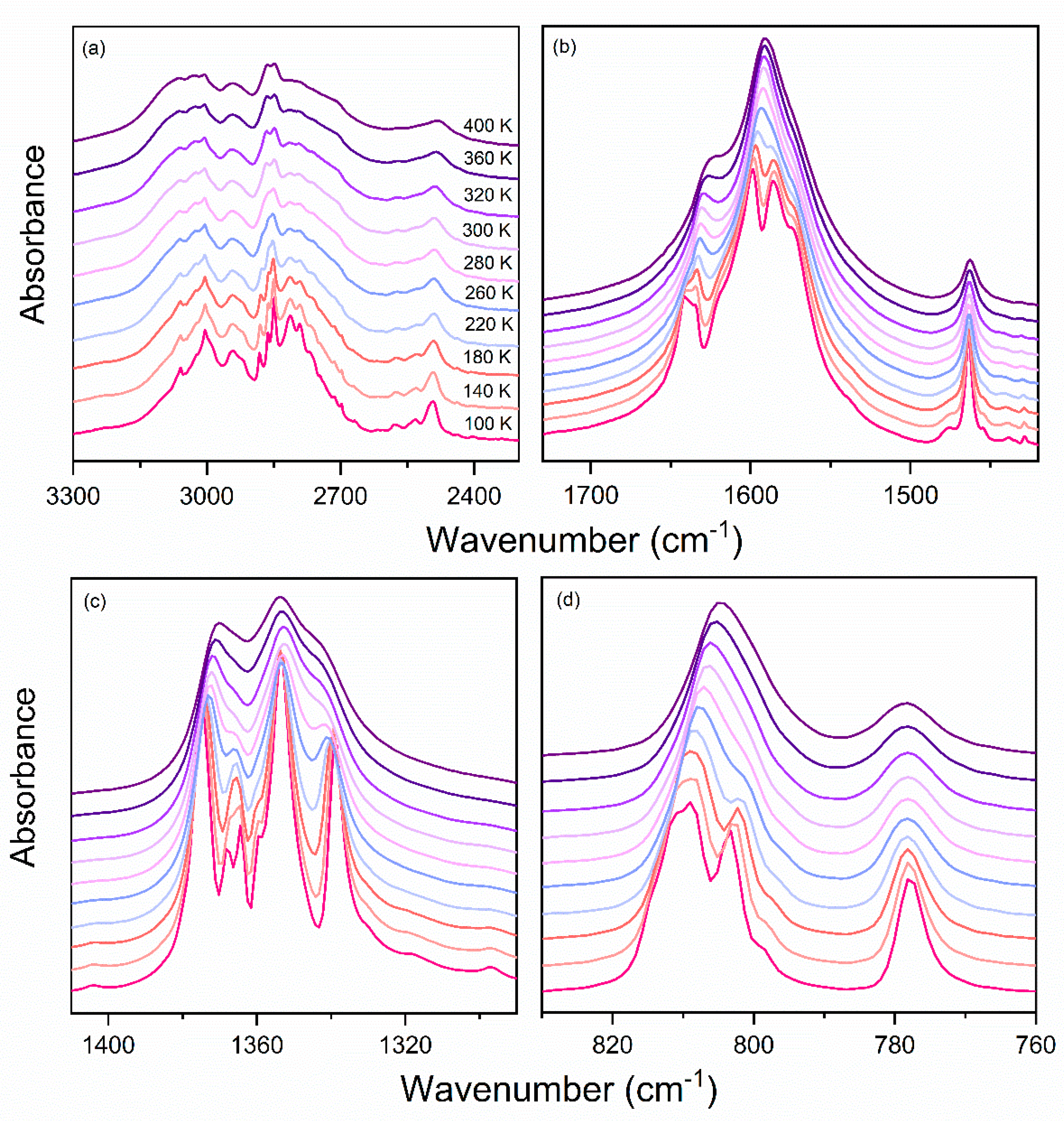
3.4. Vibrational Properties
3.4.1. Selection Rules
3.4.2. Assignment of Modes
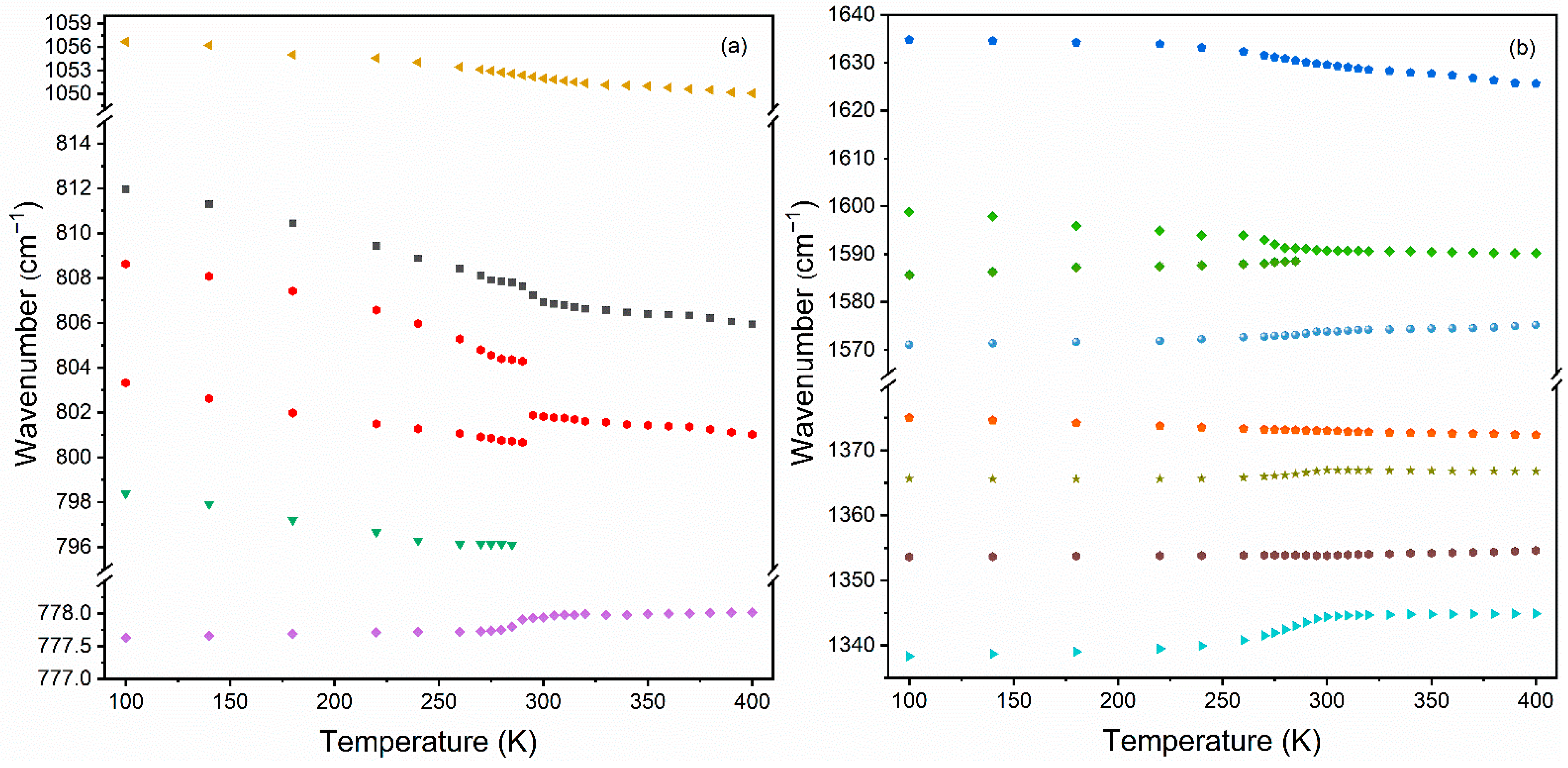
3.4.3. Temperature-Dependent IR Studies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nagabhushana, G.P.; Shivaramaiah, R.; Navrotsky, A. Thermochemistry of Multiferroic Organic–Inorganic Hybrid Perovskites [(CH3)2NH2] [M(HCOO)3] (M = Mn, Co, Ni, and Zn). J. Am. Chem. Soc. 2015, 137, 10351–10356. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, C.; Julian, B.; Belleville, P.; Popall, M. Applications of hybrid organic–inorganic nanocomposites. J. Mater. Chem. 2005, 15, 3559–3592. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, K.; Gao, S.; Kobayashi, H. Formate—Based Magnetic Metal—Organic Frameworks Templated by Protonated Amines. Adv. Mater. 2010, 22, 1526–1533. [Google Scholar] [CrossRef]
- Jain, P.; Ramachandran, V.; Clark, R.J.; Zhou, H.D.; Toby, B.H.; Dalal, N.S.; Kroto, H.W.; Cheetham, A.K. Multiferroic behavior associated with an order-disorder hydrogen bonding transition in metal-organic frameworks (MOFs) with the perovskite ABX3 architecture. J. Am. Chem. Soc. 2009, 131, 13625–13627. [Google Scholar] [CrossRef]
- Guo, M.; Cai, H.L.; Xiong, R.G. Ferroelectric metal organic framework (MOF). Inorg. Chem. Commun. 2010, 13, 1590–1598. [Google Scholar] [CrossRef]
- Fu, D.W.; Zhang, W.; Cai, H.L.; Zhang, Y.; Ge, J.Z.; Xiong, R.G.; Huang, S.D.; Nakamura, T. A Multiferroic Perdeutero Metal–Organic Framework. Angew. Chem. Int. Ed. 2011, 50, 11947–11951. [Google Scholar] [CrossRef] [PubMed]
- Stroppa, A.; Barone, P.; Jain, P.; Perez-Mato, J.M.; Picozzi, S. Hybrid Improper Ferroelectricity in a Multiferroic and Magnetoelectric Metal–Organic Framework. Adv. Mater. 2013, 25, 2284–2290. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Yan, L.-Q.; Cong, J.-Z.; Zhao, Y.-L.; Wang, F.; Shen, S.-P.; Zhou, T.; Zhang, D.; Wang, S.-G.; Han, X.-F.; et al. Magnetoelectric coupling in the paramagnetic state of a metal-organic framework. Sci. Rep. 2013, 3, 2024. [Google Scholar] [CrossRef] [Green Version]
- Mączka, M.; Gągor, A.; Macalik, B.; Pikul, A.; Ptak, M.; Hanuza, J. Order–Disorder Transition and Weak Ferromagnetism in the Perovskite Metal Formate Frameworks of [(CH3)2NH2][M(HCOO)3] and [(CH3)2ND2][M(HCOO)3] (M = Ni, Mn). Inorg. Chem. 2014, 53, 457–467. [Google Scholar] [CrossRef]
- Šimėnas, M.; Balčiūnas, S.; Ciupa, A.; Vilčiauskas, L.; Jablonskas, D.; Kinka, M.; Sieradzki, A.; Samulionis, V.; Mączka, M.; Banys, J. Elucidation of dipolar dynamics and the nature of structural phases in the [(CH3)2NH2][Zn(HCOO)3] hybrid perovskite framework. J. Mater. Chem. C 2019, 7, 6779–6785. [Google Scholar] [CrossRef]
- Peksa, P.; Trzmiel, J.; Fedoruk, K.; Gągor, A.; Šimėnas, M.; Ciupa, A.; Pawlus, S.; Banys, J.; Mączka, M.; Sieradzki, A. Impact of the Copper-Induced Local Framework Deformation on the Mechanism of Structural Phase Transition in [(CH3)2NH2][Zn(HCOO)3] Hybrid Metal—Formate Perovskite. J. Phys. Chem. C 2019, 123, 23594–23603. [Google Scholar] [CrossRef]
- Xu, G.-C.; Zhang, W.; Ma, Z.-M.; Chen, Y.-H.; Zhang, L.; Cai, H.-L.; Wang, Z.-M.; Xiong, R.-G.; Gao, S. Coexistence of Magnetic and Electric Orderings in the Metal–Formate Frameworks of [NH4][M(HCOO)3]. J. Am. Chem. Soc. 2011, 133, 14948–14951. [Google Scholar] [CrossRef] [PubMed]
- Shang, R.; Xu, G.-C.; Wang, Z.-M.; Gao, S. Phase Transitions, Prominent Dielectric Anomalies, and Negative Thermal Expansion in Three High Thermally Stable Ammonium Magnesium–Formate Frameworks. Chem. Eur. J. 2014, 20, 1146–1158. [Google Scholar] [CrossRef]
- Li, M.-Y.; Kurmoo, M.; Wang, Z.-M.; Gao, S. Metal—Organic Niccolite: Synthesis, Structures, Phase Transition, and Magnetic Properties of [CH3NH2(CH2)2NH2CH3][M2(HCOO)6] (M=divalent Mn, Fe, Co, Ni, Cu and Zn). Chem. Asian J. 2011, 6, 3084–3096. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, X.; Batten, S.R.; Kurmoo, M.; Gao, S. [CH3NH2(CH2)2NH2CH3][M2(HCOO)6] (M = MnII and CoII): Weak Ferromagnetic Metal Formate Frameworks of Unique Binodal 6-Connected (412·63)(49·66) Topology, Templated by a Diammonium Cation. Inorg. Chem. 2007, 46, 8439–8441. [Google Scholar] [CrossRef] [PubMed]
- CrysAlis CCD and CrysAlis Red, Version 1.171.38.41; Rigaku Oxford Diffraction: Oxford, UK, 2015.
- Sheldrick, G.M. SHELXS97, Programs for Crystal Structures Solution and Refinement; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar]
- Brandenburg, K.; Putz, H. DIAMOND Version 3.0; Crystal Impact GbR: Bonn, Germany, 2006. [Google Scholar]
- Wang, Z.-M.; Zhang, B.; Fujiwara, H.; Kobayashi, H.; Kurmoo, M. Mn3(HCOO)6: A 3D porous magnet of diamond framework with nodes of Mn-centered MnMn4 tetrahedron and guest-modulated ordering temperature. Chem. Commun. 2004, 416–417. [Google Scholar] [CrossRef]
- Cornia, A.; Caneschi, A.; Dapporto, P.; Faberetti, A.C.; Gatteschi, D.; Malevasi, W.; Sangregorio, C.; Sessoli, R. Manganese(III) Formate: A Three—Dimensional Framework That Traps Carbon Dioxide Molecules. Angew. Chem. Int. Ed. 1999, 38, 1780–1781. [Google Scholar] [CrossRef]
- Rettig, S.J.; Thompson, R.C.; Trotter, J.; Xia, S.-H. Crystal Structure and Magnetic Properties of Polybis(formamide)bis(μ-formato)cobalt(II): An Extended Two-Dimensional Square Lattice Material Which Exhibits Spontaneous Magnetization below 9 K. Inorg. Chem. 1999, 38, 1360–1363. [Google Scholar] [CrossRef]
- Kubo, H.; Zenmyo, K.; Matsumura, M.; Takeda, K.; Alhara, K.; Yamagata, K. Study of Spin Configuration in Mn Formate Di-Urea by Proton NMR. J. Phys. Soc. Jpn. 1999, 68, 253–257. [Google Scholar] [CrossRef]
- Butler, K.T.; Walsh, A.; Cheetham, A.K.; Kieslich, G. Organised chaos: Entropy in hybrid inorganic–organic systems and other materials. Chem. Sci. 2016, 7, 6316–6324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mączka, M.; Ciupa, A.; Gągor, A.; Sieradzki, A.; Pikul, A.; Macalik, B.; Drozd, M. Perovskite Metal Formate Framework of [NH2-CH+-NH2]Mn(HCOO)3]: Phase Transition, Magnetic, Dielectric, and Phonon Properties. Inorg. Chem. 2014, 53, 5260–5268. [Google Scholar] [CrossRef]
- Mączka, M.; Gągor, A.; Ptak, M.; Paraguassu, W.; da Silva, T.A.; Sieradzki, A.; Pikul, A. Phase Transitions and Coexistence of Magnetic and Electric Orders in the Methylhydrazinium Metal Formate Frameworks. Chem. Mater. 2017, 29, 2264–2275. [Google Scholar] [CrossRef]
- Ciupa, A.; Mączka, M.; Gągor, A.; Sieradzki, A.; Trzmiel, J.; Pikul, A.; Ptak, M. Temperature-dependent studies of [(CH3)2NH2][FeIIIMII(HCOO)6] frameworks (MII = Fe and Mg): Structural, magnetic, dielectric and phonon properties. Dalton Trans. 2015, 44, 8846–8854. [Google Scholar] [CrossRef]
- Mączka, M.; Ptak, M.; Pawlus, S.; Paraguassu, W.; Sieradzki, A.; Belciunas, S.; Simenas, M.; Banys, J. Temperature- and pressure-dependent studies of niccolite-type formate frameworks of [NH3(CH2)4NH3][M2(HCOO)6] (M = Zn, Co, Fe). Phys. Chem. Chem. Phys. 2016, 18, 27613–27622. [Google Scholar] [CrossRef] [PubMed]
- Szeremeta, A.Z.; Nowok, A.; Sieradzki, A.; Simenas, M.; Vilciauskas, L.; Gągor, A.; Mączka, M.; Paluch, M.; Pawlus, S. Relaxing under pressure with a rigid niccolite formate framework. J. Mater. Chem. C 2020, 8, 16736–16741. [Google Scholar] [CrossRef]
- Mączka, M.; Hanuza, J.; Kamińskii, A.A. Polarized IR, spontaneous and stimulated Raman spectra of Y(HCOO)3·2H2O single crystal—a new Raman laser material. J. Raman Spectrosc. 2006, 37, 1257–1264. [Google Scholar] [CrossRef]
- Boesch, S.E.; York, S.S.; Frech, R.; Wheeler, R.A. An experimental and computational investigation of the structure and vibrations of dimethylethylenediamine, a model for poly(ethylenimine). Phys. Chem. Comm. 2001, 4, 1–10. [Google Scholar] [CrossRef]
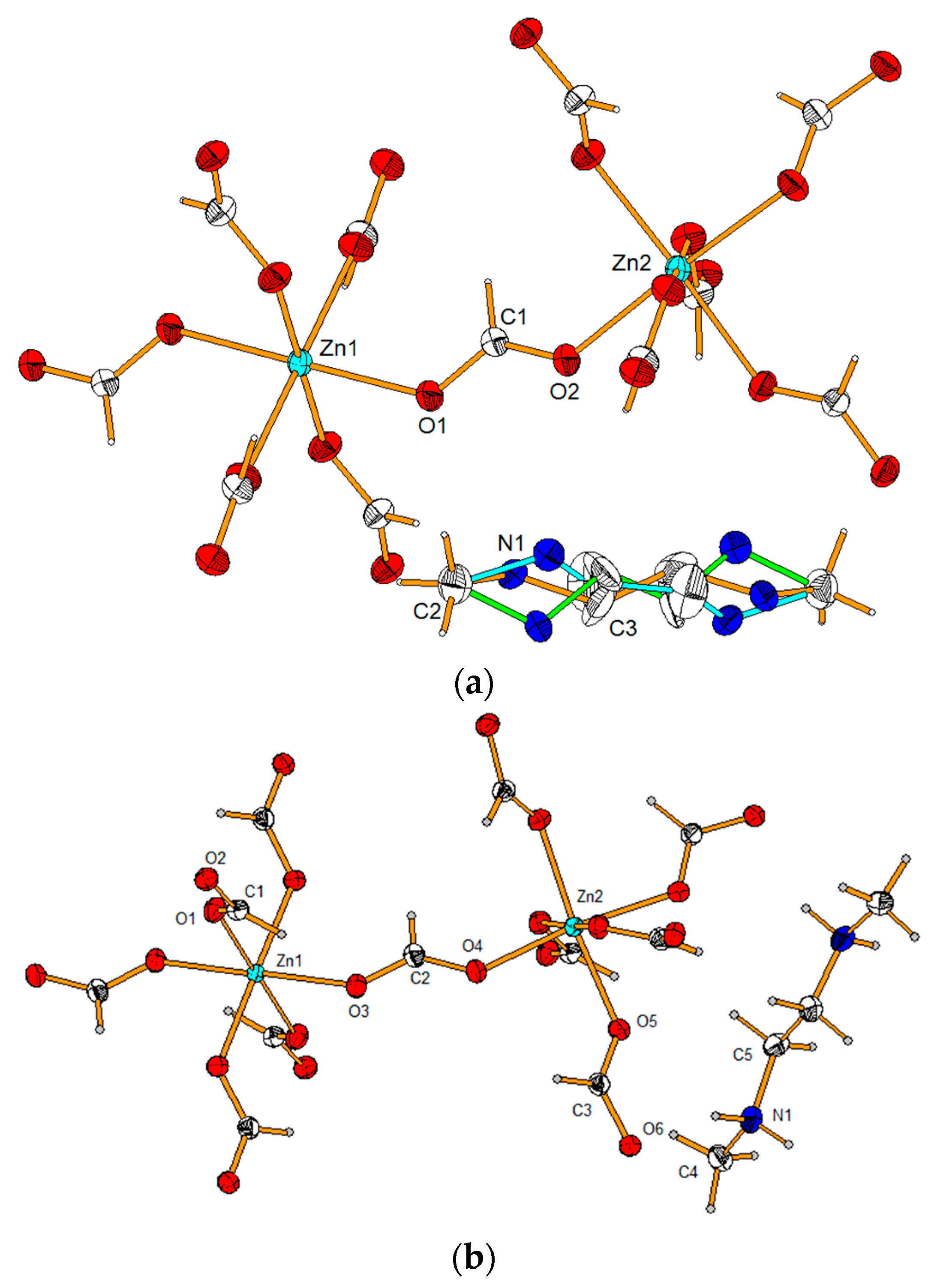
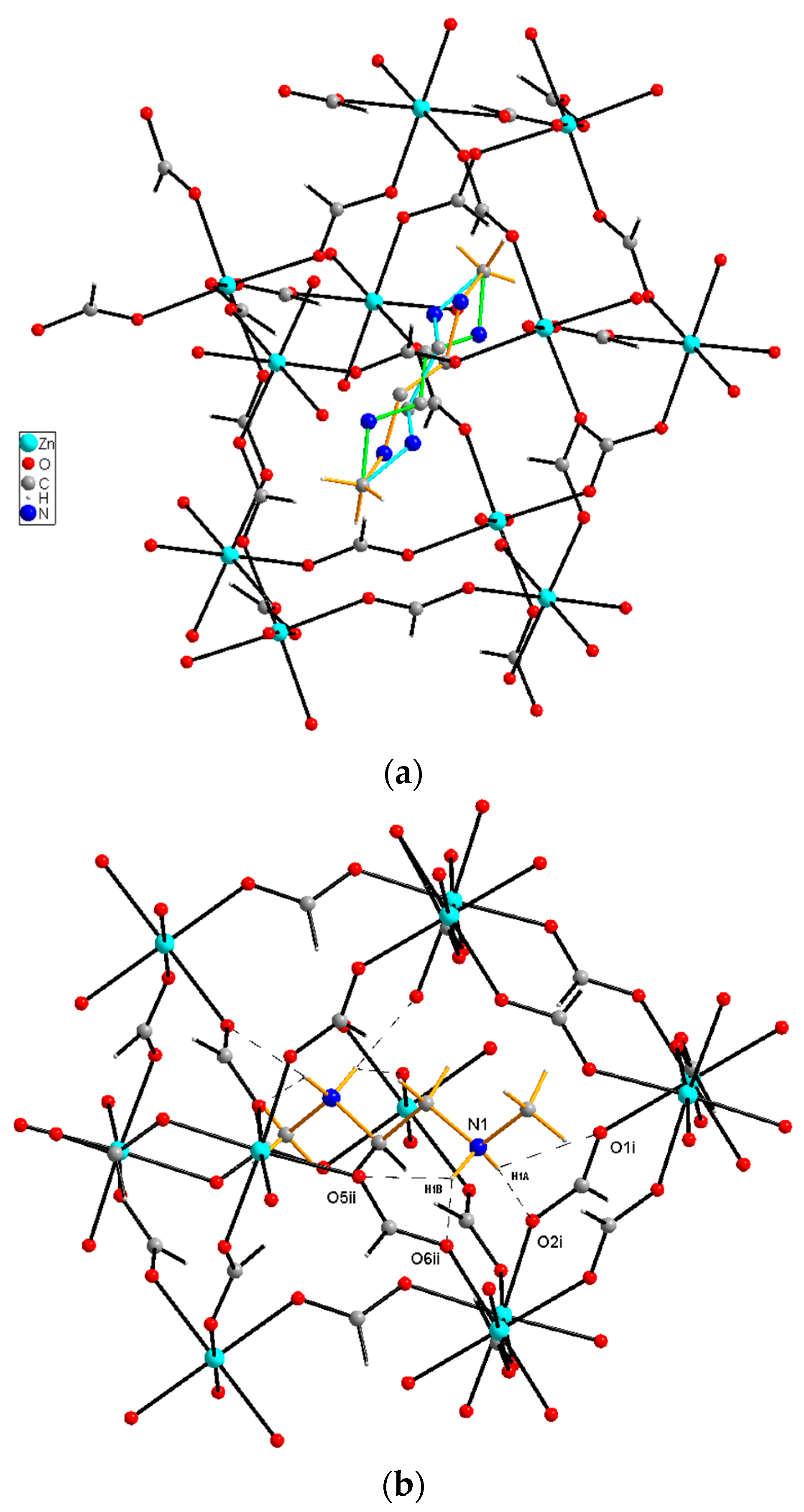
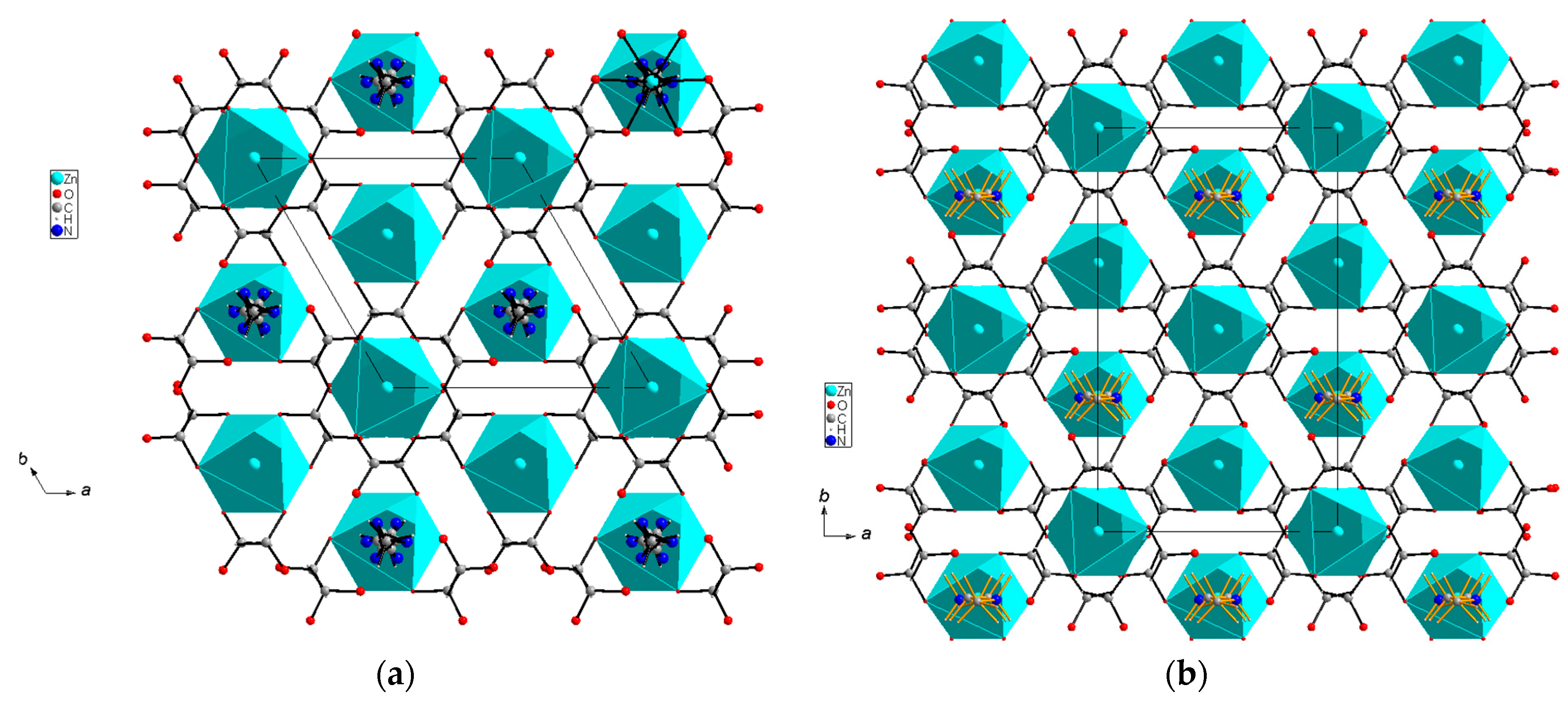
| 100(1) K | 295(1) K | |
|---|---|---|
| Empirical formula | C5H10NO6Zn | C5H10NO6Zn |
| Formula weight (g·mol–1) | 245.53 | 245.53 |
| Crystal system | monoclinic | Trigonal |
| Space group | C 2/c (No 15) | P -3 1 c (No 163) |
| a (Å) | 8.277(2) | 8.172(2) |
| b (Å) | 13.922(5) | 8.172(2) |
| c (Å) | 14.588(5) | 14.686(3) |
| α, β, γ (º) | 90, 91.16(1), 90 | 90, 90, 120 |
| V (Å3) | 1680.7(9) | 849.4(5) |
| Z | 8 | 4 |
| Dcalc (g·cm–3) | 1.941 | 1.920 |
| μ (mm–1) | 2.922 | 2.891 |
| F(000) | 1000.0 | 500.0 |
| Crystal size (mm) | 0.32 × 0.24 × 0.23 | 0.33 × 0.24 × 0.23 |
| Radiation type, λ (Å) | Mo Kα, 0.71073 | Mo Kα, 0.71073 |
| θ range(o) | 2.855—28.708 | 2.774—29.547 |
| Absorption correction | multiscan | multiscan |
| Tmin/Tmax | 0.60499 / 1.000 | 0.6474 / 1.000 |
| Refls collected / unique / observed | 5851 / 2058 / 1650 | 5994 / 763 / 619 |
| Rint | 0.0308 | 0.0329 |
| Refinement on | F2 | F2 |
| R[F2 > 2σ(F2)] | 0.0417 | 0.0247 |
| wR(F2 all reflections) * | 0.1014 | 0.0472 |
| Goodness-of-fit, S | 1.001 | 1.000 |
| Δρmax, Δρmin (e Å–3) | +1.164, −0.642 | +0.336, −0.277 |
| (a) 100(1) K | |||
| Zn1—O1 | 2.111(2) | Zn2—O4 | 2.065(2) |
| Zn1—O1i | 2.111(2) | Zn2—O4iv | 2.065(2) |
| Zn1—O3 | 2.078(2) | Zn2—O5 | 2.086(2) |
| Zn1—O3i | 2.078(2) | Zn2—O5iv | 2.086(2) |
| Zn1—O6ii | 2.115(2) | Zn2—O2v | 2.159(2) |
| Zn1—O6iii | 2.115(2) | Zn2—O2vi | 2.159(2) |
| O3—Zn1—O1 | 92.28(9) | O4—Zn2—O5 | 90.57(8) |
| O1—Zn1—O3i | 87.71(9) | O4—Zn2—O2vi | 85.73(8) |
| O3—Zn1—O3i | 180 | O4—Zn2—O5iv | 174.06(8) |
| O3—Zn1—O6ii | 88.85(8) | O4—Zn2—O2v | 90.76(8) |
| Symmetry codes: (i) −x + 1, −y + 1, −z + 1; (ii) −x + 1/2, −y + 1/2, −z + 1; (iii) x + 1/2, y + 1/2, z; (iv) −x + 1, y, −z + 3/2; (v) x + 1/2, y−1/2, z; (vi) −x + 1/2, y−1/2, −z + 3/2. | |||
| (b) 295(1) K | |||
| Zn1—O1 | 2.1099(12) | Zn2—O2 | 2.1071(12) |
| O1—Zn1—O1i | 180.0 | O2vi—Zn2—O2 | 176.07(7) |
| O1—Zn1—O1ii | 88.59(5) | O2iv—Zn2—O2 | 91.36(7) |
| O1—Zn1—O1iii | 91.41(5) | O2v—Zn2—O2 | 85.72(7) |
| Symmetry codes: (i) −x, −y, −z + 1; (ii) y, −x + y, −z + 1; (iii) −y, x−y, z; (iv) −y, −x, −z + 3/2; (v) −x + y+1, y, −z + 3/2; z; (vi) x, x−y−1, −z + 3/2. | |||
| 100(1) K | |||||
|---|---|---|---|---|---|
| D—H···A | D—H | H···A | D···A | D—H···A | D—H···A |
| N1—H1A···O1i | 0.87 (4) | 2.55 (4) | 3.171 (4) | 129 (3) | N1—H1A···O1i |
| N1—H1A···O2i | 0.87 (4) | 2.02 (4) | 2.887 (4) | 174 (4) | N1—H1A···O2i |
| N1—H1B···O5ii | 0.98 (4) | 2.33 (4) | 3.141 (4) | 139 (3) | N1—H1B···O5ii |
| N1—H1B···O6ii | 0.98 (4) | 1.96 (4) | 2.861 (4) | 151 (3) | N1—H1B···O6ii |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciupa-Litwa, A.; Janczak, J.; Peksa, P.; Sieradzki, A. Elucidation of the Mechanism of Phase Transition in a Zinc Formate Framework Templated by a Diammonium Cation—Structural, Phonon and Dielectric Studies. Crystals 2021, 11, 213. https://doi.org/10.3390/cryst11020213
Ciupa-Litwa A, Janczak J, Peksa P, Sieradzki A. Elucidation of the Mechanism of Phase Transition in a Zinc Formate Framework Templated by a Diammonium Cation—Structural, Phonon and Dielectric Studies. Crystals. 2021; 11(2):213. https://doi.org/10.3390/cryst11020213
Chicago/Turabian StyleCiupa-Litwa, Aneta, Jan Janczak, Paulina Peksa, and Adam Sieradzki. 2021. "Elucidation of the Mechanism of Phase Transition in a Zinc Formate Framework Templated by a Diammonium Cation—Structural, Phonon and Dielectric Studies" Crystals 11, no. 2: 213. https://doi.org/10.3390/cryst11020213
APA StyleCiupa-Litwa, A., Janczak, J., Peksa, P., & Sieradzki, A. (2021). Elucidation of the Mechanism of Phase Transition in a Zinc Formate Framework Templated by a Diammonium Cation—Structural, Phonon and Dielectric Studies. Crystals, 11(2), 213. https://doi.org/10.3390/cryst11020213






