Angle-Resolved Intensity of Polarized Micro-Raman Spectroscopy for 4H-SiC

Abstract

Raman spectroscopy is an indispensable method for the nondestructive testing of semiconductor materials and their microstructures. This paper presents a study on the angle-resolved intensity of polarized micro-Raman spectroscopy for a 4H silicon carbide (4H-SiC) wafer. A generalized theoretical model of polarized Raman intensity was established by considering the birefringence effect. The distributions of angle-resolved Raman intensities were achieved under normal and oblique backscattering configurations. Experiments were performed on a self-built angle-resolved Raman system, which verified the validity of the proposed model and achieved the identification of crystal orientations of the 4H-SiC sample.

1. Introduction

With the continuous development of modern advanced science and technology, there is an increasing requirement for high-performance optoelectronic devices for use in harsh environments such as those with high temperatures and high radiation levels. Traditional semiconductor devices have difficulty reaching high frequencies, high temperatures, and high power. Silicon carbide (SiC), a new-generation semiconductor material, has the advantages of a wide band gap, high thermal conductivity, high electron-drift rate, high breakdown field strength, and stable physical and chemical properties [1] and is expected to be widely used in fields with extreme environments such as aerospace, electric power transmission, and nuclear energy.

SiC has more than 200 crystal forms [2], such as 2H, 3C, 4H, 6H, and 15R, where each number represents the number of carbon-silicon diatomic layers along the (001) direction of the unit cell and C, H, and R represent cubic, hexagonal, and rhombohedral crystal systems, respectively. Cree Research Inc. developed commercial monocrystalline 6H-SiC by chemical vapor deposition (CVD) in 1991 and obtained monocrystalline 4H-SiC in 1994. Since then, many companies and scientific institutions have commercially produced 6H-SiC and 4H-SiC. Compared with 6H, 4H has higher free carrier mobility, which makes it a preferred crystal for electronic applications [3].

Performance characterization and product quality inspection are also very important for the application of SiC in advanced technology fields. Raman spectroscopy is one of the commonly used methods to analyze the physical and chemical properties of materials and structures. Due to its nondestructive, noncontact, in situ, and highly sensitive characteristics, Raman spectroscopy has been successfully applied to the field of semiconductor materials and two-dimensional materials [4,5,6]. The Raman spectra of semiconductor crystals contain structural and physical information, including crystal orientation [7], doping [8], grain size [9], stress/strain [10], and electron mobility [11]. Therefore, these properties can be characterized by quantitative analysis of the intensity, wavenumber, full width at half maximum (FWHM), and symmetry through the Raman spectra of the samples. Matsumoto [12] and Kim [13] judged that 4H-SiC underwent a phase change to 3C-SiC as the ratio of the peak intensities at 776 and 796 cm⁻¹ increased. Calabretta [14] indicated that the laser annealing effect reduced the residual stress and restored the crystallinity, which was obtained by analyzing the variation in the Raman wavenumber and Raman intensity. Tomonori [15] analyzed the relationship between stacking faults and the FWHM of the transverse optical (TO) mode of 3C-SiC Raman spectra and found that there was almost a linear relationship between the fault density and FWHM. However, most of the analysis is not based on the anisotropy of SiC. Regarding the birefringence involved in the Raman measurement of SiC, no relevant work has been found thus far.

In this paper, the polarized Raman intensity of 4H-SiC was detected by using a self-built angle-resolved polarization Raman system. By considering birefringence, the theoretical relationship between the Raman intensity and different angles (optical axis direction, incident laser direction, laser polarization direction) is derived and described in detail. The influences of these different angles on the Raman intensity are enumerated and compared.

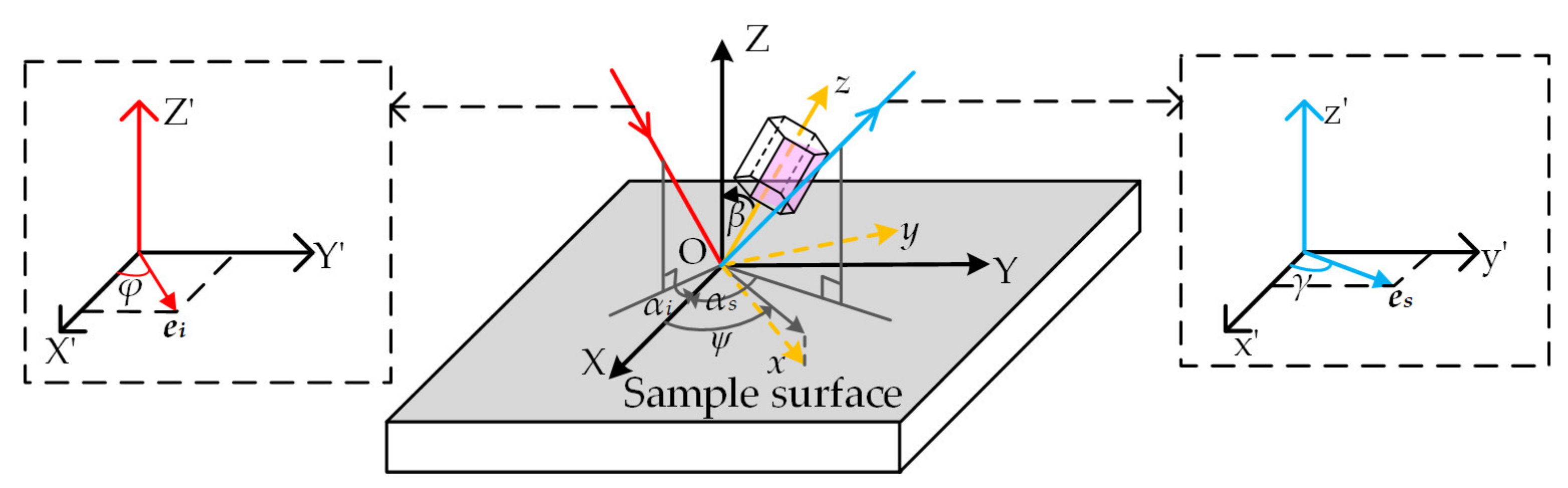
2. Materials and Experiments

The sample used in this work was a high-purity research-grade 4H-SiC wafer provided by Semicore Crystal (Shanxi Semicore Crystal Co., Ltd., Taiyuan, Shanxi, China), whose proportion of 4H crystals exceeded 94% and whose thickness was 0.5 mm. 4H-SiC has hexagonal symmetry and the stacking order is ABCB, maintaining the bonding mode of sp³ hybridization. The lattice vibration of SiC is composed of the Raman active modes A₁, E₁, E₂ and the Raman inactive mode B₁, where E₂ divides into a low-frequency mode and a high-frequency mode. Figure 1 shows the atomic displacements of the Raman active modes, where the small arrows indicate the vibration directions of atoms.

All experiments were performed by using a self-built angle-resolved polarization Raman system with a 532 nm laser and a 50× (numerical aperture, N.A. = 0.55) Mitutoyo lens, as shown in Figure 2. The self-built angle-resolved polarization Raman system includes the signal light path and the observation light path. In the signal light path, the incident laser passing through the laser filter is reflected by mirror I and then by the dichroic filter. After transmitting the half-wave plate and the objective lens, it is focused on the sample surface. The Raman signal excited from the sample by the laser is collected by the objective lens. After transmitting the half-wave plate, the dichroic filter, the analyzer, the edge filter, and the multimode optic fiber, it finally reaches the spectrometer. In the observation light path, the white light is introduced into the co-axial lens tube, reflected by mirror II, the pluggable mirror, the dichroic filter, the half-wave plate, and the objective lens, and focused the surface of the sample. The image data from the sample surface are collected by the objective lens; pass through the half-wave plate and the dichroic filter; are reflected by the pluggable mirror, mirror II; pass through the co-axial lens tube; and reach the CCD target surface to form an image. The polarization configuration was switched by an analyzer that had two adjustable gears, namely HH case and HV case, where HH case means the incident laser light is parallel to the scattering light, and HV case means the incident laser light is vertical to the scattering light. The polarization directions were controlled by the automatic polarization rotation device. During the experiments in this work, the range and step of the polarization direction were 360° and 10°, respectively. Raman spectra of five random sampling spots were detected at each step. All the experiments used a sampling time of 3 s and a grating of 1200 L/mm.

3. Method and Results

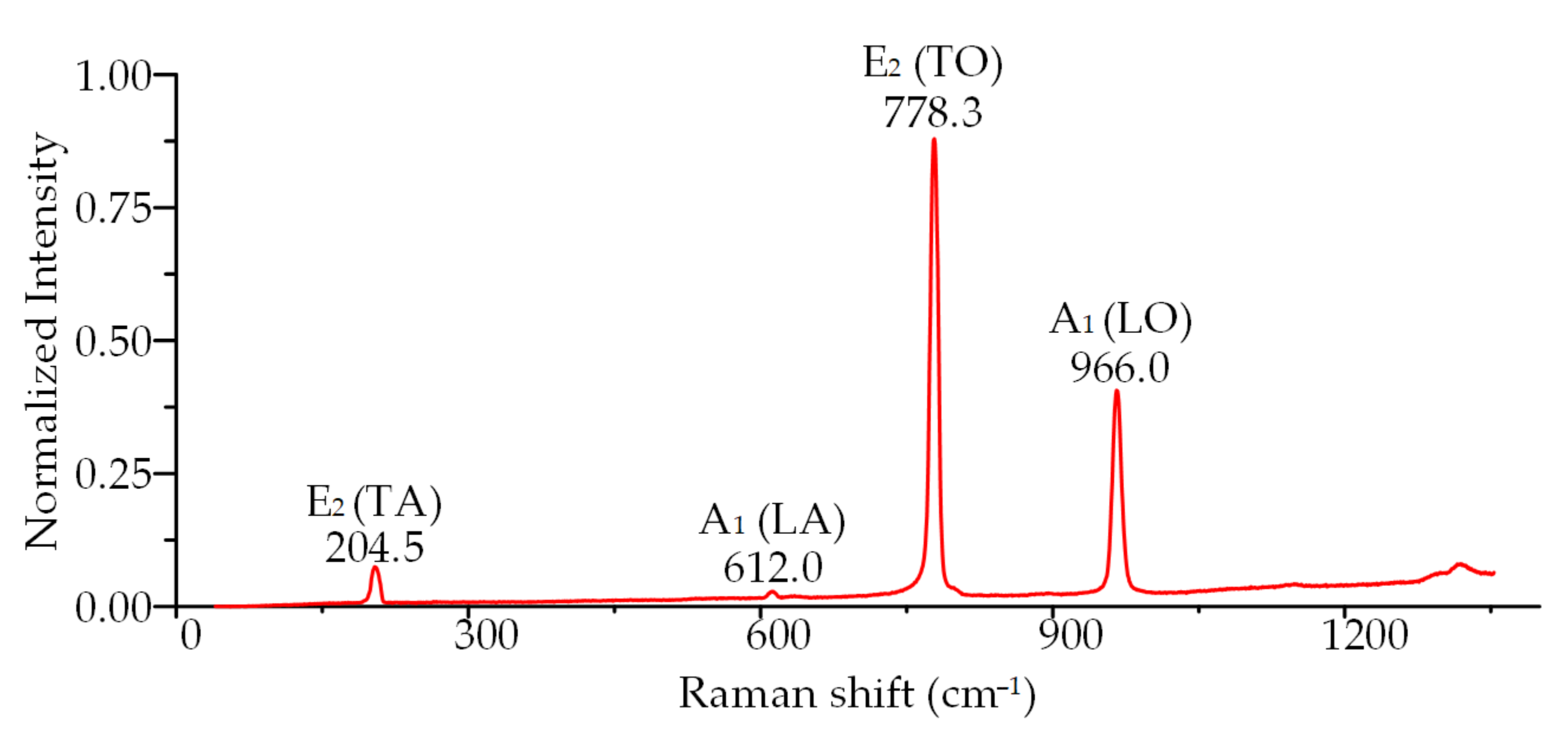
3.1. Raman Spectra of SiC

Figure 3 shows a typical Raman spectrum of the 4H-SiC sample measured by the self-built angle-resolved polarization Raman system. The incident laser was perpendicular to the surface of the sample. The scattered light was collected in backscattering mode without bias detection. The Raman spectra were normalized and fitted with multiple peaks. The Raman spectrum of 4H-SiC, shown in Figure 3, has four visible modes before 1200 cm⁻¹, including the transverse acoustic phonons E₂ (TA) at 204.5 cm⁻¹, the longitudinal acoustic phonons A₁ (LA) at 612.0 cm⁻¹, the transverse optical phonons E₂ (TO) at 778.3 cm⁻¹, and the longitudinal optical phonons A₁ (LO) at 966.0 cm⁻¹ [14]. In these modes, the Raman intensity of either A₁ (LA) or E₂ (LA) is too weak to analyze quantitively for it is always affected and even submerged by the background noise data of the spectrum. Meanwhile, the Raman intensity of the E₂ (TO) mode is regarded as relative to crystalline defects [15], which are not an intrinsic property of monocrystalline 4H-SiC, neither should they be considered when analyzing anisotropy. Therefore, the following is an analysis of the Raman anisotropy of the A₁(TO) mode.

3.2. Raman Intensity Theory of SiC

The geometrical configuration of the angle-resolved polarized Raman analysis for a 4H-SiC sample with a random crystal plane is shown in Figure 4, where X-Y-Z is the sample coordinate system, x-y-z is the crystal coordinate system, X′-Y′-Z′ is the coordinate system of the incident laser, and x′-y′-z′ is the coordinate system of scattered light; hence, β is the angle between the Z-axis and z-axis, ψ is the angle between the X-axis and the projection of the x-axis onto the X-Y plane (viz. the measured surface of the sample), α_i is the angle between the X-axis and the projection of the incident laser onto the X-Y plane, α_s is the angle between the X-axis and the projection of the scattered light onto the X-Y plane, i_i and i_s are the angles between the incident laser or scattered light direction and Z-axis, respectively, and γ and φ are the polarization directions of the incident laser and scattered light, respectively. The z-axis is both the [001]-axis and the optical axis.

The model of the polarized Raman intensity for 4H-SiC with an in-axis/off-axis geometric configuration was established based on the general theory as follows. The polarization vectors of the incident laser e_i′ and scattered light e_s′ are expressed in the coordinate system of the incident laser and the coordinate system of scattered light, respectively, as follows, where T means transpose of matrix or vector.

$$e_{\mathit{i}}{}^{\prime }={\left[\begin{array}{ccc}\cos \phi & \sin \phi & 0\end{array}\right]}^{\mathrm{T}}, e_s{}^{\prime }={\left[\begin{array}{ccc}\cos \gamma & \sin \gamma & 0\end{array}\right]}^{\mathrm{T}}$$

(1)

4H-SiC is a birefringence crystal. If the incident laser does not coincide with the optical axis of the 4H-SiC sample, the incident light is split into ordinary light (O light) and extraordinary light (E light). O light obeys the usual law of refraction, i.e., the refractive index is constant, and the refracted light is in the incident plane. E light does not obey the usual law of refraction and is not necessarily in the incident plane.

In Figure 4, the direction of the optical axis in the X-Y-Z system is expressed as a vector in Equation (2).

$$e_a={\left[\begin{array}{ccc}-\sin \psi \sin \beta & \cos \psi \sin \beta & \cos \beta \end{array}\right]}^{\mathrm{T}}$$

(2)

The incident laser irradiated the sample at an incident angle i. As shown in Figure 5, the incident surface is represented by a green plane, and the angles θ_o and θ_t are within the incident surface. θ_o is defined as the angle of the O light refraction angle, and θ_t is defined as E light. The principal plane of O light is represented by a blue plane, which is formed by the z-axis and the O light vector, where θ_oa is the angle between the O light and the z-axis in the principal plane of O light. The principal plane of E light is represented by a red plane, which is formed by the z-axis and the E light vector, where θ_ta is the angle between the E light and the z-axis in the principal plane of E light.

The directions of O light and E light are expressed as vectors e_o and e_t in Equation (3).

$$\begin{array}{l}{e}_o={\left[\begin{array}{ccc}\cos \psi \cos {\theta }_o& \sin \psi \cos {\theta }_o& \sin {\theta }_o\end{array}\right]}^{\mathrm{T}}\\ e_t={\left[\begin{array}{ccc}\cos \psi \cos {\theta }_t& \sin \psi \cos {\theta }_t& \sin {\theta }_t\end{array}\right]}^{\mathrm{T}}\end{array}$$

(3)

According to the refraction law and Fresnel’s law in a crystal [16,17] and taking the refractive index n = 1 in air, the refractions of O light and E light are expressed as Equation (4).

$$\begin{array}{l}\sin {\theta }_o=\sin i/n_o\\ \sin {\theta }_t=\sin i/n_t\end{array}$$

(4)

where n_o is the principal refractive index of O light, and n_t is the refractive index of E light under general circumstances. n_o is a constant of the 4H-SiC material, while n_t is a function of θ_ta, which is determined by Equation (5).

$$\begin{array}{l}{n}_t=n_o{n}_e/\sqrt{n_o{}^2{\sin }^2{\theta }_{ta}+n_e{}^2{\cos }^2{\theta }_{ta}}\\ \cos {\theta }_{ta}=e_t·e_a=\sin {\theta }_t\cos \beta \end{array}$$

(5)

where n_e is the principal refractive index of E light, which is a constant of the 4H-SiC material. n_t = n_e when the vibration direction of the incident light wave is perpendicular to the z-axis. The refraction angle θ_t and refractive index n_t of E light are expressed as Equation (6) using the angle of incidence and crystal parameters.

$$\begin{array}{l}\sin {\theta }_t=n_o\sin i/\sqrt{n_o{}^2{n}_e{}^2+{\sin }^{2}i{\cos }^2\beta \left(n_o{}^2-n_e{}^2\right)}\\ n_t=\sqrt{n_o{}^2{n}_e{}^2+{\sin }^{2}i{\cos }^2\beta \left(n_o{}^2-n_e{}^2\right)}/n_o\end{array}$$

(6)

According to Equations (4)–(6), the principal planes of O light and E light overlap with each other when and only when i = 0 (viz. vertical incidence). In the case of oblique incidence, it is obvious that O light and E light travel in different directions, and the principal planes of O light and E light no longer overlap. The normal directions of the principal plane of O light and E light are expressed as Equation (7).

$$\begin{array}{l}{n}_o=\left[\begin{array}{c}\frac{\sin {\theta }_o\sin \beta \cos \psi -\cos {\theta }_o\cos \beta \sin \psi }{\sin {\theta }_{oa}}\\ \frac{\cos {\theta }_o\cos \beta \cos \psi +\sin {\theta }_o\sin \beta \sin \psi }{\sin {\theta }_{oa}}\\ \frac{-\cos {\theta }_o\sin \beta }{\sin {\theta }_{oa}}\end{array}\right]\\ n_t=\left[\begin{array}{c}\frac{\sin {\theta }_t\sin \beta \cos \psi -\cos {\theta }_t\cos \beta \sin \psi }{\sin {\theta }_{ta}}\\ \frac{\cos {\theta }_t\cos \beta \cos \psi +\sin {\theta }_t\sin \beta \sin \psi }{\sin {\theta }_{ta}}\\ \frac{-\cos {\theta }_t\sin \beta }{\sin {\theta }_{ta}}\end{array}\right]\\ \cos {\theta }_{oa}=e_o·e_a=\sin {\theta }_o\cos \beta \end{array}$$

(7)

The polarization direction of O light is the normal direction of the principal plane of O light, i.e., v_o = n_o. The polarization direction v_t of E light is in the principal plane of E light and perpendicular to e_t, that is, v_t = n_t × e_t.

$$\begin{array}{l}{v}_o=n_o\\ v_t=\left[\begin{array}{c}\frac{-\sin \beta \sin \psi -0.5\sin 2{\theta }_t\cos \beta \cos \psi }{\sin {\theta }_{ta}}\\ \frac{\sin \beta \cos \psi +0.5\sin 2{\theta }_t\cos \beta \sin \psi }{\sin {\theta }_{ta}}\\ \frac{-{\cos }^2{\theta }_t\cos \beta }{\sin {\theta }_{ta}}\end{array}\right]\end{array}$$

(8)

with the difference in the incident angle i, the polarization directions of the two lights are no longer perpendicular, and the angle between the O light and E light is also not fixed.

The polarization states of O light and E light in the crystal are expressed in Equation (8). Because the basis vectors are e₁ = (100), e₂ = (010), and e₃ = (001) in the sample coordinate system X-Y-Z, the crystal Jones matrix is inferred in the sample coordinate system X-Y-Z [18], as shown in Equation (9).

$$f_o=\left[\begin{array}{ccc}{v}_o{}_1& 0& 0\\ 0& v_o{}_2& 0\\ 0& 0& v_o{}_3\end{array}\right], f_t=\left[\begin{array}{ccc}{v}_t{}_1& 0& 0\\ 0& v_t{}_2& 0\\ 0& 0& v_t{}_3\end{array}\right]$$

(9)

In the sample coordinate system, polarization vectors e_i and e_s are obtained based on e_i’ and e_s’ by a coordinate transformation and Jones matrix. T₁ and T₂ are coordinate transformation matrixes [19] of the incident laser and scattering light, respectively.

$$e_{oi}=f_o·T_1·e_i{}^{\prime }, e_{ti}=f_t·T_1·e_i{}^{\prime }$$

(10)

$$\begin{array}{l}{T}_1=\left[\begin{array}{ccc}\cos {\alpha }_i\cos i_i& -\sin {\alpha }_i& -\cos {\alpha }_i\sin i_i\\ \sin {\alpha }_i\cos i_i& \cos {\alpha }_i& -\sin {\alpha }_i\sin i_i\\ \sin i_i& 0& \cos i_i\end{array}\right]\\ {{\rm T}}_2=\left[\begin{array}{ccc}\cos {\alpha }_s\cos i_s& -\sin {\alpha }_s& -\cos {\alpha }_s\sin i_s\\ \sin {\alpha }_s\cos i_s& \cos {\alpha }_s& -\sin {\alpha }_s\sin i_s\\ \sin i_s& 0& \cos i_s\end{array}\right]\end{array}$$

(11)

The polarization vector of the scattered light is Equation (12).

$$e_s=T_2·e_s{}^{\prime }$$

(12)

The Raman tensor of the A₁ mode is expressed in the crystal coordinate system x-y-z as Equation (13) [20], where a, b are the components of the Raman tensor.

$$R_{\left({\mathrm{A}}_1\right)}{}^{\prime }=\left[\begin{array}{ccc}a& 0& 0\\ 0& a& 0\\ 0& 0& b\end{array}\right]$$

(13)

In practical measurement, the Raman tensor should be converted to the sample coordinate system using the rotation matrix A [19] shown in Equation (14). Hence, the Raman tensor in the sample coordinate system is Equation (15).

$$A=\left[\begin{array}{ccc}\cos \psi & \sin \psi & 0\\ -\cos \beta \sin \psi & \cos \beta \cos \psi & -\sin \beta \\ -\sin \beta \sin \psi & \sin \beta \cos \psi & \cos \beta \end{array}\right]$$

(14)

$$R_{\left({\mathrm{A}}_1\right)}=A{R}_{\left({\mathrm{A}}_1\right)}{}^{\prime }{A}^{\mathsf{{\rm T}}}$$

(15)

For general Raman scattering, the Raman intensity is related to the Raman tensor and laser polarization direction, as shown in Equation (16).

$$I_j\propto {\left|e_i{}^{\mathrm{T}}·R_j·e_s\right|}^2$$

(16)

From Equations (1)–(16), the Raman intensity of 4H-SiC is obtained as Equation (17) in the sample coordinate system.

$$I\propto C_1{\left|e_{oi}{}^{\mathrm{T}}·R_{\left(A_1\right)}{}^{\prime }·e_s\right|}^2+C_2{\left|e_{ti}{}^{\mathrm{T}}·R_{\left(A_1\right)}{}^{\prime }·e_s\right|}^2$$

(17)

C₁ and C₂ are related to the transmittance of the crystal for O light and E light. The transmittance of O light and E light is related to parameters such as the incident laser wavelength and sample thickness.

The angle between the polarization direction of the incident laser and that of the scattered light is usually fixed during actual measurement, where γ = φ is usually named the HH configuration and γ = φ + 90° is the HV configuration.

When β = 90°, ψ = 0°, and i_i = i_s = 0°, the configuration is similar to those used in Pezzotti [20] and Zhao [21]. Under such a configuration, the Raman intensity of 4H-SiC is described by Equation (18),

$$\begin{array}{c}{I}_{HH}\propto C_1{b}^2{\cos }^4\phi \\ I_{HV}\propto 0.25C_1{b}^2{\sin }^{2}2\phi \end{array}$$

(18)

where it should be noted that the distribution of Raman intensity described by Equation (18) is the same as the experimental results measured by Pezzotti [20] and Zhao [21].

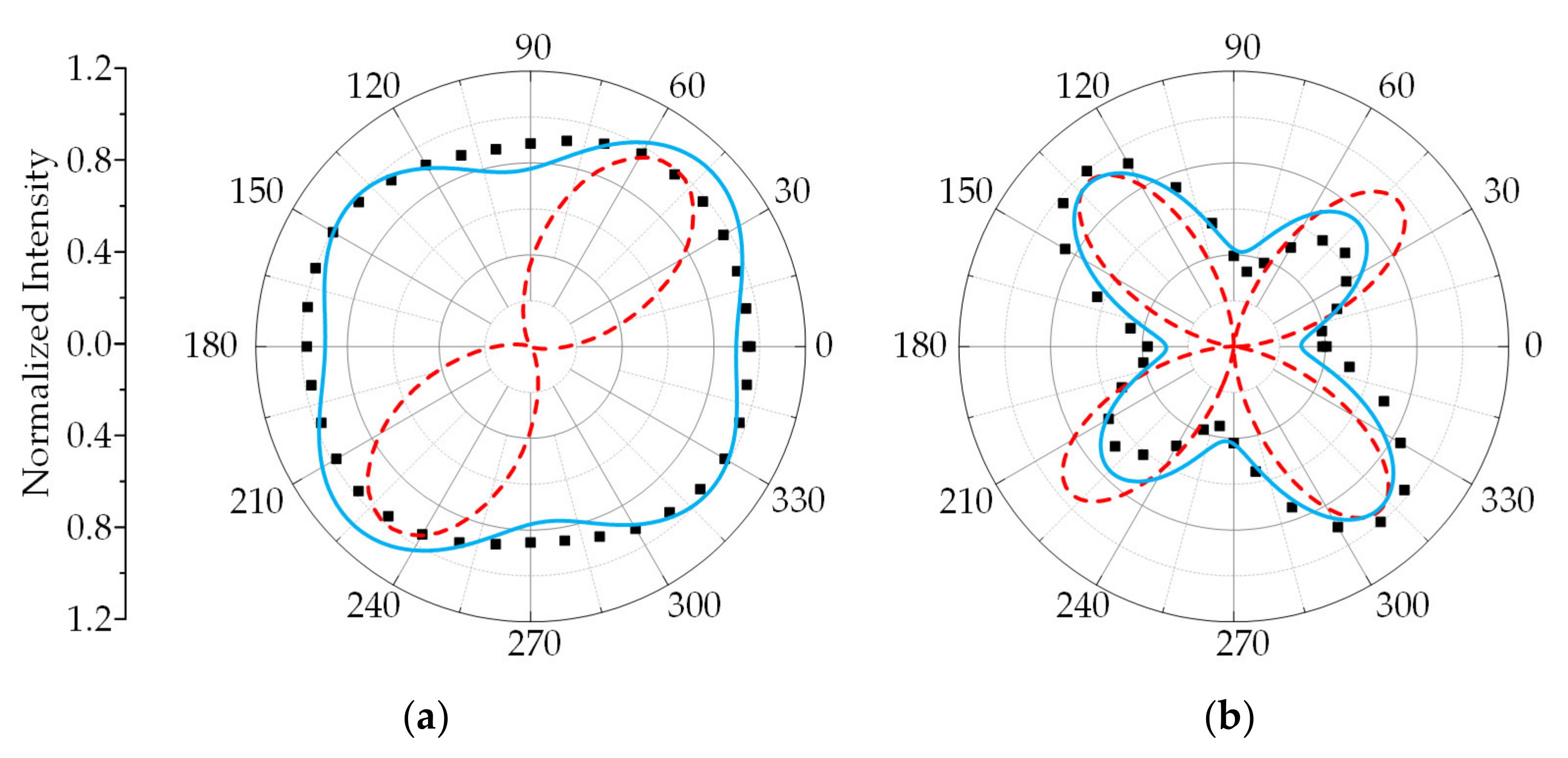
3.3. Analysis of Raman Intensity of SiC

For a commonly used 4H-SiC (0001) crystal plane, when the z-axis coincides with the Z-axis, Equation (17) can be simplified as Equation (19) by using n_o² = 7.1163 and n_e² = 7.4165 under a 532 nm laser measured by Wang [22] at room temperature.

$$\begin{array}{l}I\propto C_1{a}^2{\left[\sin \left({\alpha }_i+\psi \right)\cos i_i\cos \phi +\cos \left({\alpha }_i+\psi \right)\sin \phi \right]}^2\cdot \\ {\left[\sin \left({\alpha }_s+\psi \right)\cos i_s\cos \gamma +\cos \left({\alpha }_s+\psi \right)\sin \gamma \right]}^2\\ +C_2{\left\{\begin{array}{l}\sin {\theta }_{t}a\left[\cos \left({\alpha }_i+\psi \right)\cos i_i\cos \phi -\sin \left({\alpha }_i+\psi \right)\sin \phi \right]\cdot \\ \left[\cos \left({\alpha }_s+\psi \right)\cos i_s\cos \gamma -\sin \left({\alpha }_s+\psi \right)\sin \gamma \right]\\ +b\cos {\theta }_t\sin i_i\sin i_s\cos \phi \cos \gamma \end{array}\right\}}^2\\ \mathrm{where} {\theta }_t=\arcsin \left(7.116\sin i/\sqrt{52.778-0.300{\sin }^{2}i}\right)\end{array}$$

(19)

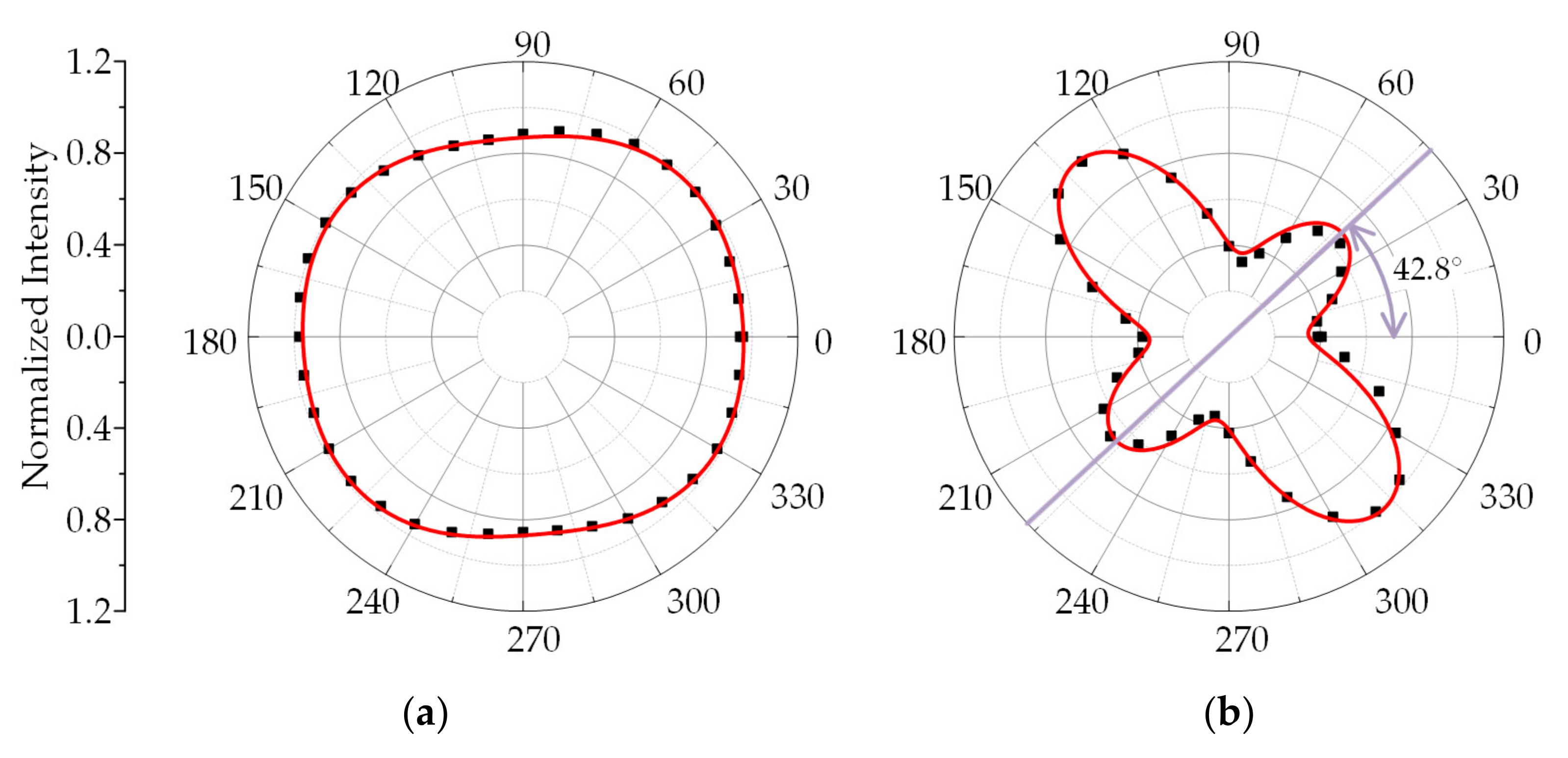
3.3.1. Vertical Backscattering

In the vertical backscattering configuration, both the incident laser and the scattered light are normal to the sample surface. It holds that α_i = α_s = α and i_i = i_s = 0°. The Raman intensity of 4H-SiC is shown in Equation (20).

$$I_{\mathrm{vertical}}\propto C_1{a}^2{\sin }^2\left(\alpha +\psi +\phi \right){\sin }^2\left(\alpha +\psi +\gamma \right)$$

(20)

The Raman intensity is actually the sum of all the scattered light in the range of the optic cone of the materials of the sample that is excited by the incident laser and illuminated within the same cone range. The model that takes into account the influence of a large N.A. could be presented as the integral of the Raman intensity caused by the laser in a cone whose inclination angle i ∈ [0°, arcsin (N.A.)] = [0°, i′] and rotation angle α ∈ [0°, 360°]. Assuming that the light intensity of each inclination angle is uniform, the expression of the Raman intensity is presented as shown in Equation (21) when considering the influence of N.A. The specific calculation result is shown in Equation (A1) in Appendix A.

$$I_{\mathrm{vertical}-\mathrm{N}.\mathrm{A}.}\propto {\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{i^{\prime }}{\int }}{C}_1{\left|e_{oi}{}^{\mathrm{T}}·R_{\left(A_1\right)}{}^{\prime }·e_s\right|}^2+C_2{\left|e_{ti}{}^{\mathrm{T}}·R_{\left(A_1\right)}{}^{\prime }·e_s\right|}^2}}did\alpha$$

(21)

• HH case

In this case, γ = φ. The Raman intensity of the A₁ Raman mode is expressed as Equation (A2) in Appendix A.

• HV case

In this case, γ = φ + 90°. The Raman intensity of the A₁ Raman mode is expressed as Equation (A3) in Appendix A.

The Raman intensity of the 4H-SiC sample under vertical backscattering was measured, as shown in Figure 6, which shows that most, except for a few, experimental points (black solid points) are identical to the theoretical results (red solid line).

In the configuration of vertical backscattering, the experimental data of the HH case and HV case are fitted by Equations (A2) and (A3), and the fitting results are shown as I_V-HH and I_V-HV curves in Figure 6a,b. The I_V-HH curve in Figure 6a is shaped like a potato without a dominant direction, which shows that the anisotropy of 4H-SiC is not obvious in the HH case under the vertical backscattering configuration. The I_V-HV curve in Figure 6b appears to be the superposition of two orthogonal spindles, one long and the other short, which has two unequal maxima corresponding to two orthogonal spindle vertices. The two maxima were defined as I_EL and I_ES (I_EL > I_ES) and corresponded to the polarization directions φ_EL and φ_ES. The crystal direction ψ is the normal direction of the a-plane (I_a-N), corresponding to φ_ES. The parallel direction of the a-plane (I_a-P) corresponds to φ_EL, viz. ψ = φ_ES = φ_EL ± 90°. The crystal direction ψ can be roughly identified by the shape of the experimental data in Figure 6b, precisely determined as one of the fitting parameters. Therefore, ψ = φ_ES = 42.8° in Figure 6b.

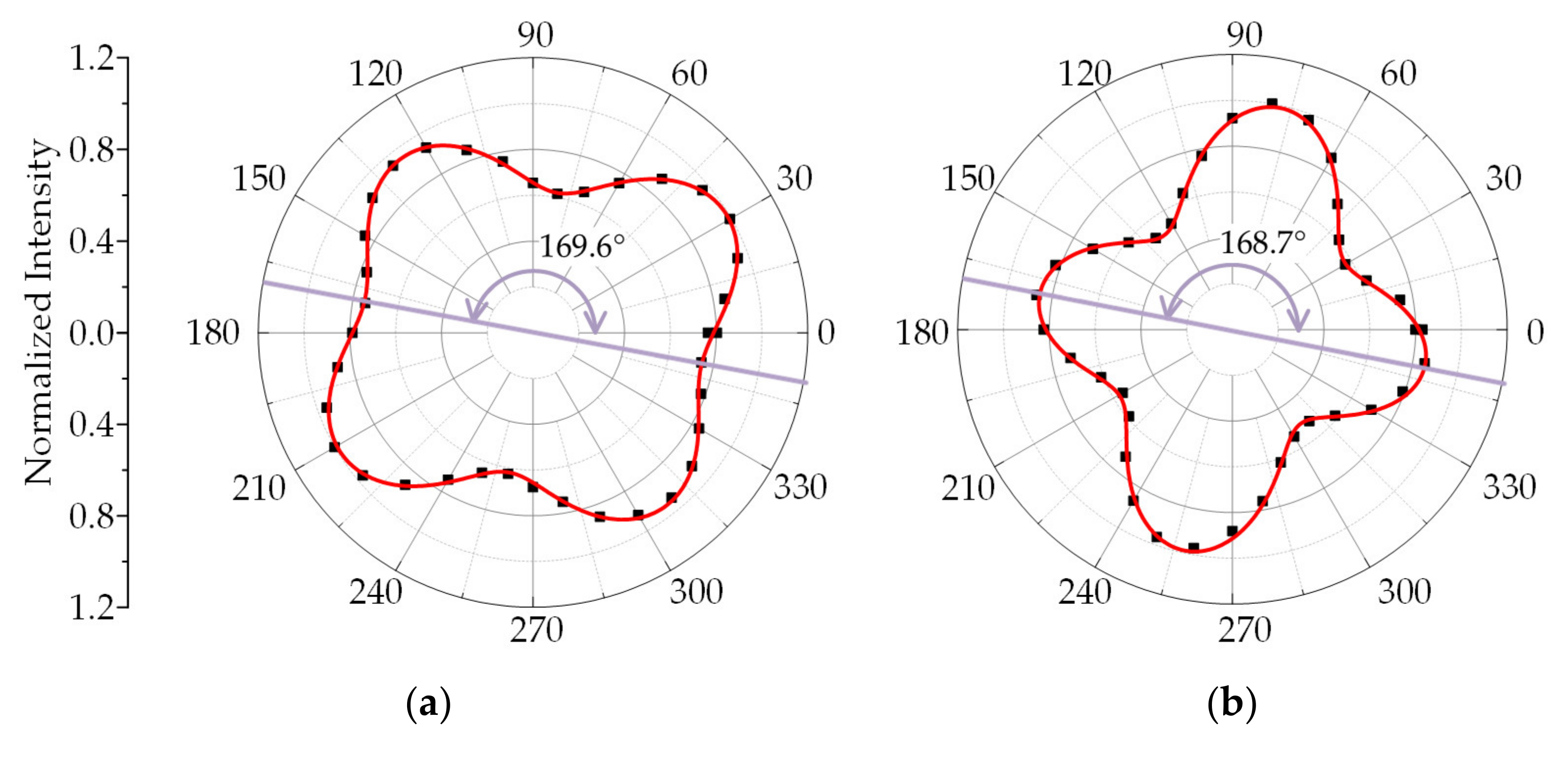
3.3.2. Oblique Backscattering i_i = i_s = i > 0°

In the state of oblique backscattering, i_i equals i_s but does not equal 0. According to the general theory described in Section 3.2, the universal formula of the polarized Raman intensity under the geomatical configuration of oblique backscattering is as follows.

$$\begin{array}{l}{I}_{\mathrm{oblique}}\propto C_1{a}^2{\left[\begin{array}{l}\sin \gamma \cos \left(\alpha +\psi \right)\\ +\cos \gamma \cos i\sin \left(\alpha +\psi \right)\end{array}\right]}^2\times {\left[\begin{array}{l}\sin \phi \cos \left(\alpha +\psi \right)\\ +\cos i\cos \phi \sin \left(\alpha +\psi \right)\end{array}\right]}^2\\ +C_2{\left\{\begin{array}{l}a\left[\begin{array}{l}\sin \phi \sin {\theta }_t\sin \left(\alpha +\psi \right)\\ -\cos i\cos \phi \sin {\theta }_t\cos \left(\alpha +\psi \right)\end{array}\right]\times \left[\begin{array}{l}\sin \gamma \sin \left(\alpha +\psi \right)\\ -\cos \gamma \cos i\cos \left(\alpha +\psi \right)\end{array}\right]\\ +b\cos \gamma \cos \phi \cos {\theta }_t{\sin }^{2}i\end{array}\right\}}^2\end{array}$$

(22)

In the configuration of oblique backscattering, the model considering the influence of a large N.A. could be presented as the integral of the Raman intensity caused by the laser in a cone whose inclination angle is i ∈ [i₁ − arcsin(N.A.), i₁ + arcsin(N.A.)] = [i₁ − i′, i₁ + i′] and rotation angle is α ∈ [−i′, i′]. When i₁ = 30° is the tilt angle of the self-built angle-resolved Raman system, the expression of the Raman intensity is presented as shown in Equation (23) when considering the N.A.

$$I_{\mathrm{oblique}-\mathrm{N}.\mathrm{A}.}\propto {\displaystyle \underset{-i^{\prime }}{\overset{i^{\prime }}{\int }}{\displaystyle \underset{\pi /6-i^{\prime }}{\overset{\pi /6+i^{\prime }}{\int }}{C}_1{\left|e_{oi}{}^{\mathrm{T}}·R_{\left(A_1\right)}{}^{\prime }·e_s\right|}^2+C_2{\left|e_{ti}{}^{\mathrm{T}}·R_{\left(A_1\right)}{}^{\prime }·e_s\right|}^2}}did\alpha$$

(23)

• HH case

In this case, γ = φ. The Raman intensity of the A₁ Raman mode is expressed as Equation (24).

$$\begin{array}{l}{I}_{\mathrm{oblique}-\mathrm{N}.\mathrm{A}.}\propto C_1{a}^2{\displaystyle \underset{-i^{\prime }}{\overset{i^{\prime }}{\int }}{\displaystyle \underset{\pi /6-i^{\prime }}{\overset{\pi /6+i^{\prime }}{\int }}{\left[\begin{array}{l}\sin \phi \cos \left(\alpha +\psi \right)\\ +\cos \phi \cos i\sin \left(\alpha +\psi \right)\end{array}\right]}^4}}did\alpha \\ +C_2{\displaystyle \underset{-i^{\prime }}{\overset{i^{\prime }}{\int }}{\displaystyle \underset{\pi /6-i^{\prime }}{\overset{\pi /6+i^{\prime }}{\int }}{\left\{\begin{array}{l}a\left[\begin{array}{l}\sin \phi \sin {\theta }_t\sin \left(\alpha +\psi \right)\\ -\cos i\cos \phi \sin {\theta }_t\cos \left(\alpha +\psi \right)\end{array}\right]\times \left[\begin{array}{l}\sin \phi \sin \left(\alpha +\psi \right)\\ -\cos \phi \cos i\cos \left(\alpha +\psi \right)\end{array}\right]\\ +b{\cos }^2\phi \cos {\theta }_t{\sin }^{2}i\end{array}\right\}}^2}}did\alpha \end{array}$$

(24)

• HV case

In this case, γ = φ + 90°. The Raman intensity of the A₁ Raman mode is expressed as Equation (25).

$$\begin{array}{l}{I}_{\mathrm{oblique}-\mathrm{N}.\mathrm{A}.}\propto C_1{a}^2{\displaystyle \underset{-i^{\prime }}{\overset{i^{\prime }}{\int }}{\displaystyle \underset{\pi /6-i^{\prime }}{\overset{\pi /6+i^{\prime }}{\int }}{\left[\begin{array}{l}\sin \phi \cos i\sin \left(\alpha +\psi \right)\\ -\cos \phi \cos \left(\alpha +\psi \right)\end{array}\right]}^2\times {\left[\begin{array}{l}\cos i\cos \phi \sin \left(\alpha +\psi \right)\\ +\sin \phi \cos \left(\alpha +\psi \right)\end{array}\right]}^2}}did\alpha \\ +C_2{\displaystyle \underset{-i^{\prime }}{\overset{i^{\prime }}{\int }}{\displaystyle \underset{\pi /6-i^{\prime }}{\overset{\pi /6+i^{\prime }}{\int }}{\left\{\begin{array}{l}a\left[\begin{array}{l}\cos i\cos \phi \sin {\theta }_t\cos \left(\alpha +\psi \right)\\ -\sin \phi \sin {\theta }_t\sin \left(\alpha +\psi \right)\end{array}\right]\times \left[\begin{array}{l}\sin \phi \cos i\cos \left(\alpha +\psi \right)\\ +\cos \phi \sin \left(\alpha +\psi \right)\end{array}\right]\\ +0.5b\sin 2\phi \cos {\theta }_t{\sin }^{2}i\end{array}\right\}}^2}}did\alpha \end{array}$$

(25)

The Raman intensity of the 4H-SiC sample under oblique backscattering was measured, as shown in Figure 7, which shows that most of the experimental points (black solid points) are identical to the theoretical results (red solid line), except for a few.

In the state of oblique backscattering, the experimental data of the HH case and HV case are fitted through Equations (24) and (25), and the fitting results are the I_O-HH and I_O-HV curves in Figure 6b and Figure 7a. The I_O-HH curve in Figure 7a has a butterfly shape with two symmetry axes. The Raman intensities along the directions of two symmetry axes are defined as I_SL and I_SS (I_SL > I_SS), corresponding to the polarization directions φ_SL and φ_SS. The I_O-HH curve in Figure 7b seems to be a superposition of two orthogonal spindles, one long and the other short, which has two unequal maxima corresponding to two orthogonal spindle vertices. The two maxima are defined as I_EL and I_ES (I_EL > I_ES), corresponding to the polarization directions φ_EL and φ_ES. Both φ_SL and φ_ES should be similar to the crystal direction, viz. ψ= φ_SL = φ_ES. According to the fitting results, φ_SL = 169.6° and φ_ES = 168.7°, which are quite similar.

4. Discussion

In Figure 6 and Figure 7, the experimental data are not completely consistent with the theoretical curve, which may be due to defects in the sample, laser incident angle error, and so on.

According to the current processing level, the qualification rate of silicon carbide wafers is 65–80% [23]. Even for wafers qualified for scientific research, the proportion of 4H crystals in a wafer is rarely 100%. Generally, the 4H crystal formation rate of a qualified wafer is 95–99%. In addition, 4H-SiC undergoes a phase transformation after mechanical loading during manufacturing. Matsumoto [12] proved that there was a phase transition from 4H to 3C in the indentation process. Nakashima [24] found that stacking faults can cause a new Raman band to increase, and this new Raman band influences other Raman band intensities. In addition, the residual stress in the SiC will also affect the Raman signal of the SiC [25,26].

In addition to the 4H-SiC wafer quality, another deviation is the angle error in the process of Raman measurement, such as the inclination angle of incident light and the control error of the polarization angle. Furthermore, for optical measurement, the roughness of the crystal surface would also affect the shape of the laser incident into the crystal, resulting in a change in laser polarization.

More importantly, when the N.A. of the microscope objective lens used is less than 0.2, the incident light is close to the parallel light [27], and the influence of numerical aperture can be ignored. However, the Raman experiments in this work used a lens with an N.A. = 0.55, which means that the influence of the numerical aperture cannot be ignored.

With the vertical backscattering measurement as an example, the measured values of Raman intensity are listed again in Figure 8. According to the theoretical model that does not consider the influence of N.A., the intensity curves are as shown with the red dotted lines, which are quite far from the actually measured results, showing that the effect of N.A. is not negligible.

The Raman intensity is the sum of all the scattered light in the range of the optic cone of the materials of the sample that is excited by the incident laser illuminated within the same cone range. If the optic cone of N.A. is divided into numbers of co-axial layers with different radii, each layer has its unique contribution to the total Raman intensity, and has its unique Raman intensity relative to the geometrical configuration and polarization direction. For example, the blue solid lines give the normalized Raman intensity from one layer of the optic cone where the incident angle i =30° and α is integrated from 0° to 360°. Compared with the shape of the red line, the shape of the blue line is much closer to that of the measured data. When all the layers inside the optic cone of N.A. are calculated, the fitted lines shown in Figure 6 and Figure 7 successfully describe the distribution patterns of the measured data.

5. Conclusions

In this paper, the angle-resolved Raman intensity of 4H-SiC is analyzed by developing a polarized Raman theory that quantifies the influences of birefringence and numerical aperture. The theoretical model was verified through angle-resolved Raman experiments on the (0001) surface of a 4H-SiC sample under both vertical and oblique backscattering configurations using a self-built system. The anisotropy of 4H-SiC is more obvious in the HV case than in the HH case under both vertical and oblique backscattering configurations, which were beneficial to the identification of crystal orientation. In addition, the influence of the numerical aperture on the Raman measurement of silicon carbide is not negligible. This work is helpful for analyses of the crystallographic anisotropy, Raman tensor calibration, stress/strain measurement, and performance modification of 4H-SiC based on angle-resolved in-axis/off-axis polarized Raman spectroscopy.