Crystal Plasticity with Micromorphic Regularization in Assessing Scale Dependent Deformation of Polycrystalline Doped Copper Alloys
Abstract
:1. Introduction
2. Materials and Methods
Crystal Plasticity Modeling
3. Results and Discussion
3.1. Material Model Parameters
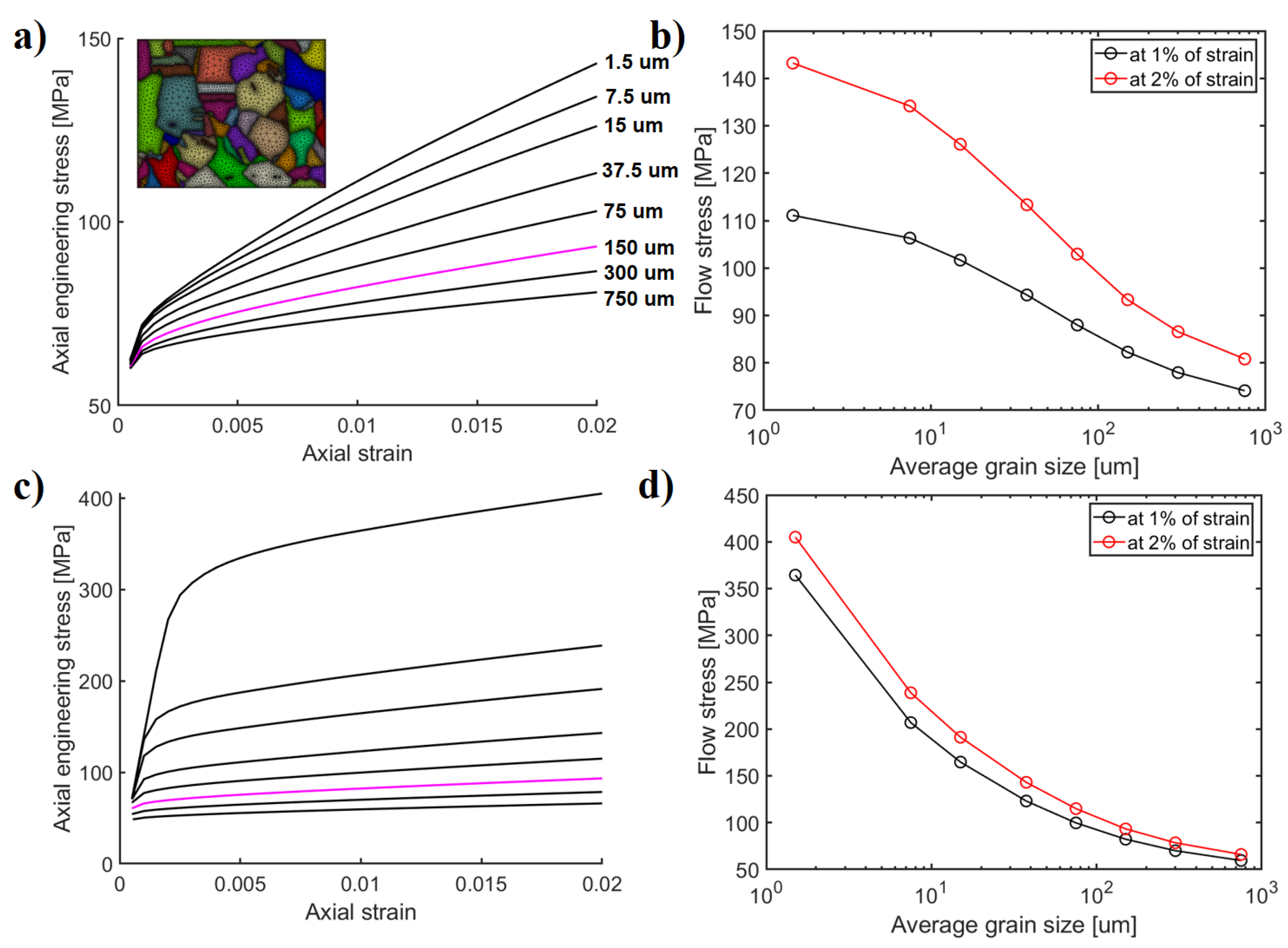
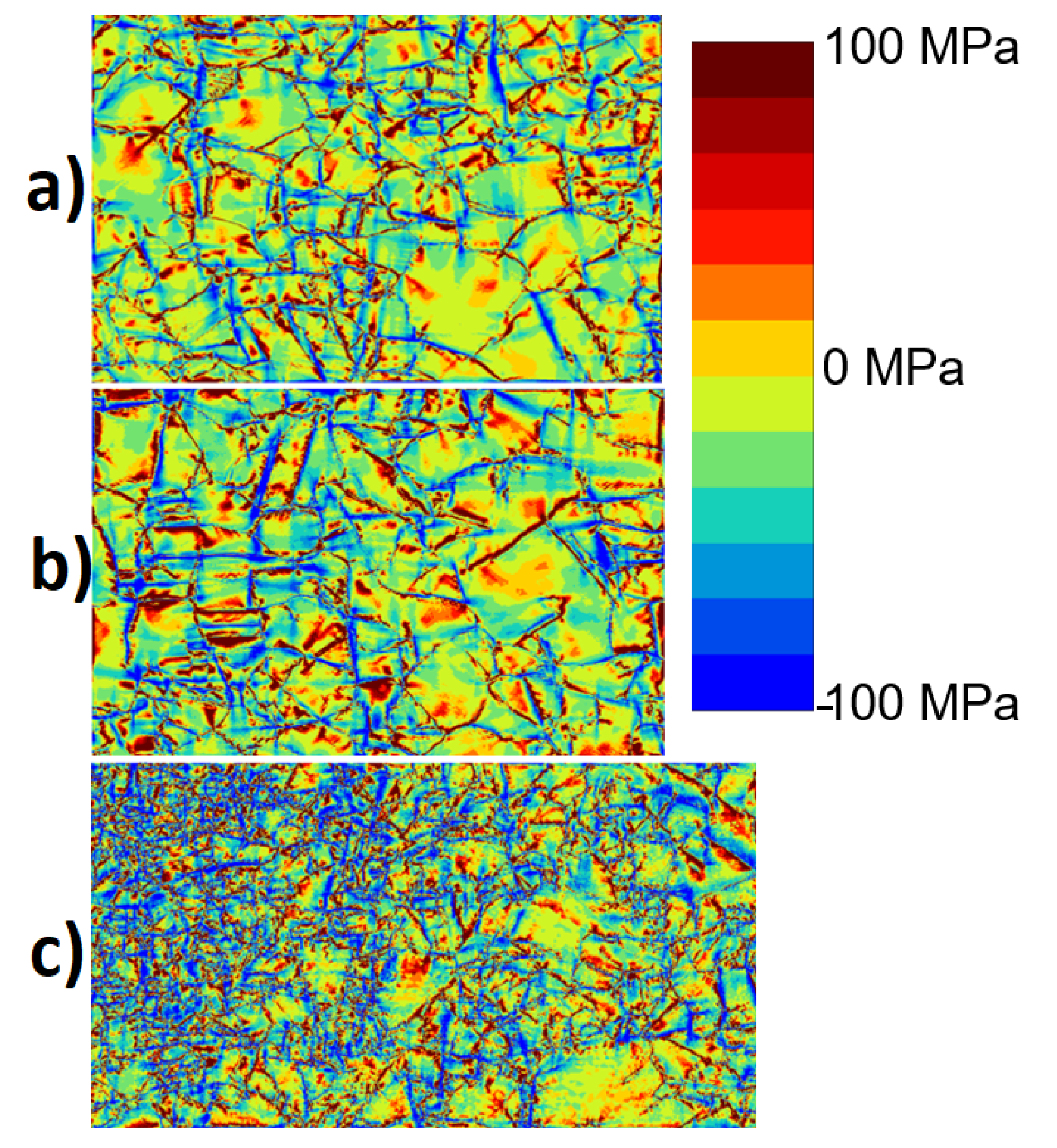
3.2. Model Scaling Effect
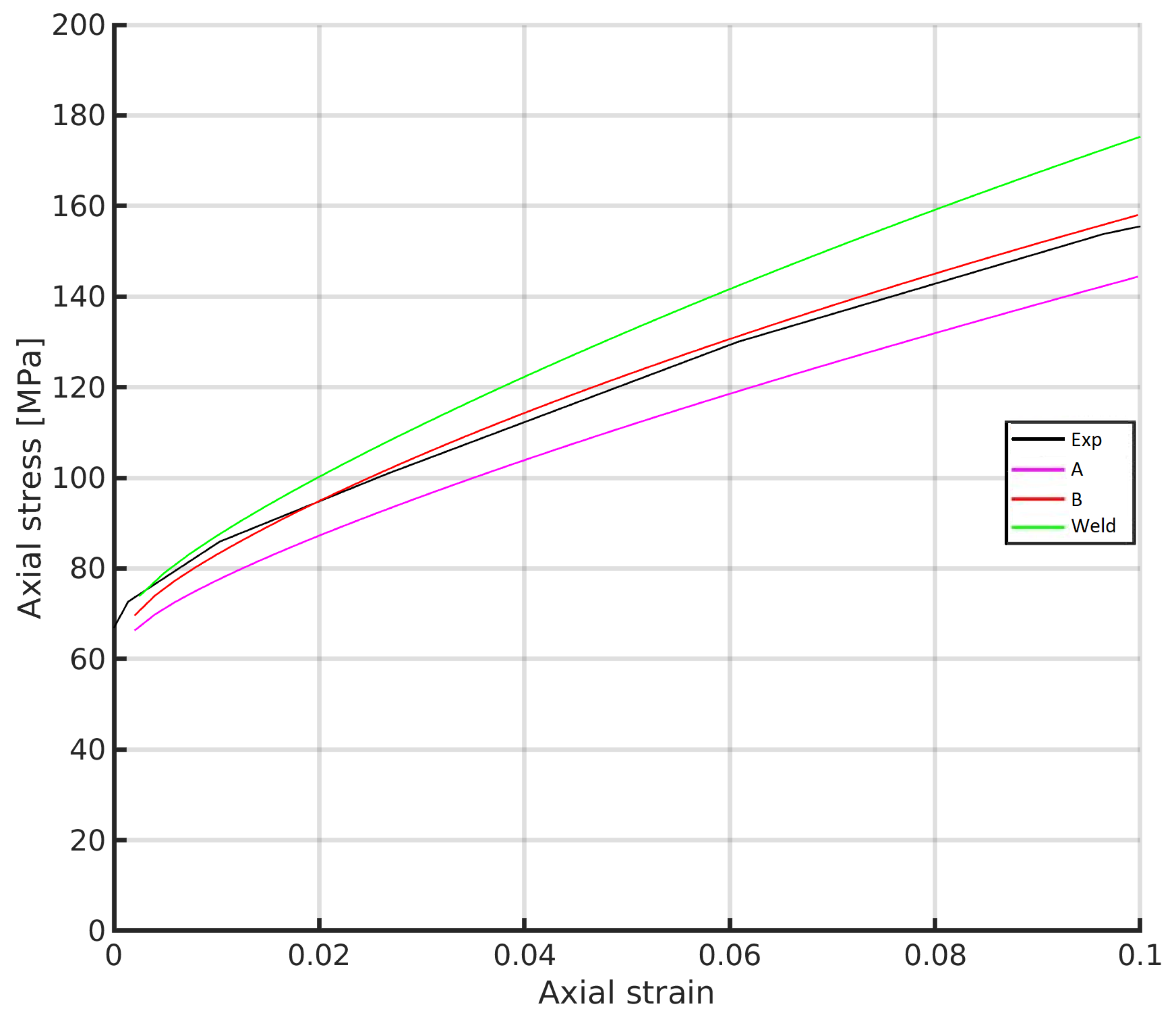
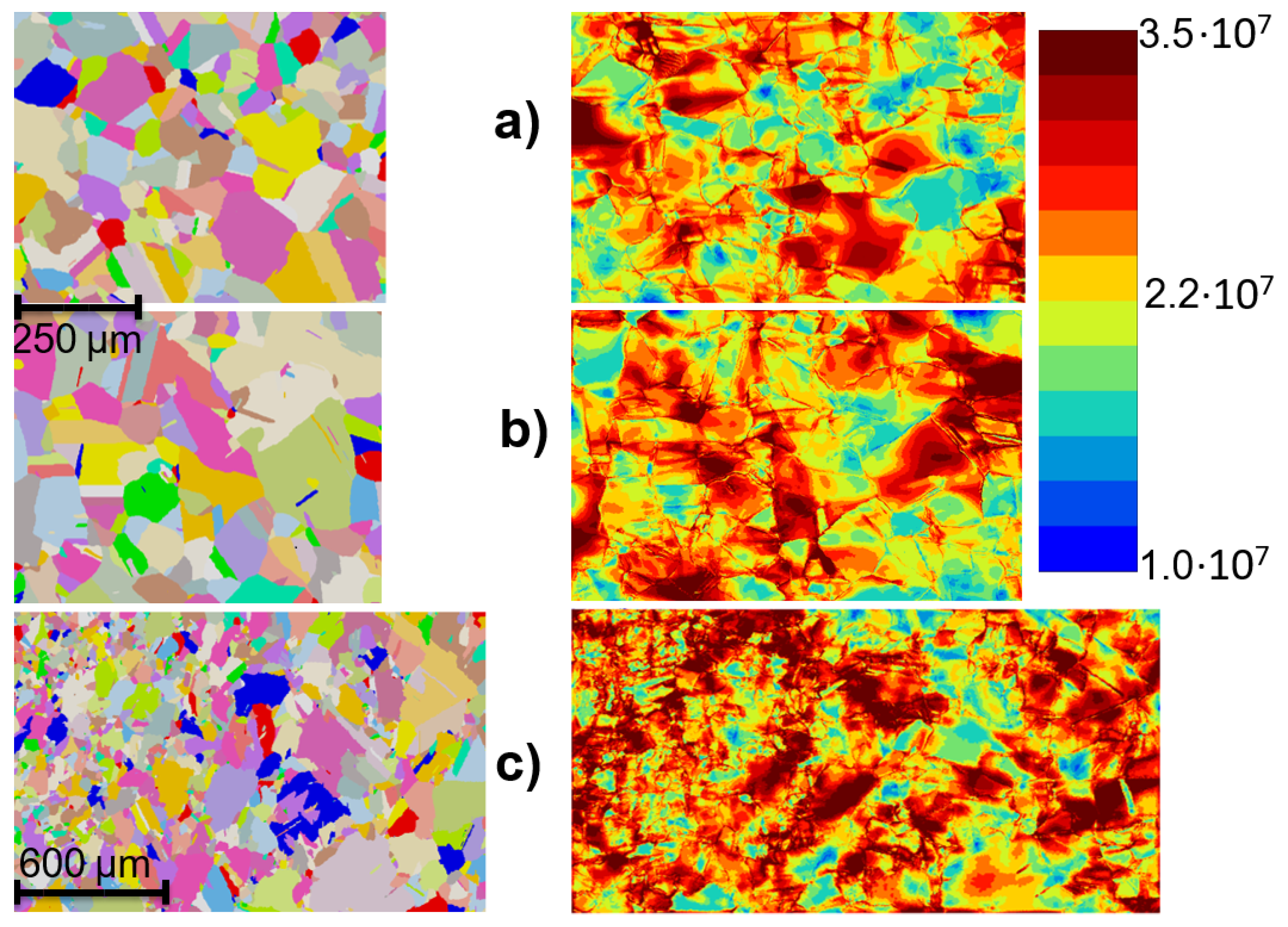
3.3. Simulation of Copper Canister Microstructure Deformation
4. Conclusions
- Various length-scale related hardening responses can be achieved with the reduced micromorphic model which is akin to strain gradient models. Significant differences occur with respect to the resulting grain size dependencies. A typical tanh-shaped grain size dependency is obtained with saturation of the hardening at the extreme ends of grain sizes. Intrinsic length-scale then can be adjusted according to the Hall-Petch tanh curvature when the necessary experimental or multiscale modeling data is available. If the Hall-Petch yield offset is used, the dislocation slip based hardening coming from the length-scale model is masked and the grain size dependent curve resembles a typical square root dependency.
- The modeling approach is usable to investigate grain size dependent plasticity in copper alloys of the overpack with heterogeneous grain distribution in the microstructures. Strain localization is controlled with the model by a regularization placed over the plastic slip. The model can produce length-scale dependent plasticity in the range of the typical grain sizes for the material. The greatest hardening accumulates near grain boundaries where dislocation pile-ups are generally expected, and small grains produce further pronounced intra-grain hardening associated with the local spreading of gradient enhanced hardening. The model is computationally robust; however, the limiting feature is that the hardening is introduced mainly as a source of enhanced isotropic hardening in the present context. It is possible to derive a variant to describe more closely kinematic hardening effects [15,18,26].
- Three polycrystalline microstructural aggregates were simulated which represent different sections of the copper overpack: (i) The cylindrical part of the canister (A), (ii) the lid of the canister (B) and (iii) the welded zone. The hardening response of the cylindrical and lid regions is quite similar, but the lid contains more small grains that increase strain hardening potential. The welded microstructure has the greatest tendency to develop higher local stresses and distinctive strain localization networks throughout the microstructure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Posiva. Safety Case for the Disposal of Spent Nuclear Fuel at Olkiluoto—Description of the Disposal System; Posiva: Eurajoki, Finland, 2012. [Google Scholar]
- Uniaxial and Multiaxial Creep Testing of Copper. SKIReport-2003:06; 2003. Available online: https://www.osti.gov/etdeweb/servlets/purl/20452367 (accessed on 5 May 2021).
- Material Integrity of Welded Copper Overpack—Final Report 2011. VTT 2011, VTT-R-01384-12. 2011. Available online: https://www.vttresearch.com/sites/default/files/julkaisut/muut/2012/VTT-R-01384-12.pdf (accessed on 1 May 2021).
- Holmström, S.; Rantala, J.; Laukkanen, A.; Kolari, K.; Keinänen, H.; Lehtinen, O. Modeling and Verification of Creep Strain and Exhaustion in a Welded Steam Mixer. J. Press. Vessel Technol. 2009, 131, 061405. [Google Scholar] [CrossRef]
- Auerkari, P.; Salonen, J.; Holmström, S.; Laukkanen, A.; Rantala, J.; Nikkarila, R. Creep damage and long term life modelling of an X20 steam line component. Eng. Fail. Anal. 2013, 35, 508–515, Special Issue on ICEFA V—Part 1. [Google Scholar] [CrossRef]
- Monnet, G.; Mai, C. Multiscale modeling of crystal plasticity in steels: Prediction of irradiation hardening. J. Nucl. Mater. 2019, 514, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Fleck, N.; Hutchinson, J. Strain gradient plasticity. Adv. Appl. Mech. 1997, 33, 296–361. [Google Scholar]
- Kocks, U.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Acharya, A.; Bassani, J. Lattice incompatibility and a gradient theory of crystal plasticity. Acta Mater. 2000, 47, 1565–1595. [Google Scholar] [CrossRef]
- Gurtin, M.E. A gradient theory of single-crystal viscoplasticity that accounts for geometrically necessary dislocations. J. Mech. Phys. Solids 2002, 50, 5–32. [Google Scholar] [CrossRef]
- Rys, M.; Forest, S.; Petryk, H. A micromorphic crystal plasticity model with the gradient-enhanced incremental hardening law. Int. J. Plast. 2020, 128, 102655. [Google Scholar] [CrossRef]
- Eringen, A.; Suhubi, E. Nonlinear theory of simple micro-elastic solids—I. Int. J. Eng. Sci. 1964, 2, 189–203. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Rational Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Forest, S.; Mayeur, J.R.; Mcdowell, D.L. Micromorphic Crystal Plasticity. In Handbook of Nonlocal Continuum Mechanics for Materials and Structures; Voyiadjis, G., Ed.; Springer: Cham, Switzerland, 2018; pp. 1–44. [Google Scholar] [CrossRef]
- Lindroos, M.; Laukkanen, A.; Andersson, T.; Vaara, J.; Mäntylä, A.; Frondelius, T. Micromechanical modeling of short crack nucleation and growth in high cycle fatigue of martensitic microstructures. Comput. Mater. Sci. 2019, 170, 109185. [Google Scholar] [CrossRef]
- Wulfinghoff, S.; Böhlke, T. Equivalent plastic strain gradient enhancement of single crystal plasticity: Theory and numerics. Proc. R. Soc. A 2012, 468, 2682–2703. [Google Scholar] [CrossRef] [Green Version]
- Ling, C.; Forest, S.; Besson, J.; Tanguy, B.; Latourte, F. A reduced micromorphic single crystal plasticity model at finite deformations. Application to strain localization and void growth in ductile metals. Int. J. Solids Struct. 2018, 134, 143–169. [Google Scholar] [CrossRef]
- Scherer, J.M.; Besson, J.; Forest, S.; Hure, J.; Tanguy, B. Strain gradient crystal plasticity with evolving length scale: Application to voided irradiated materials. Eur. J. Mech. A 2019, 77, 103768. [Google Scholar] [CrossRef] [Green Version]
- Besson, J.; Foerch, R. Object-oriented programming applied to the finite element method part I. general concepts. Rev. Eur. Des Eléments Finis 1998, 7, 535–566. [Google Scholar] [CrossRef]
- Z–Set Package. Non-Linear Material & Structure Analysis Suite. 2013. Available online: www.zset-software.com (accessed on 1 May 2021).
- Scherer, J.M.; Phalke, V.; Besson, J.; Forest, S.; Hure, J.; Tanguy, B. Lagrange multiplier based vs micromorphic gradient-enhanced rate-(in) dependent crystal plasticity modelling and simulation. Comput. Methods Appl. Mech. Eng. 2020, 372, 113426. [Google Scholar] [CrossRef]
- Forest, S. Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech. 2009, 135, 117–131. [Google Scholar] [CrossRef]
- Sandström, R.; Hallgren, J.; Burman, G. Stress Strain Flow Curves for Cu-OFP; Technical Report, SKB Rapport R-09-14; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2009. [Google Scholar]
- Rassoulinejad-Mousavi, S.; Mao, Y.; Zhang, Y. Evaluation of copper, aluminum, and nickel interatomic potentials on predicting the elastic properties. J. Appl. Phys. 2016, 119, 244304. [Google Scholar] [CrossRef]
- Cordero, N.; Forest, S.; Busso, E. Micromorphic modelling of grain size effects in metal polycrystals. Ges. Angew. Math. Mech. 2013, 36, 186–202. [Google Scholar] [CrossRef]
- Scherer, J.M.; Hure, J. A size-dependent ductile fracture model: Constitutive equations, numerical implementation and validation. Eur. J. Mech. A 2019, 76, 135–145. [Google Scholar] [CrossRef] [Green Version]
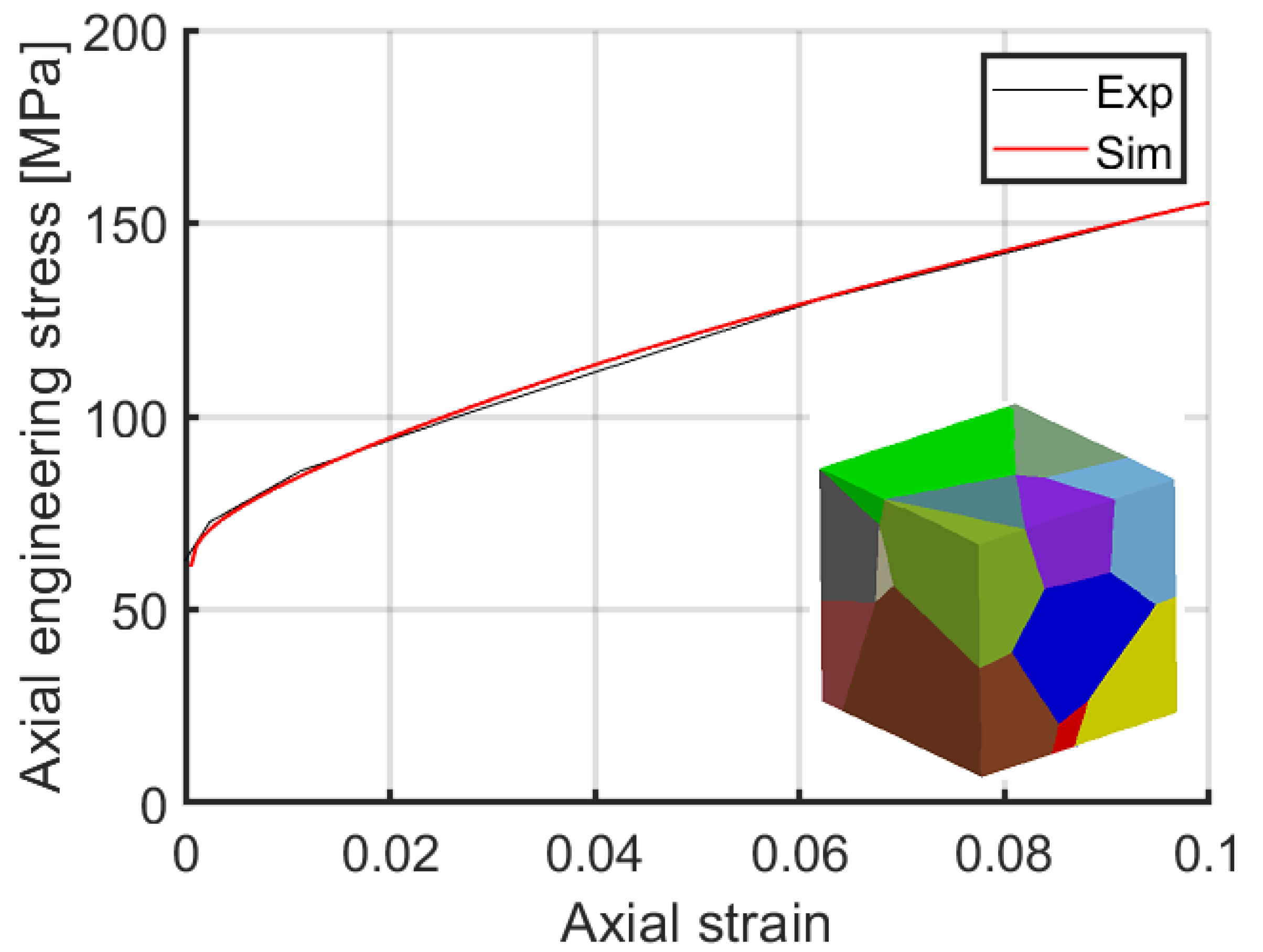

| Elasticity | ||
|---|---|---|
| Elastic constants [GPa] | ||
| Reference [25] | ||
| = 75.4 | ||
| Shear modulus [GPa] | = 42.5 | |
| Reference [24] | ||
| Plasticity | ||
| Slip parameters | ||
| Viscous parameter | K [MPa·s] | 3.0 |
| Strain rate parameter | N | 10.0 |
| Interaction slip-slip | – () | 0.124; 0.124; 0.625; 0.137; 0.122; 0.07 |
| Hall-Petch coefficient | [MPa ] | |
| Effective grain size | d [m] | 150.0 or variable |
| Initial dislocation density | [m] | |
| Dislocation obstacles | 130.0 | |
| Dislocation annihilation | 10.0 | |
| Length of Burgers vector | [m] | |
| Gradient penalty | [MPa] | 10,000.0 |
| Gradient parameter | A [MPa·mm] | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindroos, M.; Andersson, T.; Metsäjoki, J.; Laukkanen, A. Crystal Plasticity with Micromorphic Regularization in Assessing Scale Dependent Deformation of Polycrystalline Doped Copper Alloys. Crystals 2021, 11, 994. https://doi.org/10.3390/cryst11080994
Lindroos M, Andersson T, Metsäjoki J, Laukkanen A. Crystal Plasticity with Micromorphic Regularization in Assessing Scale Dependent Deformation of Polycrystalline Doped Copper Alloys. Crystals. 2021; 11(8):994. https://doi.org/10.3390/cryst11080994
Chicago/Turabian StyleLindroos, Matti, Tom Andersson, Jarkko Metsäjoki, and Anssi Laukkanen. 2021. "Crystal Plasticity with Micromorphic Regularization in Assessing Scale Dependent Deformation of Polycrystalline Doped Copper Alloys" Crystals 11, no. 8: 994. https://doi.org/10.3390/cryst11080994
APA StyleLindroos, M., Andersson, T., Metsäjoki, J., & Laukkanen, A. (2021). Crystal Plasticity with Micromorphic Regularization in Assessing Scale Dependent Deformation of Polycrystalline Doped Copper Alloys. Crystals, 11(8), 994. https://doi.org/10.3390/cryst11080994







