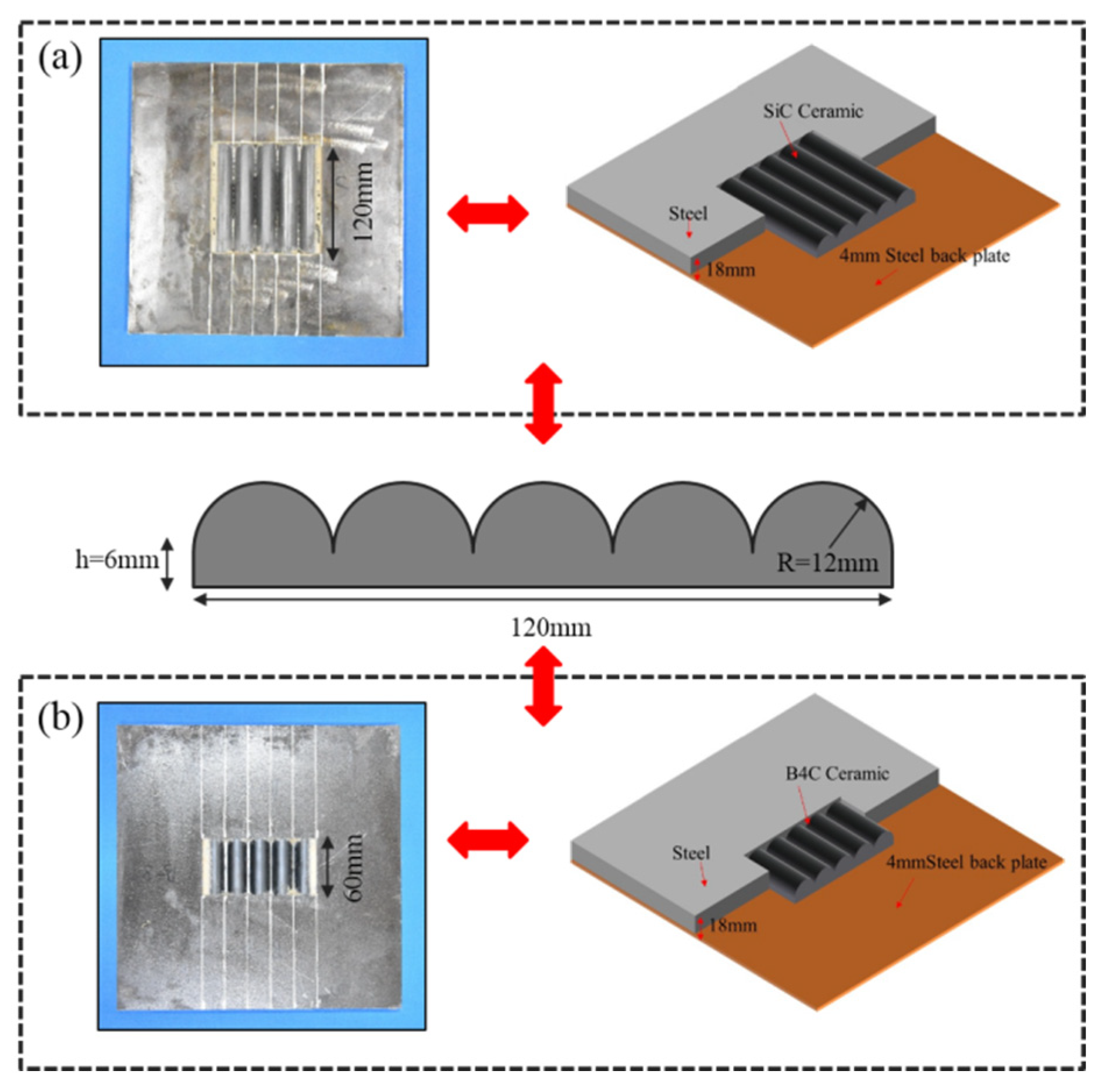
1. Introduction
A lightweight and high-performance armor protection structure has always been an important goal of research on modern protection technology, as its lightweight and high ballistic performance can help ensure the mobility of military weapons, while reaching the protection goal [
1,
2]. Ceramic materials have lower densities than metal materials, as well as high hardness and compressive strength and are widely used in lightweight and high-performance armor [
3,
4,
5]. On the other hand, because of the brittleness and low tensile strength of ceramics, they cannot absorb a large amount of energy in the penetration process. So, in practical applications, ceramic is usually used as the front plate and metal or fiber-reinforced composite as the back plate, so that ceramic/metal or ceramic/composite material armor can be developed with improved ballistic performance [
6]. In the process of projectile penetrating ceramic composite armor, the ceramic material first blunts and erodes the projectile to dissipate energy, and then the composite back plate absorbs the remaining kinetic energy to prevent projectile penetration [
7,
8]. Therefore, ceramic composite armor has a wide range of applications because of its high protection coefficient and good ballistic performance.
The conventional ceramic composite armor has good anti-penetration performance, but as projectiles have increasingly stronger penetration capabilities, to achieve the protection goal, the armor needs to have a larger mass and size. In practice, the ballistic impact on the armor is not perpendicular to its surface [
9]. Therefore, researchers have carried out extensive research on the oblique penetration into the ceramic composite armor. It is found that when the projectile penetrates the ceramic composite armor with a non-ideal attitude, the projectile axis deviates from its initial impact angle under the action of the deflection moment because the axis of the projectile does not coincide with the normal line of the ceramic plate [
10]. If the penetration angle keeps increasing, projectile ricochet may happen. In addition, the increase in penetration angle also leads to the increase in the effective target thickness during projectile penetration, and projectile deflection and yaw occur, making the penetration path of the projectile longer. The longer the interaction between the projectile and the ceramic armor lasts, the greater the erosion of the projectile [
11] and the break-up degree of the ceramic [
12], resulting in more kinetic energy dissipation [
13]. In the study on the oblique penetration of the long-rod projectile into the ceramic composite armor, it has been also found that oblique penetration makes the dwell time of the long-rod projectile on the interface longer compared with vertical penetration [
14]. These factors finally lead to a faster decline in projectile velocity [
15], a reduction in penetration depth [
16], an increase in the ballistic limit of the armor, and a significant improvement in the anti-penetration performance under the condition of oblique penetration into the ceramic composite armor.
In practical applications, such as personal protective equipment and other usage scenarios with space limitations, when the conditions do not allow the ceramic composite armor to be placed obliquely, by designing specially shaped ceramics to cover the armor surface [
17] or be set inside the armor [
18], the nominal normal penetration can be transformed into the actual local oblique penetration, penetration with an angle of attack or a combination of the two.
In terms of realizing the ceramic slope, S. Stanislawek [
19] designed a pyramidal ceramic armor. The results showed that when the pyramids had large dimensions compared with the projectile and the impact point of the projectile was situated on the pyramid side wall, projectile turning could be especially observed, but the energy dissipation capacity of the composite armor was weaker than that of the homogeneous ceramic composite armor with equal mass. In addition, there was an obvious weak point where the pyramids adjoined, and the pyramid top was the tip of the inclined section that should be avoided, as pointed out in Ref. [
15]. Based on Cohen. M’s patent [
20], W. L. Liu [
21] carried out a study on a specially shaped ceramic composite armor with a hemispherical top and a cylindrical lower part. Compared with planar ceramics, closely arranged ceramic cylinders can transfer energy to the surrounding ceramic cylinders, and can also greatly dissipate the projectile’s energy through break-up. However, it is obvious that with such a design, gaps exist between the adjacent ceramic cylinders, which may lead to anti-penetration performance reduction. J. M. Chen [
22] improved the above-mentioned specially shaped ceramics by cutting the congruent circles of the cylinder into regular hexagons, so that there can be no gap between each ceramic unit. However, this also brings more seams to the whole composite armor, and the decreased ballistic performance at the seams leads to more weak areas in the improved protective structure. The positive side of the above structure is that, due to the included angle between the projectile and the ceramic surface, the projectile is subject to the longitudinal and lateral resistances that unevenly vary in size and direction. This leads to ballistic deviation, serious deformation and damage to the projectile, thus improving the ballistic performance of the ceramic plate. M. Aydin [
23] and R.Z. Shao [
24] proposed a protective structure using ceramic balls, which provide a large number of slopes. Unlike the fixed-shaped ceramics, the reason for the deflection, yaw and fracture of the projectile against this type of ceramic armor is the rotation, movement and brittle fracture of the ceramic balls under impact loading. In addition, under this concept, the ceramic balls that break after each impact will soon be replaced by the adjacent new balls. Therefore, the armor can continuously resist multiple rounds of impact loads, without removing the damaged ceramic balls. The authors called this armor design “self-healing armor”.
Based on the advantages and disadvantages of the above-mentioned specially shaped ceramics, this paper proposes a ceramic composite armor, which is mainly divided into the following two parts: specially shaped ceramic and metal back plate. Through ballistic impact experiments combined with FEM (finite element method) and SPH (smooth particle hydrodynamics) numerical calculations, the anti-penetration performance of the composite armor structure against the 12.7 mm API projectile is mainly studied; at the same time, the penetration and deflection processes of the projectile, the deformation and failure mode of the metal back plate are analyzed.
3. Results and Analysis
3.1. Analysis of Penetration Process
In order to better reveal the penetration process of the 12.7 mm API projectile into the ceramic composite armor, the penetration process of the projectile body under working condition 11 (
η = 0.5) is analyzed.
Figure 11 shows the velocity–time–history curve of the projectile. For the convenience of analysis, the lateral and vertical acceleration time–history curves of the projectile and three typical process pictures are also added in the velocity–time–history curve. According to
Figure 11, the penetration process can be divided into the following four stages: asymmetric erosion of the projectile, ceramic cone squeezing movement, back plate failure and projectile exit.
In the asymmetric erosion stage, when the projectile hits the ceramic, the tip part of the projectile head rapidly breaks, and the ogive nose head characteristics of the projectile body gradually disappear. At the same time, due to the semi-cylindrical surface of the ceramic, the erosion failure of the projectile is asymmetric, the length of the projectile is greatly eroded, and the velocity of the projectile decreases greatly. The projectile penetrates further into the ceramic, and cracks and fragments appear in the ceramic and form ceramic cones. During the formation of ceramic cones, the vertical force of the projectile core increases sharply. At this stage, the back plate has not been squeezed by the ceramic cone, and the back plate almost has no deformation. The duration of this stage is denoted as t1.
In the phase of the ceramic cone squeezing movement, the projectile penetrates further into the ceramic interior, and the asymmetric erosion failure degree of the warhead decreases. When the projectile extrudes the ceramic cone, the particles in the cone are accelerated and crushed continuously, and the diameter and thickness of the bottom of the ceramic cone become smaller and smaller. The vertical force of the projectile core starts to decrease. The projectile compresses the ceramic cone and acts on the back plate, which starts to produce local bulging deformation. When the velocity of the remaining ceramic cone reaches the velocity of the projectile, the remaining ceramic crushing cone moves with the projectile at the same speed, and the ceramic cone stops being abrasive on the projectile, and the vertical force of the projectile core continues to decrease. The plastic deformation of the back plate expands, and when the deformation of the plastic bulge area reaches a certain degree, the back plate begins to undergo tensile failure. The duration of this stage is denoted as t2.
In the failure stage of the back plate, the projectile penetrates further. Due to the failure of the back plate, the vertical force of the projectile decreases greatly, and the velocity decrease rate decreases greatly. The left and right sides of the projectile head touch the back plate successively. At this time, the projectile has a large deflection, and the contact area between the right side of the projectile and the back plate is large, so that the velocity of the projectile decreases and the “secondary deceleration” begins. The duration of this phase is denoted as t3.
In the phase of projectile exit, after the projectile exits out of the back plate, the attitude of the projectile is greatly deflected compared with the incident, and the velocity direction of the projectile is also changed.
When the deviation degree of the impact point changes, the penetration process will be partially different. When the deviation of the impact point is close to 0 or 1, the degree of asymmetric erosion in the first stage of the penetration process will be significantly reduced. As a result, the attitude deflection of the projectile is small during the penetration process, and the secondary deceleration process is not obvious during the penetration process of the projectile. The whole penetration process is similar to that of homogeneous ceramic composite armor.
The projectile deflection process in this study is similar to that reported in the literature [
27], but in the process of projectile penetration, due to the ogive nose of the projectile head, the contact area between the projectile head and the ceramic is large at the initial moment when the projectile hits the ceramic. This allows the projectile to deflect slightly more than the flat-ended rod projectile in the first stage. In the next penetration stage, the rapid erosion failure oval head did not play a significant role. In addition, because the 12.7 mm API projectile has a long body and a relatively low velocity, the contact area between the projectile and the back plate was large for a long time in the failure stage of the back plate. As a result, the negative angular acceleration of the projectile at this stage was large, the angular velocity of the projectile decreased to a negative value, the deflection angle of the projectile decreased to 0, and then the inverse direction increased.
3.2. Backplate Failure Mode Analysis
As the 12.7 mm API projectile penetrates the ceramic part, the geometric characteristics of the ogive nose of the projectile have been completely destroyed, and the damaged nose becomes similar to that of the flat-nosed projectile. However, during the projectile penetration into the semi-cylindrical ceramic composite armor, the ceramic in front of the projectile is broken and a ceramic cone is formed; the projectile squeezes the ceramic cone to move forward, causing bulging deformation in a large area of the back plate around the projectile nose. Such an impact response is similar to that of an ogive-nosed projectile perforating a thin plate armor at a low velocity. During the penetration, at the impact center, the tensile deformation of the back plate increases sharply as it is squeezed by the projectile and the broken ceramic cone, so necking occurs, and cracks are generated and gradually expand to form petals. The projectile and the broken ceramic cone continue to press forward, and the petals bend and turn outward, forming the dishing deformation-petaling failure (
Figure 12). If the projectile does not perforate the back plate, the back plate displays asymmetric bulging-dishing deformation (
Figure 13).
In the working conditions where the projectile attitude and trajectory apparently change during penetration, the forces on the broken ceramic cone and the deformation area of the back plate bulge are obviously asymmetric. Meanwhile, due to the large projectile deflection, the breach shape is elliptical. The long axis direction of the ellipse is consistent with the axis direction of the projectile, and petals appear on both sides of the elliptical breaches (
Figure 14). Taking working condition 11 as an example, the failure mode is analyzed as follows. When the projectile perforates and exits the back plate, the projectile first hits one side of the back plate obliquely, and further moves in this direction, resulting in a strip crack in the back plate in the direction parallel to the
Z-axis (
Figure 15 (T = 75 µs)), and the crack keeps expanding at both ends. When the crack expands to a certain degree, the projectile squeezes the back plate on the side of the crack (
Figure 15 (T = 88 µs)), making the petals on one side of the back plate higher, whose width is roughly equal to that of the projectile, but less than the length of the original strip crack. Then, two smaller cracks appear near the short axis of the ellipse (
Figure 15 (T = 114 µs)). When one side of the projectile tail hits the other side of the back plate, the petals on the other side also become higher. However, on this side, the projectile moves in the direction of gradually moving away from the petals; both the height and size of the petals on the projectile tail side are smaller than those on the nose side (
Figure 15 (T = 194 µs)).
In the working conditions where the projectile attitude and trajectory change little during penetration, the petals on the back plate appear more evenly, the breach shape is relatively regular, and the petal height is roughly the same (
Figure 16). Taking working condition 17 as an example, when petaling failure occurs to the back plate and since there are many ceramic fragments in the front of the projectile and the deflection is small, the back plate is subjected to a relatively uniform force, resulting in a relatively uniform distribution of cracks. As the back plate damage continues along the crack, petals with large areas and good integrity are formed (
Figure 17).
3.3. Influence of Impact Point on Anti-Penetration Performance
The ceramic composite armor designed in this paper has periodic inhomogeneity in the direction perpendicular to the length of the ceramic column, so that the anti-penetration performance of the composite armor will be affected by the change in the impact point. In this section, under the condition that the initial velocity of the projectile is 810 m/s and the ratio of the diameter of the semi-cylindrical ceramic to the core is unchanged, the influence of the impact point on the anti-penetration performance of the semi-cylindrical ceramic composite armor is explored by changing the deviation degree of the impact point.
Figure 18 shows the relationship between the residual projectile velocity
and the impact point deviation degree
. As shown in the figure, with the gradual increase
, the residual velocity
displays an overall decreasing trend first and then increases. For the residual velocity
, the change in impact point leads to the variation in two influencing factors, with the first being (1) ceramic thickness. The influence of the ceramic thickness below the projectile on the residual projectile velocity is mainly reflected in the change in the time
t1 +
t2 from the beginning of projectile penetration to back plate failure, when projectile velocity experiences a significant reduction. The thicker the ceramic, the longer
t1 +
t2, and the greater the velocity reduction. After the back plate is damaged, the velocity reduction rate of the projectile slows down rapidly. In the working conditions with large ceramic thicknesses, when the back plate starts to be damaged, the projectile velocity is smaller than that in the conditions with small ceramic thicknesses, so the projectile and the composite armor have an increased action time, causing greater velocity reductions in the third and fourth stages of penetration than that in the conditions with small thicknesses. Therefore, without considering projectile deflection, the thicker the ceramic below the projectile, the greater the deceleration capability of the composite armor to the projectile. (2) The second influencing factor is the maximum attitude deflection angle
of the projectile. As shown in
Figure 19, with the increase
, the
increases first and then decreases. The change in
mainly affects the projectile’s deceleration process in the third stage. The greater the
, the greater the effect of the back plate on the projectile and the greater the deceleration degree in the third stage. Therefore, with the increase
, although the ceramic material below the projectile decreases gradually, the
in the penetration process gradually increases first, and projectile deceleration in the third stage of penetration is obvious, resulting in the decrease in the residual projectile velocity. When
is further increased and the impact point is gradually close to the seam, the
in during penetration is gradually decreased, and meanwhile, the ceramic material below the projectile is further reduced, so the residual projectile velocity is significantly increased.
In order to reflect the anti-penetration performance of the semi-cylindrical ceramic composite armor more directly, the area of the composite armor is divided according to the different anti-penetration performance. The division criteria are the same as in the literature [
27], and the remaining characteristics of the projectile body are shown in
Table 5, where
is the residual kinetic energy of the projectile with the same initial velocity when penetrating the equivalent homogeneous ceramic composite armor. According to the division criteria and the above residual characteristics of the projectile body, the composite armor can be divided into three areas, whose penetration resistance decreases successively, which are named as the strong protection zone, secondary protection zone, and weak protection zone. The distribution is shown in
Figure 20, accounting for 66.67%, 16.67% and 16.67%, respectively.
3.4. Influence of the Ratio of Semi-Cylindrical Ceramic Diameter to Core Diameter on Anti-Penetration Performance
In order to investigate the effect of the ratio of the semi-cylindrical ceramic diameter to core diameter on the anti-penetration performance, the areal density of the semi-cylindrical ceramic and the initial projectile velocity are left unchanged, and = 0.56, 1.11, 2.22 and 2.78 are used. For the three typical impact points when = 0, 0.5 and 1, a total of twelve working conditions are calculated respectively to study the anti-penetration performance of the semi-cylindrical ceramic composite armor under different semi-cylindrical ceramic diameters.
Figure 21 gives a comparison of the residual velocities of the projectile when penetrating ceramic composite armors with different
values, under the above three impact point conditions. By comparing the residual velocities of the projectile with the same diameter but different impact point deviation degrees
, it can be concluded that when
= 0.56, 1.11, the residual velocity difference under the three typical impact point deviation degrees is relatively small. This is mainly because the semi-cylindrical ceramic diameter is too small; in the first stage of penetration, it does not cause large asymmetric erosion to the projectile, resulting in small projectile deflection during penetration (
Figure 22). In the third stage of penetration, the secondary deceleration of the projectile in the case of
= 0.5 is not apparent.
Regarding the anti-penetration performance of composite armors with different
values, as can be observed from
Figure 21, when
= 0.56, 1.11, the residual velocities under the three typical impact point deviation degrees are slightly less than or slightly greater than the residual velocity
in the case of homogeneous ceramic composite armor with equal areal density, and the projectile attitude deflection angle does not change significantly. So, the semi-cylinder design does not play a positive role in improving the anti-penetration performance of the armor. When
= 2.78, under the same areal density, the distribution of the ceramic material in the X direction is extremely uneven, resulting in the fact that the residual velocities in the case of
= 0, 0.5 are smaller than
, but the residual velocity with
= 1 is much greater than
; meanwhile, the theoretical value of the projectile attitude deflection angle is 0 in this case, which is unfavorable for armor protection. The anti-penetration performance of the ceramic composite armor with
= 2.22 has been described in
Section 3.3. The comprehensive comparison shows that the composite armor with
= 2.22 performs the best in resisting penetration among the designed four types of composite armor with different semi-cylindrical ceramic diameters, under the areal density conditions adopted in this paper.
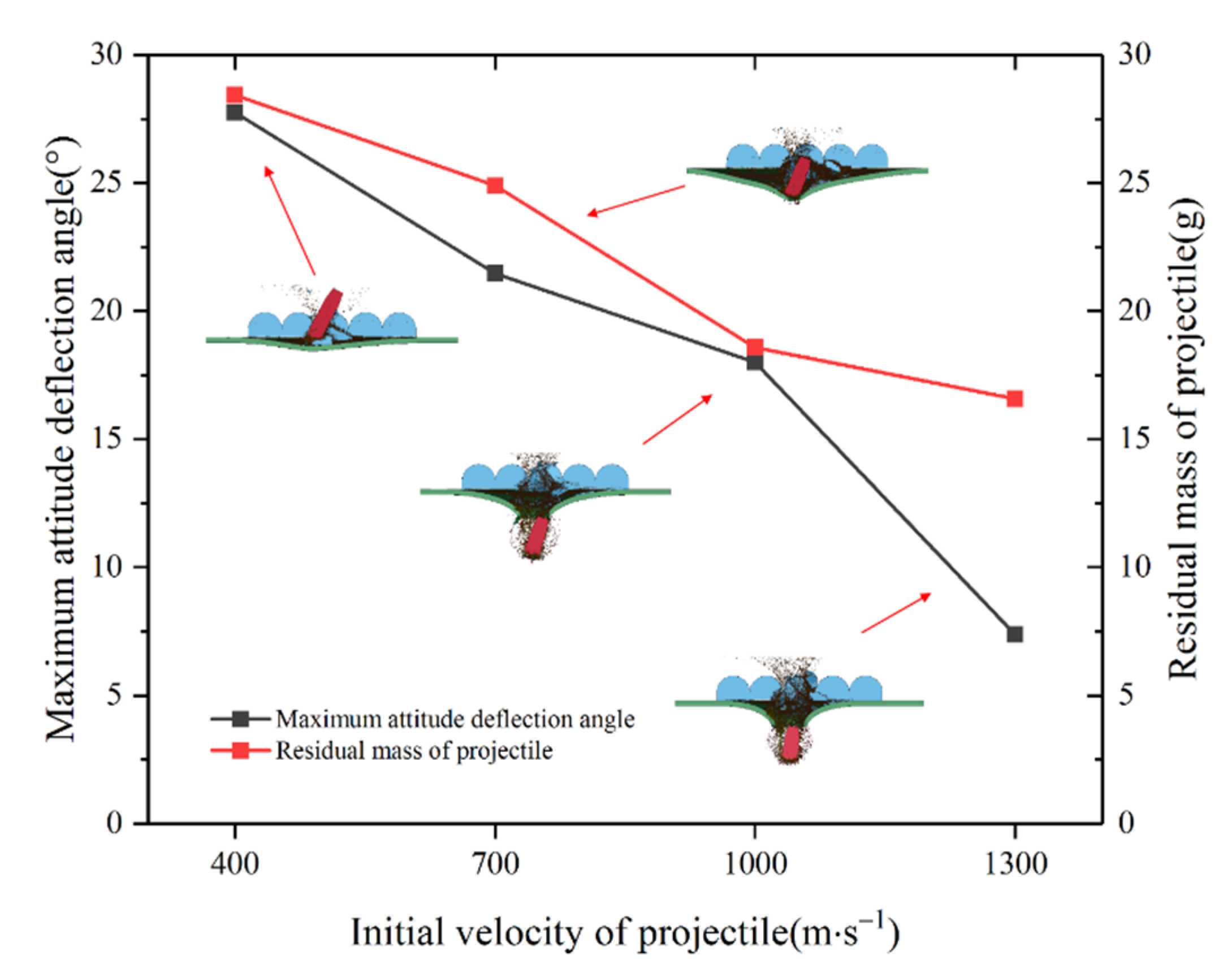
3.5. Influence of Projectile Initial Velocity
In order to explore the anti-penetration performance of the semi-cylindrical ceramic composite armor against the projectile with different initial velocities, the initial velocities of
= 400, 700, 1000 and 1300 m/s are used, while keeping the deviation of the impact point of the projectile at
= 0.5. Under different initial velocity conditions, the maximum attitude deflection angle (before it completely hits the target) and residual mass of the projectile are shown in
Figure 23. As can be observed from the figure, when the initial velocity of the projectile increases, the erosion degree of the projectile increases continuously, and the maximum attitude deflection angle decreases.
The increase in the initial projectile velocity directly leads to the decrease in its target penetration time. Under the working condition of
ν0 = 1000 m/s, at t = 34 µs, the displacement of the center of mass of the projectile is Δy = −3.22 cm.
Figure 24 presents the Y-direction displacement–time curve of the node at the center of mass of the projectile under different initial velocities. As illustrated, Δy = −3.22 cm under the working conditions of
= 700, 1000 and 1300 m/s corresponds to 52 µs, 34 µs and 25 µs, respectively. In the working condition of
= 400 m/s, the deflection of the projectile is too large, which cannot be displayed in the figure, and the corresponding time is t = 112 µs.
Figure 25 shows the penetration under different working conditions with the same displacement of Δy = −3.22 cm. It can be observed from the figure that the projectile nose is near the bottom of the ceramic half cylinder in the three working conditions, i.e., the asymmetric erosion stage of the projectile ends. In other words, due to the increase in the initial projectile velocity, the time required for the projectile to go through this stage is shortened, and the angular acceleration differences between the three working conditions at this stage are small, all within the range of 0~0.008 rad∙µs
−1. Therefore, the time of the projectile in this phase is proportional to its attitude deflection angle, which is 13.74°, 4.42°, 1.37°, and 0.37° in the three conditions. The magnitude of the attitude deflection angle of the projectile has a positive feedback effect on its further deflection. The larger the attitude deflection angle, the stronger the asymmetric action on the projectile, resulting in a further increase in the deflection of the projectile, which further promotes its self-deflection; otherwise, the further deflection will be smaller. Therefore, as the velocity increases, the deflection effect of the projectile decreases continuously. At the same time, the increase in the initial projectile velocity leads to the increase in the projectile-target acting force during the projectile’s penetration into the composite armor, which then results in an increased degree of projectile erosion.
To sum up, the anti-penetration performance of the semi-cylindrical ceramic composite armor against projectiles with different initial velocities shows the following trend: under low initial projectile velocities, the composite armor mainly exhibits large deflection and a relatively small erosion effect on the projectile; as the initial velocity increases, the erosion effect of the composite armor on the projectile gradually increases, while the deflection effect decreases.
4. Conclusions
A semi-cylindrical ceramic composite armor structure is designed in this paper. The processes of projectile penetration deflection and the deformation and failure mode of the back plate are analyzed by the method of combining experiment and numerical calculations. The protective effect of the composite armor with different ratios of semi-cylindrical ceramic to core diameter on 12.7 mm armor-piercing firebombs in different areas and under the condition of equal areal density is mainly explored, and the trend of anti-penetration performance of the composite armor to projectiles with different initial velocities is reported.
(1) The process of the 12.7 mm API projectile penetrating ceramic composite armor can be divided into four stages. Projectile attitude deflection during penetration is mainly attributed to the non-axial force on the projectile, due to the asymmetric erosion of the projectile nose by the specially shaped ceramic and the non-ideal attitude of the projectile when penetrating the back plate. Due to projectile deflection, the projectile velocity experiences a significant secondary decline at the stage of back plate failure. After exiting the target plate, the projectile has an attitude deflection angle and angular velocity.
(2) After the projectile perforated and exited the target plate, dishing deformation-petaling failure occurred at the back plate, which is similar to the deformation/failure mode of an ogive-nosed projectile perforating a thin plate at a low velocity. When the projectile deflected to a certain extent during penetration, the breaches in the back plate showed elliptical shapes of varying degrees, and the size and height of the petals were also significantly different. When the attitude deflection was small, the breaches were regular, and the difference in the size and height of petals was relatively small.
(3) Due to the periodic inhomogeneity of the structure in the direction perpendicular to the length of the semi-cylinder, the impact point of the projectile has a great influence on the anti-penetration performance of the composite armor to 12.7 mm API projectiles. According to the remaining characteristics of the projectile, the composite armor can be divided into strong protection area, secondary protection area and weak protection area, and the proportion of each area is 67.67%, 16.67% and 16.67%, respectively.
(4) For the semi-cylindrical ceramic composite armor designed in this paper, when the ratio of semi-cylindrical ceramic diameter to core diameter is less than 2, it leads to a small deflection during projectile penetration, and the design of the semi-cylinder contributes very little to improving the anti-penetration performance of the composite armor. Among the tested composite armor with = 0.56, 1.11, 2.22 and 2.78, the armor with = 2.22 has the best anti-penetration performance.
(5) The anti-penetration performance of the semi-cylindrical ceramic composite armor against projectiles with different initial velocities shows the following trend: under low initial projectile velocities, the composite armor mainly exhibits large deflection and a relatively small erosion effect on the projectile; as the initial velocity increases, the erosion effect of the composite armor on the projectile gradually increases, while the deflection effect decreases.