Abstract
Liquid crystal elastomers are attractive materials featuring promising applications in emerging technologies, but their structure–property relationship has yet to be thoroughly explored. Some mechanical properties of these materials are the focus of this article. Three tensile experiments of monodomain nematic liquid crystal elastomers have been theoretically analyzed using a free energy density expression describing mechanical and orientational deformations and their interaction. As a result, a theoretical relation is obtained that relates the quantities measured in experiments with the elasticity coefficients entering the expression of the free energy density. Five of these elasticity coefficients were estimated for monodomain nematic liquid crystal elastomers with different compositions using available experimental data from the literature.
1. Introduction
Liquid crystal elastomers (LCEs) are complex media that have the elastic properties of traditional elastomers combined with the orientational properties of liquid crystals [1,2,3,4]. Due to their unique mechanical properties, based on the coupling between the director, which defines the macroscopic orientation of the mesogens, and the polymer network, they offer significant application potential. The ability to change their form reversibly in response to particular external stimuli is among their most fascinating characteristics. Given the properties indicated, LCEs have emerged as a viable choice for various applications such as actuators, sensors, artificial muscles, and other intelligent devices in soft robotics and biomedical engineering [5,6,7,8,9,10,11,12,13,14,15,16]. It is also crucial to study their mechanical behavior to manufacture commercial products using this material. Although much theoretical and experimental work has been done in this area, the mechanical properties observed in experiments with these complex media have not been fully studied yet [4,17,18,19,20,21,22,23,24,25,26,27,28].
The beginning of theoretical investigations of the elastic response of liquid crystal polymers was the proposed theory in [29] that incorporates additional terms in the free energy linking the director rotations to the permanent network. As reported in [1,4], the insertion of rigid and anisotropic molecules along a polymeric chain may induce a nematic property in a polymeric sample, which attracted much attention. The density of the free energy of mechanical deformation of nematic liquid crystal elastomers was written in its general form [30,31]. The structure-dependent elastic properties of these materials include elastic anisotropy, spontaneous contraction (elongation) induced by a temperature change, auxeticity, and more. Another interesting feature of the mechanical properties of these materials is the elastic plateau in the stress–strain curve, which was observed when a monodomain nematic elastomer is stretched perpendicularly to the director’s initial direction [4,23,32]. The initial region of the corresponding stress–strain curve (small strain region) represents the response of conventional rubbers. After that, there is a plateau region, where an almost constant stress leads to a significant increase in strain. The characteristic elastic modulus of the plateau region is reduced compared to the moduli of the pre- and post-plateau regions (the latter are also different). Thus, it was clear that elastic constants (Young’s moduli and Poisson’s ratios) for nematic elastomers must depend on the orientational distribution of the director. The temperature variation of Young’s moduli for parallel and perpendicular extensions to the director, and , respectively, as well as the ratio , were reported in [33]. The Young’s moduli, transverse and longitudinal shear moduli, and transverse bulk modulus for different types of nematic liquid crystal elastomer samples with varying azo-dye concentrations have recently been determined experimentally [34]. The present work is the first report on the determination of the five elasticity coefficients entering the expression of the elastic free energy density of these materials written in [35]. First, we describe three simple tensile experiments. Using the mentioned expression of the free energy density for these materials, a system of equations is obtained linking the elasticity coefficients with the strains that can be directly measured in experiments. Then, the corresponding constants were calculated using available experimental data for monodomain nematic LCE samples. In addition, the theoretical constraints for the mechanical behavior of the nematic LCE are also discussed and applied to the elastic constants using available experimental data.
2. Theory
We begin with a brief review of the expression of free energy density of nematic liquid crystal elastomers. As initially proposed by P.G. de Gennes in [2], the total free energy density of this system is composed of three parts: the elastic free energy for uniaxial materials; the Frank free energy related to deformations in the director field, and the coupling terms considering the interaction between mechanical and orientational deformations:
Considering the description of the elastic free energy of the deformed monodomain nematic elastomer in [35], the total free energy density can be written in the following form:
where is the symmetric part of the strain tensor, u is the displacement vector and , n is a unit vector called the director, is the antisymmetric part of the strain tensor, and describes the director rotation given by , is the totally antisymmetric Levi-Civita tensor, are Frank elastic constants, and are nematic-rubber coupling constants that depend on the anisotropy parameter [4]. The elastic part of the free energy density is represented by the first five coefficients, taking into account the symmetry of these materials [35]. These coefficients are related to those given in [2,31] by the following relations:
When the material is in its isotropic phase, the constants , , , and are equal to zero. The comparison of the free energy density for the isotropic case [36] with Equation (2) reveals that and are the μ and λ Lame coefficients, respectively. or μ is known as the shear modulus. Given this, one can express the transverse bulk modulus K with these constants:
The total stress tensor can be obtained by differentiating the total free energy density by the strain tensor
Three experiments are considered to obtain the first five elastic constants () in the free energy expression (2).
The first experiment is a simple extension of the nematic elastomer sample (Figure 1a). The symmetry axis and the nematic director are along the z-axis (nx = ny = 0, nz = 1). The sample is stretched in both directions by applying forces to its ends. These forces operate uniformly over the specimen’s end surfaces, and p denotes the force per unit area. Since the strain is homogenous, that is, uik is constant throughout the body, the stress tensor σik is similarly constant and can thus be derived from the boundary conditions. Because there is no external force on the specimen’s sides, σikSk = 0. So, all of the components σik except σzz are zero since the unit vector S on the side of the specimen is perpendicular to the z-axis. As a result, we get σzkSk = p, or σzz = p on the end surface. Using the total stress tensor expression (5) and the actions described in [37], a system of equations for stress–strain relations has been derived based on geometry of the first experiment. Since, in the experiments, one directly measures the normal strains in x, y, and z directions, it is more convenient to write the relevant equations in the following way:
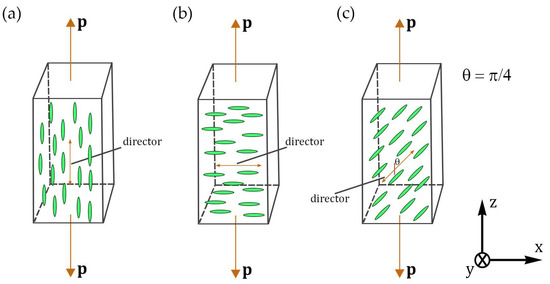
Figure 1.
A schematic depiction of three experiments. (a) The forces are applied along the z-axis parallel to the nematic director. (b) The forces are applied along the z-axis perpendicular to the nematic director. (c) The NLC director forms an angle of 45° with the z-axis (loading direction). The force per unit area is denoted by p.
The free energy coefficients can also be used to determine the main elastic constants by solving the system of equations with the uik components as unknown variables. Accordingly, for Young’s modulus, which is the ratio of tensile stress to strain, we get
where . For Poisson’s ratios, which are the ratios of transverse strain to axial strain, we have
In the second experiment (Figure 1b), the forces are applied perpendicular to the nematic director (nz = ny = 0, nx = 1). Similarly, the required equations can be written as follows:
In this case, the main elastic constants are determined similarly. For Young’s modulus, we obtain
where . The Poisson’s ratios are
The third experiment (Figure 1c) represents the case when the nematic director forms an angle of 45° with the loading direction: ny = 0, nx = nz = . Then, from Equation (5), we can obtain the following equations:
where .
So, based on the measurements of normal strains, one can determine the five elastic constants in the free energy expression (2).
The monodomain nematic elastomers are transversely isotropic media. Notably, one can derive the constraints on elastic constants from the basic principle of positive strain energy density [38]. The following is a summary of these thermodynamic constraints:
These constraints should be satisfied by experimentally obtained values.
3. Application to Azobenzene-Functionalized Liquid Crystal Elastomers
Measurements of the mechanical properties of various monodomain nematic liquid crystal elastomers have been intensively carried out to describe the characteristics of these types of LCEs. The experiments conducted so far are mainly measurements of load (stress–strain) curves. In some cases, when strains along two orthogonal axes have been measured for a particular type of LCE, the strain along the other orthogonal axis has usually been determined from the condition of volume conservation. However, these data are insufficient to calculate the five elasticity coefficients in the free energy density expression. To apply the theoretical approach described above, three experiments for a monodomain nematic liquid crystal elastomer must be performed. A similar complete characterization of the mechanical properties was carried out in [34] for azobenzene-functionalized nematic LCEs. Figure 4 in [34] contains experimental data that can be used to estimate the mentioned elasticity coefficients. For the experiments performed, three films were cut from prepared nematic elastomer samples with a nematic director at 0°, 45°, and 90° relative to the longitudinal direction. The experiments were carried out with a simple setup allowing the measurements of three normal strain components. The complete description of the experimental procedure and setup is described in the paper [34]. It is also important to note that the authors mentioned that their LCE samples exhibit viscoelastic behavior. Unlike conventional liquid crystals, the viscoelastic properties of which have been studied in detail in many works [39,40,41], the dynamics of the viscoelastic response in the case of elastomers need further research, although significant progress has been made in this direction.
In our case, the free energy density was taken in its quadratic form in the theoretical section, and we considered that mechanical deformations are small. Those tests were carried out in the small strain range (the measured strains were in the 0–10% range). We can estimate these five elasticity coefficients for the three geometries from the experimental data, using the strain values for the corresponding stress value and solving the corresponding equations. For example, in the case of the first experiment: , , , ; thus, using Equation (6) for the elastic coefficients, we obtain the following equations:
Similarly, for the second experiment: , , , ; and from Equation (9), we have the following equations:
From Equation (17), the following elastic coefficients can be determined: , , ; in units of MPa, where . Alternatively, the value of can be calculated using Equation (18), which yields 41.95 MPa. Values for the same elastic constant estimated in two ways give fairly comparable results. By using Equation (18), we were able to determine that the constant of the nematic elastomer is 197.5 MPa. As was mentioned above, here, we are considering sufficiently small deformations, so we assume that the direction of the director does not change during the deformation. It means that there is no interaction between mechanical and orientational parts of deformations. We get the following from the obtained system of equations of stress–strain relations for the third experiment by doing some calculations and considering :
where ; ; ; ; ; . Finally, from Equations (19) and (20), we have
In the case of the third experiment (): , , ; then, using the already estimated and constants, we calculated the and constants to be 0.8 and 55.5 MPa, respectively. Table 1 shows the values of the five elasticity coefficients for three different LCE samples. These are the first calculations of coefficients, and we do not exclude that in the case of such complex media, the results obtained for these coefficients may even differ by order of magnitude from one LCE to another because of many factors. First of all, the values of the elastic coefficients will be quite different depending on the material chemistries and procedures used to synthesize those LCEs. As for the future, these materials will be synthesized using the same techniques (with exactly the same conditions) and will become widely available for industrial applications. In that case, the coefficients for different samples will be the same.

Table 1.
Compositions of samples and calculation results.
It is important to note that the elastic constants measured experimentally reasonably satisfy the theoretical inequalities indicated above for transversely isotropic materials (Equations (14)–(16)). To verify the satisfaction of the reciprocity condition (Equation (13)), let us write it in a more convenient way
The constraint (23) is mainly satisfied quite well by the experimental results.
Figure 5 in [34] shows that those LCE samples are practically incompressible. Therefore, the coefficient, which characterizes the compressibility of the sample, is quite large. Since and therefore are always positive in the condition of thermodynamic equilibrium, and here and are negative, the logical theoretical condition for to be positive can be derived from Equation (9):
where is the relative volume change in the second experiment. Thus, the value and the sign of the coefficient critically depend on the volume change during deformation.
4. Conclusions
The primary outcome of the work is that it is the first report on calculating the five elasticity coefficients entering the elastic free energy density expression written in [35] for a monodomain nematic LCE. To achieve this, we first developed a connection between measured strains and elasticity coefficients. We then used the available data from the tensile experiments to estimate the values of those coefficients for three different LCE samples. The theoretical constraints on the elastic constants imposed by the material’s symmetry have also been discussed. The experimentally calculated constants reasonably satisfy those constraints.
Further experiments involving more precise measurements of the elastic constants of nematic liquid crystal elastomers with different compositions and measurements of coupling constants will complete the reported results in the future.
Author Contributions
Conceptualization, R.H.; methodology, R.H.; validation, M.S., G.G. and M.H.; investigation, M.S., G.G. and M.H.; writing—original draft preparation, M.S.; writing—review and editing, R.H., G.G. and M.S.; supervision, R.H.; project administration, R.H.; funding acquisition, R.H. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Science Committee of the Republic of Armenia in the frames of research projects 21AA-1C007 and 21AG-1C088.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All supporting data are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- de Gennes, P.G. Physique moléculaire-réflexions sur un type de polymères nématiques. Comptes Rendus De L’académie Des. Sci. B 1975, 281, 101–103. [Google Scholar]
- de Gennes, P.G. Liquid Crystals of One and Two-Dimensional Order; Helfrich, W., Heppke, G., Eds.; Springer: New York, NY, USA, 1980. [Google Scholar]
- Finkelmann, H.; Koch, H.J.; Rehage, G. Investigations on liquid crystalline polysiloxanes 3, Liquid crystalline elastomers-a new type of liquid crystalline material. Makromol. Chem. Rapid Commun. 1981, 2, 317–322. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Ohm, C.; Brehmer, M.; Zentel, R. Liquid crystalline elastomers as actuators and sensors. Adv. Mater. 2010, 22, 3366–3387. [Google Scholar]
- Guin, T.; Settle, M.J.; Kowalski, B.A.; Auguste, A.D.; Beblo, R.V.; Reich, G.W.; White, T.J. Layered liquid crystal elastomer actuators. Nat. Commun. 2018, 9, 2531. [Google Scholar] [CrossRef]
- Mistry, D.; Traugutt, N.A.; Yu, K.; Yakacki, C.M. Processing and reprocessing liquid crystal elastomer actuators. J. Appl. Phys. 2021, 129, 130901. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, J.; Ikeda, T.; Jiang, L. Bio-inspired liquid crystal actuator materials. J. Mater. Chem. C 2019, 7, 3413–3428. [Google Scholar] [CrossRef]
- Petsch, S.; Rix, R.; Khatri, B.; Schuhladen, S.; Müller, P.; Zentel, R.; Zappe, H. Smart artificial muscle actuators: Liquid crystal elastomers with integrated temperature feedback. Sens. Actuators A Phys. 2015, 231, 44–51. [Google Scholar] [CrossRef]
- Jaggessar, A.; Shahali, H.; Mathew, A.; Yarlagadda, P.K. Bio-mimicking nano and micro-structured surface fabrication for antibacterial properties in medical implants. J. Nanobiotechnol. 2017, 15, 64. [Google Scholar] [CrossRef]
- Schuhladen, S.; Preller, F.; Rix, R.; Petsch, S.; Zentel, R.; Zappe, H. Iris-Like Tunable Aperture Employing Liquid-Crystal Elastomers. Adv. Mater. 2014, 26, 7247–7251. [Google Scholar] [CrossRef]
- Shahsavan, H.; Salili, S.M.; Jákli, A.; Zhao, B. Smart Muscle-Driven Self-Cleaning of Biomimetic Microstructures from Liquid Crystal Elastomers. Adv. Mater. 2015, 27, 6828–6833. [Google Scholar] [CrossRef]
- Montero de Espinosa, L.; Meesorn, W.; Moatsou, D.; Weder, C. Bioinspired Polymer Systems with Stimuli-Responsive Mechanical Properties. Chem. Rev. 2017, 117, 12851–12892. [Google Scholar] [CrossRef] [PubMed]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft Robotics for Chemists. Angew. Chem. Int. Ed. 2011, 50, 1890–1895. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Zhang, J.; Li, H.; Shi, Z.; Meng, Q.; Liu, S.; Chen, J.; Liu, X. Toward Application of Liquid Crystalline Elastomer for Smart Robotics: State of the Art and Challenges. Polymers 2021, 13, 1889. [Google Scholar] [CrossRef] [PubMed]
- Ula, S.W.; Traugutt, N.A.; Volpe, R.H.; Patel, R.R.; Yu, K.; Yakacki, C.M. Liquid crystal elastomers: An introduction and review of emerging technologies. Liq. Cryst. Rev. 2018, 6, 78–107. [Google Scholar] [CrossRef]
- Martinoty, P.; Stein, P.; Finkelmann, H.; Pleiner, H.; Brand, H.R. Mechanical properties of mono-domain side chain nematic elastomers. Eur. Phys. J. E Soft Matter 2004, 14, 311–321. [Google Scholar] [CrossRef]
- Martinoty, P.; Stein, P.; Finkelmann, H.; Pleiner, H.; Brand, H.R. Reply to the commentary by Terentjev EM, Warner M on “Mechanical properties of monodomain side chain nematic elastomers”. Eur. Phys. J. E 2004, 14, 329–332. [Google Scholar] [CrossRef]
- Martinoty, P.; Stein, P.; Finkelmann, H.; Pleiner, H.; Brand, H.R. Reply to the commentary by Stenull O, and Lubensky TC on “Mechanical properties of monodomain side chain nematic elastomers”. Eur. Phys. J. E 2004, 14, 339–340. [Google Scholar] [CrossRef]
- Stenull, O.; Lubensky, T.C. Commentary on “Mechanical properties of monodomain sidechain nematic elastomers” by Martinoty, P.; et al. Eur. Phys. J. E 2004, 14, 333–337. [Google Scholar] [CrossRef]
- Terentjev, E.M.; Warner, M. Commentary on “Mechanical properties of monodomain side chain nematic elastomers” by Martinoty, P., Stein, P., Finkelmann, H., Pleiner, H., Brand, H.R. Eur. Phys. J. E 2004, 14, 323–327. [Google Scholar] [CrossRef]
- Warner, M. New elastic behaviour arising from the unusual constitutive relation of nematic solids. J. Mech Phys. Solids 1999, 47, 1355–1377. [Google Scholar] [CrossRef]
- Mistry, D.; Morgan, P.B.; Clamp, J.H.; Gleeson, H.F. New insights into the nature of semi-soft elasticity and “mechanical-Fréedericksz transitions” in liquid crystal elastomers. Soft Matter 2018, 14, 1301–1310. [Google Scholar] [CrossRef] [PubMed]
- Mistry, D.; Gleeson, H.F. Mechanical deformations of a liquid crystal elastomer at director angles between 0° and 90°: Deducing an empirical model encompassing anisotropic nonlinearity. J. Polym. Sci. B Polym. Phys. 2019, 57, 1367–1377. [Google Scholar] [CrossRef]
- Mistry, D.; Connell, S.D.; Mickthwaite, S.L.; Morgan, P.B.; Clamp, J.H.; Gleeson, H.F. Coincident molecular auxeticity and negative order parameter in a liquid crystal elastomer. Nat. Commun. 2018, 9, 5095. [Google Scholar] [CrossRef] [PubMed]
- Mihai, L.A.; Goriely, A. A plate theory for nematic liquid crystalline solids. J. Mech. Phys. Solids 2020, 144, 104101. [Google Scholar] [CrossRef]
- Mihai, L.A.; Goriely, A. Likely striping in stochastic nematic elastomers. Math. Mech. Solids 2020, 25, 108128652091495. [Google Scholar] [CrossRef]
- Okamoto, S.; Sakurai, S.; Urayama, K. Effect of stretching angle on the stress plateau behavior of main-chain liquid crystal elastomers. Soft Matter 2021, 17, 3128–3136. [Google Scholar] [CrossRef]
- De Gennes, P.G. Possibilites Offertes Par La Reticulation de Polymeres En Presence d’un Cristal Liquide. Phys. Lett. A 1969, 28, 725–726. [Google Scholar] [CrossRef]
- Golubovic, L.; Lubensky, T.C. Nonlinear elasticity of amorphous solids. Phys. Rev. Lett. 1989, 63, 1082. [Google Scholar] [CrossRef] [PubMed]
- Lubensky, T.C.; Mukhopadhyay, R.; Radzihovsky, L.; Xing, X. Symmetries and elasticity of nematic gels. Phys. Rev. E 2002, 66, 011702. [Google Scholar] [CrossRef]
- Dey, S.; Agra-Kooijman, D.M.; Ren, W.; McMullan, P.J.; Griffin, A.C.; Kumar, S. Soft Elasticity in Main Chain Liquid Crystal Elastomers. Crystals 2013, 3, 363–390. [Google Scholar] [CrossRef]
- Finkelmann, H.; Greve, A.; Warner, M. The elastic anisotropy of nematic elastomers. Eur. J. Phys. E 2001, 5, 281. [Google Scholar] [CrossRef]
- Oh, S.W.; Guo, T.; Kuenstler, A.S.; Hayward, R.; Palffy-Muhoray, P.; Zheng, X. Measuring the five elastic constants of a nematic liquid crystal elastomer. Liquid Crystals 2020, 48, 511–520. [Google Scholar] [CrossRef]
- Hakobyan, M.R.; Hakobyan, R.S. Some elastic properties of solid nematics. J. Contemp. Phys. (Armenian Ac. Sci.) 2017, 52, 295–302. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity (Volume 7 of a Course of Theoretical Physics); Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Hovakimyan, M.T.; Sargsyan, M.L.; Hakobyan, R.S.; Hakobyan, M.R. Elastic properties of solid nematics. Mol. Cryst. Liq. Cryst. 2020, 713, 55–64. [Google Scholar] [CrossRef]
- Lempriere, B.M. Poisson’s ratio in orthotropic materials. AIAA J 1968, 6, 2226–2227. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Kröger, M.; Sellers, S. On the Signs of the Leslie Viscosities α2 and α3 for Nematics and Discotic Nematics. Molecular Crystals and Liquid Crystals Science and Technology. Section A. Mol. Cryst. Liq. Cryst. 1997, 293, 17–27. [Google Scholar] [CrossRef]
- Pasechnik, S.V.; Chigrinov, V.G.; Shmeliova, D.V. Liquid Crystals: Viscous and Elastic Properties in Theory and Applications; Wiley: New York, NY, USA, 2009; p. 424. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).