Development of a Computational Fluid Dynamics (CFD) Numerical Approach of Thermoelectric Module for Power Generation
Abstract
:1. Introduction
2. Model Design and Theoretical Background
3. Methodology
3.1. Model Design
3.2. Theoretical Formulations
3.2.1. Governing Equations
3.2.2. Boundary Conditions
3.3. Numerical Approach and Validation
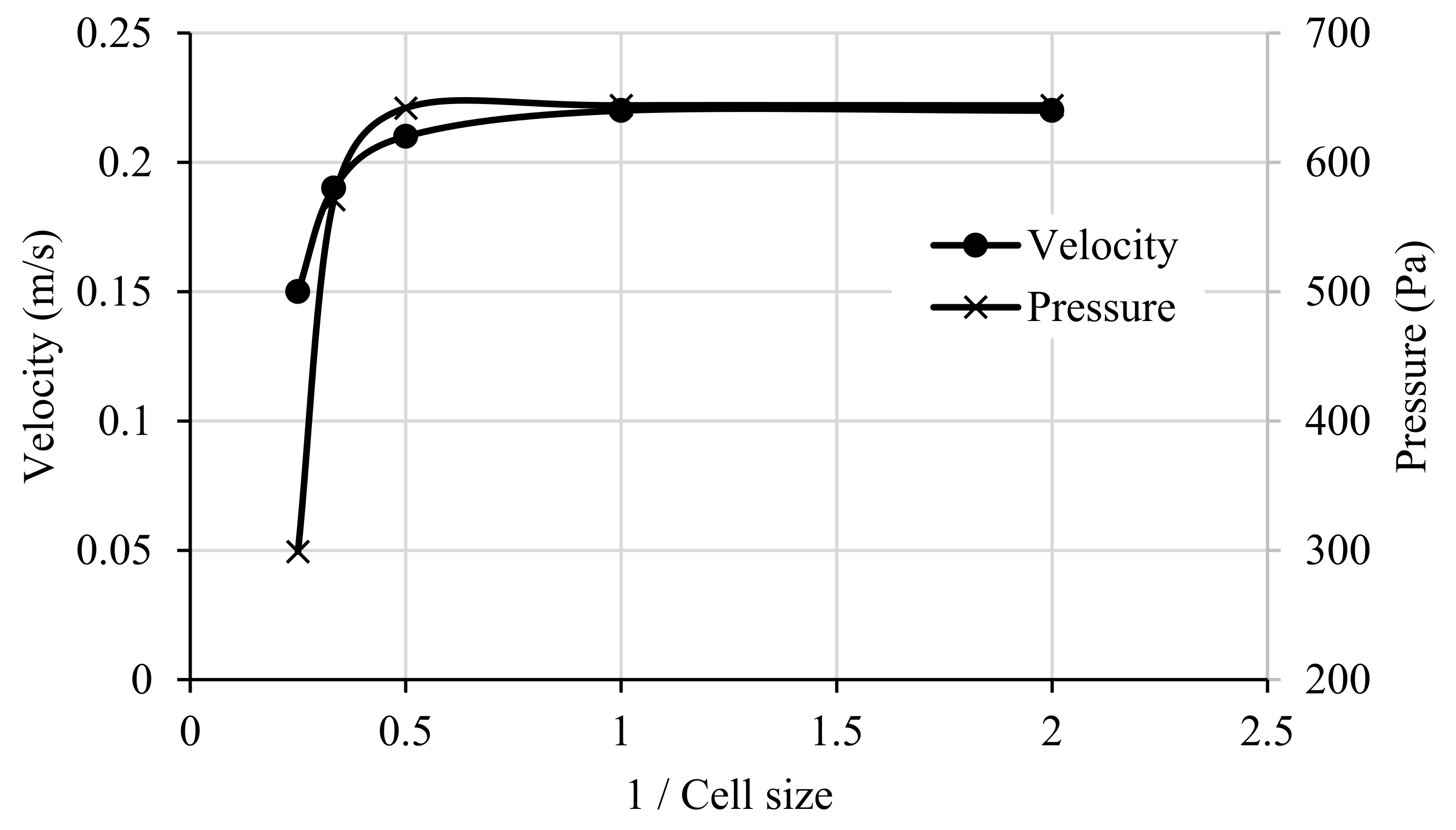
3.3.1. Mesh Study
3.3.2. Model Validation
4. Results and Discussion
4.1. Solar Plate Thickness
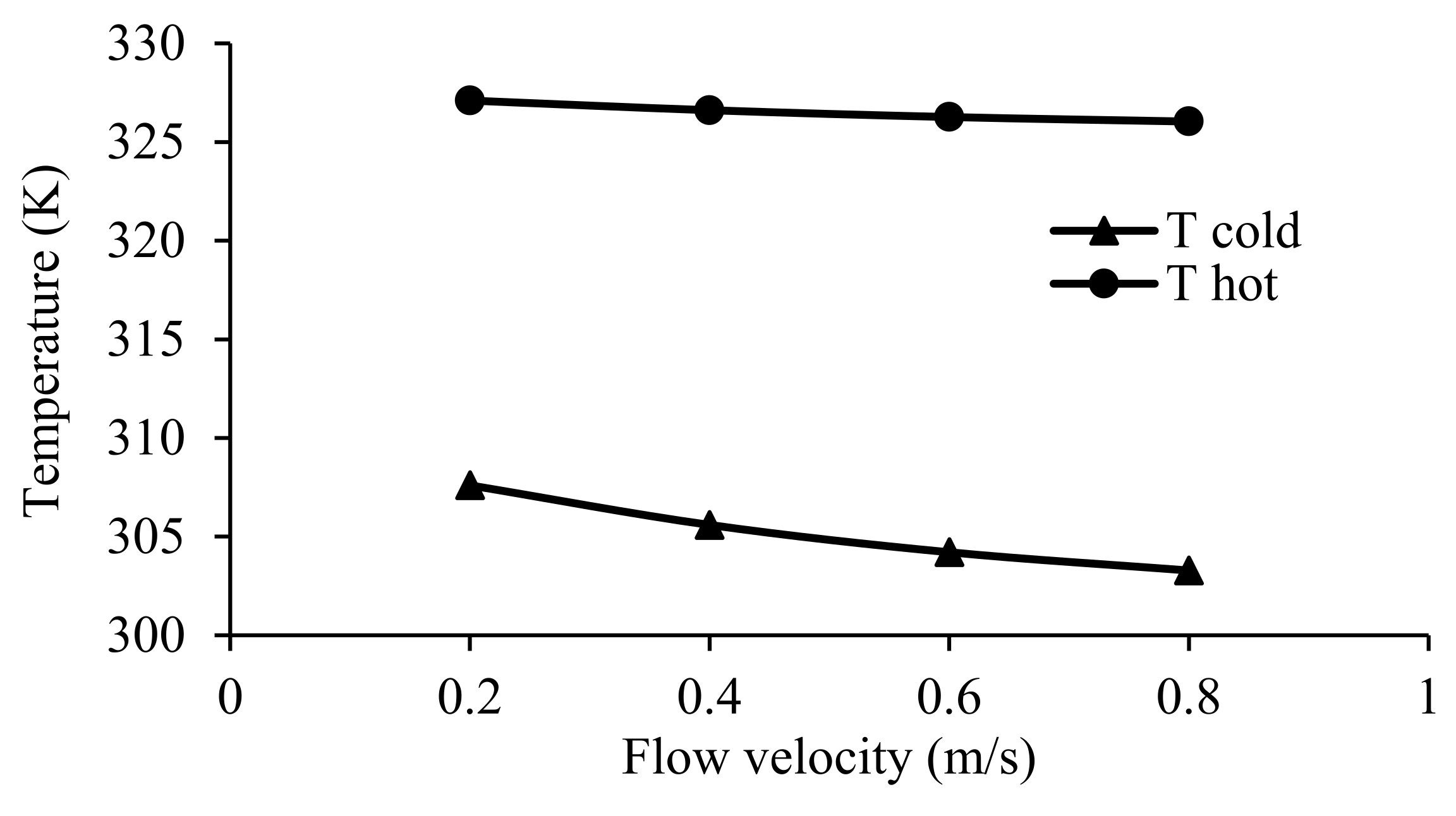
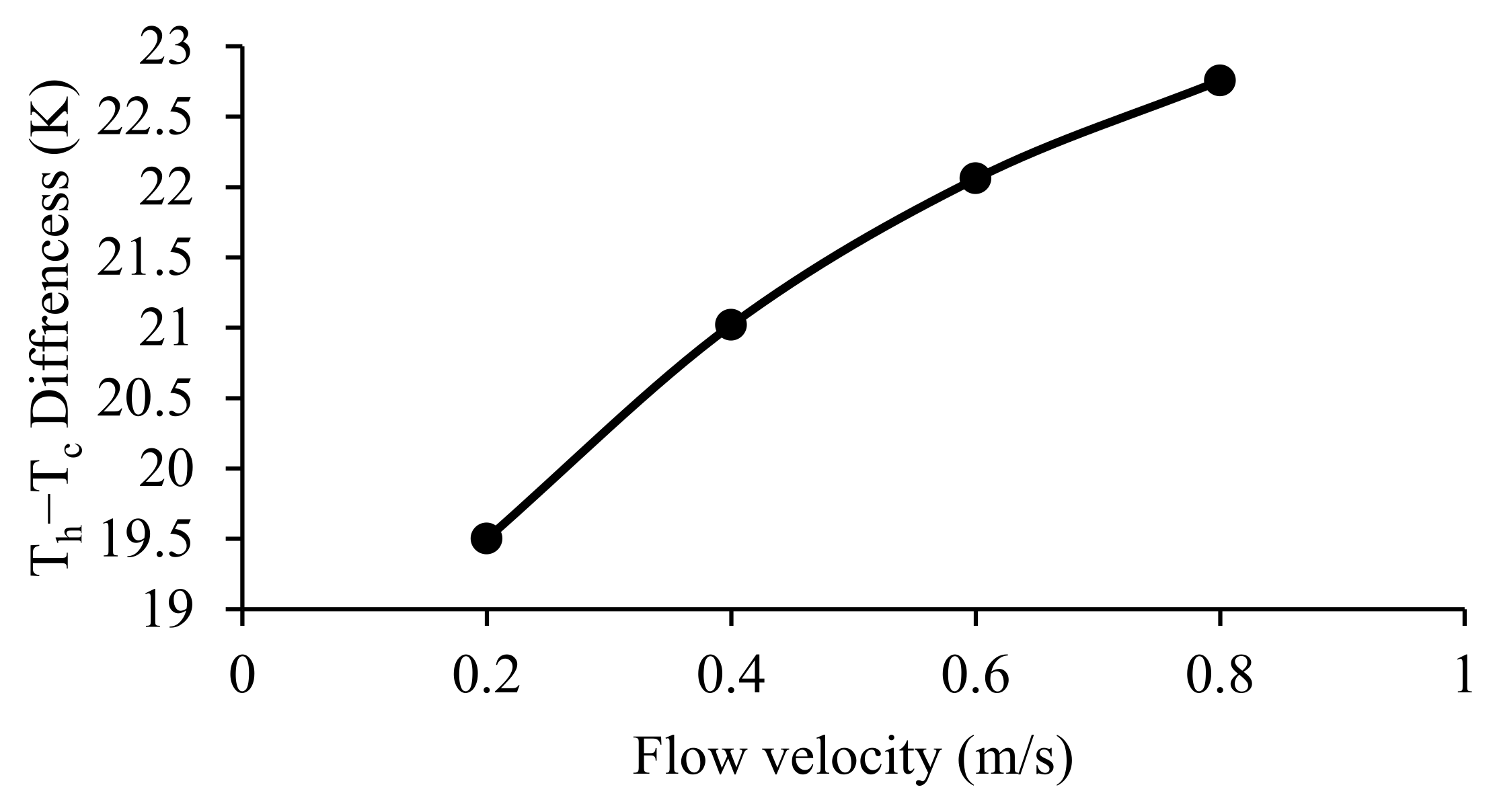
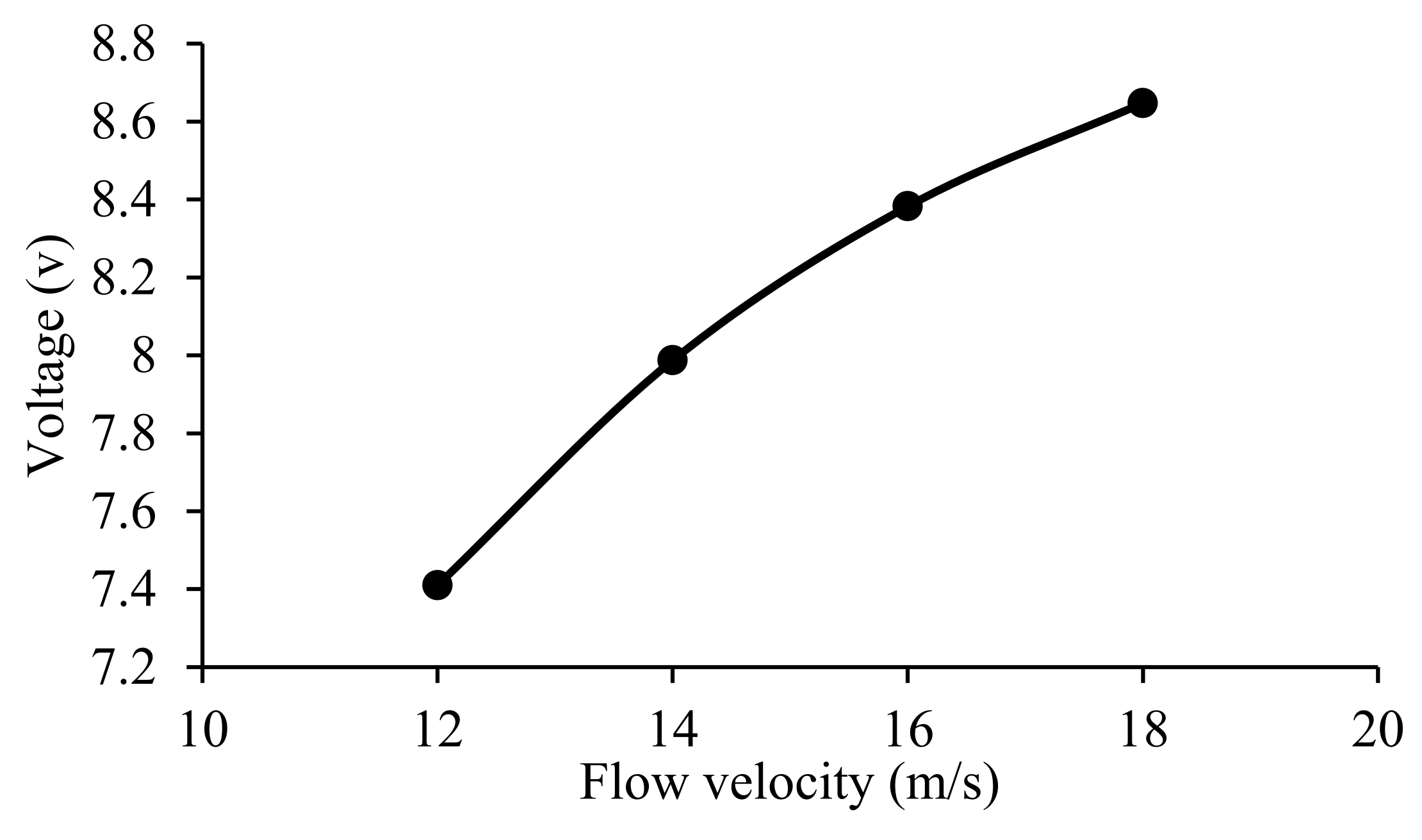
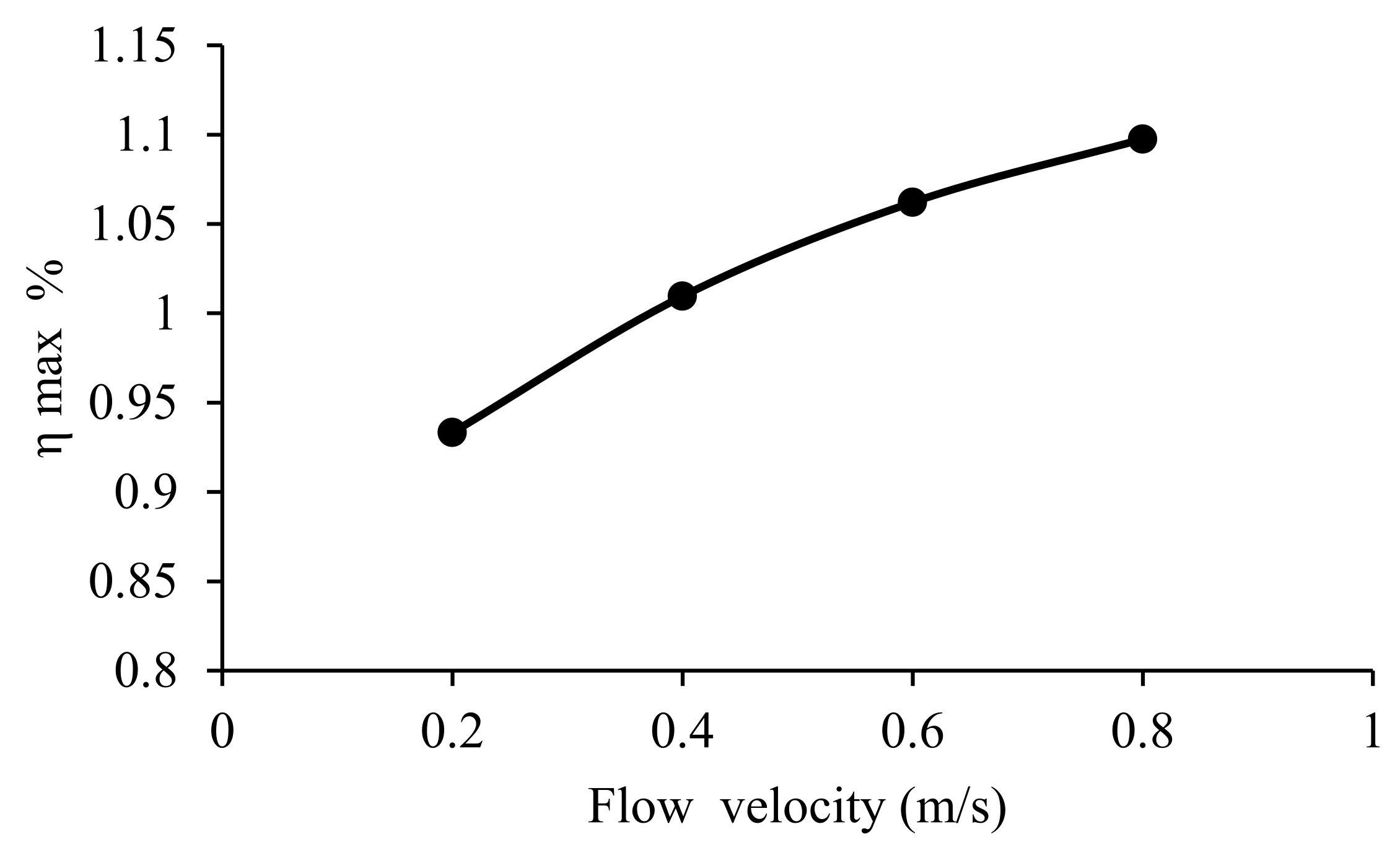
4.2. Flow Velocity
5. Conclusions and Future Research Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qasim, M.A.; Velkin, V.I.; Shcheklein, S.E. The Experimental Investigation of a New Panel Design for Thermoelectric Power Generation to Maximize Output Power Using Solar Radiation. Energies 2022, 15, 3124. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, X.; Lu, H.; Ni, T.; Li, Y. Waste energy recovery and energy efficiency improvement in China’s iron and steel industry. Appl. Energy 2017, 191, 502–520. [Google Scholar] [CrossRef]
- Dolz, V.; Novella, R.; García, A.; Sánchez, J. HD Diesel engine equipped with a bottoming Rankine cycle as a waste heat recovery system. Part 1: Study and analysis of the waste heat energy. Appl. Therm. Eng. 2012, 36, 269–278. [Google Scholar] [CrossRef]
- Chen, W.H.; Lin, Y.X.; Chiou, Y.B.; Lin, Y.L.; Wang, X.D. A computational fluid dynamics (CFD) approach of thermoelectric generator (TEG) for power generation. Appl. Therm. Eng. 2020, 173, 115203. [Google Scholar] [CrossRef]
- Barati, M.; Esfahani, S.; Utigard, T. Energy recovery from high temperature slags. Energy 2011, 36, 5440–5449. [Google Scholar] [CrossRef]
- Jouhara, H.; Khordehgah, N.; Almahmoud, S.; Delpech, B.; Chauhan, A.; Tassou, S.A. Waste heat recovery technologies and applications. Therm. Sci. Eng. Prog. 2018, 6, 268–289. [Google Scholar] [CrossRef]
- Aranguren, P.; Astrain, D.; Pérez, M.G. Computational and experimental study of a complete heat dissipation system using water as heat carrier placed on a thermoelectric generator. Energy 2014, 74, 346–358. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.S.; Bai, K.L.; Li, J. Thermodynamic analysis and parametric optimization of CDTPC-ARC based on cascade use of waste heat of heavy-duty internal combustion engines (ICEs). Appl. Therm. Eng. 2016, 106, 661–673. [Google Scholar] [CrossRef]
- Shu, G.; Liu, P.; Tian, H.; Wang, X.; Jing, D. Operational profile based thermal-economic analysis on an Organic Rankine cycle using for harvesting marine engine’s exhaust waste heat. Energy Convers. Manag. 2017, 146, 107–123. [Google Scholar] [CrossRef]
- Wang, X.; Shu, G.; Tian, H.; Liu, P.; Jing, D.; Li, X. Dynamic analysis of the dual-loop Organic Rankine Cycle for waste heat recovery of a natural gas engine. Energy Convers. Manag. 2017, 148, 724–736. [Google Scholar] [CrossRef]
- Song, J.; Gu, C.W.; Ren, X. Influence of the radial-inflow turbine efficiency prediction on the design and analysis of the Organic Rankine Cycle (ORC) system. Energy Convers. Manag. 2016, 123, 308–316. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.C.; Du, F.R.; Ding, S.T. Algorithm to construct line-shaped feature point clouds of single-value ruled blades for gas turbines. J. Manuf. Sci. Eng. 2014, 136, 041022. [Google Scholar] [CrossRef]
- Ennil, A.B.; Al-Dadah, R.; Mahmoud, S.; Rahbar, K.; AlJubori, A. Minimization of loss in small scale axial air turbine using CFD modeling and evolutionary algorithm optimization. Appl. Therm. Eng. 2016, 102, 841–848. [Google Scholar] [CrossRef]
- Li, G.; Bao, M.; Ding, S.; Li, Y. A system for accurate measuring of thermal-structure displacement on a high speed rotating turbine disk by using digital image correlation technology. Appl. Therm. Eng. 2017, 113, 36–46. [Google Scholar] [CrossRef]
- Habhab, M.B.; Ismail, T.; Lo, J.F. A laminar flow-based microfluidic tesla pump via lithography enabled 3D printing. Sensors 2016, 16, 1970. [Google Scholar] [CrossRef]
- Guha, A.; Sengupta, S. Similitude and scaling laws for the rotating flow between concentric discs. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 429–439. [Google Scholar] [CrossRef]
- Song, J.; Ren, X.D.; Li, X.S.; Gu, C.W.; Zhang, M.M. One-dimensional model analysis and performance assessment of Tesla turbine. Appl. Therm. Eng. 2018, 134, 546–554. [Google Scholar] [CrossRef]
- Krishnan, V.G.; Romanin, V.; Carey, V.P.; Maharbiz, M.M. Design and scaling of microscale Tesla turbines. J. Micromech. Microeng. 2013, 23, 125001. [Google Scholar] [CrossRef]
- Zhang, M.; Miao, L.; Kang, Y.P.; Tanemura, S.; Fisher, C.A.J.; Xu, G.; Li, C.X.; Fan, G.Z. Efficient, low-cost solar thermoelectric cogenerators comprising evacuated tubular solar collectors and thermoelectric modules. Appl. Energy 2013, 109, 51–59. [Google Scholar] [CrossRef]
- Suter, C.; Jovanovic, Z.; Steinfeld, A. A 1 kWe thermoelectric stack for geothermal power generation–Modeling and geometrical optimization. Appl. Energy 2012, 99, 379–385. [Google Scholar] [CrossRef]
- Whalen, S.A.; Dykhuizen, R.C. Thermoelectric energy harvesting from diurnal heat flow in the upper soil layer. Energy Convers. Manag. 2012, 64, 397–402. [Google Scholar] [CrossRef]
- Li, B.; Huang, K.; Yan, Y.; Li, Y.; Twaha, S.; Zhu, J. Heat transfer enhancement of a modularised thermoelectric power generator for passenger vehicles. Appl. Energy 2017, 205, 868–879. [Google Scholar] [CrossRef]
- Nonthakarn, P.; Ekpanyapong, M.; Nontakaew, U.; Bohez, E. Design and Optimization of an Integrated Turbo-Generator and Thermoelectric Generator for Vehicle Exhaust Electrical Energy Recovery. Energies 2019, 12, 3134. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Saber, H.H. Performance analysis of cascaded thermoelectric converters for advanced radioisotope power systems. Energy Convers. Manag. 2005, 46, 1083–1105. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, C.; Wang, S. Theoretical analysis of a thermoelectric generator using exhaust gas of vehicles as heat source. Appl. Energy 2013, 112, 1171–1180. [Google Scholar] [CrossRef]
- Weng, C.-C.; Huang, M.-J. A simulation study of automotive waste heat recovery using a thermoelectric power generator. Int. J. Therm. Sci. 2013, 71, 302–309. [Google Scholar] [CrossRef]
- Champier, D.; Bédécarrats, J.P.; Kousksou, T.; Rivaletto, M.; Strub, F.; Pignolet, P. Study of a TE (thermoelectric) generator incorporated in a multifunction wood stove. Energy 2011, 36, 1518–1526. [Google Scholar] [CrossRef]
- Chen, W.-H.; Lin, Y.X.; Wang, X.D.; Lin, Y.L. A comprehensive analysis of the performance of thermoelectric generators with constant and variable properties. Appl. Energy 2019, 241, 11–24. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, H.; Xie, K. Analysis of optimum configuration of two-stage thermoelectric modules. Cryogenics 2007, 47, 89–93. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wu, P.-H.; Lin, Y.-L. Performance optimization of thermoelectric generators designed by multi-objective genetic algorithm. Appl. Energy 2018, 209, 211–223. [Google Scholar] [CrossRef]
- Qasim, M.A.; Alwan, N.T.; PraveenKumar, S.; Velkin, V.I.; Agyekum, E.B. A New Maximum Power Point Tracking Technique for Thermoelectric Generator Modules. Inventions 2021, 6, 88. [Google Scholar] [CrossRef]
- Meng, F.; Chen, L.; Sun, F. Extreme working temperature differences for thermoelectric refrigerating and heat pumping devices driven by thermoelectric generator. J. Energy Inst. 2010, 83, 108–113. [Google Scholar] [CrossRef]
- Yu, J.; Wang, B. Enhancing the maximum coefficient of performance of thermoelectric cooling modules using internally cascaded thermoelectric couples. Int. J. Refrig. 2009, 32, 32–39. [Google Scholar] [CrossRef]
- Chakraborty, A.; Saha, B.B.; Koyama, S.; Ng, K.C. Thermodynamic modelling of a solid state thermoelectric cooling device: Temperature–entropy analysis. Int. J. Heat Mass Transf. 2006, 49, 3547–3554. [Google Scholar] [CrossRef]
- Huang, M.-J.; Yen, R.-H.; Wang, A.-B. The influence of the Thomson effect on the performance of a thermoelectric cooler. Int. J. Heat Mass Transf. 2005, 48, 413–418. [Google Scholar] [CrossRef]
- Chen, W.-H.; Liao, C.-Y.; Hung, C.-I. A numerical study on the performance of miniature thermoelectric cooler affected by Thomson effect. Appl. Energy 2012, 89, 464–473. [Google Scholar] [CrossRef]
- Chen, M.; Rosendahl, L.A.; Condra, T. A three-dimensional numerical model of thermoelectric generators in fluid power systems. Int. J. Heat Mass Transf. 2011, 54, 345–355. [Google Scholar] [CrossRef]
- Shen, R.; Gou, X.; Zhong, J. A Three-dimensional Dynamic Analysis CFD Tool for Thermoelectric Generators. Int. J. Thermophys. 2020, 41, 1–19. [Google Scholar] [CrossRef]
- Högblom, O.; Andersson, R. Multiphysics CFD Simulation for Design and Analysis of Thermoelectric Power Generation. Energies 2020, 13, 4344. [Google Scholar] [CrossRef]
- Bejjam, R.B.; Dabot, M.; Wondatir, T.; Negash, S. Performance evaluation of thermoelectric generator using CFD. Mater. Today Proc. 2021, 47, 2498–2504. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Ge, M.; Li, Y.; Yang, Y. Energy and exergy analysis of thermoelectric generator system with humidified flue gas. Energy Convers. Manag. 2018, 156, 140–149. [Google Scholar] [CrossRef]
- Nagaraj, N.N.A.; Kumar, L.S. Electrical Energy Harvesting Using Thermo Electric Generator for Rural Communities in India. Int. J. Energy Power Eng. 2019, 13, 663–667. [Google Scholar]
- Tsai, H.-L.; Lin, J.-M. Model building and simulation of thermoelectric module using Matlab/Simulink. J. Electron. Mater. 2010, 39, 2105. [Google Scholar] [CrossRef]
- Hsu, C.-T.; Huang, G.Y.; Chu, H.S.; Yu, B.; Yao, D.J. An effective Seebeck coefficient obtained by experimental results of a thermoelectric generator module. Appl. Energy 2011, 88, 5173–5179. [Google Scholar] [CrossRef]
- Pfeiffelmann, B.; Benim, A.C.; Joos, F. Water-Cooled Thermoelectric Generators for Improved Net Output Power: A Review. Energies 2021, 14, 8329. [Google Scholar] [CrossRef]
- Su, C.Q.; Xu, M.; Wang, W.S.; Deng, Y.D.; Liu, X.; Tang, Z.B. Optimization of cooling unit design for automotive exhaust-based thermoelectric generators. J. Electron. Mater. 2015, 44, 1876–1883. [Google Scholar] [CrossRef]
- Qasim, M.A.; Velkin, V.I.; Hassan, A.K. Seebeck Generators and Their Performance in Generating Electricity. J. Oper. Autom. Power Eng. JOAPE 2022, 10, 200–205. [Google Scholar]
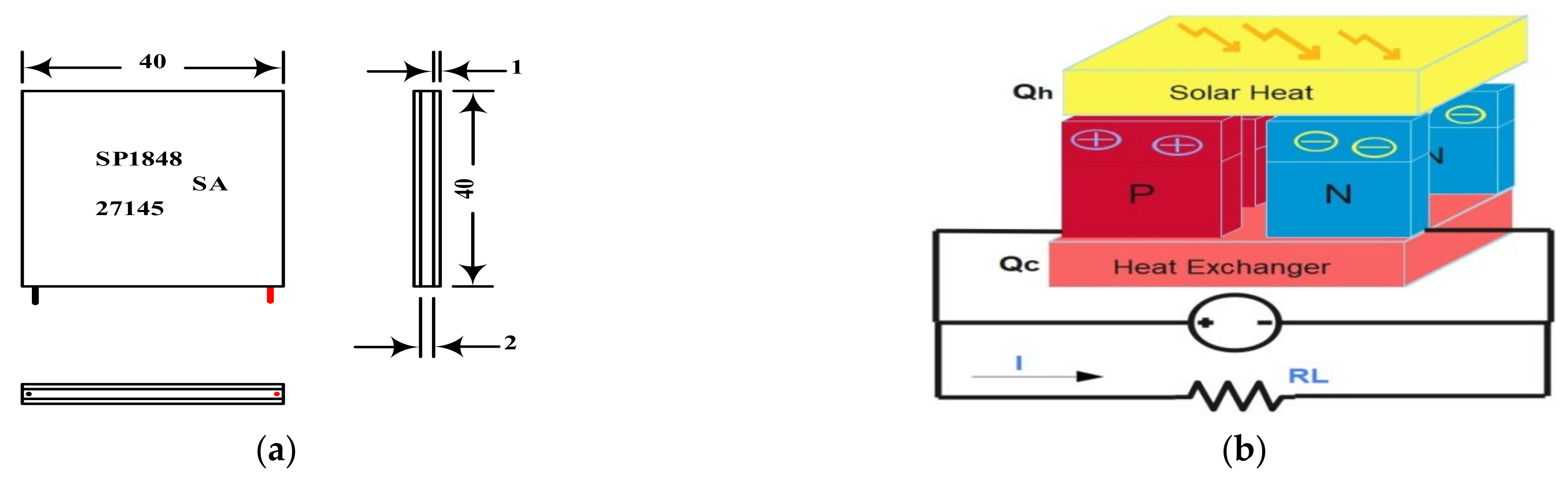









| Specification | Value |
|---|---|
| Material | Ceramic/Bismuth Telluride |
| Color | White |
| Temperature () | 150 |
| Open-circuit voltage (V) | 4.8 |
| Short-circuit current (mA) | 20/0.97/225; 40/1.8/368; 60/2.4/469; 80/3.6/559; 100/4.8/669 |
| Module size (L × W × H) | 40 × 40 × 4 mm3 |
| Weight | 25 g |
| Property | Value |
|---|---|
| Density | 2.70 kg/m3 |
| Thermal expansion | 23.5 × 10−6/K |
| Thermal conductivity | 200 W/m·K |
| Electrical resistivity | 0.035 × 10−6 Ω · m |
| Cell Size | Total Number of Cells |
|---|---|
| 4.00 | 4861 |
| 3.00 | 6759 |
| 2.00 | 19,551 |
| 1.00 | 128,474 |
| 0.50 | 964,572 |
| Time | Qasim, Velkin [1] | Predicted | Diff. (%) | ||||
|---|---|---|---|---|---|---|---|
| 11:30 a.m. | 51 | 27 | 24 | 51 | 29 | 22 | 8.3 |
| 12:30 p.m. | 62 | 32 | 30 | 62 | 31 | 31 | 3.3 |
| 1:30 p.m. | 72 | 37 | 35 | 72 | 35 | 37 | 5.7 |
| 3:30 p.m. | 63 | 32 | 31 | 63 | 31 | 32 | 3.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasim, M.A.; Velkin, V.I.; Shcheklein, S.E. Development of a Computational Fluid Dynamics (CFD) Numerical Approach of Thermoelectric Module for Power Generation. Crystals 2022, 12, 828. https://doi.org/10.3390/cryst12060828
Qasim MA, Velkin VI, Shcheklein SE. Development of a Computational Fluid Dynamics (CFD) Numerical Approach of Thermoelectric Module for Power Generation. Crystals. 2022; 12(6):828. https://doi.org/10.3390/cryst12060828
Chicago/Turabian StyleQasim, Mohammed A., Vladimir I. Velkin, and Sergey E. Shcheklein. 2022. "Development of a Computational Fluid Dynamics (CFD) Numerical Approach of Thermoelectric Module for Power Generation" Crystals 12, no. 6: 828. https://doi.org/10.3390/cryst12060828
APA StyleQasim, M. A., Velkin, V. I., & Shcheklein, S. E. (2022). Development of a Computational Fluid Dynamics (CFD) Numerical Approach of Thermoelectric Module for Power Generation. Crystals, 12(6), 828. https://doi.org/10.3390/cryst12060828







