Design of Porous Shape Memory Alloys with Small Mechanical Hysteresis
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
3.1. Experiment and Simulation for Bulk SMA
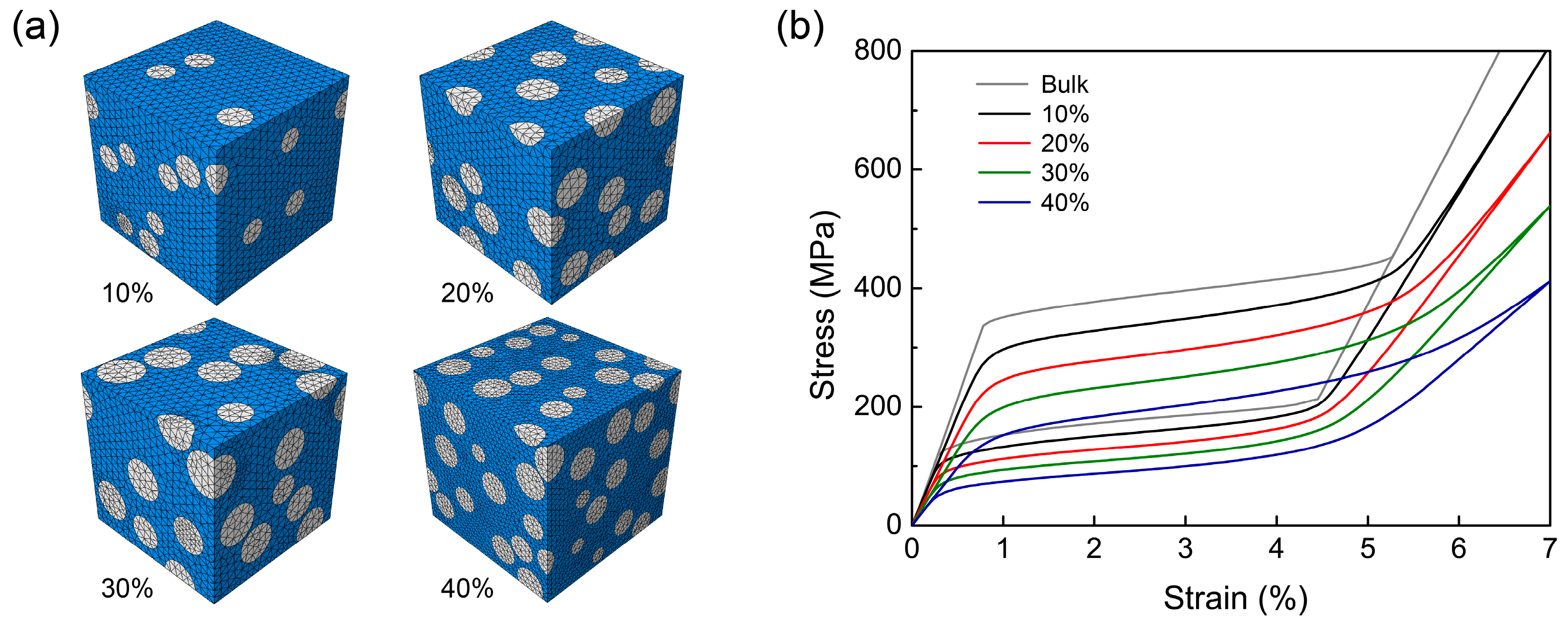
3.2. Effect of Porosity on Hysteresis Loops of the Random Porous SMAs
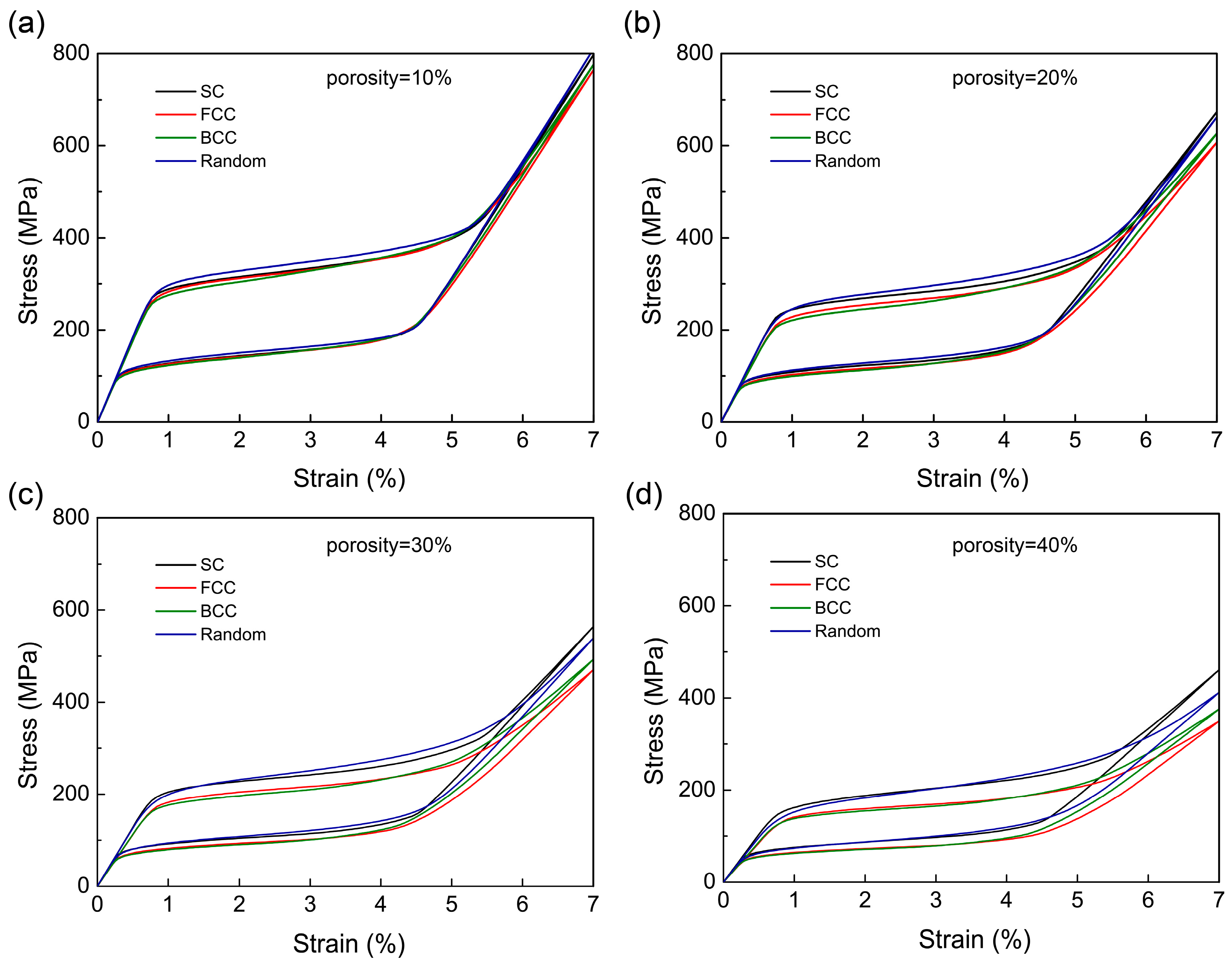
3.3. Microstructure Design of Porous SMAs to Achieve Narrow Hysteresis
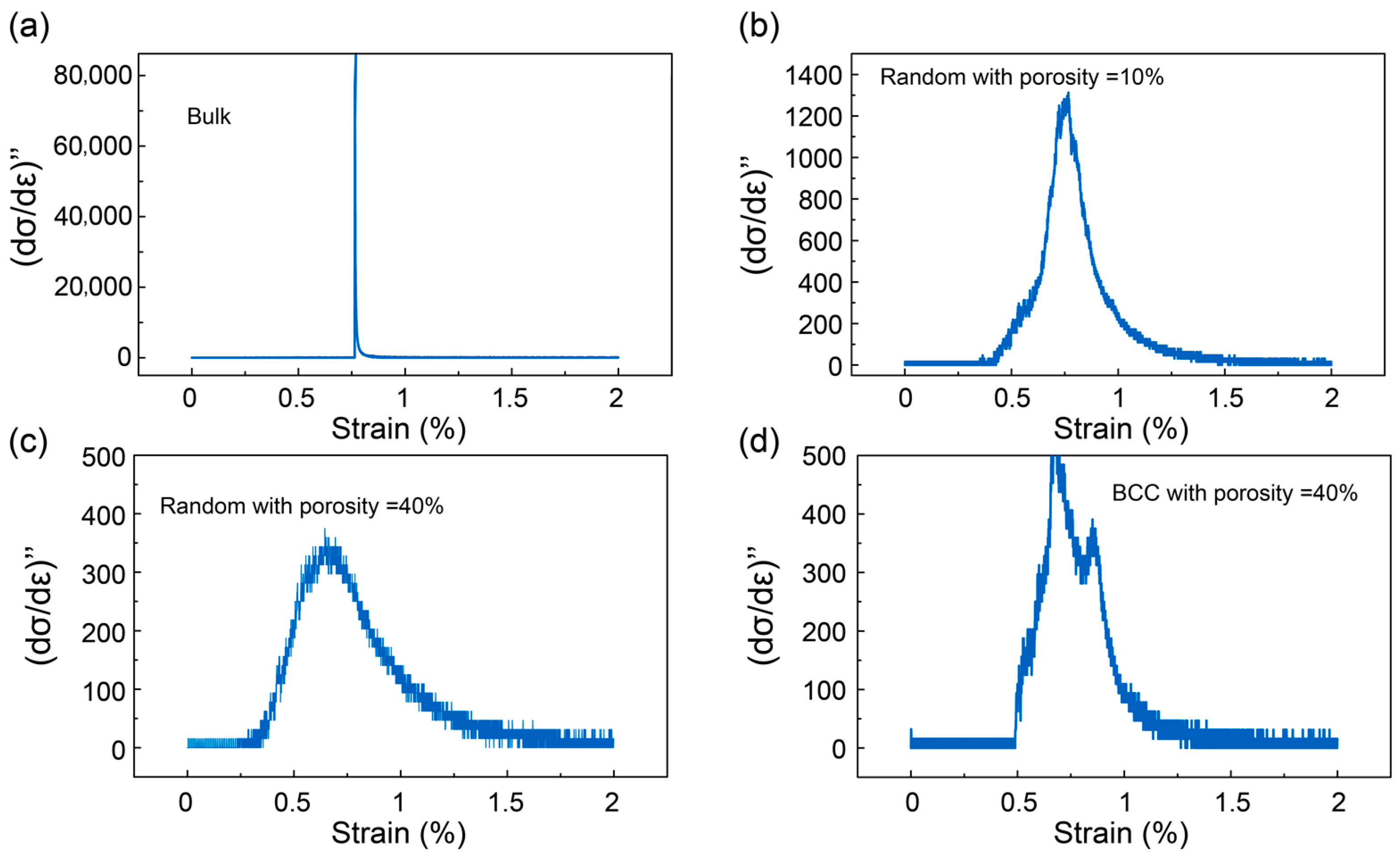
3.4. Martensitic Transformation Behavior of Porous SMAs during the Loading Processes
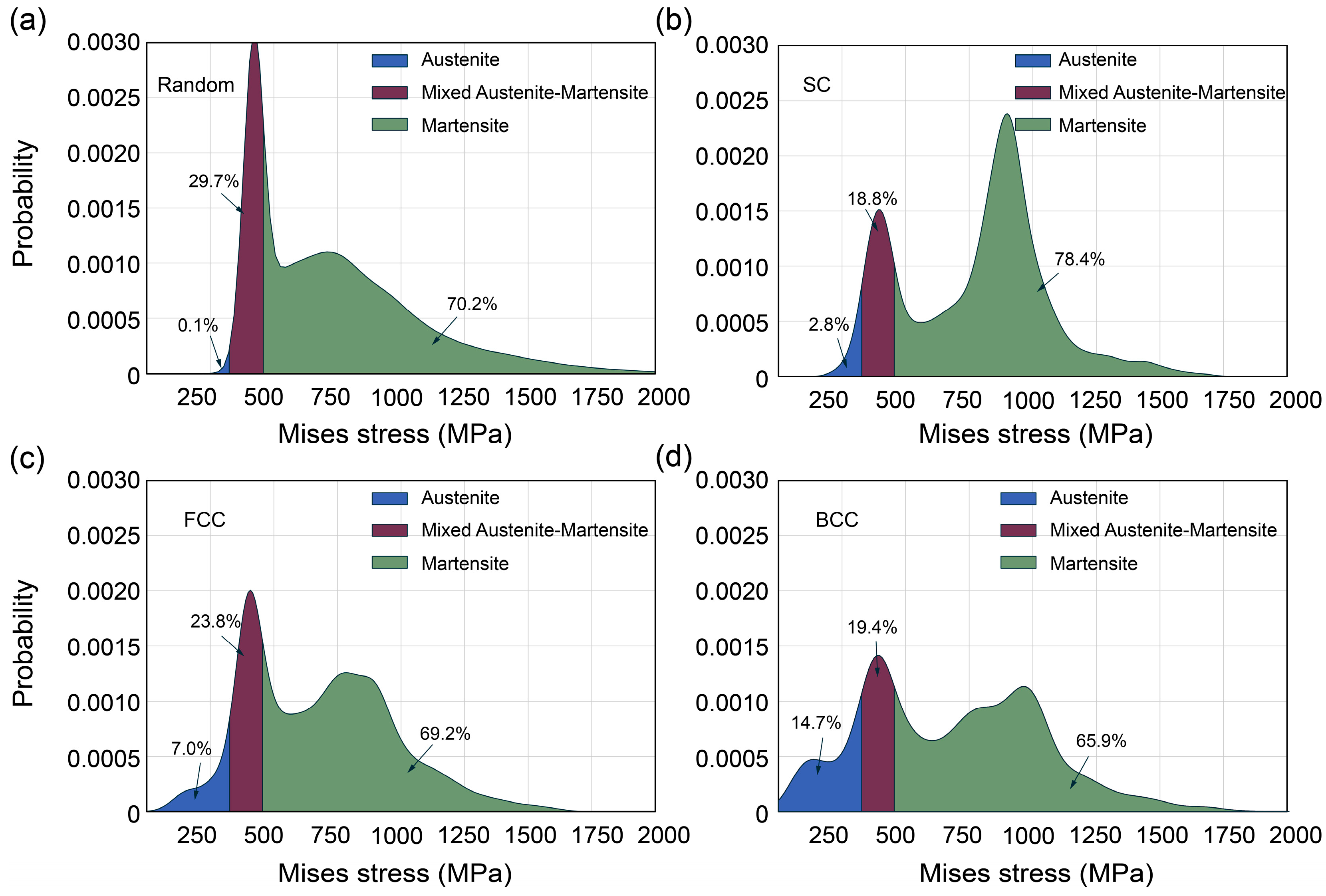
3.5. Probability Statistics and Stress Analysis in Random and BCC-Type Porous SMAs
4. Conclusions
- (1)
- The mechanical hysteresis loops of SMAs can be effectively modulated by introducing porous structures. Higher porosity helps the SMAs achieve a smaller hysteresis loop area, indicating less energy dissipation.
- (2)
- The lowest damping performance can be obtained when the pores are distributed in a BCC-type fashion. This characteristic can be attributed to the gradual martensitic-phase-transformation behavior caused by inhomogeneous local stress in porous SMAs.
- (3)
- In BCC-type porous SMAs, the phase transformations occur more homogeneously, and the stress concentration can be effectively avoided compared to a random porous structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Otsuka, K.; Shimizu, K. Memory Effect and Thermoelastic Martensite Transformation in Cu-Al-Ni Alloy. Scr. Metall. Mater. 1970, 4, 469–472. [Google Scholar] [CrossRef]
- Duerig, T.; Pelton, A.; Stöckel, D. An overview of nitinol medical applications. Mater. Sci. Eng. A 1999, 273, 149–160. [Google Scholar] [CrossRef]
- Santosh, S.; Thomas, J.K.; Pavithran, M.; Nithyanandh, G.; Ashwath, J. An experimental analysis on the influence of CO2 laser machining parameters on a copper-based shape memory alloy. Opt. Laser Technol. 2022, 153, 108210. [Google Scholar] [CrossRef]
- Sampath, S.; Vedamanickam, S. Effect of Vanadium on the Microstructure, TransformationTemperatures, and Corrosion Behavior of NiTi Shape Memory Alloys. J. Eng. Mater. Technol. 2023, 145, 011008. [Google Scholar] [CrossRef]
- Jani, J.M.; Learg, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Humbeeck, J.V. Non-medical applications of shape memory alloys. Mater. Sci. Eng. A 1999, 273, 134–148. [Google Scholar] [CrossRef]
- Kahn, H.; Huff, M.A.; Heuer, A.H. The TiNi shape-memory alloy and its applications for MEMS. J. Micromech. Microeng. 1998, 8, 213–221. [Google Scholar] [CrossRef]
- Fujita, H.; Toshiyoshi, H. Micro actuators and their applications. Microelectron. J. 1998, 29, 637–640. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Ding, Z.; Zhao, Y.; Wang, C.C.; Purnawali, H.; Tang, C. Stimulus-responsive shape memory materials: A review. Mater. Des. 2012, 33, 577–640. [Google Scholar] [CrossRef]
- Humbeeck, J.V. Shape memory alloys: A material and a technology. Adv. Eng. Mater. 2001, 3, 837–850. [Google Scholar] [CrossRef]
- Cui, J.; Chu, Y.S.; Famodu, O.O.; Furuya, Y.; Hattrick-Simpers, J.; James, R.D.; Ludwig, A.; Thienhaus, S.; Wuttig, M.; Zhang, Z.; et al. Combinatorial search of thermoelastic shape-memory alloys with extremely small hysteresis width. Nat. Mater. 2006, 5, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.P.; He, Y.J. A multiscale continuum model of the grain-size dependence of the stress hysteresis in shape memory alloy polycrystals. Int. J. Solids Struct. 2008, 45, 3868–3896. [Google Scholar] [CrossRef]
- Zhu, J.; Gao, M.; Wang, D.; Li, J.; Zhang, T.Y.; Wang, Y. Making metals linear super-elastic with ultralow modulus and nearly zero hysteresis. Mater. Horiz. 2019, 6, 515–523. [Google Scholar] [CrossRef] [Green Version]
- Hao, S.; Cui, L.; Jiang, D.; Yu, C.; Jiang, J.; Shi, X.; Liu, Z.; Wang, S.; Wang, Y.; Brown, D.E.; et al. Nanostructured Nb reinforced NiTi shape memory alloy composite with high strength and narrow hysteresis. Appl. Phys. Lett. 2013, 102, 231905. [Google Scholar] [CrossRef]
- Hao, S.J.; Cui, L.S.; Wang, Y.D.; Jiang, D.Q.; Yu, C.; Jiang, J.; Brown, D.E.; Ren, Y. The ultrahigh mechanical energy-absorption capability evidenced in a high-strength NbTi/NiTi nanocomposite. Appl. Phys. Lett. 2011, 99, 024102. [Google Scholar] [CrossRef]
- Wang, D.; Hou, S.; Wang, Y.; Ding, X.; Ren, S.; Ren, X.; Wang, Y. Superelasticity of slim hysteresis over a wide temperature range by nanodomains of martensite. Acta Mater. 2014, 66, 349–359. [Google Scholar] [CrossRef]
- Elahinia, M.; Moghaddam, N.S.; Andani, M.T.; Amerinatanzi, A.; Bimber, B.A.; Hamilton, R.F. Fabrication of NiTi through additive manufacturing: A review. Prog. Mater. Sci. 2016, 83, 630–663. [Google Scholar] [CrossRef] [Green Version]
- Neurohr, A.J.; Dunand, D.C. Shape-Memory NiTi with two-dimensional networks of micro-channels. Acta Biomater. 2011, 7, 1862–1872. [Google Scholar] [CrossRef]
- Bewerse, C.; Brinson, L.C.; Dunand, D.C. Porous shape-memory NiTi-Nb with microchannel arrays. Acta Mater. 2016, 115, 83–93. [Google Scholar] [CrossRef]
- Saedi, S.; Saghaian, S.E.; Jahadakbar, A.; Moghaddam, N.S.; Andani, M.T.; Saghaian, S.M.; Lu, Y.C.; Elahinia, M.; Karaca, H.E. Shape memory response of porous NiTi shape memory alloys fabricated by selective laser melting. J. Mater. Sci. Mater. Med. 2018, 29, 40. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Qing, H.; Wang, Y.; Liang, J.; Zhao, M.; Geng, Y.; Liang, J.; Lu, B. Superelastic behaviors of additively manufactured porous NiTi shape memory alloys designed with Menger sponge-like fractal structures. Mater. Des. 2021, 200, 109448. [Google Scholar] [CrossRef]
- Lester, B.T.; Baxevanis, T.; Chemisky, Y.; Lagoudas, D.C. Review and perspectives: Shape memory alloy composite systems. Acta Mech. 2015, 226, 3907–3960. [Google Scholar] [CrossRef] [Green Version]
- Auricchio, F.; Taylor, R.L. Shape-Memory alloys: Modelling and numerical simulations of the finite-strain superelastic behavior. Comput. Meth. Appl. Mech. Eng. 1997, 143, 175–194. [Google Scholar] [CrossRef]
- Auricchio, F.; Taylor, R.L.; Lubliner, J. Shape-Memory alloys: Macromodelling and numerical simulations of the superelastic behavior. Comput. Meth. Appl. Mech. Eng. 1997, 146, 281–312. [Google Scholar] [CrossRef]
- Segurado, J.; Llorca, J. A numerical approximation to the elastic properties of sphere-reinforced composites. J. Mech. Phys. Solids 2002, 50, 2107–2121. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Zhou, J.; Guan, J. Effects of the fiber orientation and fiber aspect ratio on the tensile strength of C-sf/Mg composites. Comput. Mater. Sci. 2014, 89, 6–11. [Google Scholar] [CrossRef]
- Ashrafi, M.J.; Arghavani, J.; Naghdabadi, R.; Sohrabpour, S. A 3-D constitutive model for pressure-dependent phase transformation of porous shape memory alloys. J. Mech. Behav. Biomed. Mater. 2015, 42, 292–310. [Google Scholar] [CrossRef]
- Panico, M.; Brinson, L.C. Computational modeling of porous shape memory alloys. Int. J. Solids Struct. 2008, 45, 5613–5626. [Google Scholar] [CrossRef] [Green Version]
- Dhondt, G. The Finite Element Method for Three-Dimensional Thermomechanical Applications; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Xia, Z.; Zhang, Y.; Ellyin, F. A unified periodical boundary conditions for representative volume elements of composites and applications. Int. J. Solids Struct. 2003, 40, 1907–1921. [Google Scholar] [CrossRef]
- Xia, Z.H.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef] [Green Version]
- Şopu, D.; Soyarslan, C.; Sarac, B.; Bargmann, S.; Stoica, M.; Eckert, J. Structure-property relationships in nanoporous metallic glasses. Acta Mater. 2016, 106, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Sarac, B.; Wilmers, J.; Bargmann, S. Property optimization of porous metallic glasses via structural design. Mater. Lett. 2014, 134, 306–310. [Google Scholar] [CrossRef]
- Jiang, Y.; Sun, L.; Wu, Q.; Qiu, K. Enhanced tensile ductility of metallic glass matrix composites with novel microstructure. J. Non-Cryst. Solids 2017, 459, 26–31. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, F.; Liu, B.; Deng, J. Design of Menger sponge fractal structural NiTi as bone implants. Model. Simul. Mater. Sci. Eng. 2021, 29, 084001. [Google Scholar] [CrossRef]
- Hao, S.; Cui, L.; Jiang, Q.; Han, X.; Ren, Y.; Jiang, J.; Liu, Y.; Liu, Z.; Mao, S.; Wang, Y.; et al. A Transforming Metal Nanocomposite with Large Elastic Strain, Low Modulus, and High Strength. Science 2013, 339, 1191–1194. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zong, H.; Cui, L.; Fan, X.; Ding, X.; Sun, J. Origin of high strength, low modulus superelasticity in nanowire-shape memory alloy composites. Sci. Rep. 2017, 7, 46360. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ren, J.; Wang, X.; Zong, H.; Cui, L.; Ding, X. Insight into the Effects of Reinforcement Shape on Achieving Continuous Martensite Transformation in Phase Transforming Matrix Composites. Appl. Compos. Mater. 2018, 25, 1369–1384. [Google Scholar] [CrossRef]
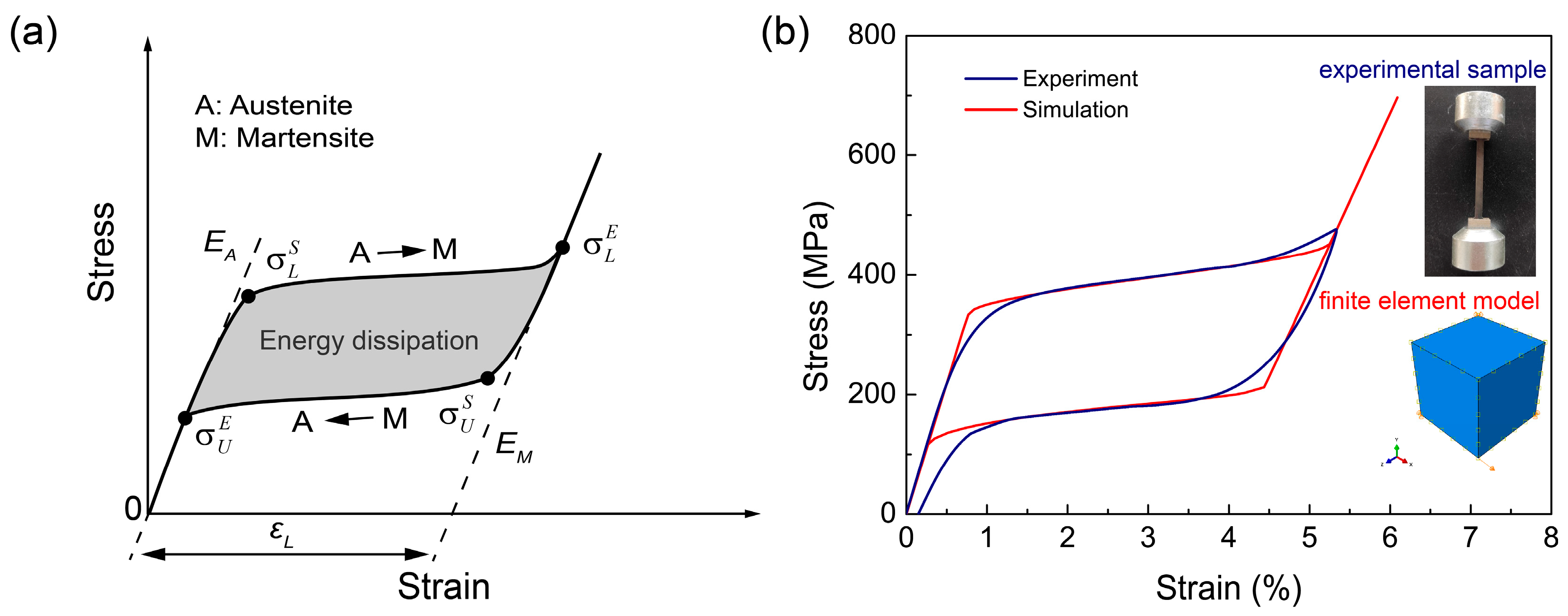



| Material Parameter | Value |
|---|---|
| Martensite elastic modulus (MPa) | 43,708 |
| Austenite elastic modulus (MPa) | 29,400 |
| Starting stress for austenite to martensite transformation (MPa) | 334 |
| Finishing stress for austenite to martensite transformation (MPa) | 454 |
| Starting stress for martensite to austenite transformation (MPa) | 214 |
| Finishing stress for martensite to austenite transformation (MPa) | 115 |
| Transformation strain | 0.0372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Liu, B.; Wei, J.; Yang, Y.; Zhang, X.; Deng, J. Design of Porous Shape Memory Alloys with Small Mechanical Hysteresis. Crystals 2023, 13, 34. https://doi.org/10.3390/cryst13010034
Wu Z, Liu B, Wei J, Yang Y, Zhang X, Deng J. Design of Porous Shape Memory Alloys with Small Mechanical Hysteresis. Crystals. 2023; 13(1):34. https://doi.org/10.3390/cryst13010034
Chicago/Turabian StyleWu, Zheng, Baosheng Liu, Jiali Wei, Yuanxi Yang, Xudong Zhang, and Junkai Deng. 2023. "Design of Porous Shape Memory Alloys with Small Mechanical Hysteresis" Crystals 13, no. 1: 34. https://doi.org/10.3390/cryst13010034
APA StyleWu, Z., Liu, B., Wei, J., Yang, Y., Zhang, X., & Deng, J. (2023). Design of Porous Shape Memory Alloys with Small Mechanical Hysteresis. Crystals, 13(1), 34. https://doi.org/10.3390/cryst13010034








