Residual Stress Testing and Simulation Analysis of Crystal Structures of Electronic Device Materials

Abstract

In this paper, we analyze the residual stress of different components of the crystal structures of electronic device materials following exposure to elevated temperatures using a combination of experimental tests and finite element simulations. X-ray diffraction (XRD) and LXRD micro-area residual stress analyzer were employed to determine the residual strain and stress of the CBGA sample encapsulation cover and solder joints. Subsequently, the experimental data were utilized to verify the accuracy of the simulation. The discrepancy between experimental measurements and simulation outcomes of the residual stress following reflow soldering of CBGA-assembled micro-solder joints is below 14%. The analysis also included thermal warping deformation of the CBGA encapsulation cover and how the residual stress was influenced by the diameter, spacing, and height of the solder joints. The study reveals that the residual stress following reflow soldering of BGA solder joints is non-uniformly distributed within the array. Within a single solder joint, residual stress gradually increases in distribution from its middle to the point where it make contact with the PCB and chip, with the highest level of residual stress observed where the solder joint contacts the chip. The variation in material parameters, such as the coefficient of thermal expansion, is the primary cause of thermal warping deformation on the surface of CBGA encapsulation covers. Three primary factors significantly impact the residual stress on BGA solder joints: solder joint diameter, spacing, and height. The maximum value is inversely proportional to the height of the solder joints and the residual stress. Conversely, the diameter and spacing of the joints are positively proportional to the highest value. When the diameter of the solder joint is increased from 0.55 mm to 0.75 mm, the maximum residual stress in the BGA solder joint increases from 37.243 MPa to 36.835 MPa. Conversely, increasing the height of the solder joint from 0.36 mm to 0.44 mm reduces the stress from 39.776 MPa to 36.835 MPa.

1. Introduction

With the swift advancement of modern science and technology, microelectronics has become an inextricable component, gaining increased importance. The level of development of microelectronics corresponds with a country’s overall strength and is presently one of the foremost industries in the world. The modern microelectronics industry has evolved into three distinct sectors: design, manufacturing, and encapsulation [1]. Microelectronic encapsulation is now a key technology for the IT industry’s development and an essential component of the microelectronics industry. The primary purpose of microelectronic encapsulation technology is to assemble tens of thousands of semiconductor electronic components into a compact package that can receive power and exchange information with the external environment [2]. However, electronic encapsulation devices are widely used in various fields, including communication satellites, automotive electronics, medical devices, and consumer electronics. As a result, they are vulnerable to various external environmental loads during production and service, such as residual stress, surface strain, chemical corrosion, electromigration caused by ambient humidity or current density, physical impact, and random vibration factors [3]. The failure of electronic encapsulation devices can be caused by a combination of factors. To ensure their normal function and stability, a comprehensive analysis needs to be conducted, considering the materials, structure, and process. This will help to reduce the risk of device failure and improve reliability.

Since the 1990s, semiconductor technology has continuously developed and integrated, resulting in an increase in the number of pins on a chip. However, traditional pin socket technology has been unable to fulfil the need for high-density interconnections [4]. Consequently, pin-less encapsulation technologies such as Ball Grid Array (BGA) have been introduced. BGA is an electronic encapsulation method known for connecting a chip’s pins to a grid of small balls, allowing for high-density micro-interconnections. Various types of BGA encapsulation are available on the market, differing in terms of substrate materials such as PBGA (plastic), CBGA (ceramic), CCGA (ceramic column arrays), and MBGA (metal) [5,6]. Each type of BGA encapsulation has its own characteristics and advantages in industrial applications.

Ceramic materials are preferred as they offer excellent properties, including good abrasion resistance, insulating properties, and thermal stability, making them an important material for microelectronic components [7]. Ceramic Ball Grid Array (CBGA) is a type of BGA encapsulation that employs ceramic materials. It has excellent electrical properties, high-density integration, good airtightness, moisture resistance, and effective soldering performance. Due to its remarkable reliability, CBGA is widely utilized in national defense, military, and aerospace sectors, as well as other high-precision special equipment fields. 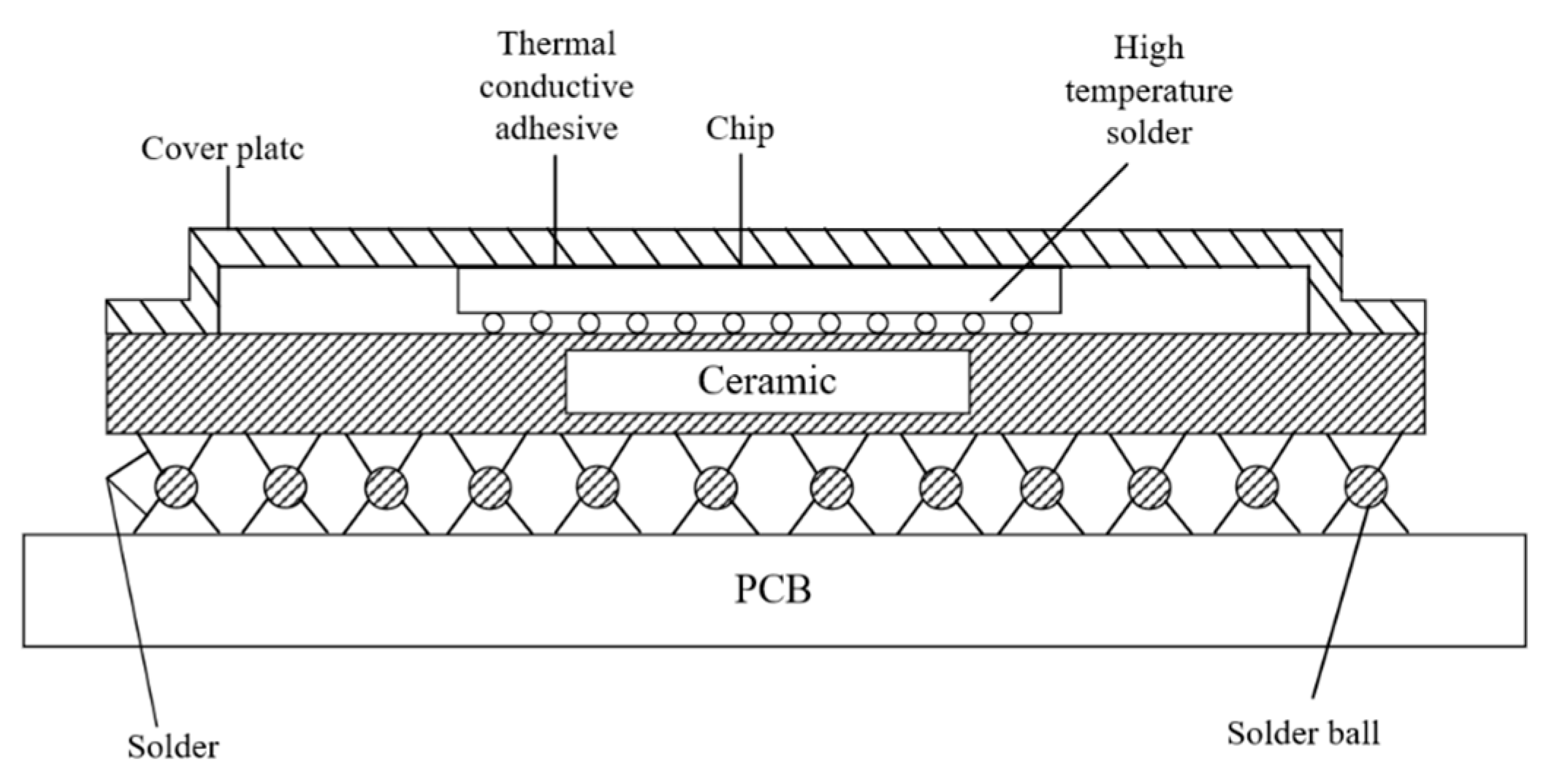Figure 1 illustrates the typical encapsulation structure of CBGA [8,9].

In general, there are two primary reasons for electronic device failure: low-cycle thermal fatigue from temperature loading and high-cycle mechanical fatigue resulting from shock drops, vibration, and other loads [10]. Based on statistical data published by the US military, 55% and 20% of electronic device failures were attributed to temperature loading and shock and vibration, correspondingly, as depicted in Figure 2 [11]. Most electronic device failures are caused by the malfunction of crystal structures in materials, such as solder balls and columns. Therefore, it is necessary to investigate the mechanical properties and failure mechanisms of these crystal structures when they are subjected to thermal loading. This research will facilitate the study of their performance and reliability.

During the welding process, the impact of temperature fluctuations on the crystal structures of electronic device materials is primarily demonstrated by the following factors: due to the large thermal expansion coefficient of the material’s constituent parts, the crystal structures itself experiences residual stress and thermal deformation during device cooling contraction. This, in turn, causes mismatched thermal stress between the constituent materials, increasing the stress and strain experienced by critical nodes in the crystal structures during subsequent service, and ultimately leading to deformation [12,13]. Figure 3 illustrates problems, including solder joint cracking and fracture, caused by temperature that significantly impede the reliable and safe operation of electronic equipment. Electronic device failure problems are a serious concern that must be addressed.

Wang and colleagues conducted research on the structure and thermal fatigue properties of solderless solder joints in ceramic ball array packaging (CBGA) structures through thermal cycling experiments and finite element modeling while sweeping the electrical observation point cross-section [14]. Li and colleagues utilized the ANSYS software for finite element analysis to simulate stress and strain distribution and plastic work accumulation in the solder ball array of the CBGA packaging device. The reliability of the solder joints was then examined from the perspective of thermal cycling damage using Darveaux’s plastic energy accumulation damage equation. Lastly, a comparison was made between the performance of the single-solder-joint-array device and the composite-solder-joint-array packaging device [15]. Lv et al. investigated the failure mechanism of surface-mounted solder joints at the board level of CBGA ball-implanted devices under cyclic loading conditions within a temperature range from −55 to 105 °C. The authors’ objective was to understand the relations between temperature, loading cycles, and solder joint reliability. The study results indicated that the key areas of failure in the solder joints of surface-mounted CBGA devices were the interfaces between the solder and ceramic ball, and the interfaces between solder joints and pads on two locations. In addition, there was a preference for the fracture of edge solder joints, which was a critical finding in failure analysis. Furthermore, the inboard link’s breakage failures occurred sequentially as the cyclic cycle increased [16]. According to Guo’s test results, a high level of straight-through rate is achievable in the electronic assembly of CBGA through reasonable process design and management. Device defects and other factors primarily cause soldering defects. The overall reliability is dependent on the weakest link, and process control must prioritize addressing the weak link [17]. Wang et al. used CBGA256 and CBGA500 circuit packages as examples to investigate the effects of ceramic shell quality on the quality of the CBGA ball planting process. They examined three aspects: pad coplanarity, positional accuracy, and ceramic surface flatness [18].

In this paper, we analyze the residual stress of different parts of crystal structures of electronic device materials following exposure to high temperatures using experimental tests and finite element simulations. X-ray diffraction (XRD) and LXRD micro-area residual stress analyzer were used to determine the residual strain and residual stress of the CBGA sample encapsulation cover and BGA solder joints. The experimental data were then utilized to verify the accuracy of the simulation part, which also involved analyzing the thermal warping deformation of the CBGA encapsulation cover. The influence of the diameter, spacing, and height of the solder joints on the residual stress was also examined.

2. Experimental Methodologies

When electronic devices are manufactured, they undergo various processes and environmental factors that can cause residual stress in the components. Even when these factors are no longer present, some amount of residual stress remains. In the production and servicing of crystal structures of electronic device materials, temperature loading is a frequent occurrence. Due to the large material coefficient of thermal expansion differences, the interface between various components is susceptible to delamination and cracking caused by temperature load, leading to device failure. During the curing process, the device transitions from a liquid to a solid state and undergoes cooling contraction, resulting in the creation of residual stress and thermal deformation. The appearance of residual stress generates a thermal stress mismatch between the constituent materials, leading to the failure of the entire device.

The residual stress test of BGA micro-solder joints assembled in high-density packaging presents a challenging industry test point. Traditional destructive measurement methods are inadequate to meet this demand. The “Macro-area Destructive Lossy Measurement System” is appropriate for assessing extensive structural components that require drilling holes, cutting strips, etc., resulting in a certain degree of destructive structure with accuracy of the test area at the centimeter level. The widely used LABVIEW strain test and analysis system is primarily employed for residual strain testing of assembled parts, with a test accuracy of typically 0.01 micro-strain. However, direct measurement of residual stress is not feasible because the test involves pasting BGA solder joints. The mainstream LABVIEW strain testing and analysis system is primarily utilized for residual strain testing during assembly. The testing accuracy usually amounts to 0.01 micro-strains, although the system cannot directly measure residual stresses. The accuracy of the test area is also limited to centimeter-level precision due to the installation of strain gauges. To achieve micron-level positioning accuracy, high-powered research-level equipment for residual stress testing, specifically the LXRD micro-area model, must be utilized.

In this paper, we utilize the LXRD micro-zone residual stress analyzer to conduct tests on residual stress. Additionally, we establish a nondestructive microstructure residual stress test platform surrounding the LXRD micro-zone residual stress analyzer to analyze residual stress on CBGA micro-soldered joints. The overall and internal structure can be seen in Figure 4.

The specific parameters of the LXRD micro-area residual stress analyzer are as follows: Size: 1.1 × 0.8 × 1.9 m; Recommended Maximum Part Size: 300 mm; Focusing axis (Z): 300 mm; Optional Cloud Mapping Platform (X, Y): 100 × 100 mm; Phi Rotary Table: 300 mm, angle of rotation (0–360°); Specimen stage: 180 mm; High Voltage Generator Power: 3000 W; Goniometer: MG2000 + chi axis.

The LXRD micro-area residual stress analyzer employs X-ray diffraction to irradiate crystalline material with X-rays of a certain wavelength. Due to the regular arrangement of atoms or ions encountered within the crystallization and scattering, the X-rays are scattered in some directions, and the phase is strengthened, resulting in a unique diffraction phenomenon corresponding to the crystalline structure. This is manifested in the drift of peaks in the X-ray diffraction spectra. When compressive stress is present, the distance between the crystal faces reduces, leading to a shift in the diffraction peaks towards a higher angle. In contrast, tensile stress causes the distance between the crystal faces to expand, resulting in the diffraction peaks shifting towards a lower angle.

2.1. X-ray Diffraction (XRD)

X-ray diffraction has been used extensively for residual stress measurements in tests [19,20,21], and XRD measurements of stress are based on the Bragg equation.

The principle of the X-ray diffraction method [22,23] is based on the phenomenon that the crystallographic plane spacing changes with residual stress, which leads to a shift in the Bragg diffraction peaks, and the distance of this shift is related to the magnitude of the stress. The method uses X-rays with a wavelength of $\lambda$ to irradiate the specimen at different angles of incidence, measure the corresponding diffraction angle $2\theta$, and calculate the corresponding slope $M$. The residual stress ${\sigma }_{\phi }$ can be calculated.

$${\sigma }_{\phi }=-\frac{E}{2(1+v)}\mathrm{c}\mathrm{o}\mathrm{t}{\theta }_0\frac{\pi }{180}\frac{\partial \left(2\theta \right)}{\partial \left({\mathrm{s}\mathrm{i}\mathrm{n}}^2\psi \right)}$$

(1)

where $E$ is modulus of elasticity, $v$ is the Poisson’s ratio, ${\theta }_0$ is the Bragg angle of the diffraction peak of the unstressed specimen. Thus,

$$K=-\frac{E}{2\left(1+v\right)}\cot {\theta }_0\frac{\pi }{180}, M=\frac{\partial \left(2\theta \right)}{\partial \left({\mathrm{s}\mathrm{i}\mathrm{n}}^2\psi \right)}$$

(2)

Then,

$${\sigma }_{\phi }=K\cdot M$$

(3)

where $K$ is a constant related only to the nature of the material, the selected diffracting surface HKL, when the measured samples are of the same material and the selected diffracting surface indices are the same, $K$ is a fixed value and is called the stress coefficient. $M$ is the slope of $2\theta$ versus ${\mathrm{s}\mathrm{i}\mathrm{n}}^2\psi$.

The principle of the XRD method is shown in Figure 5.

Before conducting the residual stress test, it is essential to perform a physical phase analysis of the device micro-solder joints. First, utilize XRD equipment to gather high angle information on the micro-solder joint material exceeding 120–150° and the surface information of the 2 crystalline structures. This process will help you to select the suitable target material for testing residual stress using the LXRD micro-area residual stress analyzer. The physical phase analysis equipment and device test samples are presented in Figure 6, featuring identical structural dimensions and a finite element calculation model.

The instrument utilized for this experiment was a Bruker D8a X-ray diffractometer. The machine was manufactured by Bruker Company and operated under the following working conditions. Cu-Kα radiation was produced by a source with a wavelength (λ) of 0.15406 nm, whilst employing a working tube current of 40 mA and a tube voltage of 40 kV, with continuous scanning mode at 4°/min. Data were gathered between 10° and 80°. The physical phases were identified, and macrostructural information was analyzed using MDI Jade5.0 software.

2.1.1. XRD Pattern of the Encapsulated Cover on the Front Side of the Sample

The test sample is CBGA, and the specific structural parameters are shown in

Table 1. Parameters of the main structure of the CBGA.

	Number	Size
PCB	1	150.00 mm × 150.00 mm × 2 mm
Solder ball	64	Diameter: 0.6 mm Spacing: 1.2 mm
Chip	1	42.36 mm × 40.16 mm × 450 μm
Ceramic	1	50.00 mm × 50.00 mm × 1.00 mm
Cover	1	48.36 mm × 48.36 mm × 600 μm

. Temperature conditions of the experiment: 23 ± 2 °C.

The cover material consists of 4J29 alloy, also referred to as Kovar alloy. This alloy has a linear expansion coefficient similar to silica–boron hard glass from 20 to 450 °C, boasts a high Curie point, and exhibits exceptional low-temperature organizational stability. The oxide film of the alloy is compact and easily penetrable by the glass. The alloy’s modulus of elasticity E is 138 GPa, with specific physical properties listed in

Table 2. Physical properties of Kovar.

Properties	Temperature (°C)/Treatment	Numerical Value
Density	/	8.35	$\mathrm{g}/{\mathrm{c}\mathrm{m}}^3$
Melting point	/	1450	${}^{\circ }\mathrm{C}$
Specific heat capacity	0 430	439.61 648.95	$\mathrm{J}/(\mathrm{k}\mathrm{g}\cdot \mathrm{k})$
Coefficient of linear expansion	30–200 20–300 20–400 20–500	43–53 45–55 44–52 56–64	${10}^{-6} {}^{\circ }\mathrm{C}$
Brinell hardness	Annealing Cold working	150 200–250	$\mathrm{k}\mathrm{g}/{\mathrm{m}\mathrm{m}}^2$
Young’s modulus	/	14,000	/
Resistivity	25	49	$\mathsf{\Omega }·\mathrm{c}\mathrm{m}$

.

In this study, the X-ray diffraction (XRD) phase search software was utilized to analyze the XRD patterns between 120–150° of the encapsulated cover plate on the front side of the test sample. After a comparison with the PDF standard diffraction patterns, it was identified that the plate may contain two phases, namely Au_9.9 Fe_0.1 (PDF No:00–040–1295) and CoSc (PDF No:00–019–0360). As the concentration of other phases is too low to be detected through XRD phase analysis, they cannot be confirmed. The XRD pattern between 120–150° on the front side of the sample is presented in Figure 7b. Partial phase retrieval results are shown in Figure 8.

2.1.2. XRD Pattern of BGA Solder Joints on the Back Side of the Sample

The back side of the test sample, which is at the BGA solder joints, was analyzed using XRD phase search software and shown in Figure 9. After a comparison with the PDF standard diffraction pattern, the main composition of the measured sample may be Rh₃Zr (PDF NO:00-017-0049) and Nb₆C₅ (PDF NO:00-037-1201), but also some Au₉Hg, RuZr, Cu_9.9 Fe_0.1, Cu_0.948 Sn_0.052, CuGe, Na_0.66Au_2.66O₄, etc. Some of the main phase XRD patterns at 120–150° are shown in Figure 10.

2.2. Measurement of Residual Stress

After completing the preparation work, the front and back side tests are conducted. The operation process for the LXRD micro-area residual stress analyzer is as follows: turn on the power supply, excite the high-voltage generator of the X-ray tube, and bombard the target material with high-pressure electrons, resulting in the production of X-rays. First, the device will be positioned on the carrier platform. The X-ray tube and goniometer will be rotated to different angles to radiate the surface of the welded joints. Dual detectors will accept X-ray diffraction cones at various angles and convert them into photoelectric digital signals for the computer. Secondly, the analysis and processing software examines the diffraction peaks gathered by the detectors to determine the alteration of diffraction angle, and subsequently, the alteration of lattice spacing. Lastly, the stress equation is used to compute the residual stress of the material after ellipse fitting in accordance with Hooke’s Law and elastic mechanics. The test site and samples are illustrated in Figure 11 and Figure 12.

3. Finite Element Methods

Welding is a multi-physical field process that generates a melting zone with uneven and unstable temperature fields of the weldment due to time-dependent heat input. This creates residual stress and weld distortion. The weld’s temperature field drives residual stress by inducing phase changes and strains caused by thermal stress and fluctuations in metal state and crystal structures. Therefore, analyzing the weld temperature field is necessary to conduct finite element analysis of weld residual stress.

3.1. Theory of the Welding Temperature Field

Since this paper employs ANSYS APDL as the finite element simulation software to investigate residual stress in crystal structures of electronic device materials, and since there is no welding heat source needed for the welding process in this software, it is necessary to customize the welding heat source parameters, such as the density of heat flow, shape, and moving path. Since the temperature field constantly changes during welding, the welding process can be considered a transient heat-transfer process. This process can be expressed by Equation (4) [24,25].

$$\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+q$$

(4)

where $q$ is the strength of the heat source, $\rho$ is the density of the material, $c$ is the specific heat capacity, $T$ is the temperature, $k$ is the coefficient of thermal conductivity, and $t$ is the time.

The equation above represents the basic principle used to simulate the temperature distribution via finite element analysis. However, to ensure consistency with the actual welding heat source, a Gaussian heat source model was chosen for the finite element simulation of the welding heat source in this study [26,27,28,29]. Equation (5) displays the selected model.

$$q(r)=q_m{e}^{-\left(\frac{3r^2}{R^2}\right)}$$

(5)

where $q_m$ is the maximum heat flow density in the center of the heating spot; $R$ is the effective heating radius of the arc; $r$ is the distance from the center of the arc heating spot.

For the moving heat source, the maximum heat flow density in the center of the arc heating spot is:

$$q_m=\frac{3}{\pi R^2}Q$$

(6)

where $Q$ is the effective thermal power of welding.

3.2. Finite Element Simulation of CBGA Residual Stress

ANSYS finite element analysis software is utilized to simulate and analyze the residual stress following reflow soldering of both the sample encapsulation cover and BGA solder joints [30,31,32]. Material interfaces are fully connected with each other in the established finite element model, as demonstrated in Figure 13. Technical abbreviations will be defined when first used throughout the remaining document. In order to maintain generality, the model comprises four identical chips, with BGA solder joints and a PCB assembly. The chip connects to the PCB substrate through lead-free BGA solder joints. ANSYS software is used to establish the connection between the chip, solder joints, and PCB using the GLUE command. Technical abbreviations will be explained on their first usage. To ensure accurate calculation results, we utilized a software simulation based on the principle of minimum energy surface to obtain the structural dimensions of the BGA solder joints. We then employed the mapping mesh delineation method for finite element model meshing, performing local mesh refinement where necessary. This resulted in a finite element model meshed according to 337,152 cells and 414,317 nodes.

Table 3. Material properties.

Material	Thermal Conductivity [W/(m·K)]	Coefficient of Thermal Expansion (10–6/°C)	Modulus of Elasticity (GPa)	Poisson’s Ratio	Density (kg·m−3)	Specific Heat Capacity [J/(kg·K)]
SAC305	50	25	38.70– 0.176 t*	0.35	8410	192
Chip	84	2.6	130	0.28	2320	750
PCB	0.32	13.62	6.50	0.28	1870	1150

Note: t* means the temperature of the SAC305 solder.

shows the parameters of the material used in the model, broken down by each part of the finite element model.

4. Results and Discussion

The ANSYS software is used for finite element analysis of residual stress after reflow soldering in the sample encapsulation cover and BGA solder joints [33,34,35]. The process considers the interaction between two physical fields: temperature and structure. To conduct multi-physical field analysis, ANSYS software offers two methods: direct coupling and indirect coupling. This project uses the indirect coupling analysis method. That is, the methodology involves conducting transient thermal analysis of the model to obtain the temperature field of the finite element analysis model, and then utilizing the obtained temperature field results as a body load in the thermal–structural coupling analysis. The thermal analysis unit type employed is Solid70, while the structural analysis unit type used is Solid185. The initial and reference temperatures are set to 25 °C. The thermal convection coefficient is 125 W/(m·K). Thermal convection is selected to thermally load the outer surface of the model.

In this paper, we present an experimental and transient temperature field thermal analysis simulation of a loaded reflow temperature profile for lead-free solder. As shown in Figure 14, the temperature profile comprises four regions: preheating, holding, reflow, and cooling zones. We provide a detailed analysis and causal connections between the different zones. SAC305 solder has a melting point temperature of 217 °C with a difference of 29.8 °C between its solidification and melting points. This means that the cooling solidification temperature of the joints is 187.2 °C, which corresponds to point a in Figure 14.

When analyzing residual stress in the BGA solder joint model after reflow soldering, a convective load is applied uniformly to all model outer surfaces while the initial temperature of the model is set at the cooling and solidification temperature of the solder joints (187.2 °C). Please refer to Figure 14 for further clarification. The simulation analysis begins at the 210th second, which corresponds to the cooling and solidification temperature of the lead-free solder joints in the reflow soldering temperature curve’s cooling section. From here, the cooling temperature is gradually lowered for 150 s until the 360th second, and then continues cooling for another 600 s until the 960th second. The simulation analysis concludes at the 960th second. Cooling continues until the 360th second (point b), then for another 600 s until the 960th second (point c). The 960th second is considered to be the conclusion of the simulation analysis.

Displacement constraints are applied to the four corners of the bottom surface of the PCB in the model. Von Mises equivalent stress is used to describe the residual stress of the encapsulation cover and solder joints after soldering. Then, the residual stress in the model is simulated and analyzed. The resulting residual stress distribution structure of the encapsulation cover is shown in Figure 15, while the results of residual stress and strain distributions of the BGA solder joints after soldering are shown in Figure 16. Remember to explain all technical term abbreviations when first using them.

Based on the symmetry of the chip, we use the Z-coordinate constraint at the center of the bottom surface of the substrate as the reference displacement. We observe the warping and deformation of the encapsulated cover under this constraint after the thermal process. Initially, we assume the bottom’s surface of the encapsulation substrate to be an absolute plane, which corresponds to the reference surface in the actual measurement. When the temperature fluctuates, the warpage value of the CBGA encapsulation cover also fluctuates accordingly.

It is evident that the initial state samples exhibit some degree of warpage, resulting from the product’s manufacturing process and other influencing factors. However, the finite element simulation represents an ideal state that cannot replicate the warping deformation of the sample’s initial state. From the simulation results of warpage deformation of the CBGA encapsulation cover, it is evident that the warpage value gradually increases with rising temperatures and decreases and returns to its initial state as temperatures decrease. The maximum warpage value and its trend are consistent with the measured value.

Due to the simulation analysis of thermal deformation, the model has been suitably simplified. However, there are structural disparities between the model and the actual product, and the simulation does not account for material heterogeneity and other factors, which leads to a deviation between the obtained simulation results and the measured ones. From the above analysis, it is evident that simpler packaging structures and uniform material composition lead to a smaller discrepancy between thermal deformation simulation and measurement outcomes. Therefore, simulation analysis is more effective when studying the influence of a single structure and material on the law of thermal deformation. However, it is challenging to use it as a quantitative method for characterizing thermal deformation in complex structures like the crystal structures of electronic device materials.

As shown in Figure 15, the residual stress distribution on the encapsulation cover is highly imbalanced, which is closely tied to varying moduli of elasticity and coefficients of thermal expansion among different materials. Residual stress distribution is predominantly concentrated in the contact region between the chip and different materials, with highly uneven distribution. With temperature changes, the value of residual stress on the encapsulation cover plate also changes; however, its distribution remains relatively unchanged. The area of residual stress concentration on the encapsulation cover is consistently found in the combination of different materials. It is the variation in material parameters, such as the coefficient of thermal expansion, that causes significant residual stress and strains in the encapsulation cover at high temperatures. This is the underlying cause of the CBGA encapsulation cover’s thermal warping and surface deformation.

As shown in Figure 16, the residual stress of BGA solder joints is unevenly distributed throughout the array after soldering. The stress exhibits a gradual increase from the middle to the area where the solder joints make contact with the PCB and the chip in a single joint. The maximum residual stress value is 39.1 MPa, and it occurs in the area where the solder joints make contact with the chip. Among the three materials in the model, the BGA solder ball has the highest thermal expansion coefficient, and the chip has the lowest. The difference in thermal expansion coefficient between these two materials is also the greatest, resulting in higher residual stress in the area where the BGA solder joint comes into contact with the chip.

The weld ball diagonal to the weld joint array and furthest from its center exhibits the highest residual stress. Residual strain in the solder joint array is also unevenly distributed, with the greatest residual strain values occurring farther away from the center of the array. As shown in Figure 16b, the maximum residual strain value reaches $0.772\times {10}^{-3}$. Technical abbreviations will be explained when first used. The maximum residual strain occurs at the same location as the maximum residual stress. This is because the thermal deformation is greater the farther away from the center of the BGA, resulting in increased stress and strain at the BGA welded joints located in that area. This is because thermal deformation increases with the distance from the center of the BGA. As a result, BGA solder joints located in these areas generate greater stress and strain. This also results in the highest residual stress and strain after reflow soldering.

As the residual stress position measured in the test was at the edge of the solder joint, the simulation results show the residual stress value at the node of the same position.

Table 4. Comparison of residual stress values between simulation and test for soldered joints.

Maximum Value of Residual Stress	Test (MPa)	Simulation (MPa)	Standard Deviation *
Edge Solder Joints	35.3	39.1	10.76%
Middle Solder Joints	20.9	23.7	13.40%

Note: $\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{d} \mathrm{d}\mathrm{e}\mathrm{v}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{*}=\left|\left(\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{s}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}-\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}\right)/\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}\right|\times 100\%$.

presents a comparison of the aforementioned test results with the simulation results, using the experimental modulus of elasticity value of SAC305 in the simulation and calculating the stress value as the Young’s modulus multiplied by the maximum strain of the material. According to the experimental measurements, the simulation results show good agreement, verifying the paper’s finite element simulation method as more accurate for analyzing post-soldering residual stress within BGA-soldered joints.

Next, we varied the solder joint diameter, solder joint height, and solder joint spacing in the finite element model of BGA solder joints to evaluate the impacts of these parameters on the maximum post-solder residual stress of BGA solder joints.

The height of the solder joint, pad diameter, and spacing between solder joints was set to 0.40 mm, 0.48 mm, and 1.20 mm, respectively, during a one-way analysis of the solder joint diameter. Other parameters remained consistent with those used in the sensitivity analysis. Only the diameter of the solder joints was changed, and was set to 0.55 mm, 0.60 mm, 0.65 mm, 0.70 mm, and 0.75 mm, respectively. Five finite element models were established to analyze residual stress in reflow soldering.

Table 5. Effect of solder joint diameter on residual stress.

Diameter (mm)	0.55	0.6	0.65	0.7	0.75
Maximum value of residual stress (MPa)	37.243	38.304	38.828	39.516	40.632

presents the results of the finite element analysis of post-soldering residual stress for five different diameters of BGA solder joints.

A one-way analysis was conducted with regard to the height of solder joints. The solder joint diameter, pad diameter, and solder joint spacing were fixed at 0.60 mm, 0.48 mm, and 1.20 mm, respectively. Only the height of the solder joint was varied, with values of 0.36 mm, 0.38 mm, 0.40 mm, 0.42 mm, and 0.44 mm. Other parameters and sensitivity analysis factors were kept consistent. Accordingly, the establishment of five finite element models and analysis of post-solder residual stress after reflow soldering resulted in finite element analysis results being obtained for maximum post-solder residual stress values of BGA solder joints of different heights. These results are presented in

Table 6. Effect of solder joint height on residual stress.

Height (mm)	0.36	0.38	0.40	0.42	0.44
Maximum value of residual stress (MPa)	39.776	39.473	38.163	38.022	36.835

.

We conducted a one-way analysis of the spacing of solder joints. The solder joint diameter was set to 0.60 mm, the solder joint height to 0.40 mm, and the pad diameter to 0.48 mm. Sensitivity analysis was performed on other parameters while maintaining their values, with only the solder joint pitch being varied at 0.80 mm, 0.90 mm, 1.0 mm, 1.1 mm, and 1.2 mm. Abbreviations will be explained when first used. Following the establishment of finite element models and re-flow soldering residual stress analysis, the results of maximum residual stress for BGA solder joints with five different pitches are presented in

Table 7. Effect of solder joint spacing on residual stress.

Spacing (mm)	0.8	0.9	1.0	1.1	1.2
Maximum value of residual stress (MPa)	38.512	38.657	38.828	39.425	40.162

.

As indicated in Table 5, the highest residual stress within the BGA joints rises as the joint diameter increases; while in Table 6, the highest residual stress in the BGA joints decreases as the joint height increases. Table 7 demonstrates that the peak residual stress in the BGA joints climbs as the spacing between joints increases.

5. Conclusions

In this paper, we analyze the residual stress of different components in crystal structures of electronic device materials following exposure to elevated temperatures using a combination of experimental tests and finite element simulations. We can infer the following conclusions.

• In this study, a micro-area residual stress test system was constructed to examine the residual stress of CBGA after welding. The system was based on the Bragg’s equation, a three-dimensional stress model of X-ray measurement, and the diffraction conditions of each material of CBGA. To calculate the stress equation in accordance with Hooke’s law and the theory of Elasticity, an ellipse fitting approach was applied. The final results of the test revealed the distinctive features of the residual stress distribution of the CBGA cover plate and the soldering joints following welding.
• As temperatures fluctuate, the residual stress on the encapsulation cover will shift correspondingly, but its distribution will remain largely unchanged. The combination of different materials always creates a residual stress concentration area on the encapsulation cover. This is due to differences in material parameters such as thermal expansion coefficients, which generate significant residual stress and strain in the encapsulation cover at high temperatures. As such, thermal warping and deformation of the surface of the CBGA encapsulation cover occur.
• The distribution of residual stress after reflow soldering of BGA solder joints is non-uniform throughout the solder joint array. Additionally, within each solder joint, the residual stress gradually increases from the central portion to the contact area between the solder joint and both the PCB and the chip. The region of maximum residual stress is located in the area where the solder joint connects with the chip.
• The discrepancy between experimental measurements and simulation outcomes of the residual stress following reflow soldering of CBGA-assembled micro-solder joints is less than 14%. Therefore, it can be inferred that the simulation results are well-suited to the intended purpose. The residual stress of BGA solder joints is heavily impacted by three factors: solder joint diameter, spacing, and height. The height of the solder joint is inversely proportional to the maximum residual stress, whereas the diameter and spacing of the joint are positively proportional to it.