The Effects of Chlorine Doping on the Thermoelectric Properties of Bi2O2Se
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussions
3.1. Structural Properties of Pristine and Cl-Doped Bi2O2Se
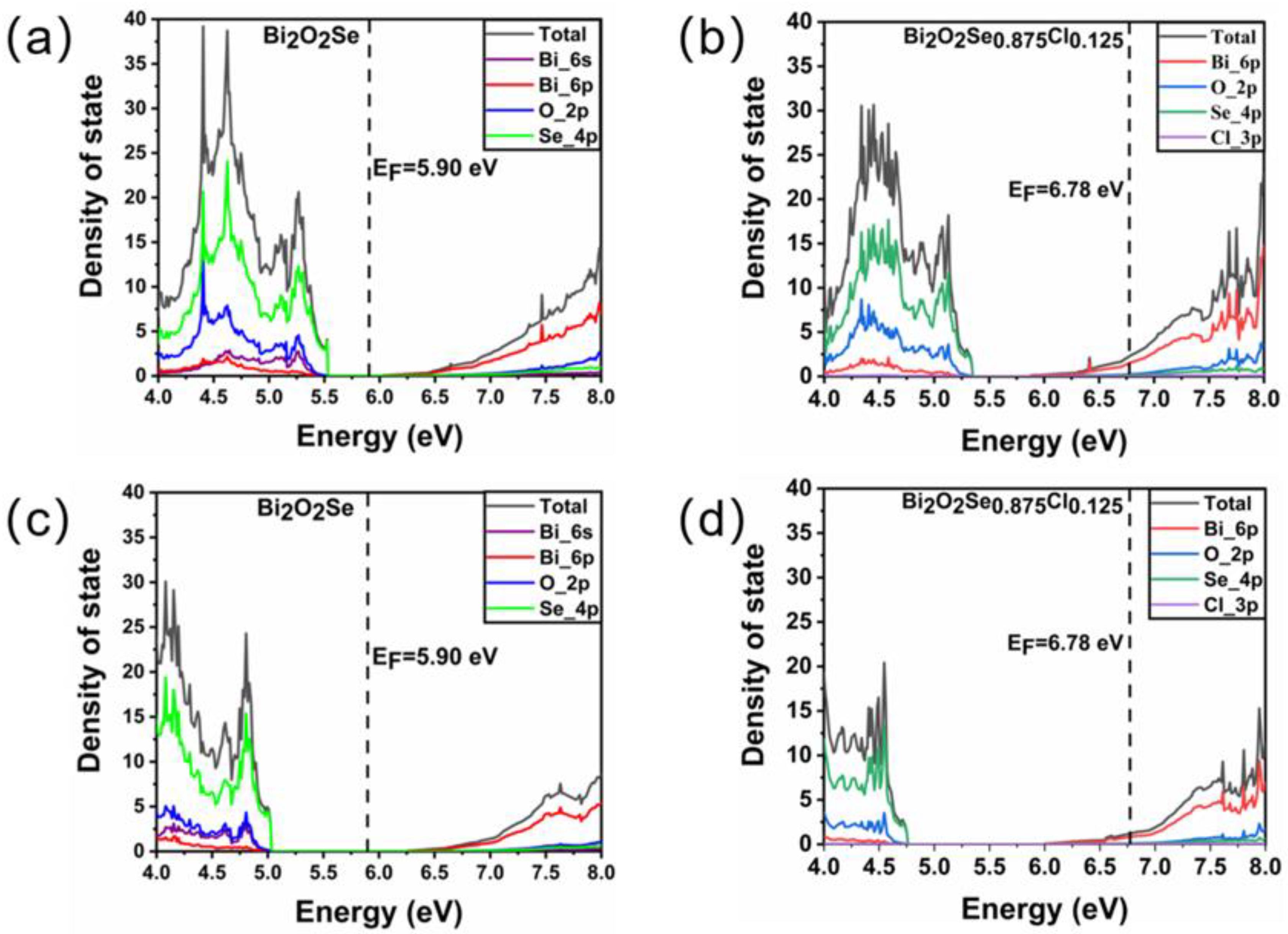
3.2. The Influence of Cl Doping on the Electronic Structure of Bi2O2Se
3.3. Thermal Transport Properties of Bi2O2Se and Bi2O2Se0.875Cl0.125
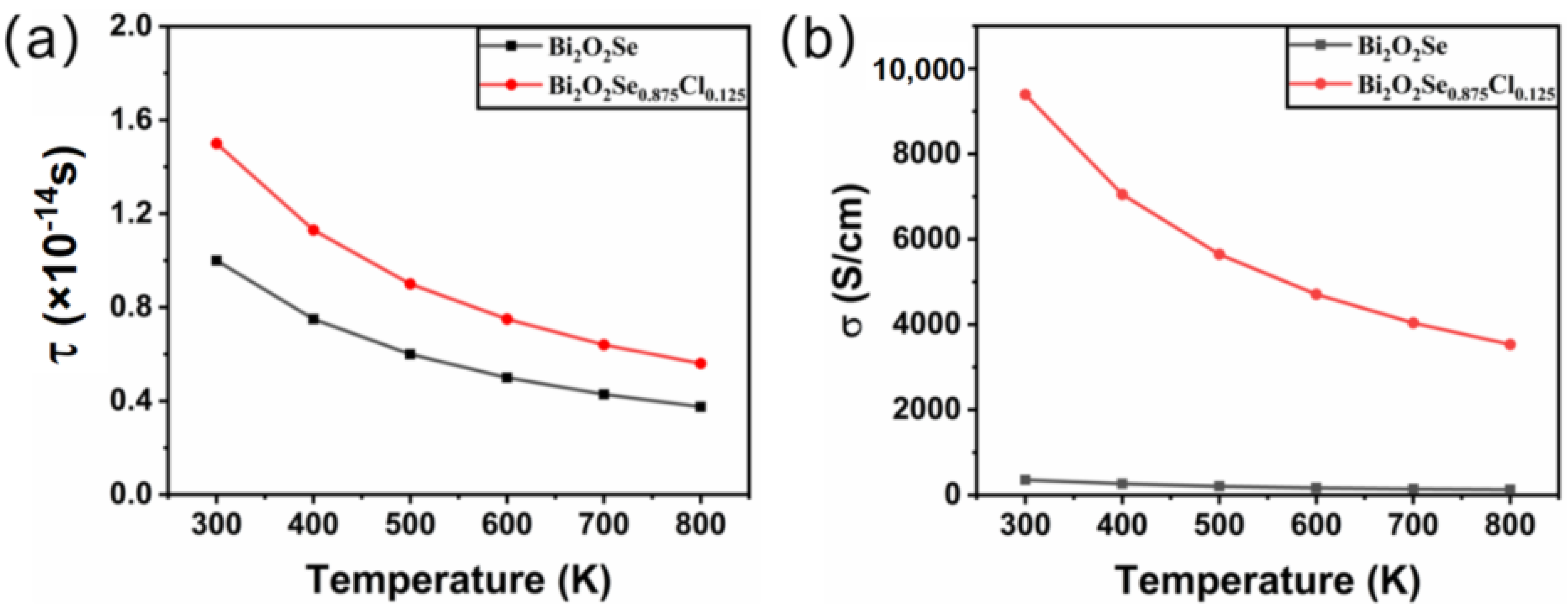
3.3.1. Relaxation Time and Electrical Conductivity of Pure and Cl-Doped Bi2O2Se
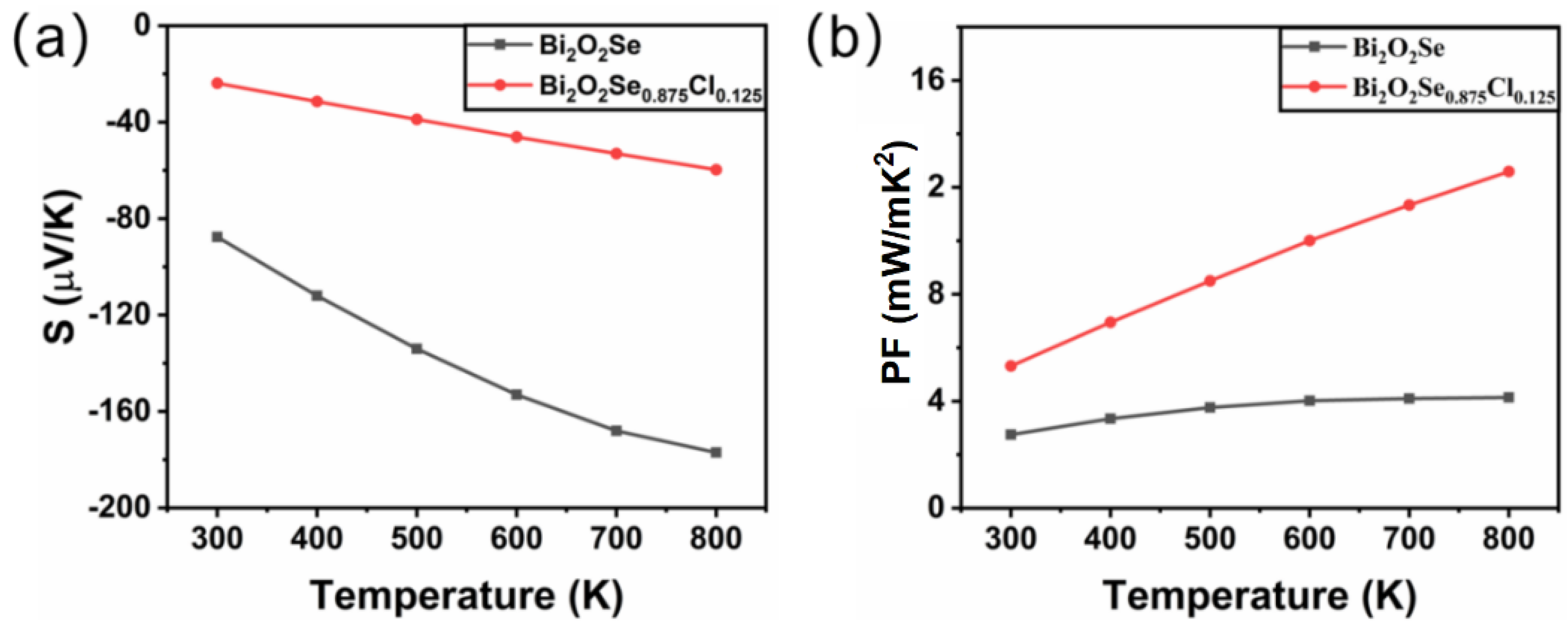
3.3.2. Seebeck Coefficient and Power Factor of Bi2O2Se and Bi2O2Se0.875Cl0.125
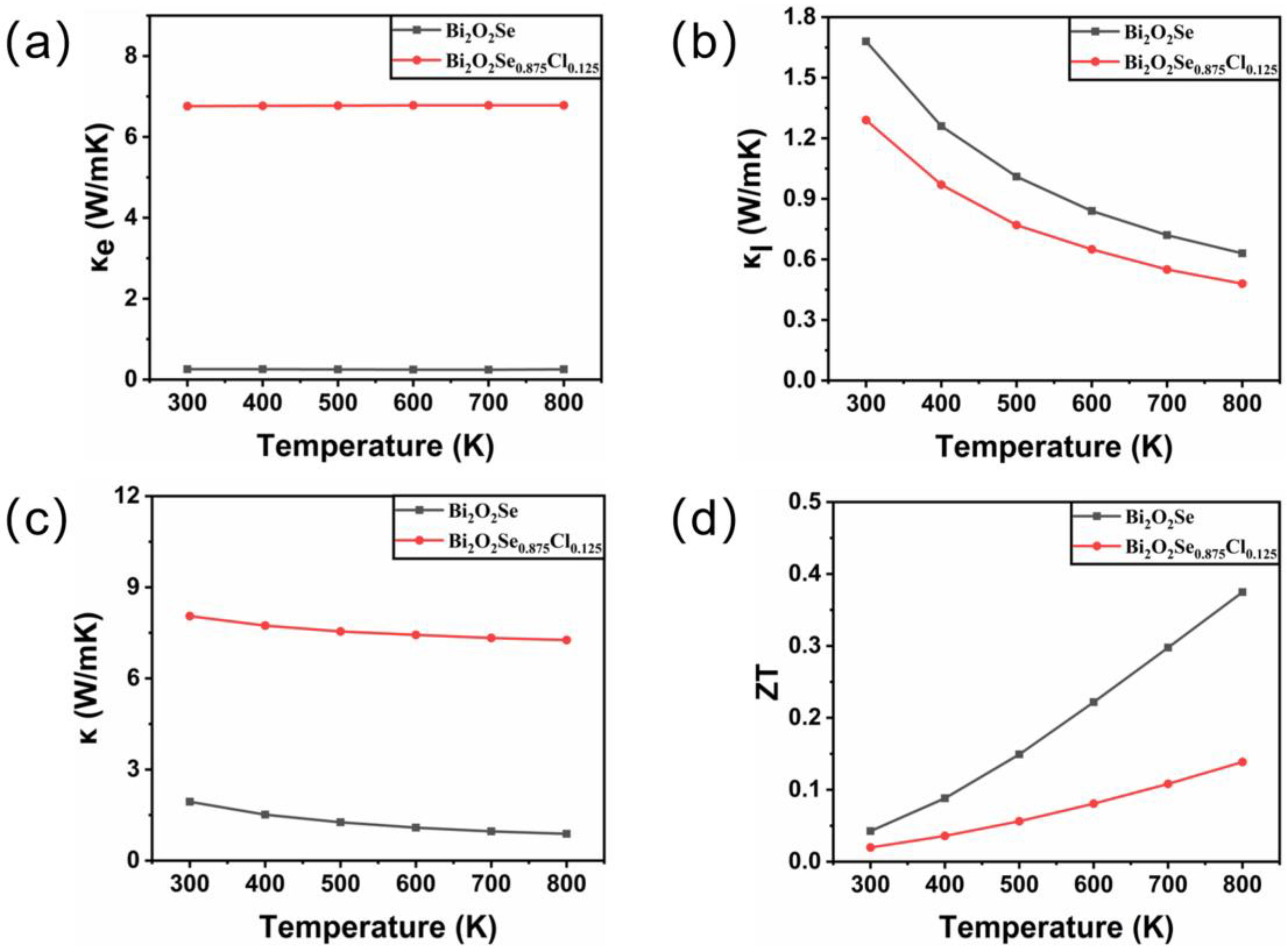
3.3.3. Thermal Conductivity and Figure of Merit ZT of Pure and Cl-Doped Bi2O2Se
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen production, storage, transportation and key challenges with applications: A review. Energy Convers. Manag. 2018, 165, 602–627. [Google Scholar] [CrossRef]
- Ren, J.; Musyoka, N.M.; Langmi, H.W.; Mathe, M.; Liao, S. Current research trends and perspectives on materials-based hydrogen storage solutions: A critical review. Int. J. Hydrogen Energy 2017, 42, 289–311. [Google Scholar] [CrossRef]
- Yu, X.; Tang, Z.; Sun, D.; Ouyang, L.; Zhu, M. Recent advances and remaining challenges of nanostructured materials for hydrogen storage applications. Prog. Mater. Sci. 2017, 88, 1–48. [Google Scholar] [CrossRef]
- Liu, W.; Jie, Q.; Kim, H.S.; Ren, Z. Current progress and future challenges in thermoelectric power generation: From materials to devices. Acta Mater. 2015, 87, 357–376. [Google Scholar] [CrossRef]
- Zhu, H.; Xiao, C.; Xie, Y. Design of Highly Efficient Thermoelectric Materials: Tailoring Reciprocal-Space Properties by Real-Space Modification. Adv. Mater. 2018, 30, e1802000. [Google Scholar] [CrossRef] [PubMed]
- Boukai, A.I.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.K.; Goddard, W.A., 3rd; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef]
- Wang, N.; Li, M.; Xiao, H.; Gong, H.; Liu, Z.; Zu, X.; Qiao, L. Optimizing the thermoelectric transport properties of Bi2O2Se monolayer via biaxial strain. Phys. Chem. Chem. Phys. 2019, 21, 15097–15105. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 2008, 321, 554–557. [Google Scholar] [CrossRef]
- Tan, G.; Zhao, L.D.; Kanatzidis, M.G. Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 2016, 116, 12123–12149. [Google Scholar] [CrossRef]
- Hochbaum, A.I.; Chen, R.; Delgado, R.D.; Liang, W.; Garnett, E.C.; Najarian, M.; Majumdar, A.; Yang, P. Enhanced thermoelectric performance of rough silicon nanowires. Nature 2008, 451, 163–167. [Google Scholar] [CrossRef]
- Lu, W.; Ji, Z.; Pfeiffer, L.; West, K.W.; Rimberg, A.J. Real-time detection of electron tunnelling in a quantum dot. Nature 2003, 423, 422–425. [Google Scholar] [CrossRef]
- Heikes, R.; Ure, R., Jr. Thermo Electricity: Science and Engineering Intersciences; Interscience Publishers: New York, NY, USA, 1961; Volume 285, p. 40. [Google Scholar]
- Gelbstein, Y.; Dashevsky, Z.; Dariel, M.P. High performance n-type PbTe-based materials for thermoelectric applications. Phy. B 2005, 363, 196–205. [Google Scholar] [CrossRef]
- Fleischmann, H.; Luy, H.; Rupprecht, J. Neuere Untersuchungen an halbleitenden IV VI-1 V VI2-Mischkristallen. Zeitschri’ Für Naturforschung A 1963, 18, 646–649. [Google Scholar] [CrossRef]
- Wood, C. Materials for thermoelectric energy conversion. Rep. Prog. Phys. 1988, 51, 459–539. [Google Scholar] [CrossRef]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.K.; Kanatzidis, M.G. Cubic AgPb(m)SbTe(2+m): Bulk thermoelectric materials with high figure of merit. Science 2004, 303, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Rosi, F.; Hockings, E.; Lindenblad, N. Semiconducting materials for thermoelectric power generation. RCA Rev. 1961, 22, 82–121. [Google Scholar]
- Zhan, B.; Liu, Y.; Tan, X.; Lan, J.l.; Lin, Y.h.; Nan, C.W.; Zhou, X.D. Enhanced Thermoelectric Properties of Bi2O2Se Ceramics by Bi Deficiencies. J. Am. Ceram. Soc. 2015, 98, 2465–2469. [Google Scholar] [CrossRef]
- Li, Y.; Huo, H.; Huang, H.; Guo, K.; Yang, X.; Xing, J.; Luo, J.; Rao, G.-H.; Zhao, J.-T. Optimization of electrical and thermal transport properties of layered Bi2O2Se via Nb doping. J. Mater. Sci 2021, 56, 12732–12739. [Google Scholar] [CrossRef]
- Hong, H.Y.; Kim, D.H.; Won, S.O.; Park, K. Enhancement of the thermoelectric performance of n−type Bi2O2Se by Ce4+ doping. J. Mater. Res. Technol. 2021, 15, 4161–4172. [Google Scholar] [CrossRef]
- Song, C.; Song, Y.; Pan, L.; Chen, C.; Zong, P.; Wang, Y. Thermoelectric properties of Bi2TiO2Se with the shear exfoliation-restacking process. J. Alloys Compd. 2022, 892, 162147. [Google Scholar] [CrossRef]
- Yang, N.; Pan, L.; Chen, C.; Wang, Y. Effects of Sb-doping on the electron-phonon transport properties of Bi2O2Se. J. Alloys Compd. 2021, 858, 157748. [Google Scholar] [CrossRef]
- Pan, L.; Zhao, Z.; Yang, N.; Xing, W.; Zhang, J.; Liu, Y.; Chen, C.; Li, D.; Wang, Y. Effects of sulfur substitution for oxygen on the thermoelectric properties of Bi2O2Se. J. Eur. Ceram. Soc. 2020, 40, 5543–5548. [Google Scholar] [CrossRef]
- Fu, Z.; Jiang, J.-L.; Dong, S.-T.; Yu, M.-C.; Zhao, L.; Wang, L.; Yao, S.-H. Effects of Zr substitution on structure and thermoelectric properties of Bi2O2Se. J. Mater. Res. Thechnol. 2022, 21, 640–647. [Google Scholar] [CrossRef]
- Song, C.; Zhou, H.; Gu, Y.; Pan, L.; Chen, C.; Wang, Y. Enhanced thermoelectric properties of Bi2O2Se by Bi2Te2.7Se0.3 addition. J. Alloys Compd. 2023, 930, 167439. [Google Scholar] [CrossRef]
- Wang, S.; Su, L.; Qiu, Y.; Xiao, Y.; Zhao, L.-D. Enhanced thermoelectric performance in Cl-doped BiSbSe3 with optimal carrier concentration and effective mass. J. Mater. Sci. Technol. 2021, 70, 67–72. [Google Scholar] [CrossRef]
- Tan, G.; Hao, S.; Zhao, J.; Wolverton, C.; Kanatzidis, M.G. High thermoelectric performance in electron-doped AgBi3S5 with ultralow thermal conductivity. J. Am. Chem. Soc. 2017, 139, 6467–6473. [Google Scholar] [CrossRef]
- Zhang, Q.; Lan, Y.; Yang, S.; Cao, F.; Yao, M.; Opeil, C.; Broido, D.; Chen, G.; Ren, Z. Increased thermoelectric performance by Cl doping in nanostructured AgPb18SbSe20−xClx. Nano Energy 2013, 2, 1121–1127. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmu¨ller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, S.; Xiao, H.Y.; Singh, D.J.; Zhang, K.H.L.; Liu, Z.J.; Zu, X.T.; Li, S. Orbital controlled band gap engineering of tetragonal BiFeO3 for optoelectronic applications. J. Mater. Chem. C 2018, 6, 1239–1247. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J.; BoltzTra, P. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Morelli, D.T.; Slack, G.A. High Lattice Thermal Conductivity of Solids; Springer: New York, NY, USA, 2006; pp. 37–68. [Google Scholar]
- Serier, H.; Gaudon, M.; Ménétrier, M. Al-doped ZnO powdered materials: Al solubility limit and IR absorption properties. Solid State Sci. 2009, 11, 1192–1197. [Google Scholar] [CrossRef]
- Martínez, V.d.P.; Aguilar, C.; Marín, J.; Ordoñez, S.; Castro, F. Mechanical alloying of Cu–Mo powder mixtures and thermodynamic study of solubility. Mater. Lett. 2007, 61, 929–933. [Google Scholar] [CrossRef]
- Zhou, E.; Suryanarayana, C.; Froes, F.S. Effect of premilling elemental powders on solid solubility extension of magnesium in titanium by mechanical alloying. Mater. Lett. 1995, 23, 27–31. [Google Scholar] [CrossRef]
- Liu, R.; Lan, J.-L.; Tan, X.; Liu, Y.-C.; Ren, G.-K.; Liu, C.; Zhou, Z.-F.; Nan, C.-W.; Lin, Y.-H. Carrier concentration optimization for thermoelectric performance enhancement in n-type Bi2O2Se. J. Eur. Ceram. Soc. 2018, 38, 2742–2746. [Google Scholar] [CrossRef]
- Wu, J.; Tan, C.; Tan, Z.; Liu, Y.; Yin, J.; Dang, W.; Wang, M.; Peng, H. Controlled Synthesis of High-Mobility Atomically Thin Bismuth Oxyselenide Crystals. Nano Lett. 2017, 17, 3021–3026. [Google Scholar] [CrossRef]
- Boiler, I. Die Kristallstruktur von Bi2O2Se. Monatsh. Chem. 1973, 104, 916–919. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, P.; Qin, M.; Lou, Z.; Gong, L.; Xu, J.; Kong, J.; Yan, H.; Gao, F. Effect of La3+, Ag+ and Bi3+ doping on thermoelectric properties of SrTiO3: First-principles investigation. Ceram. Int. 2022, 48, 13803–13816. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, H.; Meng, M.; Chen, C.; Sun, Y.; Chen, Z.; Dang, W.; Tan, C.; Liu, Y.; Yin, J.; et al. High electron mobility and quantum oscillations in non-encapsulated ultrathin semiconducting Bi2O2Se. Nat. Commun. 2017, 12, 530–534. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Han, J.; Xu, B.; Lin, Y.H. Thermoelectric power factor of doped Bi2O2Se: A computational study. Phys. Chem. Chem. Phys. 2020, 22, 27096–27104. [Google Scholar] [CrossRef]
- Li, J.Q.; Cheng, C.; Duan, M.Y. The electronic and optical properties of multi-layer Bi2O2X (X = S, Se, Te) by first-principles calculations. Appl. Surf. Sci. 2023, 618, 156541. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, B.; Yu, G.; Zhang, J.; Ma, S.; Yuan, S.; Sun, T.; Wang, Y. Electronic structure and thermoelectric properties of Bi2O2Se with GGA and TB-mBJ potentials. Jpn. J. Appl. Phys. 2019, 58, 015501. [Google Scholar] [CrossRef]
- Tan, X.; Lan, J.-l.; Ren, G.; Liu, Y.; Lin, Y.-H.; Nan, C.-W. Enhanced thermoelectric performance of n-type Bi2O2Se by Cl-doping at Se site. J. Am. Ceram. Soc. 2017, 100, 1494–1501. [Google Scholar] [CrossRef]
- Li, M.; Wang, N.; Jiang, M.; Xiao, H.; Zhang, H.; Liu, Z.; Zu, X.; Qiao, L. Improved thermoelectric performance of bilayer Bi2O2Se by the band convergence approach. J. Mater. Chem. C 2019, 7, 11029–11039. [Google Scholar] [CrossRef]
- Liu, J.; Tian, L.; Mou, Y.; Jia, W.; Zhang, L.; Liu, R. Electronic and mechanical property of high electron mobility semiconductor Bi2O2Se. J. Alloys Compd. 2018, 764, 674–678. [Google Scholar] [CrossRef]
- Zhu, X.L.; Liu, P.F.; Xie, G.; Wang, B.T. First-principles study of thermal transport properties in the two- and three-dimensional forms of Bi2O2Se. Phys. Chem. Chem. Phys. 2019, 21, 10931–10938. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Y.; Pan, L.; Chen, C.; Zong, P.; Wang, Y. Enhancing thermoelectric performance of Bi2O2Se by W-doping with the shear exfoliation-restacking process. Mater. Lett. 2022, 308, 131291. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, J.; Chen, C.; Wang, Y. Enhanced thermoelectric properties of highly textured Bi2O2-Se1+ with liquid-phase mechanical exfoliation. Scr. Mater. 2020, 178, 376–381. [Google Scholar] [CrossRef]
- Smith, J.B.; Ehrenreich, H. Frequency dependence of the optical relaxation time in metals. Phys. Rev. B 1982, 25, 923–930. [Google Scholar] [CrossRef]
- Guo, D.; Hu, C.; Xi, Y.; Zhang, K. Strain Effects To Optimize Thermoelectric Properties of Doped Bi2O2Se via Tran–Blaha Modified Becke–Johnson Density Functional Theory. J. Phys. Chem. C 2013, 117, 21597–21602. [Google Scholar] [CrossRef]
- Sikam, P.; Moontragoon, P.; Ikonic, Z.; Kaewmaraya, T.; Thongbai, P. The study of structural, morphological and optical properties of (Al, Ga)-doped ZnO: DFT and experimental approaches. Appl. Surf. Sci. 2019, 480, 621–635. [Google Scholar] [CrossRef]
- Pei, Y.; Wang, H.; Snyder, G.J. Band engineering of thermoelectric materials. Adv. Mater. 2012, 24, 6125–6135. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, D.; He, D.; Feng, D.; Yin, M.; Qin, X.; He, J. Extraordinary Thermoelectric Performance Realized in n-Type PbTe through Multiphase Nanostructure Engineering. Adv. Mater. 2017, 29, 1703148. [Google Scholar] [CrossRef]
- Ruleova, P.; Drasar, C.; Lostak, P.; Li, C.P.; Ballikaya, S.; Uher, C. Thermoelectric properties of Bi2O2Se. Mater. Chem. Phys. 2010, 119, 299–302. [Google Scholar] [CrossRef]
- Islam, M.A.; Serles, P.; Kumral, B.; Demingos, P.G.; Qureshi, T.; Meiyazhagan, A.; Puthirath, A.B.; Abdullah, M.S.B.; Faysal, S.R.; Ajayan, P.M.; et al. Exfoliation Mechanisms of 2D Materials and Their Applications. Appl. Phys. Rev. 2022, 9, 041301. [Google Scholar] [CrossRef]
- Kim, M.; Park, D.; Kim, J. Enhancement of Bi2O2Se thermoelectric power factor via Nb doping. J. Alloys Compd. 2021, 851, 156905. [Google Scholar] [CrossRef]
- Stojanovic, N.; Maithripala, D.H.S.; Berg, J.M.; Holtz, M. Thermal conductivity in metallic nanostructures at high temperature: Electrons, phonons, and the Wiedemann-Franz law. Phys. Rev. B 2010, 82, 075418. [Google Scholar] [CrossRef]
- Wang, D.; He, W.; Chang, C.; Wang, G.; Wang, J.; Zhao, L.-D. Thermoelectric transport properties of rock-salt SnSe: First-principles investigation. J. Mater. Chem. C 2018, 6, 12016–12022. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Wang, J. Approaching extremely low thermal conductivity by crystal structure engineering in Mg2Al4Si5O18. J. Mater. Res. 2015, 30, 3729–3739. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Y.; Tian, Z.; Wang, J.; Wang, J. Theoretical exploration of the abnormal trend in lattice thermal conductivity for monosilicates RE2SiO5 (RE = Dy, Ho, Er, Tm, Yb and Lu). J. Eur. Ceram. Soc. 2018, 38, 3539–3546. [Google Scholar] [CrossRef]
- Shindé, S.L.; Goela, J. (Eds.) High Thermal Conductivity Materials; Springer: New York, NY, USA, 2006; p. 91. [Google Scholar]

| a0 | c0 | Volume | <Bi-O> | <Bi-Se> | ||
|---|---|---|---|---|---|---|
| Bi2O2Se | Our cal. | 3.917 | 12.357 | 189.592 | 2.337 | 3.311 |
| Exp. [42] | 3.88 | 12.16 | 183.06 | --- | --- | |
| Other cal. [43] | 3.90 | 12.39 | 188.45 | --- | --- | |
| Bi2O2Se0.875Cl0.125 | Our cal. | 3.946 | 12.287 | 191.320 | 2.339 | 3.336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Li, M.; Qi, H.; Zu, X.; Qiao, L.; Xiao, H. The Effects of Chlorine Doping on the Thermoelectric Properties of Bi2O2Se. Crystals 2023, 13, 1586. https://doi.org/10.3390/cryst13111586
Li B, Li M, Qi H, Zu X, Qiao L, Xiao H. The Effects of Chlorine Doping on the Thermoelectric Properties of Bi2O2Se. Crystals. 2023; 13(11):1586. https://doi.org/10.3390/cryst13111586
Chicago/Turabian StyleLi, Buda, Menglu Li, Hangbo Qi, Xiaotao Zu, Liang Qiao, and Haiyan Xiao. 2023. "The Effects of Chlorine Doping on the Thermoelectric Properties of Bi2O2Se" Crystals 13, no. 11: 1586. https://doi.org/10.3390/cryst13111586
APA StyleLi, B., Li, M., Qi, H., Zu, X., Qiao, L., & Xiao, H. (2023). The Effects of Chlorine Doping on the Thermoelectric Properties of Bi2O2Se. Crystals, 13(11), 1586. https://doi.org/10.3390/cryst13111586










