Superdense Hexagonal BP and AlP with Quartz Topology: Crystal Chemistry and DFT Study
Abstract
:1. Introduction
2. Computational Methodology
3. Results and Discussion
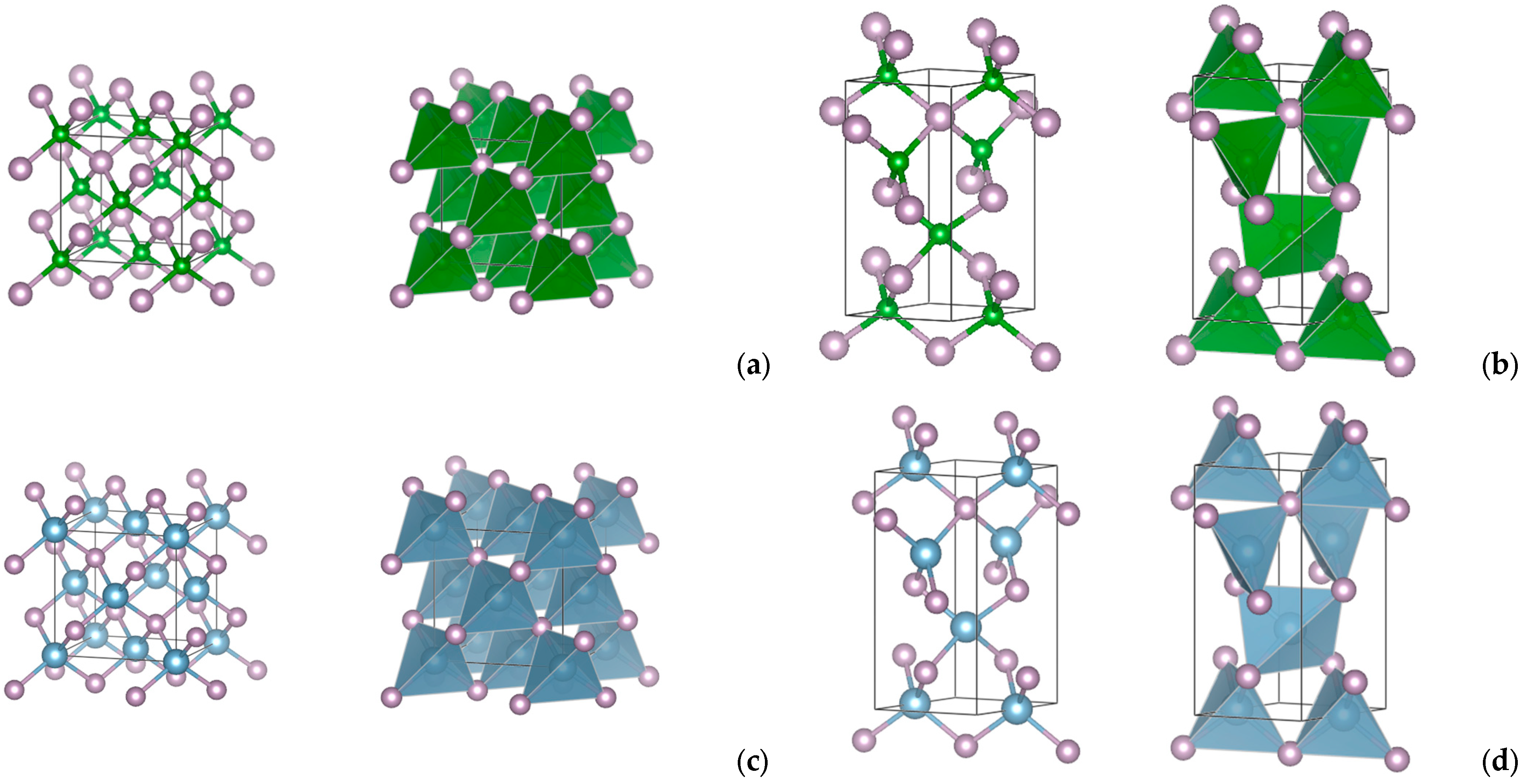
3.1. Crystal Structure
- In tetrahedral coordination as zinc-blende ZnS (space group , No. 216; dia topology) and wurtzite ZnO (space group P63mc, No. 186; lon topology);
- In octahedral coordination as rock salt NaCl (space group , No. 225; pcu topology) and NiAs (space group P63/mmc, No. 194; seh topology).
3.2. Projections of the Charge Densities
3.3. Mechanical Properties
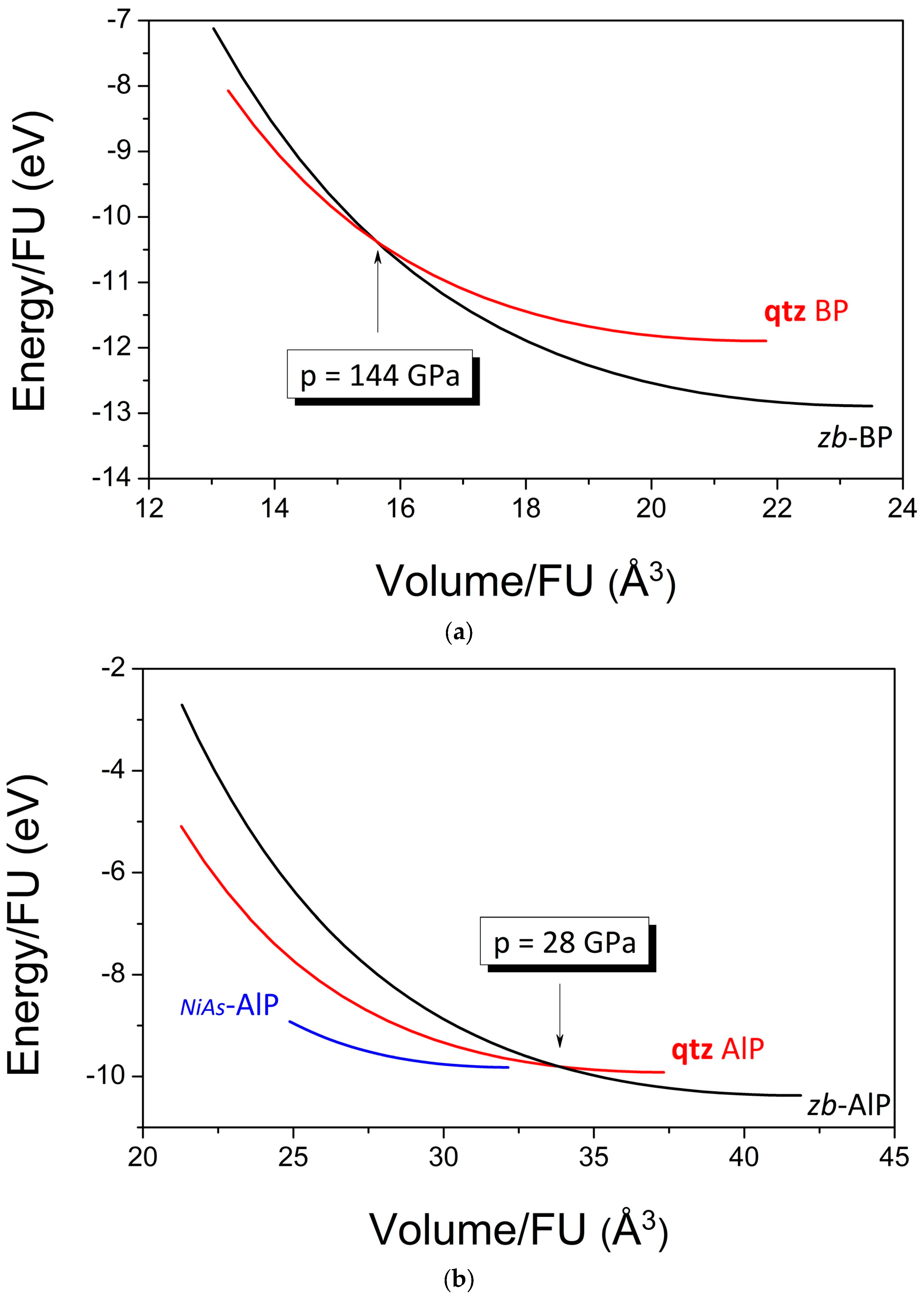
3.4. Equations of State and Possible High-Pressure Phase Transitions
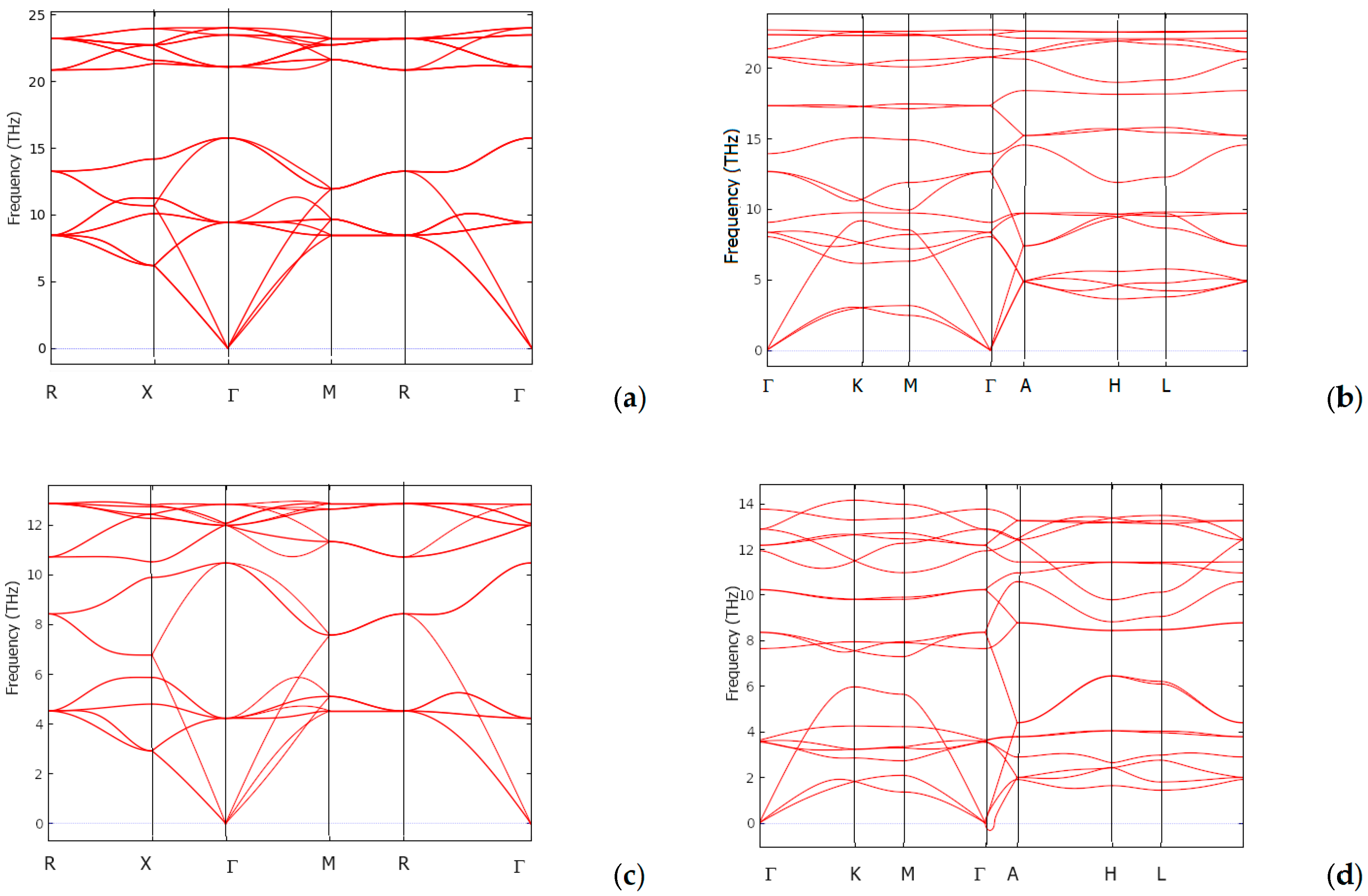
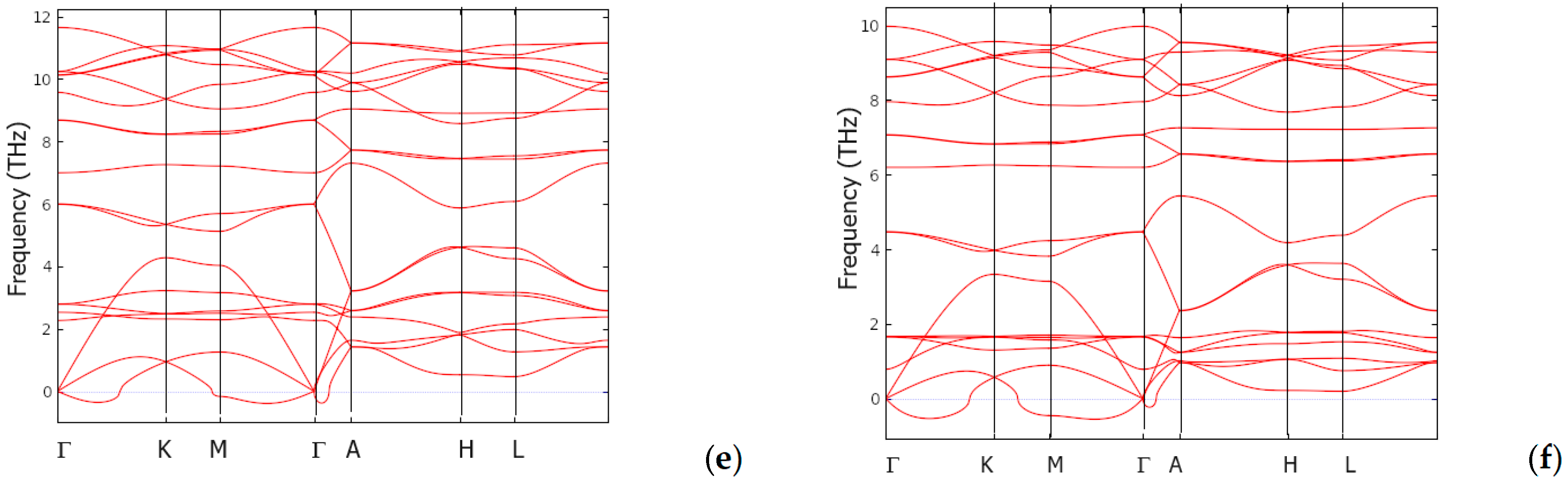
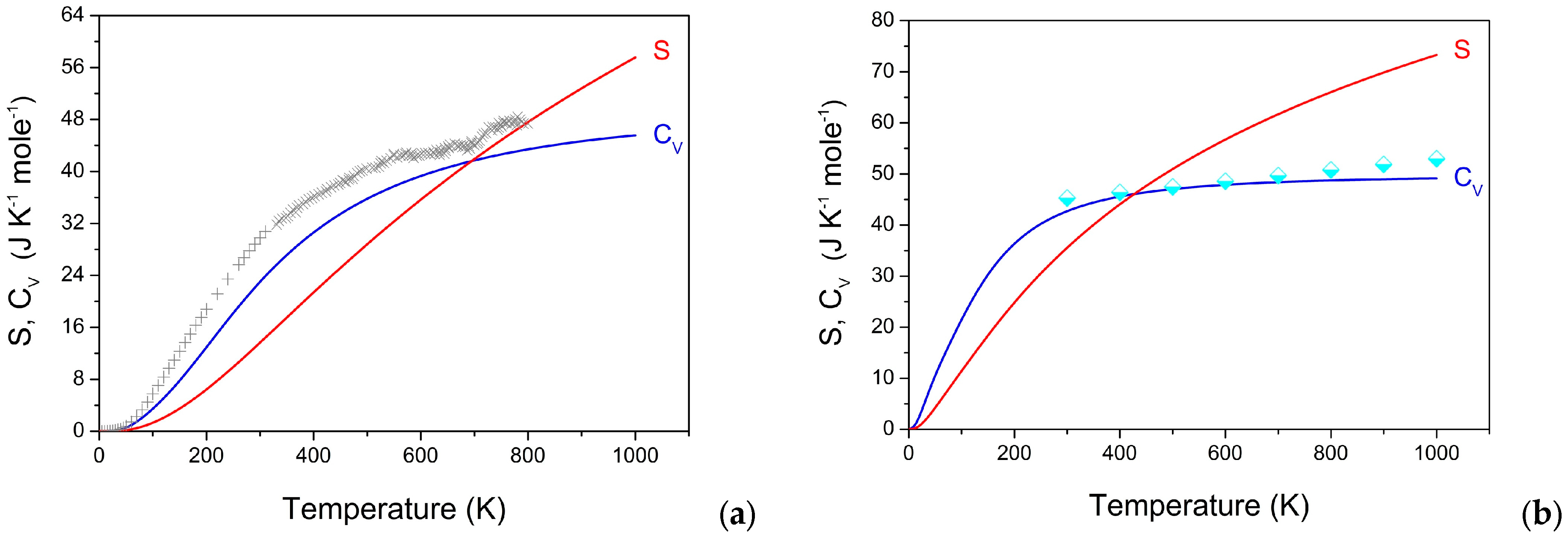
3.5. Dynamic and Thermodynamic Properties from the Phonons
3.6. Electronic Band Structures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Quillec, M. (Ed.) Materials for Optoelectronics; Kluwer Academic: Boston, MA, USA, 1996. [Google Scholar]
- Levinshtein, M.; Rumyantsev, S.; Shur, M. Handbook Series on Semiconductor Parameters; World Scientific: Singapore, 1999; Volume 1. [Google Scholar]
- Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band parameters for III-V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Adachi, S. Physical Properties of III-V Semiconductor Compounds. Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Evans, D.A.; McGlynn, A.G.; Towlson, B.M.; Gunn, M.; Jones, D.; Jenkins, T.E.; Winter, R.; Poolton, N.R.J. Determination of the optical band-gap energy of cubic and hexagonal boron nitride using luminescence excitation spectroscopy. J. Phys. Condens. Matter 2008, 20, 075233. [Google Scholar] [CrossRef]
- Agui, A.; Shin, S.; Kumashiro, Y. Electronic structure of BP studied by resonant soft X-ray emission spectroscopy. J. Phys. Soc. Jpn. 1999, 68, 166–169. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Matar, S.F. Polymorphism of boron phosphide: Theoretical and experimental assessments. J. Mater. Chem. C 2022, 10, 3937–3943. [Google Scholar] [CrossRef]
- Matar, S.F.; Solozhenko, V.L. Ultrahigh-density superhard hexagonal BN and SiC with quartz topology from crystal chemistry and first principles. Crystals 2023, 13, 1498. [Google Scholar] [CrossRef]
- McMahon, M.I.; Nelmes, R.J.; Wright, N.G.; Allan, D.R. Crystal structure studies of II-VI semiconductors using angle-dispersive diffraction techniques with an image-plate detector. AIP Conf. Proc. 1994, 309, 633–636. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.; Burke, K.; Ernzerhof, M. The Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Blöchl, P.; Jepsen, O.; Anderson, O. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef] [PubMed]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special k-points for Brillouin Zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef] [PubMed]
- Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Eyert, V. Basic notions and applications of the augmented spherical wave method. Int. J. Quantum Chem. 2000, 77, 1007–1031. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Shevchenko, A.P.; Shabalin, A.A.; Karpukhin, I.Y.; Blatov, V.A. Topological representations of crystal structures: Generation, analysis and implementation in the TopCryst system. Sci. Technol. Adv. Mat. 2022, 2, 250–265. [Google Scholar] [CrossRef]
- Luo, B.; Wu, L.; Zhang, Z.; Li, G.; Tian, E. A triatomic carbon and derived pentacarbides with superstrong mechanical properties. iScience 2022, 25, 104712. [Google Scholar] [CrossRef] [PubMed]
- Matar, S.F.; Solozhenko, V.L. First principles search for novel ultrahard high-density carbon allotropes: Hexagonal C6, C9 and C12. J. Superhard Mater. 2023, 45, 239–248. [Google Scholar] [CrossRef]
- Rundqvist, S. Crystal structure of boron phosphide BP. In Proceedings of the Congres International de Chimie Pure et Applique, Paris, France, 18–24 July 1957; Volume 16, pp. 539–540. [Google Scholar]
- Richman, D. Vapor phase growth and properties of aluminum phosphide. J. Electrochem. Soc. 1968, 115, 945–947. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Voigt, W. Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annal. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. The interrelation between hardness and compressibility of substances and their structure and thermodynamic properties. J. Superhard Mater. 2008, 30, 368–378. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Bushlya, V. Mechanical properties of boron phosphides. J. Superhard Mater. 2019, 41, 84–89. [Google Scholar] [CrossRef]
- Solozhenko, V.L. Hardness of new boron-rich chalcogenides B12S and B12Se. J. Superhard Mater. 2021, 43, 375–377. [Google Scholar] [CrossRef]
- Solozhenko, V.L. On hardness of boron subarsenide B12As2. J. Superhard Mater. 2022, 44, 377–378. [Google Scholar] [CrossRef]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Kurakevych, O.O.; Le Godec, Y.; Kurnosov, A.V.; Oganov, A.R. Boron phosphide under pressure: In situ study by Raman scattering and X-ray diffraction. J. Appl. Phys. 2014, 116, 033501. [Google Scholar] [CrossRef]
- Wiley, J.D. Semiconductors and Semimetals; Willardson, R.K., Beer, A.C., Eds.; Academic Press: New York, NY, USA, 1975; Volume 10. [Google Scholar]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Nation. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Xia, Q.; Ruoff, A.L. BP at megabar pressures and its equation of state to 110 GPa. J. Appl. Phys. 1993, 74, 1660–1662. [Google Scholar] [CrossRef]
- Greene, R.G.; Luo, H.; Ruoff, A.L. High pressure study of AIP: Transformation to a metallic NiAs phase. J. Appl. Phys. 1994, 76, 7296–7299. [Google Scholar] [CrossRef]
- Dove, M.T. Introduction to Lattice Dynamics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Ohsawa, J.; Nishinaga, T.; Uchiyama, S. Measurement of specific heat of boron monophosphide by AC calorimetry. Jpn. J. Appl. Phys. 1978, 17, 1059–1065. [Google Scholar] [CrossRef]
- Koshchenko, V.I.; Grinberg, Y.K.; Demidenko, A.F. Thermodynamic properties of AlN (5-2700 K), GaP (5-1500 K) and BP (5-800 K). Izv. Akad. Nauk SSSR Neorg. Mater. 1984, 20, 1787–1790. (In Russian) [Google Scholar]
- Neviak, S.O.; Sandulova, A.V. Thermodynamic characteristics of aluminum phosphide. Izv. Akad. Nauk SSSR Neorg. Mater. 1974, 10, 146–147. (In Russian) [Google Scholar]


| zb-BP (Z = 4) (No. 216) | qtz BP (Z = 3) P6422 (No. 181) | zb-AlP (Z = 4) (No. 216) | qtz AlP (Z = 3) P6422 (No. 181) | |
|---|---|---|---|---|
| a, Å | 4.541 (4.538 [28]) | 3.274 | 5.501 (5.463 [29]) | 3.854 |
| c, Å | – | 6.983 | – | 8.658 |
| Vcell, Å3 | 93.64 | 64.82 | 166.50 | 111.25 |
| V/FU, Å3 | 23.41 | 21.61 ΔVzb-qtz/FU = 1.80 | 41.63 | 37.08 ΔVzb-qtz/FU = 4.55 |
| Shortest bond, Å | 1.97 | 2.00 | 2.38 | 2.40 |
| Angles (deg.) | 109.47 | 109.17/90.2 | 109.47 | 106.39/92.20 |
| Atomic positions | B (4a) 0, 0, 0 P (4c) ¼, ¼, ¼ | B (3c) ½, 0, 0 P (3d) ½, 0, ½ | Al (4a) 0, 0, 0 P (4c) ¼, ¼, ¼ | Al (3c) ½, 0, 0 P (3d) ½, 0, ½ |
| Etotal, eV Ecoh/atom, eV Etotal/FU, eV | −51.59 −1.16 −12.89 | −35.73 −0.67 −11.91 ΔE/FU = −0.98 eV | −41.47 −0.88 −10.36 | −29.80 −0.66 −9.94 ΔE/FU = −0.427 eV |
| C11 | C12 | C13 | C33 | C44 | C66 | BV | GV | EV | |
|---|---|---|---|---|---|---|---|---|---|
| qtz C6 [27] | 1186 | 88 | 64 | 1162 | 549 | 517 | 441 | 550 | 1165 |
| zb-BP | 336 | 77 | 77 | 336 | 180 | 180 | 163 | 160 | 362 |
| qtz BP | 417 | 45 | 62 | 380 | 186 | 199 | 172 | 186 | 411 |
| zb-AlP | 125 | 63 | 63 | 125 | 58 | 58 | 84 | 46 | 117 |
| NiAs-AlP | 166 | 81 | 68 | 166 | 42 | 46 | 106 | 47 | 123 |
| qtz AlP | 158 | 51 | 60 | 175 | 53 | 52 | 93 | 53 | 133 |
| Space Group | a = b (Å) | c (Å) | ρ (g/cm3) | HV (GPa) | ||
|---|---|---|---|---|---|---|
| T † | MO ‡ | |||||
| qtz C6 #179 [27] | P6522 | 2.5975 | 5.5859 | 3.666 | 102 | 105 |
| zb-BP #216 | 4.5410 | 2.964 | 30 | 28 | ||
| qtz BP #180 | P6222 | 3.2739 | 3.211 | 3.211 | 33 | 34 |
| zb-AlP #216 | 5.4625 | 2.362 | 10 | 6 | ||
| NiAs-AlP #194 | P63/mmc | 3.6084 | 2.967 | 2.967 | 8 | 6 |
| qtz AlP #180 | P6222 | 3.8535 | 2.595 | 2.595 | 11 | 6 |
| BP | AlP | |||||
|---|---|---|---|---|---|---|
| zb | qtz | zb | qtz | |||
| calc. | exp. | calc. | calc. | exp. | calc. | |
| B0 (GPa) | 158 | 174(2) [37] | 165 | 83 | 88 [38] | 86.0 |
| B0′ | 3.89 | 3.2(2) [37] | 4.0 | 3.86 | 4 [38] | 4.07 |
| E0/FU (eV) | −12.90 | – | −11.89 | −10.37 | – | −9.92 |
| V0/FU (Å3) | 23.41 | 23.36 [28] | 21.61 | 41.63 | 40.75 [29] | 37.08 |
| Vtr/V0 | 0.67 | – | – | 0.81 | – | – |
| ptr (GPa) | 144 | – | – | 28 | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solozhenko, V.L.; Matar, S.F. Superdense Hexagonal BP and AlP with Quartz Topology: Crystal Chemistry and DFT Study. Crystals 2023, 13, 1622. https://doi.org/10.3390/cryst13121622
Solozhenko VL, Matar SF. Superdense Hexagonal BP and AlP with Quartz Topology: Crystal Chemistry and DFT Study. Crystals. 2023; 13(12):1622. https://doi.org/10.3390/cryst13121622
Chicago/Turabian StyleSolozhenko, Vladimir L., and Samir F. Matar. 2023. "Superdense Hexagonal BP and AlP with Quartz Topology: Crystal Chemistry and DFT Study" Crystals 13, no. 12: 1622. https://doi.org/10.3390/cryst13121622
APA StyleSolozhenko, V. L., & Matar, S. F. (2023). Superdense Hexagonal BP and AlP with Quartz Topology: Crystal Chemistry and DFT Study. Crystals, 13(12), 1622. https://doi.org/10.3390/cryst13121622






