Aluminum Phosphide van der Waals Bilayers with Tunable Optoelectronic Properties under Biaxial Strain
Abstract
:1. Introduction
2. Methods
3. Results and Discussions
3.1. Structural Properties
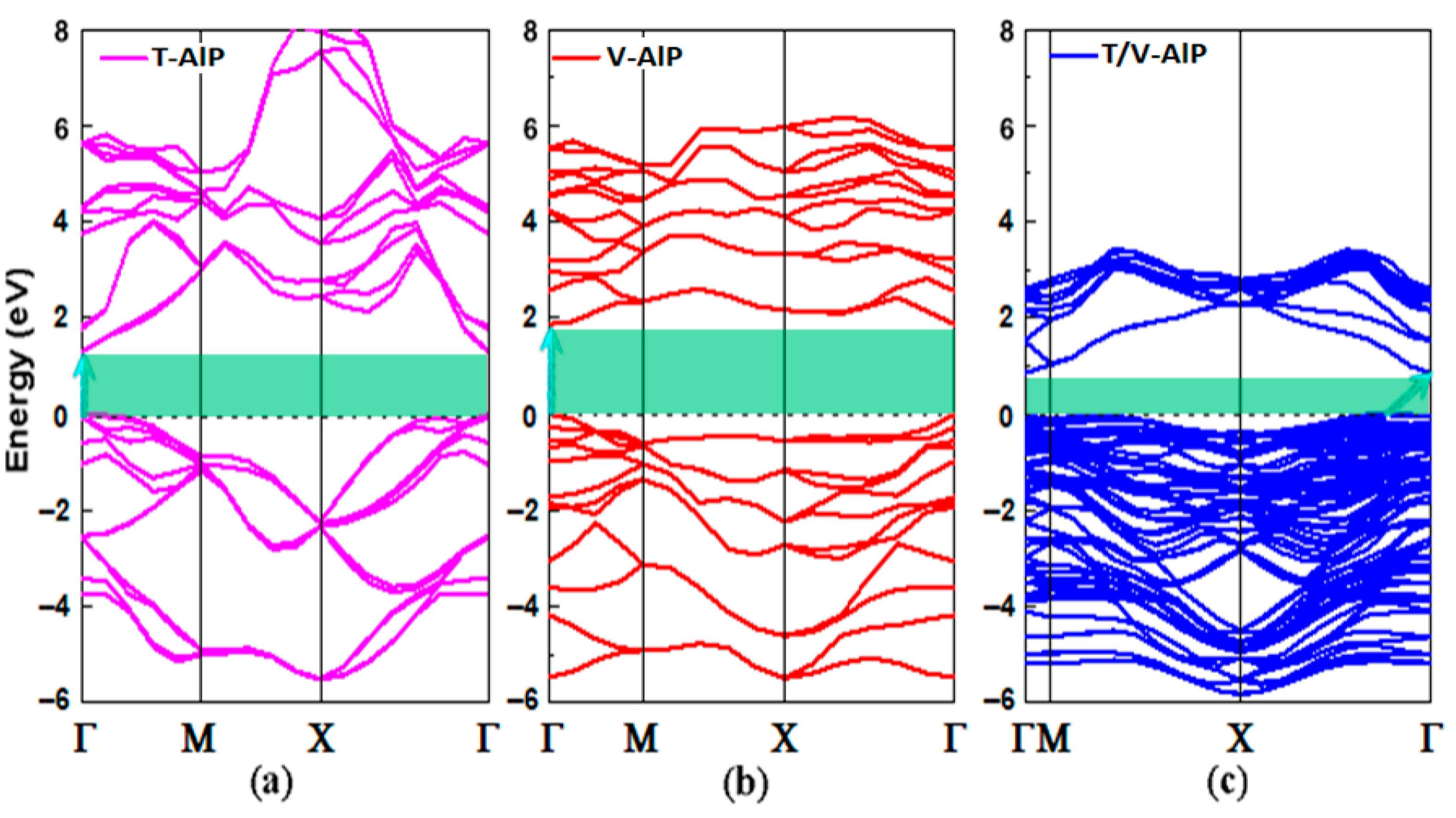
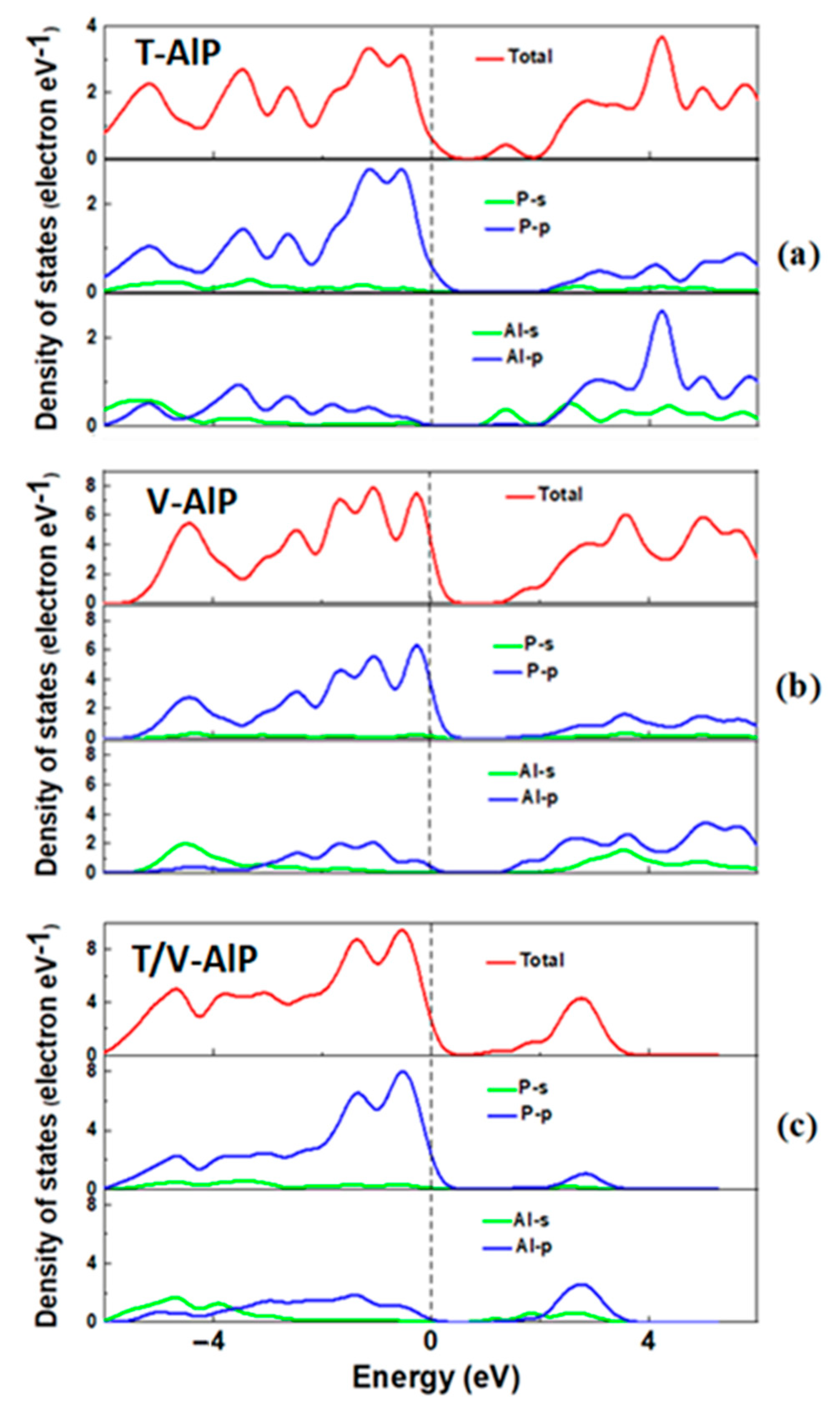
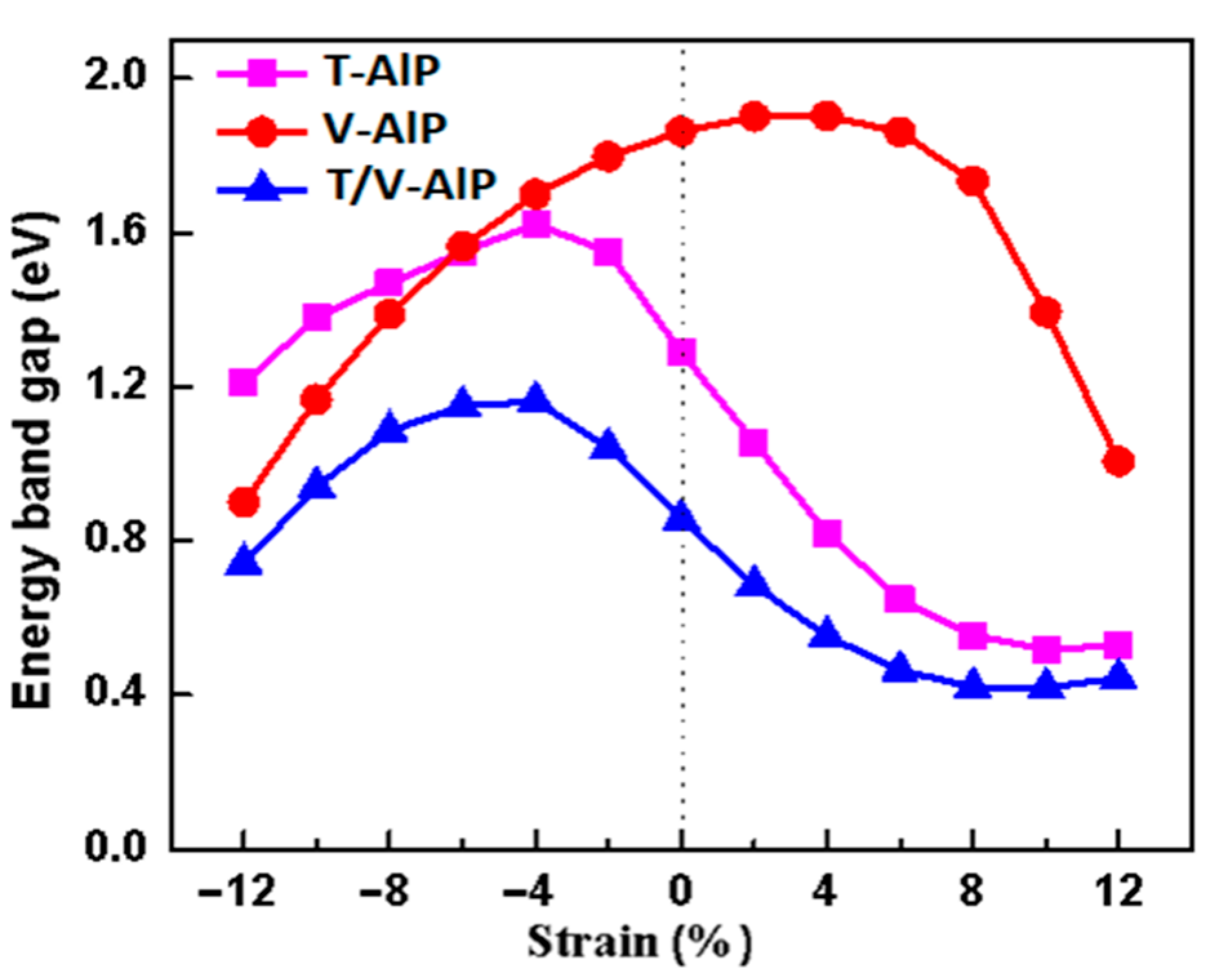
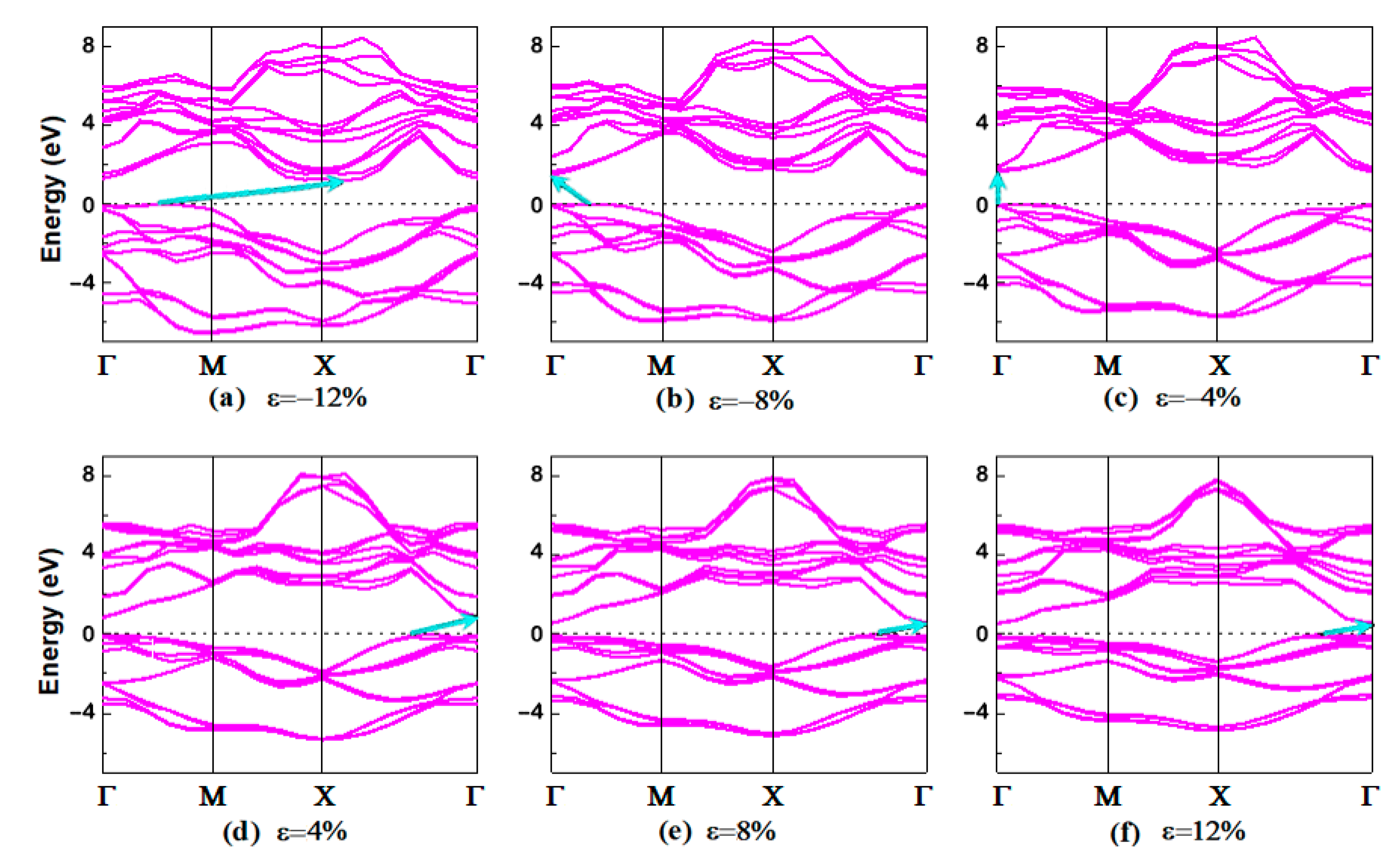
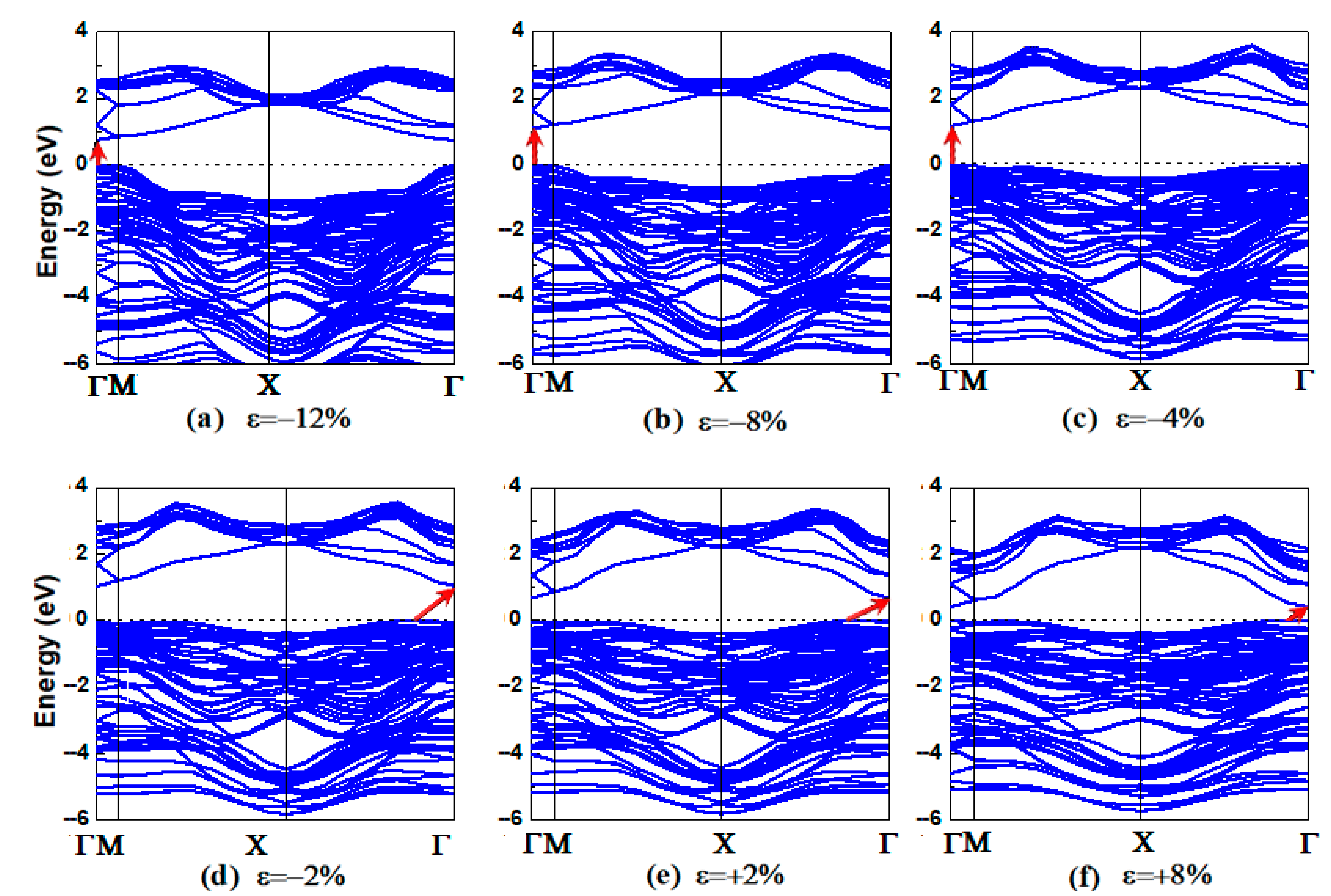
3.2. Electronic Properties
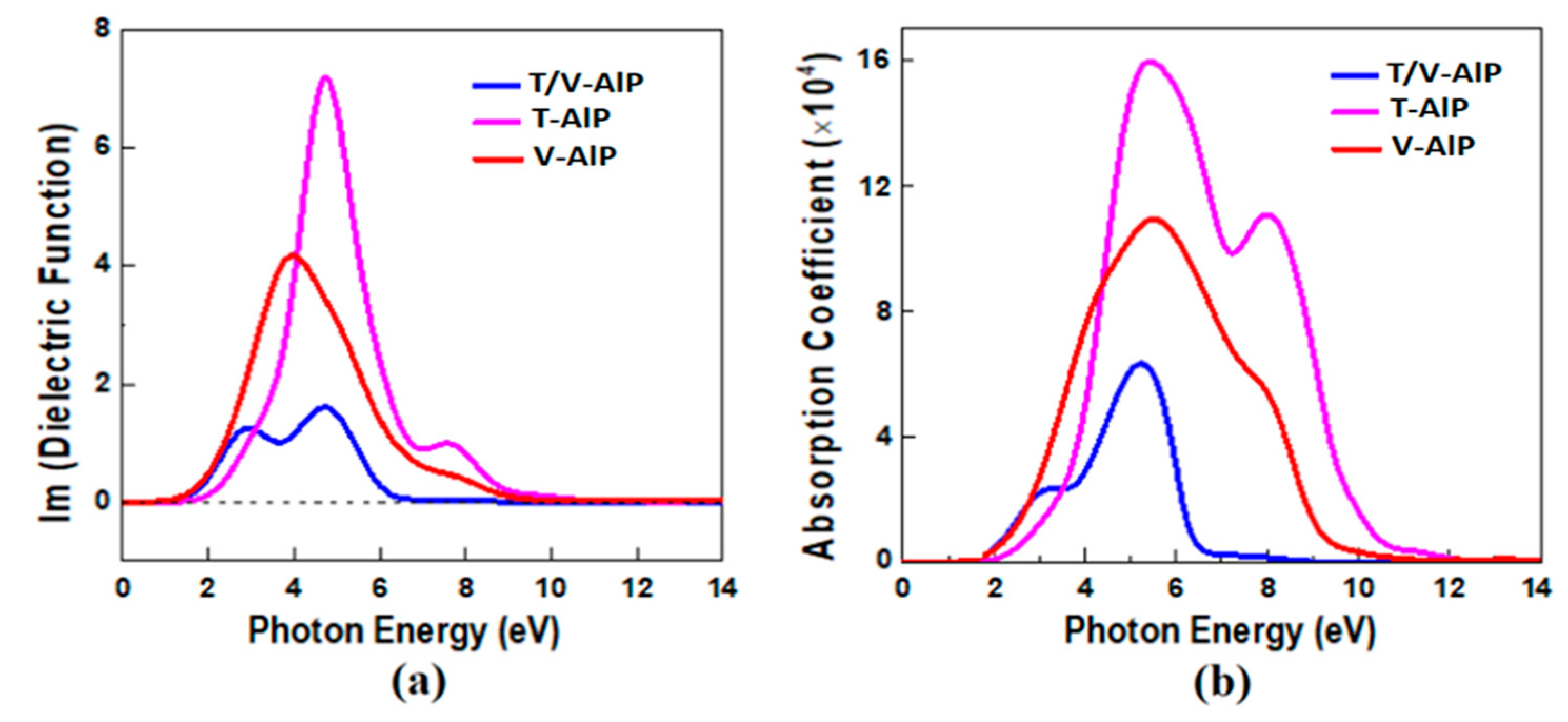
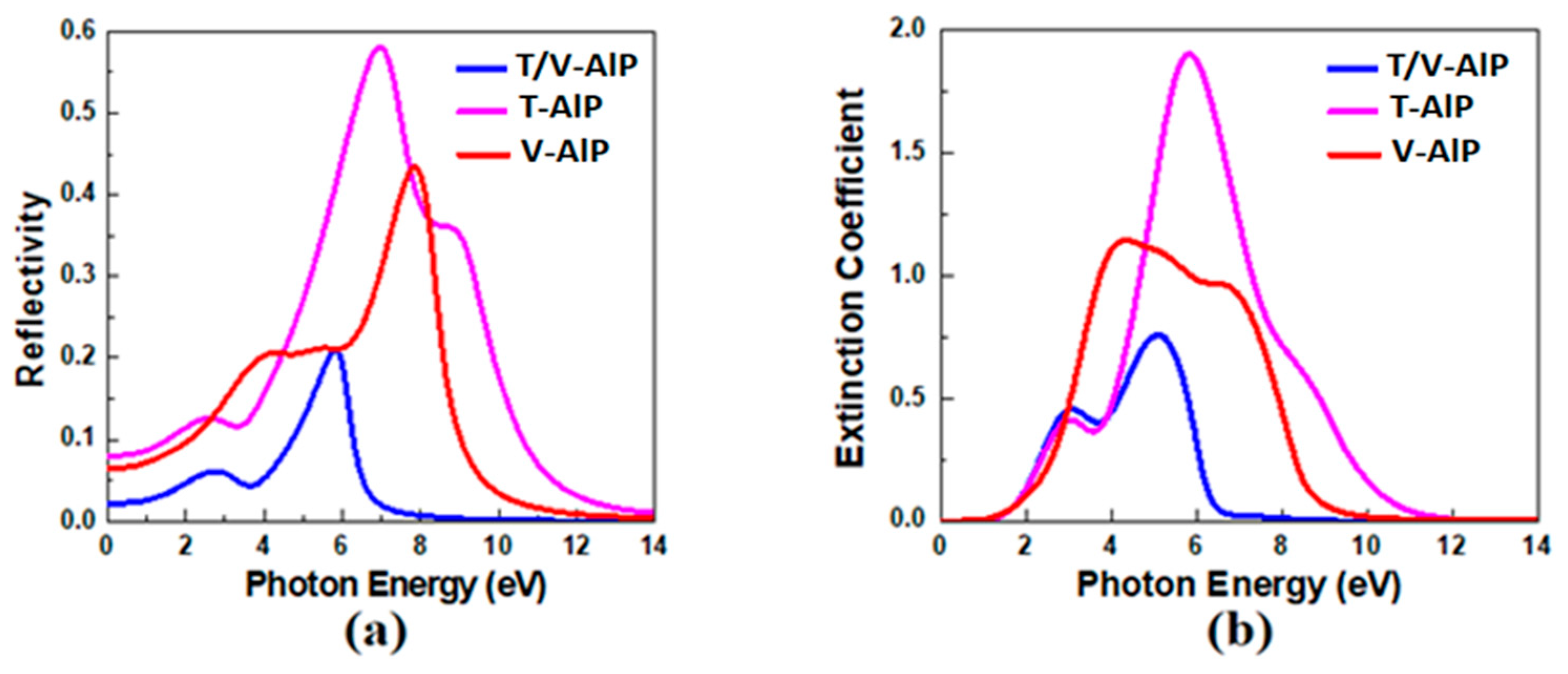
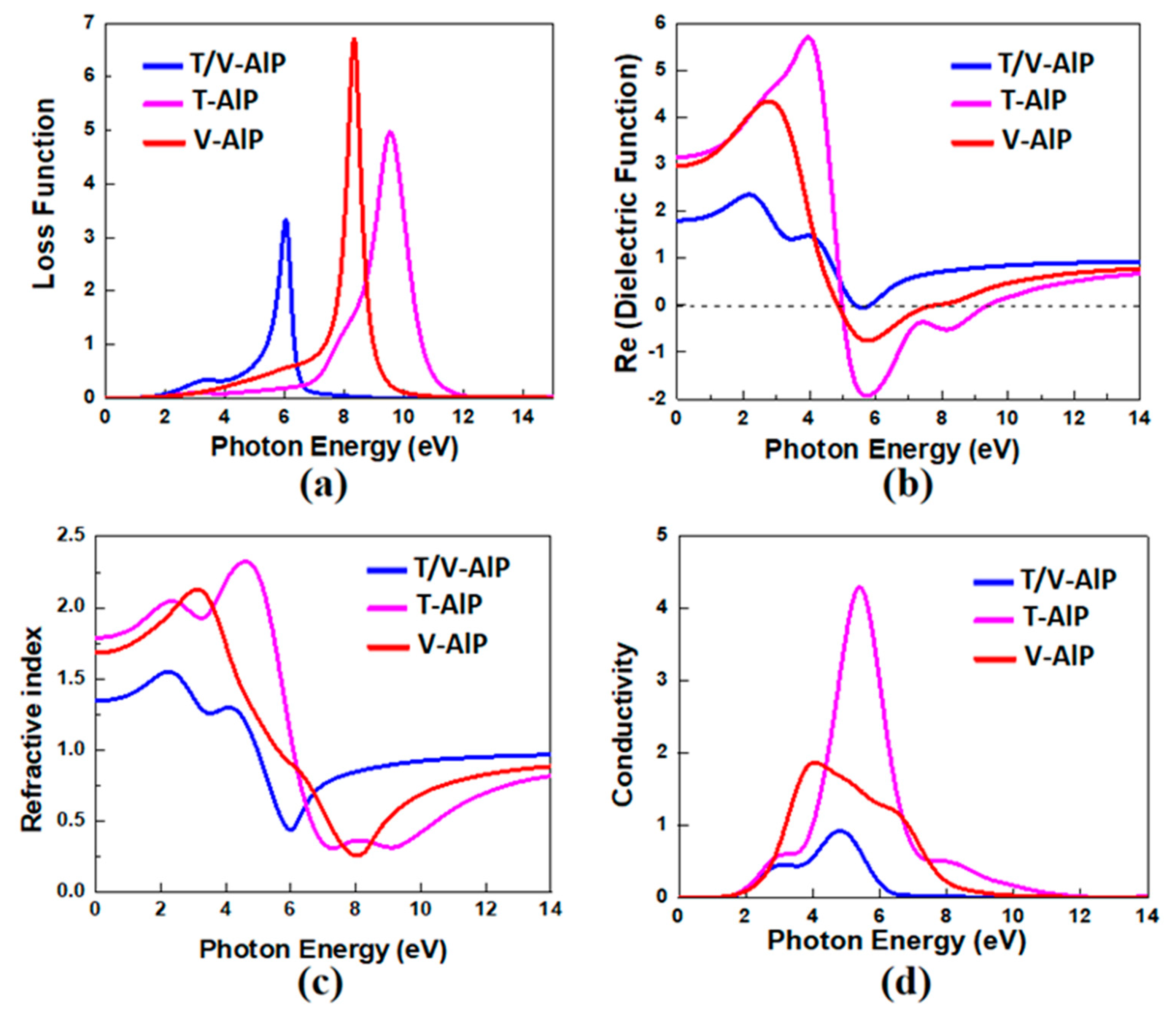
3.3. Optical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect inatomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhu, C.; Zhang, S.; Hu, X.; Zhang, K.; Zhou, W.; Guo, S.; Xu, F.; Zeng, H. Ultrathin Bismuth Nanosheets for Stable Na-Ion Batteries: Clarification of Structure and Phase Transition by in Situ Observation. Nano Lett. 2019, 19, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Ashton, M.; Mathew, K.; Hennig, R.G.; Sinnott, S.B. Predicted Surface Composition and Thermodynamic Stability of MXenes in Solution. J. Phys. Chem. C 2016, 120, 3550–3556. [Google Scholar] [CrossRef]
- Ashton, M.; Paul, J.; Sinnott, S.B.; Hennig, R.G. Topology-Scaling Identification of Layered Solids and Stable Exfoliated 2D Materials. Phys. Rev. Lett. 2017, 118, 10610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Dong, N.; Tao, H.; Yan, C.; Huang, J.; Liu, T.; Robertson, A.W.; Texter, J.; Wang, J.; Sun, Z.Y. Exfoliation of stable 2D black phosphorus for device fabrication. Chem. Mater. 2017, 29, 6445–6456. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, S.; Ma, Y.; Chen, Z.; Wang, Y.; Gao, H.; Herrero, J.G.; Ares, P.; Zamora, F.; Zhou, Z.; et al. Recent progress in 2D group-VA semiconductors: From theory to experiment. Chem. Soc. Rev. 2018, 47, 982–1021. [Google Scholar] [CrossRef] [Green Version]
- Niu, T.; Zhou, W.; Zhou, D.; Hu, X.; Zhang, S.; Zhang, K.; Zhou, M.; Fuchs, H.; Zeng, H. Modulating Epitaxial Atomic Structure of Antimonene through Interface Design. Adv. Mater. 2019, 31, 1902606. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Niu, H. Half-metallic ferromagnetism in Cr-doped AlP—Density functional calculations. Solid State Commun. 2008, 145, 590–593. [Google Scholar] [CrossRef]
- Zhang, Y. Possible room temperature ferromagnetism in Ca-doped AlP: First-principles study. J. Magn. Magn. Mater. 2013, 342, 35–37. [Google Scholar] [CrossRef]
- Liang, P.; Liu, Y.; Hu, X.; Wang, L.; Dong, Q.; Jing, X. The half metallic property and electronic structure of the Ti doped AlP systems investigated by first principle. J. Magn. Magn. Mater. 2014, 355, 295–299. [Google Scholar] [CrossRef]
- Yan, Z.; Wu, H.; Zheng, R. Ferromagnetism in alkali-metal-doped AlP: An ab initio study. Comput. Mater. Sci. 2015, 99, 16–20. [Google Scholar] [CrossRef]
- Boutaleb, M.; Doumi, B.; Tadjer, A.; Sayede, A. Half-metallic ferromagnetic properties of Cr- and V-doped AlP semiconductors. J. Magn. Magn. Mater. 2016, 397, 132–138. [Google Scholar] [CrossRef]
- Wang, S.; Fan, X.; An, Y. Room-temperature ferromagnetism in alkaline-earth-metal doped AlP: First-principle calculations. Comput. Mater. Sci. 2018, 142, 338–345. [Google Scholar] [CrossRef]
- Chen, Y.; Xing, Y.; Jiang, A.; Zhou, C.; Lu, S. Enhanced optical absorption in visible range in Mn doped AlP: A density functional theory study. J. Magn. Magn. Mater. 2018, 457, 13–16. [Google Scholar] [CrossRef]
- Sun, J. Stability and Electronic Structures of Single-Walled Alp Nanotubes by First Principle Study. Procedia Eng. 2011, 15, 5062–5066. [Google Scholar]
- Tong, C.; Zhang, H.; Zhang, Y.; Liu, H.; Liu, L. New manifold two-dimensional single-layer structures of zinc-blende compounds. J. Mater. Chem. A 2014, 2, 17971–17978. [Google Scholar] [CrossRef]
- Liu, C.; Teng, Z.; Ye, X.; Yan, X. Two-dimensional tetragonal AlP monolayer: Strain-tunable direct–indirect band-gap and semiconductor–metal transitions. J. Mater. Chem. C 2017, 5, 5999–6004. [Google Scholar] [CrossRef]
- Yang, X.; Mao, C.; Hu, Y.; Cao, H.; Zhang, Y.; Zhao, D.; Chen, Z.; Xie, M. Two-dimensional aluminum phosphide semiconductor with tunable direct band gap for nanoelectricapplications. RSC Adv. 2020, 10, 25170–25176. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 207–8215. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Xu, C.; Yuan, J.; Zhao, H. Effect of stacking order and in-plane strain on the electronic properties of bilayer GeSe. Phys. Chem. Chem. Phys. 2018, 20, 6929–6935. [Google Scholar] [CrossRef]
- Zhang, K.; Feng, S.; Wang, J.; Azcatl, A.; Lu, N.; Addou, R.; Wang, N.; Zhou, C.; Lerach, J.; Bojan, V. Correction to manganese doping of monolayer MoS2: The substrate is critical. Nano Lett. 2016, 16, 2125. [Google Scholar] [CrossRef]
- Qu, H.; Zhou, W.; Guo, S.; Li, Z.; Wang, Y.; Zhang, S. Ballistic Quantum Transport of Sub-10 nm 2D Sb2Te2Se Transistors. Adv. Bioelectron. Mater. 2019, 5, 1900813. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, Y.; Hu, Z.; Cai, B.; Zeng, H. Hydrogenated arsenenes as planar magnet and Dirac material. Appl. Phys. Lett. 2015, 107, 022102. [Google Scholar] [CrossRef]
- Choi, S.M.; Jhi, S.H.; Son, Y.W. Effects of strain on electronic properties of graphene. Phys. Rev. B 2010, 81, 081407. [Google Scholar] [CrossRef] [Green Version]
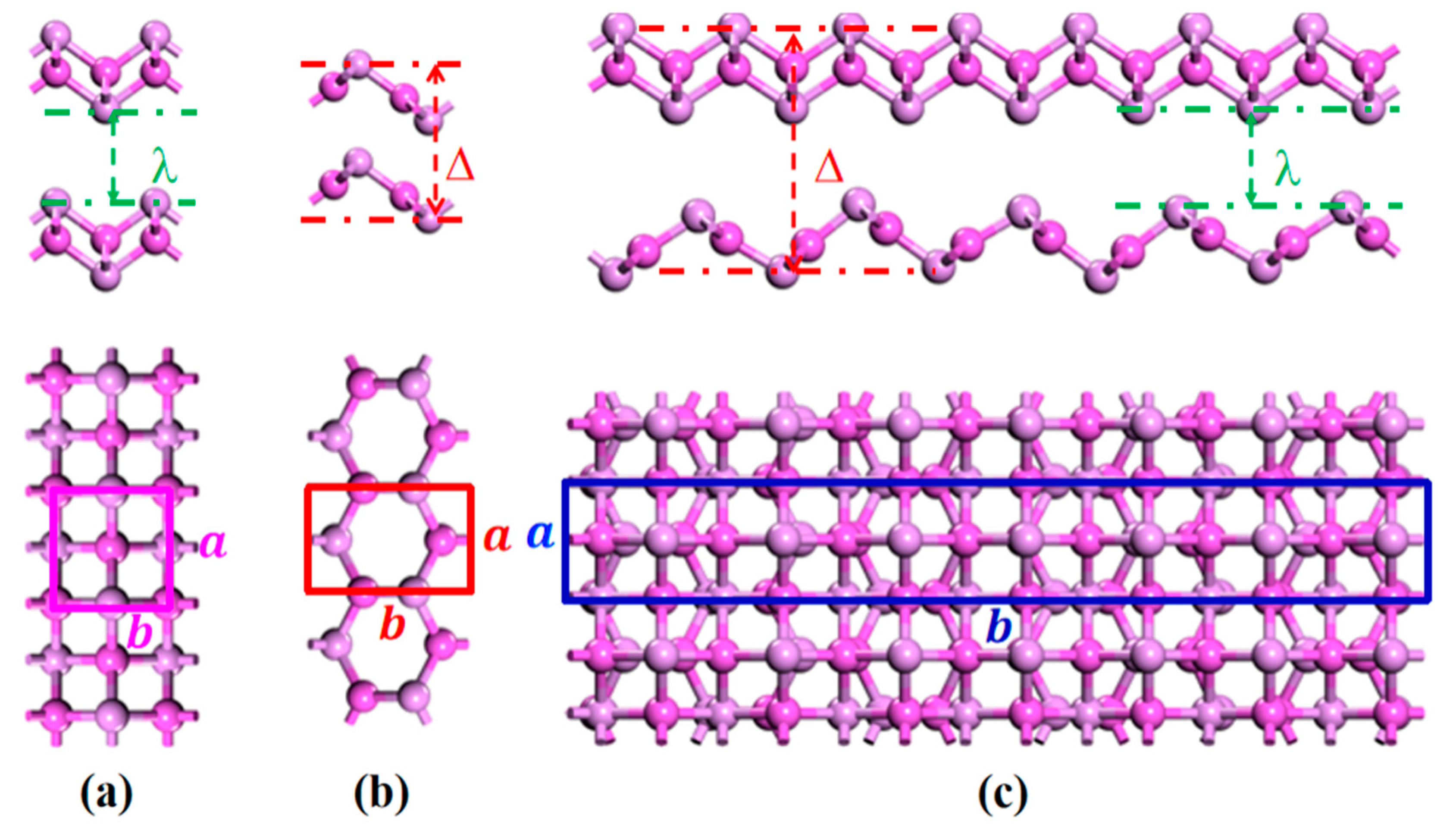
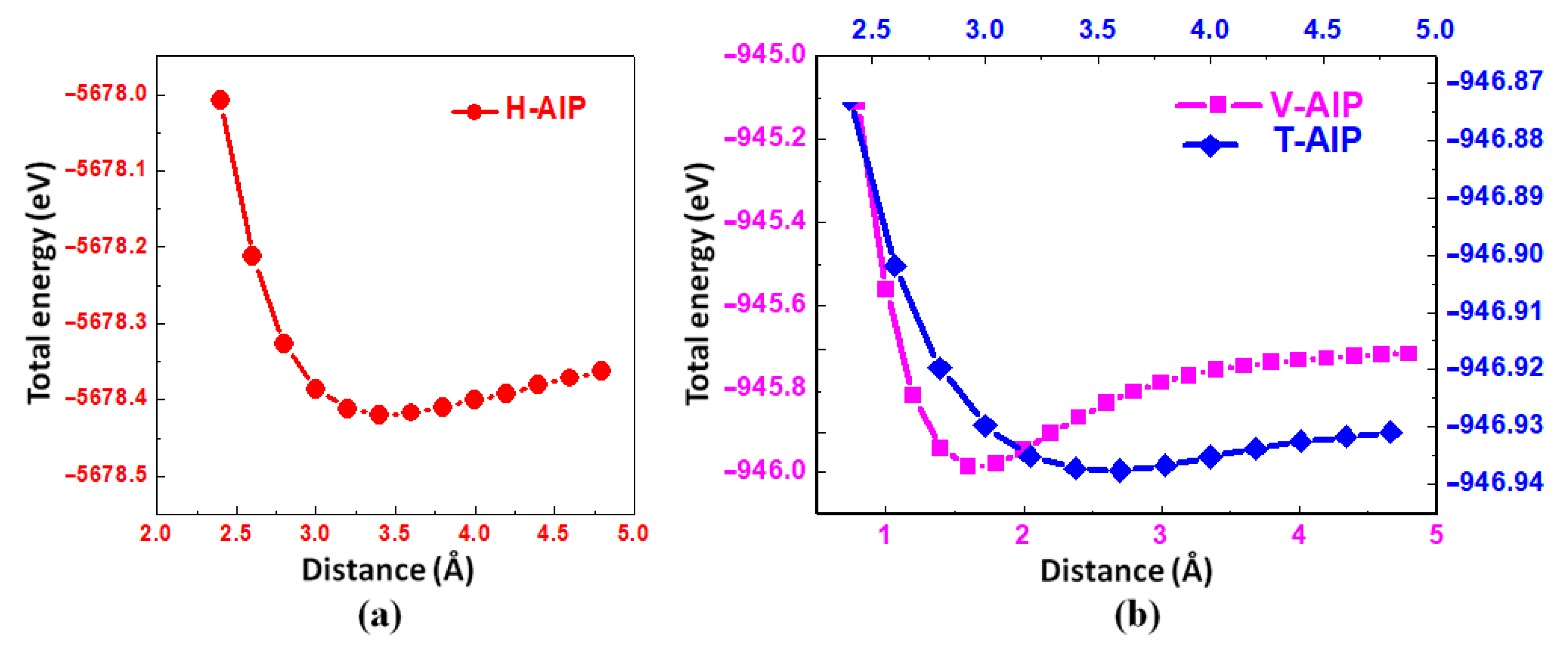

| Model | , (Å) | λ | ||||
|---|---|---|---|---|---|---|
| V-AlP monolayer | = 3.81, = 5.68 | 2.32 | 2.2 | --- | −5.12 | 2.62 |
| T-AlP monolayer | = = 3.91 | 2.43 | 2.9 | --- | −5.35 | 0.97 |
| V-AlP bilayer | = 3.81, = 5.68 | 2.34 | 6.2 | 1.6 | −5.00 | 1.86 |
| T-AlP bilayer | = = 3.89 | 2.27 | 8.8 | 3.6 | −4.85 | 1.29 |
| T/V-AlP bilayer | = 3.85, = 28.4 | 2.37 | 8.6 | 3.4 | −4.94 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, C.; Ni, H.; Qian, L.; Hu, Y.; Huang, H. Aluminum Phosphide van der Waals Bilayers with Tunable Optoelectronic Properties under Biaxial Strain. Crystals 2023, 13, 597. https://doi.org/10.3390/cryst13040597
Mao C, Ni H, Qian L, Hu Y, Huang H. Aluminum Phosphide van der Waals Bilayers with Tunable Optoelectronic Properties under Biaxial Strain. Crystals. 2023; 13(4):597. https://doi.org/10.3390/cryst13040597
Chicago/Turabian StyleMao, Caixia, Hao Ni, Libing Qian, Yonghong Hu, and Haiming Huang. 2023. "Aluminum Phosphide van der Waals Bilayers with Tunable Optoelectronic Properties under Biaxial Strain" Crystals 13, no. 4: 597. https://doi.org/10.3390/cryst13040597
APA StyleMao, C., Ni, H., Qian, L., Hu, Y., & Huang, H. (2023). Aluminum Phosphide van der Waals Bilayers with Tunable Optoelectronic Properties under Biaxial Strain. Crystals, 13(4), 597. https://doi.org/10.3390/cryst13040597






