Experimental Observation of Possible Pressure-Induced Phase Transformation in GdAlO₃ Perovskite Using In Situ X-ray Diffraction

Abstract

Gadolinium aluminate perovskite (GdAlO₃) was studied at high pressures of up to 23 GPa in a diamond anvil cell (DAC) using monochromatic synchrotron X-ray powder diffraction. Evidence of a pressure-induced phase transformation from orthorhombic (Pbnm) to rhombohedral (R$\overline{3}$c) structure was observed at 21 GPa and further proved by DFT calculations. Before phase transition, the volumetric ratio of polyhedron A and B (i.e., V_A/V_B for ABX₃ general notation) in the Pbnm phase continuously increased towards the ideal value of five at the transition, indicating a pressure-induced decrease in the structural distortion as opposed to the trend in many other orthorhombic perovskites (e.g., CaSnO₃, CaGeO₃, MgSiO₃ and NaMgF₃). Pressure–volume data of the Pbnm phase were fitted to the third-order Birch–Murnaghan equation of state yielding a bulk modulus (K_o) of 216 ± 7 GPa with a pressure derivative of the bulk modulus ($K_o^{\prime }$) of 5.8 GPa (fixed). This work confirms the pressure-induced phase transformation from orthorhombic to a higher symmetry structure previously predicted in GdAlO₃ perovskite.

1. Introduction

Perovskite materials are well-known solids with the general formula of ABO₃, where A is a large cation occupying the voids with coordination number 12 (in the ideal cubic perovskite structure) and B is a smaller cation in octahedral oxygen coordination. Rare-earth aluminates with perovskite structure are potential materials for optical, electronic, structural, and magnetic applications such as colossal magneto resistant materials, substrates for high-temperature superconductors, solid oxide fuel cells and microwave dielectric materials [1,2,3,4,5,6,7]. A large number of rare-earth perovskite-type oxides have been studied because of their interesting properties. Many of those ABO₃ compounds crystallize into an orthorhombic structure which deviates from the ideal cubic structure via the titling and distortion of the BO₆ octahedra [8,9]. The distortion degree of perovskites can be described with the following parameters: the BO₆ octahedral tilting and rotation, the Goldschmidt’s tolerance factor(t) and the polyhedron volume ratio V_A/V_B, where V_A is the volume of A-site polyhedron and V_B is that of the B-site octahedron. The values for the tilting angle ($\sphericalangle$B–O1–B), the rotation angle ($\sphericalangle$B–O2–B), t and V_A/V_B for an ideal perovskite are 180°, 180°, 1 and 5, respectively. The nature of this distortion has been related to the existence of different ionic radii within the crystal [10,11,12,13,14,15,16].

Pressure, as one of the important thermodynamic parameters plays a critical role in altering material properties. Under pressure, shortening of the effective ionic radius may vary depending on the ion itself and its coordinating environment. Zhao et al. [17] developed a model using the bond valence concept to predict the structural behavior of oxide perovskites at high pressure, introducing the ratio M_A/M_B, which determines the relative compressibility of the AO₁₂ and BO₆ sites due to the change in the average bond distance, where M_A and M_B describe the variation of the bond valence sum at the central cation in a polyhedral site. Based on this model, the relative polyhedral compressibility (i.e., V_A/V_B) determines the influence of pressure on the crystal structure of perovskite [18]. Some orthorhombic rare-earth perovskites such as LaFeO₃ and PrFeO₃ undergo a first-order transition to high-pressure phases, among which the high-pressure phase of LaFeO₃ was reported to have a tetragonal symmetry with unknown structural details [19]. First-order reversible structural phase transition from the orthorhombic to rhombohedral R$\overline{3}$c structure was observed in SmAlO₃ and LaGaO₃ near 10 GPa [20] and 2.5 GPa [21], respectively, by X-ray synchrotron powder diffraction.

GdAlO₃ orthorhombic perovskite has been studied as a potential material for industrial applications considering its magnetic, optical, electronic, and structural properties [22,23,24,25,26,27]. The crystal structure of gadolinium aluminate has been reported at ambient conditions [22,28,29]. Ross et al. [30,31] studied the structural behavior of GdAlO₃ at high pressures of up to 8 GPa and found that the abovementioned structural distortion decreases with increasing pressure. By extrapolating the metrical deviation of the orthorhombic perovskite from tetragonal symmetry (proportional to (b−a)/a₀ where a₀ is the value of the phase with a higher symmetry), they predicted an orthorhombic to higher-symmetry transition at about 12 GPa in GdAlO₃. Nevertheless, such a transition has never been directly observed in any experimental study. In this work, we compressed GdAlO₃ up to 23 GPa and observed signs of the predicted transition but at a higher pressure (21 GPa). Density functional theory (DFT) calculations indicate that the rhombohedral structure (R$\overline{3}$c) found in LaGaO₃ is favorable at high pressure over the low-pressure orthorhombic structure (Pbnm) of GdAlO₃ and the tetragonal structure (I4/mcm) found in CeAlO₃ [32].

2. Materials and Methods

The GdAlO₃ sample was prepared through the solid-state reaction of Gd₂O₃ and Al₂O₃ by arc-melting in argon atmosphere. Details of the procedure can be found elsewhere [9,32,33]. High pressures were generated using a Mao–Bell diamond anvil cell (DAC). Two opposed diamond anvils with 300 µm diameter culets were compressed on a 302 stainless steel gasket with an initial thickness of 250 µm. The gasket was pre-indented with the anvils to a thickness of 60 µm and a hole of a 125 µm diameter was drilled at the center of the indentation to hold the sample. The synthesized sample was grounded into fine powder in an agate mortar and loaded into the 125 µm diameter sample chamber. A methanol–ethanol (4:1) mixture was loaded together with the sample and a small ruby sphere (pressure calibrant) as a pressure transmitting medium. The in situ high-pressure powder X-ray diffraction experiments were performed at the 16-IDB beamline of HPCAT (High Pressure Collaborative Access Team) at Advanced Photon Source (APS) of Argonne National Laboratory, Lemont, IL, USA. The monochromatic X-ray beam of a 0.3757 Å wavelength was focused to a spot size of 5 µm. Diffraction patterns were recorded using a MAR345 detector. During the experiment, the sample pressure was increased stepwise; fluorescence of the ruby sphere and sample diffraction were collected at each step. The sample pressure was determined using ruby fluorescence pressure scale [34,35]. The FIT2D software [36] was used to integrate the recorded 2-dimensional diffraction patterns to obtain intensity versus 2θ plots. Rietveld refinements were performed for both the ambient-pressure phase and the high-pressure phase at 21 GPa using the GSAS software with a GUI interface [37,38]. The volumetric compression data of the ambient-pressure phase were derived through full-spectrum Le Bail analysis of the in-situ X-ray diffraction patterns.

Density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP 6.3) [39,40]. The generalized gradient approximation (GGA) [41] with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional [42] was used to describe exchange and correlation effects. Electron wave functions were expanded by a plane wave with a cutoff energy of 520 eV. The Gaussian smearing method was used with a width of 0.05 eV. A Monkhorst–Pack [43] k-point grid was set with a 0.03 1/Å k-point separation which provides a mesh density of >1000 per reciprocal atom. Atomic relaxation was performed until the changes in the electronic and ionic steps were less than 10⁻⁶ eV and 10⁻⁵ eV, respectively.

3. Results

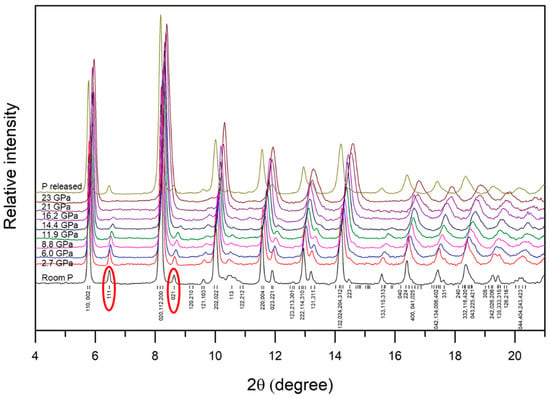
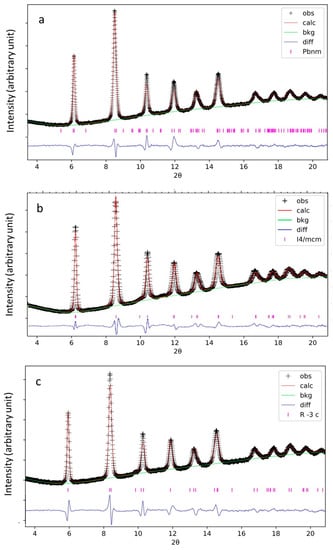
A sequence of in situ X-ray diffraction patterns of the sample was taken up to 23 GPa (Figure 1). All the diffraction peaks in the initial diffraction pattern were identified as the Pbnm perovskite phase in agreement with previous works [9,29,31,44]. Disappearance of (111), (021), (113), (023)/(221), and (133) peaks indicates a possible pressure-induced structural phase transition at a pressure between 16.2 GPa and 21 GPa, and this transition is reversible as all these disappeared peaks reappear when the pressure is released back to ambient. From the symmetry relationship point of view, there are three higher symmetry phases for perovskite in the pathway from its Pbnm orthorhombic to $Pm\overline{3}m$ cubic polymorphs, i.e., P4/mbm, I4/mcm and R$\overline{3}$c [16]. However, differences in symmetry operations require that the (111) and (021) peaks in the Pbnm orthorhombic phase disappear in the I4/mcm tetragonal phase (i.e., hkl: h + k + l = 2n and 0kl: k, l = 2n) and the R$\overline{3}$c rhombohedral phase while they are allowed in the P4/mbm tetragonal phase. Since the (111) and (021) peaks in the Pbnm orthorhombic phase completely disappeared when sample pressure increased to 21 GPa (Figure 1), the P4/mbm tetragonal phase was not considered. Therefore, we examined three possible structural models using the diffraction pattern at 21 GPa, i.e., Pbnm (the ambient pressure phase), R$\overline{3}$c (the high-pressure phase observed in SmAlO₃ [20] and I4/mcm (the structure of CeAlO₃). As shown in Figure 2 and Table 1, the differences in structure refinements using the three different space groups are not significant enough to conclusively determine the favorable structure for the high-pressure phase. We then calculated the total energy of the three structure models as a function of pressure using DFT (Figure 3). The calculation results indicate that Pbnm is favorable at low pressures, whereas R$\overline{3}$c is favorable at high pressures, although the calculated transition pressure (75 GPa) is much higher than the experimental pressure where the disappearance of diffraction peaks was observed. We realize that the methanol–ethanol (4:1) pressure medium solidifies at a pressure above 10 GPa [45], creating a non-hydrostatic pressure environment and therefore the sample may experience significant stresses at 21 GPa. Zhao et al. [46,47] were able to quantify the stress field using single-crystal X-ray diffraction and indicate that such a non-hydrostatic pressure environment in a DAC may affect and even induce the phase transition as stress fields can influence the structural distortions in perovskites. A more recent experimental study [48] demonstrated that applying non-hydrostatic pressure may lower the transition pressure in a DAC. Taking this stress influence and possibly large uncertainty in determining transition pressure using DFT calculations into consideration, we propose that the theoretically predicted Pbnm to R$\overline{3}$c phase transition may occur at a pressure between 16.2 GPa and 21 GPa promoted by non-hydrostatic pressure. As shown in Table 1, the volume per formula unit of the R$\overline{3}$c structure is nearly identical to the Pbnm structure within the experimental uncertainty. To further confirm the symmetry of the high-pressure phase, higher resolution structure characterization, e.g., in situ single crystal X-ray diffraction, is needed.

Figure 1. In situ synchrotron X-ray diffraction patterns of GdAlO₃ at different pressures as indicated and room temperature (λ = 0.3757 Å). Red circles indicate the characteristic peaks that disappear when Pbnm to R$\overline{3}$c phase transition occurs.

Figure 2. Result of Rietveld refinement of the diffraction pattern of GdAlO₃ at 21 GPa with (a) Pbnm, (b) I4/mcm and (c) R$\overline{3}$c space groups. Crosses are experimentally observed data, red solid line is calculated data, vertical bars are locations of expected diffraction peaks, and blue line at the bottom is the difference between the observed and calculated data.

Table 1. Results of Rietveld refinement of the diffraction pattern of GdAlO₃ at 21 GPa using Pbnm, I4/mcm and R$\overline{3}$c space groups.

	Atom	x	y	Z	a (Å)	b (Å)	c (Å)	V (Å3)	V/Z (Å3)	wR
Pbnm	Gd	0.998(7)	0.003(4)	0.25	5.093(1)	5.146(1)	7.322(1)	191.89(2)	47.97	2.9%
	Al	0	0.5	0
	O1	0.5(4)	0.98(18)	0.25
	O2	0.75(8)	0.25(10)	0.00(7)
I4/mcm	Gd	0	0.5	0.25	5.123(2)	5.123(2)	7.25(1)	190.76(4)	47.69	1.9%
	Al	0	0	0
	O1	0	0	0.25
	O2	0.32(5)	0.82(5)	0
R$\overline{3}$c	Gd	0	0	0	5.111(2)	5.111(2)	12.713(5)	287.55(21)	47.93	2.9%
	Al	0.421(3)	0	0.25
	O1	0	0	0.25

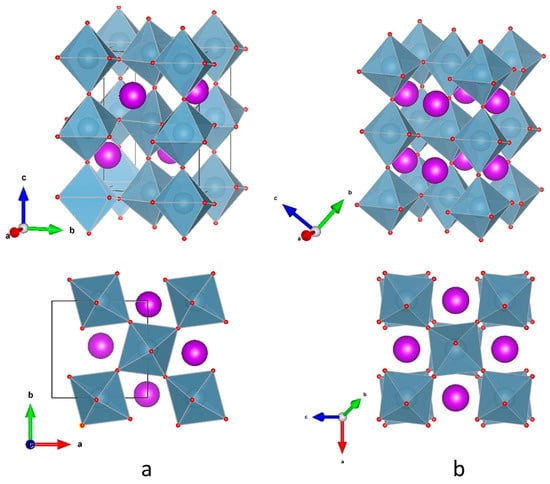
Figure 3. Crystal structure of GdAlO₃ at (a) ambient pressure (Pbnm space group, a⁻a⁻c⁺ tilt system), and (b) 21 GPa (R$\overline{3}$c space group, a⁻a⁻a⁻ tilt system). Solid black lines indicate unit cell. Small red dots represent oxygen atoms and large pink spheres gadolinium atoms. Grey areas denote AlO₆ octahedra.

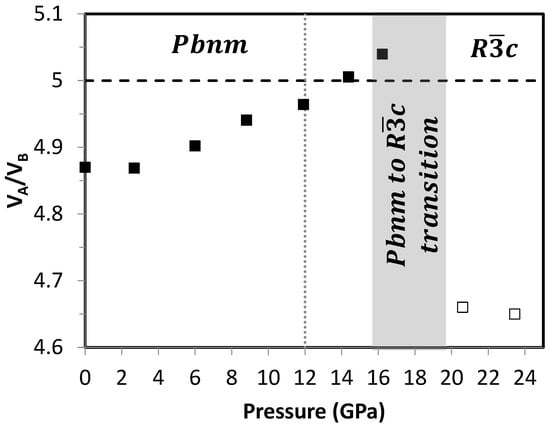
The structural deviation of the perovskite (ABX₃) structure from its ideal cubic structure is commonly characterized by its BX₆ octahedral titling. The Pbnm perovskite has a simple tilt system of a⁻a⁻c⁺ [49,50] (the superscript + and − indicate that successive octahedra along an axis have the same tilt and opposite tilt respectively). Figure 3a shows the GdAlO₃ structure model based on the refinement of the X-ray diffraction at ambient condition. The tilting angles along the a-axis and the b-axis are identical, and successive octahedra along each of these axes have opposite tilt, whereas successive octahedra along the c-axis have the same tilt. The R$\overline{3}$c perovskite has a tilt system of a⁻a⁻a⁻ [49,50]. Figure 3b shows the high-pressure phase structure model of GdAlO₃ based on the refinement of the X-ray diffraction at 21 GPa. There are three identical tilts along the a, b and c-axis, and successive octahedra along each of the axes have opposite tilt. The degree of structure distortion of perovskite can be evaluated using the volumetric ratio (V_A/V_B) between AX₁₂ and BX₆ polyhedron with an ideal value of five for undistorted cubic structure [15]. Assuming regular BX₆ octahedra throughout the Pbnm perovskite structure, V_A and V_B can be calculated through its unit cell dimensions [15,51]. Evolution of the V_A/V_B ratio of the low-pressure phase in GdAlO₃ with pressure is given in Figure 4 shows the V_A/V_B ratio as a function of pressure (Table 2). As pressure increases, the V_A/V_B ratio of the Pbnm phase approaches the value of five, indicating a transition to a higher symmetry. Note that during the phase transition (between 16.2 and 21 GPa), V_A/V_B goes beyond five at 16.2 GPa, indicating large pre-transition straining. Detailed reasoning for these phenomena is unclear. While coexistence of two phases may compromise refinement accuracy, simultaneously fitting two phases did not solve this issue in the Pbnm phase. Although the pure high-pressure phase was observed at 21 GPa, the transition likely starts at 16.2 GPa since significant weakening of (111), (021), (113), (023)/(221), and (133) peaks occurs at this pressure, which is still higher than the transition pressure (12 GPa) predicted by Ross et al. [30,31].

Figure 4. Variations of V_A/V_B of the Pbnm (solid symbols) and R$\overline{3}$c (open symbols) phase of GdAlO₃ as a function of pressure. The broken line indicates the ideal value of V_A/V_B for undistorted cubic perovskite structure. The dotted line indicates the pressure of the predicted structural transition to from Pbnm to a higher symmetry [30,31]. The shaded area shows the pressure range where the Pbnm to R$\overline{3}$c transition may actually happen under non-hydrostatic pressure.

Table 2. Unit cell parameters of GdAlO₃ measured in the diamond anvil cell from 1 bar to 23 GPa. The figures in parentheses represent 1 esd of the last decimal place shown.

	P (GPa)	σ * (GPa)	a (Å)	b (Å)	c (Å)	V (Å3)	Va/Vb **
Pbnm	0.00	0	5.2534(7)	5.2910(6)	7.458(1)	207.29(1)	4.87
	2.7	0.3	5.2289(9)	5.2823(6)	7.401(2)	204.4(2)	4.87
	6.0	0.5	5.212(1)	5.2558(8)	7.368(2)	201.82(2)	4.90
	8.8	0.8	5.2050(7)	5.2373(8)	7.352(1)	200.42(1)	4.94
	11.9	1.0	5.188(1)	5.218(1)	7.316(2)	198.06(3)	4.96
	14.4	1.0	5.173(4)	5.176(3)	7.308(3)	195.64(3)	5.01
	16.2	1.2	5.175(1)	5.120(1)	7.371(1)	195.29(3)	5.04
R$\overline{3}$c	20.6	2.0	5.111(2)	5.111(2)	12.713(5)	287.55(21)	4.66
	23.4	2.0	5.094(1)	5.094(1)	12.682(3)	285.02(6)	4.65

* Experimental uncertainty taking the nonhydrostatic pressure due to solidification of pressure medium into account [45]. ** V_a and V_b are calculated from the unit cell dimensions.

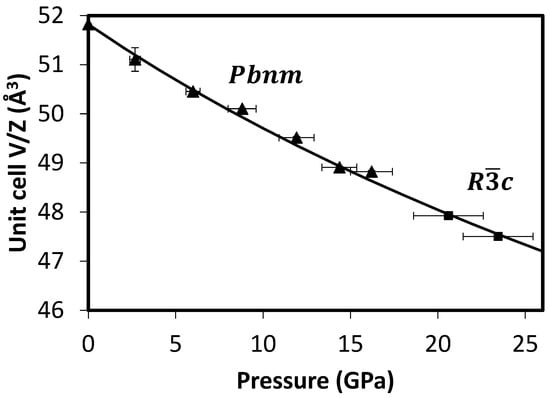
The compression data (Figure 5) show that the transition from the Pbnm to R$\overline{3}$c phase in GdAlO₃ at a pressure between 16.2 GPa and 21 GPa accompanied nearly no volumetric discontinuity. Nevertheless, the space group–subgroup theory indicates that the Pbnm to R$\overline{3}$c transformation is a first-order phase transition [16]. Likely, the volumetric discontinuity is so small that it is unrecognizable with the experimental uncertainty of this study. The orthorhombic (Pnma) to rhombohedral (R$\overline{3}$c) transition observed in GdAlO₃ and LaGaO₃ has a similar unrecognizable volume discontinuity [20,21].

Figure 5. Variation of the volume per formula unit of GdAlO₃ perovskite (triangles: the Pbnm phase, squares: the R$\overline{3}$c phase) as a function of pressure. The experimental errors are either indicated by the bars or less than the size of the symbols. The solid line represents the third-order Birch–Murnaghan EoS fitting for the data of the Pbnm phase (triangles).

The obtained volumetric data of the Pbnm phase were fitted into the third–order Birch–Murnaghan equation of state (EoS) [52]:

$$P=\frac{3}{2}{K}_0\left[{\left(\frac{V}{V_0}\right)}^{-7/3}-{\left(\frac{V}{V_0}\right)}^{-5/3}\right]x\left\{1+\frac{3}{4}\left(K_o^{\prime }-4)\right)\left[{\left(\frac{V}{V_0}\right)}^{-2/3}-1\right]\right\},$$

where P is the pressure applied, V is the volume of the unit cell under pressure, K₀ is the bulk modulus, subscript 0 indicates the ambient pressure, and K₀′ is the pressure derivative of bulk modulus. EoSFit 7.0 software [53] was used for fitting the experimental P–V data into the EoS. The fitting was weighted according to the uncertainty of each point [53] and K₀′ was fixed at 5.8 based on the previous experimental data by Ross et al. [31]. The V₀ and K₀ determined through the fitting are 207.29 ± 0.01 ų and 216 ± 7 GPa, respectively. Due to the very limited data for the high-pressure R$\overline{3}$c phase (only two points), no EoS fitting was performed.

4. Discussion

While temperature influence on the structure of perovskite has been extensively studied, investigations of pressure influence on perovskite structure are still limited. Pressure influence on the Pbnm perovskite structure is twofold. Some structural studies on MgSiO₃ [54,55] and NaMgF₃ [11,56] perovskite showed that the V_A/V_B ratio of the Pbnm perovskite structure decreases further away from the ideal value of five upon compression, i.e., pressure increases the distortion of the perovskite. Experimental studies of pressure effect on CaGeO₃ perovskite structure presented controversial results. In situ extended X-ray absorption fine structure (EXAFS) study inferred a trend of reduced distortion under high pressure [57], while X-ray diffraction study indicated a reversed pressure effect [58]. Controversial results about the pressure influence also exist in theoretical calculations on CaSiO₃ perovskite [59,60]. CaSnO₃ is another example of perovskites that show increased distortion with increasing pressure [61]. Whether pressure enhances the distortion or reduces it depends on the relative compressibility of the AX₆ octahedra and the BX₁₂ polyhedron. In the case of GdAlO₃ of this study, the GdO₆ octahedra are less compressible than the AlO₁₂ polyhedron, yielding an increase in the V_A/V_B ratio towards five. This is consistent with previous single-crystal X-ray diffraction study on GdAlO₃ by Ross et al. [30,31], although their experiment was limited to the high pressure of 8 GPa and therefore did not observe any phase transition. An ab initio calculation [62] and a single-crystal X-ray diffraction study [63] on another rare-earth aluminate perovskite, YAlO₃, also show that the AX₆ octahedra are less compressible than the BX₁₂ polyhedron. All of these align nicely with the model developed by Zhao et al. [17] which shows that in GdFeO₃-type orthorhombic perovskites with both cations possessing a formal charge of 3+, the structural distortion decreases with increasing pressure and the structure evolves towards a higher symmetry at high pressure.

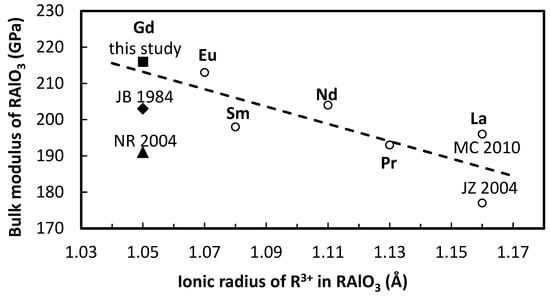
The bulk modulus (216 GPa) of Pbnm GdAlO₃ derived in this study is higher than those reported previously by Bass et al. [64] using Brillouin spectroscopy (204 GPa) and by Ross et al. [31] using single-crystal X-ray diffraction (191 GPa). In perovskite-structured alkaline earth silicates, germanates, and titanates, a simple trend of a smaller unit formula volume leading to a larger bulk modulus has been observed [65]. In the case of rare-earth aluminate perovskite, a summary of the available bulk moduli is listed in Table 3. Figure 6 shows a plot of the bulk moduli at ambient conditions as a function of ionic radius of R³⁺ [66] in the rare-earth aluminate perovskite RAlO₃ (R = La, Pr, Nd, Sm, Eu and Gd). The linear trendline defined by the data of LaAlO₃, PrAlO₃, NdAlO₃, SmAlO₃ and EuAlO₃ indicates that the bulk modulus of RAlO₃ increases as the ionic radius of R³⁺ decreases. The bulk modulus value of GdAlO₃ derived from the current study agrees well with the general trend of bulk moduli as a function of the ionic radius (Figure 6). More systematic studies on the bulk moduli of the perovskite-structured RAlO₃ aluminates for the entire rare-earth family will be interesting to generalize the influence of ionic radius on bulk modulus of the rare-earth aluminate perovskite. We also realize that the methanol–ethanol pressure medium may yield non-hydrostatic environment when the pressure rises above 10 GPa due to solidification [45]. Although enlarged experimental uncertainties because of the non-hydrostatic pressure have been taken into account through weighted EoS fitting, a future study using nearly hydrostatic pressure medium such as helium or neon is more desirable for a better characterization of the compression behavior and the phase transition.

Table 3. Summary of the available bulk moduli (K) of rare-earth aluminate perovskite RAlO₃.

Composition	Space Group	K (GPa)	Reference	Note	Use for the Trendline
LaAlO3	$R\overline{3}c$	190 ± 5	[67]	$\mathrm{XRD}, \mathrm{fit} \mathrm{using} Pm\overline{3}m$, up to 40 GPa (improper space group and pressure range)	no
LaAlO3	$R\overline{3}c$	177 ± 4	[68]	XRD, up to 7 GPa	yes
LaAlO3	$R\overline{3}c$	196	[69]	Brillouin scattering	yes
PrAlO3	Pnma	193 ± 1	[70]	XRD, up to 7 GPa	yes
NdAlO3	$R\overline{3}c$	204	[71]	Ab-initio calculation	yes
SmAlO3	Pnma	178 ± 14	[72]	Ultrasound, at 0.6 GPa, 2.2% porosity	no
SmAlO3	Pnma	198 ± 4	[64]	Brillouin scattering	yes
EuAlO3	Pnma	203 ± 15	[72]	Ultrasound, at 0.6 GPa, 2.4% porosity	no
EuAlO3	Pnma	213	[73]	Ultrasound, sample of [72], corrected for porosity	yes
GdAlO3	Pnma	179 ± 15	[72]	Ultrasound, at 0.6 GPa, 2.4% porosity	no
GdAlO3	Pnma	203 ± 4	[64]	Brillouin scattering	no
GdAlO3	Pnma	191 ± 1	[31]	XRD, up to 8 GPa	no
GdAlO3	Pnma	216 ± 7	this study	XRD, up to 16 GPa	no

Table 3. Summary of the available bulk moduli (K) of rare-earth aluminate perovskite RAlO₃.

Composition	Space Group	K (GPa)	Reference	Note	Use for the Trendline
LaAlO3	$R\overline{3}c$	190 ± 5	[67]	$\mathrm{XRD}, \mathrm{fit} \mathrm{using} Pm\overline{3}m$, up to 40 GPa (improper space group and pressure range)	no
LaAlO3	$R\overline{3}c$	177 ± 4	[68]	XRD, up to 7 GPa	yes
LaAlO3	$R\overline{3}c$	196	[69]	Brillouin scattering	yes
PrAlO3	Pnma	193 ± 1	[70]	XRD, up to 7 GPa	yes
NdAlO3	$R\overline{3}c$	204	[71]	Ab-initio calculation	yes
SmAlO3	Pnma	178 ± 14	[72]	Ultrasound, at 0.6 GPa, 2.2% porosity	no
SmAlO3	Pnma	198 ± 4	[64]	Brillouin scattering	yes
EuAlO3	Pnma	203 ± 15	[72]	Ultrasound, at 0.6 GPa, 2.4% porosity	no
EuAlO3	Pnma	213	[73]	Ultrasound, sample of [72], corrected for porosity	yes
GdAlO3	Pnma	179 ± 15	[72]	Ultrasound, at 0.6 GPa, 2.4% porosity	no
GdAlO3	Pnma	203 ± 4	[64]	Brillouin scattering	no
GdAlO3	Pnma	191 ± 1	[31]	XRD, up to 8 GPa	no
GdAlO3	Pnma	216 ± 7	this study	XRD, up to 16 GPa	no

Figure 6. Bulk moduli of rare-earth aluminate perovskite RAlO₃ (R = La, Pr, Nd, Sm, Eu and Gd) as a function of the ionic radius of R³⁺. The broken line represents the linear trendline based on the data of LaAlO₃ (JZ 2004 [68], MC 2010 [69]), PrAlO₃ [70], NdAlO₃ [71], SmAlO₃ [64] and EuAlO₃ [73]. Data for GdAlO₃ of this study, JB 1984 [64] and NR 2004 [31] are plotted to show the agreement of these data with the linear trendline.

5. Conclusions

The previously predicted pressure-induced phase transformation from orthorhombic (Pbnm) to a higher-symmetry structure in GdAlO₃ has been observed in in situ X-ray diffraction and the higher-symmetry phase is identified with space group of R$\overline{3}$c with the assistant of DFT calculations. The X-ray diffraction patterns indicate that the structural phase transformation occurs between 16 and 21 GPa, although the volumetric variations V_A/V_B of the Pbnm phase suggest the transition to a higher symmetry may apparently start at around 14 GPa. The structural phase transformation is a first-order transition according to the space groups but the volumetric discontinuity is indistinguishable with the experimental uncertainty of the current study. A bulk modulus (K₀) of 216 ± 7 GPa with a fixed derivative bulk modulus (K₀′) at 5.8 was obtained for the Pbnm phase according to the third-order Birch–Murnaghan equation of state. The bulk modulus derived in this study is higher than the previously reported values but is in good agreement with the linear trend of increase in bulk modulus as the ionic radius of R³⁺ in rare-earth aluminate perovskite RAlO₃ decreases.