ab Initio DFT and MD Simulations Serving as an Anchor for Correcting Melting Curves Reported by DAC and SW Experiments—Some Transition Metals as Illustrative Examples
Abstract
:1. Introduction
2. Analysis of the Published Data
3. Ilustrative Examples
3.1. Melting Curve of Elemental Vanadium
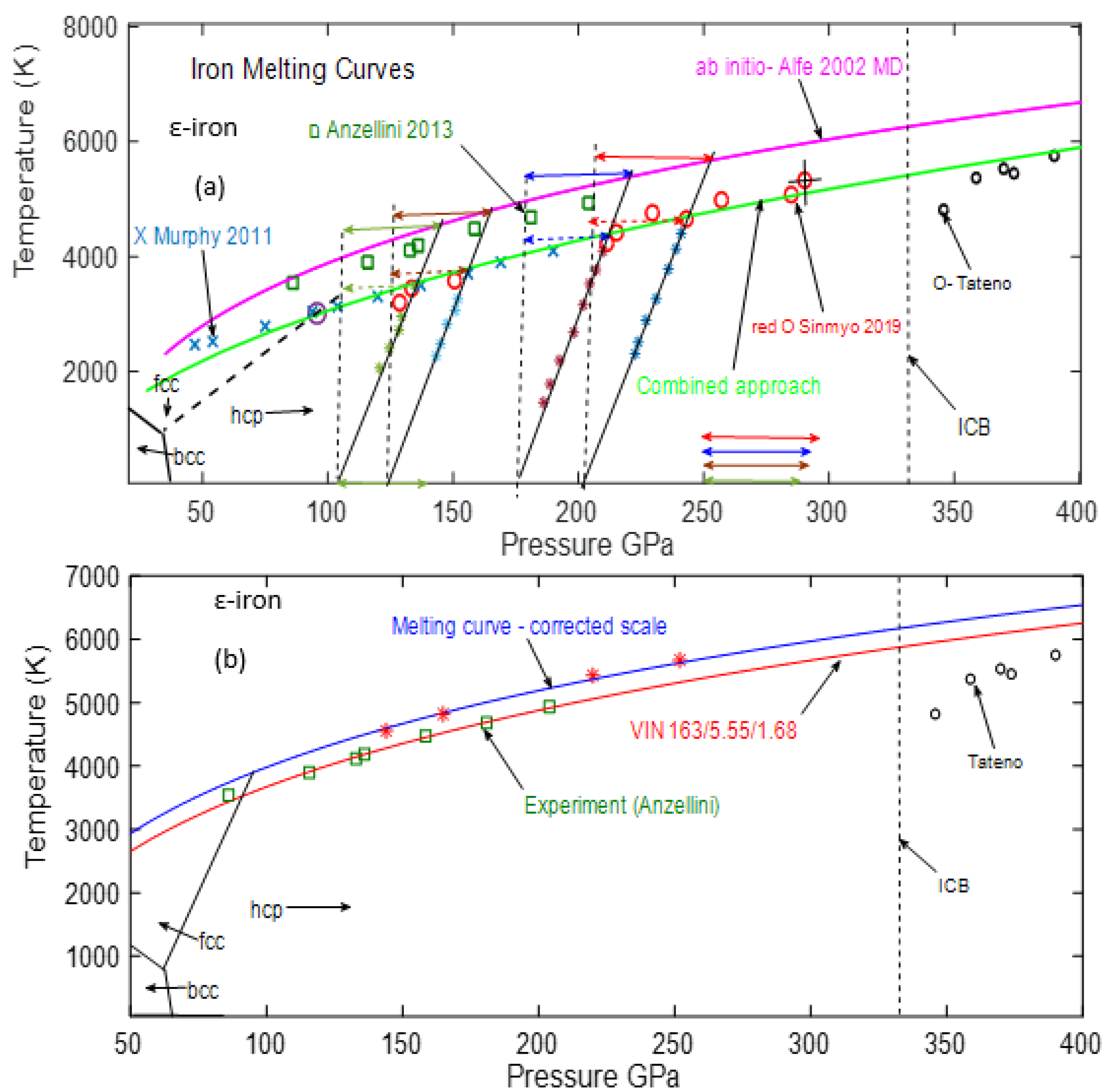
3.2. ε-Iron
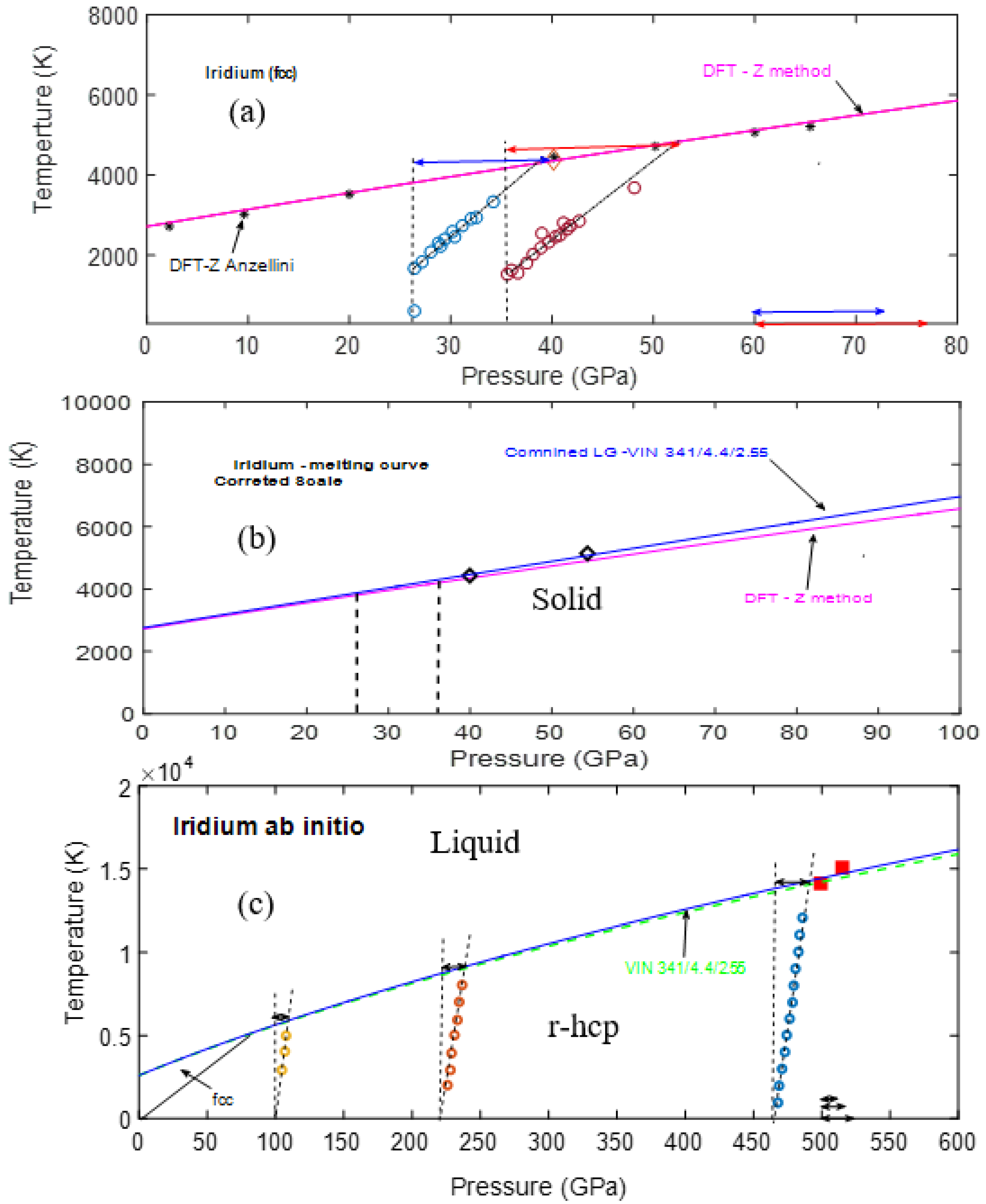
3.3. Iridium
3.4. Platinum
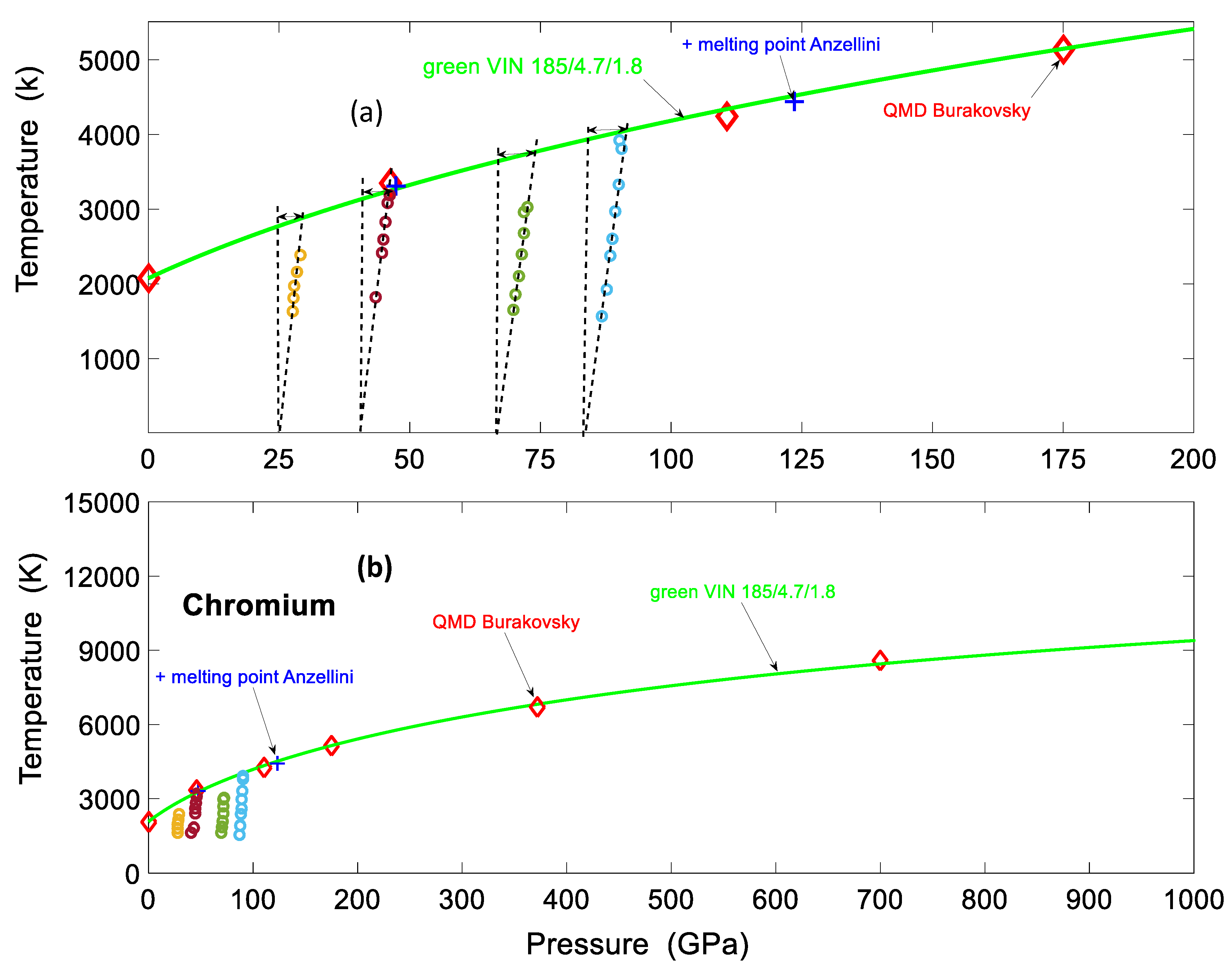
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Gilvarry–Lindemann Approximation: The Combined Approach
Appendix A.2. Lindemann–Gilvarry vs. Simon–Glatzel Fitting Curve Procedure
References
- Parisiades, P. A Review of the Melting Curves of Transition Metals at High Pressures Using Static Compression Techniques. Crystals 2021, 11, 416. [Google Scholar] [CrossRef]
- Dewaele, A.; Mezouar, M.; Guignot, N.; Loubeyre, P. High Melting Points of Tantalum in a Laser-Heated Diamond Anvil Cell. Phys. Rev. Lett. 2010, 104, 255701. [Google Scholar] [CrossRef]
- Burakovsky, L.; Burakovsky, N.; Cawkwell, M.J.; Preston, D.L.; Errandonea, D.; Simak, S.I. Ab initio phase diagram of iridium. Phys. Rev. B 2016, 94, 094112. [Google Scholar]
- Gal, J. The Influence of liquid-liquid phase transition in molten argon on the controversial melting results of Mo, Ta and W. Phys. B Condens. Matter 2021, 619, 413082. [Google Scholar] [CrossRef]
- Gal, J.; Friedlander, L. Melting curves and bulk moduli of the solid noble gasses He, Ne, Ar, Kr and Xe. Phys. B 2022, 625, 413445. [Google Scholar] [CrossRef]
- Errandonea, D.; MacLeod, S.G.; Burakovsky, L.; Santamaria-Perez, D.; Proctor, J.E.; Cynn, H.; Mezouar, M. Melting curve and phase diagram of vanadium under high-pressure and high-temperature conditions. Phys. Rev. B 2019, 100, 094111. [Google Scholar] [CrossRef]
- Gal, J.; Friedlander, L. The actual pressure and temperature at the melt of elemental vanadium. arXiv 2022, arXiv:2209.09836. [Google Scholar]
- Zhang, Y.; Tan, Y.; Geng, H.Y.; Salke, N.P.; Gao, Z.; Li, J.; Sekine, T.; Wang, Q.; Greenberg, E.; Prakapenka, V.B.; et al. Melting curve of vanadium up to 256 GPa: Consistency between experiments and theory. Phys. Rev. B 2020, 102, 214104. [Google Scholar] [CrossRef]
- Al’Tshuler, L.V.; Kormer, S.B.; Bakanova, A.A.; Trunin, R.F. Equation of state for aluminum, copper, and lead in the high pressure region. Sov. Phys. JETP 1960, 11, 573–579. [Google Scholar]
- Tummers, B. DataThief III. 2006. Available online: https://datathief.org (accessed on 5 July 2023).
- Sinmyo, R.; Hirose, K.; Ohishi, Y. Melting curve of iron to 290 GPa determined in a resistance-heated diamond-anvil cell: Implications for the earth and planetary core. Earth Planet. Sci. Lett. 2019, 510, 45–52. [Google Scholar] [CrossRef]
- Anzellini, S.; Dewaele, A.; Mezouar, M.; Loubeyre, P.; Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 2013, 340, 464–466. [Google Scholar] [CrossRef] [PubMed]
- Murphy, C.A.; Jackson, J.M.; Sturhahn, W.; Chen, B. Melting and thermal pressure of hcp-Fe from phonon density of states. Phys. Earth Planet. Inter. 2011, 188, 114–120. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Ohishi, Y.; Tatsumi, Y. The Structure of Iron in Earth’s Inner Core. Science 2010, 330, 359–361. [Google Scholar] [CrossRef] [PubMed]
- Alfe, D.; Price, G.D.; Gilan, J. Iron under Earth’s conditions: Melting curve from ab-initio calculations. Phys. Rev. B 2002, 65, 165118. [Google Scholar] [CrossRef]
- Anzellini, S.; Burakovsky, L.; Turnbull, R.; Bandiello, E.; Errandonea, D. P–V–T Equation of State of Iridium Up to 80 GPa and 3100 K. Crystals 2021, 11, 452. [Google Scholar] [CrossRef]
- Anzellini, S.; Monteseguro, V.; Bandiello, E.; Dewaele, A.; Burakovsky, L.; Errandonea, D. In situ characterization of the high pressure—High temperature melting curve of platinum. Nat. Sci. Rep. 2019, 9, 13034. [Google Scholar] [CrossRef]
- Zha, C.S.; Mibe, K.; Bassett, W.A.; Tschauner, O.; Mao, H.K.; Hemley, R.J. P-V-T equation of state of platinum to 80 GPa and 1900 K from internal resistive heating/x-ray diffraction measurements. J. Appl. Phys. 2008, 103, 054908. [Google Scholar] [CrossRef]
- Errandonea, D. High-pressure melting curves of the transition metals Cu, Ni, Pd, and Pt. Phys. Rev. B 2013, 87, 054108. [Google Scholar] [CrossRef]
- Kavner, A.; Jeanloz, R. High-pressure melting curve of platinum. J. Appl. Phys. 1998, 83, 7553–7559. [Google Scholar] [CrossRef]
- Anzellini, S.; Errandonea, D.; Burakovsky, L.; Proctor, J.E.; Turnbull, R.; Beavers, C.M. Characterization of the high-pressure and high-temperature phase diagram and equation of state of chromium. Nat. Sci. Rep. 2022, 12, 6727. [Google Scholar] [CrossRef]
- Baty, S.R.; Burakovsky, L.; Luscher, D.J.; Sjue, S.K.; Errandonea, D. Ab Initio Phase Diagram of Chromium to 2.5 TPa. Appl. Sci. 2022, 12, 7844. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gal, J. ab Initio DFT and MD Simulations Serving as an Anchor for Correcting Melting Curves Reported by DAC and SW Experiments—Some Transition Metals as Illustrative Examples. Crystals 2023, 13, 1263. https://doi.org/10.3390/cryst13081263
Gal J. ab Initio DFT and MD Simulations Serving as an Anchor for Correcting Melting Curves Reported by DAC and SW Experiments—Some Transition Metals as Illustrative Examples. Crystals. 2023; 13(8):1263. https://doi.org/10.3390/cryst13081263
Chicago/Turabian StyleGal, Joseph. 2023. "ab Initio DFT and MD Simulations Serving as an Anchor for Correcting Melting Curves Reported by DAC and SW Experiments—Some Transition Metals as Illustrative Examples" Crystals 13, no. 8: 1263. https://doi.org/10.3390/cryst13081263
APA StyleGal, J. (2023). ab Initio DFT and MD Simulations Serving as an Anchor for Correcting Melting Curves Reported by DAC and SW Experiments—Some Transition Metals as Illustrative Examples. Crystals, 13(8), 1263. https://doi.org/10.3390/cryst13081263




